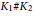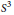Refine search
Actions for selected content:
33 results
On the genera of symmetric unions of knots
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 03 November 2025, pp. 1-26
-
- Article
- Export citation
Entropy stability and Milnor–Thurston invariants for Bowen–Series-like maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 13 October 2025, pp. 1-36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Ordered bases, order-preserving automorphisms and bi-orderable link groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 02 October 2025, pp. 1-17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CHARACTER VARIETIES, EARTHQUAKES AND ESSENTIAL SURFACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 27 June 2025, pp. 387-388
- Print publication:
- October 2025
-
- Article
-
- You have access
- HTML
- Export citation
A geometric description of the Reidemeister–Turaev torsion for abelian representations on 3-manifolds
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 2 / September 2025
- Published online by Cambridge University Press:
- 21 May 2025, pp. 233-258
- Print publication:
- September 2025
-
- Article
- Export citation
3-manifold spine cyclic presentations with seldom seen Whitehead graphs
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 04 April 2025, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Adjoint Reidemeister torsions of some 3-manifolds obtained by Dehn surgeries
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 22 April 2024, pp. 887-901
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Residual torsion-free nilpotence, bi-orderability, and two-bridge links
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 25 January 2023, pp. 394-457
- Print publication:
- April 2024
-
- Article
- Export citation
A table of n-component handlebody links of genus n+1 up to six crossings
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 17 June 2022, pp. 199-223
- Print publication:
- January 2023
-
- Article
- Export citation
Generalized torsion for knots with arbitrarily high genus
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 02 December 2021, pp. 867-881
- Print publication:
- December 2022
-
- Article
- Export citation
The first $\ell ^{2}$
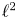 -betti number and groups acting on trees
-betti number and groups acting on trees
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 25 October 2021, pp. 916-923
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
INFINITARY COMMUTATIVITY AND ABELIANIZATION IN FUNDAMENTAL GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 23 November 2020, pp. 289-311
- Print publication:
- June 2022
-
- Article
- Export citation
Global geometry on moduli of local systems for surfaces with boundary
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 01 October 2020, pp. 1517-1559
- Print publication:
- August 2020
-
- Article
- Export citation
Twisted Alexander ideals and the isomorphism problem for a family of parafree groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 3 / August 2020
- Published online by Cambridge University Press:
- 22 June 2020, pp. 780-806
-
- Article
- Export citation
Johnson–Levine homomorphisms and the tree reduction of the LMO functor
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 27 November 2019, pp. 291-325
- Print publication:
- March 2021
-
- Article
- Export citation
A new test for asphericity and diagrammatic reducibility of group presentations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 871-895
- Print publication:
- April 2020
-
- Article
- Export citation
Generalized Torsion Elements and Bi-orderability of 3-manifold Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 60 / Issue 4 / 01 December 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 830-844
- Print publication:
- 01 December 2017
-
- Article
-
- You have access
- Export citation
On the Asphericity of a Family of Positive Relative Group Presentations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 05 January 2017, pp. 545-564
-
- Article
- Export citation
The SL(2, C) Casson Invariant for Knots and the Â-polynomial
-
- Journal:
- Canadian Journal of Mathematics / Volume 68 / Issue 1 / 01 February 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-23
- Print publication:
- 01 February 2016
-
- Article
-
- You have access
- Export citation
Non-Right-Orderable 3-Manifold Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 53 / Issue 4 / 01 December 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 706-718
- Print publication:
- 01 December 2010
-
- Article
-
- You have access
- Export citation





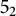
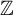
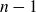
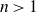
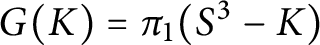
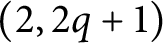
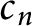
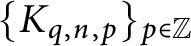
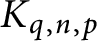
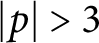
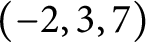
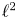
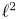

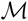
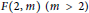
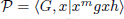 for
for