Article contents
Johnson–Levine homomorphisms and the tree reduction of the LMO functor
Published online by Cambridge University Press: 27 November 2019
Abstract
Let 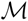 $\mathcal{M}$ denote the mapping class group of Σ, a compact connected oriented surface with one boundary component. The action of
$\mathcal{M}$ denote the mapping class group of Σ, a compact connected oriented surface with one boundary component. The action of 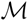 $\mathcal{M}$ on the nilpotent quotients of π1(Σ) allows to define the so-called Johnson filtration and the Johnson homomorphisms. J. Levine introduced a new filtration of
$\mathcal{M}$ on the nilpotent quotients of π1(Σ) allows to define the so-called Johnson filtration and the Johnson homomorphisms. J. Levine introduced a new filtration of 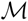 $\mathcal{M}$, called the Lagrangian filtration. He also introduced a version of the Johnson homomorphisms for this new filtration. The first term of the Lagrangian filtration is the Lagrangian mapping class group, whose definition involves a handlebody bounded by Σ, and which contains the Torelli group. These constructions extend in a natural way to the monoid of homology cobordisms. Besides, D. Cheptea, K. Habiro and G. Massuyeau constructed a functorial extension of the LMO invariant, called the LMO functor, which takes values in a category of diagrams. In this paper we give a topological interpretation of the upper part of the tree reduction of the LMO functor in terms of the homomorphisms defined by J. Levine for the Lagrangian mapping class group. We also compare the Johnson filtration with the filtration introduced by J. Levine.
$\mathcal{M}$, called the Lagrangian filtration. He also introduced a version of the Johnson homomorphisms for this new filtration. The first term of the Lagrangian filtration is the Lagrangian mapping class group, whose definition involves a handlebody bounded by Σ, and which contains the Torelli group. These constructions extend in a natural way to the monoid of homology cobordisms. Besides, D. Cheptea, K. Habiro and G. Massuyeau constructed a functorial extension of the LMO invariant, called the LMO functor, which takes values in a category of diagrams. In this paper we give a topological interpretation of the upper part of the tree reduction of the LMO functor in terms of the homomorphisms defined by J. Levine for the Lagrangian mapping class group. We also compare the Johnson filtration with the filtration introduced by J. Levine.
MSC classification
Information
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 170 , Issue 2 , March 2021 , pp. 291 - 325
- Copyright
- © Cambridge Philosophical Society 2019
References
- 1
- Cited by

