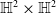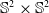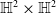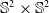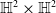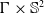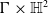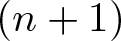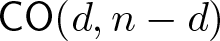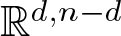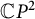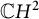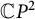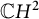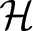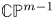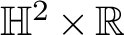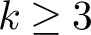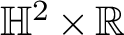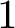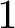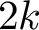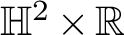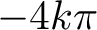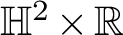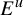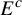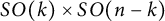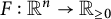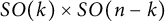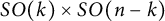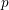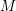Refine search
Actions for selected content:
45 results
SPHERE-LIKE ISOPARAMETRIC HYPERSURFACES IN DAMEK–RICCI SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 24 September 2025, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On hypersurfaces of
 $\mathbb{S}^2\times \mathbb{S}^2$ and
$\mathbb{S}^2\times \mathbb{S}^2$ and 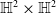 $\mathbb{H}^2\times \mathbb{H}^2$ with recurrent Ricci tensor
$\mathbb{H}^2\times \mathbb{H}^2$ with recurrent Ricci tensor
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 30 April 2025, pp. 1-21
-
- Article
- Export citation
Codazzi and totally umbilical hypersurfaces in
 $\mathrm {Sol}_1^4$
$\mathrm {Sol}_1^4$
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 03 April 2025, pp. 487-493
- Print publication:
- September 2025
-
- Article
- Export citation
On Riemannian and Ricci curvatures of homogeneous Finsler manifolds
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 73-90
- Print publication:
- March 2025
-
- Article
- Export citation
CYT and SKT manifolds with parallel Bismut torsion
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 November 2024, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Special homogeneous surfaces
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 2 / September 2024
- Published online by Cambridge University Press:
- 22 October 2024, pp. 333-362
- Print publication:
- September 2024
-
- Article
- Export citation
Invariant scalar-flat Kähler metrics on line bundles over generalized flag varieties
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 13 May 2024, pp. 1611-1636
- Print publication:
- October 2025
-
- Article
- Export citation
Projectively and affinely invariant PDEs on hypersurfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 25 April 2024, pp. 714-739
-
- Article
- Export citation
Buffon’s problem determines Gaussian curvature in three geometries
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 08 April 2024, pp. 1127-1138
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weighted nonlinear flag manifolds as coadjoint orbits
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 09 October 2023, pp. 1664-1694
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nonexistence of non-Hopf Ricci-semisymmetric real hypersurfaces in
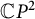 $\mathbb {C}P^{2}$ and
$\mathbb {C}P^{2}$ and 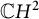 $\mathbb {C}H^{2}$
$\mathbb {C}H^{2}$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 14 August 2023, pp. 188-200
- Print publication:
- March 2024
-
- Article
- Export citation
Total mean curvature surfaces in the product space
 ${\mathbb{S}^{n}\times\mathbb{R}}$ and applications
${\mathbb{S}^{n}\times\mathbb{R}}$ and applications
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 26 April 2023, pp. 346-365
-
- Article
- Export citation
Bismut Ricci flat manifolds with symmetries
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 26 July 2022, pp. 1371-1390
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On cohomogeneity one Hermitian non-Kähler metrics
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 17 February 2022, pp. 545-587
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GENUS
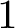 $1$ MINIMAL k-NOIDS AND SADDLE TOWERS IN
$1$ MINIMAL k-NOIDS AND SADDLE TOWERS IN 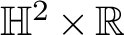 $\mathbb {H}^2\times \mathbb {R}$
$\mathbb {H}^2\times \mathbb {R}$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 06 January 2022, pp. 2155-2175
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Partially hyperbolic diffeomorphisms and Lagrangian contact structures
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 12 November 2021, pp. 2583-2629
- Print publication:
- August 2022
-
- Article
- Export citation
Proof of Laugwitz Conjecture and Landsberg Unicorn Conjecture for Minkowski norms with
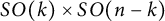 $SO(k)\times SO(n-k)$-symmetry
$SO(k)\times SO(n-k)$-symmetry
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 03 June 2021, pp. 1486-1516
- Print publication:
- October 2022
-
- Article
- Export citation
Finsler Warped Product Metrics with Relatively Isotropic Landsberg Curvature
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 12 May 2020, pp. 182-191
- Print publication:
- March 2021
-
- Article
- Export citation
WEIERSTRASS–KENMOTSU REPRESENTATION OF WILLMORE SURFACES IN SPHERES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 244 / December 2021
- Published online by Cambridge University Press:
- 27 April 2020, pp. 35-59
- Print publication:
- December 2021
-
- Article
- Export citation
Topological mixing of Weyl chamber flows
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 17 February 2020, pp. 1342-1368
- Print publication:
- May 2021
-
- Article
- Export citation