Hostname: page-component-7dd5485656-wxk4p Total loading time: 0 Render date: 2025-10-31T20:44:00.923Z Has data issue: false hasContentIssue false
  • English
  • Français

WEIERSTRASS–KENMOTSU REPRESENTATION OF WILLMORE SURFACES IN SPHERES

Part of: Classical differential geometry Global differential geometry

Published online by Cambridge University Press:  27 April 2020

JOSEF F. DORFMEISTER Open the ORCID record for JOSEF F. DORFMEISTER [Opens in a new window]  and
PENG WANG Open the ORCID record for PENG WANG [Opens in a new window]
JOSEF F. DORFMEISTER
Affiliation:
Fakultät für Mathematik, Technische Universität München, Boltzmannstr.3, D-85747, Garching, Germany email dorfm@ma.tum.de
PENG WANG
Affiliation:
College of Mathematics and Informatics, FJKLMAA, Fujian Normal University, Qishan Campus, Fuzhou 350117, PR China email pengwang@fjnu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

A Willmore surface 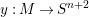$y:M\rightarrow S^{n+2}$ has a natural harmonic oriented conformal Gauss map 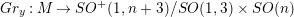$Gr_{y}:M\rightarrow SO^{+}(1,n+3)/SO(1,3)\times SO(n)$ , which maps each point 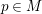$p\in M$ to its oriented mean curvature 2-sphere at 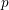$p$ . An easy observation shows that all conformal Gauss maps of Willmore surfaces satisfy a restricted nilpotency condition, which will be called “strongly conformally harmonic.” The goal of this paper is to characterize those strongly conformally harmonic maps from a Riemann surface 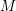$M$ to 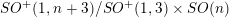$SO^{+}(1,n+3)/SO^{+}(1,3)\times SO(n)$ , which are the conformal Gauss maps of some Willmore surface in 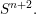$S^{n+2}.$ It turns out that generically, the condition of being strongly conformally harmonic suffices to be associated with a Willmore surface. The exceptional case will also be discussed.

MSC classification

Primary: 53A30: Conformal differential geometry 53C30: Homogeneous manifolds 53C35: Symmetric spaces

Information

Type
Article
Information
Nagoya Mathematical Journal , Volume 244 , December 2021 , pp. 35 - 59
Check for updates
Copyright
© 2020 Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The second author is thankful to the ERASMUS MUNDUS TANDEM Project for the financial supports to visit the TU München.

References

Bernard, Y. and Rivière, T., Energy quantization for Willmore surfaces and applications , Ann. of Math. (2) 180(1) (2014), 87–136.CrossRefGoogle Scholar
Blaschke, W., Vorlesungen über Differentialgeometrie, 3, Springer, Berlin, Heidelberg, New York, 1929.Google Scholar
Bryant, R., A duality theorem for Willmore surfaces , J. Diff. Geom. 20 (1984), 23–53.Google Scholar
Burstall, F., Ferus, D., Leschke, K., Pedit, F. and Pinkall, U., Conformal Geometry of Surfaces in S 4 and Quaternions, Lecture Notes in Mathematics 1772 , Springer, Berlin, 2002.Google Scholar
Burstall, F., Pedit, F. and Pinkall, U., Schwarzian Derivatives and Flows of Surfaces, Contemporary Mathematics 308 , American Mathematical Society, Providence, RI, 2002, 39–61.Google Scholar
Burstall, F. and Rawnsley, J.H., Twistor theory for Riemannian symmetric spaces: with applications to harmonic maps of Riemann surfaces, Lecture Notes in Mathematics 1424 , Springer, Berlin, 1990.CrossRefGoogle Scholar
Burstall, F., On conformal Gauss maps , Bull. Lond. Math. Soc. 51 (2019), 989–994.Google Scholar
Calabi, E., Minimal immersions of surfaces in Euclidean spheres , J. Diff. Geom. 1 (1967), 111–125.Google Scholar
Chern, S. S, “ On the minimal immersions of the two-sphere in a space of constant curvature ”, in Problems in Analysis, Princeton University Press, Princeton, NJ, 1970, 27–40.Google Scholar
Chern, S. S and Wolfson, J., Harmonic maps of the two-sphere into a complex Grassmann manifold II , Annal Math. Second Series 125(2) (1987), 301–335.Google Scholar
Dorfmeister, J., Pedit, F. and Wu, H., Weierstrass type representation of harmonic maps into symmetric spaces , Comm. Anal. Geom. 6 (1998), 633–668.CrossRefGoogle Scholar
Dorfmeister, J. and Wang, P., Willmore surfaces in spheres: the DPW approach via the conformal Gauss map , Abh. Math. Semin. Univ. Hambg 89(1) (2019), 77–103.CrossRefGoogle Scholar
Eells, J. and Sampson, J., Harmonic maps of Riemannian manifolds , Amer. J. Math. 86 (1964), 109–160.CrossRefGoogle Scholar
Ejiri, N., A counter example for Weiner’s open question , Indiana Univ. Math. J. 31(2) (1982), 209–211.CrossRefGoogle Scholar
Ejiri, N., Willmore surfaces with a duality in S n (1) , Proc. Lond. Math. Soc. (3) 57(2) (1988), 383–416.CrossRefGoogle Scholar
Hélein, F., Willmore immersions and loop groups , J. Differ. Geom. 50 (1998), 331–385.CrossRefGoogle Scholar
Hertrich, J. U., Introduction to Möbius Differential Geometry, Cambridge University Press, 2003.CrossRefGoogle Scholar
Hitchin, N., Harmonic maps from a 2-torus to the 3-sphere , J. Differ. Geom. 31 (1990), 627–710.CrossRefGoogle Scholar
Hoffman, D. and Osserman, R., The Gauss map of surfaces in ℝ n , J. Differ. Geom. 18(4) (1983), 733–754.CrossRefGoogle Scholar
Kenmotsu, K., Weierstrass formula for surfaces of prescribed mean curvature , Math. Ann. 245(2) (1979), 89–99.Google Scholar
Kuwert, E. and Schätzle, R., Removability of point singularities of Willmore surfaces , Ann. of Math. (2) 160(1) (2004), 315–357.Google Scholar
Li, P. and Yau, S. T., A new conformal invariant and its applications to the Willmore conjecture and the first eigenvalue of compact surfaces , Invent. Math. 69(2) (1982), 269–291.Google Scholar
Lü, Y. and Wang, P., The Weingarten map and the Gauss maps of submanifolds, in preparation.Google Scholar
Ma, X., Adjoint transforms of Willmore surfaces in S n , Manuscripta Math. 120(2) (2006), 163–179.CrossRefGoogle Scholar
Ma, X., Isothermic and S-Willmore surfaces as solutions to a Problem of Blaschke , Results in Math. 48 (2005), 301–309.Google Scholar
Ma, X., Willmore surfaces in $S^{n}$ : transforms and vanishing theorems, dissertation, Technische Universität Berlin, 2005.Google Scholar
Ma, X. and Wang, P., Spacelike Willmore surfaces in 4-dimensional Lorentzian space forms , Sci. China: Ser. A, Math. 51(9) (2008), 1561–1576.CrossRefGoogle Scholar
Marques, F. and Neves, A., Min-Max theory and the Willmore conjecture , Ann. of Math. (2) 179(2) (2014), 683–782.CrossRefGoogle Scholar
Montiel, S., Willmore two-spheres in the four-sphere , Trans. Amer. Math. Soc. 352 (2000), 4469–4486.Google Scholar
Pinkall, U., Hopf tori in S 3 , Invent. Math. 81(2) (1985), 379–386.Google Scholar
Rigoli, M., The conformal Gauss map of submanifolds of the Möbius space , Ann. Global Anal. Geom. 5(2) (1987), 97–116.CrossRefGoogle Scholar
Rivière, T., Analysis aspects of Willmore surfaces , Invent. Math. 174(1) (2008), 1–45.CrossRefGoogle Scholar
Ruh, E. A. and Vilms, J., The tension field of the Gauss map , Trans. Amer. Math. Soc. 149 (1970), 569–573.Google Scholar
Simon, L., Existence of surfaces minimizing the Willmore functional , Comm. Anal. Geom. 1(2) (1993), 281–326.CrossRefGoogle Scholar
Wang, C. P., Moebious geometry of submanifolds in S n , Manuscripta Math. 96(4) (1998), 517–534.Google Scholar
Wang, P., Willmore surfaces in spheres via loop groups III: on minimal surfaces in space forms , Tohoku Math. J. (2) 69(1) (2017), 141–160.CrossRefGoogle Scholar
Weiner, J. L., On a problem of Chen, Willmore, et al. , Indiana Univ. Math. J. 27 (1978), 19–35.CrossRefGoogle Scholar
Weiner, J. L., The Gauss map for surfaces: Part 1. The affine case , Trans. Amer. Math. Soc. 293(2) (1986), 431–446.Google Scholar
Xia, Q. L. and Shen, Y. B., Weierstrass type representation of Willmore surfaces in S n , Acta Math. Sinica 20(6) 1029–1046.CrossRefGoogle Scholar