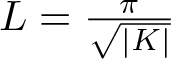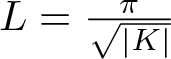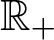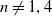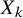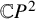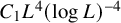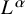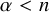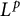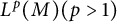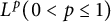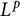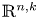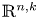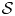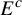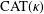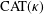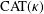Refine search
Actions for selected content:
39 results
Aspherical complex surfaces, the Singer conjecture, and Gromov–Lück inequality
 $\chi \ge |\sigma |$
$\chi \ge |\sigma |$
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 3 / November 2025
- Published online by Cambridge University Press:
- 17 July 2025, pp. 541-555
- Print publication:
- November 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DISTANCE FUNCTIONS ON CONVEX BODIES AND SYMPLECTIC TORIC MANIFOLDS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 260 / December 2025
- Published online by Cambridge University Press:
- 02 April 2025, pp. 625-647
- Print publication:
- December 2025
-
- Article
- Export citation
A Bonnet–Myers rigidity theorem for globally hyperbolic Lorentzian length spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 13 January 2025, pp. 1-42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Principal bundle structure of the space of metric measure spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 November 2024, pp. 1-31
-
- Article
- Export citation
Bishop–Jones’ theorem and the ergodic limit set
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 09 September 2024, pp. 704-718
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Simplicial volume of manifolds with amenable fundamental group at infinity
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 22 April 2024, pp. 563-570
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Degrees of maps and multiscale geometry
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 18 January 2024, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Differential Harnack estimates for a weighted nonlinear parabolic equation under a super Perelman–Ricci flow and implications
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 27 October 2023, pp. 687-717
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Topological regularity of isoperimetric sets in PI spaces having a deformation property
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 09 October 2023, pp. 611-633
- Print publication:
- April 2025
-
- Article
- Export citation
A universal inequality for Neumann eigenvalues of the Laplacian on a convex domain in Euclidean space
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 19 September 2023, pp. 222-226
- Print publication:
- March 2024
-
- Article
- Export citation
A note about charts built by Eriksson-Bique and Soultanis on metric measure spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 09 June 2023, pp. 49-59
- Print publication:
- March 2024
-
- Article
- Export citation
Uniqueness of
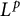 $L^p$ subsolutions to the heat equation on Finsler measure spaces
$L^p$ subsolutions to the heat equation on Finsler measure spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 05 June 2023, pp. 166-175
- Print publication:
- March 2024
-
- Article
- Export citation
Coisotropic Ekeland–Hofer capacities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 05 September 2022, pp. 1564-1608
- Print publication:
- October 2023
-
- Article
- Export citation
Leafwise quasigeodesic foliations in dimension three and the funnel property
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 8 / August 2023
- Published online by Cambridge University Press:
- 31 August 2022, pp. 2624-2650
- Print publication:
- August 2023
-
- Article
- Export citation
Non-Hilbertian tangents to Hilbertian spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 05 April 2022, pp. 811-832
- Print publication:
- June 2023
-
- Article
- Export citation
Continuity of critical exponent of quasiconvex-cocompact groups under Gromov–Hausdorff convergence
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 4 / April 2023
- Published online by Cambridge University Press:
- 10 February 2022, pp. 1189-1221
- Print publication:
- April 2023
-
- Article
- Export citation
Partially hyperbolic diffeomorphisms and Lagrangian contact structures
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 12 November 2021, pp. 2583-2629
- Print publication:
- August 2022
-
- Article
- Export citation
Topological volumes of fibrations: a note on open covers
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 11 October 2021, pp. 1340-1360
- Print publication:
- October 2022
-
- Article
- Export citation
Hardy type inequalities on closed manifolds via Ricci curvature
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 21 July 2020, pp. 993-1020
- Print publication:
- June 2021
-
- Article
- Export citation
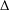 $\unicode[STIX]{x1D6E5}$-CONVERGENCES OF WEIGHTED AVERAGED PROJECTIONS IN
$\unicode[STIX]{x1D6E5}$-CONVERGENCES OF WEIGHTED AVERAGED PROJECTIONS IN 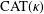 $\text{CAT}(\unicode[STIX]{x1D705})$ SPACES
$\text{CAT}(\unicode[STIX]{x1D705})$ SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 110 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 14 May 2020, pp. 289-301
- Print publication:
- June 2021
-
- Article
- Export citation