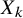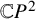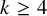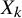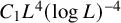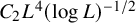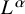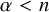1. Introduction
1.1. Background
Given an oriented Riemannian manifold M, how does the Lipschitz constant of a map
![]() $M \to M$
control its degree? In all cases, if M is an n-manifold, an L-Lipschitz map
$M \to M$
control its degree? In all cases, if M is an n-manifold, an L-Lipschitz map
![]() $M \to M$
multiplies n-dimensional volumes by at most
$M \to M$
multiplies n-dimensional volumes by at most
![]() $L^n$
, and so its degree is at most
$L^n$
, and so its degree is at most
![]() $L^n$
. In [Reference Gromov15, Ch. 2], Gromov studied the extent to which this estimate is sharp. For example, he showed that if M admits a sequence of self-maps
$L^n$
. In [Reference Gromov15, Ch. 2], Gromov studied the extent to which this estimate is sharp. For example, he showed that if M admits a sequence of self-maps
![]() $f_k$
with
$f_k$
with
then M must be flat [Reference Gromov15, 2.32]. He also asked the following question: for what M are there
![]() $f_k$
with unbounded degree such that the ratio
$f_k$
with unbounded degree such that the ratio
![]() $\operatorname {\mathrm {Lip}}(f_k)^n/\deg (f_k)$
is bounded [Reference Gromov15, 2.40(c)]? The answer to this modified question only depends on the topology of M. Gromov constructed such maps when M is a sphere or a product of spheres. He singled out
$\operatorname {\mathrm {Lip}}(f_k)^n/\deg (f_k)$
is bounded [Reference Gromov15, 2.40(c)]? The answer to this modified question only depends on the topology of M. Gromov constructed such maps when M is a sphere or a product of spheres. He singled out
![]() $(S^2 \times S^2) \mathbin{\#} (S^2 \times S^2)$
as a case in which he did not know whether such maps exist.
$(S^2 \times S^2) \mathbin{\#} (S^2 \times S^2)$
as a case in which he did not know whether such maps exist.
We now know that the answer for connected sums of copies of
![]() $S^2 \times S^2$
or of
$S^2 \times S^2$
or of
![]() ${\mathbb {C}} P^2$
is rather subtle. (The behavior is similar for both families.) Consider the manifold
${\mathbb {C}} P^2$
is rather subtle. (The behavior is similar for both families.) Consider the manifold
![]() $X_k = \#_k \mathbb CP^2$
. Volume considerations show that an L-Lipschitz self-map of any
$X_k = \#_k \mathbb CP^2$
. Volume considerations show that an L-Lipschitz self-map of any
![]() $4$
-manifold has degree at most
$4$
-manifold has degree at most
![]() $L^4$
. It is not difficult to construct an L-Lipschitz self-map of
$L^4$
. It is not difficult to construct an L-Lipschitz self-map of
![]() $\mathbb CP^2$
with degree
$\mathbb CP^2$
with degree
![]() $\sim L^4$
. When
$\sim L^4$
. When
![]() $k=2$
or
$k=2$
or
![]() $3$
, then [Reference Berdnikov and Manin3] shows that there are also L-Lipschitz self-maps of
$3$
, then [Reference Berdnikov and Manin3] shows that there are also L-Lipschitz self-maps of
![]() $X_k$
with degree
$X_k$
with degree
![]() $\sim L^4$
. But when
$\sim L^4$
. But when
![]() $k \ge 4$
, [Reference Berdnikov and Manin3] shows that every L-Lipschitz self-map of
$k \ge 4$
, [Reference Berdnikov and Manin3] shows that every L-Lipschitz self-map of
![]() $X_k$
has degree
$X_k$
has degree
![]() $o(L^4)$
. Before this paper, the most efficient known maps had degree
$o(L^4)$
. Before this paper, the most efficient known maps had degree
![]() $\sim L^3$
.
$\sim L^3$
.
One of our goals in this paper is to give sharper quantitative estimates for the case
![]() $k \ge 4$
. We will show that the maximal degree p lies in the range
$k \ge 4$
. We will show that the maximal degree p lies in the range
This phase transition between
![]() $k=3$
and
$k=3$
and
![]() $k=4$
is an example of a broader phenomenon. Our second goal in the paper is to develop the general theory of this phenomenon.
$k=4$
is an example of a broader phenomenon. Our second goal in the paper is to develop the general theory of this phenomenon.
For a given M, the maximally efficient relationship
![]() $\operatorname {\mathrm {Lip}} f \sim (\deg f)^{1/n}$
may not be achievable for several reasons. For example, M may be inflexible, meaning that it does not have self-maps of degree
$\operatorname {\mathrm {Lip}} f \sim (\deg f)^{1/n}$
may not be achievable for several reasons. For example, M may be inflexible, meaning that it does not have self-maps of degree
![]() $>1$
. (Examples of inflexible simply connected manifolds are given in [Reference Arkowitz and Lupton2, Reference Crowley and Löh10, Reference Costoya and Viruel9, Reference Amann1].) Or it may be the case that any self-map of M of degree D multiplies some k-dimensional homology class by a factor greater than
$>1$
. (Examples of inflexible simply connected manifolds are given in [Reference Arkowitz and Lupton2, Reference Crowley and Löh10, Reference Costoya and Viruel9, Reference Amann1].) Or it may be the case that any self-map of M of degree D multiplies some k-dimensional homology class by a factor greater than
![]() $D^{k/n}$
, giving a stronger bound on the Lipschitz constant.
$D^{k/n}$
, giving a stronger bound on the Lipschitz constant.
A compact manifold M is formal if it has a self-map
![]() $M \to M$
which, for some p, induces multiplication by
$M \to M$
which, for some p, induces multiplication by
![]() $p^k$
on
$p^k$
on
![]() $H_k(M;\mathbb R)$
, for every
$H_k(M;\mathbb R)$
, for every
![]() $k \geq 1$
. This notion, first defined by Sullivan and coauthors in terms of rational homotopy theory, has played a role in many other geometric applications, starting with [Reference Deligne, Griffiths, Morgan and Sullivan11]. If M is a formal n-manifold, then obstructions to obtaining an L-Lipschitz map
$k \geq 1$
. This notion, first defined by Sullivan and coauthors in terms of rational homotopy theory, has played a role in many other geometric applications, starting with [Reference Deligne, Griffiths, Morgan and Sullivan11]. If M is a formal n-manifold, then obstructions to obtaining an L-Lipschitz map
![]() $M \to M$
of degree
$M \to M$
of degree
![]() $L^n$
cannot come from measuring volumes of cycles. However, in [Reference Berdnikov and Manin3] it was shown that more subtle obstructions may exist. This motivates the definition of a scalable manifold to be one which has
$L^n$
cannot come from measuring volumes of cycles. However, in [Reference Berdnikov and Manin3] it was shown that more subtle obstructions may exist. This motivates the definition of a scalable manifold to be one which has
![]() $O(L)$
-Lipschitz self-maps of degree
$O(L)$
-Lipschitz self-maps of degree
![]() $L^n$
. The paper [Reference Berdnikov and Manin3] shows that scalability is equivalent to several other conditions; most importantly, a manifold M (perhaps with boundary) is scalable if and only if there is a ring homomorphism
$L^n$
. The paper [Reference Berdnikov and Manin3] shows that scalability is equivalent to several other conditions; most importantly, a manifold M (perhaps with boundary) is scalable if and only if there is a ring homomorphism
![]() $H^*(M;{\mathbb {R}}) \to \Omega ^*(M)$
which realizes cohomology classes as differential forms representing them.
$H^*(M;{\mathbb {R}}) \to \Omega ^*(M)$
which realizes cohomology classes as differential forms representing them.
1.2. Main results
For nonscalable formal spaces, [Reference Berdnikov and Manin3] proves that any L-Lipschitz self-map has degree
![]() $o(L^n)$
. Before this paper, the examples that had been constructed had degree
$o(L^n)$
. Before this paper, the examples that had been constructed had degree
![]() $O(L^{n-1})$
. In this paper, we gain a sharper quantitative understanding:
$O(L^{n-1})$
. In this paper, we gain a sharper quantitative understanding:
Theorem A. Let M be a formal, simply connected closed n-manifold which is not scalable. Then the maximal degree p of an L-Lipschitz map
![]() $M \to M$
satisfies
$M \to M$
satisfies
where
![]() $\beta (M) \geq \alpha (M)>0$
are constants depending only on the real cohomology ring of M.
$\beta (M) \geq \alpha (M)>0$
are constants depending only on the real cohomology ring of M.
For example, in the case of
![]() $M=\#_k {\mathbb {C}} P^2$
,
$M=\#_k {\mathbb {C}} P^2$
,
![]() $\beta (M)=4$
and
$\beta (M)=4$
and
![]() $\alpha (M)=1/2$
.
$\alpha (M)=1/2$
.
The lower bound of Theorem A generalizes to compact manifolds with boundary with a slightly more complicated statement (see Theorem 3.1).
We obtain a similar result for sizes of nullhomotopies of L-Lipschitz maps to a nonscalable formal space:
Theorem B. Let Y be a formal, simply connected compact Riemannian n-manifold (perhaps with boundary). Then for any finite simplicial complex X, any nullhomotopic L-Lipschitz map
![]() $f:X \to Y$
is
$f:X \to Y$
is
![]() $O(L(\log L)^{n-2})$
-Lipschitz nullhomotopic.
$O(L(\log L)^{n-2})$
-Lipschitz nullhomotopic.
For scalable spaces, a linear bound was proved in [Reference Berdnikov and Manin3]; thus, this result is interesting mainly for nonscalable formal spaces. In contrast, in nonformal spaces, it is often impossible to do better than a bound of the form
![]() $L^\alpha $
for some
$L^\alpha $
for some
![]() $\alpha>1$
.
$\alpha>1$
.
One of the main theorems of [Reference Berdnikov and Manin3] says that a manifold Y is scalable if and only if there is a ring homomorphism from
![]() $H^*(Y; {\mathbb {R}})$
to
$H^*(Y; {\mathbb {R}})$
to
![]() $\Omega ^*(Y)$
which takes each cohomology class to a differential form in that class. Because
$\Omega ^*(Y)$
which takes each cohomology class to a differential form in that class. Because
![]() $\Omega ^*(Y)$
is infinite-dimensional, this condition is not so easy to check. We verify the conjecture given in [Reference Berdnikov and Manin3] which states that scalability is equivalent to a simple homological criterion:
$\Omega ^*(Y)$
is infinite-dimensional, this condition is not so easy to check. We verify the conjecture given in [Reference Berdnikov and Manin3] which states that scalability is equivalent to a simple homological criterion:
Theorem C. Let Y be a formal, simply connected compact Riemannian n-manifold (perhaps with boundary). Then Y is scalable if and only if there is an injective ring homomorphism
 $$\begin{align*}h:H^*(Y; {\mathbb{R}}) \to \bigoplus_{i=1}^N \Lambda^*{\mathbb{R}}^{n_i}\end{align*}$$
$$\begin{align*}h:H^*(Y; {\mathbb{R}}) \to \bigoplus_{i=1}^N \Lambda^*{\mathbb{R}}^{n_i}\end{align*}$$
for some integers
![]() $n_1,\ldots ,n_N$
. In particular, if Y is a closed manifold, then it is scalable if and only if there is an injective ring homomorphism
$n_1,\ldots ,n_N$
. In particular, if Y is a closed manifold, then it is scalable if and only if there is an injective ring homomorphism
![]() $H^*(Y;\mathbb R) \to \Lambda ^*\mathbb R^n$
.
$H^*(Y;\mathbb R) \to \Lambda ^*\mathbb R^n$
.
In particular, scalability is an invariant not only of rational but of real homotopy type.
Example 1.1. If M is an
![]() $(n-1)$
-connected
$(n-1)$
-connected
![]() $2n$
-manifold, then its real cohomology ring is completely described by the signature
$2n$
-manifold, then its real cohomology ring is completely described by the signature
![]() $(k,\ell )$
of the bilinear form
$(k,\ell )$
of the bilinear form
Then M is scalable if and only if k and
![]() $\ell $
are both at most
$\ell $
are both at most
![]() ${2n \choose n}/2$
.
${2n \choose n}/2$
.
Theorem C is closely related to another idea studied by Gromov in [Reference Gromov15, 2.41]. For a closed n-manifold M, say a map
![]() $f:\mathbb R^n \to M$
has positive asymptotic degree if
$f:\mathbb R^n \to M$
has positive asymptotic degree if
 $$\begin{align*}\limsup_{R \to \infty} \frac{\int_{B_R(0)} f^*d\operatorname{\mathrm{vol}}_M}{R^n}=\delta>0.\end{align*}$$
$$\begin{align*}\limsup_{R \to \infty} \frac{\int_{B_R(0)} f^*d\operatorname{\mathrm{vol}}_M}{R^n}=\delta>0.\end{align*}$$
Given an efficient self-map
![]() $M \to M$
of high degree, you can zoom in and find a map of positive asymptotic degree on a large ball. If M is formal, then the converse also holds:
$M \to M$
of high degree, you can zoom in and find a map of positive asymptotic degree on a large ball. If M is formal, then the converse also holds:
Theorem C′. Let M be a formal, simply connected closed n-manifold. Then a
![]() $1$
-Lipschitz map
$1$
-Lipschitz map
![]() ${f:\mathbb R^n \to M}$
of positive asymptotic degree exists if and only if M is scalable.
${f:\mathbb R^n \to M}$
of positive asymptotic degree exists if and only if M is scalable.
Remark 1.2. Gromov refers to manifolds with this property as elliptic, suggesting a connection with the notion of elliptic spaces from rational homotopy theory. However, this notion is not closely connected to scalability.
Question 1.3. Can a nonformal simply connected manifold be Gromov-elliptic?
Finally, we explore the behavior of nonformal manifolds:
Theorem D. Let M be a closed simply connected n-manifold which is not formal. Then either M is inflexible (has no self-maps of degree
![]() $>1$
) or the maximal degree of an L-Lipschitz map
$>1$
) or the maximal degree of an L-Lipschitz map
![]() $M \to M$
is bounded by
$M \to M$
is bounded by
![]() $L^\alpha $
for some real number
$L^\alpha $
for some real number
![]() $\alpha <n$
.
$\alpha <n$
.
To see how the latter situation arises, consider the simplest example of a nonformal simply connected manifold, given in [Reference Félix, Oprea and Tanré13, p. 94]. This is the total space M of a fiber bundle
![]() $S^3 \to M \to S^2 \times S^2$
obtained by pulling back the Hopf fibration
$S^3 \to M \to S^2 \times S^2$
obtained by pulling back the Hopf fibration
![]() $S^3 \to S^7 \to S^4$
along the degree
$S^3 \to S^7 \to S^4$
along the degree
![]() $1$
map
$1$
map
![]() $S^2 \times S^2 \to S^4$
.
$S^2 \times S^2 \to S^4$
.
A self-map of M is determined by its action on
![]() $H^2(M) \cong \mathbb Z^2$
. This is because the generators of
$H^2(M) \cong \mathbb Z^2$
. This is because the generators of
![]() $H^5(M)$
can be obtained from the generators of
$H^5(M)$
can be obtained from the generators of
![]() $H^2(M)$
by taking Massey products (a higher cohomology operation) of order 3. An L-Lipschitz self-map takes the generators of
$H^2(M)$
by taking Massey products (a higher cohomology operation) of order 3. An L-Lipschitz self-map takes the generators of
![]() $H^5(M)$
to vectors of length
$H^5(M)$
to vectors of length
![]() $O(L^5)$
, and therefore, it takes the generators of
$O(L^5)$
, and therefore, it takes the generators of
![]() $H^2(M)$
to vectors of length
$H^2(M)$
to vectors of length
![]() $O(L^{5/3})$
. This means the degree of such a map is
$O(L^{5/3})$
. This means the degree of such a map is
![]() $O(L^{20/3}) \prec L^7$
.
$O(L^{20/3}) \prec L^7$
.
Something similar happens for any nonformal space: an alternate definition of formality is that a formal space has no nontrivial higher-order rational cohomology operations.
1.3. Proof ideas
The key idea behind Theorem A is that efficient self-maps of a formal but nonscalable space must behave nontrivially on many scales. We explain the intuition here.
In [Reference Berdnikov and Manin3], the
![]() $o(L^n)$
upper bound for the degree of an L-Lipschitz map
$o(L^n)$
upper bound for the degree of an L-Lipschitz map
![]() $M \to M$
is obtained by looking at the induced pullbacks of differential forms representing cohomology classes of M and taking flat limits. To get the sharper upper bound of Theorem A, we analyze the same pullback forms using Fourier analysis – namely, Littlewood–Paley theory. These pullback forms can be decomposed into summands concentrated in different frequency ranges.
$M \to M$
is obtained by looking at the induced pullbacks of differential forms representing cohomology classes of M and taking flat limits. To get the sharper upper bound of Theorem A, we analyze the same pullback forms using Fourier analysis – namely, Littlewood–Paley theory. These pullback forms can be decomposed into summands concentrated in different frequency ranges.
To start to get an idea how the proof works, first imagine that all the pullback forms are concentrated in a single frequency range. If the frequency range is high, then we got a lot of cancellation when we integrate the forms, leading to a nontrivial bound for the degree. If the frequency range is low, then we use the fact that M is not scalable to get a nontrivial bound for the degree – roughly speaking, if all the relevant forms were large and low frequency, we could use them to build a ring homomorphism from
![]() $H^*(M; {\mathbb {R}})$
to
$H^*(M; {\mathbb {R}})$
to
![]() $\Omega ^*(M)$
.
$\Omega ^*(M)$
.
In general, the pullback forms have contributions from many frequency ranges. We carefully break up the integral for the degree into pieces involving different frequency ranges, and we use the two ideas above to bound the pieces. It turns out that the interaction of different frequency ranges is important in this estimate. In the worst case, the forms have roughly equal contributions in every frequency range. Indeed, a self-map of M which comes close to the upper bound must have pieces in a wide range of frequencies (see Proposition 2.16 for a precise statement).
Let us see what such a self-map might look like in the case of
![]() $M=\#_k {\mathbb {C}} P^2$
. We think of M as a CW complex with one
$M=\#_k {\mathbb {C}} P^2$
. We think of M as a CW complex with one
![]() $0$
-cell,
$0$
-cell,
![]() $k 2$
-cells and one
$k 2$
-cells and one
![]() $4$
-cell. We construct self-maps
$4$
-cell. We construct self-maps
![]() ${r}_\ell :M \to M$
which have degree
${r}_\ell :M \to M$
which have degree
![]() $2^{4\ell }$
on the top cell. We would like to arrange that
$2^{4\ell }$
on the top cell. We would like to arrange that
![]() ${r}_\ell $
has Lipschitz constant at most
${r}_\ell $
has Lipschitz constant at most
![]() $C \ell \cdot 2^{\ell }$
. A naive way to build a map
$C \ell \cdot 2^{\ell }$
. A naive way to build a map
![]() ${r}_\ell $
of the right degree is to start with some
${r}_\ell $
of the right degree is to start with some
![]() ${r}_1$
and iterate it
${r}_1$
and iterate it
![]() $\ell $
times to get
$\ell $
times to get
![]() ${r}_\ell $
. In this case,
${r}_\ell $
. In this case,
![]() $\operatorname {\mathrm {Lip}}({r}_\ell ) \le \operatorname {\mathrm {Lip}}({r}_1)^\ell $
. However,
$\operatorname {\mathrm {Lip}}({r}_\ell ) \le \operatorname {\mathrm {Lip}}({r}_1)^\ell $
. However,
![]() $\operatorname {\mathrm {Lip}}({r}_1)$
is strictly bigger than 2 (by [Reference Gromov15, 2.32], the Lipschitz constant could only be 2 if
$\operatorname {\mathrm {Lip}}({r}_1)$
is strictly bigger than 2 (by [Reference Gromov15, 2.32], the Lipschitz constant could only be 2 if
![]() $M = \#_k {\mathbb {C}} P^2$
had a flat metric). Therefore, the bound
$M = \#_k {\mathbb {C}} P^2$
had a flat metric). Therefore, the bound
![]() $\operatorname {\mathrm {Lip}}({r}_1)^\ell $
is too big. By performing some optimization each time we iterate, we can bring
$\operatorname {\mathrm {Lip}}({r}_1)^\ell $
is too big. By performing some optimization each time we iterate, we can bring
![]() $\operatorname {\mathrm {Lip}}({r}_\ell )$
down to the target value.
$\operatorname {\mathrm {Lip}}({r}_\ell )$
down to the target value.
We may build
![]() ${r}_1$
, which has degree
${r}_1$
, which has degree
![]() $16$
, as follows: the top cell
$16$
, as follows: the top cell
![]() $e_4$
contains 16 cubical regions that each map homeomorphically, even homothetically, to the whole cell, whereas the area outside those cubical regions maps to the
$e_4$
contains 16 cubical regions that each map homeomorphically, even homothetically, to the whole cell, whereas the area outside those cubical regions maps to the
![]() $2$
-skeleton. To try to make this map efficient, we can arrange the cubical regions in a
$2$
-skeleton. To try to make this map efficient, we can arrange the cubical regions in a
![]() $2 \times 2 \times 2 \times 2$
grid. But when we iterate this map many times, the regions that map homothetically to the
$2 \times 2 \times 2 \times 2$
grid. But when we iterate this map many times, the regions that map homothetically to the
![]() $4$
-cell become tiny, and most of the
$4$
-cell become tiny, and most of the
![]() $4$
-cell maps to the
$4$
-cell maps to the
![]() $2$
-skeleton.
$2$
-skeleton.
The main idea of the construction is that we can actually expand the homothetic regions so that they take up a much larger part of the cell, while compressing the parts that map to the
![]() $2$
-skeleton to a thin layer. This has to do with the fact that self-maps of
$2$
-skeleton to a thin layer. This has to do with the fact that self-maps of
![]() $S^2$
of high degree are easy to produce and modify. In the end, each of the
$S^2$
of high degree are easy to produce and modify. In the end, each of the
![]() $\ell $
iterations contributes a layer of roughly the same thickness, leading to an estimate of
$\ell $
iterations contributes a layer of roughly the same thickness, leading to an estimate of
![]() $O(\ell \cdot 2^\ell )$
for the Lipschitz constant, or
$O(\ell \cdot 2^\ell )$
for the Lipschitz constant, or
![]() $O(d^{1/4}\log d)$
in terms of the degree
$O(d^{1/4}\log d)$
in terms of the degree
![]() $d=2^{4\ell }$
. See Figure 1 for a rough illustration.
$d=2^{4\ell }$
. See Figure 1 for a rough illustration.

Figure 1 Rescaling the ‘layers’ of the iterated map.
The proof of the lower bound of Theorem A is a straightforward generalization of this idea.
To end this introduction, we consider the Littlewood–Paley pieces of the differential forms from this map and from other maps we have discussed. For simplicity, let us first discuss a self-map
![]() $S^2 \to S^2$
with degree
$S^2 \to S^2$
with degree
![]() $2^{2p}$
and Lipschitz constant
$2^{2p}$
and Lipschitz constant
![]() $2^p$
. The pullback of the volume form is very repetitive, so that after averaging on scale
$2^p$
. The pullback of the volume form is very repetitive, so that after averaging on scale
![]() $2^{-p}$
, it becomes essentially constant. Therefore, the Littlewood–Paley pieces of the pullback are large at the highest frequency scale
$2^{-p}$
, it becomes essentially constant. Therefore, the Littlewood–Paley pieces of the pullback are large at the highest frequency scale
![]() $2^p$
and at frequency 1, but they can be very small at all the in-between frequencies.
$2^p$
and at frequency 1, but they can be very small at all the in-between frequencies.
The maps between scalable spaces constructed in [Reference Berdnikov and Manin3] have a similar Littlewood–Paley profile. These maps are highly regular ‘rescalings’. In fact, we prove Theorem C by building maps which are modeled on constant forms—the lowest possible frequency. Such maps are built on each cell and patched together using previous results from quantitative homotopy theory. The patching introduces high-frequency pieces, but there do not need to be any contributions from the intermediate frequencies.
The Littlewood–Paley decomposition for the self-map of
![]() $\#_k {\mathbb {C}} P^2$
sketched above is very different. The outermost layer is dominated by very low-frequency terms (at scale around the diameter of the space) and very high-frequency terms (at scale
$\#_k {\mathbb {C}} P^2$
sketched above is very different. The outermost layer is dominated by very low-frequency terms (at scale around the diameter of the space) and very high-frequency terms (at scale
![]() $\sim 2^{-\ell }$
). Similarly, the kth layer, which looks like the outermost layer but on a different scale, is dominated by terms at scale
$\sim 2^{-\ell }$
). Similarly, the kth layer, which looks like the outermost layer but on a different scale, is dominated by terms at scale
![]() $2^{-k}$
and
$2^{-k}$
and
![]() $2^{-\ell }$
. Overall, the map has pieces at every frequency range, as suggested by its fractal-like self-similarity.
$2^{-\ell }$
. Overall, the map has pieces at every frequency range, as suggested by its fractal-like self-similarity.
1.4. Structure of the paper
Section 2 contains the Fourier-analytic proof of the upper bound of Theorem A; it is independent of the remainder of the paper. Section 3 discusses the corresponding lower bound and is likewise largely self-contained. Section 4 introduces some necessary results from rational and quantitative homotopy theory. In Section 5, we use this machinery to prove Theorems C and C′, and in Section 6, we use it to prove Theorem B. Finally, in Section 7, we discuss what our techniques can say about nonformal spaces, proving Theorem D as well as some complementary bounds.
2. Upper bounds on degree using Fourier analysis
In this section, we show the upper bound of Theorem A. To introduce the method, we first handle the case of a connected sum of
![]() ${\mathbb {C}} P^2$
s:
${\mathbb {C}} P^2$
s:
Theorem 2.1. Let
![]() $X_k = \#_k {\mathbb {C}} P^2$
. Fix a metric g on
$X_k = \#_k {\mathbb {C}} P^2$
. Fix a metric g on
![]() $X_k$
. Suppose that
$X_k$
. Suppose that
![]() $f: X_k \rightarrow X_k$
is L-Lipschitz. If
$f: X_k \rightarrow X_k$
is L-Lipschitz. If
![]() $k \ge 4$
, then
$k \ge 4$
, then
We then use the same method to prove the general result:
Theorem 2.2. Suppose that M is a closed connected oriented n-manifold such that
![]() $H^*(M; {\mathbb {R}})$
does not embed into
$H^*(M; {\mathbb {R}})$
does not embed into
![]() $\Lambda ^* {\mathbb {R}}^n$
, and N is any closed oriented n-manifold. Then there is an
$\Lambda ^* {\mathbb {R}}^n$
, and N is any closed oriented n-manifold. Then there is an
![]() $\alpha (M)> 0$
so that for any metric g on M and
$\alpha (M)> 0$
so that for any metric g on M and
![]() $g'$
on N and any L-Lipschitz map
$g'$
on N and any L-Lipschitz map
![]() $f: N \rightarrow M$
,
$f: N \rightarrow M$
,
Note that by Theorem C, proved later in the paper, if M is simply connected and formal, then this condition holds if and only if M is not scalable. However, the theorem also holds for nonformal manifolds as well as those with nontrivial fundamental group.
A similar result also holds for many nonclosed domain manifolds. We give the proof for a unit ball, although it extends easily to any compact manifold with boundary:
Theorem 2.3. Suppose that M is a closed connected oriented n-manifold such that
![]() $H^*(M; {\mathbb {R}})$
does not embed into
$H^*(M; {\mathbb {R}})$
does not embed into
![]() $\Lambda ^* {\mathbb {R}}^n$
, and let
$\Lambda ^* {\mathbb {R}}^n$
, and let
![]() $\alpha (M)>0$
be as in the statement of Theorem 2.2. Let
$\alpha (M)>0$
be as in the statement of Theorem 2.2. Let
![]() $B^n \subseteq {\mathbb {R}}^n$
be the unit ball. Then for any metric g on M and any L-Lipschitz map
$B^n \subseteq {\mathbb {R}}^n$
be the unit ball. Then for any metric g on M and any L-Lipschitz map
![]() $f:B^n \to M$
,
$f:B^n \to M$
,
As discussed in the introduction, we prove these results by using Littlewood–Paley theory to divide the forms into pieces at different frequency ranges. In the first subsection, we review the tools from Littlewood–Paley theory that we need. In the second part, we prove Theorem 2.1. In the third part, we introduce the modifications needed to prove the more general estimate in Theorem 2.2.
2.1. Littlewood–Paley theory
If a denotes a differential form on
![]() ${\mathbb {R}}^d$
, then we can define its Fourier transform term by term. In other words, if I is a multi-index and
${\mathbb {R}}^d$
, then we can define its Fourier transform term by term. In other words, if I is a multi-index and
![]() $ a = \sum _I a_I(x) dx^I$
, then
$ a = \sum _I a_I(x) dx^I$
, then
To set up Littlewood–Paley theory, pick a partition of unity on Fourier space:
where
![]() $\eta _k$
is supported in the annulus
$\eta _k$
is supported in the annulus
![]() $\operatorname {\mathrm {Ann}}_k := \{ \xi : 2^{k-1} \le |\xi | \le 2^{k+1} \}$
. We can also arrange that
$\operatorname {\mathrm {Ann}}_k := \{ \xi : 2^{k-1} \le |\xi | \le 2^{k+1} \}$
. We can also arrange that
![]() $0 \le \eta _k \le 1$
and that
$0 \le \eta _k \le 1$
and that
![]() $\eta _k$
are smooth with appropriate bounds on their derivatives.
$\eta _k$
are smooth with appropriate bounds on their derivatives.
Then define
where
![]() $\vee $
denotes the inverse Fourier transform. We have
$\vee $
denotes the inverse Fourier transform. We have
![]() $a = \sum _{k \in {\mathbb {Z}}} P_k a$
, and we know that
$a = \sum _{k \in {\mathbb {Z}}} P_k a$
, and we know that
![]() $\widehat {P_k a} = \eta _k \hat a$
is supported in
$\widehat {P_k a} = \eta _k \hat a$
is supported in
![]() $\operatorname {\mathrm {Ann}}_k$
.
$\operatorname {\mathrm {Ann}}_k$
.
We also write
![]() $P_{\le k} a = \sum _{k' \le k} P_{k'} a$
, and
$P_{\le k} a = \sum _{k' \le k} P_{k'} a$
, and
![]() $\eta _{\le k} = \sum _{k' \le k} \eta _k$
, so
$\eta _{\le k} = \sum _{k' \le k} \eta _k$
, so
![]() $P_{\le k} a = (\eta _{\le k} \hat a)^\vee $
.
$P_{\le k} a = (\eta _{\le k} \hat a)^\vee $
.
We say that a form
![]() $a = \sum _I a_I(x) dx^I$
is Schwartz if each function
$a = \sum _I a_I(x) dx^I$
is Schwartz if each function
![]() $a_I(x)$
is Schwartz. A form a is Schwartz if and only if
$a_I(x)$
is Schwartz. A form a is Schwartz if and only if
![]() $\hat a$
is Schwartz. Therefore, if a is Schwartz, then
$\hat a$
is Schwartz. Therefore, if a is Schwartz, then
![]() $P_k a$
and
$P_k a$
and
![]() $P_{\le k} a$
are also Schwartz.
$P_{\le k} a$
are also Schwartz.
In this section, we review some estimates related to the
![]() $P_k a$
. These results are proven using some inequalities about the inverse Fourier transform of smooth bump functions.
$P_k a$
. These results are proven using some inequalities about the inverse Fourier transform of smooth bump functions.
Lemma 2.4. Suppose that
![]() $\eta (\omega )$
is a smooth function supported on a ball
$\eta (\omega )$
is a smooth function supported on a ball
![]() $B\subset {\mathbb {R}}^d$
of radius 1 such that
$B\subset {\mathbb {R}}^d$
of radius 1 such that
-
•
 $| \eta (\omega ) | \le A$
for all
$| \eta (\omega ) | \le A$
for all
 $\omega $
.
$\omega $
. -
•
 $| \partial _J \eta (\omega ) | \le A_N$
for all multi-indices J with
$| \partial _J \eta (\omega ) | \le A_N$
for all multi-indices J with
 $|J| \le N$
.
$|J| \le N$
.
Then
 $$ \begin{align*} \lvert\eta^\vee(x)\rvert &\lesssim_d A \qquad\text{for every } x \in {\mathbb{R}}^d. \\ \lvert \eta^\vee(x) \rvert &\lesssim_d A_N \lvert x \rvert^{-N} \qquad \text{for every } x \in {\mathbb{R}}^d. \end{align*} $$
$$ \begin{align*} \lvert\eta^\vee(x)\rvert &\lesssim_d A \qquad\text{for every } x \in {\mathbb{R}}^d. \\ \lvert \eta^\vee(x) \rvert &\lesssim_d A_N \lvert x \rvert^{-N} \qquad \text{for every } x \in {\mathbb{R}}^d. \end{align*} $$
Therefore, if
![]() $N> d$
,
$N> d$
,
Proof. For the first bound, we write
For the second bound, we integrate by parts N times. For a given
![]() $x \in {\mathbb {R}}^d$
, we choose a multi-index J with
$x \in {\mathbb {R}}^d$
, we choose a multi-index J with
![]() $|J| =N$
and
$|J| =N$
and
![]() $|x|^N \sim x^J$
. Then
$|x|^N \sim x^J$
. Then
To bound
![]() $\int |\eta ^\vee (x)| dx$
, we use the first bound when
$\int |\eta ^\vee (x)| dx$
, we use the first bound when
![]() $|x| \le 1$
and the second bound when
$|x| \le 1$
and the second bound when
![]() $|x| \ge 1$
.
$|x| \ge 1$
.
Lemma 2.5. Suppose that
![]() $\eta (\omega )$
is a smooth function supported on a ball
$\eta (\omega )$
is a smooth function supported on a ball
![]() $B\subset {\mathbb {R}}^d$
of radius R such that
$B\subset {\mathbb {R}}^d$
of radius R such that
-
•
 $| \eta (\omega ) | \le A$
for all
$| \eta (\omega ) | \le A$
for all
 $\omega $
.
$\omega $
. -
•
 $| \partial _J \eta (\omega ) | \le A_N R^{-|J|}$
for all multi-indices J with
$| \partial _J \eta (\omega ) | \le A_N R^{-|J|}$
for all multi-indices J with
 $|J| \le N$
.
$|J| \le N$
.
Then
 $$ \begin{align*} | \eta^\vee(x) | &\lesssim_d A R^d \qquad\textrm{ for every } x \in {\mathbb{R}}^d. \\ | \eta^\vee(x) | &\lesssim_d A_N R^d \lvert Rx \rvert^{-N} \qquad\textrm{ for every } x \in {\mathbb{R}}^d. \end{align*} $$
$$ \begin{align*} | \eta^\vee(x) | &\lesssim_d A R^d \qquad\textrm{ for every } x \in {\mathbb{R}}^d. \\ | \eta^\vee(x) | &\lesssim_d A_N R^d \lvert Rx \rvert^{-N} \qquad\textrm{ for every } x \in {\mathbb{R}}^d. \end{align*} $$
Therefore, if
![]() $N> d$
,
$N> d$
,
Proof. The first two bounds follow from Lemma 2.4 by a change of variables. Alternatively, one can use the same method as in Lemma 2.4.
To bound
![]() $\int |\eta ^\vee (x)| dx$
, we use the first bound when
$\int |\eta ^\vee (x)| dx$
, we use the first bound when
![]() $|x| \le 1/R$
and the second bound when
$|x| \le 1/R$
and the second bound when
![]() $|x| \ge 1/R$
.
$|x| \ge 1/R$
.
Lemma 2.6. Suppose that
![]() $\eta (\omega )$
is a smooth function supported on a ball
$\eta (\omega )$
is a smooth function supported on a ball
![]() $B\subset {\mathbb {R}}^d$
of radius R such that
$B\subset {\mathbb {R}}^d$
of radius R such that
-
•
 $| \eta (\omega ) | \le A$
for all
$| \eta (\omega ) | \le A$
for all
 $\omega $
.
$\omega $
. -
•
 $| \partial _J \eta (\omega ) | \le A_N R^{-|J|}$
for all multi-indices J with
$| \partial _J \eta (\omega ) | \le A_N R^{-|J|}$
for all multi-indices J with
 $|J| \le N$
.
$|J| \le N$
.
Write
![]() $M f = \big ( \eta \hat f \big )^\vee $
. Then if
$M f = \big ( \eta \hat f \big )^\vee $
. Then if
![]() $N>d$
,
$N>d$
,
Proof. We have
![]() $Mf = f * \eta ^\vee $
. So
$Mf = f * \eta ^\vee $
. So
![]() $\| M f \|_{L^p} \le \| f \|_{L^p} \| \eta ^\vee \|_{L^1}$
. Now apply the bound for
$\| M f \|_{L^p} \le \| f \|_{L^p} \| \eta ^\vee \|_{L^1}$
. Now apply the bound for
![]() $\| \eta ^\vee \|_{L^1}$
from Lemma 2.5.
$\| \eta ^\vee \|_{L^1}$
from Lemma 2.5.
We apply these bounds to study the Littlewood–Paley projections
![]() $P_k$
.
$P_k$
.
Lemma 2.7.
![]() $\| \eta _k^\vee \|_{L^1} \lesssim 1$
uniformly in k.
$\| \eta _k^\vee \|_{L^1} \lesssim 1$
uniformly in k.
![]() $\| d \eta _k^\vee \|_{L^1} \lesssim 2^k$
uniformly in k.
$\| d \eta _k^\vee \|_{L^1} \lesssim 2^k$
uniformly in k.
Proof. We can first arrange that
![]() $\eta _k(\omega ) = \eta _0(2^{-k} \omega )$
. Then the function
$\eta _k(\omega ) = \eta _0(2^{-k} \omega )$
. Then the function
![]() $\eta _k$
obeys the hypotheses of Lemma 2.5 with
$\eta _k$
obeys the hypotheses of Lemma 2.5 with
![]() $R = 2^k$
, with bounds that are uniform in k. Then Lemma 2.5 gives the estimate
$R = 2^k$
, with bounds that are uniform in k. Then Lemma 2.5 gives the estimate
![]() $\| \eta _k^\vee \|_{L^1} \lesssim _d 1$
.
$\| \eta _k^\vee \|_{L^1} \lesssim _d 1$
.
Next, we will show that
![]() $\| \partial _j \eta _k^\vee \|_{L^1} \lesssim _d 2^k$
. This will imply
$\| \partial _j \eta _k^\vee \|_{L^1} \lesssim _d 2^k$
. This will imply
![]() $\| d \eta _k^\vee \|_{L^1} \lesssim _d 2^k$
as desired.
$\| d \eta _k^\vee \|_{L^1} \lesssim _d 2^k$
as desired.
The Fourier transform of
![]() $\partial _j \eta _k^\vee $
is
$\partial _j \eta _k^\vee $
is
![]() $2 \pi i \omega _j \eta _k(\omega )$
. Notice that
$2 \pi i \omega _j \eta _k(\omega )$
. Notice that
![]() $|\omega _j| \lesssim 2^k$
on
$|\omega _j| \lesssim 2^k$
on
![]() $\operatorname {\mathrm {Ann}}_k$
. We write
$\operatorname {\mathrm {Ann}}_k$
. We write
 $$\begin{align*}2 \pi i \omega_j \eta_k = 2^k \cdot \underbrace{ 2 \pi i \frac{\omega_j}{2^k} \eta_k }_{\psi}.\end{align*}$$
$$\begin{align*}2 \pi i \omega_j \eta_k = 2^k \cdot \underbrace{ 2 \pi i \frac{\omega_j}{2^k} \eta_k }_{\psi}.\end{align*}$$
The function
![]() $\psi $
obeys the hypotheses of Lemma 2.5. Therefore,
$\psi $
obeys the hypotheses of Lemma 2.5. Therefore,
![]() $\| \psi ^\vee \|_{L^1} \lesssim _d 1.$
And so
$\| \psi ^\vee \|_{L^1} \lesssim _d 1.$
And so
Lemma 2.8.
![]() $\| P_k a \|_{L^p} \le C \| a \|_{L^p}$
, for all k and all
$\| P_k a \|_{L^p} \le C \| a \|_{L^p}$
, for all k and all
![]() $1 \le p \le \infty $
with a uniform constant C.
$1 \le p \le \infty $
with a uniform constant C.
Proof.
![]() $\|P_k a \|_{L^p} = \| \eta _k^\vee * a \|_{L^p} \le \| \eta _k^\vee \|_{L^1} \| a \|_{L^p}$
. Now
$\|P_k a \|_{L^p} = \| \eta _k^\vee * a \|_{L^p} \le \| \eta _k^\vee \|_{L^1} \| a \|_{L^p}$
. Now
![]() $\| \eta _k^\vee \|_{L^1}$
is bounded uniformly in k by Lemma 2.7.
$\| \eta _k^\vee \|_{L^1}$
is bounded uniformly in k by Lemma 2.7.
Lemma 2.9. The projection operator
![]() $P_k$
commutes with the exterior derivative d:
$P_k$
commutes with the exterior derivative d:
Proof. We can see this by taking the Fourier transform on both sides. The exterior derivative d becomes pointwise multiplication by a matrix on the Fourier side. The projection operator
![]() $P_k$
becomes pointwise multiplication by the scalar
$P_k$
becomes pointwise multiplication by the scalar
![]() $\eta _k$
. These commute.
$\eta _k$
. These commute.
Lemma 2.10. Suppose that a is a Schwartz form on
![]() ${\mathbb {R}}^d$
with
${\mathbb {R}}^d$
with
![]() $da = 0$
and with
$da = 0$
and with
![]() $\hat a$
is supported in
$\hat a$
is supported in
![]() $\operatorname {\mathrm {Ann}}_k:= \{ \xi : 2^{k-1} \le |\xi | \le 2^{k+1} \}$
. Then a has a primitive, which we denote
$\operatorname {\mathrm {Ann}}_k:= \{ \xi : 2^{k-1} \le |\xi | \le 2^{k+1} \}$
. Then a has a primitive, which we denote
![]() $\operatorname {\mathrm {Prim}}(a)$
, so that
$\operatorname {\mathrm {Prim}}(a)$
, so that
-
•
 $ d \operatorname {\mathrm {Prim}}(a) = a$
. (This is what the word ‘primitive’ means.)
$ d \operatorname {\mathrm {Prim}}(a) = a$
. (This is what the word ‘primitive’ means.) -
•
 $\operatorname {\mathrm {Prim}}(a)$
is a Schwartz form.
$\operatorname {\mathrm {Prim}}(a)$
is a Schwartz form. -
•
 $ \lVert \operatorname {\mathrm {Prim}}(a)\rVert _{L^p} \le C 2^{-k} \lVert a \rVert _{L^p}$
for all
$ \lVert \operatorname {\mathrm {Prim}}(a)\rVert _{L^p} \le C 2^{-k} \lVert a \rVert _{L^p}$
for all
 $1 \le p \le \infty $
, with a uniform constant C.
$1 \le p \le \infty $
, with a uniform constant C.
This is really the key property of frequency localized forms. The intuition is that
![]() $\operatorname {\mathrm {Prim}}(a)$
is defined by integrating a, and the integral cancels at length scales larger than
$\operatorname {\mathrm {Prim}}(a)$
is defined by integrating a, and the integral cancels at length scales larger than
![]() $2^{-k}$
.
$2^{-k}$
.
Before starting the proof, we make a quick remark about top-dimensional forms. If a is a d-form on
![]() ${\mathbb {R}}^d$
, then the condition
${\mathbb {R}}^d$
, then the condition
![]() $da=0$
is automatic. In order for a to have a Schwartz primitive, we need to know that
$da=0$
is automatic. In order for a to have a Schwartz primitive, we need to know that
![]() $\int _{{\mathbb {R}}^d} a = 0$
. This fact is implied by our assumption that
$\int _{{\mathbb {R}}^d} a = 0$
. This fact is implied by our assumption that
![]() $\hat a$
is supported in
$\hat a$
is supported in
![]() $\operatorname {\mathrm {Ann}}_k$
because
$\operatorname {\mathrm {Ann}}_k$
because
![]() $\int _{{\mathbb {R}}^d} a = \hat a(0) = 0$
.
$\int _{{\mathbb {R}}^d} a = \hat a(0) = 0$
.
Proof. First cover
![]() $\operatorname {\mathrm {Ann}}_k$
with
$\operatorname {\mathrm {Ann}}_k$
with
![]() $\sim 1$
balls B so that the radius of each ball is
$\sim 1$
balls B so that the radius of each ball is
![]() $\sim 2^k$
and the distance from each ball to the origin is also
$\sim 2^k$
and the distance from each ball to the origin is also
![]() $\sim 2^k$
. Let
$\sim 2^k$
. Let
![]() $\psi _B$
be a partition of unity:
$\psi _B$
be a partition of unity:
![]() $\sum _B \psi _B = 1$
on
$\sum _B \psi _B = 1$
on
![]() $\operatorname {\mathrm {Ann}}_k$
and
$\operatorname {\mathrm {Ann}}_k$
and
![]() $\psi _B$
is supported in B. Decompose
$\psi _B$
is supported in B. Decompose
![]() $a = \sum _B a_B$
where
$a = \sum _B a_B$
where
The form
![]() $\hat a_B$
is smooth and supported in
$\hat a_B$
is smooth and supported in
![]() $\operatorname {\mathrm {Ann}}_k \cup \operatorname {\mathrm {Ann}}_{k-1} \cup \operatorname {\mathrm {Ann}}_{k+1}$
. Just as in the proof of Lemma 2.9, it follows that
$\operatorname {\mathrm {Ann}}_k \cup \operatorname {\mathrm {Ann}}_{k-1} \cup \operatorname {\mathrm {Ann}}_{k+1}$
. Just as in the proof of Lemma 2.9, it follows that
![]() $d a_B = 0$
. Using Lemma 2.6,
$d a_B = 0$
. Using Lemma 2.6,
![]() $ \| a_B \|_{L^p} \le C \| a \|_{L^p}$
for all
$ \| a_B \|_{L^p} \le C \| a \|_{L^p}$
for all
![]() $1 \le p \le \infty $
.
$1 \le p \le \infty $
.
We will construct a primitive
![]() $\operatorname {\mathrm {Prim}}(a_B)$
for each form
$\operatorname {\mathrm {Prim}}(a_B)$
for each form
![]() $a_B$
such that
$a_B$
such that
-
•
 $ d \operatorname {\mathrm {Prim}}(a_B) = a_B$
.
$ d \operatorname {\mathrm {Prim}}(a_B) = a_B$
. -
•
 $\operatorname {\mathrm {Prim}}(a_B)$
is a Schwartz form.
$\operatorname {\mathrm {Prim}}(a_B)$
is a Schwartz form. -
•
 $ \lVert \operatorname {\mathrm {Prim}}(a_B) \rVert _{L^p} \le C 2^{-k} \lVert a_B \rVert _{L^p}$
for all
$ \lVert \operatorname {\mathrm {Prim}}(a_B) \rVert _{L^p} \le C 2^{-k} \lVert a_B \rVert _{L^p}$
for all
 $1 \le p \le \infty $
, with a uniform constant C.
$1 \le p \le \infty $
, with a uniform constant C.
Finally, we define
![]() $\operatorname {\mathrm {Prim}}(a) = \sum _B \operatorname {\mathrm {Prim}}(a_B)$
. Since
$\operatorname {\mathrm {Prim}}(a) = \sum _B \operatorname {\mathrm {Prim}}(a_B)$
. Since
![]() $\operatorname {\mathrm {Prim}}(a_B)$
has the desired properties, it follows that
$\operatorname {\mathrm {Prim}}(a_B)$
has the desired properties, it follows that
![]() $\operatorname {\mathrm {Prim}}(a)$
does also.
$\operatorname {\mathrm {Prim}}(a)$
does also.
Now we have to construct
![]() $\operatorname {\mathrm {Prim}}(a_B)$
. For ease of notation, we will abbreviate
$\operatorname {\mathrm {Prim}}(a_B)$
. For ease of notation, we will abbreviate
![]() $a_B$
by a. We know that
$a_B$
by a. We know that
![]() $\hat a$
is supported on B. We can choose coordinates so that
$\hat a$
is supported on B. We can choose coordinates so that
![]() $\omega _1 \sim 2^k$
on B.
$\omega _1 \sim 2^k$
on B.
We write the form a as
We define the antiderivative
![]() $\int a_I dx_1$
via the Fourier transform by the formula
$\int a_I dx_1$
via the Fourier transform by the formula
Since
![]() $\omega _1> 0$
on B, and
$\omega _1> 0$
on B, and
![]() $\hat a_I(\omega )$
is supported in B, the right-hand side is a smooth compactly supported function on Fourier space. Therefore,
$\hat a_I(\omega )$
is supported in B, the right-hand side is a smooth compactly supported function on Fourier space. Therefore,
![]() $\int a_I dx_1$
is a Schwartz function on
$\int a_I dx_1$
is a Schwartz function on
![]() ${\mathbb {R}}^d$
. From (1), we can also check that
${\mathbb {R}}^d$
. From (1), we can also check that
We can also define
![]() $\int a_I dx_1$
using definite integrals:
$\int a_I dx_1$
using definite integrals:
This definite integral formula is equivalent to (1). From the definite integral formula, it takes a little work to check that
![]() $\int a_I dx_1$
is, in fact, a Schwartz function on
$\int a_I dx_1$
is, in fact, a Schwartz function on
![]() ${\mathbb {R}}^d$
, although it is not that difficult. In our proof, we will only need (1).)
${\mathbb {R}}^d$
, although it is not that difficult. In our proof, we will only need (1).)
We now define
This is a standard construction for primitives of forms which appears in the proof of the Poincaré lemma, cf. [Reference Bott and Tu6, p. 38]. We will check that
![]() $d \operatorname {\mathrm {Prim}}(a) = a$
, following the same general method as in [Reference Bott and Tu6].
$d \operatorname {\mathrm {Prim}}(a) = a$
, following the same general method as in [Reference Bott and Tu6].
We first compute
![]() $d( \int a_I dx_1)$
:
$d( \int a_I dx_1)$
:
 $$\begin{align*}d({\textstyle\int} a_I dx_1) = \partial_1 ({\textstyle\int} a_I dx_1) dx_1 + \sum_{j=2}^d \partial_j ({\textstyle\int} a_I dx_1) dx_j = a_I dx_1 + \sum_{j=2}^d {\textstyle\int} \partial_j a_I dx_1.\end{align*}$$
$$\begin{align*}d({\textstyle\int} a_I dx_1) = \partial_1 ({\textstyle\int} a_I dx_1) dx_1 + \sum_{j=2}^d \partial_j ({\textstyle\int} a_I dx_1) dx_j = a_I dx_1 + \sum_{j=2}^d {\textstyle\int} \partial_j a_I dx_1.\end{align*}$$
Now,
 $$\begin{align*}d \operatorname{\mathrm{Prim}}(a) = \sum_{I = 1 \cup J} d ({\textstyle\int a_I dx_1}) dx_J = \sum_{I = 1 \cup J} a_I dx_1 \wedge dx_J + \sum_{I = 1 \cup J} \sum_{j=2}^d ({\textstyle\int \partial_j a_I dx_1}) dx_j \wedge dx_J.\end{align*}$$
$$\begin{align*}d \operatorname{\mathrm{Prim}}(a) = \sum_{I = 1 \cup J} d ({\textstyle\int a_I dx_1}) dx_J = \sum_{I = 1 \cup J} a_I dx_1 \wedge dx_J + \sum_{I = 1 \cup J} \sum_{j=2}^d ({\textstyle\int \partial_j a_I dx_1}) dx_j \wedge dx_J.\end{align*}$$
The first term is
![]() $\sum _{I = 1 \cup J} a_I dx_I$
. So we have to check that the second term is the rest of a. In other words, we want to show that
$\sum _{I = 1 \cup J} a_I dx_I$
. So we have to check that the second term is the rest of a. In other words, we want to show that
 $$ \begin{align} \sum_{I = 1 \cup J} \sum_{j=2}^d ({\textstyle\int} \partial_j a_I dx_1) dx_j \wedge dx_J = \sum_{1 \notin I'} a_{I'} dx_{I'}. \end{align} $$
$$ \begin{align} \sum_{I = 1 \cup J} \sum_{j=2}^d ({\textstyle\int} \partial_j a_I dx_1) dx_j \wedge dx_J = \sum_{1 \notin I'} a_{I'} dx_{I'}. \end{align} $$
Since both forms are Schwartz, it suffices to check that
![]() $\partial _1$
of both sides are equal:
$\partial _1$
of both sides are equal:
 $$ \begin{align} \sum_{I = 1 \cup J} \sum_{j=2}^d \partial_j a_I dx_j \wedge dx_J = \sum_{1 \notin I'} \partial_1 a_{I'} dx_{I'}. \end{align} $$
$$ \begin{align} \sum_{I = 1 \cup J} \sum_{j=2}^d \partial_j a_I dx_j \wedge dx_J = \sum_{1 \notin I'} \partial_1 a_{I'} dx_{I'}. \end{align} $$
Since there is no 1 in J or j or
![]() $I'$
, it suffices to check that
$I'$
, it suffices to check that
![]() $dx_1$
wedged with both sides are equal:
$dx_1$
wedged with both sides are equal:
 $$ \begin{align} \sum_{I = 1 \cup J} \sum_{j=2}^d \partial_j a_I dx_1 \wedge dx_j \wedge dx_J = \sum_{1 \notin I'} \partial_1 a_{I'} dx_1 \wedge dx_{I'}. \end{align} $$
$$ \begin{align} \sum_{I = 1 \cup J} \sum_{j=2}^d \partial_j a_I dx_1 \wedge dx_j \wedge dx_J = \sum_{1 \notin I'} \partial_1 a_{I'} dx_1 \wedge dx_{I'}. \end{align} $$
This, in turn, follows from
![]() $da = 0$
.
$da = 0$
.
To bound
![]() $\operatorname {\mathrm {Prim}}(a)$
, the main point is that
$\operatorname {\mathrm {Prim}}(a)$
, the main point is that
![]() $| \frac {1}{2 \pi i \omega _1}| \sim 2^{-k}$
on the ball B. Define
$| \frac {1}{2 \pi i \omega _1}| \sim 2^{-k}$
on the ball B. Define
![]() $\eta _B = 1 $
on B, and
$\eta _B = 1 $
on B, and
![]() $0 \le \eta _B \le 1$
and with
$0 \le \eta _B \le 1$
and with
![]() $\eta _B$
supported in a slightly larger ball
$\eta _B$
supported in a slightly larger ball
![]() $\tilde B = 1.01 B$
. We can assume that
$\tilde B = 1.01 B$
. We can assume that
![]() $\omega _1 \sim 2^k$
on
$\omega _1 \sim 2^k$
on
![]() $\tilde B$
. Then
$\tilde B$
. Then
 $$\begin{align*}\frac{1}{2 \pi i \omega_1} \hat a_I(\omega) = 2^{-k} \underbrace{\frac{1}{2 \pi i} \frac{2^k}{\omega_1} \eta_B}_{\tilde \eta_B} \hat a_I (\omega).\end{align*}$$
$$\begin{align*}\frac{1}{2 \pi i \omega_1} \hat a_I(\omega) = 2^{-k} \underbrace{\frac{1}{2 \pi i} \frac{2^k}{\omega_1} \eta_B}_{\tilde \eta_B} \hat a_I (\omega).\end{align*}$$
The function
![]() $\tilde \eta _B$
is supported on
$\tilde \eta _B$
is supported on
![]() $\tilde B$
, and it obeys the bounds from Lemma 2.6. The lemma tells us that
$\tilde B$
, and it obeys the bounds from Lemma 2.6. The lemma tells us that
Therefore,
![]() $\lVert \operatorname {\mathrm {Prim}}(a)\rVert _{L^p} \le C 2^{-k} \lVert a \rVert _{L^p}$
as desired.
$\lVert \operatorname {\mathrm {Prim}}(a)\rVert _{L^p} \le C 2^{-k} \lVert a \rVert _{L^p}$
as desired.
Lemma 2.11. For any function f,
Similarly, for any form a,
Proof. By the Plancherel theorem,
 $$\begin{align*}\sum_{k \in {\mathbb{Z}}} \| P_k f \|_{L^2}^2 = \sum_{k \in {\mathbb{Z}}} \int_{{\mathbb{R}}^d} \big\lvert \widehat{P_k f} \big\rvert^2 = \sum_{k \in {\mathbb{Z}}} \int_{{\mathbb{R}}^d} \lvert\eta_k(\omega)\rvert^2 \lvert\hat f(\omega)\rvert^2 d \omega.\end{align*}$$
$$\begin{align*}\sum_{k \in {\mathbb{Z}}} \| P_k f \|_{L^2}^2 = \sum_{k \in {\mathbb{Z}}} \int_{{\mathbb{R}}^d} \big\lvert \widehat{P_k f} \big\rvert^2 = \sum_{k \in {\mathbb{Z}}} \int_{{\mathbb{R}}^d} \lvert\eta_k(\omega)\rvert^2 \lvert\hat f(\omega)\rvert^2 d \omega.\end{align*}$$
Now for every
![]() $\omega $
,
$\omega $
,
![]() $(1/10) \le \sum _{k \in {\mathbb {Z}}} \eta _k(\omega )^2 \le 1$
. This holds because
$(1/10) \le \sum _{k \in {\mathbb {Z}}} \eta _k(\omega )^2 \le 1$
. This holds because
![]() $\sum _{k \in {\mathbb {Z}}} \eta _k(\omega ) = 1$
and each
$\sum _{k \in {\mathbb {Z}}} \eta _k(\omega ) = 1$
and each
![]() $\eta _k (\omega ) \ge 0$
, and each
$\eta _k (\omega ) \ge 0$
, and each
![]() $\omega $
lies in the support of
$\omega $
lies in the support of
![]() $\eta _k$
for at most 5 values of k. Therefore,
$\eta _k$
for at most 5 values of k. Therefore,
 $$\begin{align*}\sum_{k \in {\mathbb{Z}}} \| P_k f \|_{L^2}^2 = \int_{{\mathbb{R}}^d} \bigg( \sum_{k \in {\mathbb{Z}}} \eta_k(\omega)^2 \bigg) |\hat f(\omega)|^2 d \omega \sim \int_{{\mathbb{R}}^d} |\hat f (\omega)|^2 d \omega = \int_{{\mathbb{R}}^d} |f(x)|^2 dx.\end{align*}$$
$$\begin{align*}\sum_{k \in {\mathbb{Z}}} \| P_k f \|_{L^2}^2 = \int_{{\mathbb{R}}^d} \bigg( \sum_{k \in {\mathbb{Z}}} \eta_k(\omega)^2 \bigg) |\hat f(\omega)|^2 d \omega \sim \int_{{\mathbb{R}}^d} |\hat f (\omega)|^2 d \omega = \int_{{\mathbb{R}}^d} |f(x)|^2 dx.\end{align*}$$
For a form
![]() $a = \sum _{I} a_I(x) dx_I$
,
$a = \sum _{I} a_I(x) dx_I$
,
![]() $P_k(a) = \sum _I P_k a_I(x) dx_I$
and
$P_k(a) = \sum _I P_k a_I(x) dx_I$
and
![]() $\| a \|_{L^2}^2 := \sum _I \int |a_I(x)|^2 dx$
. So the case of forms follows from the case of functions.
$\| a \|_{L^2}^2 := \sum _I \int |a_I(x)|^2 dx$
. So the case of forms follows from the case of functions.
Lemma 2.12. The Fourier support of
![]() $P_{\le k} a_1 \wedge P_{\le k} a_2$
is contained in the ball of radius
$P_{\le k} a_1 \wedge P_{\le k} a_2$
is contained in the ball of radius
![]() $2^{k+2}$
around 0. Therefore,
$2^{k+2}$
around 0. Therefore,
Proof. The Fourier support of
![]() $P_{\le k} a$
is contained in the ball
$P_{\le k} a$
is contained in the ball
![]() $B(2^{k+1}, 0)$
. For any functions f and g, the Fourier transform of
$B(2^{k+1}, 0)$
. For any functions f and g, the Fourier transform of
![]() $fg$
is given by
$fg$
is given by
If
![]() $\hat f$
and
$\hat f$
and
![]() $\hat g$
are supported in
$\hat g$
are supported in
![]() $B(2^{k+1}, 0)$
, then
$B(2^{k+1}, 0)$
, then
![]() $\widehat {fg}$
is supported in
$\widehat {fg}$
is supported in
![]() $B( 2\cdot 2^{k+1}, 0)$
.
$B( 2\cdot 2^{k+1}, 0)$
.
This argument also applies to wedge products of forms instead of products of functions, just by writing out the components of the forms. This shows that the Fourier transform of
![]() $P_{\le k} a_1 \wedge P_{\le k} a_2$
is supported in
$P_{\le k} a_1 \wedge P_{\le k} a_2$
is supported in
![]() $B(2^{k+2}, 0)$
. Now,
$B(2^{k+2}, 0)$
. Now,
![]() $\eta _{\le k+3}(\omega )$
is identically 1 on this ball, and so
$\eta _{\le k+3}(\omega )$
is identically 1 on this ball, and so
2.2. Bounds for connected sums of
 $\mathbb CP^2$
s
$\mathbb CP^2$
s
2.2.1. Setup
In this section, we will prove Theorem 2.1. We recall the statement.
Theorem. Let
![]() $X_k = ({\mathbb {C}} P^2)^{\# k}$
. Fix a metric g on
$X_k = ({\mathbb {C}} P^2)^{\# k}$
. Fix a metric g on
![]() $X_k$
. Suppose that
$X_k$
. Suppose that
![]() $f: X_k \rightarrow X_k$
is L-Lipschitz. If
$f: X_k \rightarrow X_k$
is L-Lipschitz. If
![]() $k \ge 4$
, then
$k \ge 4$
, then
Proof. Let
![]() $u_i \in H^2(X_k; {\mathbb {R}})$
be a cohomology class dual to the ith copy of
$u_i \in H^2(X_k; {\mathbb {R}})$
be a cohomology class dual to the ith copy of
![]() ${\mathbb {C}} P^1$
in
${\mathbb {C}} P^1$
in
![]() $X_k$
, for
$X_k$
, for
![]() $i = 1, \ldots , k$
. Let
$i = 1, \ldots , k$
. Let
![]() $\alpha _i$
be a 2-form in the cohomology class
$\alpha _i$
be a 2-form in the cohomology class
![]() $u_i$
. We can assume that the
$u_i$
. We can assume that the
![]() $\alpha _i$
have disjoint supports. For any i, we can write
$\alpha _i$
have disjoint supports. For any i, we can write
We will use Littlewood–Paley theory to estimate the right-hand side. Because Littlewood–Paley theory is by far nicest on
![]() ${\mathbb {R}}^d$
, we first switch to charts. Fix an atlas of charts for
${\mathbb {R}}^d$
, we first switch to charts. Fix an atlas of charts for
![]() $X_k$
: suppose that
$X_k$
: suppose that
![]() $X_k = \cup U'$
, and
$X_k = \cup U'$
, and
![]() $\phi _U: U \rightarrow U'$
are parametrizations. Suppose that
$\phi _U: U \rightarrow U'$
are parametrizations. Suppose that
![]() $\sum _{U'} \psi _{U'} = 1$
is a partition of unity on
$\sum _{U'} \psi _{U'} = 1$
is a partition of unity on
![]() $X_k$
subordinate to these charts. Define
$X_k$
subordinate to these charts. Define
![]() $\psi _U:{\mathbb {R}}^4 \to {\mathbb {R}}$
by
$\psi _U:{\mathbb {R}}^4 \to {\mathbb {R}}$
by
 $$\begin{align*}\psi_U(x) = \begin{cases} \phi^{*} \psi_{U'}(x) & x \in U \\ 0 & x \notin U. \end{cases}\end{align*}$$
$$\begin{align*}\psi_U(x) = \begin{cases} \phi^{*} \psi_{U'}(x) & x \in U \\ 0 & x \notin U. \end{cases}\end{align*}$$
Now, we can extend
![]() $\phi _U|_{\operatorname {\mathrm {supp}}(U)}$
to a smooth map
$\phi _U|_{\operatorname {\mathrm {supp}}(U)}$
to a smooth map
![]() $\tilde \phi _U:\mathbb R^4 \to X_k$
, and we can do it so that
$\tilde \phi _U:\mathbb R^4 \to X_k$
, and we can do it so that
![]() $\tilde \phi _U$
sends the complement of a compact set to a single point. Then define differential forms
$\tilde \phi _U$
sends the complement of a compact set to a single point. Then define differential forms
![]() $a_i$
on
$a_i$
on
![]() ${\mathbb {R}}^4$
by
${\mathbb {R}}^4$
by
(The forms
![]() $a_i$
also implicitly depend on U.) Plugging this definition into (5), we get
$a_i$
also implicitly depend on U.) Plugging this definition into (5), we get
 $$ \begin{align} \deg (f) = \sum_U \int_{{\mathbb{R}}^4} \psi_U a_i \wedge a_i. \end{align} $$
$$ \begin{align} \deg (f) = \sum_U \int_{{\mathbb{R}}^4} \psi_U a_i \wedge a_i. \end{align} $$
We will bound each of these integrals.
Before going on, we discuss properties of the
![]() $a_i$
. We made sure these forms are defined on all of
$a_i$
. We made sure these forms are defined on all of
![]() ${\mathbb {R}}^4$
so that we can apply Littlewood–Paley theory. We have
${\mathbb {R}}^4$
so that we can apply Littlewood–Paley theory. We have
![]() $\| a_i \|_{L^\infty } \lesssim L^2$
. We also know that
$\| a_i \|_{L^\infty } \lesssim L^2$
. We also know that
![]() $d a_i = 0$
. The form
$d a_i = 0$
. The form
![]() $a_i$
is supported on a fixed ball, and so for every
$a_i$
is supported on a fixed ball, and so for every
![]() $1 \le p \le \infty $
, we also have
$1 \le p \le \infty $
, we also have
![]() $\| a_i \|_{L^p} \lesssim \| a_i \|_{L^\infty } \lesssim L^2$
.
$\| a_i \|_{L^p} \lesssim \| a_i \|_{L^\infty } \lesssim L^2$
.
2.2.2. Using that k is large
In this section, we prove a lemma that takes advantage of the fact that
![]() $k \ge 4$
. This lemma is similar to a lemma in [Reference Berdnikov and Manin3].
$k \ge 4$
. This lemma is similar to a lemma in [Reference Berdnikov and Manin3].
Lemma 2.13. Suppose that
![]() $k \ge 4$
and that
$k \ge 4$
and that
![]() $b_1, \ldots , b_k$
are 2-forms on
$b_1, \ldots , b_k$
are 2-forms on
![]() ${\mathbb {R}}^4$
. Then at each point x, we have
${\mathbb {R}}^4$
. Then at each point x, we have
Proof. Suppose not. By scaling, we can assume that
![]() $b_1 \wedge b_1(x) = dx_1 \wedge \cdots \wedge dx_4$
. Then we must have
$b_1 \wedge b_1(x) = dx_1 \wedge \cdots \wedge dx_4$
. Then we must have
![]() $b_j \wedge b_j(x)$
is almost
$b_j \wedge b_j(x)$
is almost
![]() $dx_1 \wedge \cdots \wedge dx_4$
for every j and
$dx_1 \wedge \cdots \wedge dx_4$
for every j and
![]() $b_i \wedge b_j(x)$
is almost zero for every
$b_i \wedge b_j(x)$
is almost zero for every
![]() $i \neq j$
. Next, we will get a contradiction by considering the wedge product.
$i \neq j$
. Next, we will get a contradiction by considering the wedge product.
Let
![]() $W: \Lambda ^2 {\mathbb {R}}^4 \times \Lambda ^2 {\mathbb {R}}^4 \rightarrow \Lambda ^4 {\mathbb {R}}^4$
be the quadratic form given by the wedge product. It has signature (3,3). Now, let
$W: \Lambda ^2 {\mathbb {R}}^4 \times \Lambda ^2 {\mathbb {R}}^4 \rightarrow \Lambda ^4 {\mathbb {R}}^4$
be the quadratic form given by the wedge product. It has signature (3,3). Now, let
![]() $B \subset \Lambda ^2 {\mathbb {R}}^4$
be the subspace spanned by
$B \subset \Lambda ^2 {\mathbb {R}}^4$
be the subspace spanned by
![]() $b_1, \ldots , b_k$
. When we restrict W to the subspace B, we will check that it has signature
$b_1, \ldots , b_k$
. When we restrict W to the subspace B, we will check that it has signature
![]() $(k,0)$
. Since
$(k,0)$
. Since
![]() $k \ge 4$
, this gives the desired contradiction.
$k \ge 4$
, this gives the desired contradiction.
It remains to compute the signature of the quadratic form W restricted to B. This is isomorphic to the quadratic form
![]() $(c_1, \ldots , c_k) \mapsto (\sum c_i b_i(x)) \wedge (\sum c_i b_i(x))$
. Expanding out the right-hand side, we get
$(c_1, \ldots , c_k) \mapsto (\sum c_i b_i(x)) \wedge (\sum c_i b_i(x))$
. Expanding out the right-hand side, we get
Since
![]() $b_i \wedge b_j$
is almost 0 for every
$b_i \wedge b_j$
is almost 0 for every
![]() $i \neq j$
and
$i \neq j$
and
![]() $b_i \wedge b_i$
is almost
$b_i \wedge b_i$
is almost
![]() $dx_1 \wedge \cdots \wedge dx_4$
for every i, we see that this form is almost
$dx_1 \wedge \cdots \wedge dx_4$
for every i, we see that this form is almost
In particular, the form has signature
![]() $(k,0)$
.
$(k,0)$
.
2.2.3. Relations in cohomology and low-frequency bounds
Let
![]() $u_i \in H^2(X_k; {\mathbb {R}})$
be a cohomology class dual to the ith copy of
$u_i \in H^2(X_k; {\mathbb {R}})$
be a cohomology class dual to the ith copy of
![]() ${\mathbb {C}} P^1$
in
${\mathbb {C}} P^1$
in
![]() $X_k$
, for
$X_k$
, for
![]() $i = 1, \ldots , k$
. Let
$i = 1, \ldots , k$
. Let
![]() $\alpha _i$
be a 2-form in the cohomology class
$\alpha _i$
be a 2-form in the cohomology class
![]() $u_i$
.
$u_i$
.
We know that
![]() $u_i \smile u_i - u_j \smile u_j = 0$
in
$u_i \smile u_i - u_j \smile u_j = 0$
in
![]() $H^4(X_k; {\mathbb {R}})$
. Therefore, the corresponding differential forms
$H^4(X_k; {\mathbb {R}})$
. Therefore, the corresponding differential forms
![]() $\alpha _i \wedge \alpha _i - \alpha _j \wedge \alpha _j $
are exact. Similarly, for
$\alpha _i \wedge \alpha _i - \alpha _j \wedge \alpha _j $
are exact. Similarly, for
![]() $i \neq j$
,
$i \neq j$
,
![]() $u_i \smile u_j = 0$
, and so the forms
$u_i \smile u_j = 0$
, and so the forms
![]() $\alpha _i \wedge \alpha _j$
are exact. Let
$\alpha _i \wedge \alpha _j$
are exact. Let
![]() $\gamma _r$
be primitives for these forms. We have
$\gamma _r$
be primitives for these forms. We have
![]() $2{k \choose 2}$
exact forms total, and so r goes from
$2{k \choose 2}$
exact forms total, and so r goes from
![]() $1$
to
$1$
to
![]() $2{k \choose 2}$
.
$2{k \choose 2}$
.
Define
![]() $g_r = \phi ^* f^* \gamma _r$
. Since
$g_r = \phi ^* f^* \gamma _r$
. Since
![]() $\gamma _r$
is a 3-form,
$\gamma _r$
is a 3-form,
Depending on r, we have
![]() $dg_r = a_i \wedge a_i - a_j \wedge a_j$
or
$dg_r = a_i \wedge a_i - a_j \wedge a_j$
or
![]() $dg_r = a_i \wedge a_j$
with
$dg_r = a_i \wedge a_j$
with
![]() $i \neq j$
.
$i \neq j$
.
The bound
![]() $\| g_r \|_{L^\infty } \lesssim L^3$
gives extra information about
$\| g_r \|_{L^\infty } \lesssim L^3$
gives extra information about
![]() $a_i \wedge a_j$
. In particular, we get bounds on the low-frequency parts of
$a_i \wedge a_j$
. In particular, we get bounds on the low-frequency parts of
![]() $a_i \wedge a_j$
.
$a_i \wedge a_j$
.
Lemma 2.14. If
![]() $i \neq j$
, then
$i \neq j$
, then
 $$ \begin{align*} \lVert P_{ k} ( a_i \wedge a_j) \rVert_{L^\infty} &\lesssim 2^k L^3 \\ \lVert P_{k} ( a_i \wedge a_i - a_j \wedge a_j) \rVert_{L^\infty} &\lesssim 2^k L^3. \end{align*} $$
$$ \begin{align*} \lVert P_{ k} ( a_i \wedge a_j) \rVert_{L^\infty} &\lesssim 2^k L^3 \\ \lVert P_{k} ( a_i \wedge a_i - a_j \wedge a_j) \rVert_{L^\infty} &\lesssim 2^k L^3. \end{align*} $$
The same bounds hold with
![]() $P_{\le k}$
in place of
$P_{\le k}$
in place of
![]() $P_k$
.
$P_k$
.
Notice that
![]() $\| a_i \|_{L^\infty } \lesssim L^2$
, and so we have
$\| a_i \|_{L^\infty } \lesssim L^2$
, and so we have
![]() $\| a_i \wedge a_j \|_{L^\infty } \lesssim L^4$
. But the low-frequency part of
$\| a_i \wedge a_j \|_{L^\infty } \lesssim L^4$
. But the low-frequency part of
![]() $a_i \wedge a_j$
obeys a much stronger bound.
$a_i \wedge a_j$
obeys a much stronger bound.
Proof. We write
 $$\begin{align*}\left\lvert P_{k} (a_i \wedge a_j) (x) \right\rvert = \left\lvert \int \eta_{k}^\vee (y) a_i \wedge a_j (x-y) dy \right\rvert.\end{align*}$$
$$\begin{align*}\left\lvert P_{k} (a_i \wedge a_j) (x) \right\rvert = \left\lvert \int \eta_{k}^\vee (y) a_i \wedge a_j (x-y) dy \right\rvert.\end{align*}$$
We now substitute in
![]() $a_i \wedge a_j = d g_r$
and then integrate by parts:
$a_i \wedge a_j = d g_r$
and then integrate by parts:
 $$\begin{align*}\left\lvert \int \eta_{k}^\vee (y) d g_r (x-y) dy \right\rvert = \left\lvert \int d \eta_{k}^\vee (y) g_r(x-y) dy \right\rvert.\end{align*}$$
$$\begin{align*}\left\lvert \int \eta_{k}^\vee (y) d g_r (x-y) dy \right\rvert = \left\lvert \int d \eta_{k}^\vee (y) g_r(x-y) dy \right\rvert.\end{align*}$$
Since
![]() $\| g_r \|_{L^\infty } \lesssim L^3$
, and
$\| g_r \|_{L^\infty } \lesssim L^3$
, and
![]() $\int |d \eta _k^\vee | \lesssim 2^k$
by Lemma 2.7, our expression is bounded by
$\int |d \eta _k^\vee | \lesssim 2^k$
by Lemma 2.7, our expression is bounded by
The same proof applies to
![]() $ \| P_{k} ( a_i \wedge a_i - a_j \wedge a_j) \|_{L^\infty }$
and with
$ \| P_{k} ( a_i \wedge a_i - a_j \wedge a_j) \|_{L^\infty }$
and with
![]() $P_{\le k}$
in place of
$P_{\le k}$
in place of
![]() $P_k$
.
$P_k$
.
2.2.4. Toy case: all forms are low frequency
To illustrate how the tools we have developed work together, we now do a toy case of our main theorem: the case where all forms have low frequency.
Suppose that the forms
![]() $a_i$
are all low-frequency:
$a_i$
are all low-frequency:
![]() $P_{\le 1} a_i = a_i$
for every i. It follows that the wedge products are also fairly low frequency:
$P_{\le 1} a_i = a_i$
for every i. It follows that the wedge products are also fairly low frequency:
![]() $P_{\le 2} (a_i \wedge a_j) = a_i \wedge a_j$
for every
$P_{\le 2} (a_i \wedge a_j) = a_i \wedge a_j$
for every
![]() $i, j$
.
$i, j$
.
We can now bound
![]() $\int \psi _U a_1 \wedge a_1$
using the tools we have developed. First, Lemma 2.13 tells us that
$\int \psi _U a_1 \wedge a_1$
using the tools we have developed. First, Lemma 2.13 tells us that
 $$\begin{align*}\int \psi_U a_1 \wedge a_1 \le \int \psi_U |a_1 \wedge a_1| \le \sum_{i \neq j} \int \psi_U | a_i \wedge a_j| + \int \psi_U |a_i \wedge a_i - a_j \wedge a_j|.\end{align*}$$
$$\begin{align*}\int \psi_U a_1 \wedge a_1 \le \int \psi_U |a_1 \wedge a_1| \le \sum_{i \neq j} \int \psi_U | a_i \wedge a_j| + \int \psi_U |a_i \wedge a_i - a_j \wedge a_j|.\end{align*}$$
We are discussing the low-frequency special case, where
![]() $|a_i \wedge a_j| = | P_{\le 2} (a_i \wedge a_j) |$
. By Lemma 2.14, we have
$|a_i \wedge a_j| = | P_{\le 2} (a_i \wedge a_j) |$
. By Lemma 2.14, we have
Similarly,
Therefore,
![]() $\int \psi _U a_1 \wedge a_1 \lesssim L^3$
, and so finally, we have
$\int \psi _U a_1 \wedge a_1 \lesssim L^3$
, and so finally, we have
![]() $\deg f \lesssim L^3$
.
$\deg f \lesssim L^3$
.
If we have a weaker low-frequency assumption that
![]() $P_{\le \bar \ell } a_i = a_i$
for every i, then the same argument shows that
$P_{\le \bar \ell } a_i = a_i$
for every i, then the same argument shows that
![]() $\deg f \lesssim 2^{\bar \ell } L^3$
. As long as the frequency range
$\deg f \lesssim 2^{\bar \ell } L^3$
. As long as the frequency range
![]() $2^{\bar \ell }$
is significantly less than L, then we get a strong estimate. For instance, if
$2^{\bar \ell }$
is significantly less than L, then we get a strong estimate. For instance, if
![]() $2^{\bar \ell } = L^{.9}$
, then
$2^{\bar \ell } = L^{.9}$
, then
![]() $\deg f \le L^{3.9}$
.
$\deg f \le L^{3.9}$
.
2.2.5. Bounding high-frequency contributions
We use the Littlewood–Paley decomposition to write
 $$\begin{align*}\int_{{\mathbb{R}}^d} \psi_U a_i \wedge a_i = \int_{{\mathbb{R}}^d} \psi_U \sum_{k \in {\mathbb{Z}}} P_k a_i \wedge \sum_{\ell \in {\mathbb{Z}}} P_\ell a_i.\end{align*}$$
$$\begin{align*}\int_{{\mathbb{R}}^d} \psi_U a_i \wedge a_i = \int_{{\mathbb{R}}^d} \psi_U \sum_{k \in {\mathbb{Z}}} P_k a_i \wedge \sum_{\ell \in {\mathbb{Z}}} P_\ell a_i.\end{align*}$$
We can bound each term on the right-hand side by using our primitive estimate, Lemma 2.10, and integration by parts:
 $$ \begin{align*} \left\lvert\int_{{\mathbb{R}}^d} \psi_U P_k a_i \wedge P_\ell a_i \right\rvert &= \left\lvert\int_{{\mathbb{R}}^d} \psi_U P_k a_i \wedge d( \operatorname{\mathrm{Prim}}(P_\ell a_i) )\right\rvert \\ &= \left\lvert\int d \psi_U \wedge P_k a_i \wedge \operatorname{\mathrm{Prim}}( P_\ell a_i)\right\rvert \\ &\le \int \lvert d\psi_U \rvert \lvert P_k a_i \rvert \lvert\operatorname{\mathrm{Prim}} (P_\ell a_i)\rvert. \end{align*} $$
$$ \begin{align*} \left\lvert\int_{{\mathbb{R}}^d} \psi_U P_k a_i \wedge P_\ell a_i \right\rvert &= \left\lvert\int_{{\mathbb{R}}^d} \psi_U P_k a_i \wedge d( \operatorname{\mathrm{Prim}}(P_\ell a_i) )\right\rvert \\ &= \left\lvert\int d \psi_U \wedge P_k a_i \wedge \operatorname{\mathrm{Prim}}( P_\ell a_i)\right\rvert \\ &\le \int \lvert d\psi_U \rvert \lvert P_k a_i \rvert \lvert\operatorname{\mathrm{Prim}} (P_\ell a_i)\rvert. \end{align*} $$
Now
![]() $d \psi _U$
is a fixed
$d \psi _U$
is a fixed
![]() $C^\infty _{comp}$
form, and we have
$C^\infty _{comp}$
form, and we have
![]() $|P_k a_i| \lesssim L^2$
and
$|P_k a_i| \lesssim L^2$
and
![]() $| \operatorname {\mathrm {Prim}} P_\ell (a_i)| \lesssim 2^{-\ell } L^2$
. All together, we get the bound
$| \operatorname {\mathrm {Prim}} P_\ell (a_i)| \lesssim 2^{-\ell } L^2$
. All together, we get the bound
 $$ \begin{align} \left\lvert\int_{{\mathbb{R}}^d} \psi_U P_k a_i \wedge P_\ell a_i\right\rvert \lesssim 2^{-\ell} L^4. \end{align} $$
$$ \begin{align} \left\lvert\int_{{\mathbb{R}}^d} \psi_U P_k a_i \wedge P_\ell a_i\right\rvert \lesssim 2^{-\ell} L^4. \end{align} $$
This shows that the high-frequency parts of
![]() $a_i$
contribute little to the integral for the degree. By summing this geometric series of error terms, we see the following:
$a_i$
contribute little to the integral for the degree. By summing this geometric series of error terms, we see the following:
Lemma 2.15. For any frequency cutoff
![]() $\bar \ell $
,
$\bar \ell $
,
 $$\begin{align*}\left\lvert\int_{{\mathbb{R}}^d} \psi_U a_i \wedge a_i\right\rvert \lesssim \left\lvert\int \psi_U P_{\le \bar \ell} a_i \wedge P_{\le \bar \ell} a_i \right\rvert + O(2^{-\bar \ell} L^4).\end{align*}$$
$$\begin{align*}\left\lvert\int_{{\mathbb{R}}^d} \psi_U a_i \wedge a_i\right\rvert \lesssim \left\lvert\int \psi_U P_{\le \bar \ell} a_i \wedge P_{\le \bar \ell} a_i \right\rvert + O(2^{-\bar \ell} L^4).\end{align*}$$
In particular, Lemma 2.15 allows us to resolve another toy case of our problem. If every form
![]() $a_i$
is purely high-frequency, in the sense that
$a_i$
is purely high-frequency, in the sense that
![]() $P_{\le \bar \ell } a_i = 0$
, then Lemma 2.15 gives the bound
$P_{\le \bar \ell } a_i = 0$
, then Lemma 2.15 gives the bound
![]() $\deg f \lesssim 2^{- \bar \ell } L^4$
. For instance, if
$\deg f \lesssim 2^{- \bar \ell } L^4$
. For instance, if
![]() $2^{\bar \ell }$
is at least
$2^{\bar \ell }$
is at least
![]() $L^{1/10}$
, then we get a strong estimate:
$L^{1/10}$
, then we get a strong estimate:
![]() $\deg f \lesssim L^{3.9}$
.
$\deg f \lesssim L^{3.9}$
.
We now have strong bounds in two toy cases: the pure low-frequency case and the pure high-frequency case. We will prove bounds in the general case by combining these tools.
However, combining the tools is not completely straightforward. Based on the discussion above, it initially sounds like we might get a bound of the form
![]() $\deg f \lesssim L^{4 - \beta }$
for some
$\deg f \lesssim L^{4 - \beta }$
for some
![]() $\beta> 0$
. But there are maps f with Lipschitz constant L and degree at least
$\beta> 0$
. But there are maps f with Lipschitz constant L and degree at least
![]() $L^4 (\log L)^{-C}$
for some constant C. The forms coming from these maps crucially have signifinant contributions at all frequency levels.
$L^4 (\log L)^{-C}$
for some constant C. The forms coming from these maps crucially have signifinant contributions at all frequency levels.
2.2.6. Bounds in the general case
We begin by applying Lemma 2.15. For any frequency cutoff
![]() $\bar \ell $
, the lemma tells us that
$\bar \ell $
, the lemma tells us that
 $$ \begin{align} \left\lvert\int_{{\mathbb{R}}^d} \psi_U a_1 \wedge a_1\right\rvert \lesssim \int \psi_U \left\lvert P_{\le \bar \ell} a_1 \wedge P_{\le \bar \ell} a_1\right\rvert + 2^{-\bar \ell} L^4. \end{align} $$
$$ \begin{align} \left\lvert\int_{{\mathbb{R}}^d} \psi_U a_1 \wedge a_1\right\rvert \lesssim \int \psi_U \left\lvert P_{\le \bar \ell} a_1 \wedge P_{\le \bar \ell} a_1\right\rvert + 2^{-\bar \ell} L^4. \end{align} $$
We will choose
![]() $\bar \ell $
later, in the range
$\bar \ell $
later, in the range
![]() $2^{\bar \ell } \ge L^{1/10}$
. This guarantees that the last term is
$2^{\bar \ell } \ge L^{1/10}$
. This guarantees that the last term is
![]() $\lesssim L^{3.9}$
, which is much smaller than our goal.
$\lesssim L^{3.9}$
, which is much smaller than our goal.
To control the first term, we apply Lemma 2.13 with
![]() $b_i = P_{\le \bar \ell } a_i(x)$
at each point x. Lemma 2.13 tells us that at each point,
$b_i = P_{\le \bar \ell } a_i(x)$
at each point x. Lemma 2.13 tells us that at each point,
Plugging into the integral, we get
 $$\begin{align*}\int \psi_U | P_{\le \bar \ell} a_1 \wedge P_{\le \bar \ell} a_1 | \lesssim \sum_{i \neq j} \underbrace{\int \psi_U |P_{\le \bar \ell} a_i \wedge P_{\le \bar \ell} a_j|}_{I} + \underbrace{\int \psi_U |P_{\le \bar \ell} a_i \wedge P_{\le \bar \ell} a_i - P_{\le \bar \ell} a_j \wedge P_{\le \bar \ell} a_j|}_{II}.\end{align*}$$
$$\begin{align*}\int \psi_U | P_{\le \bar \ell} a_1 \wedge P_{\le \bar \ell} a_1 | \lesssim \sum_{i \neq j} \underbrace{\int \psi_U |P_{\le \bar \ell} a_i \wedge P_{\le \bar \ell} a_j|}_{I} + \underbrace{\int \psi_U |P_{\le \bar \ell} a_i \wedge P_{\le \bar \ell} a_i - P_{\le \bar \ell} a_j \wedge P_{\le \bar \ell} a_j|}_{II}.\end{align*}$$
The two terms are similar to each other. We focus on the terms of type I first. The same arguments apply to type II.
The form
![]() $P_{\le \bar \ell } a_i \wedge P_{\le \bar \ell } a_j$
looks a little bit like
$P_{\le \bar \ell } a_i \wedge P_{\le \bar \ell } a_j$
looks a little bit like
![]() $P_{\le \bar \ell } (a_i \wedge a_j)$
, which has strong bounds coming from Lemma 2.14. However, these forms are not equal to each other. We will examine the situation more carefully and find that
$P_{\le \bar \ell } (a_i \wedge a_j)$
, which has strong bounds coming from Lemma 2.14. However, these forms are not equal to each other. We will examine the situation more carefully and find that
The additional terms are crucial to our story – they actually make the largest contribution in our bound for the degree of f.
To work out the details of (11), we begin by doing the Littlewood–Paley expansion of
![]() $a_i$
and
$a_i$
and
![]() $a_j$
:
$a_j$
:
Grouping the terms according to whether
![]() $k_1$
or
$k_1$
or
![]() $k_2$
is bigger, we get
$k_2$
is bigger, we get
 $$ \begin{align} a_i \wedge a_j = P_{\le \bar \ell} a_i \wedge P_{\le \bar \ell} a_j + \sum_{k_1 = \bar \ell+1}^\infty P_{k_1} a_i \wedge P_{\le k_1} a_j + \sum_{k_2 = \bar \ell+1}^\infty P_{< k_2} a_i \wedge P_{k_2} a_j. \end{align} $$
$$ \begin{align} a_i \wedge a_j = P_{\le \bar \ell} a_i \wedge P_{\le \bar \ell} a_j + \sum_{k_1 = \bar \ell+1}^\infty P_{k_1} a_i \wedge P_{\le k_1} a_j + \sum_{k_2 = \bar \ell+1}^\infty P_{< k_2} a_i \wedge P_{k_2} a_j. \end{align} $$
Note that the Fourier transform of
![]() $P_{\le \bar \ell } a_i \wedge P_{\le \bar \ell } a_j$
is supported in
$P_{\le \bar \ell } a_i \wedge P_{\le \bar \ell } a_j$
is supported in
![]() $|\omega | \le 4 \cdot 2^{\bar \ell }$
(cf. Lemma 2.12). Therefore,
$|\omega | \le 4 \cdot 2^{\bar \ell }$
(cf. Lemma 2.12). Therefore,
We apply
![]() $P_{\le \bar \ell + 3}$
to both sides of (12) to get
$P_{\le \bar \ell + 3}$
to both sides of (12) to get
 $$ \begin{align} \begin{aligned} P_{\le \bar \ell +3} ( a_i \wedge a_j ) &= P_{\le \bar \ell} a_i \wedge P_{\le \bar \ell} a_j \\ & \qquad {}+ \sum_{k_1 = \bar \ell+1}^\infty P_{\le \bar \ell +3} (P_{k_1} a_i \wedge P_{\le k_1} a_j) + \sum_{k_2 = \bar \ell+1}^\infty P_{\le \bar \ell + 3} (P_{< k_2} a_i \wedge P_{k_2} a_j). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} P_{\le \bar \ell +3} ( a_i \wedge a_j ) &= P_{\le \bar \ell} a_i \wedge P_{\le \bar \ell} a_j \\ & \qquad {}+ \sum_{k_1 = \bar \ell+1}^\infty P_{\le \bar \ell +3} (P_{k_1} a_i \wedge P_{\le k_1} a_j) + \sum_{k_2 = \bar \ell+1}^\infty P_{\le \bar \ell + 3} (P_{< k_2} a_i \wedge P_{k_2} a_j). \end{aligned} \end{align} $$
This gives us our fleshed out version of (11):
 $$ \begin{align} \begin{aligned} P_{\le \bar \ell} a_i \wedge P_{\le \bar \ell} a_j &= \underbrace{P_{\le \bar \ell + 3} (a_i \wedge a_j)}_{\textrm{Term 1}} \\ & \qquad {} - \underbrace{ \sum_{k_1 = \bar \ell+1}^\infty P_{\le \bar \ell +3} (P_{k_1} a_i \wedge P_{\le k_1} a_j) }_{\textrm{Term 2.1}}- \underbrace{\sum_{k_2 = \bar \ell+1}^\infty P_{\le \bar \ell + 3} (P_{< k_2} a_i \wedge P_{k_2} a_j)}_{\textrm{Term 2.2}}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} P_{\le \bar \ell} a_i \wedge P_{\le \bar \ell} a_j &= \underbrace{P_{\le \bar \ell + 3} (a_i \wedge a_j)}_{\textrm{Term 1}} \\ & \qquad {} - \underbrace{ \sum_{k_1 = \bar \ell+1}^\infty P_{\le \bar \ell +3} (P_{k_1} a_i \wedge P_{\le k_1} a_j) }_{\textrm{Term 2.1}}- \underbrace{\sum_{k_2 = \bar \ell+1}^\infty P_{\le \bar \ell + 3} (P_{< k_2} a_i \wedge P_{k_2} a_j)}_{\textrm{Term 2.2}}. \end{aligned} \end{align} $$
We want to bound
![]() $\int \psi _U | P_{\le \bar \ell } a_i \wedge P_{\le \bar \ell } a_j |$
. We plug in (14), and then we have to bound the contributions of term 1, term 2.1 and term 2.2. The contribution of Term 1 is bounded using Lemma 2.14:
$\int \psi _U | P_{\le \bar \ell } a_i \wedge P_{\le \bar \ell } a_j |$
. We plug in (14), and then we have to bound the contributions of term 1, term 2.1 and term 2.2. The contribution of Term 1 is bounded using Lemma 2.14:
We will choose
![]() $\bar \ell $
in the range
$\bar \ell $
in the range
![]() $2^{\bar \ell } \le L^{9/10}$
, and so the right-hand side is
$2^{\bar \ell } \le L^{9/10}$
, and so the right-hand side is
![]() $\lesssim L^{3.9}$
, much smaller than our goal.
$\lesssim L^{3.9}$
, much smaller than our goal.
Terms 2.1 and 2.2 are similar, so we just explain Term 2.1. The contribution of Term 2.1 is at most
 $$ \begin{align} \sum_{k_1 = \bar \ell+1}^\infty \int \psi_U \lvert P_{\le \bar \ell +3} (P_{k_1} a_i \wedge P_{\le k_1} a_j) \rvert \le \sum_{k_1 = \bar \ell + 1}^\infty \lVert P_{\le \bar \ell +3} (P_{k_1} a_i \wedge P_{\le k_1} a_j) \rVert_{L^1}. \end{align} $$
$$ \begin{align} \sum_{k_1 = \bar \ell+1}^\infty \int \psi_U \lvert P_{\le \bar \ell +3} (P_{k_1} a_i \wedge P_{\le k_1} a_j) \rvert \le \sum_{k_1 = \bar \ell + 1}^\infty \lVert P_{\le \bar \ell +3} (P_{k_1} a_i \wedge P_{\le k_1} a_j) \rVert_{L^1}. \end{align} $$
We start with a direct bound for this
![]() $L^1$
norm. Lemma 2.8 gives
$L^1$
norm. Lemma 2.8 gives
Now, Lemma 2.8 again gives
![]() $\| P_{\le k_1} a_j \|_{L^\infty } \lesssim \| a_j \|_{L^\infty } \lesssim L^2$
. All together this gives
$\| P_{\le k_1} a_j \|_{L^\infty } \lesssim \| a_j \|_{L^\infty } \lesssim L^2$
. All together this gives
If
![]() $k_1 = \bar \ell $
, this is the best bound we know. But if
$k_1 = \bar \ell $
, this is the best bound we know. But if
![]() $k_1$
is much larger than
$k_1$
is much larger than
![]() $\bar \ell $
, then we can get a better estimate by using the primitive of
$\bar \ell $
, then we can get a better estimate by using the primitive of
![]() $P_{k_1} a_i$
and integrating by parts.
$P_{k_1} a_i$
and integrating by parts.
Writing out what this means and integrating by parts, we get the following:
 $$ \begin{align*} \left\lvert P_{\le \bar \ell +3} (P_{k_1} a_i \wedge P_{\le k_1} a_j) (x)\right\rvert &= \left\lvert \int \eta_{\le \bar \ell + 3}^\vee(y) ( d \operatorname{\mathrm{Prim}} ( P_{k_1} a_i))(x-y) \wedge P_{\le k_1} a_j (x-y) dy \right\rvert \\ &= \left\lvert \int d \eta_{\le \bar \ell + 3}^\vee(y) ( \operatorname{\mathrm{Prim}} ( P_{k_1} a_i))(x-y) \wedge P_{\le k_1} a_j (x-y) dy \right\rvert. \end{align*} $$
$$ \begin{align*} \left\lvert P_{\le \bar \ell +3} (P_{k_1} a_i \wedge P_{\le k_1} a_j) (x)\right\rvert &= \left\lvert \int \eta_{\le \bar \ell + 3}^\vee(y) ( d \operatorname{\mathrm{Prim}} ( P_{k_1} a_i))(x-y) \wedge P_{\le k_1} a_j (x-y) dy \right\rvert \\ &= \left\lvert \int d \eta_{\le \bar \ell + 3}^\vee(y) ( \operatorname{\mathrm{Prim}} ( P_{k_1} a_i))(x-y) \wedge P_{\le k_1} a_j (x-y) dy \right\rvert. \end{align*} $$
Therefore, we have a pointwise bound
Taking
![]() $L^1$
norms, we get
$L^1$
norms, we get
Now Lemma 2.7 gives
![]() $ \| d \eta _{\le \bar \ell + 3} \|_{L^1} \lesssim 2^{\bar \ell }$
and Lemma 2.10 gives
$ \| d \eta _{\le \bar \ell + 3} \|_{L^1} \lesssim 2^{\bar \ell }$
and Lemma 2.10 gives
We also know by Lemma 2.8 that
![]() $\lVert P_{k_1} a_j \rVert _{L^\infty } \lesssim \lVert a_j \rVert _{L^\infty } \lesssim L^2$
. Putting these bounds together, we see that
$\lVert P_{k_1} a_j \rVert _{L^\infty } \lesssim \lVert a_j \rVert _{L^\infty } \lesssim L^2$
. Putting these bounds together, we see that
Returning to the contribution of Term 2.1 in (16), we have the bound
 $$ \begin{align} \sum_{k_1 = \bar \ell+1}^\infty \int \psi_U \lvert P_{\le \bar \ell +3} (P_{k_1} a_i \wedge P_{\le k_1} a_j) \rvert \le \sum_{k_1 = \bar \ell + 1}^\infty 2^{\bar \ell - k_1} L^2 \lVert P_{k_1} a_i \rVert_{L^1}. \end{align} $$
$$ \begin{align} \sum_{k_1 = \bar \ell+1}^\infty \int \psi_U \lvert P_{\le \bar \ell +3} (P_{k_1} a_i \wedge P_{\le k_1} a_j) \rvert \le \sum_{k_1 = \bar \ell + 1}^\infty 2^{\bar \ell - k_1} L^2 \lVert P_{k_1} a_i \rVert_{L^1}. \end{align} $$
Putting together our bounds for all the different terms, we get the following estimate for any choice of scale
![]() $\bar \ell $
:
$\bar \ell $
:
 $$ \begin{align} \left\lvert\int_{{\mathbb{R}}^d} \psi_U a_1 \wedge a_1\right\rvert \lesssim 2^{- \bar \ell} L^4 + 2^{\bar \ell} L^3 + \sum_{k_1 = \bar \ell + 1}^\infty 2^{\bar \ell - k_1} L^2 \| P_{k_1} a_i \|_{L^1}. \end{align} $$
$$ \begin{align} \left\lvert\int_{{\mathbb{R}}^d} \psi_U a_1 \wedge a_1\right\rvert \lesssim 2^{- \bar \ell} L^4 + 2^{\bar \ell} L^3 + \sum_{k_1 = \bar \ell + 1}^\infty 2^{\bar \ell - k_1} L^2 \| P_{k_1} a_i \|_{L^1}. \end{align} $$
(On the right-hand side, the first term comes from high-frequency pieces, the next term comes from Term 1 and is bounded using the low-frequency method, and the final term comes from Terms 2.1 and 2.2. The fact that
![]() $k \ge 4$
is used in the bound for Term 1.)
$k \ge 4$
is used in the bound for Term 1.)
Let us pause to digest this bound. To begin, note that the first two terms,
![]() $2^{- \bar \ell } L^4 + 2^{\bar \ell } L^3$
, can be made much smaller than
$2^{- \bar \ell } L^4 + 2^{\bar \ell } L^3$
, can be made much smaller than
![]() $L^4$
. For instance, we can choose
$L^4$
. For instance, we can choose
![]() $\bar \ell $
so that
$\bar \ell $
so that
![]() $2^{\bar \ell } = L^{1/2}$
, and then these first two terms give
$2^{\bar \ell } = L^{1/2}$
, and then these first two terms give
![]() $L^{3.5}$
. The final term is often the most important.
$L^{3.5}$
. The final term is often the most important.
Now let us try to get some intuition about the last term. Because of the exponentially decaying factor
![]() $2^{\bar \ell - k_1}$
, the final term comes mainly from
$2^{\bar \ell - k_1}$
, the final term comes mainly from
![]() $k_1$
close to
$k_1$
close to
![]() $\bar \ell $
. If
$\bar \ell $
. If
![]() $\| P_{k_1} a_i \|_{L^1}$
is very small for a range of
$\| P_{k_1} a_i \|_{L^1}$
is very small for a range of
![]() $k_1$
, then it is strategic for us to choose
$k_1$
, then it is strategic for us to choose
![]() $\bar \ell $
at the start of this range. This scenario could lead to a bound which is much stronger than
$\bar \ell $
at the start of this range. This scenario could lead to a bound which is much stronger than
![]() $L^4 (\log L)^{-1/2}$
– see Proposition 2.16 below. However, it may happen that
$L^4 (\log L)^{-1/2}$
– see Proposition 2.16 below. However, it may happen that
![]() $\| P_{k_1} a_i \|_{L^1}$
are all roughly equal. This is actually the worst scenario from the point of view of Theorem 2.1. In this case, we can improve on the bound
$\| P_{k_1} a_i \|_{L^1}$
are all roughly equal. This is actually the worst scenario from the point of view of Theorem 2.1. In this case, we can improve on the bound
![]() $\| P_{k_1} a_i \|_{L^1} \lesssim \| a_i \|_{L^1} = L^2$
by using the orthogonality of the
$\| P_{k_1} a_i \|_{L^1} \lesssim \| a_i \|_{L^1} = L^2$
by using the orthogonality of the
![]() $P_{k_1} a_i$
. By Cauchy–Schwarz,
$P_{k_1} a_i$
. By Cauchy–Schwarz,
![]() $\| P_{k_1} a_i \|_{L^1} \lesssim \|P_{k_1} a_i \|_{L^2}$
, and
$\| P_{k_1} a_i \|_{L^1} \lesssim \|P_{k_1} a_i \|_{L^2}$
, and
![]() $\sum _{k_1} \| P_{k_1} a_i \|_{L^2}^2 \lesssim \| a_i \|_{L^2}^2 \lesssim L^4$
. If
$\sum _{k_1} \| P_{k_1} a_i \|_{L^2}^2 \lesssim \| a_i \|_{L^2}^2 \lesssim L^4$
. If
![]() $\|P_{k_1} a_i \|_{L^1}$
are all equal, then we can compute
$\|P_{k_1} a_i \|_{L^1}$
are all equal, then we can compute
![]() $\| P_{k_1} a_i \|_{L^1} \lesssim L^2 (\log L)^{-1/2}$
. Plugging this into the last term, and summing the geometric series, the last term contributes
$\| P_{k_1} a_i \|_{L^1} \lesssim L^2 (\log L)^{-1/2}$
. Plugging this into the last term, and summing the geometric series, the last term contributes
![]() $L^4 (\log L)^{-1/2}$
.
$L^4 (\log L)^{-1/2}$
.
We now finish the formal proof of Theorem 2.1. We apply our estimates for those
![]() $\bar \ell $
satisfying
$\bar \ell $
satisfying
![]() $L^{1/10} \le 2^{\bar \ell } \le L^{9/10}$
. The number of different
$L^{1/10} \le 2^{\bar \ell } \le L^{9/10}$
. The number of different
![]() $\bar \ell $
in this range is
$\bar \ell $
in this range is
![]() $\sim \log L$
. For each
$\sim \log L$
. For each
![]() $\bar \ell $
in this range, (20) gives
$\bar \ell $
in this range, (20) gives
 $$\begin{align*}\left\lvert\int_{{\mathbb{R}}^d} \psi_U a_1 \wedge a_1\right\rvert \lesssim L^{3.9} + \sum_{k_1 = \bar \ell + 1}^\infty 2^{\bar \ell - k_1} L^2 \| P_{k_1} a_i \|_{L^1}.\end{align*}$$
$$\begin{align*}\left\lvert\int_{{\mathbb{R}}^d} \psi_U a_1 \wedge a_1\right\rvert \lesssim L^{3.9} + \sum_{k_1 = \bar \ell + 1}^\infty 2^{\bar \ell - k_1} L^2 \| P_{k_1} a_i \|_{L^1}.\end{align*}$$
Summing the formula over all the
![]() $\bar \ell $
in this range, we get
$\bar \ell $
in this range, we get
 $$ \begin{align} \log L \left\lvert\int_{{\mathbb{R}}^d} \psi_U a_1 \wedge a_1\right\rvert \lesssim L^{3.91} + \sum_{L^{1/10} \le 2^{\bar \ell} \le L^{9/10}} \sum_{k_1 = \bar \ell + 1}^\infty 2^{\bar \ell - k_1} L^2 \| P_{k_1} a_i \|_{L^1}. \end{align} $$
$$ \begin{align} \log L \left\lvert\int_{{\mathbb{R}}^d} \psi_U a_1 \wedge a_1\right\rvert \lesssim L^{3.91} + \sum_{L^{1/10} \le 2^{\bar \ell} \le L^{9/10}} \sum_{k_1 = \bar \ell + 1}^\infty 2^{\bar \ell - k_1} L^2 \| P_{k_1} a_i \|_{L^1}. \end{align} $$
In this sum, the terms with
![]() $2^{k_1}> L$
can be bounded by
$2^{k_1}> L$
can be bounded by
![]() $L^{3.9}$
and absorbed into the first term. The remaining terms are
$L^{3.9}$
and absorbed into the first term. The remaining terms are
 $$\begin{align*}\sum_{L^{1/10} \le 2^{k_1} \le L} \sum_{L^{1/10} \le 2^{\bar \ell} \le 2^{k_1}-1} 2^{\bar \ell - k_1} L^2 \| P_{k_1} a_i \|_{L^1} \lesssim \sum_{L^{1/10} \le 2^{k_1} \le L} L^2 \|P_{k_1} a_i \|_{L^1}.\end{align*}$$
$$\begin{align*}\sum_{L^{1/10} \le 2^{k_1} \le L} \sum_{L^{1/10} \le 2^{\bar \ell} \le 2^{k_1}-1} 2^{\bar \ell - k_1} L^2 \| P_{k_1} a_i \|_{L^1} \lesssim \sum_{L^{1/10} \le 2^{k_1} \le L} L^2 \|P_{k_1} a_i \|_{L^1}.\end{align*}$$
Next, we want to use orthogonality from Lemma 2.11:
![]() $\| a_i \|_{L^2}^2 \sim \sum _k \| P_k a_i \|_{L^2}^2$
. To get these
$\| a_i \|_{L^2}^2 \sim \sum _k \| P_k a_i \|_{L^2}^2$
. To get these
![]() $L^2$
norms into play, we apply Cauchy–Schwarz. Since the
$L^2$
norms into play, we apply Cauchy–Schwarz. Since the
![]() $a_i$
are supported in a fixed ball, and since the
$a_i$
are supported in a fixed ball, and since the
![]() $P_{k_1} a_i$
are rapidly decaying away from that ball, we have
$P_{k_1} a_i$
are rapidly decaying away from that ball, we have
![]() $\| P_{k_1} a_i \|_{L^1} \lesssim \| P_{k_1} a_i \|_{L^2}$
. Since there are
$\| P_{k_1} a_i \|_{L^1} \lesssim \| P_{k_1} a_i \|_{L^2}$
. Since there are
![]() $\sim \log L$
values of
$\sim \log L$
values of
![]() $k_1$
in the range
$k_1$
in the range
![]() $L^{1/10} \le 2^{k_1} \le L$
, we have
$L^{1/10} \le 2^{k_1} \le L$
, we have
 $$ \begin{align*} \sum_{L^{1/10} \le 2^{k_1} \le L} L^2 \|P_{k_1} a_i \|_{L^1} &\lesssim (\log L)^{1/2} L^2 \left( \sum_{L^{1/10} \le 2^{k_1} \le L} \|P_{k_1} a_i \|_{L^2}^2 \right)^{1/2} \\ &\lesssim (\log L)^{1/2} L^2 \| a_i \|_{L^2} \lesssim (\log L)^{1/2} L^4. \end{align*} $$
$$ \begin{align*} \sum_{L^{1/10} \le 2^{k_1} \le L} L^2 \|P_{k_1} a_i \|_{L^1} &\lesssim (\log L)^{1/2} L^2 \left( \sum_{L^{1/10} \le 2^{k_1} \le L} \|P_{k_1} a_i \|_{L^2}^2 \right)^{1/2} \\ &\lesssim (\log L)^{1/2} L^2 \| a_i \|_{L^2} \lesssim (\log L)^{1/2} L^4. \end{align*} $$
Plugging this back into (21), we see that
 $$\begin{align*}\log L \left\lvert\int_{{\mathbb{R}}^d} \psi_U a_1 \wedge a_1\right\rvert \lesssim L^{3.91} + (\log L)^{1/2} L^4 \end{align*}$$
$$\begin{align*}\log L \left\lvert\int_{{\mathbb{R}}^d} \psi_U a_1 \wedge a_1\right\rvert \lesssim L^{3.91} + (\log L)^{1/2} L^4 \end{align*}$$
and so
 $$\begin{align*}\left\lvert\int_{{\mathbb{R}}^d} \psi_U a_1 \wedge a_1\right\rvert \lesssim (\log L)^{-1/2} L^4.\end{align*}$$
$$\begin{align*}\left\lvert\int_{{\mathbb{R}}^d} \psi_U a_1 \wedge a_1\right\rvert \lesssim (\log L)^{-1/2} L^4.\end{align*}$$
But the degree of f is given by (7):
 $$\begin{align*}\deg (f) = \sum_U \int \psi_U a_1 \wedge a_1 \lesssim (\log L)^{-1/2} L^4.\end{align*}$$
$$\begin{align*}\deg (f) = \sum_U \int \psi_U a_1 \wedge a_1 \lesssim (\log L)^{-1/2} L^4.\end{align*}$$
This finishes the proof of Theorem 2.1.
The bound (20) contains somewhat more information than Theorem 2.1. It also tells us that if the degree of f is close to
![]() $L^4 (\log L)^{-1/2}$
, then the forms
$L^4 (\log L)^{-1/2}$
, then the forms
![]() $a_i$
must have contributions from essentially all frequency ranges. We make this precise in the following proposition.
$a_i$
must have contributions from essentially all frequency ranges. We make this precise in the following proposition.
Proposition 2.16. Suppose that
![]() $k \ge 4$
. Suppose
$k \ge 4$
. Suppose
![]() $f: X_k \rightarrow X_k$
is L-Lipschitz. Let the forms
$f: X_k \rightarrow X_k$
is L-Lipschitz. Let the forms
![]() $a_i$
be as in (6), and fix
$a_i$
be as in (6), and fix
![]() $0 < \beta _1 < \beta _2 < 1$
.
$0 < \beta _1 < \beta _2 < 1$
.
Suppose that for every chart and every i, and every
![]() $k_1$
in the range
$k_1$
in the range
![]() $L^{\beta _1} < 2^{k_1} < L^{\beta _2}$
,
$L^{\beta _1} < 2^{k_1} < L^{\beta _2}$
,
Then the degree of f is bounded by
![]() $C(g) L^{4 - \eta }$
, where
$C(g) L^{4 - \eta }$
, where
Proof. Recall that
![]() $\| P_{k_1} a_i \|_{L^1} \lesssim \| a_i \|_{L^1} \lesssim L^2$
. The hypothesis (22) says that we have a stronger bound on
$\| P_{k_1} a_i \|_{L^1} \lesssim \| a_i \|_{L^1} \lesssim L^2$
. The hypothesis (22) says that we have a stronger bound on
![]() $\| P_{k_1} a_i \|_{L^1}$
when
$\| P_{k_1} a_i \|_{L^1}$
when
![]() $2^{k_1}$
lies in the range
$2^{k_1}$
lies in the range
![]() $[L^{\beta _1}, L^{\beta _2}]$
.
$[L^{\beta _1}, L^{\beta _2}]$
.
To prove the bound, we plug all our hypotheses into the bound (20). That shows that the degree is bounded by
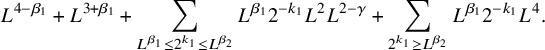 $$\begin{align*}L^{4 - \beta_1} + L^{3 + \beta_1} + \sum_{L^{\beta_1} \le 2^{k_1} \le L^{\beta_2}} L^{\beta_1} 2^{-k_1} L^2 L^{2 - \gamma} + \sum_{2^{k_1} \ge L^{\beta_2}} L^{\beta_1} 2^{-k_1} L^4.\end{align*}$$
$$\begin{align*}L^{4 - \beta_1} + L^{3 + \beta_1} + \sum_{L^{\beta_1} \le 2^{k_1} \le L^{\beta_2}} L^{\beta_1} 2^{-k_1} L^2 L^{2 - \gamma} + \sum_{2^{k_1} \ge L^{\beta_2}} L^{\beta_1} 2^{-k_1} L^4.\end{align*}$$
Carrying out the geometric series and grouping terms finishes the proof.
2.3. General estimate
In this section, we prove theorem 2.2. We recall the statement.
Theorem. Suppose that M is a closed connected oriented n-manifold such that
![]() $H^*(M; {\mathbb {R}})$
does not embed into
$H^*(M; {\mathbb {R}})$
does not embed into
![]() $\Lambda ^* {\mathbb {R}}^n$
, and N is any closed oriented n-manifold. Then there exists
$\Lambda ^* {\mathbb {R}}^n$
, and N is any closed oriented n-manifold. Then there exists
![]() $\alpha (M)> 0$
so that for any metric g on M and
$\alpha (M)> 0$
so that for any metric g on M and
![]() $g'$
on N and any map
$g'$
on N and any map
![]() $f: N \rightarrow M$
with
$f: N \rightarrow M$
with
![]() $\operatorname {\mathrm {Lip}}(f) = L$
,
$\operatorname {\mathrm {Lip}}(f) = L$
,
Remark 2.17. The constant
![]() $\alpha (M)$
depends only on the real cohomology algebra of M,
$\alpha (M)$
depends only on the real cohomology algebra of M,
![]() $H^*(M; {\mathbb {R}})$
.
$H^*(M; {\mathbb {R}})$
.
Remark 2.18. Because the constant
![]() $C(M,g)$
depends on g, it suffices to prove the estimate for any one metric g.
$C(M,g)$
depends on g, it suffices to prove the estimate for any one metric g.
The main difference between the general situation in Theorem 2.2 and the special case
![]() $X_k = ({\mathbb {C}} P^2)^{\# k}$
in Theorem 2.1 is to find the right analogue of Lemma 2.13. Lemma 2.13 takes advantage of the hypothesis that
$X_k = ({\mathbb {C}} P^2)^{\# k}$
in Theorem 2.1 is to find the right analogue of Lemma 2.13. Lemma 2.13 takes advantage of the hypothesis that
![]() $k \ge 4$
for
$k \ge 4$
for
![]() $X_k$
. Similarly, the following lemma takes advantage of the hypothesis that
$X_k$
. Similarly, the following lemma takes advantage of the hypothesis that
![]() $H^*(M; {\mathbb {R}})$
does not embed into
$H^*(M; {\mathbb {R}})$
does not embed into
![]() $\Lambda ^* {\mathbb {R}}^n$
.
$\Lambda ^* {\mathbb {R}}^n$
.
Lemma 2.19. Suppose that M is a closed connected oriented n-manifold such that
![]() $H^*(M; {\mathbb {R}})$
does not embed into
$H^*(M; {\mathbb {R}})$
does not embed into
![]() $\Lambda ^* {\mathbb {R}}^n$
. Then there exists an integer
$\Lambda ^* {\mathbb {R}}^n$
. Then there exists an integer
![]() $m(M)$
so that the following holds.
$m(M)$
so that the following holds.
Let
![]() $u_j \in H^{d_j} (M; {\mathbb {R}})$
be a set of generators for the cohomology algebra of M, including a generator
$u_j \in H^{d_j} (M; {\mathbb {R}})$
be a set of generators for the cohomology algebra of M, including a generator
![]() $u_{\operatorname {\mathrm {top}}} \in H^n(M; {\mathbb {R}})$
. Suppose that the relations of the cohomology algebra are given by
$u_{\operatorname {\mathrm {top}}} \in H^n(M; {\mathbb {R}})$
. Suppose that the relations of the cohomology algebra are given by
![]() $R_r(u_1, \ldots , u_J) = 0$
.
$R_r(u_1, \ldots , u_J) = 0$
.
Fix
![]() $\beta _j \in \Lambda ^{d_j} {\mathbb {R}}^n$
for each
$\beta _j \in \Lambda ^{d_j} {\mathbb {R}}^n$
for each
![]() $j =1, \ldots , J$
such that
$j =1, \ldots , J$
such that
![]() $|\beta _j| \le 1$
for each j and
$|\beta _j| \le 1$
for each j and
![]() $| R_r(\vec \beta )| \le {\epsilon }$
for each r. Then
$| R_r(\vec \beta )| \le {\epsilon }$
for each r. Then
![]() $| \beta _{\operatorname {\mathrm {top}}} | \le C_M {\epsilon }^{\frac {1}{2m}}$
.
$| \beta _{\operatorname {\mathrm {top}}} | \le C_M {\epsilon }^{\frac {1}{2m}}$
.
Proof. The tuple
![]() $(\beta _1, \ldots , \beta _J)$
belongs to the space
$(\beta _1, \ldots , \beta _J)$
belongs to the space
![]() $\prod _{j=1}^J \Lambda ^{d_j} {\mathbb {R}}^n$
, which is isomorphic to
$\prod _{j=1}^J \Lambda ^{d_j} {\mathbb {R}}^n$
, which is isomorphic to
![]() ${\mathbb {R}}^N$
. We can think of (each component of)
${\mathbb {R}}^N$
. We can think of (each component of)
![]() $\beta _j$
as a coordinate on this space, and we can think of
$\beta _j$
as a coordinate on this space, and we can think of
![]() $R_r$
as a polynomial on this space. We let
$R_r$
as a polynomial on this space. We let
![]() $V(R_1, \ldots , R_k)$
be the set of
$V(R_1, \ldots , R_k)$
be the set of
![]() $\vec \beta $
where all the polynomials
$\vec \beta $
where all the polynomials
![]() $R_r$
vanish.
$R_r$
vanish.
Each
![]() $(\beta _1, \ldots , \beta _J) \in V(R_1, \ldots , R_k)$
corresponds to a homomorphism
$(\beta _1, \ldots , \beta _J) \in V(R_1, \ldots , R_k)$
corresponds to a homomorphism
![]() $\phi : H^*(M; {\mathbb {R}}) \rightarrow \Lambda ^* {\mathbb {R}}^n$
with
$\phi : H^*(M; {\mathbb {R}}) \rightarrow \Lambda ^* {\mathbb {R}}^n$
with
![]() $\beta _j = \phi (u_j)$
. By hypothesis, each such homomorphism is noninjective. By Poincaré duality, we have that each such homomorphism sends
$\beta _j = \phi (u_j)$
. By hypothesis, each such homomorphism is noninjective. By Poincaré duality, we have that each such homomorphism sends
![]() $u_{\operatorname {\mathrm {top}}}$
to 0. Therefore,
$u_{\operatorname {\mathrm {top}}}$
to 0. Therefore,
![]() $\beta _{\operatorname {\mathrm {top}}} = 0$
on
$\beta _{\operatorname {\mathrm {top}}} = 0$
on
![]() $V(R_1, \ldots , R_k)$
.
$V(R_1, \ldots , R_k)$
.
For any set
![]() $X \subset {\mathbb {R}}^N$
, we let
$X \subset {\mathbb {R}}^N$
, we let
![]() $I(X)$
denote the ideal of polynomials
$I(X)$
denote the ideal of polynomials
![]() $f \in {\mathbb {R}}[\beta ]$
that vanish on X. So we see that
$f \in {\mathbb {R}}[\beta ]$
that vanish on X. So we see that
![]() $\beta _{\operatorname {\mathrm {top}}} \in I (V (R_1, \ldots , R_k))$
. The structure of
$\beta _{\operatorname {\mathrm {top}}} \in I (V (R_1, \ldots , R_k))$
. The structure of
![]() $I( V( R_1, \ldots , R_k))$
is described by the real Nullstellensatz—cf. [Reference Marshall20, §2.3]:
$I( V( R_1, \ldots , R_k))$
is described by the real Nullstellensatz—cf. [Reference Marshall20, §2.3]:
Theorem 2.20 (Real Nullstellensatz)
A polynomial
![]() $f \in {\mathbb {R}}[\beta ]$
lies in
$f \in {\mathbb {R}}[\beta ]$
lies in
![]() $I (V (R_1, \ldots , R_k))$
if and only if there is an integer
$I (V (R_1, \ldots , R_k))$
if and only if there is an integer
![]() $m \ge 1$
and polynomials
$m \ge 1$
and polynomials
![]() $g_i, h_r \in {\mathbb {R}}[\beta ]$
so that
$g_i, h_r \in {\mathbb {R}}[\beta ]$
so that
 $$\begin{align*}f^{2m} + g_1^2 + \ldots + g_s^2 = \sum_{r=1}^k h_r R_r.\end{align*}$$
$$\begin{align*}f^{2m} + g_1^2 + \ldots + g_s^2 = \sum_{r=1}^k h_r R_r.\end{align*}$$
By the real Nullstellensatz, we see that there is some integer m such that
If we also know that
![]() $|\beta _j| \le 1$
for every j and
$|\beta _j| \le 1$
for every j and
![]() $|R_r(\beta )| \le {\epsilon }$
for every r, then we see that
$|R_r(\beta )| \le {\epsilon }$
for every r, then we see that
Therefore,
![]() $| \beta _{\operatorname {\mathrm {top}}} | \le C_M {\epsilon }^{\frac {1}{2m}}$
.
$| \beta _{\operatorname {\mathrm {top}}} | \le C_M {\epsilon }^{\frac {1}{2m}}$
.
With this lemma, we can start the proof of the theorem. The ideas are the same. We just have to carry them out in a more general situation, with a little more notation.
Recall that
![]() $u_j \in H^{d_j} (M; {\mathbb {R}})$
is a set of generators for the cohomology of M, with
$u_j \in H^{d_j} (M; {\mathbb {R}})$
is a set of generators for the cohomology of M, with
![]() $u_{\operatorname {\mathrm {top}}}$
the generator of
$u_{\operatorname {\mathrm {top}}}$
the generator of
![]() $H^n(M; {\mathbb {R}})$
. Suppose that the relations of the cohomology algebra are given by
$H^n(M; {\mathbb {R}})$
. Suppose that the relations of the cohomology algebra are given by
![]() $R_r(u_1, \ldots , u_J) = 0$
.
$R_r(u_1, \ldots , u_J) = 0$
.
Choose
![]() $\alpha _j$
to be a closed form on M in the cohomology class
$\alpha _j$
to be a closed form on M in the cohomology class
![]() $u_j$
. The cohomology class of
$u_j$
. The cohomology class of
![]() $R_r(\vec \alpha )$
is zero, so
$R_r(\vec \alpha )$
is zero, so
![]() $R_r(\vec \alpha )$
is exact. Choose a primitive:
$R_r(\vec \alpha )$
is exact. Choose a primitive:
Next, suppose that
![]() $f: N \rightarrow M$
is an L-Lipschitz map. Cover N with charts
$f: N \rightarrow M$
is an L-Lipschitz map. Cover N with charts
![]() $U'$
, and let
$U'$
, and let
![]() $1 = \sum _{U'} \psi _{U'}$
be a partition of unity subordinate to the cover. Let
$1 = \sum _{U'} \psi _{U'}$
be a partition of unity subordinate to the cover. Let
![]() $\phi : U \rightarrow U'$
be a parametrization of
$\phi : U \rightarrow U'$
be a parametrization of
![]() $U'$
, where
$U'$
, where
![]() $U \subset {\mathbb {R}}^n$
, which extends to a smooth map
$U \subset {\mathbb {R}}^n$
, which extends to a smooth map
![]() $\phi : {\mathbb {R}}^n \rightarrow M$
sending the complement of a large ball in
$\phi : {\mathbb {R}}^n \rightarrow M$
sending the complement of a large ball in
![]() ${\mathbb {R}}^n$
to a single point in M. Define a smooth compactly supported function
${\mathbb {R}}^n$
to a single point in M. Define a smooth compactly supported function
 $$\begin{align*}\psi_U(x) = \begin{cases} \phi^{*} \psi_{U'}(x) & x \in U \\ 0 & x \notin U. \end{cases}\end{align*}$$
$$\begin{align*}\psi_U(x) = \begin{cases} \phi^{*} \psi_{U'}(x) & x \in U \\ 0 & x \notin U. \end{cases}\end{align*}$$
Define forms on
![]() ${\mathbb {R}}^n$
which correspond to the
${\mathbb {R}}^n$
which correspond to the
![]() $\alpha _j$
as follows:
$\alpha _j$
as follows:
With this normalization,
![]() $\| a_j \|_{L^\infty } \lesssim 1$
and the
$\| a_j \|_{L^\infty } \lesssim 1$
and the
![]() $a_j$
are smooth compactly supported differential forms. Then
$a_j$
are smooth compactly supported differential forms. Then
 $$ \begin{align} \deg(f) = L^n \sum_{U} \int_{{\mathbb{R}}^n} \psi_U a_{\operatorname{\mathrm{top}}}. \end{align} $$
$$ \begin{align} \deg(f) = L^n \sum_{U} \int_{{\mathbb{R}}^n} \psi_U a_{\operatorname{\mathrm{top}}}. \end{align} $$
Define forms on
![]() ${\mathbb {R}}^n$
which correspond to the
${\mathbb {R}}^n$
which correspond to the
![]() $\gamma _r$
as follows. If
$\gamma _r$
as follows. If
![]() $\gamma _r \in H^{d_r}(M; {\mathbb {R}})$
, then
$\gamma _r \in H^{d_r}(M; {\mathbb {R}})$
, then
The forms
![]() $g_r$
are also smooth compactly supported differential forms. The power of L is chosen so that
$g_r$
are also smooth compactly supported differential forms. The power of L is chosen so that
The power of L works out to make the forms
![]() $g_r$
very small:
$g_r$
very small:
This allows us to show that the low-frequency parts of the forms
![]() $R_r(a)$
are small.
$R_r(a)$
are small.
Lemma 2.21.
![]() $\| P_{\le k} R_r(a) \|_{L^\infty } \lesssim 2^k L^{-1}$
.
$\| P_{\le k} R_r(a) \|_{L^\infty } \lesssim 2^k L^{-1}$
.
Proof. We start by computing
Now, we can integrate by parts to get
Taking norms and using
![]() $\| g_r \|_{L^\infty } \lesssim L^{-1}$
, we see that
$\| g_r \|_{L^\infty } \lesssim L^{-1}$
, we see that
We want to bound
![]() $\int \psi _U a_{\operatorname {\mathrm {top}}}$
. We break this up into a low-frequency and high-frequency part at a frequency cutoff k which we will choose later. (Eventually we will average over many k.)
$\int \psi _U a_{\operatorname {\mathrm {top}}}$
. We break this up into a low-frequency and high-frequency part at a frequency cutoff k which we will choose later. (Eventually we will average over many k.)
 $$ \begin{align} \int \psi_U a_{\operatorname{\mathrm{top}}} = \underbrace{\int \psi_U P_{\le k} a_{\operatorname{\mathrm{top}}}}_{\textrm{low}} + \underbrace{\sum_{\ell> k} \int \psi_U P_\ell a_{\operatorname{\mathrm{top}}}}_{\textrm{high}}. \end{align} $$
$$ \begin{align} \int \psi_U a_{\operatorname{\mathrm{top}}} = \underbrace{\int \psi_U P_{\le k} a_{\operatorname{\mathrm{top}}}}_{\textrm{low}} + \underbrace{\sum_{\ell> k} \int \psi_U P_\ell a_{\operatorname{\mathrm{top}}}}_{\textrm{high}}. \end{align} $$
For the high-frequency pieces in (24), we will find a small primitive and then integrate by parts. Lemma 2.10 tells us that
![]() $P_{\ell } a_{\operatorname {\mathrm {top}}}$
has a primitive with
$P_{\ell } a_{\operatorname {\mathrm {top}}}$
has a primitive with
Then we can bound
![]() $\int \psi _U P_{\ell } a_{\operatorname {\mathrm {top}}}$
by
$\int \psi _U P_{\ell } a_{\operatorname {\mathrm {top}}}$
by
We will choose k with
![]() $2^k \ge L^{1/10}$
, and so the contribution of all the high-frequency parts is bounded by
$2^k \ge L^{1/10}$
, and so the contribution of all the high-frequency parts is bounded by
![]() $L^{-1/10}$
, which is much smaller than the bound we are aiming for.
$L^{-1/10}$
, which is much smaller than the bound we are aiming for.
For the low-frequency piece in (24)), we apply Lemma 2.19 to the forms
![]() $P_{\le k} a_j$
. Since all these forms have norm
$P_{\le k} a_j$
. Since all these forms have norm
![]() $\lesssim 1$
pointwise, the lemma gives us a pointwise bound
$\lesssim 1$
pointwise, the lemma gives us a pointwise bound
Integrating and using the Hölder inequality, we get the bound
 $$ \begin{align} \int \psi_U P_{\le k} a_{\operatorname{\mathrm{top}}} \le \sum_r \int \psi_U | R_r(P_{\le k} a)|^{\frac{1}{2m}} \lesssim \sum_r \left( \int \psi_U |R_r(P_{\le k} a)| \right)^{\frac{1}{2m}}. \end{align} $$
$$ \begin{align} \int \psi_U P_{\le k} a_{\operatorname{\mathrm{top}}} \le \sum_r \int \psi_U | R_r(P_{\le k} a)|^{\frac{1}{2m}} \lesssim \sum_r \left( \int \psi_U |R_r(P_{\le k} a)| \right)^{\frac{1}{2m}}. \end{align} $$
In the Hölder step, in detail we wrote
 $$ \begin{align*} \int \psi_U | R_r(P_{\le k} a)|^{\frac{1}{2m}} &= \int \psi_U^{\frac{2m-1}{2m}} \cdot \psi_U^{\frac{1}{2m}} |R_r(P_{\le k} a)|^{\frac{1}{2m}} \\ &\le \underbrace{\left( \int \psi_U \right)^{\frac{2m-1}{2m}}}_{\lesssim 1} \left( \int \psi_U |R_r(P_{\le k} a)| \right)^{\frac{1}{2m}}. \end{align*} $$
$$ \begin{align*} \int \psi_U | R_r(P_{\le k} a)|^{\frac{1}{2m}} &= \int \psi_U^{\frac{2m-1}{2m}} \cdot \psi_U^{\frac{1}{2m}} |R_r(P_{\le k} a)|^{\frac{1}{2m}} \\ &\le \underbrace{\left( \int \psi_U \right)^{\frac{2m-1}{2m}}}_{\lesssim 1} \left( \int \psi_U |R_r(P_{\le k} a)| \right)^{\frac{1}{2m}}. \end{align*} $$
Now we have to bound each integral
![]() $\int \psi _U |R_r( P_{\le k} a)|$
. Since
$\int \psi _U |R_r( P_{\le k} a)|$
. Since
![]() $\| a \|_{L^\infty } \lesssim 1$
, we get a bound
$\| a \|_{L^\infty } \lesssim 1$
, we get a bound
![]() $\int \psi _U |R_r( P_{\le k} a)|\lesssim 1$
, and to prove our theorem, we need to beat this bound by a power of
$\int \psi _U |R_r( P_{\le k} a)|\lesssim 1$
, and to prove our theorem, we need to beat this bound by a power of
![]() $\log L$
, at least for some choice of k. The key input is the bound on the low-frequency part of
$\log L$
, at least for some choice of k. The key input is the bound on the low-frequency part of
![]() $R_r(a)$
: Lemma 2.21 tells us that
$R_r(a)$
: Lemma 2.21 tells us that
![]() $\| P_{\le k} R_r(a) \|_{L^\infty } \le 2^{k} L^{-1}$
. Next, we have to relate
$\| P_{\le k} R_r(a) \|_{L^\infty } \le 2^{k} L^{-1}$
. Next, we have to relate
![]() $R_r (P_{\le k} a)$
with
$R_r (P_{\le k} a)$
with
![]() $P_{\le k} R_r(a)$
.
$P_{\le k} R_r(a)$
.
Remember that each
![]() $R_r$
is a polynomial in the
$R_r$
is a polynomial in the
![]() $a_j$
. Each
$a_j$
. Each
![]() $R_r(a_j)$
is a sum of terms of the form
$R_r(a_j)$
is a sum of terms of the form
![]() $c a_{j_1} \wedge \cdots \wedge a_{j_P}$
. If we do a Littlewood–Paley decomposition of each
$c a_{j_1} \wedge \cdots \wedge a_{j_P}$
. If we do a Littlewood–Paley decomposition of each
![]() $a_j$
, we see that
$a_j$
, we see that
For each choice of
![]() $k_1, \ldots , k_P$
, we write
$k_1, \ldots , k_P$
, we write
![]() $k_{\max } = \max _p k_p$
. We let
$k_{\max } = \max _p k_p$
. We let
![]() $p_{\max }$
be the value of p that maximizes
$p_{\max }$
be the value of p that maximizes
![]() $k_p$
. If there is a tie, we let
$k_p$
. If there is a tie, we let
![]() $p_{\max }$
be the smallest p so that
$p_{\max }$
be the smallest p so that
![]() $k_p = k_{\max }$
. We can now organize the sum on the right-hand side of (26) according to the value of
$k_p = k_{\max }$
. We can now organize the sum on the right-hand side of (26) according to the value of
![]() $k_{\max }$
and
$k_{\max }$
and
![]() $p_{\max }$
:
$p_{\max }$
:
 $$ \begin{align*} &\sum_{k_1, \ldots, k_P} P_{k_1} a_{j_1} \wedge \cdots \wedge P_{k_P} a_{j_P} = \sum_{k_{\max}} \sum_{p_{\max} = 1}^P P_{< k_{\max}} a_{j_1} \wedge \cdots \wedge \\ &\quad{} \wedge P_{< k_{\max} } a_{j_{p_{\max} - 1}} \wedge P_{k_{\max}} a_{j_{p_{\max}}} \wedge P_{\le k_{\max}} a_{j_{p_{\max}}+1} \wedge \cdots \wedge P_{\le k_{\max}} a_{j_P}. \end{align*} $$
$$ \begin{align*} &\sum_{k_1, \ldots, k_P} P_{k_1} a_{j_1} \wedge \cdots \wedge P_{k_P} a_{j_P} = \sum_{k_{\max}} \sum_{p_{\max} = 1}^P P_{< k_{\max}} a_{j_1} \wedge \cdots \wedge \\ &\quad{} \wedge P_{< k_{\max} } a_{j_{p_{\max} - 1}} \wedge P_{k_{\max}} a_{j_{p_{\max}}} \wedge P_{\le k_{\max}} a_{j_{p_{\max}}+1} \wedge \cdots \wedge P_{\le k_{\max}} a_{j_P}. \end{align*} $$
Similarly,
 $$\begin{align*}P_{\le k} a_{j_1} \wedge \cdots \wedge P_{\le k} a_{j_P}= \sum_{k_{\max} \le k } \sum_{p_{\max} = 1}^P P_{< k_{\max}} a_{j_1} \wedge \cdots \wedge P_{k_{\max}} a_{j_{p_{\max}}} \wedge \cdots \wedge P_{\le k_{\max}} a_{j_P}.\end{align*}$$
$$\begin{align*}P_{\le k} a_{j_1} \wedge \cdots \wedge P_{\le k} a_{j_P}= \sum_{k_{\max} \le k } \sum_{p_{\max} = 1}^P P_{< k_{\max}} a_{j_1} \wedge \cdots \wedge P_{k_{\max}} a_{j_{p_{\max}}} \wedge \cdots \wedge P_{\le k_{\max}} a_{j_P}.\end{align*}$$
Therefore,
 $$ \begin{align*} &P_{\le k} a_{j_1} \wedge \cdots \wedge P_{\le k} a_{j_P} \\ &\quad= a_{j_1} \wedge \cdots \wedge a_{j_P} - \sum_{k_{\max}> k } \sum_{p_{\max} = 1}^P P_{< k_{\max}} a_{j_1} \wedge \cdots \wedge P_{k_{\max}} a_{j_{p_{\max}}} \wedge \cdots \wedge P_{\le k_{\max}} a_{j_P}. \end{align*} $$
$$ \begin{align*} &P_{\le k} a_{j_1} \wedge \cdots \wedge P_{\le k} a_{j_P} \\ &\quad= a_{j_1} \wedge \cdots \wedge a_{j_P} - \sum_{k_{\max}> k } \sum_{p_{\max} = 1}^P P_{< k_{\max}} a_{j_1} \wedge \cdots \wedge P_{k_{\max}} a_{j_{p_{\max}}} \wedge \cdots \wedge P_{\le k_{\max}} a_{j_P}. \end{align*} $$
This discussion applies to each monomial of
![]() $R_r$
. Therefore,
$R_r$
. Therefore,
![]() $R_r(a)$
is equal to
$R_r(a)$
is equal to
![]() $R_r( P_{\le k} a)$
plus a finite linear combination of terms of the form
$R_r( P_{\le k} a)$
plus a finite linear combination of terms of the form
 $$ \begin{align} \sum_{k_{\max}> k } \sum_{p_{\max} = 1}^P P_{< k_{\max}} a_{j_1} \wedge \cdots \wedge P_{k_{\max}} a_{j_{p_{\max}}} \wedge \cdots \wedge P_{\le k_{\max}} a_{j_P}. \end{align} $$
$$ \begin{align} \sum_{k_{\max}> k } \sum_{p_{\max} = 1}^P P_{< k_{\max}} a_{j_1} \wedge \cdots \wedge P_{k_{\max}} a_{j_{p_{\max}}} \wedge \cdots \wedge P_{\le k_{\max}} a_{j_P}. \end{align} $$
Now, for a large constant c, we have
![]() $P_{\le k+c} R_r( P_{\le k} a_j) = R_r( P_{\le k} a_j)$
. Therefore,
$P_{\le k+c} R_r( P_{\le k} a_j) = R_r( P_{\le k} a_j)$
. Therefore,
![]() $ R_r( P_{\le k} a)$
is equal to
$ R_r( P_{\le k} a)$
is equal to
![]() $P_{\le k+c} R_r(a) $
plus a finite linear combination of terms of the form
$P_{\le k+c} R_r(a) $
plus a finite linear combination of terms of the form
 $$ \begin{align} \sum_{k_{\max}> k } \sum_{p_{\max} = 1}^P P_{\le k + c} \left( P_{< k_{\max}} a_{j_1} \wedge \cdots \wedge P_{k_{\max}} a_{j_{p_{\max}}} \wedge \cdots \wedge P_{\le k_{\max}} a_{j_P}\right). \end{align} $$
$$ \begin{align} \sum_{k_{\max}> k } \sum_{p_{\max} = 1}^P P_{\le k + c} \left( P_{< k_{\max}} a_{j_1} \wedge \cdots \wedge P_{k_{\max}} a_{j_{p_{\max}}} \wedge \cdots \wedge P_{\le k_{\max}} a_{j_P}\right). \end{align} $$
In summary,
The first term in (29) is controlled by Lemma 2.21:
![]() $\| P_{\le k+ c} R_r(a) \|_{L^\infty } \lesssim 2^{k+c} L^{-1} \lesssim 2^k L^{-1}$
. We will choose k so that
$\| P_{\le k+ c} R_r(a) \|_{L^\infty } \lesssim 2^{k+c} L^{-1} \lesssim 2^k L^{-1}$
. We will choose k so that
![]() $2^k \le L^{9/10}$
, so this term is bounded by
$2^k \le L^{9/10}$
, so this term is bounded by
![]() $L^{-1/10}$
, which is much smaller than our goal.
$L^{-1/10}$
, which is much smaller than our goal.
For each remaining term of type (28), we will again take a primitive and integrate by parts. We apply Lemma 2.10 to get a good primitive:
![]() $P_{k_{\max }} a_{j_{p_{\max }}} = d \operatorname {\mathrm {Prim}} ( P_{k_{\max }} a_{j_{p_{\max }}} )$
, where
$P_{k_{\max }} a_{j_{p_{\max }}} = d \operatorname {\mathrm {Prim}} ( P_{k_{\max }} a_{j_{p_{\max }}} )$
, where
![]() $\lVert \operatorname {\mathrm {Prim}} ( P_{k_{\max }} a_{j_{p_{\max }}} ) \rVert _{L^p} \lesssim 2^{-k_{\max }} \lVert P_{k_{\max }} a_{j_{p_{\max }}} \rVert _{L^p}$
for every
$\lVert \operatorname {\mathrm {Prim}} ( P_{k_{\max }} a_{j_{p_{\max }}} ) \rVert _{L^p} \lesssim 2^{-k_{\max }} \lVert P_{k_{\max }} a_{j_{p_{\max }}} \rVert _{L^p}$
for every
![]() $1 \le p \le \infty $
. For each fixed choice of
$1 \le p \le \infty $
. For each fixed choice of
![]() $k_{\max }$
and
$k_{\max }$
and
![]() $p_{\max }$
, we write
$p_{\max }$
, we write
 $$ \begin{align*} &P_{\le k + c} \left( P_{< k_{\max}} a_{j_1} \wedge \cdots \wedge P_{k_{\max}} a_{j_{p_{\max}}} \wedge \cdots \wedge P_{\le k_{\max}} a_{j_P}\right) \\ &\quad= \eta_{\le k + c}^\vee * \left( P_{< k_{\max}} a_{j_1} \wedge \cdots \wedge d \operatorname{\mathrm{Prim}}( P_{k_{\max}} a_{j_{p_{\max}}}) \wedge \cdots \wedge P_{\le k_{\max}} a_{j_P}\right) \\ &\quad= d \eta_{\le k + c}^\vee * \left( P_{< k_{\max}} a_{j_1} \wedge \cdots \wedge \operatorname{\mathrm{Prim}}( P_{k_{\max}} a_{j_{p_{\max}}}) \wedge \cdots \wedge P_{\le k_{\max}} a_{j_P}\right). \end{align*} $$
$$ \begin{align*} &P_{\le k + c} \left( P_{< k_{\max}} a_{j_1} \wedge \cdots \wedge P_{k_{\max}} a_{j_{p_{\max}}} \wedge \cdots \wedge P_{\le k_{\max}} a_{j_P}\right) \\ &\quad= \eta_{\le k + c}^\vee * \left( P_{< k_{\max}} a_{j_1} \wedge \cdots \wedge d \operatorname{\mathrm{Prim}}( P_{k_{\max}} a_{j_{p_{\max}}}) \wedge \cdots \wedge P_{\le k_{\max}} a_{j_P}\right) \\ &\quad= d \eta_{\le k + c}^\vee * \left( P_{< k_{\max}} a_{j_1} \wedge \cdots \wedge \operatorname{\mathrm{Prim}}( P_{k_{\max}} a_{j_{p_{\max}}}) \wedge \cdots \wedge P_{\le k_{\max}} a_{j_P}\right). \end{align*} $$
We now take the
![]() $L^1$
norm of our term. Since
$L^1$
norm of our term. Since
![]() $\| a_j\|_{L^\infty }$
and
$\| a_j\|_{L^\infty }$
and
![]() $\| P_{< k_{\max } a_j} \|_{L^\infty }$
are all
$\| P_{< k_{\max } a_j} \|_{L^\infty }$
are all
![]() $\lesssim 1$
, we see that
$\lesssim 1$
, we see that
 $$ \begin{align*} &\big\lVert d \eta_{\le k + c}^\vee * \left( P_{< k_{\max}} a_{j_1} \wedge \cdots \wedge \operatorname{\mathrm{Prim}}( P_{k_{\max}} a_{j_{p_{\max}}}) \wedge \cdots \wedge P_{\le k_{\max}} a_{j_P}\right)\big\rVert_{L^1} \\ &\quad\lesssim \big\lVert d \eta_{\le k+ c}^\vee \big\rVert_{L^1} \big\lVert \operatorname{\mathrm{Prim}} ( P_{k_{\max}} a_{j_{p_{\max}}}) \big\rVert_{L^1} \lesssim 2^{k+c} 2^{-k_{\max}} \big\lVert P_{k_{\max}} a \big\rVert_{L^1}. \end{align*} $$
$$ \begin{align*} &\big\lVert d \eta_{\le k + c}^\vee * \left( P_{< k_{\max}} a_{j_1} \wedge \cdots \wedge \operatorname{\mathrm{Prim}}( P_{k_{\max}} a_{j_{p_{\max}}}) \wedge \cdots \wedge P_{\le k_{\max}} a_{j_P}\right)\big\rVert_{L^1} \\ &\quad\lesssim \big\lVert d \eta_{\le k+ c}^\vee \big\rVert_{L^1} \big\lVert \operatorname{\mathrm{Prim}} ( P_{k_{\max}} a_{j_{p_{\max}}}) \big\rVert_{L^1} \lesssim 2^{k+c} 2^{-k_{\max}} \big\lVert P_{k_{\max}} a \big\rVert_{L^1}. \end{align*} $$
To summarize, we have proved the following bound on each summand of (28):
Now, the
![]() $L^1$
norm of each term of form (28) is bounded as follows:
$L^1$
norm of each term of form (28) is bounded as follows:
 $$ \begin{align*} &\bigg\lVert \sum_{k_{\max}> k } \sum_{p_{\max} = 1}^P P_{\le k + c} \left( P_{< k_{\max}} a_{j_1} \wedge \cdots \wedge P_{k_{\max}} a_{j_{p_{\max}}} \wedge \cdots \wedge P_{\le k_{\max}} a_{j_P}\right) \bigg\rVert_{L^1} \\ &\quad\lesssim \sum_{k_{\max}> k} 2^{k - k_{\max}} \| P_{k_{\max}} a \|_{L^1}. \end{align*} $$
$$ \begin{align*} &\bigg\lVert \sum_{k_{\max}> k } \sum_{p_{\max} = 1}^P P_{\le k + c} \left( P_{< k_{\max}} a_{j_1} \wedge \cdots \wedge P_{k_{\max}} a_{j_{p_{\max}}} \wedge \cdots \wedge P_{\le k_{\max}} a_{j_P}\right) \bigg\rVert_{L^1} \\ &\quad\lesssim \sum_{k_{\max}> k} 2^{k - k_{\max}} \| P_{k_{\max}} a \|_{L^1}. \end{align*} $$
We now have our bounds on all the terms, and we just have to put them together. Recall (25) tells us that
 $$ \begin{align} \Big(\int \psi_U P_{\le k} a_{\operatorname{\mathrm{top}}}\Big)^{2m} \lesssim \sum_r \int \psi_U |R_r(P_{\le k} a)|. \end{align} $$
$$ \begin{align} \Big(\int \psi_U P_{\le k} a_{\operatorname{\mathrm{top}}}\Big)^{2m} \lesssim \sum_r \int \psi_U |R_r(P_{\le k} a)|. \end{align} $$
By (29), we can break up
![]() $R_r(P_{\le k} a)$
into pieces:
$R_r(P_{\le k} a)$
into pieces:
We have now bounded each term on the right-hand side. Combining our bounds, we see that
 $$\begin{align*}\Big(\int \psi_U P_{\le k} a_{\operatorname{\mathrm{top}}}\Big)^{2m} \lesssim \sum_r \int \psi_U |R_r(P_{\le k} a)| \lesssim 2^k L^{-1} + \sum_{k_{\max}> k} 2^{k-k_{\max}} \| P_{k_{\max}} a \|_{L^1}.\end{align*}$$
$$\begin{align*}\Big(\int \psi_U P_{\le k} a_{\operatorname{\mathrm{top}}}\Big)^{2m} \lesssim \sum_r \int \psi_U |R_r(P_{\le k} a)| \lesssim 2^k L^{-1} + \sum_{k_{\max}> k} 2^{k-k_{\max}} \| P_{k_{\max}} a \|_{L^1}.\end{align*}$$
Let us pause to digest this bound. The first term
![]() $2^k L^{-1}$
is very small as long as
$2^k L^{-1}$
is very small as long as
![]() $2^k \le L^{9/10}$
. In the second term, there is exponential decay for
$2^k \le L^{9/10}$
. In the second term, there is exponential decay for
![]() $k_{\max }> k$
. Therefore, the main contribution on the right-hand side is when
$k_{\max }> k$
. Therefore, the main contribution on the right-hand side is when
![]() $k_{\max } = k$
, which gives
$k_{\max } = k$
, which gives
![]() $\| P_k a \|_{L^1}$
. For comparison, it would be straightforward to get an upper bound of
$\| P_k a \|_{L^1}$
. For comparison, it would be straightforward to get an upper bound of
![]() $\| a \|_{L^1} \lesssim 1$
. The upper bound
$\| a \|_{L^1} \lesssim 1$
. The upper bound
![]() $\| P_k a \|_{L^1}$
is an improvement because it includes only one Littlewood–Paley piece of a. We can take advantage of this improvement by averaging over k and using orthogonality:
$\| P_k a \|_{L^1}$
is an improvement because it includes only one Littlewood–Paley piece of a. We can take advantage of this improvement by averaging over k and using orthogonality:
![]() $\sum _k \| P_k a \|_{L^2}^2 \sim \| a \|_{L^2}^2$
. Now, we turn to the details of this estimate. We will sum over k in the range
$\sum _k \| P_k a \|_{L^2}^2 \sim \| a \|_{L^2}^2$
. Now, we turn to the details of this estimate. We will sum over k in the range
![]() $L^{1/10} \le 2^k \le L^{9/10}$
. There are
$L^{1/10} \le 2^k \le L^{9/10}$
. There are
![]() $\sim \log L$
different k in this range:
$\sim \log L$
different k in this range:
 $$\begin{align*}\sum_{L^{1/10} \le 2^k \le L^{9/10}} \Big(\int \psi_U P_{\le k} a_{\operatorname{\mathrm{top}}}\Big)^{2m} \lesssim L^{-1/10} + \sum_{L^{1/10} \le 2^k \le L^{9/10}} \sum_{2^k < 2^{k_{\max}} < L} 2^{k-k_{\max}} \| P_{k_{\max}} a \|_{L^1}.\end{align*}$$
$$\begin{align*}\sum_{L^{1/10} \le 2^k \le L^{9/10}} \Big(\int \psi_U P_{\le k} a_{\operatorname{\mathrm{top}}}\Big)^{2m} \lesssim L^{-1/10} + \sum_{L^{1/10} \le 2^k \le L^{9/10}} \sum_{2^k < 2^{k_{\max}} < L} 2^{k-k_{\max}} \| P_{k_{\max}} a \|_{L^1}.\end{align*}$$
(Here, terms with
![]() $2^{k_{\max }}> L$
are bounded by the
$2^{k_{\max }}> L$
are bounded by the
![]() $L^{-1/10}$
term). Now, the last term is bounded by
$L^{-1/10}$
term). Now, the last term is bounded by
 $$\begin{align*}\sum_{L^{1/10} \le 2^k \le L^{9/10}} \sum_{2^k < 2^{k_{\max}} < L} 2^{k-k_{\max}} \| P_{k_{\max}} a \|_{L^1} \lesssim \sum_{L^{1/10} \le k_{\max} \le L} \| P_{k_{\max}} a \|_{L^1}.\end{align*}$$
$$\begin{align*}\sum_{L^{1/10} \le 2^k \le L^{9/10}} \sum_{2^k < 2^{k_{\max}} < L} 2^{k-k_{\max}} \| P_{k_{\max}} a \|_{L^1} \lesssim \sum_{L^{1/10} \le k_{\max} \le L} \| P_{k_{\max}} a \|_{L^1}.\end{align*}$$
The number of terms in this last sum is
![]() $\sim \log L$
. Therefore, we can use the Cauchy–Schwarz inequality to get
$\sim \log L$
. Therefore, we can use the Cauchy–Schwarz inequality to get
 $$\begin{align*}\sum_{L^{1/10} \le k_{\max} \le L} \| P_{k_{\max}} a \|_{L^1} \le (\log L)^{1/2} \bigg( \sum_{L^{1/10} \le 2^{k_{\max}} \le L} \| P_{k_{\max}} a \|_{L^1}^2 \bigg)^{1/2}.\end{align*}$$
$$\begin{align*}\sum_{L^{1/10} \le k_{\max} \le L} \| P_{k_{\max}} a \|_{L^1} \le (\log L)^{1/2} \bigg( \sum_{L^{1/10} \le 2^{k_{\max}} \le L} \| P_{k_{\max}} a \|_{L^1}^2 \bigg)^{1/2}.\end{align*}$$
Since a is supported on a fixed compact set, and
![]() $P_{k_{\max }} a$
is essentially supported on that set, Cauchy–Schwarz gives
$P_{k_{\max }} a$
is essentially supported on that set, Cauchy–Schwarz gives
![]() $\| P_{k_{\max }} a \|_{L^1} \lesssim \| P_{k_{\max }} a \|_{L^2}$
. Plugging this into the last term above gives
$\| P_{k_{\max }} a \|_{L^1} \lesssim \| P_{k_{\max }} a \|_{L^2}$
. Plugging this into the last term above gives
 $$\begin{align*}(\log L)^{1/2} \bigg( \sum_{L^{1/10} \le 2^{k_{\max}} \le L} \| P_{k_{\max}} a \|_{L^2}^2 \bigg)^{1/2} \lesssim (\log L)^{1/2} \| a \|_{L^2}.\end{align*}$$
$$\begin{align*}(\log L)^{1/2} \bigg( \sum_{L^{1/10} \le 2^{k_{\max}} \le L} \| P_{k_{\max}} a \|_{L^2}^2 \bigg)^{1/2} \lesssim (\log L)^{1/2} \| a \|_{L^2}.\end{align*}$$
All together, we now have
 $$\begin{align*}\sum_{L^{1/10} \le 2^k \le L^{9/10}} \Big(\int \psi_U P_{\le k} a_{\operatorname{\mathrm{top}}} \Big)^{2m} \lesssim (\log L)^{1/2} \| a \|_{L^2}.\end{align*}$$
$$\begin{align*}\sum_{L^{1/10} \le 2^k \le L^{9/10}} \Big(\int \psi_U P_{\le k} a_{\operatorname{\mathrm{top}}} \Big)^{2m} \lesssim (\log L)^{1/2} \| a \|_{L^2}.\end{align*}$$
Since there are
![]() $\sim \log L$
terms on the left-hand side, we can find one small term; that is, we can choose k in the range
$\sim \log L$
terms on the left-hand side, we can find one small term; that is, we can choose k in the range
![]() $L^{1/10} \le 2^k \le L^{9/10}$
so that
$L^{1/10} \le 2^k \le L^{9/10}$
so that
Taking roots, we get
![]() $\int \psi _U P_{\le k} a_{\operatorname {\mathrm {top}}} \lesssim (\log L)^{-\frac {1}{4m}}$
.
$\int \psi _U P_{\le k} a_{\operatorname {\mathrm {top}}} \lesssim (\log L)^{-\frac {1}{4m}}$
.
Recall that we broke up
![]() $\int \psi _U a_{\operatorname {\mathrm {top}}}$
into low-frequency and high-frequency pieces in (24):
$\int \psi _U a_{\operatorname {\mathrm {top}}}$
into low-frequency and high-frequency pieces in (24):
 $$\begin{align*}\int \psi_U a_{\operatorname{\mathrm{top}}} = \underbrace{\int \psi_U P_{\le k} a_{\operatorname{\mathrm{top}}}}_{\textrm{low}} + \underbrace{\sum_{\ell> k} \int \psi_U P_\ell a_{\operatorname{\mathrm{top}}}}_{\textrm{high}}.\end{align*}$$
$$\begin{align*}\int \psi_U a_{\operatorname{\mathrm{top}}} = \underbrace{\int \psi_U P_{\le k} a_{\operatorname{\mathrm{top}}}}_{\textrm{low}} + \underbrace{\sum_{\ell> k} \int \psi_U P_\ell a_{\operatorname{\mathrm{top}}}}_{\textrm{high}}.\end{align*}$$
We previously showed that the high-frequency pieces are bounded by
![]() $\lesssim 2^{-k}$
. Just now, we found k with
$\lesssim 2^{-k}$
. Just now, we found k with
![]() $L^{1/10} \le 2^k \le L^{9/10}$
, where the low-frequency piece has the bound
$L^{1/10} \le 2^k \le L^{9/10}$
, where the low-frequency piece has the bound
![]() $\lesssim (\log L)^{- \frac {1}{4m}}$
. Therefore, the total is bounded:
$\lesssim (\log L)^{- \frac {1}{4m}}$
. Therefore, the total is bounded:
Recall from (23) that
![]() $\deg f = L^n \sum _U \int \psi _U a_{\operatorname {\mathrm {top}}}$
, and so
$\deg f = L^n \sum _U \int \psi _U a_{\operatorname {\mathrm {top}}}$
, and so
This proves the theorem, with
![]() $\alpha (m) = \frac {1}{4m}$
. The integer m came from the real Nullstellensatz, and it depended only on the cohomology ring
$\alpha (m) = \frac {1}{4m}$
. The integer m came from the real Nullstellensatz, and it depended only on the cohomology ring
![]() $H^*(M; {\mathbb {R}})$
.
$H^*(M; {\mathbb {R}})$
.
2.3.1. Proof of Theorem 2.3
Finally, we describe the modifications needed to prove the result on the ball, which we restate here:
Theorem. Suppose that M is a closed connected oriented n-manifold such that
![]() $H^*(M; {\mathbb {R}})$
does not embed into
$H^*(M; {\mathbb {R}})$
does not embed into
![]() $\Lambda ^* {\mathbb {R}}^n$
, and let
$\Lambda ^* {\mathbb {R}}^n$
, and let
![]() $\alpha (M)>0$
be as in the statement of Theorem 2.2. Let
$\alpha (M)>0$
be as in the statement of Theorem 2.2. Let
![]() $B^n \subseteq {\mathbb {R}}^n$
be the unit ball. Then for any metric g on M and any L-Lipschitz map
$B^n \subseteq {\mathbb {R}}^n$
be the unit ball. Then for any metric g on M and any L-Lipschitz map
![]() $f:B^n \to M$
,
$f:B^n \to M$
,
Proof. Our argument above already studies forms defined on a ball. The only difference is that above we study
![]() $\int _{B^n} \psi f^*d\operatorname {\mathrm {vol}}_M$
, where
$\int _{B^n} \psi f^*d\operatorname {\mathrm {vol}}_M$
, where
![]() $\psi :B^n \to M$
is some function which decays to
$\psi :B^n \to M$
is some function which decays to
![]() $0$
at the boundary, whereas we now want to understand
$0$
at the boundary, whereas we now want to understand
![]() $\int _{B^n} f^*d\operatorname {\mathrm {vol}}_M$
. To bridge the gap, we expand the domain. Define a function
$\int _{B^n} f^*d\operatorname {\mathrm {vol}}_M$
. To bridge the gap, we expand the domain. Define a function
![]() $\tilde f:B_2(0) \to M$
on the ball of radius
$\tilde f:B_2(0) \to M$
on the ball of radius
![]() $2$
by
$2$
by
 $$\begin{align*}\tilde f(x)=\begin{cases} f(x) & \lVert x \rVert \leq 1 \\ f(x/\lVert x \rVert) & \lVert x \rVert>1. \end{cases}\end{align*}$$
$$\begin{align*}\tilde f(x)=\begin{cases} f(x) & \lVert x \rVert \leq 1 \\ f(x/\lVert x \rVert) & \lVert x \rVert>1. \end{cases}\end{align*}$$
If f is L-Lipschitz, this function is
![]() $2L$
-Lipschitz. Moreover, since
$2L$
-Lipschitz. Moreover, since
![]() $\tilde f$
has rank
$\tilde f$
has rank
![]() $n-1$
outside the ball of radius
$n-1$
outside the ball of radius
![]() $1$
,
$1$
,
![]() $\tilde f^*d\operatorname {\mathrm {vol}}_M=0$
outside that ball. Therefore, for any
$\tilde f^*d\operatorname {\mathrm {vol}}_M=0$
outside that ball. Therefore, for any
![]() $\psi :{\mathbb {R}}^n \to {\mathbb {R}}$
such that
$\psi :{\mathbb {R}}^n \to {\mathbb {R}}$
such that
![]() $\psi |_{B^n} \equiv 1$
, we have
$\psi |_{B^n} \equiv 1$
, we have
The argument in the proof of Theorem 2.2 bounds the left side as desired.
3. Explicit construction of efficient self-maps
In this section, we discuss the lower bound of Theorem A, which follows from the following result:
Theorem 3.1. Let Y be a formal compact Riemannian manifold such that
![]() $H_n(Y;\mathbb {Q})$
is nonzero for d different values of
$H_n(Y;\mathbb {Q})$
is nonzero for d different values of
![]() $n>0$
. Then there are integers
$n>0$
. Then there are integers
![]() $a>0,p>1$
such that for every
$a>0,p>1$
such that for every
![]() $\ell \in \mathbb {N}$
and
$\ell \in \mathbb {N}$
and
![]() $q=ap^\ell $
, there is an
$q=ap^\ell $
, there is an
![]() $O(\ell ^{d-1}p^\ell )$
-Lipschitz map
$O(\ell ^{d-1}p^\ell )$
-Lipschitz map
![]() ${r}_q:Y \to Y$
which induces multiplication by
${r}_q:Y \to Y$
which induces multiplication by
![]() $q^n$
on
$q^n$
on
![]() $H_n(Y;\mathbb {Q})$
.
$H_n(Y;\mathbb {Q})$
.
For the purpose of this section, a simply connected finite CW complex Y is formal if and only if for some
![]() $q>1$
, there is a map
$q>1$
, there is a map
![]() ${r}_q:Y \to Y$
which induces multiplication by
${r}_q:Y \to Y$
which induces multiplication by
![]() $q^n$
on
$q^n$
on
![]() $H^n(Y;{\mathbb {Q}})$
for every n. Clearly, if such a map exists for some q, then it exists for
$H^n(Y;{\mathbb {Q}})$
for every n. Clearly, if such a map exists for some q, then it exists for
![]() $q^\ell $
for every
$q^\ell $
for every
![]() $\ell $
. This is not the original definition of formality due to Sullivan, which is based on the rationalization of Y [Reference Deligne, Griffiths, Morgan and Sullivan11, Reference Sullivan23]; the equivalence of our definition in the case of finite complexes was first stated by [Reference Shiga22].
$\ell $
. This is not the original definition of formality due to Sullivan, which is based on the rationalization of Y [Reference Deligne, Griffiths, Morgan and Sullivan11, Reference Sullivan23]; the equivalence of our definition in the case of finite complexes was first stated by [Reference Shiga22].
To see that Theorem 3.1 indeed implies the lower bound of Theorem A, suppose that Y is an n-manifold. Let
![]() $K(\ell )$
be the Lipschitz constant of
$K(\ell )$
be the Lipschitz constant of
![]() ${r}_{ap^\ell }:Y \to Y$
and notice that for
${r}_{ap^\ell }:Y \to Y$
and notice that for
![]() $\ell \geq 2$
,
$\ell \geq 2$
,
 $$\begin{align*}K(\ell)/K(\ell-1)=p \cdot \frac{\ell^{d-1}}{(\ell-1)^{d-1}} \leq 2p.\end{align*}$$
$$\begin{align*}K(\ell)/K(\ell-1)=p \cdot \frac{\ell^{d-1}}{(\ell-1)^{d-1}} \leq 2p.\end{align*}$$
Then for
![]() $L>>0$
, somewhere between
$L>>0$
, somewhere between
![]() $L/2p$
and L is a value of
$L/2p$
and L is a value of
![]() $K(\ell )$
for some
$K(\ell )$
for some
![]() $\ell $
. This means that for
$\ell $
. This means that for
![]() $q=ap^\ell $
,
$q=ap^\ell $
,
and therefore, there is an
![]() $O(L)$
-Lipschitz map
$O(L)$
-Lipschitz map
![]() $f:Y \to Y$
such that
$f:Y \to Y$
such that
3.1. Warmup example
We start by proving Theorem 3.1 in the simple case of connected sums of
![]() $\mathbb CP^2$
before moving on to the general case.
$\mathbb CP^2$
before moving on to the general case.
Theorem 3.2. Let
![]() $M=\#_k {\mathbb {C}} P^2$
. Then there is a constant C such that for each
$M=\#_k {\mathbb {C}} P^2$
. Then there is a constant C such that for each
![]() $\ell>0$
, there is a self-map
$\ell>0$
, there is a self-map
![]() ${r}_{2^\ell }:M \to M$
of degree
${r}_{2^\ell }:M \to M$
of degree
![]() $2^{4\ell }$
and Lipschitz constant bounded by
$2^{4\ell }$
and Lipschitz constant bounded by
![]() $C\ell \cdot 2^\ell $
.
$C\ell \cdot 2^\ell $
.
As discussed in the introduction, the strategy is to build
![]() ${r}_{2^\ell }$
inductively by gluing together several copies of
${r}_{2^\ell }$
inductively by gluing together several copies of
![]() ${r}_{2^{\ell -1}}$
without adding too much stuff in between. Before giving the detailed proof, we start with a lemma about self-maps of spheres which will also be useful for the general case of Theorem 3.1.
${r}_{2^{\ell -1}}$
without adding too much stuff in between. Before giving the detailed proof, we start with a lemma about self-maps of spheres which will also be useful for the general case of Theorem 3.1.
Lemma 3.3. For every d, there is a map
![]() $f_d:S^n \to S^n$
of degree
$f_d:S^n \to S^n$
of degree
![]() $d^n$
whose Lipschitz constant is
$d^n$
whose Lipschitz constant is
![]() $C_1(n)d$
. Moreover, for each
$C_1(n)d$
. Moreover, for each
![]() $p>1$
, there is a
$p>1$
, there is a
![]() $C_2(n)pd$
-Lipschitz homotopy
$C_2(n)pd$
-Lipschitz homotopy
![]() $H_p:S^n \times [0,1] \to S^n$
between
$H_p:S^n \times [0,1] \to S^n$
between
![]() $f_{pd}$
and
$f_{pd}$
and
![]() $f_d \circ f_p$
.
$f_d \circ f_p$
.
Proof. Give
![]() $S^n$
the metric of
$S^n$
the metric of
![]() $\partial [0,1]^{n+1}$
, which is
$\partial [0,1]^{n+1}$
, which is
![]() $C_0$
-bilipschitz to the round metric, and divide the face
$C_0$
-bilipschitz to the round metric, and divide the face
![]() $[0,1]^n \times \{0\}$
into
$[0,1]^n \times \{0\}$
into
![]() $d^n$
identical sub-cubes, d to a side. We map all other faces to a base point, and the sub-cubes to the sphere by a rescaling of a degree 1 map
$d^n$
identical sub-cubes, d to a side. We map all other faces to a base point, and the sub-cubes to the sphere by a rescaling of a degree 1 map
whose restriction to
![]() $g^{-1}([0,1]^n \times \{0\})$
is homothetic to the identity map. The resulting map has degree
$g^{-1}([0,1]^n \times \{0\})$
is homothetic to the identity map. The resulting map has degree
![]() $d^n$
, and its Lipschitz constant in the round metric is bounded by
$d^n$
, and its Lipschitz constant in the round metric is bounded by
![]() $C_0^2(\operatorname {\mathrm {Lip}} g)d$
.
$C_0^2(\operatorname {\mathrm {Lip}} g)d$
.
Now, consider the map
![]() $f_d \circ f_p$
. Like
$f_d \circ f_p$
. Like
![]() $f_{pd}$
, it consists of
$f_{pd}$
, it consists of
![]() $(pd)^n$
cubical preimages of
$(pd)^n$
cubical preimages of
![]() $S^n$
, with the rest of the sphere mapped to the basepoint. However, instead of one cluster of preimages filling a whole face of
$S^n$
, with the rest of the sphere mapped to the basepoint. However, instead of one cluster of preimages filling a whole face of
![]() $\partial [0,1]^{n+1}$
, there are
$\partial [0,1]^{n+1}$
, there are
![]() $p^n$
clusters of slightly smaller preimages. We homotope
$p^n$
clusters of slightly smaller preimages. We homotope
![]() $f_d \circ f_p$
to
$f_d \circ f_p$
to
![]() $f_{pd}$
by linearly expanding these preimages to fill the whole face. The Lipschitz constant of this homotopy is bounded by
$f_{pd}$
by linearly expanding these preimages to fill the whole face. The Lipschitz constant of this homotopy is bounded by
![]() $\operatorname {\mathrm {Lip}} f_d \cdot \operatorname {\mathrm {Lip}} f_p=C_0^4(\operatorname {\mathrm {Lip}} g)^2 pd$
.
$\operatorname {\mathrm {Lip}} f_d \cdot \operatorname {\mathrm {Lip}} f_p=C_0^4(\operatorname {\mathrm {Lip}} g)^2 pd$
.
Proof of Theorem 3.2
We fix a cell structure for
![]() $M=\#_k {\mathbb {C}} P^2$
consisting of one
$M=\#_k {\mathbb {C}} P^2$
consisting of one
![]() $0$
-cell,
$0$
-cell,
![]() $k 2$
-cells and a
$k 2$
-cells and a
![]() $4$
-cell. Let
$4$
-cell. Let
![]() $\iota :[0,1]^4 \to M$
be the inclusion map of the
$\iota :[0,1]^4 \to M$
be the inclusion map of the
![]() $4$
-cell and let
$4$
-cell and let
 $$\begin{align*}\partial=\iota|_{\partial[0,1]^4}:S^3 \to M^{(2)}=\bigvee_{i=1}^k S^2\end{align*}$$
$$\begin{align*}\partial=\iota|_{\partial[0,1]^4}:S^3 \to M^{(2)}=\bigvee_{i=1}^k S^2\end{align*}$$
be its attaching map. The projection of
![]() $\partial $
to each
$\partial $
to each
![]() $S^2$
summand has Hopf invariant one. Notice that a map
$S^2$
summand has Hopf invariant one. Notice that a map
![]() $\bigvee _{i=1}^k S^2 \to \bigvee _{i=1}^k S^2$
which sends each
$\bigvee _{i=1}^k S^2 \to \bigvee _{i=1}^k S^2$
which sends each
![]() $S^2$
to itself with degree d extends to a map
$S^2$
to itself with degree d extends to a map
![]() $M \to M$
of degree
$M \to M$
of degree
![]() $d^2$
.
$d^2$
.
We prove the theorem by induction on
![]() $\ell $
. For the base of the induction, we take
$\ell $
. For the base of the induction, we take
![]() ${r}_1:M \to M$
to be any map whose restriction to each
${r}_1:M \to M$
to be any map whose restriction to each
![]() $2$
-cell is the map
$2$
-cell is the map
![]() $f_2:S^2 \to S^2$
from Lemma 3.3.
$f_2:S^2 \to S^2$
from Lemma 3.3.
For the inductive step, assume that we have constructed a
![]() $C(\ell -1) \cdot 2^{\ell -1}$
-Lipschitz map
$C(\ell -1) \cdot 2^{\ell -1}$
-Lipschitz map
![]() ${r}_{2^{\ell -1}}:M \to M$
whose restriction to each
${r}_{2^{\ell -1}}:M \to M$
whose restriction to each
![]() $2$
-cell is
$2$
-cell is
![]() $f_{2^{\ell -1}}$
. To build
$f_{2^{\ell -1}}$
. To build
![]() ${r}_{2^\ell }$
, we take a
${r}_{2^\ell }$
, we take a
![]() $2 \times 2 \times 2 \times 2$
grid of sub-cubes inside
$2 \times 2 \times 2 \times 2$
grid of sub-cubes inside
![]() $[0,1]^4$
, each of side length
$[0,1]^4$
, each of side length
![]() $\frac {1}{2}\cdot \frac {\ell -1}{\ell }$
, and send each of them to M via a homothetic rescaling of
$\frac {1}{2}\cdot \frac {\ell -1}{\ell }$
, and send each of them to M via a homothetic rescaling of
![]() ${r}_{2^{\ell -1}} \circ \iota $
. Then the Lipschitz constant on each sub-cube is
${r}_{2^{\ell -1}} \circ \iota $
. Then the Lipschitz constant on each sub-cube is
![]() $C\ell \cdot 2^\ell $
.
$C\ell \cdot 2^\ell $
.
We must now extend the map to the rest of
![]() $[0,1]^4$
, filling the space in between with the same Lipschitz constant. These gaps have width on the order of
$[0,1]^4$
, filling the space in between with the same Lipschitz constant. These gaps have width on the order of
![]() $1/\ell $
.
$1/\ell $
.
First, we fix some notation. Let
![]() $A \subseteq [0,1]^4$
be the complement of the
$A \subseteq [0,1]^4$
be the complement of the
![]() $16$
open subcubes
$16$
open subcubes
and fix a Lipschitz map
![]() $g:A \to M^{(2)}$
which restricts to a map homothetic to
$g:A \to M^{(2)}$
which restricts to a map homothetic to
![]() $\partial $
on each
$\partial $
on each
![]() $\partial K_{\bar a}$
and to
$\partial K_{\bar a}$
and to
![]() $f_2 \circ \partial $
on
$f_2 \circ \partial $
on
![]() $\partial [0,1]^4$
. Here, we write
$\partial [0,1]^4$
. Here, we write
![]() $f_d:\bigvee _{i=1}^k S^2 \to \bigvee _{i=1}^k S^2$
for the map which induces the map from Lemma 3.3 on each wedge summand.
$f_d:\bigvee _{i=1}^k S^2 \to \bigvee _{i=1}^k S^2$
for the map which induces the map from Lemma 3.3 on each wedge summand.
Now, we construct
![]() ${r}_{2^\ell }$
as follows:
${r}_{2^\ell }$
as follows:
-
• In
 $[0,1]^4$
but outside of
$[0,1]^4$
but outside of
 $(\frac {1}{8\ell },1-\frac {1}{8\ell })^4$
, the map is a homotopy from
$(\frac {1}{8\ell },1-\frac {1}{8\ell })^4$
, the map is a homotopy from
 $f_{2^\ell } \circ \partial $
to
$f_{2^\ell } \circ \partial $
to
 $f_{2^{\ell -1}} \circ f_2 \circ \partial $
. Such a homotopy with domain
$f_{2^{\ell -1}} \circ f_2 \circ \partial $
. Such a homotopy with domain
 $S^3 \times [0,1]$
can be made
$S^3 \times [0,1]$
can be made
 $C_2 \cdot 2^\ell $
-Lipschitz by Lemma 3.3, so this map is
$C_2 \cdot 2^\ell $
-Lipschitz by Lemma 3.3, so this map is
 $C_3\ell \cdot 2^\ell $
-Lipschitz for some fixed constant
$C_3\ell \cdot 2^\ell $
-Lipschitz for some fixed constant
 $C_3$
.
$C_3$
. -
• In
 $[\frac {1}{8\ell },1-\frac {1}{8\ell }]^4$
but outside of the
$[\frac {1}{8\ell },1-\frac {1}{8\ell }]^4$
but outside of the
 $16$
sub-cubes of width
$16$
sub-cubes of width
 $2\frac {\ell -1}{\ell }$
, the map is
$2\frac {\ell -1}{\ell }$
, the map is
 $f_{2^{\ell -1}} \circ g \circ s_\ell $
, where
$f_{2^{\ell -1}} \circ g \circ s_\ell $
, where
 $s_\ell $
is a
$s_\ell $
is a
 $2\ell $
-Lipschitz piecewise linear map that sends the domain to A, as shown in Figure 2.
$2\ell $
-Lipschitz piecewise linear map that sends the domain to A, as shown in Figure 2.
Figure 2 Inductively assembling the map
 ${r}_{2^\ell }$
. The light gray regions map to
${r}_{2^\ell }$
. The light gray regions map to
 $M^{(2)}$
, and the dark gray regions map to the
$M^{(2)}$
, and the dark gray regions map to the
 $4$
-cell. Some regions are labeled with the restriction of
$4$
-cell. Some regions are labeled with the restriction of
 ${r}_{2^\ell }$
to that region.
${r}_{2^\ell }$
to that region.
Then we have
By induction, the theorem is proven with
![]() $C=\max \left\{C_2,2C_1\operatorname {\mathrm {Lip}} g,\operatorname {\mathrm {Lip}} {r}_1\right\}$
.
$C=\max \left\{C_2,2C_1\operatorname {\mathrm {Lip}} g,\operatorname {\mathrm {Lip}} {r}_1\right\}$
.
3.2. Building efficient self-maps
We give a mostly elementary proof of Theorem 3.1, building maps
![]() ${r}_q$
‘by hand’. The definition of formality gives us a self-map
${r}_q$
‘by hand’. The definition of formality gives us a self-map
![]() ${r}_p:Y \to Y$
of degree
${r}_p:Y \to Y$
of degree
![]() $p^n$
; the proof consists of homotoping the iterates
$p^n$
; the proof consists of homotoping the iterates
![]() $({r}_p)^\ell $
to maps
$({r}_p)^\ell $
to maps
![]() ${r}_{p^\ell }$
with a controlled Lipschitz constant. Although we have no control over the Lipschitz constant of the original
${r}_{p^\ell }$
with a controlled Lipschitz constant. Although we have no control over the Lipschitz constant of the original
![]() ${r}_p$
, this only affects the multiplicative constant.
${r}_p$
, this only affects the multiplicative constant.
First, we assume that Y is a finite CW complex of a particular form. We construct
![]() ${r}_{p^\ell }$
by induction on skeleta, extending along one cell at a time. Each n-cell maps to itself with degree
${r}_{p^\ell }$
by induction on skeleta, extending along one cell at a time. Each n-cell maps to itself with degree
![]() $p^{\ell n}$
and contains a grid of homeomorphic preimages of its interior,
$p^{\ell n}$
and contains a grid of homeomorphic preimages of its interior,
![]() $p^\ell $
to a side. The tricky part, and the source of the polylog factor, is filling in the area between these preimages. This is done by induction on
$p^\ell $
to a side. The tricky part, and the source of the polylog factor, is filling in the area between these preimages. This is done by induction on
![]() $\ell $
: we take
$\ell $
: we take
![]() $p^n$
copies of
$p^n$
copies of
![]() ${r}_{p^{\ell -1}}$
, arranged in a grid, and glue them together using a homotopy built in the course of the
${r}_{p^{\ell -1}}$
, arranged in a grid, and glue them together using a homotopy built in the course of the
![]() $(n-1)$
-dimensional construction. The Lipschitz constant of this homotopy is proportional to the Lipschitz constant obtained for self-maps of
$(n-1)$
-dimensional construction. The Lipschitz constant of this homotopy is proportional to the Lipschitz constant obtained for self-maps of
![]() $Y^{(n-1)}$
; since there are
$Y^{(n-1)}$
; since there are
![]() $\log \ell $
nested layers, we gain a factor of
$\log \ell $
nested layers, we gain a factor of
![]() $\log \ell $
in moving from
$\log \ell $
in moving from
![]() $Y^{(n-1)}$
to
$Y^{(n-1)}$
to
![]() $Y^{(n)}$
.
$Y^{(n)}$
.
In passing from self-maps of the CW complex to those of our original manifold, we gain an additional factor of a for the degree.
We now give the details of this argument. This is the heart of the proof of Theorem 3.1, although it only covers a special case. The remainder of the section after this proof is devoted to showing that this is sufficient to prove the general case.
Lemma 3.4. Let Z be a simply connected finite CW complex with the following properties:
-
•
 $H^i(Z)$
is nontrivial in d different dimensions (not including
$H^i(Z)$
is nontrivial in d different dimensions (not including
 $i=0$
).
$i=0$
). -
• The cellular chain complex has zero differential. (In other words, the cells are in bijection with a basis for
 $H^*(Z)$
.)
$H^*(Z)$
.) -
• The attaching maps of Z are Lipschitz maps
 $D^n \to Z^{(n-1)}$
.
$D^n \to Z^{(n-1)}$
.
Let
![]() ${r}_p:Z \to Z$
be a map which induces multiplication by
${r}_p:Z \to Z$
be a map which induces multiplication by
![]() $p^i$
on
$p^i$
on
![]() $H^i(Z;\mathbb Q)$
for every
$H^i(Z;\mathbb Q)$
for every
![]() $i>0$
. Then there is a metric on Z such that every iterate
$i>0$
. Then there is a metric on Z such that every iterate
![]() $({r}_p)^\ell $
of
$({r}_p)^\ell $
of
![]() ${r}_p$
is homotopic to a
${r}_p$
is homotopic to a
![]() $C({r}_p,Z)\ell ^{d-1}p^\ell $
-Lipschitz map
$C({r}_p,Z)\ell ^{d-1}p^\ell $
-Lipschitz map
![]() ${r}_{p^\ell }:Z \to Z$
. Moreover,
${r}_{p^\ell }:Z \to Z$
. Moreover,
![]() ${r}_{p^\ell }$
is homotopic to
${r}_{p^\ell }$
is homotopic to
![]() ${r}_{p^{\ell -1}} \circ {r}_p$
via a
${r}_{p^{\ell -1}} \circ {r}_p$
via a
![]() $C'({r}_p,Z)\ell ^{d-1}p^\ell $
-Lipschitz homotopy
$C'({r}_p,Z)\ell ^{d-1}p^\ell $
-Lipschitz homotopy
![]() $H_\ell :Z \times [0,1] \to Z$
.
$H_\ell :Z \times [0,1] \to Z$
.
The homotopy
![]() $H_\ell $
is needed for the inductive step in order to prove the lemma one dimension higher.
$H_\ell $
is needed for the inductive step in order to prove the lemma one dimension higher.
Proof. First suppose that
![]() $d=1$
and let
$d=1$
and let
![]() $n=\dim Z$
. Then Z is a wedge of n-spheres, so the base of the induction is provided by Lemma 3.3.
$n=\dim Z$
. Then Z is a wedge of n-spheres, so the base of the induction is provided by Lemma 3.3.
Now suppose that we have proved the lemma for spaces with cells in
![]() $d-1$
dimensions, in particular for
$d-1$
dimensions, in particular for
![]() $Z^{(n-1)}$
where
$Z^{(n-1)}$
where
![]() $\dim Z=n \geq 3$
. We start by building a metric on Z as follows. First, homothetically shrink
$\dim Z=n \geq 3$
. We start by building a metric on Z as follows. First, homothetically shrink
![]() $Z^{(n-1)}$
until the attaching maps of n-cells can be given by
$Z^{(n-1)}$
until the attaching maps of n-cells can be given by
![]() $1$
-Lipschitz maps from
$1$
-Lipschitz maps from
![]() $\partial [0,1]^n$
. Then give Z the nearly Euclidean metric (as defined further down in §3.3) derived from attaching cells isometric to
$\partial [0,1]^n$
. Then give Z the nearly Euclidean metric (as defined further down in §3.3) derived from attaching cells isometric to
![]() $[0,1]^n$
.
$[0,1]^n$
.
By Proposition 3.6, proved further down, we can also assume that
![]() ${r}_p:Z \to Z$
is cellular and Lipschitz. By applying a homotopy which is constant on the
${r}_p:Z \to Z$
is cellular and Lipschitz. By applying a homotopy which is constant on the
![]() $(n-1)$
-skeleton, we can also ensure that
$(n-1)$
-skeleton, we can also ensure that
![]() ${r}_p$
has the following property:
${r}_p$
has the following property:
For every open n-cell e of Z,
![]() $\overline {{r}_p^{-1}(e)}$
is a disjoint union of
$\overline {{r}_p^{-1}(e)}$
is a disjoint union of
![]() $p^n$
subcubes of
$p^n$
subcubes of
![]() $(0,1)^n$
, arranged in a grid inside e, whose interiors map homothetically to e.
$(0,1)^n$
, arranged in a grid inside e, whose interiors map homothetically to e.
Such a homotopy can be performed in several steps. First, ensure that
![]() ${r}_p$
is smooth on the preimages of the ‘middle halves’ of n-cells and that the centers of the cells are regular values. Then, by composing with a homotopy that expands a small neighborhood of the center to cover the whole cell, ensure that the preimage of each open n-cell is a disjoint union of homeomorphic copies. Then, since Z is simply connected and
${r}_p$
is smooth on the preimages of the ‘middle halves’ of n-cells and that the centers of the cells are regular values. Then, by composing with a homotopy that expands a small neighborhood of the center to cover the whole cell, ensure that the preimage of each open n-cell is a disjoint union of homeomorphic copies. Then, since Z is simply connected and
![]() $n \geq 3$
, it is possible to cancel out copies of opposite orientations. The details of this purely topological argument can be found, for example, in [Reference Griffiths and Morgan14, Lemma 5.3] or [Reference White24]. Finally, we can deform this map to obtain the desired geometry.
$n \geq 3$
, it is possible to cancel out copies of opposite orientations. The details of this purely topological argument can be found, for example, in [Reference Griffiths and Morgan14, Lemma 5.3] or [Reference White24]. Finally, we can deform this map to obtain the desired geometry.
We now construct
![]() ${r}_{p^\ell }$
and
${r}_{p^\ell }$
and
![]() $H_\ell $
by induction on
$H_\ell $
by induction on
![]() $\ell $
. Suppose we have constructed a map
$\ell $
. Suppose we have constructed a map
![]() ${r}_{p^{\ell -1}}$
that is
${r}_{p^{\ell -1}}$
that is
![]() $C({r}_p,Z)(\ell -1)^{d-1}p^{\ell -1}$
-Lipschitz and is an extension of
$C({r}_p,Z)(\ell -1)^{d-1}p^{\ell -1}$
-Lipschitz and is an extension of
![]() ${r}_{p^{\ell -1}}^{(n-1)}$
to the n-cells of Z. We will homotope
${r}_{p^{\ell -1}}^{(n-1)}$
to the n-cells of Z. We will homotope
![]() ${r}_{p^{\ell -1}} \circ {r}_p$
to the desired
${r}_{p^{\ell -1}} \circ {r}_p$
to the desired
![]() $C({r}_p,Z)\ell ^{d-1}p^\ell $
-Lipschitz map
$C({r}_p,Z)\ell ^{d-1}p^\ell $
-Lipschitz map
![]() ${r}_{p^\ell }$
.
${r}_{p^\ell }$
.
We first apply the homotopy
![]() $H_\ell ^{(n-1)}$
to
$H_\ell ^{(n-1)}$
to
![]() $Z^{(n-1)}$
. We extend this homotopy to a n-cell e as follows. Equip e with polar coordinates
$Z^{(n-1)}$
. We extend this homotopy to a n-cell e as follows. Equip e with polar coordinates
![]() $(s,\theta )$
, with
$(s,\theta )$
, with
![]() $\theta \in S^{n-1}$
and
$\theta \in S^{n-1}$
and
![]() $s \in [0,1)$
, and denote the attaching map of e by
$s \in [0,1)$
, and denote the attaching map of e by
![]() $\partial _e:S^{n-1} \to Z^{(n-1)}$
. We define a homotopy
$\partial _e:S^{n-1} \to Z^{(n-1)}$
. We define a homotopy
![]() $\tilde H:e \times [0,1] \to Z^{(n-1)}$
by
$\tilde H:e \times [0,1] \to Z^{(n-1)}$
by
 $$\begin{align*}\tilde H(s,\theta,t)=\begin{cases} H_\ell^{(n-1)}(\partial_e(\theta),t+2(s-1)), & s \geq 1-t/2, \\ {r}_{p^{\ell-1}} \circ {r}_p(\theta,(1-t/2)^{-1}s), & s \leq 1-t/2. \end{cases}\end{align*}$$
$$\begin{align*}\tilde H(s,\theta,t)=\begin{cases} H_\ell^{(n-1)}(\partial_e(\theta),t+2(s-1)), & s \geq 1-t/2, \\ {r}_{p^{\ell-1}} \circ {r}_p(\theta,(1-t/2)^{-1}s), & s \leq 1-t/2. \end{cases}\end{align*}$$
From this formula we see that
-
• When
 $s=1$
,
$s=1$
,
 $\tilde H(s,\theta ,t)$
agrees with
$\tilde H(s,\theta ,t)$
agrees with
 $H_\ell ^{(n-1)}$
.
$H_\ell ^{(n-1)}$
. -
• At
 $s=1-t/2$
,
$s=1-t/2$
,
 $\tilde H$
is continuous since
$\tilde H$
is continuous since  $$\begin{align*}H_\ell^{(n-1)}(\partial_e(\theta),t+2(s-1))=H_\ell^{(n-1)}(\partial_e(\theta),0)={r}_{p^{\ell-1}} \circ {r}_p(\theta,1).\end{align*}$$
$$\begin{align*}H_\ell^{(n-1)}(\partial_e(\theta),t+2(s-1))=H_\ell^{(n-1)}(\partial_e(\theta),0)={r}_{p^{\ell-1}} \circ {r}_p(\theta,1).\end{align*}$$

Figure 3 Stages of the homotopy
![]() $H_\ell $
, the concatenation of
$H_\ell $
, the concatenation of
![]() $\tilde H$
and J.
$\tilde H$
and J.
At this point,
![]() $\tilde H|_{e \times \{1\}}$
has different Lipschitz constants on different regions of e, which we bound by induction on
$\tilde H|_{e \times \{1\}}$
has different Lipschitz constants on different regions of e, which we bound by induction on
![]() $\ell $
and d:
$\ell $
and d:
-
(i) On the outer half of the disk, the Lipschitz constant is
 $$\begin{align*}L_1=2\operatorname{\mathrm{Lip}} H_\ell^{(n-1)} \leq 2C'({r}_p,Z^{(n-1)})\ell^{d-2}p^\ell.\end{align*}$$
$$\begin{align*}L_1=2\operatorname{\mathrm{Lip}} H_\ell^{(n-1)} \leq 2C'({r}_p,Z^{(n-1)})\ell^{d-2}p^\ell.\end{align*}$$
-
(ii) On the inner half, but outside
 $\frac {1}{2}{r}_p^{-1}(e)$
(here,
$\frac {1}{2}{r}_p^{-1}(e)$
(here,
 $\frac {1}{2}$
refers to the homothety
$\frac {1}{2}$
refers to the homothety
 $(s,\theta ) \mapsto (\frac {s}{2},\theta )$
), the Lipschitz constant is This bound holds because on this subdomain, the image of
$(s,\theta ) \mapsto (\frac {s}{2},\theta )$
), the Lipschitz constant is This bound holds because on this subdomain, the image of $$\begin{align*}L_2=2\operatorname{\mathrm{Lip}}\big({r}_{p^{\ell-1}} \circ {r}_p\big) \leq \operatorname{\mathrm{Lip}}({r}_p) \cdot 2C({r}_p,Z^{(n-1)})(\ell-1)^{d-2}p^{\ell-1}.\end{align*}$$
$$\begin{align*}L_2=2\operatorname{\mathrm{Lip}}\big({r}_{p^{\ell-1}} \circ {r}_p\big) \leq \operatorname{\mathrm{Lip}}({r}_p) \cdot 2C({r}_p,Z^{(n-1)})(\ell-1)^{d-2}p^{\ell-1}.\end{align*}$$
 ${r}_p(\theta ,s/2)$
lies in
${r}_p(\theta ,s/2)$
lies in
 $Z^{(n-1)}$
.
$Z^{(n-1)}$
.
-
(iii) In
 $\frac {1}{2}{r}_p^{-1}(e)$
, the Lipschitz constant is where D is the side length of one of the subcubes comprising
$\frac {1}{2}{r}_p^{-1}(e)$
, the Lipschitz constant is where D is the side length of one of the subcubes comprising $$\begin{align*}L_3=D^{-1}\operatorname{\mathrm{Lip}} {r}_{p^{\ell-1}} \leq D^{-1}C({r}_p,Z)(\ell-1)^{d-1}p^{\ell-1},\end{align*}$$
$$\begin{align*}L_3=D^{-1}\operatorname{\mathrm{Lip}} {r}_{p^{\ell-1}} \leq D^{-1}C({r}_p,Z)(\ell-1)^{d-1}p^{\ell-1},\end{align*}$$
 $\frac {1}{2}{r}_p^{-1}(e)$
.
$\frac {1}{2}{r}_p^{-1}(e)$
.
In the second stage
![]() $J:Z \times [0,1] \to Z$
of the homotopy, which is constant on
$J:Z \times [0,1] \to Z$
of the homotopy, which is constant on
![]() $Z^{(n-1)}$
, we expand and shrink these three regions via a product of piecewise linear homotopies of
$Z^{(n-1)}$
, we expand and shrink these three regions via a product of piecewise linear homotopies of
![]() $[0,1]$
so as to equalize the Lipschitz constants. At time
$[0,1]$
so as to equalize the Lipschitz constants. At time
![]() $1$
, e is nearly covered by a
$1$
, e is nearly covered by a
![]() $p \times \cdots \times p$
grid of subcubes which each map to Z via
$p \times \cdots \times p$
grid of subcubes which each map to Z via
![]() $r_{p^{\ell -1}}|_e$
composed with a homothety; the outer half of
$r_{p^{\ell -1}}|_e$
composed with a homothety; the outer half of
![]() $\tilde H|_{e \times \{1\}}$
is relegated to a thin shell on the outside of the cube. We can imagine expanding every part of the domain until the Lipschitz constant is
$\tilde H|_{e \times \{1\}}$
is relegated to a thin shell on the outside of the cube. We can imagine expanding every part of the domain until the Lipschitz constant is
![]() $1$
on each relevant subinterval and then shrinking the whole domain proportionally. This shows that the resulting map
$1$
on each relevant subinterval and then shrinking the whole domain proportionally. This shows that the resulting map
![]() $J|_{t=1}$
has Lipschitz constant bounded above by
$J|_{t=1}$
has Lipschitz constant bounded above by
 $$ \begin{align*} &pDL_3+\left(\frac{1}{2}-pD\right)L_2+\frac{1}{2}L_1 \\ &\quad\leq pC({r}_p,Z)(\ell-1)^{d-1}p^{\ell-1} + \operatorname{\mathrm{Lip}}({r}_p)C({r}_p,Z^{(n-1)})(\ell-1)^{d-2}p^{\ell-1} + C'({r}_p,Z^{(n-1)})\ell^{d-2}p^\ell \\ &\quad\leq C({r}_p,Z)\ell^{d-1}p^\ell, \end{align*} $$
$$ \begin{align*} &pDL_3+\left(\frac{1}{2}-pD\right)L_2+\frac{1}{2}L_1 \\ &\quad\leq pC({r}_p,Z)(\ell-1)^{d-1}p^{\ell-1} + \operatorname{\mathrm{Lip}}({r}_p)C({r}_p,Z^{(n-1)})(\ell-1)^{d-2}p^{\ell-1} + C'({r}_p,Z^{(n-1)})\ell^{d-2}p^\ell \\ &\quad\leq C({r}_p,Z)\ell^{d-1}p^\ell, \end{align*} $$
where the second inequality holds as long as
Then we set
![]() ${r}_{p^\ell }=J|_{t=1}$
and
${r}_{p^\ell }=J|_{t=1}$
and
![]() $H_\ell $
to be the concatenation of
$H_\ell $
to be the concatenation of
![]() $\tilde H$
and J. By computing derivatives of
$\tilde H$
and J. By computing derivatives of
![]() $\tilde H$
and J in the space and time directions, we see that
$\tilde H$
and J in the space and time directions, we see that
and therefore, we can set
![]() $C'({r}_p,Z) \leq \max \{2,(pD)^{-1}\}C({r}_p,Z)$
.
$C'({r}_p,Z) \leq \max \{2,(pD)^{-1}\}C({r}_p,Z)$
.
3.3. Lipschitz homotopy equivalence
To show that Lemma 3.4 implies Theorem 3.1, we need to introduce some geometric and topological facts. We start with the geometry, discussing metrics on CW complexes: we would like to show that the ‘special’ metric we imposed on the complex Z in Lemma 3.4 is not too special to be useful.
The relevant ideas date back to Gromov (see, for example, [Reference Gromov15, §7.20] and are developed more systematically in [Reference Liu, Yu and Liu17]. The basic idea is that if two homotopy equivalent metric spaces are compact and sufficiently locally nice, then they are Lipschitz homotopy equivalent (in the obvious sense).
The importance of this is that asymptotic results about Lipschitz constants are preserved under Lipschitz homotopy equivalence. That is, for metric spaces X and Y, define the Lipschitz norm of a homotopy class
![]() $\alpha \in [X,Y]$
to be
$\alpha \in [X,Y]$
to be
Suppose now that
![]() $f:X' \to X$
and
$f:X' \to X$
and
![]() $g:Y \to Y'$
are Lipschitz homotopy equivalences. Then there are constants
$g:Y \to Y'$
are Lipschitz homotopy equivalences. Then there are constants
![]() $C,K>0$
depending on f and g (but not
$C,K>0$
depending on f and g (but not
![]() $\alpha $
) such that
$\alpha $
) such that
Therefore, asymptotics such as those in Theorem A are invariant under Lipschitz homotopy equivalence.
Definition. A nearly Euclidean CW complex is a CW complex X equipped with a metric constructed inductively as follows. The 1-skeleton is a metric graph. Once we have constructed a metric on
![]() $X^{(n-1)}$
, we also fix a metric
$X^{(n-1)}$
, we also fix a metric
![]() $d_i$
on
$d_i$
on
![]() $D^n$
for every n-cell
$D^n$
for every n-cell
![]() $e_i$
, such that
$e_i$
, such that
![]() $d_i$
is bilipschitz to the standard Euclidean metric and the attaching map
$d_i$
is bilipschitz to the standard Euclidean metric and the attaching map
![]() $f_i:S^{n-1} \to X^{(n-1)}$
is Lipschitz with respect to the induced metric on
$f_i:S^{n-1} \to X^{(n-1)}$
is Lipschitz with respect to the induced metric on
![]() $S^{n-1}=\partial D^n$
. Then the metric on
$S^{n-1}=\partial D^n$
. Then the metric on
![]() $X^{(n)}$
is the quotient metric with respect to this gluing.
$X^{(n)}$
is the quotient metric with respect to this gluing.
In particular, notice that if
![]() $L=\max _i \operatorname {\mathrm {Lip}}(f_i)$
, then for points
$L=\max _i \operatorname {\mathrm {Lip}}(f_i)$
, then for points
![]() $x,y \in X^{(n-1)}$
,
$x,y \in X^{(n-1)}$
,
For example, every compact Riemannian manifold is smoothly triangulable; with any such triangulation, it is a nearly Euclidean CW complex. More generally, every simplicial complex with a simplexwise Riemannian metric is an example.
Proposition 3.5. Suppose that X and Y are homotopy equivalent nearly Euclidean finite CW complexes. Then they are Lipschitz homotopy equivalent.
In particular, the metric we constructed on Z in the proof of Lemma 3.4 is nearly Euclidean, and so Z is Lipschitz homotopy equivalent to, for example, any homotopy equivalent compact Riemannian manifold.
This follows immediately from the following more general statement:
Proposition 3.6. Let X and Y be nearly Euclidean finite CW complexes, and
![]() $A \subset X$
a subcomplex. Let
$A \subset X$
a subcomplex. Let
![]() $f:X \to Y$
be a map such that
$f:X \to Y$
be a map such that
![]() $f|_A$
is Lipschitz. Then f is homotopic rel A to a Lipschitz map. Moreover, if the original map is cellular, then so is the new map.
$f|_A$
is Lipschitz. Then f is homotopic rel A to a Lipschitz map. Moreover, if the original map is cellular, then so is the new map.
There is another useful consequence of this fact:
Corollary 3.7. Given a finite CW complex X, we can always find a homotopy equivalent complex with a nearly Euclidean metric.
Proof. We use induction on skeleta. Suppose we have constructed a complex
![]() $Y^{(k)}$
with a nearly Euclidean metric and a homotopy equivalence
$Y^{(k)}$
with a nearly Euclidean metric and a homotopy equivalence
![]() $f:X^{(k)} \to Y^{(k)}$
. Then for every
$f:X^{(k)} \to Y^{(k)}$
. Then for every
![]() $(k+1)$
-cell of X with attaching map
$(k+1)$
-cell of X with attaching map
![]() $g:S^k \to X^{(k)}$
,
$g:S^k \to X^{(k)}$
,
![]() $f \circ g$
is homotopic to a Lipschitz map
$f \circ g$
is homotopic to a Lipschitz map
![]() $\tilde g:S^k \to Y^{(k)}$
. Then we can attach a
$\tilde g:S^k \to Y^{(k)}$
. Then we can attach a
![]() $(k+1)$
-cell along
$(k+1)$
-cell along
![]() $\tilde g$
and extend f to the
$\tilde g$
and extend f to the
![]() $(k+1)$
-cell by combining
$(k+1)$
-cell by combining
![]() $\tilde g$
and the homotopy.
$\tilde g$
and the homotopy.
Proof of Prop. 3.6
We start by proving a lemma:
Lemma 3.8.
Y is locally Lipschitz contractible; that is, for every
![]() $y \in Y$
, there is a neighborhood
$y \in Y$
, there is a neighborhood
![]() $N_y \ni y$
which admits a Lipschitz deformation retraction to a point. In particular, for every n, every Lipschitz map
$N_y \ni y$
which admits a Lipschitz deformation retraction to a point. In particular, for every n, every Lipschitz map
![]() $S^n \to N_y$
extends to
$S^n \to N_y$
extends to
![]() $D^{n+1}$
(as a Lipschitz map).
$D^{n+1}$
(as a Lipschitz map).
Proof. We build such a neighborhood by induction on skeleta, using the standard construction for a contractible neighborhood inside a CW complex. Let
![]() $y \in Y$
and let k be such that y is contained in an open k-cell. Then we can take a ball in that k-cell which is Lipschitz contractible in
$y \in Y$
and let k be such that y is contained in an open k-cell. Then we can take a ball in that k-cell which is Lipschitz contractible in
![]() $Y^{(k)}$
. Now suppose we have constructed a contractible neighborhood
$Y^{(k)}$
. Now suppose we have constructed a contractible neighborhood
![]() $N(n)$
of y in
$N(n)$
of y in
![]() $Y^{(n)}$
and consider an
$Y^{(n)}$
and consider an
![]() $(n+1)$
-cell with attaching map
$(n+1)$
-cell with attaching map
![]() $f:S^n \to Y$
. Then, thinking of the cell as the cone on
$f:S^n \to Y$
. Then, thinking of the cell as the cone on
![]() $S^n$
, we can add
$S^n$
, we can add
![]() $f^{-1}(N(n)) \times [0,{\varepsilon })$
to our neighborhood. Doing this for every cell gives us a neighborhood in
$f^{-1}(N(n)) \times [0,{\varepsilon })$
to our neighborhood. Doing this for every cell gives us a neighborhood in
![]() $Y^{(n+1)}$
with an obvious deformation retraction to
$Y^{(n+1)}$
with an obvious deformation retraction to
![]() $N(n)$
, which is Lipschitz since the metric on the cell is bilipschitz to the Euclidean metric.
$N(n)$
, which is Lipschitz since the metric on the cell is bilipschitz to the Euclidean metric.
We now make f Lipschitz, also by induction on skeleta. Clearly,
![]() $f|_{X^{(0)}}$
is Lipschitz to begin with. Now suppose that
$f|_{X^{(0)}}$
is Lipschitz to begin with. Now suppose that
![]() $f|_{X^{(k)}}$
is Lipschitz (notice that this is true with respect to the metric induced from
$f|_{X^{(k)}}$
is Lipschitz (notice that this is true with respect to the metric induced from
![]() $X^{(k+1)}$
as well as that on
$X^{(k+1)}$
as well as that on
![]() $X^{(k)}$
) and consider a
$X^{(k)}$
) and consider a
![]() $(k+1)$
-cell not in A with an inclusion map
$(k+1)$
-cell not in A with an inclusion map
![]() $e:D^{k+1} \to X$
. Now take a triangulation of
$e:D^{k+1} \to X$
. Now take a triangulation of
![]() $D^{k+1}$
at a small enough scale that
$D^{k+1}$
at a small enough scale that
![]() $f \circ e$
takes every simplex into a Lipschitz contractible neighborhood. By induction on the skeleta of this triangulation, we deform
$f \circ e$
takes every simplex into a Lipschitz contractible neighborhood. By induction on the skeleta of this triangulation, we deform
![]() $f \circ e$
to a Lipschitz map, while leaving it constant on
$f \circ e$
to a Lipschitz map, while leaving it constant on
![]() $\partial D^{k+1}$
.
$\partial D^{k+1}$
.
If f is cellular, then we can construct the
![]() $(k+1)$
st stage of the homotopy as a map to
$(k+1)$
st stage of the homotopy as a map to
![]() $Y^{(k+1)}$
, rather than to Y. Then the resulting map is still cellular.
$Y^{(k+1)}$
, rather than to Y. Then the resulting map is still cellular.
3.4. Properties of formal spaces
Finally, we need to show that the topological properties of Z are also not too special to be useful. This requires some discussion of properties of formal spaces.
One property, which follows from [Reference Papadima21, Proposition 3.1], is that a map between formal spaces which induces isomorphisms on rational cohomology is rationally invertible:
Proposition 3.9. If Y is formal and
![]() $f:Z \to Y$
is a map between simply connected complexes which induces an isomorphism on rational cohomology, then Z is formal, and there is a map
$f:Z \to Y$
is a map between simply connected complexes which induces an isomorphism on rational cohomology, then Z is formal, and there is a map
![]() $g:Y \to Z$
such that
$g:Y \to Z$
such that
![]() $g \circ f$
induces multiplication by
$g \circ f$
induces multiplication by
![]() $q^n$
on
$q^n$
on
![]() $H^n(Y;\mathbb {Q})$
, for some q.
$H^n(Y;\mathbb {Q})$
, for some q.
Now, given Y, we build a rationally equivalent Z which satisfies the topological hypotheses of Lemma 3.4:
Proposition 3.10. Let Y be a simply connected space with finite-dimensional rational homology and fix a basis for
![]() $H_n(Y;\mathbb {Q})$
for every n. Then there is a CW complex Z and a map
$H_n(Y;\mathbb {Q})$
for every n. Then there is a CW complex Z and a map
![]() $f:Z \to Y$
which induces isomorphisms on rational cohomology such that:
$f:Z \to Y$
which induces isomorphisms on rational cohomology such that:
-
(i) The rational cellular chain complex of Z has zero differential; that is, rational cellular chains on Z are in bijection with
 $H_*(Z;\mathbb Q)$
.
$H_*(Z;\mathbb Q)$
. -
(ii) The induced isomorphism
 $f_*:H_n(Z;\mathbb Q) \to H_n(Y;\mathbb Q)$
maps each cell to a multiple of a basis element.
$f_*:H_n(Z;\mathbb Q) \to H_n(Y;\mathbb Q)$
maps each cell to a multiple of a basis element.
Proof. We construct Z and f by induction on skeleta. We set
![]() $Z^{(0)}=Z^{(1)}=*$
. Now suppose we have built
$Z^{(0)}=Z^{(1)}=*$
. Now suppose we have built
![]() $Z^{(n)}$
and a map
$Z^{(n)}$
and a map
![]() $f_n:Z^{(n)} \to Y$
which induces an isomorphism on
$f_n:Z^{(n)} \to Y$
which induces an isomorphism on
![]() $H_k({-};\mathbb {Q})$
,
$H_k({-};\mathbb {Q})$
,
![]() $k \leq n$
. By the rational relative Hurewicz theorem, the Hurewicz map induces an isomorphism
$k \leq n$
. By the rational relative Hurewicz theorem, the Hurewicz map induces an isomorphism
So choose elements
![]() $\alpha _1,\ldots ,\alpha _r \in \pi _{n+1}(Y,Z^{(n)})$
forming a basis for
$\alpha _1,\ldots ,\alpha _r \in \pi _{n+1}(Y,Z^{(n)})$
forming a basis for
![]() $\pi _{n+1}(Y,Z^{(n)}) \otimes \mathbb {Q}$
. We build
$\pi _{n+1}(Y,Z^{(n)}) \otimes \mathbb {Q}$
. We build
![]() $Z^{(n+1)}$
by attaching an
$Z^{(n+1)}$
by attaching an
![]() $(n+1)$
-cell
$(n+1)$
-cell
![]() $e_i$
along each
$e_i$
along each
![]() $\partial \alpha _i$
,
$\partial \alpha _i$
,
![]() $i=1,\ldots ,r$
, and extend
$i=1,\ldots ,r$
, and extend
![]() $f_n$
to
$f_n$
to
![]() $f_{n+1}:Z^{(n+1)} \to Y$
by mapping each
$f_{n+1}:Z^{(n+1)} \to Y$
by mapping each
![]() $e_i$
to Y via a representative of
$e_i$
to Y via a representative of
![]() $\alpha _i$
.
$\alpha _i$
.
Since
![]() $(f_n)_*:H_n(Z^{(n)};\mathbb {Q}) \to H_n(Y;\mathbb {Q})$
is an isomorphism, by the long exact sequence of that pair, the Hurewicz image of each
$(f_n)_*:H_n(Z^{(n)};\mathbb {Q}) \to H_n(Y;\mathbb {Q})$
is an isomorphism, by the long exact sequence of that pair, the Hurewicz image of each
![]() $\partial \alpha _i$
is zero. Therefore, the map
$\partial \alpha _i$
is zero. Therefore, the map
is an isomorphism; in other words, the cells of
![]() $Z^{(n+1)}$
form a basis for
$Z^{(n+1)}$
form a basis for
![]() $H_{n+1}(Z^{(n+1)};\mathbb {Q})$
. Moreover, by the definition of the extension
$H_{n+1}(Z^{(n+1)};\mathbb {Q})$
. Moreover, by the definition of the extension
![]() $f_{n+1}$
, the map
$f_{n+1}$
, the map
is an isomorphism. But these groups are naturally isomorphic to
![]() $H_{n+1}(Z^{(n+1)};\mathbb {Q})$
and
$H_{n+1}(Z^{(n+1)};\mathbb {Q})$
and
![]() $H_{n+1}(Y;\mathbb {Q})$
, respectively. This shows that
$H_{n+1}(Y;\mathbb {Q})$
, respectively. This shows that
![]() $f_{n+1}$
induces a bijection on
$f_{n+1}$
induces a bijection on
![]() $H_{n+1}({-};\mathbb {Q})$
as well.
$H_{n+1}({-};\mathbb {Q})$
as well.
Once we have done this in every dimension in which
![]() $H_*(Y;\mathbb {Q}) \neq 0$
, we have constructed the desired Z. To satisfy condition (ii), notice that we can always pick the
$H_*(Y;\mathbb {Q}) \neq 0$
, we have constructed the desired Z. To satisfy condition (ii), notice that we can always pick the
![]() $\alpha _i$
to be integer multiples of the elements of our chosen basis.
$\alpha _i$
to be integer multiples of the elements of our chosen basis.
Now we conclude the section:
Proof of Theorem 3.1
Let Y be a simply connected formal compact Riemannian manifold. Using Proposition 3.10, we can find a complex Z such that the cellular chain complex of Z has zero differential and a rational equivalence
![]() $g:Z \to Y$
. Moreover, by Proposition 3.9, there is a rational equivalence
$g:Z \to Y$
. Moreover, by Proposition 3.9, there is a rational equivalence
![]() $f:Y \to Z$
such that
$f:Y \to Z$
such that
![]() $f \circ g$
induces multiplication by
$f \circ g$
induces multiplication by
![]() $a^n$
on
$a^n$
on
![]() $H^n(Y;\mathbb Q)$
, for some
$H^n(Y;\mathbb Q)$
, for some
![]() $a>0$
.
$a>0$
.
By Corollary 3.7, we can put a nearly Euclidean metric on Z, and by Proposition 3.5, we can assume f and g are Lipschitz.
Now let
![]() ${r}_p:Z \to Z$
be a map that induces multiplication by
${r}_p:Z \to Z$
be a map that induces multiplication by
![]() $p^n$
on
$p^n$
on
![]() $H^n(Z;\mathbb Q)$
. By Lemma 3.4 and Proposition 3.5, for any nearly Euclidean metric on Z, and for every
$H^n(Z;\mathbb Q)$
. By Lemma 3.4 and Proposition 3.5, for any nearly Euclidean metric on Z, and for every
![]() $\ell $
, there are
$\ell $
, there are
![]() $O(p^\ell \ell ^{d-1})$
-Lipschitz maps
$O(p^\ell \ell ^{d-1})$
-Lipschitz maps
![]() ${r}_{p^\ell }$
homotopic to
${r}_{p^\ell }$
homotopic to
![]() ${r}_p^\ell $
. Then the maps
${r}_p^\ell $
. Then the maps
![]() $f \circ {r}_{p^\ell } \circ g$
are again
$f \circ {r}_{p^\ell } \circ g$
are again
![]() $O(p^\ell \ell ^{d-1})$
-Lipschitz and induce multiplication by
$O(p^\ell \ell ^{d-1})$
-Lipschitz and induce multiplication by
![]() $(ap^\ell )^n$
on
$(ap^\ell )^n$
on
![]() $H^n(Y;\mathbb R)$
.
$H^n(Y;\mathbb R)$
.
4. Rational homotopy theory
The remainder of the paper will require machinery from rational homotopy theory. We will give a very brief review of Sullivan’s theory of minimal models, referring the reader to [Reference Griffiths and Morgan14, Reference Félix, Halperin and Thomas12] for more details on the general background and [Reference Manin18, Reference Berdnikov and Manin3] for treatments geared towards quantitative topology.
Rational homotopy theory provides a way of translating the topology of simply connected spaces into algebraic language. There are several equivalent such languages, but the main one we will use is that of differential graded algebras, as developed by Sullivan.
A (commutative) differential graded algebra, or DGA, is a cochain complex over a field, typically
![]() ${\mathbb {Q}}$
or
${\mathbb {Q}}$
or
![]() ${\mathbb {R}}$
, with a graded-commutative multiplication satisfying the graded Leibniz rule. The prototypical examples are as follows:
${\mathbb {R}}$
, with a graded-commutative multiplication satisfying the graded Leibniz rule. The prototypical examples are as follows:
-
• The smooth forms
 $\Omega ^*(X)$
on a smooth manifold X, or the simplexwise smooth forms on a simplicial complex.
$\Omega ^*(X)$
on a smooth manifold X, or the simplexwise smooth forms on a simplicial complex. -
• Sullivan’s minimal DGA
 $\mathcal {M}_Y^*(\mathbb {F})$
for a simply connected space Y, which is a free-graded commutative algebra generated in degree n by a vector space of indecomposable elements
$\mathcal {M}_Y^*(\mathbb {F})$
for a simply connected space Y, which is a free-graded commutative algebra generated in degree n by a vector space of indecomposable elements
 $V_n=\operatorname {\mathrm {Hom}}(\pi _n(Y);\mathbb {F})$
and with a differential which takes elements of
$V_n=\operatorname {\mathrm {Hom}}(\pi _n(Y);\mathbb {F})$
and with a differential which takes elements of
 $V_n$
to elements of
$V_n$
to elements of
 $\Lambda _{k=2}^{n-1} V_k$
and is dual to the k-invariants in the Postnikov tower of Y,
$\Lambda _{k=2}^{n-1} V_k$
and is dual to the k-invariants in the Postnikov tower of Y,
 $k_n \in H^{n+1}(Y_{n-1};\pi _n(Y))$
. We will write noting that this isomorphism is noncanonical. We also write
$k_n \in H^{n+1}(Y_{n-1};\pi _n(Y))$
. We will write noting that this isomorphism is noncanonical. We also write $$\begin{align*}\mathcal M_Y^*=\mathcal M_Y^*({\mathbb{R}}) \cong \Lambda_{n=2}^\infty V_n,\end{align*}$$
this is the minimal DGA of the nth Postnikov stage of Y.
$$\begin{align*}\mathcal M_Y^*=\mathcal M_Y^*({\mathbb{R}}) \cong \Lambda_{n=2}^\infty V_n,\end{align*}$$
this is the minimal DGA of the nth Postnikov stage of Y. $$\begin{align*}\mathcal M_Y^*(n)=\Lambda_{k=2}^n V_k;\end{align*}$$
$$\begin{align*}\mathcal M_Y^*(n)=\Lambda_{k=2}^n V_k;\end{align*}$$
There is an algebraic notion of homotopy between morphisms of DGAs which will not figure explicitly in this paper. A quasi-isomorphism between DGAs is a map inducing an isomorphism on cohomology. The existence of such a map between
![]() $\mathcal A$
and
$\mathcal A$
and
![]() $\mathcal B$
is not an equivalence relation; therefore, we say that two DGAs are quasi-isomorphic if they are connected by a zig-zag of one or more quasi-isomorphisms
$\mathcal B$
is not an equivalence relation; therefore, we say that two DGAs are quasi-isomorphic if they are connected by a zig-zag of one or more quasi-isomorphisms
If Y is a smooth manifold or simplicial complex, then it has a (non-unique) minimal model, that is, a quasi-isomorphism
![]() $m_Y:\mathcal M_Y^* \to \Omega ^*(Y)$
realizing the generators of the minimal DGA as differential forms. The codomain of the minimal model may also be the algebra
$m_Y:\mathcal M_Y^* \to \Omega ^*(Y)$
realizing the generators of the minimal DGA as differential forms. The codomain of the minimal model may also be the algebra
![]() $\Omega ^*_\flat (Y)$
of flat forms in the sense of Whitney, which are a completion of the smooth forms with respect to the
$\Omega ^*_\flat (Y)$
of flat forms in the sense of Whitney, which are a completion of the smooth forms with respect to the
![]() $L^\infty $
norm; see [Reference Berdnikov and Manin3, §2 and 6.1] and [Reference Whitney25, Ch. IX]. When we want to be noncommittal about whether we are using smooth or flat forms, we write
$L^\infty $
norm; see [Reference Berdnikov and Manin3, §2 and 6.1] and [Reference Whitney25, Ch. IX]. When we want to be noncommittal about whether we are using smooth or flat forms, we write
![]() $\Omega ^*_{(\flat )}(Y)$
.
$\Omega ^*_{(\flat )}(Y)$
.
We will frequently leave the map
![]() $m_Y$
implicit when we speak of the rationalization of a map
$m_Y$
implicit when we speak of the rationalization of a map
![]() $f:Y \to Z$
, which is a map
$f:Y \to Z$
, which is a map
![]() $\rho $
which completes the commutative square
$\rho $
which completes the commutative square

up to homotopy. Such a map
![]() $\rho $
always exists and is unique up to homotopy of DGA homomorphisms.
$\rho $
always exists and is unique up to homotopy of DGA homomorphisms.
In the rest of this section, we introduce some prior results in quantitative homotopy theory as well as some information about formal spaces.
4.1. The shadowing principle
The main technical result of [Reference Manin18] shows a kind of coarse density of genuine maps in the space of ‘formal’ rational-homotopic maps between spaces X and Y. That is, given a homomorphism
![]() $\mathcal {M}_Y^* \to \Omega _{(\flat )}^*(X)$
, one can produce a nearby genuine map
$\mathcal {M}_Y^* \to \Omega _{(\flat )}^*(X)$
, one can produce a nearby genuine map
![]() $X \to Y$
whose Lipschitz constant depends on geometric properties of the homomorphism.
$X \to Y$
whose Lipschitz constant depends on geometric properties of the homomorphism.
To state this precisely, we first introduce some definitions. Let X and Y be finite simplicial complexes or compact Riemannian manifolds such that Y is simply connected and has a minimal model
![]() $m_Y:\mathcal {M}_Y^*\to \Omega _\flat ^*Y$
. Fix norms on the finite-dimensional vector spaces
$m_Y:\mathcal {M}_Y^*\to \Omega _\flat ^*Y$
. Fix norms on the finite-dimensional vector spaces
![]() $V_k$
of degree k indecomposables of
$V_k$
of degree k indecomposables of
![]() $\mathcal {M}_Y^*$
; then for homomorphisms
$\mathcal {M}_Y^*$
; then for homomorphisms
![]() ${\varphi }:\mathcal {M}_Y^* \to \Omega _\flat ^*(X)$
, we define the formal dilatation
${\varphi }:\mathcal {M}_Y^* \to \Omega _\flat ^*(X)$
, we define the formal dilatation
where we use the
![]() $L^\infty $
norm on
$L^\infty $
norm on
![]() $\Omega _\flat ^*(X)$
. Notice that if
$\Omega _\flat ^*(X)$
. Notice that if
![]() $f:X \to Y$
is an L-Lipschitz map, then
$f:X \to Y$
is an L-Lipschitz map, then
![]() ${\operatorname {\mathrm {Dil}}(f^*m_Y) \leq CL}$
, where the exact constant depends on the dimension of X, the minimal model on Y and the norms. Thus, the dilatation is an algebraic analogue of the Lipschitz constant.
${\operatorname {\mathrm {Dil}}(f^*m_Y) \leq CL}$
, where the exact constant depends on the dimension of X, the minimal model on Y and the norms. Thus, the dilatation is an algebraic analogue of the Lipschitz constant.
Given a formal homotopy
we can define the dilatation
![]() $\operatorname {\mathrm {Dil}}_T(\Phi )$
in a similar way. The subscript indicates that we can always rescale
$\operatorname {\mathrm {Dil}}_T(\Phi )$
in a similar way. The subscript indicates that we can always rescale
![]() $\Phi $
to spread over a smaller or larger interval, changing the dilatation; this is a formal analogue of defining separate Lipschitz constants in the time and space direction, although in the DGA world, they are not so easily separable.
$\Phi $
to spread over a smaller or larger interval, changing the dilatation; this is a formal analogue of defining separate Lipschitz constants in the time and space direction, although in the DGA world, they are not so easily separable.
Now we can state some results from [Reference Manin18]. They are stated in that paper in terms of smooth forms; for the argument that they can be adapted to flat forms, see [Reference Berdnikov and Manin3, §6].
Theorem 4.1 (A special case of the shadowing principle, [Reference Manin18, Thm. 4–1])
Let X be a Riemannian manifold or simplicial complex of locally bounded geometry, and let Y be a simply connected compact Riemmanian manifold or simplicial complex. Let
![]() ${\varphi }:\mathcal {M}_Y^* \to \Omega _{(\flat )}^*(X)$
be a homomorphism with
${\varphi }:\mathcal {M}_Y^* \to \Omega _{(\flat )}^*(X)$
be a homomorphism with
![]() $\operatorname {\mathrm {Dil}}({\varphi }) \leq L$
which is formally homotopic to
$\operatorname {\mathrm {Dil}}({\varphi }) \leq L$
which is formally homotopic to
![]() $f^*m_Y$
for some
$f^*m_Y$
for some
![]() $f:X \to Y$
. Then f is homotopic to a
$f:X \to Y$
. Then f is homotopic to a
![]() $g:X \to Y$
which is
$g:X \to Y$
which is
![]() $C(X,Y)(L+1)$
-Lipschitz and such that
$C(X,Y)(L+1)$
-Lipschitz and such that
![]() $g^*m_Y$
is homotopic to
$g^*m_Y$
is homotopic to
![]() ${\varphi }$
via a homotopy
${\varphi }$
via a homotopy
![]() $\Phi $
with
$\Phi $
with
![]() $\operatorname {\mathrm {Dil}}_{1/L}(\Phi ) \leq C(X,Y)(L+1)$
.
$\operatorname {\mathrm {Dil}}_{1/L}(\Phi ) \leq C(X,Y)(L+1)$
.
In other words, one can produce a genuine map by a small formal deformation of
![]() ${\varphi }$
. Note that in the above result, X does not have to be compact. In fact, the constants depend only on the bounds on the local geometry of X.
${\varphi }$
. Note that in the above result, X does not have to be compact. In fact, the constants depend only on the bounds on the local geometry of X.
We also present one relative version of this result:
Theorem 4.2 (Cf. [Reference Manin18, Thm. 5–7])
Let X and Y be finite simplicial complexes or compact Riemannian manifolds, with Y simply connected. Let
![]() $f,g:X \to Y$
be two nullhomotopic L-Lipschitz maps and suppose that
$f,g:X \to Y$
be two nullhomotopic L-Lipschitz maps and suppose that
![]() $f^*m_Y$
and
$f^*m_Y$
and
![]() $g^*m_Y$
are formally homotopic via a homotopy
$g^*m_Y$
are formally homotopic via a homotopy
![]() $\Phi :\mathcal {M}_Y^* \to \Omega _{(\flat )}^*(X \times [0,T])$
with
$\Phi :\mathcal {M}_Y^* \to \Omega _{(\flat )}^*(X \times [0,T])$
with
![]() $\operatorname {\mathrm {Dil}}_T(\Phi ) \leq L$
. Then there is a
$\operatorname {\mathrm {Dil}}_T(\Phi ) \leq L$
. Then there is a
![]() $C(X,Y)(L+1)$
-Lipschitz homotopy
$C(X,Y)(L+1)$
-Lipschitz homotopy
![]() $F:X \times [0,T] \to Y$
between f and g.
$F:X \times [0,T] \to Y$
between f and g.
It is important for this result that the maps be nullhomotopic, rather than just in the same homotopy class. This is because we did not require our formal homotopy to be in the relative homotopy class of a genuine homotopy. In the zero homotopy class, one can always remedy this by a small modification, but, in general, the minimal size of the modification may depend in an opaque way on the homotopy class.
4.2. Formal spaces, again
In §3.4, we introduced formal spaces as spaces which admit self-maps of a certain type. However, the original definition comes from rational homotopy theory, and there are a number of other equivalent definitions. As we will use several of these definitions, we collect a number here, most found in the work of Sullivan [Reference Sullivan23, §12] and Halperin and Stasheff [Reference Halperin and Stasheff16, §3].
For any simply connected space Y, fix an isomorphism
Now we can state some equivalent definitions of formality of Y:
Proposition 4.3. The following are equivalent for a simply connected space Y.
-
(i) The algebra of forms
 $\Omega ^*Y$
is quasi-isomorphic to
$\Omega ^*Y$
is quasi-isomorphic to
 $H^*(Y;{\mathbb {R}})$
.
$H^*(Y;{\mathbb {R}})$
. -
(ii) There is a quasi-isomorphism
 $\mathcal M_Y^* \to H^*(Y;{\mathbb {R}})$
.
$\mathcal M_Y^* \to H^*(Y;{\mathbb {R}})$
. -
(iii) The cohomology of
 $\mathcal M_Y^*$
is a quotient of the subalgebra
$\mathcal M_Y^*$
is a quotient of the subalgebra
 $W_0 \subseteq \mathcal M_Y^*$
generated by indecomposables with zero differential. (In other words, a minimal DGA is non-formal if and only if it has a cohomology class which has no representative in
$W_0 \subseteq \mathcal M_Y^*$
generated by indecomposables with zero differential. (In other words, a minimal DGA is non-formal if and only if it has a cohomology class which has no representative in
 $W_0$
.)
$W_0$
.) -
(iv) There is a (noncanonical) second grading
 $\mathcal M_Y^*=\bigoplus _i W_i$
such that
$\mathcal M_Y^*=\bigoplus _i W_i$
such that
 $H^*(Y;{\mathbb {R}})$
lives in
$H^*(Y;{\mathbb {R}})$
lives in
 $W_0$
and the differential with respect to the second grading has degree
$W_0$
and the differential with respect to the second grading has degree
 $-1$
; that is:
$-1$
; that is:-
•
 $H^*(Y;{\mathbb {R}}) \cong W_0/dW_1$
.
$H^*(Y;{\mathbb {R}}) \cong W_0/dW_1$
. -
• If
 $a \in W_i$
and
$a \in W_i$
and
 $b \in W_j$
, then
$b \in W_j$
, then
 $ab \in W_{i+j}$
.
$ab \in W_{i+j}$
. -
• If
 $a \in W_i$
, then
$a \in W_i$
, then
 $da \in W_{i-1}$
.
$da \in W_{i-1}$
.
-
-
(v) The grading automorphism
 $\rho _t:H^*(Y;{\mathbb {R}}) \to H^*(Y;{\mathbb {R}})$
sending every
$\rho _t:H^*(Y;{\mathbb {R}}) \to H^*(Y;{\mathbb {R}})$
sending every
 $\alpha \in H^n(Y;{\mathbb {R}})$
to
$\alpha \in H^n(Y;{\mathbb {R}})$
to
 $t^n\alpha $
is induced by an automorphism
$t^n\alpha $
is induced by an automorphism
 $\hat \rho _t:\mathcal M_Y^* \to \mathcal M_Y^*$
.
$\hat \rho _t:\mathcal M_Y^* \to \mathcal M_Y^*$
.
The arguments proving the equivalence of (ii)–(v) do not depend on the ground field used for the DGAs. Moreover, Sullivan [Reference Sullivan23, Thm. 12.1] shows that the definitions of formality with respect to any ground field
![]() ${\mathbb {F}} \supseteq {\mathbb {Q}}$
are equivalent. More generally, without reference to spaces, we can say a DGA is formal if it is quasi-isomorphic to its cohomology ring.
${\mathbb {F}} \supseteq {\mathbb {Q}}$
are equivalent. More generally, without reference to spaces, we can say a DGA is formal if it is quasi-isomorphic to its cohomology ring.
Proof sketch and remarks
(i)
![]() $\iff $
(ii). Since the minimal model
$\iff $
(ii). Since the minimal model
![]() $\mathcal M_Y^* \to \Omega ^*(Y)$
is a quasi-isomorphism, one is quasi-isomorphic to
$\mathcal M_Y^* \to \Omega ^*(Y)$
is a quasi-isomorphism, one is quasi-isomorphic to
![]() $H^*(Y;{\mathbb {R}})$
if and only if the other is. Moreover, it is a property of minimal DGAs that if
$H^*(Y;{\mathbb {R}})$
if and only if the other is. Moreover, it is a property of minimal DGAs that if
![]() $\mathcal M_Y^*$
is quasi-isomorphic to another DGA
$\mathcal M_Y^*$
is quasi-isomorphic to another DGA
![]() $\mathcal A$
, then there is, in fact, a quasi-isomorphism
$\mathcal A$
, then there is, in fact, a quasi-isomorphism
![]() $\mathcal M_Y^* \to \mathcal A$
.
$\mathcal M_Y^* \to \mathcal A$
.
It follows from (ii) that, while many rational homotopy types may have the same cohomology ring, exactly one of these is formal, and its minimal DGA can be constructed ‘formally’ from the cohomology ring: at stage k, one adds indecomposables in degree k that kill the relative
![]() $(k+1)$
st cohomology of the map
$(k+1)$
st cohomology of the map
![]() $\mu _{k-1}:\mathcal {M}_Y^*(k-1) \to H^*(Y;{\mathbb {R}})$
and extend
$\mu _{k-1}:\mathcal {M}_Y^*(k-1) \to H^*(Y;{\mathbb {R}})$
and extend
![]() $\mu _{k-1}$
to a map
$\mu _{k-1}$
to a map
![]() $\mu _k:\mathcal {M}_Y^*(k) \to H^*(Y;{\mathbb {R}})$
. This is the genesis of the term ‘formal’.
$\mu _k:\mathcal {M}_Y^*(k) \to H^*(Y;{\mathbb {R}})$
. This is the genesis of the term ‘formal’.
Using this construction, one inductively proves that (ii)
![]() $\Rightarrow $
(iii), by showing that for each
$\Rightarrow $
(iii), by showing that for each
![]() $\mathcal {M}_Y^*(k)$
,
$\mathcal {M}_Y^*(k)$
,
![]() $W_0$
contains cycles representing the cohomology through dimension k. For
$W_0$
contains cycles representing the cohomology through dimension k. For
![]() $\mathcal {M}_Y^*(2)$
, this is clearly true since
$\mathcal {M}_Y^*(2)$
, this is clearly true since
![]() $\mathcal {M}_Y^*(2) \subseteq W_0$
. Now suppose we have a map
$\mathcal {M}_Y^*(2) \subseteq W_0$
. Now suppose we have a map
![]() $\mu _{k-1}:\mathcal {M}_Y^*(k-1) \to H^*(Y;{\mathbb {R}})$
. By induction, the map
$\mu _{k-1}:\mathcal {M}_Y^*(k-1) \to H^*(Y;{\mathbb {R}})$
. By induction, the map
has image in the subring generated by
![]() $H^{\leq k-1}(Y;{\mathbb {R}})$
, and therefore, we can pick preimages in
$H^{\leq k-1}(Y;{\mathbb {R}})$
, and therefore, we can pick preimages in
![]() $W_0$
. The rest of
$W_0$
. The rest of
![]() $H^{k+1}(\mathcal {M}_Y^*(k-1))$
is killed by differentials of elements of
$H^{k+1}(\mathcal {M}_Y^*(k-1))$
is killed by differentials of elements of
![]() $V_k$
. However, the cokernel of
$V_k$
. However, the cokernel of
is spanned by elements of
![]() $V_k$
with zero differential, which are also in
$V_k$
with zero differential, which are also in
![]() $W_0$
. Together, these span
$W_0$
. Together, these span
![]() $H^k(\mathcal M_Y^*)$
.
$H^k(\mathcal M_Y^*)$
.
(iii)
![]() $\Rightarrow $
(iv) is also proved by induction on dimension of indecomposables. Suppose that we have defined the bigrading on
$\Rightarrow $
(iv) is also proved by induction on dimension of indecomposables. Suppose that we have defined the bigrading on
![]() $\mathcal M_Y^*(k-1)$
. By induction, the space of
$\mathcal M_Y^*(k-1)$
. By induction, the space of
![]() $(k+1)$
-cycles in
$(k+1)$
-cycles in
![]() $\mathcal M_Y^*(k-1)$
splits as a direct sum of subspaces
$\mathcal M_Y^*(k-1)$
splits as a direct sum of subspaces
![]() $Z_i \subseteq W_i$
since differentials of terms in
$Z_i \subseteq W_i$
since differentials of terms in
![]() $W_i$
can only cancel out with those of others in
$W_i$
can only cancel out with those of others in
![]() $W_i$
. Moreover, all of
$W_i$
. Moreover, all of
![]() $\bigoplus _{i \geq 1} Z_i$
must be in the image of the differential on
$\bigoplus _{i \geq 1} Z_i$
must be in the image of the differential on
![]() $V_k$
. This allows us to split
$V_k$
. This allows us to split
![]() $V_k$
as a direct sum of elements of various
$V_k$
as a direct sum of elements of various
![]() $W_i$
,
$W_i$
,
![]() $i \geq 0$
, so as to ensure
$i \geq 0$
, so as to ensure
![]() $dW_i \subseteq W_{i-1}$
. We assign
$dW_i \subseteq W_{i-1}$
. We assign
![]() $\ker d \subseteq V_k$
to
$\ker d \subseteq V_k$
to
![]() $W_0$
.
$W_0$
.
(iv)
![]() $\Rightarrow $
(ii). If a bigrading as in (iv) exists, then
$\Rightarrow $
(ii). If a bigrading as in (iv) exists, then
![]() $\mathcal M_Y^* \to W_0/dW_1$
is a quotient map of DGAs.
$\mathcal M_Y^* \to W_0/dW_1$
is a quotient map of DGAs.
(iv)
![]() $\Rightarrow $
(v). We can define
$\Rightarrow $
(v). We can define
![]() $\hat \rho _t(a)=t^{n+i}a$
for every
$\hat \rho _t(a)=t^{n+i}a$
for every
![]() $a \in W_i \cap V_n$
.
$a \in W_i \cap V_n$
.
(v)
![]() $\Rightarrow $
(iv) (see also [Reference Sullivan23, Thm. 12.7]). This argument requires some information about the automorphism group of
$\Rightarrow $
(iv) (see also [Reference Sullivan23, Thm. 12.7]). This argument requires some information about the automorphism group of
![]() $\mathcal M_Y^*$
, which is a linear algebraic subgroup of the group
$\mathcal M_Y^*$
, which is a linear algebraic subgroup of the group
![]() $\bigoplus _n \operatorname {\mathrm {Aut}}(V_n)$
. Taking the ‘diagonal part’ in the Iwasawa decomposition of
$\bigoplus _n \operatorname {\mathrm {Aut}}(V_n)$
. Taking the ‘diagonal part’ in the Iwasawa decomposition of
![]() $\hat \rho _t$
, we get another automorphism, also inducing the map
$\hat \rho _t$
, we get another automorphism, also inducing the map
![]() $\rho _t$
on cohomology, which has a basis of eigenvectors in each of the
$\rho _t$
on cohomology, which has a basis of eigenvectors in each of the
![]() $V_n$
. An inductive argument then shows that these eigenvalues are of the form
$V_n$
. An inductive argument then shows that these eigenvalues are of the form
![]() $t^{n+i}$
, and setting
$t^{n+i}$
, and setting
![]() $W_i \cap V_n$
to be the eigenspace for the eigenvalue
$W_i \cap V_n$
to be the eigenspace for the eigenvalue
![]() $t^{n+i}$
gives a bigrading as in (iv).
$t^{n+i}$
gives a bigrading as in (iv).
Now, we connect these definitions to that in the previous section. If Y is a finite complex and (v) is satisfied with
![]() $\mathbb Q$
coefficients, then any family of lifts
$\mathbb Q$
coefficients, then any family of lifts
![]() $\hat \rho _t$
can be realized by genuine maps:
$\hat \rho _t$
can be realized by genuine maps:
Theorem 4.4 [Reference Manin19, Theorem A]
Let Y be a formal, simply connected finite CW complex and let
![]() $\hat \rho _t:\mathcal M_Y \to \mathcal M_Y$
be the map
$\hat \rho _t:\mathcal M_Y \to \mathcal M_Y$
be the map
for some bigrading
![]() $\mathcal M_Y=\bigoplus _i W_i$
. Then there is an integer
$\mathcal M_Y=\bigoplus _i W_i$
. Then there is an integer
![]() $t_0 \geq 1$
such that for every
$t_0 \geq 1$
such that for every
![]() $z \in \mathbb {Z}$
, there is a genuine map
$z \in \mathbb {Z}$
, there is a genuine map
![]() ${r}_z:Y \to Y$
whose rationalization is
${r}_z:Y \to Y$
whose rationalization is
![]() $\hat \rho _{zt_0}$
.
$\hat \rho _{zt_0}$
.
The same paper also gives a stronger version of Proposition 3.9:
Theorem 4.5 [Reference Manin19, Theorem B]
Let Y be a formal, simply connected finite CW complex and let
![]() $\hat \rho _t:\mathcal M_Y \to \mathcal M_Y$
be the map
$\hat \rho _t:\mathcal M_Y \to \mathcal M_Y$
be the map
for some bigrading
![]() $\mathcal M_Y=\bigoplus _i W_i$
. Suppose that Z is another simply connected complex and
$\mathcal M_Y=\bigoplus _i W_i$
. Suppose that Z is another simply connected complex and
![]() $f:Z \to Y$
is a map inducing an isomorphism on rational cohomology. Then for some p, there is a map
$f:Z \to Y$
is a map inducing an isomorphism on rational cohomology. Then for some p, there is a map
![]() $g:Y \to Z$
such that the rationalization of
$g:Y \to Z$
such that the rationalization of
![]() $f \circ g$
is
$f \circ g$
is
![]() $\hat \rho _p$
.
$\hat \rho _p$
.
We then get the following upgraded statement of Theorem 3.1:
Theorem 4.6. Let Y be a formal, simply connected finite CW complex whose rational homology is nontrivial in d positive degrees, and let
![]() $\hat \rho _t:\mathcal M_Y \to \mathcal M_Y$
be the map
$\hat \rho _t:\mathcal M_Y \to \mathcal M_Y$
be the map
for some bigrading
![]() $\mathcal M_Y=\bigoplus _i W_i$
. Then there is a constant
$\mathcal M_Y=\bigoplus _i W_i$
. Then there is a constant
![]() $C>0$
, depending on the choice of
$C>0$
, depending on the choice of
![]() $\hat \rho _t$
as well as Y, such that for every homotopy class in
$\hat \rho _t$
as well as Y, such that for every homotopy class in
![]() $[Y,Y]$
whose rationalization is
$[Y,Y]$
whose rationalization is
![]() $\hat \rho _t$
, there is a
$\hat \rho _t$
, there is a
![]() $(Ct(\log t)^{d-1}+C)$
-Lipschitz representative
$(Ct(\log t)^{d-1}+C)$
-Lipschitz representative
![]() $f:Y \to Y$
.
$f:Y \to Y$
.
Proof. Using Theorems 4.4 and 4.5, we obtain topological control over the maps f, g and
![]() ${r}_p$
used in the proof of Theorem 3.1. Then we see that there are a and p such that for every
${r}_p$
used in the proof of Theorem 3.1. Then we see that there are a and p such that for every
![]() $q=ap^\ell $
, there is a
$q=ap^\ell $
, there is a
![]() $C_0(q(\log q)^{d-1}+1)$
-Lipschitz map
$C_0(q(\log q)^{d-1}+1)$
-Lipschitz map
![]() $f_q:Y \to Y$
whose rationalization is
$f_q:Y \to Y$
whose rationalization is
![]() $\hat \rho _q$
, where
$\hat \rho _q$
, where
![]() $C_0$
depends on the family
$C_0$
depends on the family
![]() $\hat \rho _t$
.
$\hat \rho _t$
.
Now suppose that
![]() $r_t:Y \to Y$
is a map whose rationalization is
$r_t:Y \to Y$
is a map whose rationalization is
![]() $\hat \rho _t$
, and let
$\hat \rho _t$
, and let
![]() $m_Y:\mathcal M_Y \to \Omega ^*Y$
be a minimal model of Y. Let
$m_Y:\mathcal M_Y \to \Omega ^*Y$
be a minimal model of Y. Let
![]() $q=ap^\ell $
satisfy
$q=ap^\ell $
satisfy
![]() $ap^{\ell -1} \leq t<ap^\ell $
. Then the map
$ap^{\ell -1} \leq t<ap^\ell $
. Then the map
is algebraically homotopic to
![]() $r_t^*m_Y$
. Notice also that, with an appropriate norm on indecomposables, the operator norm of
$r_t^*m_Y$
. Notice also that, with an appropriate norm on indecomposables, the operator norm of
![]() $\hat \rho _{t/q}$
is
$\hat \rho _{t/q}$
is
![]() $t/q$
. Therefore, by the shadowing principle, there is an
$t/q$
. Therefore, by the shadowing principle, there is an
![]() $C_1(Y)((t/q)\operatorname {\mathrm {Lip}} f_q+1)$
-Lipschitz map in the homotopy class of
$C_1(Y)((t/q)\operatorname {\mathrm {Lip}} f_q+1)$
-Lipschitz map in the homotopy class of
![]() $r_t$
. Then we are done because
$r_t$
. Then we are done because
5. A finite criterion for scalability
In this section, we prove Theorems C and C′. In [Reference Berdnikov and Manin3], it was shown that the following conditions are equivalent for a finite simplicial complex or compact manifold Y which is formal and simply connected:
-
(i) There is a homomorphism
 $H^*(Y) \to \Omega _\flat ^*Y$
of differential graded algebras which sends each cohomology class to a representative of that class. Here,
$H^*(Y) \to \Omega _\flat ^*Y$
of differential graded algebras which sends each cohomology class to a representative of that class. Here,
 $\Omega _\flat ^*Y$
denotes the flat forms, an algebra of not-necessarily-smooth differential forms studied by Whitney.
$\Omega _\flat ^*Y$
denotes the flat forms, an algebra of not-necessarily-smooth differential forms studied by Whitney. -
(ii) There is a constant
 $C(Y)$
such that for infinitely many
$C(Y)$
such that for infinitely many
 $p \in \mathbb {N}$
, there is a
$p \in \mathbb {N}$
, there is a
 $C(Y)(p+1)$
-Lipschitz self-map which induces multiplication by
$C(Y)(p+1)$
-Lipschitz self-map which induces multiplication by
 $p^n$
on
$p^n$
on
 $H^n(Y;\mathbb {R})$
.
$H^n(Y;\mathbb {R})$
. -
(iii) For all finite simplicial complexes X, nullhomotopic L-Lipschitz maps
 $X \to Y$
have
$X \to Y$
have
 $C(X,Y)(L+1)$
-Lipschitz nullhomotopies.
$C(X,Y)(L+1)$
-Lipschitz nullhomotopies. -
(iv) For all
 $n<\dim Y$
, homotopic L-Lipschitz maps
$n<\dim Y$
, homotopic L-Lipschitz maps
 $S^n \to Y$
have
$S^n \to Y$
have
 $C(Y)(L+1)$
-Lipschitz homotopies.
$C(Y)(L+1)$
-Lipschitz homotopies.
Spaces satisfying these conditions are called scalable. Now, we show the following.
Theorem 5.1. The following condition is also equivalent to those above:
-
(v) For some
 $n_1,\ldots ,n_N$
, there is an injective
$n_1,\ldots ,n_N$
, there is an injective
 ${\mathbb {R}}$
-algebra homomorphism
${\mathbb {R}}$
-algebra homomorphism  $$\begin{align*}h:H^*(Y;\mathbb R) \to \bigoplus_{i=1}^N \Lambda^*{\mathbb{R}}^{n_i}.\end{align*}$$
$$\begin{align*}h:H^*(Y;\mathbb R) \to \bigoplus_{i=1}^N \Lambda^*{\mathbb{R}}^{n_i}.\end{align*}$$
If Y is a closed n-manifold (or, more generally, satisfies Poincaré duality over the reals), the following conditions are also equivalent to those above:
-
(v′) There is an injective
 $\mathbb R$
-algebra homomorphism
$\mathbb R$
-algebra homomorphism
 $h:H^*(Y;\mathbb R) \to \Lambda ^*\mathbb R^n$
.
$h:H^*(Y;\mathbb R) \to \Lambda ^*\mathbb R^n$
. -
(vi) There is a
 $1$
-Lipschitz map
$1$
-Lipschitz map
 $f:\mathbb R^n \to M$
of positive asymptotic degree.
$f:\mathbb R^n \to M$
of positive asymptotic degree.
Remark 5.2. Condition (v
![]() $' $
) can also be thought of as saying that there is an injective homomorphism
$' $
) can also be thought of as saying that there is an injective homomorphism
![]() $H^*(Y;\mathbb R) \to H^*(T^n;\mathbb R)$
. When is this homomorphism induced by a genuine map
$H^*(Y;\mathbb R) \to H^*(T^n;\mathbb R)$
. When is this homomorphism induced by a genuine map
![]() $T^n \to Y$
of positive degree? A necessary condition is that the homomorphism can also be realized over the rationals. In fact, this condition is also sufficient. A homomorphism
$T^n \to Y$
of positive degree? A necessary condition is that the homomorphism can also be realized over the rationals. In fact, this condition is also sufficient. A homomorphism
![]() $H^*(Y; \mathbb Q) \to H^*(T^n;\mathbb Q)$
lifts (non-uniquely) to a homomorphism of minimal models. By [Reference Papadima21, Proposition 3.1], after composing with a self-map
$H^*(Y; \mathbb Q) \to H^*(T^n;\mathbb Q)$
lifts (non-uniquely) to a homomorphism of minimal models. By [Reference Papadima21, Proposition 3.1], after composing with a self-map
![]() $\mathcal M_Y \to \mathcal M_Y$
that induces multiplication by
$\mathcal M_Y \to \mathcal M_Y$
that induces multiplication by
![]() $p^n$
on
$p^n$
on
![]() $H^n(Y;\mathbb Q)$
for some p, this homomorphism becomes the rationalization of a genuine map
$H^n(Y;\mathbb Q)$
for some p, this homomorphism becomes the rationalization of a genuine map
![]() $T^n \to Y$
.
$T^n \to Y$
.
This does not always happen. For example, take the real Poincaré duality space
where
![]() $*$
is a basepoint. The cup product
$*$
is a basepoint. The cup product
![]() $H^2(Y) \times H^2(Y) \to H^4(Y)$
is the quadratic form
$H^2(Y) \times H^2(Y) \to H^4(Y)$
is the quadratic form
![]() $\langle 2,1,1,-1,-1,-1 \rangle $
, which has discriminant
$\langle 2,1,1,-1,-1,-1 \rangle $
, which has discriminant
![]() $-2$
and therefore is not rationally equivalent to the quadratic form induced by the cup product
$-2$
and therefore is not rationally equivalent to the quadratic form induced by the cup product
![]() $H^2(T^4) \times H^2(T^4) \to H^4(T^4)$
. However, Y is scalable, since over the reals, the two quadratic forms are equivalent.
$H^2(T^4) \times H^2(T^4) \to H^4(T^4)$
. However, Y is scalable, since over the reals, the two quadratic forms are equivalent.
To get a manifold counterexample, embed Y in
![]() $\mathbb R^{10}$
and let M be the boundary of a thickening W of this embedding. Using Alexander duality and the Mayer–Vietoris sequence, we see that the injection
$\mathbb R^{10}$
and let M be the boundary of a thickening W of this embedding. Using Alexander duality and the Mayer–Vietoris sequence, we see that the injection
![]() $M \to W$
induces an isomorphism
$M \to W$
induces an isomorphism
and the classes in
![]() $H_{\geq 5}(M)$
are Poincaré duals of those coming from W. This determines the rational and hence the real cohomology ring:
$H_{\geq 5}(M)$
are Poincaré duals of those coming from W. This determines the rational and hence the real cohomology ring:
![]() $H^*(M;{\mathbb {R}}) \cong H^*(Y;{\mathbb {R}}) \times {\mathbb {R}}\langle h^5 \rangle $
, where
$H^*(M;{\mathbb {R}}) \cong H^*(Y;{\mathbb {R}}) \times {\mathbb {R}}\langle h^5 \rangle $
, where
![]() $h^5$
is Poincaré dual to the fundamental class of Y. Clearly, this embeds in
$h^5$
is Poincaré dual to the fundamental class of Y. Clearly, this embeds in
![]() $\Lambda ^*{\mathbb {R}}^9$
. A somewhat more subtle argument shows the following:
$\Lambda ^*{\mathbb {R}}^9$
. A somewhat more subtle argument shows the following:
Proposition 5.3. M is formal.
Proof. We will show that the minimal model of M satisfies condition (iii) of Proposition 4.3. As an algebra,
![]() $H^*(M;{\mathbb {R}})$
is generated by six
$H^*(M;{\mathbb {R}})$
is generated by six
![]() $2$
-dimensional classes and the
$2$
-dimensional classes and the
![]() $5$
-dimensional class
$5$
-dimensional class
![]() $h^5$
. It suffices to show that these classes lie in
$h^5$
. It suffices to show that these classes lie in
![]() $W_0$
. To do this, we show that the Hurewicz map
$W_0$
. To do this, we show that the Hurewicz map
![]() $\pi _k(M) \otimes {\mathbb {Q}} \to H_k(M;{\mathbb {Q}})$
is surjective for
$\pi _k(M) \otimes {\mathbb {Q}} \to H_k(M;{\mathbb {Q}})$
is surjective for
![]() $k=2$
and
$k=2$
and
![]() $5$
. After dualizing, this means that all elements of
$5$
. After dualizing, this means that all elements of
![]() $H^k(M;{\mathbb {Q}})$
are represented by indecomposables in
$H^k(M;{\mathbb {Q}})$
are represented by indecomposables in
![]() $V_k$
.
$V_k$
.
For
![]() $k=2$
, this is true by the Hurewicz theorem. For
$k=2$
, this is true by the Hurewicz theorem. For
![]() $k=5$
, we apply the relative Hurewicz theorem for the pair
$k=5$
, we apply the relative Hurewicz theorem for the pair
![]() $(W,M)$
. By the long exact sequence of a pair,
$(W,M)$
. By the long exact sequence of a pair,
![]() $H_i(W,M) \cong 0$
for
$H_i(W,M) \cong 0$
for
![]() $i \leq 5$
, and so
$i \leq 5$
, and so
![]() $H_6(W,M) \cong \pi _6(W,M)$
. Then from the commutative diagram of exact sequences
$H_6(W,M) \cong \pi _6(W,M)$
. Then from the commutative diagram of exact sequences

it is evident that the Hurewicz map
![]() $\pi _5(M) \to H_5(M)$
is surjective.
$\pi _5(M) \to H_5(M)$
is surjective.
Therefore, M is scalable. However, an injection
![]() $H^*(M;\mathbb Q) \to H^*(T^9;\mathbb Q)$
, if it existed, would induce an injection
$H^*(M;\mathbb Q) \to H^*(T^9;\mathbb Q)$
, if it existed, would induce an injection
![]() $H^*(Y) \to H^*(T^4;\mathbb Q)$
, which we already showed cannot exist.
$H^*(Y) \to H^*(T^4;\mathbb Q)$
, which we already showed cannot exist.
Thus, one can distinguish a class of ‘rationally scalable’ manifolds within the larger class of scalable spaces. It would be interesting to know what other properties distinguish these two classes.
Proof of Theorem 5.1
We will prove that (i) implies (v) for all simply connected finite complexes (which is straightforward) and that (v) implies (ii) for all simply connected finite complexes (which is an application of the shadowing principle). We will also show that for closed n-manifolds, (v) implies (v
![]() $' $
); the converse is obvious. Then we will show that scalable closed n-manifolds satisfy (vi) and, conversely, (vi) implies (v
$' $
); the converse is obvious. Then we will show that scalable closed n-manifolds satisfy (vi) and, conversely, (vi) implies (v
![]() $' $
) for any closed n-manifold.
$' $
) for any closed n-manifold.
To see that (i) implies (v), choose a basis
![]() $u_1,\ldots ,u_N$
for
$u_1,\ldots ,u_N$
for
![]() $H^*(Y;{\mathbb {Q}})$
and let
$H^*(Y;{\mathbb {Q}})$
and let
![]() $\omega _1,\ldots ,\omega _N$
be the corresponding flat differential forms. Then for each i, there is a set of positive measure on which
$\omega _1,\ldots ,\omega _N$
be the corresponding flat differential forms. Then for each i, there is a set of positive measure on which
![]() $\omega _i \neq 0$
. Since the homomorphism
$\omega _i \neq 0$
. Since the homomorphism
![]() $H^*(Y) \to \Omega _\flat ^*(Y)$
is multiplicative almost everywhere, we can choose a point
$H^*(Y) \to \Omega _\flat ^*(Y)$
is multiplicative almost everywhere, we can choose a point
![]() $x_i \in Y$
such that
$x_i \in Y$
such that
![]() $uif_j \mapsto \omega _j|_{x_i}$
is a homomorphism
$uif_j \mapsto \omega _j|_{x_i}$
is a homomorphism
![]() $h_i:H^*(Y;{\mathbb {R}}) \to \Lambda ^*{\mathbb {R}}^{n_i}$
such that
$h_i:H^*(Y;{\mathbb {R}}) \to \Lambda ^*{\mathbb {R}}^{n_i}$
such that
![]() $h_i(u_i) \neq 0$
. Then we can take
$h_i(u_i) \neq 0$
. Then we can take
 $$\begin{align*}h=(h_1,\ldots,h_N):H^*(Y;\mathbb R) \to \bigoplus_{i=1}^N \Lambda^*\mathbb R^{n_i}.\end{align*}$$
$$\begin{align*}h=(h_1,\ldots,h_N):H^*(Y;\mathbb R) \to \bigoplus_{i=1}^N \Lambda^*\mathbb R^{n_i}.\end{align*}$$
If Poincaré duality is satisfied, then (v) implies (v
![]() $' $
) since we can project h to some
$' $
) since we can project h to some
![]() $\Lambda ^*\mathbb R^{n_i}$
under which the image of the fundamental class is nonzero. This projection is still injective.
$\Lambda ^*\mathbb R^{n_i}$
under which the image of the fundamental class is nonzero. This projection is still injective.
Now, we prove that if Y is a closed n-manifold, then (v
![]() $'$
) implies (vi). This argument is partly a warm-up for the more elaborate proof that (v) implies (ii). Since Y is formal, there is a quasi-isomorphism
$'$
) implies (vi). This argument is partly a warm-up for the more elaborate proof that (v) implies (ii). Since Y is formal, there is a quasi-isomorphism
![]() ${\varphi }:\mathcal M_Y^* \to H^*(Y;{\mathbb {R}})$
. Composing this with the homomorphism
${\varphi }:\mathcal M_Y^* \to H^*(Y;{\mathbb {R}})$
. Composing this with the homomorphism
![]() $h:H^*(Y;{\mathbb {R}}) \to \Lambda ^*{\mathbb {R}}^n$
, we get a homomorphism
$h:H^*(Y;{\mathbb {R}}) \to \Lambda ^*{\mathbb {R}}^n$
, we get a homomorphism
whose image consists of constant forms and such that the image of the fundamental class
![]() $\omega _{[Y{\kern-1pt}]}$
is (perhaps after rescaling) the volume form. Since
$\omega _{[Y{\kern-1pt}]}$
is (perhaps after rescaling) the volume form. Since
![]() ${\mathbb {R}}^n$
is contractible and has locally bounded geometry, we can apply the shadowing principle to
${\mathbb {R}}^n$
is contractible and has locally bounded geometry, we can apply the shadowing principle to
![]() $\eta $
to produce a Lipschitz map
$\eta $
to produce a Lipschitz map
![]() $f:{\mathbb {R}}^n \to Y$
which is related to
$f:{\mathbb {R}}^n \to Y$
which is related to
![]() $\eta $
by a formal homotopy
$\eta $
by a formal homotopy
such that
![]() $\operatorname {\mathrm {Dil}}(\Phi )<\infty $
.
$\operatorname {\mathrm {Dil}}(\Phi )<\infty $
.
The pullback map on forms induced by f should be thought of as looking on average like
![]() $\eta $
. Geometrically, f can be built so that
$\eta $
. Geometrically, f can be built so that
![]() ${\mathbb {R}}^n$
is tiled (periodically or aperiodically) by homeomorphic preimages of an open dense subset of Y. From a Fourier point of view, f has a large constant term, and the rest of the nonzero terms are at very high frequency. Intuitively, such a map must have positive asymptotic degree. To show this formally, we apply Stokes’ theorem to the form
${\mathbb {R}}^n$
is tiled (periodically or aperiodically) by homeomorphic preimages of an open dense subset of Y. From a Fourier point of view, f has a large constant term, and the rest of the nonzero terms are at very high frequency. Intuitively, such a map must have positive asymptotic degree. To show this formally, we apply Stokes’ theorem to the form
![]() $\Phi (\omega _{[Y{\kern-1pt}]})$
on
$\Phi (\omega _{[Y{\kern-1pt}]})$
on
![]() $B_R(0) \times [0,1]$
, getting
$B_R(0) \times [0,1]$
, getting
We can turn f into a
![]() $1$
-Lipschitz map of positive asymptotic degree by rescaling.
$1$
-Lipschitz map of positive asymptotic degree by rescaling.
Now we will prove that (v) implies (ii). We prove this by constructing maps skeleton-by-skeleton. When we extend to n-cells, we do it by piecing together ‘almost constant’ maps from
![]() ${\mathbb {R}}^n$
, like the map f in the previous two paragraphs.
${\mathbb {R}}^n$
, like the map f in the previous two paragraphs.
Suppose Y satisfies (v) (and therefore so does any complex in its rational homotopy class). By Proposition 3.10, we may replace Y with a rationally equivalent complex Z whose rational cellular chain complex has zero differential; in other words, the cells of Z form a basis for
![]() $H_*(Z;\mathbb R)$
. We equip Z with a nearly Euclidean metric. Theorem 4.5 implies that to show that Y satisfies (ii), it suffices to show that Z does.
$H_*(Z;\mathbb R)$
. We equip Z with a nearly Euclidean metric. Theorem 4.5 implies that to show that Y satisfies (ii), it suffices to show that Z does.
Fix a second grading
![]() $\mathcal M_Z^* \cong \bigoplus _i W_i$
as in Proposition 4.3(iv). We obtain a quasi-isomorphism
$\mathcal M_Z^* \cong \bigoplus _i W_i$
as in Proposition 4.3(iv). We obtain a quasi-isomorphism
![]() ${\varphi }:\mathcal M_Z^* \to H^*(Z;\mathbb R)$
by projecting to
${\varphi }:\mathcal M_Z^* \to H^*(Z;\mathbb R)$
by projecting to
![]() $W_0/dW_1$
, and an automorphism
$W_0/dW_1$
, and an automorphism
![]() $\rho _t:\mathcal M_Z^* \to \mathcal M_Z^*$
which takes
$\rho _t:\mathcal M_Z^* \to \mathcal M_Z^*$
which takes
![]() $w \in W_i \cap V_n$
to
$w \in W_i \cap V_n$
to
![]() $t^{n+i}w$
; then
$t^{n+i}w$
; then
![]() ${\varphi } \circ \rho _t=t^{\deg }{\varphi }$
. Moreover, by Theorem 4.4, for some
${\varphi } \circ \rho _t=t^{\deg }{\varphi }$
. Moreover, by Theorem 4.4, for some
![]() $p>1$
, there is a genuine self-map
$p>1$
, there is a genuine self-map
![]() ${r}_p:Z \to Z$
whose rationalization is
${r}_p:Z \to Z$
whose rationalization is
![]() $\rho _p$
, and in particular induces multiplication by
$\rho _p$
, and in particular induces multiplication by
![]() $p^n$
on
$p^n$
on
![]() $H^n(Z;\mathbb R)$
.
$H^n(Z;\mathbb R)$
.
We will show that Z satisfies (ii) by induction on skeleta. From (i), it follows that skeleta of scalable spaces are scalable. Conversely, we will show that if Z is an n-complex satisfying (v) and
![]() $Z^{(n-1)}$
is scalable, then so is Z. We first show that if
$Z^{(n-1)}$
is scalable, then so is Z. We first show that if
![]() $Z^{(n-1)}$
is scalable, then for every
$Z^{(n-1)}$
is scalable, then for every
![]() $\ell>0$
, the iterate
$\ell>0$
, the iterate
![]() $({r}_p)^\ell |_{Z^{(n-1)}}$
is homotopic to an
$({r}_p)^\ell |_{Z^{(n-1)}}$
is homotopic to an
![]() $O(p^\ell )$
-Lipschitz map. Moreover, for each n-cell, condition (v) lets us build an
$O(p^\ell )$
-Lipschitz map. Moreover, for each n-cell, condition (v) lets us build an
![]() $O(p^\ell )$
-Lipschitz map from
$O(p^\ell )$
-Lipschitz map from
![]() $[0,1]^n$
to Z whose degree over that cell is
$[0,1]^n$
to Z whose degree over that cell is
![]() $p^{\ell n}$
. We construct self-maps of Z satisfying (ii) by patching these together; this shows that Z is also scalable.
$p^{\ell n}$
. We construct self-maps of Z satisfying (ii) by patching these together; this shows that Z is also scalable.
Now we give the details. Let
![]() $\mathbf Z$
and its submanifold
$\mathbf Z$
and its submanifold
![]() $\mathbf Z^{(n-1)}$
be compact Riemannian manifolds with boundary homotopy equivalent to Z and
$\mathbf Z^{(n-1)}$
be compact Riemannian manifolds with boundary homotopy equivalent to Z and
![]() $Z^{(n-1)}$
. Let
$Z^{(n-1)}$
. Let
![]() ${\varphi }:\mathcal M_Z^* \to H^*(Z; {\mathbb {R}})$
be a quasi-isomorphism, which exists since Z is formal, and let
${\varphi }:\mathcal M_Z^* \to H^*(Z; {\mathbb {R}})$
be a quasi-isomorphism, which exists since Z is formal, and let
![]() $i_{n-1}:Z^{(n-1)} \to Z$
be the inclusion map.
$i_{n-1}:Z^{(n-1)} \to Z$
be the inclusion map.
Suppose, by induction, that
![]() $Z^{(n-1)}$
is scalable. By condition (i), there is an injective homomorphism
$Z^{(n-1)}$
is scalable. By condition (i), there is an injective homomorphism
![]() $H^*(Z^{(n-1)}; {\mathbb {R}}) \to \Omega _\flat ^*(\mathbf Z^{(n-1)})$
which sends each class to a representative; composing with
$H^*(Z^{(n-1)}; {\mathbb {R}}) \to \Omega _\flat ^*(\mathbf Z^{(n-1)})$
which sends each class to a representative; composing with
![]() $i_{n-1}^*{\varphi }$
gives a map
$i_{n-1}^*{\varphi }$
gives a map
![]() $\mathcal M_Z^* \to \Omega _\flat ^*(\mathbf Z^{(n-1)})$
, and by a Poincaré lemma argument, this extends to a minimal model
$\mathcal M_Z^* \to \Omega _\flat ^*(\mathbf Z^{(n-1)})$
, and by a Poincaré lemma argument, this extends to a minimal model
![]() $m_{Z}:\mathcal M_Z^* \to \Omega _\flat ^*(\mathbf Z)$
whose projection to
$m_{Z}:\mathcal M_Z^* \to \Omega _\flat ^*(\mathbf Z)$
whose projection to
![]() $\Omega _\flat ^*(\mathbf Z^{(n-1)})$
factors through
$\Omega _\flat ^*(\mathbf Z^{(n-1)})$
factors through
![]() ${\varphi }$
. Then
${\varphi }$
. Then
![]() $({r}_p^\ell )^*m_{Z}$
is formally homotopic to
$({r}_p^\ell )^*m_{Z}$
is formally homotopic to
![]() $m_{Z}\rho _p^\ell $
. By the shadowing principle 4.1 and the Lipschitz homotopy equivalence between
$m_{Z}\rho _p^\ell $
. By the shadowing principle 4.1 and the Lipschitz homotopy equivalence between
![]() $\mathbf Z$
and Z, this lets us homotope
$\mathbf Z$
and Z, this lets us homotope
![]() ${r}_p^\ell $
to a map
${r}_p^\ell $
to a map
![]() ${r}_{p^\ell ,n-1}:Z \to Z$
which is
${r}_{p^\ell ,n-1}:Z \to Z$
which is
![]() $O(p^\ell )$
-Lipschitz on
$O(p^\ell )$
-Lipschitz on
![]() $Z^{(n-1)}$
.
$Z^{(n-1)}$
.
Now, we explain how to extend this map to the n-cells. Let
![]() $\iota _1,\ldots ,\iota _r:[0,1]^{n} \to Z$
be the inclusion maps of the n-cells of Z and let
$\iota _1,\ldots ,\iota _r:[0,1]^{n} \to Z$
be the inclusion maps of the n-cells of Z and let
![]() $a_1,\ldots ,a_r \in H_n(Z)$
be the corresponding homology classes. Recall that we are assuming that there is an injective homomorphism
$a_1,\ldots ,a_r \in H_n(Z)$
be the corresponding homology classes. Recall that we are assuming that there is an injective homomorphism
![]() $h:H^*(Z;{\mathbb {R}}) \to \bigoplus _{i=1}^N \Lambda ^*{\mathbb {R}}^{n_i}$
. Since for every i,
$h:H^*(Z;{\mathbb {R}}) \to \bigoplus _{i=1}^N \Lambda ^*{\mathbb {R}}^{n_i}$
. Since for every i,
![]() $\Lambda ^n{\mathbb {R}}^{n_i}$
is spanned by simple tensors, we can choose n-dimensional subspaces
$\Lambda ^n{\mathbb {R}}^{n_i}$
is spanned by simple tensors, we can choose n-dimensional subspaces
such that the projections
collectively distinguish all elements of
![]() $H^n(Z; {\mathbb {R}})$
. Each
$H^n(Z; {\mathbb {R}})$
. Each
![]() $h_j|_{H^n(Z;{\mathbb {R}})} \in \operatorname {\mathrm {Hom}}(H^n(Z;{\mathbb {R}}),{\mathbb {R}})$
can be identified with a
$h_j|_{H^n(Z;{\mathbb {R}})} \in \operatorname {\mathrm {Hom}}(H^n(Z;{\mathbb {R}}),{\mathbb {R}})$
can be identified with a
![]() $b_j \in H_n(Z;{\mathbb {R}})$
, and we can find coefficients
$b_j \in H_n(Z;{\mathbb {R}})$
, and we can find coefficients
![]() $x_{ij}$
such that
$x_{ij}$
such that
 $$\begin{align*}a_i=\sum_{j=1}^r x_{ij}b_j.\end{align*}$$
$$\begin{align*}a_i=\sum_{j=1}^r x_{ij}b_j.\end{align*}$$
For each
![]() $j=1,\ldots ,r$
and
$j=1,\ldots ,r$
and
![]() $c \in {\mathbb {R}}$
, consider the map
$c \in {\mathbb {R}}$
, consider the map
![]() $\eta _{c,j}:\mathcal M_Z^* \to \Omega ^*([0,1]^n)$
where, for every
$\eta _{c,j}:\mathcal M_Z^* \to \Omega ^*([0,1]^n)$
where, for every
![]() $x \in [0,1]^n$
,
$x \in [0,1]^n$
,
Applying the shadowing principle, we get an
![]() $O(c)$
-Lipschitz map
$O(c)$
-Lipschitz map
![]() $f_{c,j}:[0,1]^n \to Z$
such that
$f_{c,j}:[0,1]^n \to Z$
such that
![]() $f^*_{c,j}{\varphi }$
is related to
$f^*_{c,j}{\varphi }$
is related to
![]() $\eta _{c,j}$
by a formal homotopy
$\eta _{c,j}$
by a formal homotopy
satisfying
![]() $\operatorname {\mathrm {Dil}}(\Phi )=O(c)$
. We can, moreover, assume without loss of generality that
$\operatorname {\mathrm {Dil}}(\Phi )=O(c)$
. We can, moreover, assume without loss of generality that
![]() $f_{c,j}$
sends
$f_{c,j}$
sends
![]() $\partial [0,1]^n$
to
$\partial [0,1]^n$
to
![]() $Z^{(n-1)}$
. If
$Z^{(n-1)}$
. If
![]() $f_{c,j}$
does not have this property, it has a short homotopy to a map that does, by the following lemma:
$f_{c,j}$
does not have this property, it has a short homotopy to a map that does, by the following lemma:
Lemma 5.4. Let
![]() $L \geq 1$
and let
$L \geq 1$
and let
![]() $f:[0,L]^n \to X$
be an
$f:[0,L]^n \to X$
be an
![]() $1$
-Lipschitz map to an n-dimensional CW complex X with a nearly Euclidean metric. Then there is a
$1$
-Lipschitz map to an n-dimensional CW complex X with a nearly Euclidean metric. Then there is a
![]() $C(X)$
-Lipschitz homotopy
$C(X)$
-Lipschitz homotopy
between f and a map which sends
![]() $\partial [0,L]^n$
to
$\partial [0,L]^n$
to
![]() $X^{(n-1)}$
.
$X^{(n-1)}$
.
Applying the lemma to
![]() $f_{c,j}$
, we get a map with the desired property. We modify
$f_{c,j}$
, we get a map with the desired property. We modify
![]() $\Phi $
by appending the pullback map induced by the homotopy given by the lemma.
$\Phi $
by appending the pullback map induced by the homotopy given by the lemma.
Proof. Note first that it suffices to construct the homotopy on
![]() $\partial [0,L]^n \times [0,1]$
. Then it can be extended to
$\partial [0,L]^n \times [0,1]$
. Then it can be extended to
![]() $[0,L]^n \times [0,1]$
by pulling back along a projection map
$[0,L]^n \times [0,1]$
by pulling back along a projection map
Recall that we can write
![]() $X=X^{(n-1)} \cup _{\partial _i} \bigcup _i D^n$
, where
$X=X^{(n-1)} \cup _{\partial _i} \bigcup _i D^n$
, where
![]() $\partial _i:S^n_i \to X^{(n-1)}$
are Lipschitz attaching maps, and the metric on X is the quotient metric under this identification.
$\partial _i:S^n_i \to X^{(n-1)}$
are Lipschitz attaching maps, and the metric on X is the quotient metric under this identification.
The homotopy
![]() $\partial [0,L]^n \times [0,1] \to X$
will have two steps. In the first step, we homotope
$\partial [0,L]^n \times [0,1] \to X$
will have two steps. In the first step, we homotope
![]() $f|_{\partial [0,L]^n}$
into a collar neighborhood of
$f|_{\partial [0,L]^n}$
into a collar neighborhood of
![]() $Z^{(n-1)}$
, namely,
$Z^{(n-1)}$
, namely,
while keeping the map
![]() $C(X)$
-Lipschitz. In the second step, we retract from this collar down into
$C(X)$
-Lipschitz. In the second step, we retract from this collar down into
![]() $Z^{(n-1)}$
via a straight-line homotopy, which is
$Z^{(n-1)}$
via a straight-line homotopy, which is
![]() $C(X)$
-Lipschitz by definition.
$C(X)$
-Lipschitz by definition.
To perform the first step, we first fix a
![]() $C(n)$
-Lipschitz embedding of
$C(n)$
-Lipschitz embedding of
![]() $\Delta ^n$
in
$\Delta ^n$
in
![]() $B_1(0)$
such that the interior of the image contains
$B_1(0)$
such that the interior of the image contains
![]() $B_{1/2}(0)$
. This induces an embedding
$B_{1/2}(0)$
. This induces an embedding
![]() $\iota _i:\Delta ^n \to Z$
for every n-cell. Now we triangulate
$\iota _i:\Delta ^n \to Z$
for every n-cell. Now we triangulate
![]() $\partial [0,L]^n$
using simplices uniformly bilipschitz to the standard simplex such that the diameter of each simplex is at most
$\partial [0,L]^n$
using simplices uniformly bilipschitz to the standard simplex such that the diameter of each simplex is at most
![]() $1/8$
. Then we choose the homotopy in the first step as follows:
$1/8$
. Then we choose the homotopy in the first step as follows:
-
• Vertices whose image lies in
 $B_{5/8}(0)$
inside the ith cell are homotoped linearly to the nearest vertex of
$B_{5/8}(0)$
inside the ith cell are homotoped linearly to the nearest vertex of
 $\iota _i(\Delta ^n)$
. This homotopy extends on the subcomplex spanned by these vertices (which was originally mapped to
$\iota _i(\Delta ^n)$
. This homotopy extends on the subcomplex spanned by these vertices (which was originally mapped to
 $B_{3/4}(0)$
inside the ith n-cell) to a linear homotopy to a simplicial map to
$B_{3/4}(0)$
inside the ith n-cell) to a linear homotopy to a simplicial map to
 $\iota _i(\Delta ^n)$
.
$\iota _i(\Delta ^n)$
. -
• The homotopy is constant on the subcomplex spanned by vertices whose image lies outside
 $\bigcup _i B_{5/8}(0)$
. Note that the image of this subcomplex lies outside
$\bigcup _i B_{5/8}(0)$
. Note that the image of this subcomplex lies outside
 $\bigcup _i B_{1/2}(0)$
.
$\bigcup _i B_{1/2}(0)$
. -
• On simplices that include vertices from both subcomplexes, we extend the homotopy by interpolating linearly on the join.
This homotopy is again
![]() $C(X)$
-Lipschitz.
$C(X)$
-Lipschitz.
Since
![]() $f_{c,j}$
maps the boundary of the cube to
$f_{c,j}$
maps the boundary of the cube to
![]() $Z^{(n-1)}$
, it makes sense to discuss the homology class of
$Z^{(n-1)}$
, it makes sense to discuss the homology class of
![]() $f_{c,j}$
in Z, which we write
$f_{c,j}$
in Z, which we write
![]() $a(f_{c,j}) \in H_{n}(Z;{\mathbb {R}})$
. By Stokes’ theorem, for any cohomology class
$a(f_{c,j}) \in H_{n}(Z;{\mathbb {R}})$
. By Stokes’ theorem, for any cohomology class
![]() $u \in H^{n}(Z;{\mathbb {R}})$
,
$u \in H^{n}(Z;{\mathbb {R}})$
,
In other words,
![]() $a(f_{c,j})=c^n b_j+O(c^{n-1})$
, and therefore,
$a(f_{c,j})=c^n b_j+O(c^{n-1})$
, and therefore,
 $$\begin{align*}p^{\ell n} a_i=\sum_{j=1}^r a(f_{p^\ell x_{ij}^{1/n},j}).\end{align*}$$
$$\begin{align*}p^{\ell n} a_i=\sum_{j=1}^r a(f_{p^\ell x_{ij}^{1/n},j}).\end{align*}$$
We will construct an extension of
![]() $r_{p^\ell ,n-1}$
to the ith cell by patching together
$r_{p^\ell ,n-1}$
to the ith cell by patching together
![]() $f_{p^\ell x_{ij}^{1/n},j}$
for each j together with an ‘error-correcting’ map which gets rid of the
$f_{p^\ell x_{ij}^{1/n},j}$
for each j together with an ‘error-correcting’ map which gets rid of the
![]() $O(c^{n-1})$
error term in the homology class and a homotopy which connects the map on the boundary of the cube to
$O(c^{n-1})$
error term in the homology class and a homotopy which connects the map on the boundary of the cube to
![]() $r_{p^\ell ,n-1} \circ \iota _i$
.
$r_{p^\ell ,n-1} \circ \iota _i$
.
We first build the error-correcting map. For each
![]() $i=1,\ldots ,r$
, fix a map
$i=1,\ldots ,r$
, fix a map
which maps to the ith n-cell with degree 1 and sends all but one of the faces of
![]() $[0,1]^n$
to a basepoint
$[0,1]^n$
to a basepoint
![]() $p_0$
. Splitting
$p_0$
. Splitting
![]() $[0,1]^{n-1} \times [0,p^{-\ell }]$
into an
$[0,1]^{n-1} \times [0,p^{-\ell }]$
into an
![]() $(n-1)$
-dimensional grid of subdomains,
$(n-1)$
-dimensional grid of subdomains,
![]() $O(p^\ell )$
to a side, we build an
$O(p^\ell )$
to a side, we build an
![]() $O(p^\ell )$
-Lipschitz map
$O(p^\ell )$
-Lipschitz map
by mapping each subdomain to Z via the appropriate
![]() $g_i$
(and mapping any leftover subdomains via a constant map to
$g_i$
(and mapping any leftover subdomains via a constant map to
![]() $p_0$
) so that the induced homology class is the sum of the error terms of each
$p_0$
) so that the induced homology class is the sum of the error terms of each
![]() $f_{p^\ell x_{ij}^{1/n},j}$
.
$f_{p^\ell x_{ij}^{1/n},j}$
.
Now, let
![]() $g:[0,1]^{n} \to \bigvee _{r+1} [0,1]^{n}$
be an
$g:[0,1]^{n} \to \bigvee _{r+1} [0,1]^{n}$
be an
![]() $\text {const}(r)$
-Lipschitz map whose relative degree over each cube is
$\text {const}(r)$
-Lipschitz map whose relative degree over each cube is
![]() $1$
. Then the map
$1$
. Then the map
is in the homotopy class of
![]() $p^{\ell n}[\iota _i] \in \pi _n(Z,Z^{(n-1)})$
. Since
$p^{\ell n}[\iota _i] \in \pi _n(Z,Z^{(n-1)})$
. Since
![]() $\tilde f$
and
$\tilde f$
and
![]() $r_{p^\ell ,n-1} \circ \iota _i$
are in the same class in
$r_{p^\ell ,n-1} \circ \iota _i$
are in the same class in
![]() $\pi _n(Z,Z^{(n-1)})$
, their restrictions to the boundary are in the same class in
$\pi _n(Z,Z^{(n-1)})$
, their restrictions to the boundary are in the same class in
![]() $\pi _{n-1}(Z^{(n-1)})$
.
$\pi _{n-1}(Z^{(n-1)})$
.
Therefore, since
![]() $Z^{(n-1)}$
is scalable, using condition (iii), we can construct an
$Z^{(n-1)}$
is scalable, using condition (iii), we can construct an
![]() $O(p^\ell )$
-Lipschitz homotopy in
$O(p^\ell )$
-Lipschitz homotopy in
![]() $Z^{(n-1)}$
between
$Z^{(n-1)}$
between
![]() $\tilde f|_{\partial [0,1]^n}$
and
$\tilde f|_{\partial [0,1]^n}$
and
![]() ${r}_{p^\ell ,n-1} \circ \iota _i|_{\partial [0,1]^n}$
. We then extend
${r}_{p^\ell ,n-1} \circ \iota _i|_{\partial [0,1]^n}$
. We then extend
![]() ${r}_{p^\ell ,n-1}|_{Z^{(n-1)}}$
to our n-cell in an
${r}_{p^\ell ,n-1}|_{Z^{(n-1)}}$
to our n-cell in an
![]() $O(p^\ell )$
-Lipschitz way using this homotopy on the outer part of the cell and
$O(p^\ell )$
-Lipschitz way using this homotopy on the outer part of the cell and
![]() $\tilde f$
on the inner part.
$\tilde f$
on the inner part.
After we do this for every n-cell, we get an
![]() $O(p^\ell )$
-Lipschitz map
$O(p^\ell )$
-Lipschitz map
![]() $Z \to Z$
that induces the right action on homology. Although this map may not be homotopic to
$Z \to Z$
that induces the right action on homology. Although this map may not be homotopic to
![]() ${r}_p^\ell |_{Z}$
, this is sufficient to prove condition (ii) and therefore the inductive step.
${r}_p^\ell |_{Z}$
, this is sufficient to prove condition (ii) and therefore the inductive step.
Now we argue that (vi) implies (v
![]() $' $
). One way to see this is by a direct application of Theorem 2.3, which shows that (vi) implies (v
$' $
). One way to see this is by a direct application of Theorem 2.3, which shows that (vi) implies (v
![]() $' $
) for any closed n-manifold, as well as giving a quantitative result describing how fast the degree goes to
$' $
) for any closed n-manifold, as well as giving a quantitative result describing how fast the degree goes to
![]() $0$
asymptotically if (v
$0$
asymptotically if (v
![]() $'$
) is not satisfied.
$'$
) is not satisfied.
We can also use a softer, less technical argument related to Lemma 2.19. Suppose there is a
![]() $1$
-Lipschitz map
$1$
-Lipschitz map
![]() $f:{\mathbb {R}}^n \to Y$
of positive asymptotic degree. Let
$f:{\mathbb {R}}^n \to Y$
of positive asymptotic degree. Let
![]() $u_j \in H^{d_j}(Y;{\mathbb {R}})$
be a set of generators for the cohomology algebra of Y. Suppose that the relations of the cohomology algebra are given by
$u_j \in H^{d_j}(Y;{\mathbb {R}})$
be a set of generators for the cohomology algebra of Y. Suppose that the relations of the cohomology algebra are given by
![]() $R_r(u_1,\ldots ,u_J)=0$
, where
$R_r(u_1,\ldots ,u_J)=0$
, where
![]() $R_r$
is a homogeneous polynomial of graded degree
$R_r$
is a homogeneous polynomial of graded degree
![]() $D_r$
in the free exterior algebra
$D_r$
in the free exterior algebra
![]() $\Lambda (u_1,\ldots ,u_J)$
. Define forms
$\Lambda (u_1,\ldots ,u_J)$
. Define forms
![]() $\omega _j \in \Omega ^{d_j}(Y)$
representing the
$\omega _j \in \Omega ^{d_j}(Y)$
representing the
![]() $u_j$
and
$u_j$
and
![]() $\alpha _r \in \Omega ^{D_r-1}(Y)$
such that
$\alpha _r \in \Omega ^{D_r-1}(Y)$
such that
![]() $d\alpha _r=R_r(\omega _1,\ldots ,\omega _J)$
.
$d\alpha _r=R_r(\omega _1,\ldots ,\omega _J)$
.
For every
![]() $t>0$
, define
$t>0$
, define
![]() $f_t(x)=f(tx)$
; this is a t-Lipschitz map. Now, we consider forms
$f_t(x)=f(tx)$
; this is a t-Lipschitz map. Now, we consider forms
Since pulling back along a t-Lipschitz map multiplies the infinity-norm of a k-form by at most
![]() $t^k$
, we have
$t^k$
, we have
By definition of positive asymptotic degree, there is an
![]() ${\varepsilon }>0$
and a sequence of
${\varepsilon }>0$
and a sequence of
![]() $t \to \infty $
such that
$t \to \infty $
such that
![]() $\int _{B_1({\mathbb {R}}^n)} f_t^*d\operatorname {\mathrm {vol}}_M \geq {\varepsilon }$
. By the Arzelà–Ascoli theorem, this sequence has a subsequence
$\int _{B_1({\mathbb {R}}^n)} f_t^*d\operatorname {\mathrm {vol}}_M \geq {\varepsilon }$
. By the Arzelà–Ascoli theorem, this sequence has a subsequence
![]() $t_1,t_2,\ldots \to \infty $
for which the
$t_1,t_2,\ldots \to \infty $
for which the
![]() $\omega _{j,t_k}$
converge in the flat norm; we have
$\omega _{j,t_k}$
converge in the flat norm; we have
This means that the ring homomorphism
![]() $\Lambda (u_1,\ldots ,u_J) \to \Omega ^*_\flat ({\mathbb {R}}^n)$
defined by
$\Lambda (u_1,\ldots ,u_J) \to \Omega ^*_\flat ({\mathbb {R}}^n)$
defined by
![]() $wu_j \mapsto \omega _{j,\infty }$
passes to a well-defined map on the quotient ring by the relations
$wu_j \mapsto \omega _{j,\infty }$
passes to a well-defined map on the quotient ring by the relations
![]() $R_r$
, giving a ring homomorphism
$R_r$
, giving a ring homomorphism
Moreover, flat convergence implies that
In particular,
![]() ${\varphi }_\infty (d\operatorname {\mathrm {vol}}_M)$
is nonzero on some set of positive measure. While flat forms are not well defined pointwise, they are well defined up to a measure zero set, so we can choose representatives and then choose a point in this set of positive measure where these representatives actually restrict to a ring homomorphism
${\varphi }_\infty (d\operatorname {\mathrm {vol}}_M)$
is nonzero on some set of positive measure. While flat forms are not well defined pointwise, they are well defined up to a measure zero set, so we can choose representatives and then choose a point in this set of positive measure where these representatives actually restrict to a ring homomorphism
This homomorphism sends the fundamental class to a nonzero element, so by Poincaré duality, it is injective.
6. Efficient nullhomotopies
Now, we prove Theorem B, which we restate here:
Theorem 6.1. Let Y be a finite formal CW complex with a piecewise Riemannian metric and Lipschitz attaching maps such that
![]() $H_n(Y;\mathbb {Q})$
is nonzero for d different values of
$H_n(Y;\mathbb {Q})$
is nonzero for d different values of
![]() $n>0$
. Then for any finite simplicial complex X, any nullhomotopic L-Lipschitz map
$n>0$
. Then for any finite simplicial complex X, any nullhomotopic L-Lipschitz map
![]() $f:X \to Y$
is
$f:X \to Y$
is
![]() $O(L(\log L)^{d-1})$
-Lipschitz nullhomotopic.
$O(L(\log L)^{d-1})$
-Lipschitz nullhomotopic.
We will use Theorem 3.1 to prove Theorem 6.1. The argument is similar to the proof of (ii)
![]() $\Rightarrow $
(iii) of the main theorem of [Reference Berdnikov and Manin3].
$\Rightarrow $
(iii) of the main theorem of [Reference Berdnikov and Manin3].
Proof. Let X be a finite simplicial complex and
![]() $f:X \to Y$
a nullhomotopic L-Lipschitz map. Fix a minimal model
$f:X \to Y$
a nullhomotopic L-Lipschitz map. Fix a minimal model
![]() $m_Y:\mathcal M_Y \to \Omega ^*Y$
and a family of automorphisms
$m_Y:\mathcal M_Y \to \Omega ^*Y$
and a family of automorphisms
![]() $\rho _t:\mathcal M_Y \to \mathcal M_Y$
which induce the grading automorphisms on cohomology sending a class
$\rho _t:\mathcal M_Y \to \mathcal M_Y$
which induce the grading automorphisms on cohomology sending a class
![]() $z \in H^n(Y;{\mathbb {R}})$
to
$z \in H^n(Y;{\mathbb {R}})$
to
![]() $t^n z$
. By Theorem 4.4, there is a
$t^n z$
. By Theorem 4.4, there is a
![]() $p>1$
and a self-map
$p>1$
and a self-map
![]() ${r}_p:Y \to Y$
whose rationalization is
${r}_p:Y \to Y$
whose rationalization is
![]() $\rho _p$
. Moreover, by Theorem 4.6, there is a sequence of
$\rho _p$
. Moreover, by Theorem 4.6, there is a sequence of
![]() $O(\ell ^{d-1}p^\ell )$
-Lipschitz maps
$O(\ell ^{d-1}p^\ell )$
-Lipschitz maps
![]() ${r}_{p^\ell }$
homotopic to the
${r}_{p^\ell }$
homotopic to the
![]() $\ell $
th iterate
$\ell $
th iterate
![]() ${r}_p^\ell $
.
${r}_p^\ell $
.
We will define a nullhomotopy of f by homotoping through a series of maps which are more and more ‘locally organized’. Specifically, for
![]() $1 \leq \ell \leq s=\lceil \log _pL\rceil $
, we look at the map
$1 \leq \ell \leq s=\lceil \log _pL\rceil $
, we look at the map
![]() $\rho _{p^{-\ell }}$
which multiplies each degree d generator by
$\rho _{p^{-\ell }}$
which multiplies each degree d generator by
![]() $p^{-\ell k}$
where
$p^{-\ell k}$
where
![]() $k \geq d$
. Thus, applying the shadowing principle 4.1 to the map
$k \geq d$
. Thus, applying the shadowing principle 4.1 to the map
gives a
![]() $C(X,Y)(L/p^\ell +1)$
-Lipschitz map
$C(X,Y)(L/p^\ell +1)$
-Lipschitz map
![]() $f_\ell :X \to Y$
. Similarly, we get a
$f_\ell :X \to Y$
. Similarly, we get a
![]() $C(Y)(s^{d-1}p^\ell +1)$
-Lipschitz self-map
$C(Y)(s^{d-1}p^\ell +1)$
-Lipschitz self-map
![]() $g_\ell :Y \to Y$
homotopic to
$g_\ell :Y \to Y$
homotopic to
![]() ${r}_{p^\ell }$
by applying the shadowing principle to the map
${r}_{p^\ell }$
by applying the shadowing principle to the map
We will build a nullhomotopy of f through the sequence of maps

As we go right, the length (Lipschitz constant in the time direction) of the
![]() $\ell $
th intermediate homotopy increases – it is
$\ell $
th intermediate homotopy increases – it is
![]() $O(s^{d-1} p^\ell )$
– while the thickness (Lipschitz constant in the space direction) stays a constant
$O(s^{d-1} p^\ell )$
– while the thickness (Lipschitz constant in the space direction) stays a constant
![]() $O(s^{d-1}L)$
. Thus, all together, these homotopies can be glued into an
$O(s^{d-1}L)$
. Thus, all together, these homotopies can be glued into an
![]() $O(s^{d-1}p^s)$
-Lipschitz nullhomotopy of f.
$O(s^{d-1}p^s)$
-Lipschitz nullhomotopy of f.
Informally, the intermediate maps
![]() $g_\ell \circ f_\ell $
look at scale
$g_\ell \circ f_\ell $
look at scale
![]() $p^\ell /L$
like thickness-
$p^\ell /L$
like thickness-
![]() $p^\ell $
‘bundles’ or ‘cables’ of identical standard maps at scale
$p^\ell $
‘bundles’ or ‘cables’ of identical standard maps at scale
![]() $1/L$
. This structure makes them essentially as easy to nullhomotope as
$1/L$
. This structure makes them essentially as easy to nullhomotope as
![]() $L/p^\ell $
-Lipschitz maps.
$L/p^\ell $
-Lipschitz maps.
We now build the aforementioned homotopies:
Lemma 6.2. There is a homotopy
![]() $G_\ell :Y \times [0,1] \to Y$
between
$G_\ell :Y \times [0,1] \to Y$
between
![]() $g_\ell $
and
$g_\ell $
and
![]() $g_{\ell -1} \circ {r}_p$
which has constant length and thickness
$g_{\ell -1} \circ {r}_p$
which has constant length and thickness
![]() $O(s^{d-1} p^\ell )$
.
$O(s^{d-1} p^\ell )$
.
Note that the conclusion of Lemma 6.2 is similar to that of Lemma 3.4 but applies to a larger class of spaces.
Lemma 6.3. There is a homotopy
![]() $F_\ell :X \times [0,1] \to Y$
between
$F_\ell :X \times [0,1] \to Y$
between
![]() $f_\ell $
and
$f_\ell $
and
![]() ${r}_p \circ f_{\ell +1}$
which has constant length and thickness
${r}_p \circ f_{\ell +1}$
which has constant length and thickness
![]() $O(p^\ell )$
.
$O(p^\ell )$
.
This induces homotopies of thickness
![]() $O(s^{d-1}p^s)$
and length
$O(s^{d-1}p^s)$
and length
![]() $O(s^{d-1} p^\ell )$
:
$O(s^{d-1} p^\ell )$
:
-
•
 $G_\ell \circ (f_\ell \times \operatorname {\mathrm {id}})$
from
$G_\ell \circ (f_\ell \times \operatorname {\mathrm {id}})$
from
 $g_{\ell -1} \circ r_p \circ f_\ell $
to
$g_{\ell -1} \circ r_p \circ f_\ell $
to
 $g_\ell \circ f_\ell $
of thickness
$g_\ell \circ f_\ell $
of thickness
 $O(s^{d-1}p^s)$
and length
$O(s^{d-1}p^s)$
and length
 $O(p^\ell )$
;
$O(p^\ell )$
; -
•
 $g_\ell \circ F_\ell $
from
$g_\ell \circ F_\ell $
from
 $g_\ell \circ f_\ell $
to
$g_\ell \circ f_\ell $
to
 $g_\ell \circ r_p \circ f_{\ell +1}$
of thickness
$g_\ell \circ r_p \circ f_{\ell +1}$
of thickness
 $O(s^{d-1}p^s)$
and length
$O(s^{d-1}p^s)$
and length
 $O(s^{d-1}p^\ell )$
.
$O(s^{d-1}p^\ell )$
.
It remains to build a homotopy from
![]() $r_p$
to the
$r_p$
to the
![]() $C(Y)(s^{d-1}p+1)$
-Lipschitz map
$C(Y)(s^{d-1}p+1)$
-Lipschitz map
![]() $g_1$
. By [Reference Manin18, Theorem 5–6], such a homotopy
$g_1$
. By [Reference Manin18, Theorem 5–6], such a homotopy
![]() $\tilde G: Y \times [0,1] \to Y$
can be chosen to have thickness
$\tilde G: Y \times [0,1] \to Y$
can be chosen to have thickness
![]() $O(s^{d-1})$
and length
$O(s^{d-1})$
and length
![]() $O(s^{d(d-1)})$
. Thus, the homotopy
$O(s^{d(d-1)})$
. Thus, the homotopy
![]() $\tilde G \circ (f_1 \times \operatorname {\mathrm {id}})$
has thickness
$\tilde G \circ (f_1 \times \operatorname {\mathrm {id}})$
has thickness
![]() $O(s^{d-1}p^s)$
and length
$O(s^{d-1}p^s)$
and length
![]() $O(s^{d(d-1)})$
.
$O(s^{d(d-1)})$
.
Finally, the map
![]() $f_s$
is
$f_s$
is
![]() $C(X,Y)$
-Lipschitz and therefore has a short homotopy to one of a finite set of nullhomotopic simplicial maps
$C(X,Y)$
-Lipschitz and therefore has a short homotopy to one of a finite set of nullhomotopic simplicial maps
![]() $X \to Y$
. For each map in this finite set, we can pick a fixed nullhomotopy, giving a constant bound for the Lipschitz constant of a nullhomotopy of
$X \to Y$
. For each map in this finite set, we can pick a fixed nullhomotopy, giving a constant bound for the Lipschitz constant of a nullhomotopy of
![]() $f_s$
and therefore a linear one for
$f_s$
and therefore a linear one for
![]() $r_{p^s} \circ f_s$
.
$r_{p^s} \circ f_s$
.
The lengths of these homotopies are bounded above by a geometric series which sums to
![]() $O(L(\log L)^d)$
, completing the proof of the theorem modulo the two lemmas above.
$O(L(\log L)^d)$
, completing the proof of the theorem modulo the two lemmas above.
Proof of Lemma 6.2
We use the fact that the maps
![]() $g_\ell $
were built using the shadowing principle. Thus, there are formal homotopies
$g_\ell $
were built using the shadowing principle. Thus, there are formal homotopies
![]() $\Psi _i$
of length
$\Psi _i$
of length
![]() $C(X,Y)$
between
$C(X,Y)$
between
![]() ${r}_{p^s}^*m_Y\rho _{p^{s-i}}$
and
${r}_{p^s}^*m_Y\rho _{p^{s-i}}$
and
![]() $g_i^*m_Y$
. There is also a formal homotopy
$g_i^*m_Y$
. There is also a formal homotopy
![]() $\Upsilon $
between
$\Upsilon $
between
![]() ${r}_p^*m_Y$
and
${r}_p^*m_Y$
and
![]() $m_Y\rho _p$
. This allows us to construct the following formal homotopies:
$m_Y\rho _p$
. This allows us to construct the following formal homotopies:
-
•
 $\Psi _\ell $
, time-reversed, between
$\Psi _\ell $
, time-reversed, between
 $g_\ell ^*m_Y$
and
$g_\ell ^*m_Y$
and
 ${r}_{p^s}^*m_Y\rho _{p^{s-\ell }}$
, of length
${r}_{p^s}^*m_Y\rho _{p^{s-\ell }}$
, of length
 $C(Y)$
;
$C(Y)$
; -
•
 $\Psi _{\ell -1}\rho _p$
between
$\Psi _{\ell -1}\rho _p$
between
 ${r}_{p^s}^*m_Y\rho _{p^{s-\ell }}$
and
${r}_{p^s}^*m_Y\rho _{p^{s-\ell }}$
and
 $g_{\ell -1}^*m_Y\rho _p$
, of length
$g_{\ell -1}^*m_Y\rho _p$
, of length
 $C(Y)p$
;
$C(Y)p$
; -
• and
 $(g_{\ell -1}^* \otimes \operatorname {\mathrm {id}})\Upsilon $
between
$(g_{\ell -1}^* \otimes \operatorname {\mathrm {id}})\Upsilon $
between
 $g_{\ell -1}^*m_Y\rho _p$
and
$g_{\ell -1}^*m_Y\rho _p$
and
 $g_{\ell -1}^*{r}_p^*m_Y$
, of length
$g_{\ell -1}^*{r}_p^*m_Y$
, of length
 $C(Y)$
.
$C(Y)$
.
Concatenating these three homotopies and applying the relative shadowing principle 4.2 to the resulting map
![]() $\mathcal {M}^*_Y \to \Omega ^*(Y \times [0,1])$
rel ends, we get a linear thickness homotopy of length
$\mathcal {M}^*_Y \to \Omega ^*(Y \times [0,1])$
rel ends, we get a linear thickness homotopy of length
![]() $O(p)$
between the two maps.
$O(p)$
between the two maps.
Proof of Lemma 6.3
We use the fact that the maps
![]() $f_\ell $
and
$f_\ell $
and
![]() $f_{\ell +1}$
were built using the shadowing principle. Thus, there are formal homotopies
$f_{\ell +1}$
were built using the shadowing principle. Thus, there are formal homotopies
![]() $\Phi _i$
of length
$\Phi _i$
of length
![]() $C(X,Y)$
between
$C(X,Y)$
between
![]() $f^*m_Y\rho _{p^{-i}}$
and
$f^*m_Y\rho _{p^{-i}}$
and
![]() $f_i$
. This allows us to construct the following formal homotopies:
$f_i$
. This allows us to construct the following formal homotopies:
-
•
 $\Phi _\ell $
, time-reversed, between
$\Phi _\ell $
, time-reversed, between
 $f_\ell $
and
$f_\ell $
and
 $f^*m_Y\rho _{p^{-\ell }}$
, of length
$f^*m_Y\rho _{p^{-\ell }}$
, of length
 $C(X,Y)$
;
$C(X,Y)$
; -
•
 $\Phi _{\ell +1}\rho _p$
between
$\Phi _{\ell +1}\rho _p$
between
 $f^*m_Y\rho _{p^{-\ell }}$
and
$f^*m_Y\rho _{p^{-\ell }}$
and
 $f_{\ell +1}^*m_Y\rho _p$
, of length
$f_{\ell +1}^*m_Y\rho _p$
, of length
 $C(X,Y)p$
;
$C(X,Y)p$
; -
• and
 $(f_{\ell +1}^* \otimes \operatorname {\mathrm {id}})\Upsilon $
between
$(f_{\ell +1}^* \otimes \operatorname {\mathrm {id}})\Upsilon $
between
 $f_{\ell +1}^*m_Y\rho _p$
and
$f_{\ell +1}^*m_Y\rho _p$
and
 $f_{\ell +1}^*{r}_p^*m_Y$
, of length
$f_{\ell +1}^*{r}_p^*m_Y$
, of length
 $C(X,Y)$
.
$C(X,Y)$
.
Concatenating these three homotopies and applying the relative shadowing principle 4.2 to the resulting map
![]() $\mathcal {M}^*_Y \to \Omega ^*(X \times [0,1])$
rel ends, we get a linear thickness homotopy of length
$\mathcal {M}^*_Y \to \Omega ^*(X \times [0,1])$
rel ends, we get a linear thickness homotopy of length
![]() $O(p)$
between the two maps.
$O(p)$
between the two maps.
7. Nonformal spaces
In this section, we discuss the relationship between the degree and Lipschitz constants of self-maps of nonformal manifolds.
First, we note that such manifolds may have no self-maps of degree
![]() $>1$
at all. Such manifolds are called inflexible; examples of this phenomenon are given in [Reference Arkowitz and Lupton2, Reference Crowley and Löh10, Reference Costoya and Viruel9, Reference Amann1]. Manifolds which have self-maps of high degree are called flexible.
$>1$
at all. Such manifolds are called inflexible; examples of this phenomenon are given in [Reference Arkowitz and Lupton2, Reference Crowley and Löh10, Reference Costoya and Viruel9, Reference Amann1]. Manifolds which have self-maps of high degree are called flexible.
Among flexible manifolds, a distinguished class are those with positive weights. A space Y has positive weights if its minimal model
![]() $\mathcal M_Y$
has a one-parameter family of ‘rescaling’ automorphisms; that is, there is a basis
$\mathcal M_Y$
has a one-parameter family of ‘rescaling’ automorphisms; that is, there is a basis
![]() $\{v_i\}$
for the indecomposables and integers
$\{v_i\}$
for the indecomposables and integers
![]() $n_i$
such that the map
$n_i$
such that the map
![]() $\lambda _t:\mathcal M_Y \to \mathcal M_Y$
sending
$\lambda _t:\mathcal M_Y \to \mathcal M_Y$
sending
![]() $v_i \mapsto t^{n_i}v_i$
is a DGA automorphism for any
$v_i \mapsto t^{n_i}v_i$
is a DGA automorphism for any
![]() $t \in (0,\infty )$
. This can be thought of as a generalization of formality: formal spaces are distinguished by the fact that one can define rescaling automorphisms that send every cohomology class
$t \in (0,\infty )$
. This can be thought of as a generalization of formality: formal spaces are distinguished by the fact that one can define rescaling automorphisms that send every cohomology class
![]() $z \mapsto t^{\dim z} z$
; see §4.2.
$z \mapsto t^{\dim z} z$
; see §4.2.
Example 7.1. One nonformal manifold with positive weights is the example given in the introduction, the total space M of the bundle
![]() $S^3 \to M \to S^2 \times S^2$
obtained by pulling back the Hopf fibration along a degree 1 map
$S^3 \to M \to S^2 \times S^2$
obtained by pulling back the Hopf fibration along a degree 1 map
![]() $S^2 \times S^2 \to S^4$
. According to [Reference Félix, Oprea and Tanré13, p. 95], its minimal model is given by
$S^2 \times S^2 \to S^4$
. According to [Reference Félix, Oprea and Tanré13, p. 95], its minimal model is given by
and therefore, for any t, it has an automorphism which takes
![]() $a_i \mapsto ta_i$
and
$a_i \mapsto ta_i$
and
![]() $b_{ij} \mapsto t^2b_{ij}$
. Now,
$b_{ij} \mapsto t^2b_{ij}$
. Now,
 $$ \begin{align*} H^5(M;\mathbb Q) &\cong \langle b_{11}a_2-a_1b_{12}, b_{12}a_2-a_1b_{22} \rangle \\ H^7(M;\mathbb Q) &\cong \langle b_{11}a_2^2-a_1a_2b_{12} \sim a_1^2b_{22}-a_1a_2b_{12} \rangle, \end{align*} $$
$$ \begin{align*} H^5(M;\mathbb Q) &\cong \langle b_{11}a_2-a_1b_{12}, b_{12}a_2-a_1b_{22} \rangle \\ H^7(M;\mathbb Q) &\cong \langle b_{11}a_2^2-a_1a_2b_{12} \sim a_1^2b_{22}-a_1a_2b_{12} \rangle, \end{align*} $$
and therefore, this automorphism multiplies elements of
![]() $H^5(M;\mathbb Q)$
by
$H^5(M;\mathbb Q)$
by
![]() $t^3$
and elements of
$t^3$
and elements of
![]() $H^7(M;\mathbb Q)$
by
$H^7(M;\mathbb Q)$
by
![]() $t^4$
.
$t^4$
.
A priori, automorphisms of the minimal model need not be realized by genuine maps of finite complexes. But manifolds with positive weights have self-maps of arbitrarily high degree [Reference Costoya, Muñoz and Viruel8, Theorem 3.2]. In fact, for any family of scaling automorphisms
![]() $\lambda _t$
, there is some
$\lambda _t$
, there is some
![]() $t_0>0$
such that for every
$t_0>0$
such that for every
![]() $z \in \mathbb Z$
,
$z \in \mathbb Z$
,
![]() $\lambda _{zt_0}$
is the rationalization of a genuine map
$\lambda _{zt_0}$
is the rationalization of a genuine map
![]() $Y \to Y$
[Reference Manin19, Theorem A].
$Y \to Y$
[Reference Manin19, Theorem A].
Of course, not every flexible manifold has positive weights. For example, if M is inflexible and N has positive weights, then
![]() $M \times N$
is flexible but does not have positive weights.
$M \times N$
is flexible but does not have positive weights.
7.1. Upper bounds on degree
Having introduced the main actors, we prove Theorem D, which we restate here for convenience:
Theorem. Let M be a closed simply connected n-manifold which is not formal. Then either M is inflexible (has no self-maps of degree
![]() $>1$
) or the maximal degree of an L-Lipschitz map
$>1$
) or the maximal degree of an L-Lipschitz map
![]() $M \to M$
is bounded by
$M \to M$
is bounded by
![]() $L^\alpha $
for some rational
$L^\alpha $
for some rational
![]() $\alpha <n$
.
$\alpha <n$
.
Example 7.2. As stated in the introduction, for the
![]() $7$
-manifold M described in Example 7.1, we get
$7$
-manifold M described in Example 7.1, we get
![]() $\alpha =20/3<7$
. To see this, consider an automorphism
$\alpha =20/3<7$
. To see this, consider an automorphism
![]() $\rho :\mathcal M_M \to \mathcal M_M$
of the minimal model of M. Such an automorphism is determined by the images
$\rho :\mathcal M_M \to \mathcal M_M$
of the minimal model of M. Such an automorphism is determined by the images
 $$ \begin{align*} \rho(a_1) &= t_{11}a_1+t_{12}a_2 \\ \rho(a_2) &= t_{21}a_1+t_{22}a_2. \end{align*} $$
$$ \begin{align*} \rho(a_1) &= t_{11}a_1+t_{12}a_2 \\ \rho(a_2) &= t_{21}a_1+t_{22}a_2. \end{align*} $$
Then a computation determines that
where
 $T=\begin {pmatrix} t_{11}&t_{12} \\ t_{21}&t_{22} \end {pmatrix}$
, and the action of
$T=\begin {pmatrix} t_{11}&t_{12} \\ t_{21}&t_{22} \end {pmatrix}$
, and the action of
![]() $\rho $
on
$\rho $
on
![]() $H^5(M;\mathbb R)$
with respect to the given basis has matrix
$H^5(M;\mathbb R)$
with respect to the given basis has matrix
![]() $(\det T)T$
. Let
$(\det T)T$
. Let
![]() $\lambda _1,\lambda _2$
be the eigenvalues of T with
$\lambda _1,\lambda _2$
be the eigenvalues of T with
![]() $\lvert \lambda _1\rvert \leq \lvert \lambda _2\rvert $
. Then by Lemma 7.3 below, for any self-map
$\lvert \lambda _1\rvert \leq \lvert \lambda _2\rvert $
. Then by Lemma 7.3 below, for any self-map
![]() $f:M \to M$
whose rationalization is
$f:M \to M$
whose rationalization is
![]() $\rho $
,
$\rho $
,
Proof of Theorem D
We prove the contrapositive. Suppose that there is a sequence of maps
![]() $f_i:M \to M$
with strictly increasing degrees such that for every
$f_i:M \to M$
with strictly increasing degrees such that for every
![]() $\alpha <n$
,
$\alpha <n$
,
![]() $\deg f_i$
eventually grows faster than
$\deg f_i$
eventually grows faster than
![]() $(\operatorname {\mathrm {Lip}} f_i)^\alpha $
. We will show that M must be formal.
$(\operatorname {\mathrm {Lip}} f_i)^\alpha $
. We will show that M must be formal.
This requires a lemma:
Lemma 7.3. Let
![]() $f:M \to M$
and suppose the induced map
$f:M \to M$
and suppose the induced map
![]() $f_*:H^k(M;{\mathbb {C}}) \to H^k(M;{\mathbb {C}})$
has an eigenvalue
$f_*:H^k(M;{\mathbb {C}}) \to H^k(M;{\mathbb {C}})$
has an eigenvalue
![]() $\lambda $
. Then
$\lambda $
. Then
Proof. The eigenvalue
![]() $\lambda $
is either real or one of a conjugate pair of complex eigenvalues. If it is real, choose a
$\lambda $
is either real or one of a conjugate pair of complex eigenvalues. If it is real, choose a
![]() $\lVert {\cdot }\rVert _\infty $
-minimizing form
$\lVert {\cdot }\rVert _\infty $
-minimizing form
![]() $\omega \in \Omega ^k_\flat (M)$
among those which represent an eigenvector
$\omega \in \Omega ^k_\flat (M)$
among those which represent an eigenvector
![]() $a \in H^k(M;{\mathbb {R}})$
. Then
$a \in H^k(M;{\mathbb {R}})$
. Then
If
![]() $\lambda $
is not real, choose an invariant two-dimensional subspace of
$\lambda $
is not real, choose an invariant two-dimensional subspace of
![]() $H^k(M;{\mathbb {R}})$
whose complexification contains eigenvectors for
$H^k(M;{\mathbb {R}})$
whose complexification contains eigenvectors for
![]() $\lambda $
and
$\lambda $
and
![]() $\overline \lambda $
and, within this, an
$\overline \lambda $
and, within this, an
![]() $f^*/\lvert \lambda \rvert $
-invariant ellipse E. Let
$f^*/\lvert \lambda \rvert $
-invariant ellipse E. Let
![]() $\omega \in \Omega ^k_\flat (M)$
be a
$\omega \in \Omega ^k_\flat (M)$
be a
![]() $\lVert {\cdot }\rVert _\infty $
-minimizing form among those representing elements of E. Then once again,
$\lVert {\cdot }\rVert _\infty $
-minimizing form among those representing elements of E. Then once again,
Now, suppose
![]() $f:M \to M$
is of degree d and
$f:M \to M$
is of degree d and
![]() $f_*:H^k(M;{\mathbb {C}}) \to H^k(M;{\mathbb {C}})$
has some eigenvalue
$f_*:H^k(M;{\mathbb {C}}) \to H^k(M;{\mathbb {C}})$
has some eigenvalue
![]() $\lambda $
such that
$\lambda $
such that
![]() $\lvert \lambda \rvert \neq d^{k/n}$
. Then either
$\lvert \lambda \rvert \neq d^{k/n}$
. Then either
![]() $\lvert \lambda \rvert>d^{k/n}$
, or by Poincaré duality, the induced map on
$\lvert \lambda \rvert>d^{k/n}$
, or by Poincaré duality, the induced map on
![]() $H^{n-k}(M;{\mathbb {C}})$
has an eigenvalue
$H^{n-k}(M;{\mathbb {C}})$
has an eigenvalue
![]() $\mu $
with
$\mu $
with
![]() $\lvert \mu \rvert>d^{\frac {n-k}{n}}$
. Therefore, by our hypotheses and Lemma 7.3, as
$\lvert \mu \rvert>d^{\frac {n-k}{n}}$
. Therefore, by our hypotheses and Lemma 7.3, as
![]() $i \to \infty $
, the absolute values of eigenvalues of
$i \to \infty $
, the absolute values of eigenvalues of
![]() $(f_i)_*:H_k(M;{\mathbb {C}}) \to H_k(M;{\mathbb {C}})$
uniformly approach
$(f_i)_*:H_k(M;{\mathbb {C}}) \to H_k(M;{\mathbb {C}})$
uniformly approach
![]() $(\deg f_i)^{k/n}$
. That is, for any such eigenvalue
$(\deg f_i)^{k/n}$
. That is, for any such eigenvalue
![]() $\lambda $
,
$\lambda $
,
Now consider the automorphisms
![]() ${\varphi }_i:\mathcal L_M({\mathbb {C}}) \to \mathcal L_M({\mathbb {C}})$
induced by the
${\varphi }_i:\mathcal L_M({\mathbb {C}}) \to \mathcal L_M({\mathbb {C}})$
induced by the
![]() $f_i$
. Here,
$f_i$
. Here,
![]() $\mathcal L_M({\mathbb {C}})$
is the complexified Lie minimal model of M, a free differential graded Lie algebra whose indecomposables in degree k are
$\mathcal L_M({\mathbb {C}})$
is the complexified Lie minimal model of M, a free differential graded Lie algebra whose indecomposables in degree k are
![]() $L_k \cong H_k(M;{\mathbb {C}})$
, and
$L_k \cong H_k(M;{\mathbb {C}})$
, and
![]() ${\varphi }_i|_{L_k}=(f_i)_*$
. The Lie minimal model is in many ways dual to the Sullivan minimal model; see [Reference Félix, Halperin and Thomas12, Part IV] for the detailed theory. The endomorphisms of
${\varphi }_i|_{L_k}=(f_i)_*$
. The Lie minimal model is in many ways dual to the Sullivan minimal model; see [Reference Félix, Halperin and Thomas12, Part IV] for the detailed theory. The endomorphisms of
![]() $\mathcal L_M$
form an affine variety in the vector space of graded linear maps
$\mathcal L_M$
form an affine variety in the vector space of graded linear maps
![]() $H_*(M;{\mathbb {C}}) \to H_*(M;{\mathbb {C}})$
, and the automorphisms
$H_*(M;{\mathbb {C}}) \to H_*(M;{\mathbb {C}})$
, and the automorphisms
![]() $\operatorname {\mathrm {Aut}}(\mathcal L_M({\mathbb {C}}))$
form a linear algebraic group which is Zariski open inside that variety. Moreover, the Zariski closure of
$\operatorname {\mathrm {Aut}}(\mathcal L_M({\mathbb {C}}))$
form a linear algebraic group which is Zariski open inside that variety. Moreover, the Zariski closure of
![]() $\operatorname {\mathrm {Aut}}(\mathcal L_M({\mathbb {C}}))$
, which is the same as its metric closure, is contained in the endomorphism variety.
$\operatorname {\mathrm {Aut}}(\mathcal L_M({\mathbb {C}}))$
, which is the same as its metric closure, is contained in the endomorphism variety.
We now apply the theory of linear algebraic groups; see, for example, [Reference Borel5, §III.10 and IV.11]. (A similar argument is applied to rational homotopy theory in [Reference Body, Mimura, Shiga and Sullivan4, §2].) Choose a Borel subgroup
![]() $G \subseteq \operatorname {\mathrm {Aut}}(\mathcal L_M({\mathbb {C}}))$
; by the Lie–Kolchin theorem [Reference Borel5, Ch. III, Theorem 10.5], this is the subgroup of matrices which are upper triangular with respect to some basis
$G \subseteq \operatorname {\mathrm {Aut}}(\mathcal L_M({\mathbb {C}}))$
; by the Lie–Kolchin theorem [Reference Borel5, Ch. III, Theorem 10.5], this is the subgroup of matrices which are upper triangular with respect to some basis
![]() $\mathcal B$
of
$\mathcal B$
of
![]() $H_*(M;{\mathbb {C}})$
. Moreover, since elements of
$H_*(M;{\mathbb {C}})$
. Moreover, since elements of
![]() $\operatorname {\mathrm {Aut}}(\mathcal L_M({\mathbb {C}}))$
preserve the grading of
$\operatorname {\mathrm {Aut}}(\mathcal L_M({\mathbb {C}}))$
preserve the grading of
![]() $H_*(M;{\mathbb {C}})$
, we can assume that
$H_*(M;{\mathbb {C}})$
, we can assume that
![]() $\mathcal B$
is a graded basis. By [Reference Borel5, Ch. IV, Theorem 11.10], every
$\mathcal B$
is a graded basis. By [Reference Borel5, Ch. IV, Theorem 11.10], every
![]() ${\varphi }_i$
is conjugate to some
${\varphi }_i$
is conjugate to some
![]() ${\varphi }_i' \in G$
. Moreover, by [Reference Borel5, Ch. III, Theorem 10.6], for every
${\varphi }_i' \in G$
. Moreover, by [Reference Borel5, Ch. III, Theorem 10.6], for every
![]() ${\varphi }_i'$
, G also contains the diagonal matrix
${\varphi }_i'$
, G also contains the diagonal matrix
![]() ${\varphi }_i"$
obtained by zeroing out the off-diagonal entries of
${\varphi }_i"$
obtained by zeroing out the off-diagonal entries of
![]() ${\varphi }_i'$
.
${\varphi }_i'$
.
As a vector space,
![]() $\mathcal L_M({\mathbb {C}})$
is spanned by iterated Lie brackets of elements of
$\mathcal L_M({\mathbb {C}})$
is spanned by iterated Lie brackets of elements of
![]() $\mathcal B$
. Therefore, each
$\mathcal B$
. Therefore, each
![]() ${\varphi }_i"$
is diagonal on all of
${\varphi }_i"$
is diagonal on all of
![]() $\mathcal L_M({\mathbb {C}})$
with respect to a basis of iterated brackets of elements of
$\mathcal L_M({\mathbb {C}})$
with respect to a basis of iterated brackets of elements of
![]() $\mathcal B$
. Moreover, if
$\mathcal B$
. Moreover, if
![]() $a \in L_k$
is an eigenvector of
$a \in L_k$
is an eigenvector of
![]() ${\varphi }_i"$
, then
${\varphi }_i"$
, then
![]() $\partial a$
is also an eigenvector with the same eigenvalue. Therefore, there are well-defined automorphisms
$\partial a$
is also an eigenvector with the same eigenvalue. Therefore, there are well-defined automorphisms
The sequence
![]() $\{\psi _i\}$
lies in a compact set of automorphisms and therefore has a subsequence which converges to some
$\{\psi _i\}$
lies in a compact set of automorphisms and therefore has a subsequence which converges to some
![]() $\psi _\infty :\mathcal L_M({\mathbb {C}}) \to \mathcal L_M({\mathbb {C}})$
. This
$\psi _\infty :\mathcal L_M({\mathbb {C}}) \to \mathcal L_M({\mathbb {C}})$
. This
![]() $\psi _\infty $
is also diagonal with respect to
$\psi _\infty $
is also diagonal with respect to
![]() $\mathcal B$
, and its eigenvalues on
$\mathcal B$
, and its eigenvalues on
![]() $L_k$
have absolute value
$L_k$
have absolute value
![]() $2^k$
.
$2^k$
.
As with the
![]() ${\varphi }_i"$
,
${\varphi }_i"$
,
![]() $\psi _\infty $
is also diagonalizable as a linear automorphism of
$\psi _\infty $
is also diagonalizable as a linear automorphism of
![]() $\mathcal L_M({\mathbb {C}})$
, and if
$\mathcal L_M({\mathbb {C}})$
, and if
![]() $a \in L_k$
is an eigenvector of
$a \in L_k$
is an eigenvector of
![]() $\psi _\infty $
, then so is
$\psi _\infty $
, then so is
![]() $\partial a \in \mathcal L_M({\mathbb {C}})_{k-1}$
. Therefore, if we replace each eigenvalue of
$\partial a \in \mathcal L_M({\mathbb {C}})_{k-1}$
. Therefore, if we replace each eigenvalue of
![]() $\psi _\infty $
with its absolute value, then the resulting linear map, which sends every element
$\psi _\infty $
with its absolute value, then the resulting linear map, which sends every element
![]() $a \in L_k$
to
$a \in L_k$
to
![]() $2^k a$
, is still an automorphism of
$2^k a$
, is still an automorphism of
![]() $\mathcal L_M({\mathbb {C}})$
. This automorphism descends to
$\mathcal L_M({\mathbb {C}})$
. This automorphism descends to
![]() $\mathcal L_M({\mathbb {Q}})$
. Since the automorphisms of a rational minimal model are the same as those of the rationalized space
$\mathcal L_M({\mathbb {Q}})$
. Since the automorphisms of a rational minimal model are the same as those of the rationalized space
![]() $M_{(0)}$
, this shows that M is formal.
$M_{(0)}$
, this shows that M is formal.
7.2. Lower bounds on degree
Using the techniques of §3, we can give lower bounds on the maximal degree of an L-Lipschitz self-map of a manifold with positive weights that complement the upper bound of Theorem D:
Theorem 7.4. Let Y be a compact manifold with positive weights and
![]() $\rho _t:\mathcal M_Y \to \mathcal M_Y$
a scaling automorphism of its minimal model. Let
$\rho _t:\mathcal M_Y \to \mathcal M_Y$
a scaling automorphism of its minimal model. Let
![]() $\{z_i\}$
be a graded basis for the rational homology of Y such that
$\{z_i\}$
be a graded basis for the rational homology of Y such that
![]() $\rho _t$
induces the map
$\rho _t$
induces the map
![]() $z_i \mapsto t^{n_i}z_i$
, and let
$z_i \mapsto t^{n_i}z_i$
, and let
 $$ \begin{align*} \gamma_n &= \max \{n_i/n \mid \dim z_i=n\} \\ \alpha_n &= \max_{k \leq n} \gamma_n \\ \alpha &= \alpha_{dim Y} \\ d &= \#\{n \mid \gamma_n=\alpha\}. \end{align*} $$
$$ \begin{align*} \gamma_n &= \max \{n_i/n \mid \dim z_i=n\} \\ \alpha_n &= \max_{k \leq n} \gamma_n \\ \alpha &= \alpha_{dim Y} \\ d &= \#\{n \mid \gamma_n=\alpha\}. \end{align*} $$
Then there are integers
![]() $a>0$
and
$a>0$
and
![]() $p>1$
such that for every
$p>1$
such that for every
![]() $q=ap^\ell $
, there is an
$q=ap^\ell $
, there is an
![]() $O(q^\alpha (\log q)^{d-1})$
-Lipschitz map whose rationalization is
$O(q^\alpha (\log q)^{d-1})$
-Lipschitz map whose rationalization is
![]() $\rho _q$
.
$\rho _q$
.
Example 7.5. In particular, this shows that the
![]() $7$
-manifold M described in Example 7.1 has L-Lipschitz self-maps of degree
$7$
-manifold M described in Example 7.1 has L-Lipschitz self-maps of degree
![]() $\sim L^{20/3}$
: the bound of Theorem D is asymptotically sharp in this case.
$\sim L^{20/3}$
: the bound of Theorem D is asymptotically sharp in this case.
This is because for the automorphism
![]() $\rho _t:\mathcal M_M \to \mathcal M_M$
defined by
$\rho _t:\mathcal M_M \to \mathcal M_M$
defined by
we get
![]() $n_i/\dim z_i=1/2$
when
$n_i/\dim z_i=1/2$
when
![]() $z_i$
is any
$z_i$
is any
![]() $2$
-cycle,
$2$
-cycle,
![]() $3/5$
when
$3/5$
when
![]() $z_i$
is any
$z_i$
is any
![]() $5$
-cycle, and
$5$
-cycle, and
![]() $4/7$
when
$4/7$
when
![]() $z_i$
is any 7-cycle. Thus, the maximum is only attained in dimension 5, and therefore, the number d defined in the statement of Theorem 7.4 is
$z_i$
is any 7-cycle. Thus, the maximum is only attained in dimension 5, and therefore, the number d defined in the statement of Theorem 7.4 is
![]() $1$
in this case. For a map
$1$
in this case. For a map
![]() $f:M \to M$
whose rationalization is
$f:M \to M$
whose rationalization is
![]() $\rho _t$
, we have
$\rho _t$
, we have
![]() $\deg f=t^4$
; by Theorem 7.4, there are such maps which are
$\deg f=t^4$
; by Theorem 7.4, there are such maps which are
![]() $O(t^{3/5})$
-Lipschitz.
$O(t^{3/5})$
-Lipschitz.
Proof of Theorem 7.4
The proof is almost identical to that of Theorem 3.1, so we give an outline and indicate the main differences.
As with Theorem 3.1, we first reduce to the case of a nearly Euclidean cell complex Z whose cells are in bijection with the basis for
![]() $H_*(Z;\mathbb Q) \cong H_*(Y;\mathbb Q)$
specified in the positive weight decomposition. Such a complex exists by Proposition 3.10. The reduction is exactly the same as before but requires a generalization of Proposition 3.9:
$H_*(Z;\mathbb Q) \cong H_*(Y;\mathbb Q)$
specified in the positive weight decomposition. Such a complex exists by Proposition 3.10. The reduction is exactly the same as before but requires a generalization of Proposition 3.9:
Proposition 7.6 [Reference Manin19, Thm. B]; see also the slightly weaker [Reference Buijs, Cantero Morán and Cirici7, Thm. 3.4]
Let Y be a space with positive weights and let
![]() $\rho _t:\mathcal M_Y \to \mathcal M_Y$
be a one-parameter family of automorphisms. If
$\rho _t:\mathcal M_Y \to \mathcal M_Y$
be a one-parameter family of automorphisms. If
![]() $f:Z \to Y$
is a map between simply connected complexes inducing an isomorphism on rational cohomology, then it is a rational equivalence, and there is a map
$f:Z \to Y$
is a map between simply connected complexes inducing an isomorphism on rational cohomology, then it is a rational equivalence, and there is a map
![]() $g:Y \to Z$
and a
$g:Y \to Z$
and a
![]() $t \in {\mathbb {Z}}$
such that the rationalization of
$t \in {\mathbb {Z}}$
such that the rationalization of
![]() $f \circ g$
is
$f \circ g$
is
![]() $\rho _t$
.
$\rho _t$
.
Now, by [Reference Manin19, Theorem A], there is a
![]() $p>1$
and a map
$p>1$
and a map
![]() ${r}_p:Z \to Z$
whose rationalization is
${r}_p:Z \to Z$
whose rationalization is
![]() $\rho _p$
. As in Lemma 3.4, we construct maps
$\rho _p$
. As in Lemma 3.4, we construct maps
![]() ${r}_{p^\ell }$
homotopic to the iterates
${r}_{p^\ell }$
homotopic to the iterates
![]() ${r}_p^\ell $
, bounding the Lipschitz constant by induction on both
${r}_p^\ell $
, bounding the Lipschitz constant by induction on both
![]() $\ell $
and the dimension. We also construct controlled homotopies
$\ell $
and the dimension. We also construct controlled homotopies
![]() $H_\ell $
from
$H_\ell $
from
![]() ${r}_{p^{\ell -1}} \circ {r}_p$
to
${r}_{p^{\ell -1}} \circ {r}_p$
to
![]() ${r}_{p^\ell }$
. There are two main points on which the proof differs from that of Lemma 3.4.
${r}_{p^\ell }$
. There are two main points on which the proof differs from that of Lemma 3.4.
First, as in Lemma 3.4, we assume that
![]() ${r}_p$
has a nice geometric form. Specifically, we assume that for every n-cell
${r}_p$
has a nice geometric form. Specifically, we assume that for every n-cell
![]() $e_i$
,
$e_i$
,
![]() $\overline {{r}_p^{-1}(e_i)}$
is a grid inside e of homothetic preimages of e. Rather than p to a side, this grid has
$\overline {{r}_p^{-1}(e_i)}$
is a grid inside e of homothetic preimages of e. Rather than p to a side, this grid has
![]() $p^{n_i/n}$
subcubes to a side, where
$p^{n_i/n}$
subcubes to a side, where
![]() $n_i$
is the ‘weight’ of the homology class
$n_i$
is the ‘weight’ of the homology class
![]() $[e_i]$
. For this to make sense,
$[e_i]$
. For this to make sense,
![]() $p^{n_i/\dim z_i}$
must be an integer; we can make sure this is true for every i by iterating
$p^{n_i/\dim z_i}$
must be an integer; we can make sure this is true for every i by iterating
![]() ${r}_p$
at most
${r}_p$
at most
![]() $(\dim Z)!$
times.
$(\dim Z)!$
times.
The other main difference is in the Lipschitz constant estimate. As before, we set
 $$ \begin{align*} L_1 &= 2\operatorname{\mathrm{Lip}}(H_\ell|_{Z^{(n-1)}}) \\ L_2 &= 2\operatorname{\mathrm{Lip}}({r}_p)\operatorname{\mathrm{Lip}}({r}_{p^{\ell-1}}|_{Z^{(n-1)}}) \\ L_3 &= D^{-1}\operatorname{\mathrm{Lip}}({r}_{p^{\ell-1}}), \end{align*} $$
$$ \begin{align*} L_1 &= 2\operatorname{\mathrm{Lip}}(H_\ell|_{Z^{(n-1)}}) \\ L_2 &= 2\operatorname{\mathrm{Lip}}({r}_p)\operatorname{\mathrm{Lip}}({r}_{p^{\ell-1}}|_{Z^{(n-1)}}) \\ L_3 &= D^{-1}\operatorname{\mathrm{Lip}}({r}_{p^{\ell-1}}), \end{align*} $$
where D is the side length of a subcube. Then the Lipschitz constant of
![]() ${r}_{p^\ell }$
on a cell
${r}_{p^\ell }$
on a cell
![]() $e_i$
is bounded by
$e_i$
is bounded by
 $$\begin{align*}p^{n_i/n}DL_3+\left(\frac{1}{2}-p^{\alpha_n}D\right)L_2+\frac{1}{2}L_1.\end{align*}$$
$$\begin{align*}p^{n_i/n}DL_3+\left(\frac{1}{2}-p^{\alpha_n}D\right)L_2+\frac{1}{2}L_1.\end{align*}$$
Now, the proof splits into cases. Suppose, by induction, that
 $$ \begin{align*} \operatorname{\mathrm{Lip}}({r}_{p^\ell}|_{Z^{(n-1)}}) &\leq C(n-1)\ell^{d_{n-1}}p^{\alpha_{n-1}\ell} \\ \operatorname{\mathrm{Lip}}(H_\ell|_{Z^{(n-1)}}) &\leq C'(n-1)\ell^{d_{n-1}}p^{\alpha_{n-1}\ell}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Lip}}({r}_{p^\ell}|_{Z^{(n-1)}}) &\leq C(n-1)\ell^{d_{n-1}}p^{\alpha_{n-1}\ell} \\ \operatorname{\mathrm{Lip}}(H_\ell|_{Z^{(n-1)}}) &\leq C'(n-1)\ell^{d_{n-1}}p^{\alpha_{n-1}\ell}. \end{align*} $$
If
![]() $\alpha _{n-1}=n_i/n$
, then the proof is exactly as before and
$\alpha _{n-1}=n_i/n$
, then the proof is exactly as before and
 $$ \begin{align*} \operatorname{\mathrm{Lip}}({r}_{p^\ell}|_e) &\leq C(n)\ell^{d_{n-1}+1}p^{\alpha_{n-1}\ell} \\ \operatorname{\mathrm{Lip}}(H_\ell|_e) &\leq C'(n)\ell^{d_{n-1}+1}p^{\alpha_{n-1}\ell} \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Lip}}({r}_{p^\ell}|_e) &\leq C(n)\ell^{d_{n-1}+1}p^{\alpha_{n-1}\ell} \\ \operatorname{\mathrm{Lip}}(H_\ell|_e) &\leq C'(n)\ell^{d_{n-1}+1}p^{\alpha_{n-1}\ell} \end{align*} $$
for sufficiently large
![]() $C(n)$
and
$C(n)$
and
![]() $C'(n)$
, depending on Z and
$C'(n)$
, depending on Z and
![]() ${r}_p$
.
${r}_p$
.
If
![]() $\alpha _{n-1}<n_i/n$
, then the estimate for the Lipschitz constant is dominated by the
$\alpha _{n-1}<n_i/n$
, then the estimate for the Lipschitz constant is dominated by the
![]() $L_3$
term. After substituting the expression for the bound on
$L_3$
term. After substituting the expression for the bound on
![]() $\operatorname {\mathrm {Lip}}({r}_{p^{\ell -1}})$
and summing a geometric series, we see that
$\operatorname {\mathrm {Lip}}({r}_{p^{\ell -1}})$
and summing a geometric series, we see that
for sufficiently large
![]() $C(n)$
.
$C(n)$
.
Finally, if
![]() $\alpha _{n-1}>n_i/n$
, then the estimate for the Lipschitz constant is dominated by the
$\alpha _{n-1}>n_i/n$
, then the estimate for the Lipschitz constant is dominated by the
![]() $L_1$
and
$L_1$
and
![]() $L_2$
terms, and therefore, for sufficiently large
$L_2$
terms, and therefore, for sufficiently large
![]() $C(n)$
,
$C(n)$
,
Similar estimates hold for the Lipschitz constant of
![]() $H_\ell $
.
$H_\ell $
.
This gives the estimate in the theorem: the polynomial power in the Lipschitz constant is governed by the largest possible value of
![]() $n_i/n$
, and the power of the polylogarithm is governed by the number of n for which that value is attained.
$n_i/n$
, and the power of the polylogarithm is governed by the number of n for which that value is attained.
Remark 7.7. The methods of this theorem do not extend to manifolds without positive weights because Proposition 7.6 fails. For example, suppose that M is rationally equivalent to
![]() $N=P \times Q$
, where P has positive weights and Q does not. Then if
$N=P \times Q$
, where P has positive weights and Q does not. Then if
![]() $f:P \to P$
is a map of degree
$f:P \to P$
is a map of degree
![]() $>1$
, so is
$>1$
, so is
![]() $f \times \operatorname {\mathrm {id}}_Q:N \to N$
, and Theorem 7.4 lets us find efficient maps homotopic to
$f \times \operatorname {\mathrm {id}}_Q:N \to N$
, and Theorem 7.4 lets us find efficient maps homotopic to
![]() $f^\ell $
for
$f^\ell $
for
![]() $\ell \geq 1$
. However, this does not automatically tell us whether M has self-maps of positive degree or, if it does, anything about the Lipschitz constants of these maps. It would be interesting to either show that these properties are rationally invariant or to find examples in which they are not.
$\ell \geq 1$
. However, this does not automatically tell us whether M has self-maps of positive degree or, if it does, anything about the Lipschitz constants of these maps. It would be interesting to either show that these properties are rationally invariant or to find examples in which they are not.
Acknowledgements
We are grateful to an anonymous referee for a number of comments, including one catching a significant error.
Competing interest
The authors have no competing interest to declare.
Financial support
The second author is supported by a Simons Investigator Award. The third author was partially supported by NSF individual grant DMS-2001042 and a Sloan Fellowship.