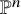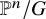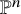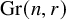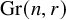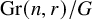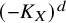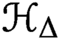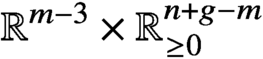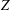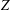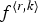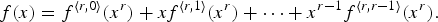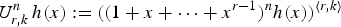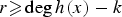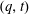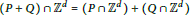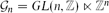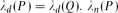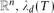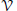Refine search
Actions for selected content:
25 results
Unimodular valuations beyond Ehrhart
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 19 November 2025, e188
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Initial degenerations of flag varieties
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 10 November 2025, pp. 1-29
-
- Article
- Export citation
Equivariant Ehrhart theory of hypersimplices
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 27 October 2025, e178
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE UNIFICATION TYPE OF ŁUKASIEWICZ LOGIC WITH A BOUNDED NUMBER OF VARIABLES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 08 October 2025, pp. 1-18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Empty simplices of large width
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 03 February 2025, e21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lattice points in slices of prisms
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 08 March 2024, pp. 1013-1040
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unwinding Toric Degenerations and Mirror Symmetry for Grassmannians
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 14 December 2022, e111
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the maximum dual volume of a canonical Fano polytope
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 13 December 2022, e109
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The moduli space of Harnack curves in toric surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 27 May 2021, e43
-
- Article
-
- You have access
- Open access
- Export citation
GEOMETRIC BIJECTIONS FOR REGULAR MATROIDS, ZONOTOPES, AND EHRHART THEORY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 04 December 2019, e45
-
- Article
-
- You have access
- Open access
- Export citation
Interlacing polynomials and the veronese construction for rational formal power series
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 30 January 2019, pp. 1-16
- Print publication:
- February 2020
-
- Article
- Export citation
Flow Polytopes and the Space of Diagonal Harmonics
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 1495-1521
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Galois theory for general systems of polynomial equations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 2 / February 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 229-245
- Print publication:
- February 2019
-
- Article
- Export citation
Convex-normal (Pairs of) Polytopes
-
- Journal:
- Canadian Mathematical Bulletin / Volume 60 / Issue 3 / 01 September 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 510-521
- Print publication:
- 01 September 2017
-
- Article
-
- You have access
- Export citation
On the equations and classification of toric quiver varieties
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 03 March 2016, pp. 265-295
- Print publication:
- April 2016
-
- Article
- Export citation
Invariant Measure Under the Affine Group Over
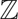 ${\mathbb{Z}$
${\mathbb{Z}$
-
- Journal:
- Combinatorics, Probability and Computing / Volume 23 / Issue 2 / March 2014
- Published online by Cambridge University Press:
- 02 January 2014, pp. 248-268
-
- Article
- Export citation
Centrally Symmetric Configurations of Integer Matrices
-
- Journal:
- Nagoya Mathematical Journal / Volume 216 / 2014
- Published online by Cambridge University Press:
- 11 January 2016, pp. 153-170
- Print publication:
- 2014
-
- Article
-
- You have access
- Export citation
GOLDIE RANK OF PRIMITIVE QUOTIENTS VIA LATTICE POINT ENUMERATION
-
- Journal:
- Glasgow Mathematical Journal / Volume 55 / Issue A / October 2013
- Published online by Cambridge University Press:
- 01 October 2013, pp. 149-168
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
Seven new champion linear codes
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 January 2013, pp. 109-117
-
- Article
-
- You have access
- Export citation
A Note on Toric Varieties Associated with Moduli Spaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 54 / Issue 3 / 01 September 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 561-565
- Print publication:
- 01 September 2011
-
- Article
-
- You have access
- Export citation