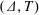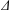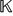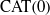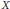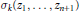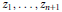Refine search
Actions for selected content:
15 results
Isogeny graphs on superspecial abelian varieties: eigenvalues and connection to Bruhat–Tits buildings
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 20 October 2023, pp. 1891-1916
- Print publication:
- December 2024
-
- Article
- Export citation
Automorphisms and opposition in spherical buildings of exceptional type, I
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 05 July 2021, pp. 1517-1578
- Print publication:
- December 2022
-
- Article
- Export citation
On exceptional Lie geometries
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 11 January 2021, e2
-
- Article
-
- You have access
- Open access
- Export citation
Tits Triangles
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 15 November 2018, pp. 583-601
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
A COMBINATORIAL CHARACTERIZATION OF THE LAGRANGIAN GRASSMANNIAN LG(3,6)(
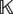 ${\mathbb{K}}$)
${\mathbb{K}}$)
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 293-311
- Print publication:
- May 2016
-
- Article
-
- You have access
- Export citation
Simplicity of Some Twin Tree Automorphism Groups with Trivial Commutation Relations
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 2 / 14 June 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 390-400
- Print publication:
- 14 June 2014
-
- Article
-
- You have access
- Export citation
Buildings, spiders, and geometric Satake
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 11 / November 2013
- Published online by Cambridge University Press:
- 10 July 2013, pp. 1871-1912
- Print publication:
- November 2013
-
- Article
- Export citation
The norm of a Ree group
-
- Journal:
- Nagoya Mathematical Journal / Volume 199 / September 2010
- Published online by Cambridge University Press:
- 11 January 2016, pp. 15-41
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
On Geometric Flats in the CAT(0) Realization of Coxeter Groups and Tits Buildings
-
- Journal:
- Canadian Journal of Mathematics / Volume 61 / Issue 4 / 01 August 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 740-761
- Print publication:
- 01 August 2009
-
- Article
-
- You have access
- Export citation
Groupes de Kac–Moody déployés sur un corps local, immeubles microaffines
-
- Journal:
- Compositio Mathematica / Volume 142 / Issue 2 / March 2006
- Published online by Cambridge University Press:
- 13 March 2006, pp. 501-528
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
ON A $p$-LOCAL GEOMETRY ASSOCIATED WITH A COMPLEX OF NON-TRIVIAL $p$-SUBGROUPS
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 35 / Issue 2 / March 2003
- Published online by Cambridge University Press:
- 20 March 2003, pp. 196-202
- Print publication:
- March 2003
-
- Article
- Export citation
Elementary Symmetric Polynomials in Numbers of Modulus 1
-
- Journal:
- Canadian Journal of Mathematics / Volume 54 / Issue 2 / 01 April 2002
- Published online by Cambridge University Press:
- 20 November 2018, pp. 239-262
- Print publication:
- 01 April 2002
-
- Article
-
- You have access
- Export citation
Asymptotic K-Theory for Groups Acting on à 2 Buildings
-
- Journal:
- Canadian Journal of Mathematics / Volume 53 / Issue 4 / 01 August 2001
- Published online by Cambridge University Press:
- 20 November 2018, pp. 809-833
- Print publication:
- 01 August 2001
-
- Article
-
- You have access
- Export citation
Exceptional Moufang Quadrangles of Type F4
-
- Journal:
- Canadian Journal of Mathematics / Volume 51 / Issue 2 / 01 April 1999
- Published online by Cambridge University Press:
- 20 November 2018, pp. 347-371
- Print publication:
- 01 April 1999
-
- Article
-
- You have access
- Export citation
Sporadic group geometries and the action of involutions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 1 / August 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 35-48
- Print publication:
- August 1994
-
- Article
-
- You have access
- Export citation