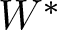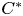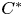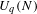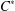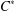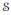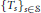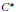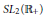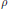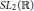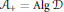Refine search
Actions for selected content:
16 results
On Fock covariance for product systems and the reduced Hao–Ng isomorphism problem by discrete actions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 April 2025, pp. 1-53
-
- Article
- Export citation
The lattice of C
 $^*$-covers of an operator algebra
$^*$-covers of an operator algebra
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 14 February 2025, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
 $C^*$-ALGEBRAS OF UNSATURATED FELL BUNDLES OVER ÉTALE GROUPOIDS
$C^*$-ALGEBRAS OF UNSATURATED FELL BUNDLES OVER ÉTALE GROUPOIDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 13 January 2025, pp. 366-379
- Print publication:
- October 2025
-
- Article
- Export citation
Isometric dilations for representations of product systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 November 2024, pp. 1-42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The isomorphism problem for tensor algebras of multivariable dynamical systems
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 19 September 2022, e81
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Classification of irreversible and reversible Pimsner operator algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 13 January 2021, pp. 2510-2535
- Print publication:
- December 2020
-
- Article
- Export citation
All finite transitive graphs admit a self-adjoint free semigroupoid algebra
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 30 March 2020, pp. 391-406
- Print publication:
- February 2021
-
- Article
- Export citation
Type classification of extreme quantized characters
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 06 September 2019, pp. 593-605
- Print publication:
- February 2021
-
- Article
- Export citation
APPROXIMATIONS OF SUBHOMOGENEOUS ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 07 February 2019, pp. 328-337
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
Unitary Equivalence and Similarity to Jordan Models for Weak Contractions of Class C0
-
- Journal:
- Canadian Journal of Mathematics / Volume 67 / Issue 1 / 01 February 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 132-151
- Print publication:
- 01 February 2015
-
- Article
-
- You have access
- Export citation
Nonself-adjoint Semicrossed Products by Abelian Semigroups
-
- Journal:
- Canadian Journal of Mathematics / Volume 65 / Issue 4 / 01 August 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 768-782
- Print publication:
- 01 August 2013
-
- Article
-
- You have access
- Export citation
Periodicity in Rank 2 Graph Algebras
-
- Journal:
- Canadian Journal of Mathematics / Volume 61 / Issue 6 / 01 December 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1239-1261
- Print publication:
- 01 December 2009
-
- Article
-
- You have access
- Export citation
AUTOMORPHISMS OF NONSELFADJOINT DIRECTED GRAPH OPERATOR ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 87 / Issue 2 / October 2009
- Published online by Cambridge University Press:
- 09 October 2009, pp. 175-196
- Print publication:
- October 2009
-
- Article
-
- You have access
- Export citation
NEST REPRESENTATIONS OF DIRECTED GRAPH ALGEBRAS
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 92 / Issue 3 / May 2006
- Published online by Cambridge University Press:
- 18 April 2006, pp. 762-790
- Print publication:
- May 2006
-
- Article
- Export citation
A Double Triangle Operator Algebra From SL 2(ℝ+)
-
- Journal:
- Canadian Mathematical Bulletin / Volume 49 / Issue 1 / 01 March 2006
- Published online by Cambridge University Press:
- 20 November 2018, pp. 117-126
- Print publication:
- 01 March 2006
-
- Article
-
- You have access
- Export citation
The Curvature and Index of Completely Positive Maps
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 87 / Issue 3 / November 2003
- Published online by Cambridge University Press:
- 23 October 2003, pp. 748-778
- Print publication:
- November 2003
-
- Article
- Export citation