No CrossRef data available.
Article contents
All finite transitive graphs admit a self-adjoint free semigroupoid algebra
Published online by Cambridge University Press: 30 March 2020
Abstract
In this paper we show that every non-cycle finite transitive directed graph has a Cuntz–Krieger family whose WOT-closed algebra is 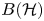 $B(\mathcal {H})$. This is accomplished through a new construction that reduces this problem to in-degree 2-regular graphs, which is then treated by applying the periodic Road Colouring Theorem of Béal and Perrin. As a consequence we show that finite disjoint unions of finite transitive directed graphs are exactly those finite graphs which admit self-adjoint free semigroupoid algebras.
$B(\mathcal {H})$. This is accomplished through a new construction that reduces this problem to in-degree 2-regular graphs, which is then treated by applying the periodic Road Colouring Theorem of Béal and Perrin. As a consequence we show that finite disjoint unions of finite transitive directed graphs are exactly those finite graphs which admit self-adjoint free semigroupoid algebras.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 151 , Issue 1 , February 2021 , pp. 391 - 406
- Copyright
- Copyright © The Author(s), 2020. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh
References
1Adler, R. L. and Weiss, B.. Similarity of automorphisms of the torus. Memoirs of the American Mathematical Society, vol. 98 (Providence, RI: American Mathematical Society, 1970).CrossRefGoogle Scholar
2Arias, A. and Popescu, G.. Noncommutative interpolation and poisson transforms. Isr. J. Math. 115 (2000), 205–234.CrossRefGoogle Scholar
3Bezuglyi, S. and Jorgensen, P.. Representations of Cuntz-Krieger relations, dynamics on Bratteli diagrams, and path-space measures. In Trends in harmonic analysis and its applications. Contemp. Math., vol. 650, pp. 57–88 (Providence, RI: American Mathematical Society, 2015).CrossRefGoogle Scholar
4Béal, M.-P. and Perrin, D.. A quadratic algorithm for road coloring. Discrete Appl. Math. 169 (2014), 15–29.CrossRefGoogle Scholar
5Bratteli, O. and Jorgensen, P.. Iterated function systems and permutation representations of the Cuntz algebra. Mem. Am. Math. Soc. 139 (1999), x+89 pp.Google Scholar
6Cuntz, J. and Krieger, W.. A class of C*-algebras and topological Markov chains. Invent. Math. 56 (1980), 251–268.CrossRefGoogle Scholar
7Davidson, K. R..  $B(\mathcal {H})$ is a free semigroup algebra. Proc. Am. Math. Soc. 134 (2006), 1753–1757.CrossRefGoogle Scholar
$B(\mathcal {H})$ is a free semigroup algebra. Proc. Am. Math. Soc. 134 (2006), 1753–1757.CrossRefGoogle Scholar
8Davidson, K. R. and Pitts, D. R.. The algebraic structure of non-commutative analytic Toeplitz algebras. Math. Ann. 311 (1998), 275–303.CrossRefGoogle Scholar
9Davidson, K. R. and Pitts, D. R.. Invariant subspaces and hyper-reflexivity for free semi-group algebras. Proc. London Math. Soc. 78 (1999), 401–430.CrossRefGoogle Scholar
10Davidson, K. R., Dor-On, A. and Li, B.. Structure of free semigroupoid algebras. J. Funct. Anal. arXiv preprint: 1709.06637.Google Scholar
11Davidson, K. R., Katsoulis, E. and Pitts, D. R.. The structure of free semigroup algebras. J. Reine Angew. Math. 533 (2001), 99–125.Google Scholar
12Davidson, K. R., Li, J. and Pitts, D. R.. Absolutely continuous representations and a Kaplansky density theorem for free semigroup algebras. J. Funct. Anal. 224 (2005), 160–191.CrossRefGoogle Scholar
14Jury, M. T. and Kribs, D. W.. Ideal structure in free semigroupoid algebras from directed graphs. J. Oper. Theory 53 (2005), 273–302.Google Scholar
15Katsoulis, E. and Kribs, D. W.. Applications of the Wold decomposition to the study of row contractions associated with directed graphs. Trans. Am. Math. Soc. 357 (2005), 3739–3755.CrossRefGoogle Scholar
16Kennedy, M.. Wandering vectors and the reflexivity of free semigroup algebras. J. Reine Angew. Math. (Crelle) 653 (2011), 47–73.Google Scholar
17Kennedy, M.. The structure of an isometric tuple. Proc. London Math. Soc. 106 (2013), 1157–1177.CrossRefGoogle Scholar
18Kribs, D. W. and Power, S. C.. Free semigroupoid algebras. J. Ramanujan Math. Soc. 19 (2004), 117–159.Google Scholar
19Linden, C.. Slow continued fractions and permutative representations of  $\mathcal {O}_{N}$. Can. Math. Bull. arxiv preprint: 1810.05948.Google Scholar
$\mathcal {O}_{N}$. Can. Math. Bull. arxiv preprint: 1810.05948.Google Scholar
20Marcolli, M. and Maria Paolucci, A.. Cuntz-Krieger algebras and wavelets on fractals. Complex Anal. Oper. Theory 5 (2011), 41–81.CrossRefGoogle Scholar
21Muhly, P. S. and Solel, B.. Representations of Hardy algebras: absolute continuity, intertwiners, and superharmonic operators. Integral Equ. Oper. Theory 70 (2011), 151–203.CrossRefGoogle Scholar
22Popescu, G.. Non-commutative disc algebras and their representations. Proc. Am. Math. Soc. 124 (1996), 2137–2148.CrossRefGoogle Scholar
24Read, C. J.. A large weak operator closure for the algebra generated by two isometries. J. Oper. Theory 54 (2005), 305–316.Google Scholar


