The loop space of a string manifold supports an infinite-dimensional Fock space bundle, which is an analog of the spinor bundle on a spin manifold. This spinor bundle on loop space appears in the description of two-dimensional sigma models as the bundle of states over the configuration space of the superstring. We construct a product on this bundle that covers the fusion of loops, i.e. the merging of two loops along a common segment. For this purpose, we exhibit it as a bundle of bimodules over a certain von Neumann algebra bundle, and realize our product fibrewise using the Connes fusion of von Neumann bimodules. Our main technique is to establish novel relations between string structures, loop fusion, and the Connes fusion of Fock spaces. The fusion product on the spinor bundle on loop space was proposed by Stolz and Teichner as part of a programme to explore the relation between generalized cohomology theories, functorial field theories, and index theory. It is related to the pair of pants worldsheet of the superstring, to the extension of the corresponding smooth functorial field theory down to the point, and to a higher-categorical bundle on the underlying string manifold, the stringor bundle.

We study a class of left-invertible operators which we call weakly concave operators. It includes the class of concave operators and some subclasses of expansive strict $m$-isometries with $m > 2$. We prove a Wold-type decomposition for weakly concave operators. We also obtain a Berger–Shaw-type theorem for analytic finitely cyclic weakly concave operators. The proofs of these results rely heavily on a spectral dichotomy for left-invertible operators. It provides a fairly close relationship, written in terms of the reciprocal automorphism of the Riemann sphere, between the spectra of a left-invertible operator and any of its left inverses. We further place the class of weakly concave operators, as the term $\mathcal {A}_1$, in the chain $\mathcal {A}_0 \subseteq \mathcal {A}_1 \subseteq \ldots \subseteq \mathcal {A}_{\infty }$ of collections of left-invertible operators. We show that most of the aforementioned results can be proved for members of these classes. Subtleties arise depending on whether the index $k$ of the class $\mathcal {A}_k$ is finite or not. In particular, a Berger–Shaw-type theorem fails to be true for members of $\mathcal {A}_{\infty }$. This discrepancy is better revealed in the context of $C^*$- and $W^*$-algebras.

In this paper, we will show that the unitary equivalence of two multiplication operators on the Bergman spaces on polygons depends on the geometry of the polygon.

Our first result is a noncommutative form of the Jessen-Marcinkiewicz-Zygmund theorem for the maximal limit of multiparametric martingales or ergodic means. It implies bilateral almost uniform convergence (a noncommutative analogue of almost everywhere convergence) with initial data in the expected Orlicz spaces. A key ingredient is the introduction of the $L_p$ -norm of the $\limsup $ of a sequence of operators as a localized version of a $\ell _\infty /c_0$ -valued $L_p$ -space. In particular, our main result gives a strong $L_1$ -estimate for the $\limsup $ —as opposed to the usual weak $L_{1,\infty }$ -estimate for the $\mathop {\mathrm {sup}}\limits $ —with interesting consequences for the free group algebra.

Let $\mathcal{L} \mathbf{F} _2$ denote the free group algebra with $2$ generators, and consider the free Poisson semigroup generated by the usual length function. It is an open problem to determine the largest class inside $L_1(\mathcal{L} \mathbf{F} _2)$ for which the free Poisson semigroup converges to the initial data. Currently, the best known result is $L \log ^2 L(\mathcal{L} \mathbf{F} _2)$ . We improve this result by adding to it the operators in $L_1(\mathcal{L} \mathbf{F} _2)$ spanned by words without signs changes. Contrary to other related results in the literature, this set grows exponentially with length. The proof relies on our estimates for the noncommutative $\limsup $ together with new transference techniques.

We also establish a noncommutative form of Córdoba/Feffermann/Guzmán inequality for the strong maximal: more precisely, a weak $(\Phi ,\Phi )$ inequality—as opposed to weak $(\Phi ,1)$ —for noncommutative multiparametric martingales and $\Phi (s) = s (1 + \log _+ s)^{2 + \varepsilon }$ . This logarithmic power is an $\varepsilon $ -perturbation of the expected optimal one. The proof combines a refinement of Cuculescu’s construction with a quantum probabilistic interpretation of M. de Guzmán’s original argument. The commutative form of our argument gives the simplest known proof of this classical inequality. A few interesting consequences are derived for Cuculescu’s projections.

The joint Brown measure and joint Haagerup–Schultz projections for tuples of commuting operators in a von Neumann algebra equipped with a faithful tracial state are investigated, and several natural properties are proved for these. It is shown that the support of the joint Brown measure is contained in the Taylor joint spectrum of the tuple, and also in the ostensibly smaller left Harte spectrum. A simultaneous upper triangularization result for finite commuting tuples is proved, and the joint Brown measure and joint Haagerup–Schultz projections are shown to behave well under the Arens multivariate holomorphic functional calculus of such a commuting tuple.

Main result: If a ${{C}^{*}}$-algebra $\mathcal{A}$ is simple, $\sigma $-unital, has finitely many extremal traces, and has strict comparison of positive elements by traces, then its multiplier algebra $\mathcal{M}\left( \mathcal{A} \right)$ also has strict comparison of positive elements by traces. The same results holds if finitely many extremal traces is replaced by quasicontinuous scale. A key ingredient in the proof is that every positive element in the multiplier algebra of an arbitrary $\sigma $-unital ${{C}^{*}}$ -algebra can be approximated by a bi-diagonal series. As an application of strict comparison, if $\mathcal{A}$ is a simple separable stable ${{C}^{*}}$ -algebra with real rank zero, stable rank one, and strict comparison of positive elements by traces, then whether a positive element is a positive linear combination of projections is determined by the trace values of its range projection.

In this paper we generalize the notion of the C-numerical range of a matrix to operators in arbitrary tracial von Neumann algebras. For each self-adjoint operator C, the C-numerical range of such an operator is defined; it is a compact, convex subset of ℂ. We explicitly describe the C-numerical ranges of several operators and classes of operators.

In this paper, we develop a generalized Jordan canonical form theorem for a certain class of operators in $L\left( H \right)$ . A complete criterion for similarity for this class of operators in terms of $K$ -theory for Banach algebras is given.

In the finite von Neumann algebra setting, we introduce the concept of a perturbation determinant associated with a pair of self-adjoint elements ${{H}_{0}}$ and $H$ in the algebra and relate it to the concept of the de la Harpe–Skandalis homotopy invariant determinant associated with piecewise ${{C}^{1}}$-paths of operators joining ${{H}_{0}}$ and $H$. We obtain an analog of Krein's formula that relates the perturbation determinant and the spectral shift function and, based on this relation, we derive subsequently (i) the Birman–Solomyak formula for a general non-linear perturbation, (ii) a universality of a spectral averaging, and (iii) a generalization of the Dixmier–Fuglede–Kadison differentiation formula.

Let $\mathcal{H}$ be a complex separable Hilbert space and $\mathcal{L}\left( \mathcal{H} \right)$ denote the collection of bounded linear operators on $\mathcal{H}$. An operator $A$ in $\mathcal{L}\left( \mathcal{H} \right)$ is said to be strongly irreducible, if ${{\mathcal{A}}^{\prime }}(T)$, the commutant of $A$, has no non-trivial idempotent. An operator $A$ in $\mathcal{L}\left( \mathcal{H} \right)$ is said to be a Cowen-Douglas operator, if there exists $\Omega $, a connected open subset of $C$, and $n$, a positive integer, such that

1. (a)

   $$\Omega \,\subset \,\sigma (A)\,=\,\left\{ z\,\in \,C|\,A-z\,\text{not}\,\text{invertible} \right\};$$

2. (b)

   $$\text{ran(A}-z\text{)}\,\text{=}\,\mathcal{H}\text{,}\,\text{for}\,z\,\text{in}\,\Omega \text{;}$$

3. (c)

   $${{\vee }_{z\in \Omega }}\,\ker (A-\,z)\,=\,\mathcal{H}\,\text{and}$$

4. (d)

   $$\dim\,\ker (A-z)\,=\,n\,\text{for}\,z\,\text{in}\,\Omega $$

In the paper, we give a similarity classification of strongly irreducible Cowen-Douglas operators by using the ${{K}_{0}}$-group of the commutant algebra as an invariant.

Jensen's operator inequality and Jensen's trace inequality for real functions defined on an interval are established in what might be called their definitive versions. This is accomplished by the introduction of genuine non-commutative convex combinations of operators, as opposed to the contractions considered in earlier versions of the theory by the authors, and by Brown and Kosaki. As a consequence, one no longer needs to impose conditions on the interval of definition. It is shown how this relates to the pinching inequality of Davis, and how Jensen's trace inequality generalizes to C*-algebras.

In a beautiful result, Herrero (D. A. Herrero, ‘Normal limits of nilpotent operators’, Indiana Univ. Math. J. 23 (1973/74) 1097–1108) showed that a normal operator on $l^2$ lies in the closure of the set of nilpotent operators if and only if its spectrum is connected and contains zero. In the quest for an automatic continuity result for algebra homomorphisms between ${\rm C}^*$-algebras, Dales showed that, if a discontinuous algebra homomorphism $\theta :{\cal A} \rightarrow {\cal U}$ exists between ${\rm C}^*$-algebras ${\cal A}$ and ${\cal U}$, and if $\theta({\cal A})$ is dense in ${\cal U}$, then there is a ${\rm C}^*$-algebra ${\cal U}_2$ with a dense subalgebra ${\cal N} \subset {\cal U}_2$ such that every $x \in {\cal N}$ is quasinilpotent (see p. 685 of H. G. Dales, Banach algebras and automatic continuity, London Mathematical Society Monographs 24, Oxford University Press, 2001). (A discontinuous homomorphism $\theta_2 :{\cal A}_2 \rightarrow {\cal U}_2$ can be defined with the same basic properties as $\theta$, but the revised target space ${\cal U}_2$ has a dense subalgebra consisting of quasinilpotent elements.) As remarked by Dales, no such ${\rm C}^*$-algebra was then known; but here we present one. Indeed, using the full power of Herrero's result, one may arrange that every $x \in {\cal N}$ is nilpotent. The ${\rm C}^*$-algebra is constructed in a ‘neat’ way; it is most naturally constructed as a non-separable, concrete ${\rm C}^*$-algebra of operators on a separable Hilbert space ${\cal K}$; but one can arrange that the algebra ${\cal U}$ itself be separable if desired.

It is known that the Toeplitz algebra associated with any flow which is both minimal and uniquely ergodic always has a trivial ${{K}_{1}}$-group. We show in this note that if the unique ergodicity is dropped, then such ${{K}_{1}}$-group can be non-trivial. Therefore, in the general setting of minimal flows, even the $K$-theoretical index is not sufficient for the classification of Toeplitz operators which are invertible modulo the commutator ideal.

We prove that given an operator space structure on a dual Banach space Y*, it is not necessarily the dual one of some operator space structure on Y. This allows us to show that Sakai's theorem providing the identification between C*-algebras having a predual and von Neumann algebras does not extend to the category of operator spaces. We also include a related result about completely bounded operators from B(ℓ2)* into the operator Hilbert space OH.

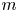
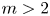
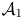
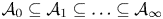
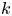
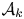
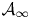
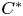
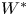
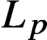
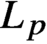
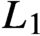
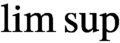
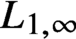
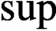
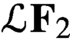
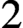
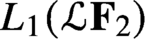
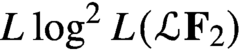
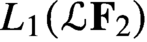
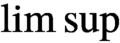
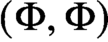
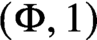
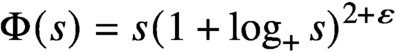
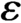
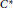
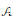
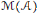
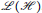
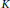
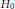
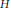
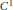
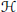
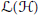
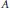
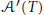
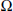
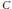
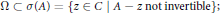
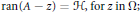
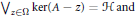
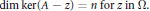
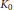
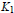
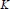
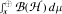In recent years there has been a growing interest in problems of factorization for bounded linear operators. We first show that many of these problems properly belong to the category of C*-algebras. With this interpretation, it becomes evident that the problem is fundamental both to the structure of operator algebras and the elements therein. In this paper we consider the direct integral algebra with 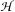separable and infinite dimensional. We generalize a theorem of Wu (1988) and characterize those decomposable operators which are products of non-negative decomposable operators. We do this by first showing that various results on operator ranges may be generalized to “measurable fields of operator ranges”.

We give characterizations of Toeplitz operators on generalised H2 spaces and derive some properties of the corresponding Toeplitz algebras. The proofs depend essentially on having a "sufficient" supply of inner functions.

The spectrum of the Laplacian or more generally of a Schrödinger operator on an open manifold may have possibly a complicated aspect. For example, a Cantor set in the real axis may appear as the spectrum even for an innocent looking potential on a standard Riemannian manifold (see J. Moser [10]). The fundamental result of the spectral theory of periodic Schrödinger operators, however, says that the picture of the spectrum of a Schrödinger operator on ℝn with a periodic potential is simple; indeed the spectrum consists of a series of closed intervals of the real axis without accumulation, separated in general by gaps outside the spectrum (see M. Reed and B. Simon [13] or M. M. Skriganov [15] for instance).

The C*-algebras associated with irrational rotations of the circle were classified up to strong Morita equivalence by M. A. Rieffel. As a corollary, he gave a complete classification of the C*-algebras arising from irrational or Kronecker flows on the 2-torus up to *-isomorphism. Here, we extend the result to the socalled Denjoy homeomorphisms. Specifically, we give a necessary and sufficient condition for the strong Morita equivalence of two C*-algebras arising from homeomorphisms of the circle without periodic points. As a corollary, we show that two C*-algebras arising from flows on the 2-torus obtained from such homeomorphisms by the “flow under constant function” construction are *-isomorphic if and only if the flows themselves are topologically conjugate.