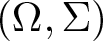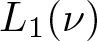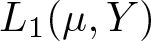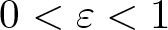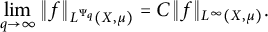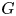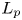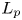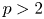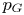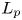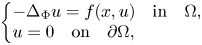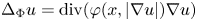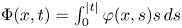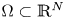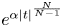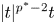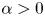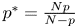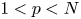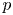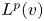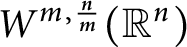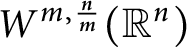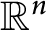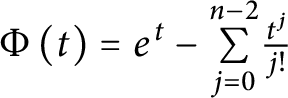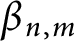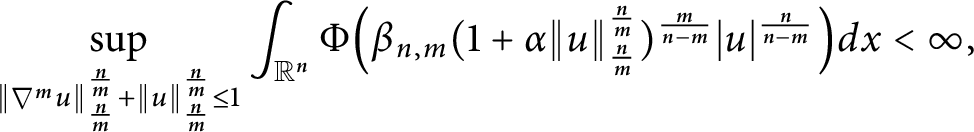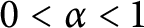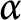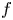Refine search
Actions for selected content:
94 results
An extension-restriction theorem for weighted Besov spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 26 August 2025, pp. 1-48
-
- Article
- Export citation
Well-posedness of Naiver–Stokes equations in logarithmic Q spaces covering
 $BMO^{-1}$ and its fractional counterpart
$BMO^{-1}$ and its fractional counterpart
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 11 August 2025, pp. 1-64
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal function spaces in weighted Sobolev embeddings with α-homogeneous weights
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 19 June 2025, pp. 1-30
-
- Article
- Export citation
Trudinger-type inequalities in Musielak–Orlicz spaces and double phase functionals
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 27 March 2025, pp. 1192-1209
- Print publication:
- December 2025
-
- Article
- Export citation
Functions with small BMO norm
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 08 January 2025, pp. 1-15
-
- Article
- Export citation
A note on continuity and asymptotic consistency of measures of risk and variability
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 55 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 16 December 2024, pp. 168-177
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Maximal noncompactness of limiting Sobolev embeddings
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 November 2024, pp. 1-19
-
- Article
- Export citation
A class of Hausdorff–Berezin operators on the unit ball
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 23 October 2024, pp. 1069-1080
- Print publication:
- December 2024
-
- Article
- Export citation
On weakly almost square Banach spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 05 October 2023, pp. 979-997
-
- Article
- Export citation
Families of Young functions and limits of Orlicz norms
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 29 May 2023, pp. 26-39
- Print publication:
- March 2024
-
- Article
- Export citation
Isometric actions on Lp-spaces: dependence on the value of p
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 26 May 2023, pp. 1300-1313
- Print publication:
- June 2023
-
- Article
- Export citation
Multiple solutions for a class of quasilinear problems with double criticality
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 4 / November 2022
- Published online by Cambridge University Press:
- 21 October 2022, pp. 1011-1047
-
- Article
- Export citation
Harnack inequality for the nonlocal equations with general growth
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 23 August 2022, pp. 1479-1502
- Print publication:
- October 2023
-
- Article
- Export citation
Measure data elliptic problems with generalized Orlicz growth
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 02 March 2022, pp. 588-618
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weighted estimates for Bochner–Riesz operators on Lorentz spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 28 February 2022, pp. 654-678
- Print publication:
- April 2023
-
- Article
- Export citation
Trudinger’s inequalities for Riesz potentials in Morrey spaces of double phase functionals on half spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 27 December 2021, pp. 924-935
- Print publication:
- December 2022
-
- Article
- Export citation
A sharpened form of Adams-type inequalities on higher-order Sobolev spaces
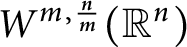 $W^{m,\frac {n}{m}}(\mathbb {R}^n)$: a simple approach
$W^{m,\frac {n}{m}}(\mathbb {R}^n)$: a simple approach
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 15 December 2021, pp. 895-905
- Print publication:
- December 2022
-
- Article
- Export citation
Partial regularity for minimizers of discontinuous quasiconvex integrals with general growth
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 01 December 2021, pp. 1191-1232
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Extrapolation to weighted Morrey spaces with variable exponents and applications
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 09 November 2021, pp. 1002-1027
-
- Article
- Export citation
Lorentz and Gale–Ryser theorems on general measure spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 09 August 2021, pp. 857-878
- Print publication:
- August 2022
-
- Article
- Export citation