Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-01-10T22:35:01.676Z Has data issue: false hasContentIssue false
  • English
  • Français

Functions with small BMO norm

Part of: Linear function spaces and their duals Harmonic analysis in several variables

Published online by Cambridge University Press:  08 January 2025

Arturo Popoli Open the ORCID record for Arturo Popoli [Opens in a new window]
Arturo Popoli*
Affiliation:
Dipartimento di Matematica e Applicazioni “R. Caccioppoli”, Università di Napoli “Federico II”, Napoli, 80126 Via Cintia, (arturo.popoli@unina.it)
Get access Rights & Permissions [Opens in a new window]

Abstract

We characterize the functions with ‘small’ bounded mean oscillation (BMO) norm by establishing the precise connection between the space BMO and class 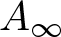$A_\infty$ of Muckenhoupt weights. We prove that there exists a universal constant $c^*_2$ such that $\Vert f \Vert_{BMO} \lt c^*_2$ if and only if $\exp f \in A_2$, where 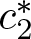$c^*_2$ is the sharp constant in the John and Nirenberg inequality. Similarly, in dimension one, we prove that $\Vert f \Vert_{BLO} \lt 1$ if and only if $\exp f \in A_1$. As application we introduce a structure of metric space in $A_\infty$ and prove that the closed unit ball of $A_\infty$ is a Banach space.

Keywords

Bounded Mean OscillationBounded Lower OscillationMuckenhoupt weightsJohn and Nirenberg InequalityBanach Spaces

MSC classification

Primary: 46E30: Spaces of measurable functions ($L^p$-spaces, Orlicz spaces, Köthe function spaces, Lorentz spaces, rearrangement invariant spaces, ideal spaces, etc.)
Secondary: 42B35: Function spaces arising in harmonic analysis
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 15
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Coifman, R. R. and Rochberg, R.. Another characterization of BMO. Proc. Am. Math. Soc. 79 (1980), 249–254.CrossRefGoogle Scholar
Dafni, G., Gibara, R. and Lavigne, A.. BMO and the John-Nirenberg inequality on measure spaces. Anal. Geom. Metr. Spaces 8 (2020), 335–362.CrossRefGoogle Scholar
Fefferman, C.. Characterizations of bounded mean oscillation. Bull. Amer. Math. Soc. 77 (1971), 587–588.CrossRefGoogle Scholar
Garcia-Cuerva, J. and Rubio de Francia, J. L.. Weighted norm inequalities and related topics. North-Holland Math. Stud. 116 (1985).Google Scholar
Hytönen, T. and Pérez, C.. Sharp weighted bounds involving $A_\infty$. Analysis & PDE 6 (2013), 777–818.CrossRefGoogle Scholar
John, F. and Nirenberg, L.. On functions of bounded mean oscillation. Comm. Pure Appl. Math. 14 (1961), 415–426.CrossRefGoogle Scholar
Jones, P. W.. Homeomorphisms of the line which preserve BMO. Arkiv för Matematik 21 (1983), 229–231.CrossRefGoogle Scholar
Kinnunen, J. and Shula, P.. The distance of $L^\infty$ from BMO on metric measure spaces. Adv. Pure Appl. Math. 5 (2014), 117–129.CrossRefGoogle Scholar
Korenovskii, A.. Mean oscillations and equimeasurable rearrangements of functions, Lecture Notes of the Unione Matematica Italiana, Vol. 4 (Springer, Berlin, 2007).Google Scholar
Korey, M. B.. Ideal weights: asymptotically optimal versions of doubling absolute continuity and mean oscillation. J. Fourier Anal. Appl. 4 (1998), 491–519.CrossRefGoogle Scholar
Lerner, A.. The John–Nirenberg inequality with sharp constants. C. R. Acad. Sci. Paris, Ser. I. 351 (2013), 463–466.CrossRefGoogle Scholar
Nielsen, M. and Šikić, H.. Muckenhoupt class weight decomposition and BMO distance to bounded functions. Proc. Edinb. Math. Soc. 62 (2019), 1017–1031.CrossRefGoogle Scholar
Osȩkowski, A.. Sharp estimates for functions of bounded lower oscillation. Bull. Aust. Math. Soc. 87 (2013), 68–81.CrossRefGoogle Scholar
Ou, W.. Near-symmetry in $A_\infty$ and refined Jones factorization. Proc. Am. Math. Soc. 136 (2008), 3239–3245.CrossRefGoogle Scholar
Pattakos, N. and Volberg, A.. The Muckenhoupt $A_\infty$ class as a metric space and continuity of weighted estimates. Math. Res. Lett. 19 (2012), 499–510.CrossRefGoogle Scholar
Popoli, A.. Limits of the Ap constants. J. Math. Anal. Appl. 478 (2019), 1218–1229.CrossRefGoogle Scholar
Popoli, A.. Homeomorphisms preserving BMO and BLO. Anal. Math. 47 (2021), 893–906.CrossRefGoogle Scholar