We consider the Bernstein–Sato polynomial of a locally quasi-homogeneous polynomial $f \in R = \mathbb{C}[x_{1}, x_{2}, x_{3}]$. We construct, in the analytic category, a complex of $\mathscr{D}_{X}[s]$-modules that can be used to compute the $\mathscr{D}_{X}[s]$-dual of $\mathscr{D}_{X}[s] f^{s-1}$ as the middle term of a short exact sequence where the outer terms are well understood. This extends a result by Narváez Macarro where a freeness assumption was required. We derive many results about the zeros of the Bernstein–Sato polynomial. First, we prove each nonvanishing degree of the zeroth local cohomology of the Milnor algebra $H_{\mathfrak{m}}^{0} (R / (\partial f))$ contributes a root to the Bernstein–Sato polynomial, generalizing a result of M. Saito (where the argument cannot weaken homogeneity to quasi-homogeneity). Second, we prove the zeros of the Bernstein–Sato polynomial admit a partial symmetry about $-1$, extending a result of Narváez Macarro that again required freeness. We give applications to very small roots, the twisted logarithmic comparison theorem, and more precise statements when f is additionally assumed to be homogeneous. Finally, when f defines a hyperplane arrangement in $\mathbb{C}^{3}$ we give a complete formula for the zeros of the Bernstein–Sato polynomial of f. We show all zeros except the candidate root $-2 + (2 / \deg(f))$ are (easily) combinatorially given; we give many equivalent characterizations of when the only noncombinatorial candidate root $-2 + (2/ \deg(f))$ is in fact a zero of the Bernstein–Sato polynomial. One equivalent condition is the nonvanishing of $H_{\mathfrak{m}}^{0}( R / (\partial f))_{\deg(f) - 1}$.

We develop the theory of relative regular holonomic $\mathcal {D}$-modules with a smooth complex manifold $S$ of arbitrary dimension as parameter space, together with their main functorial properties. In particular, we establish in this general setting the relative Riemann–Hilbert correspondence proved in a previous work in the one-dimensional case.

We define Bernstein–Sato polynomials for meromorphic functions and study their basic properties. In particular, we prove a Kashiwara–Malgrange-type theorem on their geometric monodromies, which would also be useful in relation with the monodromy conjecture. A new feature in the meromorphic setting is that we have several b-functions whose roots yield the same set of the eigenvalues of the Milnor monodromies. We also introduce multiplier ideal sheaves for meromorphic functions and show that their jumping numbers are related to our b-functions.

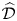We develop a dimension theory for coadmissible $\widehat {\mathcal {D}}$-modules on rigid analytic spaces and study those which are of minimal dimension, in analogy to the theory of holonomic $\mathcal {D}$-modules in the algebraic setting. We discuss a number of pathologies contained in this subcategory (modules of infinite length, infinite-dimensional fibres). We prove stability results for closed immersions and the duality functor, and show that all higher direct images of integrable connections restricted to a Zariski open subspace are coadmissible of minimal dimension. It follows that the local cohomology sheaves $\underline {H}^{i}_Z(\mathcal {M})$ with support in a closed analytic subset $Z$ of $X$ are also coadmissible of minimal dimension for any integrable connection $\mathcal {M}$ on $X$.

We establish some cohomological bounds in $D$-module theory that are known in the holonomic case and folklore in general. The method rests on a generalization of the $b$-function lemma for non-holonomic $D$-modules.

For a commutative ring R, we define the notions of deformed Picard algebroids and deformed twisted differential operators on a smooth, separated, locally of finite type R-scheme and prove these are in a natural bijection. We then define the pullback of a sheaf of twisted differential operators that reduces to the classical definition when R = ℂ. Finally, for modules over twisted differential operators, we prove a theorem for the descent under a locally trivial torsor.

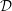We study Fourier transforms of regular holonomic ${\mathcal{D}}$-modules. In particular, we show that their solution complexes are monodromic. An application to direct images of some irregular holonomic ${\mathcal{D}}$-modules will be given. Moreover, we give a new proof of the classical theorem of Brylinski and improve it by showing its converse.

We determine the irregular Hodge filtration, as introduced by Sabbah, for the purely irregular hypergeometric ${\mathcal{D}}$-modules. We obtain, in particular, a formula for the irregular Hodge numbers of these systems. We use the reduction of hypergeometric systems from GKZ-systems as well as comparison results to Gauss–Manin systems of Laurent polynomials via Fourier–Laplace and Radon transformations.

We introduce the notion of regularity for a relative holonomic ${\mathcal{D}}$-module in the sense of Monteiro Fernandes and Sabbah [Internat. Math. Res. Not. (21) (2013), 4961–4984]. We prove that the solution functor from the bounded derived category of regular relative holonomic modules to that of relative constructible complexes is essentially surjective by constructing a right quasi-inverse functor. 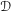When restricted to relative ${\mathcal{D}}$-modules underlying a regular mixed twistor ${\mathcal{D}}$-module, this functor satisfies the left quasi-inverse property.

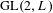In this paper we study certain sheaves of $p$-adically complete rings of differential operators on semistable models of 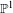the projective line over the ring of integers in a finite extension $L$ of $\mathbb{Q}_{p}$. The global sections of these sheaves can be identified with (central reductions of) analytic distribution algebras of wide open congruence subgroups. It is shown that the global sections functor furnishes an equivalence between the categories of coherent module sheaves and finitely presented modules over the distribution algebras. Using the work of M. Emerton, we then describe admissible representations of $\text{GL}_{2}(L)$ in terms of sheaves on the projective limit of these formal schemes. As an application, we show that representations coming from certain equivariant line bundles on Drinfeld’s first étale covering of the $p$-adic upper half plane are admissible.

Using Beilinson–Bernstein localisation, we give another proof of Levasseur's theorem on the Krull dimension of the enveloping algebra of a complex semisimple Lie algebra. The proof also extends to the case of affinoid enveloping algebras.

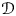
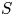
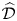
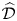
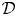
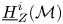
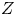
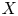
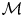
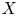
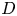
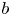
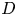
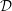
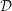
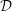
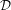
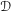
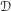
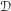
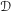
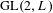
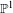
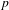
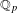
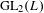
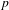
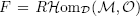We prove that the k-truncated microsupport of the specialization of a complex of sheaves F along a submanifold is contained in the normal cone to the conormal bundle along the k-truncated microsupport of F. In the complex case, applying our estimates to , where 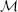is a coherent 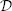-module, we obtain new estimates for the truncated microsupport of real analytic and hyperfunction solutions. When is regular along Y we also obtain estimates for the truncated microsupport of the holomorphic solutions of the induced system along Y as well as for the nearby-cycle sheaf of when Y is a hypersurface.

We prove that holonomic arithmetical ${\mathcal{D}}$-modules over curves have finite fibers. We also define L-functions associated with arithmetical ${\mathcal{D}}$-modules and, when the scheme is a curve, we show a cohomological formula. Furthermore, we prove that F-isocrystals over curves are holonomic.

We compute the category of perverse sheaves on Hermitian symmetric spaces in types $\text{A}$ and $\text{D}$ , constructible with respect to the Schubert stratification. The calculation is microlocal, and uses the action of the Borel group to study the geometry of the conormal variety $\Lambda$ .