Article contents
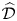 $\widehat {\mathcal {D}}$-modules on rigid analytic spaces III: weak holonomicity and operations
$\widehat {\mathcal {D}}$-modules on rigid analytic spaces III: weak holonomicity and operations
Published online by Cambridge University Press: 28 October 2021
Abstract
We develop a dimension theory for coadmissible 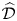 $\widehat {\mathcal {D}}$-modules on rigid analytic spaces and study those which are of minimal dimension, in analogy to the theory of holonomic
$\widehat {\mathcal {D}}$-modules on rigid analytic spaces and study those which are of minimal dimension, in analogy to the theory of holonomic 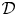 $\mathcal {D}$-modules in the algebraic setting. We discuss a number of pathologies contained in this subcategory (modules of infinite length, infinite-dimensional fibres). We prove stability results for closed immersions and the duality functor, and show that all higher direct images of integrable connections restricted to a Zariski open subspace are coadmissible of minimal dimension. It follows that the local cohomology sheaves
$\mathcal {D}$-modules in the algebraic setting. We discuss a number of pathologies contained in this subcategory (modules of infinite length, infinite-dimensional fibres). We prove stability results for closed immersions and the duality functor, and show that all higher direct images of integrable connections restricted to a Zariski open subspace are coadmissible of minimal dimension. It follows that the local cohomology sheaves  $\underline {H}^{i}_Z(\mathcal {M})$ with support in a closed analytic subset
$\underline {H}^{i}_Z(\mathcal {M})$ with support in a closed analytic subset 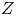 $Z$ of
$Z$ of 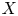 $X$ are also coadmissible of minimal dimension for any integrable connection
$X$ are also coadmissible of minimal dimension for any integrable connection  $\mathcal {M}$ on
$\mathcal {M}$ on 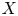 $X$.
$X$.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © 2021 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence
Footnotes
The first and second authors acknowledge support from the EPSRC grant EP/L005190/1.
References
- 1
- Cited by

