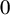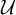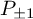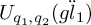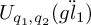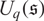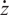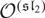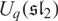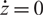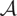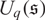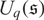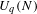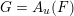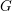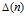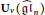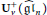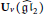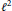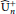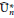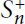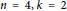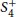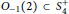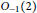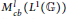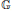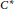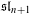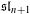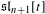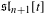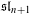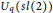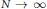Refine search
Actions for selected content:
28 results
A categorical action of the shifted
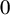 $0$-affine algebra
$0$-affine algebra
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 15 April 2025, e74
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generalised Temperley–Lieb algebras of type G(r, p, n)
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 08 April 2025, pp. 193-227
- Print publication:
- March 2025
-
- Article
- Export citation
Quantum symmetries of Cayley graphs of abelian groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 12 October 2023, pp. 655-686
- Print publication:
- September 2023
-
- Article
- Export citation
On the primality of totally ordered q-factorization graphs
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 20 March 2023, pp. 594-637
- Print publication:
- April 2024
-
- Article
- Export citation
A CATEGORICAL QUANTUM TOROIDAL ACTION ON THE HILBERT SCHEMES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 06 March 2023, pp. 897-940
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GENERALISED QUANTUM DETERMINANTAL RINGS ARE MAXIMAL ORDERS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 04 August 2020, pp. 515-525
- Print publication:
- September 2021
-
- Article
- Export citation
BGG CATEGORY FOR THE QUANTUM SCHRÖDINGER ALGEBRA
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 20 April 2020, pp. 266-279
- Print publication:
- May 2021
-
- Article
- Export citation
QUANTUM INCREASING SEQUENCES GENERATE QUANTUM PERMUTATION GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 27 September 2019, pp. 631-639
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
Type classification of extreme quantized characters
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 06 September 2019, pp. 593-605
- Print publication:
- February 2021
-
- Article
- Export citation
Martin boundaries of the duals of free unitary quantum groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 6 / June 2019
- Published online by Cambridge University Press:
- 31 May 2019, pp. 1171-1193
- Print publication:
- June 2019
-
- Article
- Export citation
Induction for locally compact quantum groups revisited
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 1071-1093
- Print publication:
- April 2020
-
- Article
- Export citation
Multiplication Formulas and Canonical Bases for Quantum Affine gln
-
- Journal:
- Canadian Journal of Mathematics / Volume 70 / Issue 4 / 01 August 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 773-803
- Print publication:
- 01 August 2018
-
- Article
-
- You have access
- Export citation
Higher ℓ 2-Betti Numbers of Universal Quantum Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 61 / Issue 2 / 01 June 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 225-235
- Print publication:
- 01 June 2018
-
- Article
-
- You have access
- Export citation
Remarks on Hopf Images and Quantum Permutation Groups
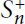 $S_{n}^{+}$
$S_{n}^{+}$
-
- Journal:
- Canadian Mathematical Bulletin / Volume 61 / Issue 2 / 01 June 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 301-317
- Print publication:
- 01 June 2018
-
- Article
-
- You have access
- Export citation
On Positive Definiteness Over Locally Compact Quantum Groups
-
- Journal:
- Canadian Journal of Mathematics / Volume 68 / Issue 5 / 01 October 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1067-1095
- Print publication:
- 01 October 2016
-
- Article
-
- You have access
- Export citation
Categorical Aspects of Quantum Groups: Multipliers and Intrinsic Groups
-
- Journal:
- Canadian Journal of Mathematics / Volume 68 / Issue 2 / 01 April 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 309-333
- Print publication:
- 01 April 2016
-
- Article
-
- You have access
- Export citation
DEMAZURE MODULES OF LEVEL TWO AND PRIME REPRESENTATIONS OF QUANTUM AFFINE
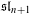 $\mathfrak{sl}_{n+1}$
$\mathfrak{sl}_{n+1}$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 09 November 2015, pp. 75-105
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
Affine Actions of Uq(sl(2)) on Polynomial Rings
-
- Journal:
- Canadian Mathematical Bulletin / Volume 58 / Issue 2 / 01 June 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 233-240
- Print publication:
- 01 June 2015
-
- Article
-
- You have access
- Export citation
Strong Asymptotic Freeness for Free Orthogonal Quantum Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 4 / 01 December 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 708-720
- Print publication:
- 01 December 2014
-
- Article
-
- You have access
- Export citation
A Note on Amenability of Locally Compact Quantum Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 2 / 14 June 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 424-430
- Print publication:
- 14 June 2014
-
- Article
-
- You have access
- Export citation