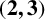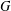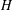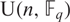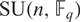Refine search
Actions for selected content:
41 results
A GEOMETRIC APPROACH TO POLYNOMIAL PROPERTY FOR PATTERN SUBGROUPS IN
 ${{\mathrm {\mathbf {U}}}}_{\boldsymbol {a,b,c,d}}$
${{\mathrm {\mathbf {U}}}}_{\boldsymbol {a,b,c,d}}$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 19 November 2025, pp. 1-18
-
- Article
- Export citation
Picky elements, subnormalisers, and character correspondences
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 30 September 2025, e161
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The stack of G-zips is a Mori dream space
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 19 September 2025, pp. 1-36
-
- Article
- Export citation
Moments, Exponential Sums, and Monodromy Groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 26 June 2025, e101
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Polishchuk’s conjecture and Kazhdan–Laumon representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 26 August 2025, pp. 993-1020
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE COHOMOLOGY OF p-ADIC DELIGNE-LUSZTIG SCHEMES OF COXETER TYPE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 10 February 2025, pp. 1429-1462
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Orthogonality relations for deep level Deligne–Lusztig schemes of Coxeter type
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 22 May 2024, e66
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE
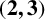 $\boldsymbol {(2,3)}$-GENERATION OF THE FINITE SIMPLE ODD-DIMENSIONAL ORTHOGONAL GROUPS
$\boldsymbol {(2,3)}$-GENERATION OF THE FINITE SIMPLE ODD-DIMENSIONAL ORTHOGONAL GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 28 February 2024, pp. 130-148
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CHARACTER STACKS ARE PORC COUNT
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 23 September 2022, pp. 289-310
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Products of derangements in simple permutation groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 23 September 2022, e83
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SYLOW CLASSES OF REFLECTION SUBGROUPS AND PSEUDO-LEVI SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 30 August 2022, pp. 508-510
- Print publication:
- December 2022
-
- Article
-
- You have access
- HTML
- Export citation
Overgroups of regular unipotent elements in reductive groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 24 February 2022, e13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Corrigendum to ‘Endoscopy for Hecke categories, character sheaves and representations’
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 9 / 2021
- Published online by Cambridge University Press:
- 30 November 2021, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GENERALIZED GREEN FUNCTIONS AND UNIPOTENT CLASSES FOR FINITE REDUCTIVE GROUPS, III
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 247 / September 2022
- Published online by Cambridge University Press:
- 03 September 2021, pp. 552-573
- Print publication:
- September 2022
-
- Article
- Export citation
Automorphic vector bundles on the stack of G-zips
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 03 May 2021, e37
-
- Article
-
- You have access
- Open access
- Export citation
Low-dimensional representations of finite orthogonal groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 3 / November 2021
- Published online by Cambridge University Press:
- 26 January 2021, pp. 585-606
- Print publication:
- November 2021
-
- Article
- Export citation
ENDOSCOPY FOR HECKE CATEGORIES, CHARACTER SHEAVES AND REPRESENTATIONS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 28 May 2020, e12
-
- Article
-
- You have access
- Open access
- Export citation
Surjectivity of near-square random matrices
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 06 November 2019, pp. 267-292
-
- Article
- Export citation
ON THE NUMBER OF REAL CLASSES IN THE FINITE PROJECTIVE LINEAR AND UNITARY GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 31 January 2019, pp. 93-107
- Print publication:
- January 2020
-
- Article
-
- You have access
- Export citation
Normalization of Closed Ekedahl—Oort Strata
-
- Journal:
- Canadian Mathematical Bulletin / Volume 61 / Issue 3 / 01 September 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 572-587
- Print publication:
- 01 September 2018
-
- Article
-
- You have access
- Export citation