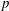 $p$-subgroups of finite Chevalley groups of rank six and seven
$p$-subgroups of finite Chevalley groups of rank six and sevenPublished online by Cambridge University Press: 01 April 2014
Let 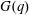 $G(q)$ be a finite Chevalley group, where
$G(q)$ be a finite Chevalley group, where 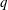 $q$ is a power of a good prime
$q$ is a power of a good prime 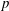 $p$, and let
$p$, and let 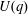 $U(q)$ be a Sylow
$U(q)$ be a Sylow 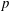 $p$-subgroup of
$p$-subgroup of 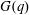 $G(q)$. Then a generalized version of a conjecture of Higman asserts that the number
$G(q)$. Then a generalized version of a conjecture of Higman asserts that the number 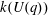 $k(U(q))$ of conjugacy classes in
$k(U(q))$ of conjugacy classes in 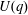 $U(q)$ is given by a polynomial in
$U(q)$ is given by a polynomial in 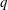 $q$ with integer coefficients. In [S. M. Goodwin and G. Röhrle, J. Algebra 321 (2009) 3321–3334], the first and the third authors of the present paper developed an algorithm to calculate the values of
$q$ with integer coefficients. In [S. M. Goodwin and G. Röhrle, J. Algebra 321 (2009) 3321–3334], the first and the third authors of the present paper developed an algorithm to calculate the values of 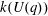 $k(U(q))$. By implementing it into a computer program using
$k(U(q))$. By implementing it into a computer program using  $\mathsf{GAP}$, they were able to calculate
$\mathsf{GAP}$, they were able to calculate 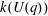 $k(U(q))$ for
$k(U(q))$ for 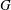 $G$ of rank at most five, thereby proving that for these cases
$G$ of rank at most five, thereby proving that for these cases 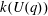 $k(U(q))$ is given by a polynomial in
$k(U(q))$ is given by a polynomial in 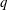 $q$. In this paper we present some refinements and improvements of the algorithm that allow us to calculate the values of
$q$. In this paper we present some refinements and improvements of the algorithm that allow us to calculate the values of 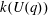 $k(U(q))$ for finite Chevalley groups of rank six and seven, except
$k(U(q))$ for finite Chevalley groups of rank six and seven, except 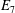 $E_7$. We observe that
$E_7$. We observe that 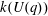 $k(U(q))$ is a polynomial, so that the generalized Higman conjecture holds for these groups. Moreover, if we write
$k(U(q))$ is a polynomial, so that the generalized Higman conjecture holds for these groups. Moreover, if we write 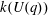 $k(U(q))$ as a polynomial in
$k(U(q))$ as a polynomial in 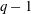 $q-1$, then the coefficients are non-negative.
$q-1$, then the coefficients are non-negative.
Under the assumption that 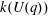 $k(U(q))$ is a polynomial in
$k(U(q))$ is a polynomial in 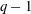 $q-1$, we also give an explicit formula for the coefficients of
$q-1$, we also give an explicit formula for the coefficients of 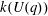 $k(U(q))$ of degrees zero, one and two.
$k(U(q))$ of degrees zero, one and two.