Hostname: page-component-669899f699-8p65j Total loading time: 0 Render date: 2025-04-25T16:03:27.140Z Has data issue: false hasContentIssue false
  • English
  • Français

Lifting Representations of Finite Reductive Groups I: Semisimple Conjugacy Classes

Published online by Cambridge University Press:  20 November 2018

Jeffrey D. Adler  and
Joshua M. Lansky
Jeffrey D. Adler
Affiliation:
Department of Mathematics and Statistics, American University, Washington, DC 20016-8050, USA. e-mail: (Adler) jadler@american.edu (Lansky) lansky@american.edu
Joshua M. Lansky
Affiliation:
Department of Mathematics and Statistics, American University, Washington, DC 20016-8050, USA. e-mail: (Adler) jadler@american.edu (Lansky) lansky@american.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Suppose that 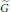$\widetilde{G}$ is a connected reductive group defined over a field 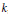$k$, and 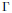$\Gamma$ is a finite group acting via 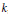$k$-automorphisms of 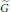$\widetilde{G}$ satisfying a certain quasi-semisimplicity condition. Then the identity component of the group of 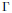$\Gamma$-fixed points in 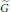$\widetilde{G}$ is reductive. We axiomatize the main features of the relationship between this fixed-point group and the pair 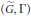$\left( \tilde{G},\Gamma \right)$, and consider any group 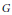$G$ satisfying the axioms. If both 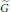$\widetilde{G}$ and 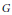$G$ are 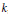$k$-quasisplit, then we can consider their duals 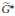$\widetilde{{{G}^{*}}}$ and 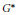${{G}^{*}}$. We show the existence of and give an explicit formula for a natural map from the set of semisimple stable conjugacy classes in 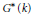${{G}^{*}}\,(k)$ to the analogous set for 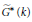$\widetilde{{{G}^{*}}}\,(k)$. If 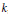$k$ is finite, then our groups are automatically quasisplit, and our result specializes to give a map of semisimple conjugacy classes. Since such classes parametrize packets of irreducible representations of 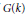$G(k)$ and 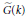$\widetilde{G}\,(k)$, one obtains a mapping of such packets.

Keywords

20G1520G4020C3322E35reductive groupliftingconjugacy classrepresentationLusztig series
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 66 , Issue 6 , 01 December 2014 , pp. 1201 - 1224
Copyright
Copyright © Canadian Mathematical Society 2014

References

[1] Adler, Jeffrey D. and Lansky, Joshua M., Depth-zero base change for ramified U(2; 1). Trans. Amer. Math. Soc. 362(2010), 5569–5599.http://dx.doi.org/10.1090/S0002-9947-10-05212-8 Google Scholar
[2] Adler, Jeffrey D. and Lansky, Joshua M., Lifting representations of finite reductive groups II: Explicit conorm functions. arxiv:1109.0794 Google Scholar
[3] Adler, Jeffrey D. and Lansky, Joshua M., Quasi-semisimple actions of finite groups on p-adic groups and buildings. In preparation.Google Scholar
[4] Borel, Armand, Linear algebraic groups. Graduate Texts in Math. 126, Springer-Verlag, New York, 1991.Google Scholar
[5] Carter, Roger W., Finite groups of Lie type. John Wiley & Sons Ltd., Chichester, 1993.Google Scholar
[6] Deligne, Pierre and Lusztig, George, Representations of reductive groups over finite fields. Ann. of Math. (2) 103(1976), 103–161.http://dx.doi.org/10.2307/1971021 Google Scholar
[7] Digne, François and Michel, Jean, Representations of finite groups of Lie type. London Math. Soc. Stud. Texts 21, Cambridge University Press, Cambridge, 1991.Google Scholar
[8] Howard, Tatiana K., Lifting of characters on p-adic orthogonal and metaplectic groups. Compos. Math. 146(2010), 795–810.http://dx.doi.org/10.1112/S0010437X09004618 Google Scholar
[9] Kottwitz, Robert E., Rational conjugacy classes in reductive groups. Duke Math. J. 49(1982), 785–806.http://dx.doi.org/10.1215/S0012-7094-82-04939-0 Google Scholar
[10] Kottwitz, Robert E. and Diana, Shelstad, Foundations of twisted endoscopy. Astérisque 255(1999).Google Scholar
[11] Lemaire, Bertrand, Caractères tordus des représentations admissibles. arxiv:1007.3576v2 Google Scholar
[12] Prasad, Gopal and Yu, Jiu-Kang, On finite group actions on reductive groups and buildings. Invent. Math. 147(2002), 545–560.http://dx.doi.org/10.1007/s002220100182 Google Scholar
[13] Raghunathan, M. S., Tori in quasi-split groups. J. Ramanujan Math. Soc. 19(2004), 281–287.Google Scholar
[14] Reeder, Mark, Elliptic centralizers in Weyl groups and their coinvariant representations. Represent. Theory 15(2011), 63–111.http://dx.doi.org/10.1090/S1088-4165-2011-00377-0 Google Scholar
[15] Serre, Jean-Pierre, Galois cohomology. Springer Monogr. Math., Springer-Verlag, Berlin, 2002.Google Scholar
[16] Springer, Tonny A., Linear algebraic groups. Progr. Math. 9, Biräkhuser Boston Inc., Boston, MA, 1998.Google Scholar
[17] Steinberg, Robert, Endomorphisms of linear algebraic groups. Mem. Amer. Math. Soc. 80, American Mathematical Society, Providence, RI, 1968.Google Scholar
[18] Weibel, Charles A., An introduction to homological algebra. Cambridge Stud. Adv. Math. 38, Cambridge University Press, Cambridge, 1994.Google Scholar