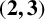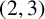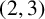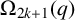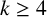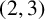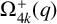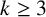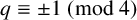1 Introduction
A group is said to be
![]() $(2,3)$
-generated if it can be generated by an involution and an element of order
$(2,3)$
-generated if it can be generated by an involution and an element of order
![]() $3$
, equivalently if it is an epimorphic image of
$3$
, equivalently if it is an epimorphic image of
![]() $C_2 \ast C_3\cong \mathrm {PSL}_2(\mathbb {Z})$
. In 1996 (see [Reference Liebeck and Shalev6]), it was shown that the symplectic groups
$C_2 \ast C_3\cong \mathrm {PSL}_2(\mathbb {Z})$
. In 1996 (see [Reference Liebeck and Shalev6]), it was shown that the symplectic groups
![]() $\mathrm {PSp}_4(q)$
, with
$\mathrm {PSp}_4(q)$
, with
![]() $q=2^f,3^f$
, are not
$q=2^f,3^f$
, are not
![]() $(2,3)$
-generated and that, apart from the members of these two infinite families and a finite number of undetermined exceptions, the finite simple classical groups, defined over the Galois field
$(2,3)$
-generated and that, apart from the members of these two infinite families and a finite number of undetermined exceptions, the finite simple classical groups, defined over the Galois field
![]() $\mathbb {F}_q$
, are
$\mathbb {F}_q$
, are
![]() $(2,3)$
-generated. Since then, many authors contributed to a constructive solution of the
$(2,3)$
-generated. Since then, many authors contributed to a constructive solution of the
![]() $(2,3)$
-generation problem of these groups (for example, see [Reference Tamburini and Wilson13, Reference Tamburini, Wilson and Gavioli14]). As a consequence, the list
$(2,3)$
-generation problem of these groups (for example, see [Reference Tamburini and Wilson13, Reference Tamburini, Wilson and Gavioli14]). As a consequence, the list
![]() $\mathcal {L}$
of the known exceptions consists now of the following ten groups:
$\mathcal {L}$
of the known exceptions consists now of the following ten groups:
![]() $\mathrm {PSL}_2(9)$
,
$\mathrm {PSL}_2(9)$
,
![]() $\mathrm {PSL}_3(4)$
,
$\mathrm {PSL}_3(4)$
,
![]() $\mathrm {PSL}_4(2)$
,
$\mathrm {PSL}_4(2)$
,
![]() $\mathrm {PSU}_3(3^2)$
,
$\mathrm {PSU}_3(3^2)$
,
![]() $\mathrm {PSU}_3(5^2)$
,
$\mathrm {PSU}_3(5^2)$
,
![]() $\mathrm {PSU}_4(2^2)\cong \mathrm {PSp}_4(3)$
,
$\mathrm {PSU}_4(2^2)\cong \mathrm {PSp}_4(3)$
,
![]() $\mathrm {PSU}_4(3^2)$
,
$\mathrm {PSU}_4(3^2)$
,
![]() $\mathrm {PSU}_5(2^2)$
,
$\mathrm {PSU}_5(2^2)$
,
![]() $\mathrm {P}\Omega _8^+(2)$
and
$\mathrm {P}\Omega _8^+(2)$
and
![]() $\mathrm {P}\Omega _8^+(3)$
. This list is complete for linear, unitary and symplectic groups, as shown in [Reference Pellegrini8–Reference Pellegrini and Tamburini Bellani10].
$\mathrm {P}\Omega _8^+(3)$
. This list is complete for linear, unitary and symplectic groups, as shown in [Reference Pellegrini8–Reference Pellegrini and Tamburini Bellani10].
In [Reference Pellegrini and Tamburini Bellani11], we proved that the finite simple
![]() $8$
-dimensional orthogonal groups are
$8$
-dimensional orthogonal groups are
![]() $(2,3)$
-generated, with the exceptions of
$(2,3)$
-generated, with the exceptions of
![]() $\mathrm {P}\Omega _8^+(2)$
and
$\mathrm {P}\Omega _8^+(2)$
and
![]() $\mathrm {P}\Omega _8^+(3)$
found by Vsemirnov [Reference Vsemirnov16]. In this paper, we consider orthogonal groups of dimension
$\mathrm {P}\Omega _8^+(3)$
found by Vsemirnov [Reference Vsemirnov16]. In this paper, we consider orthogonal groups of dimension
![]() $n\geq 9$
and prove the following constructive result.
$n\geq 9$
and prove the following constructive result.
Theorem 1.1. Assume q is odd. The following orthogonal groups are
![]() $(2,3)$
-generated:
$(2,3)$
-generated:
-
(i)
 $\Omega _{2k+1}(q)$
with
$\Omega _{2k+1}(q)$
with
 $k\geq 4$
;
$k\geq 4$
; -
(ii)
 $\Omega _{4k}^+(q)$
with
$\Omega _{4k}^+(q)$
with
 $k\geq 3$
;
$k\geq 3$
; -
(iii)
 $\Omega _{4k+2}^+(q)$
with
$\Omega _{4k+2}^+(q)$
with
 $k\geq 4$
and
$k\geq 4$
and
 $q\equiv 1 ~\mathrm {(mod~ 4)}$
;
$q\equiv 1 ~\mathrm {(mod~ 4)}$
; -
(iv)
 $\Omega _{4k+2}^-(q)$
with
$\Omega _{4k+2}^-(q)$
with
 $k\geq 4$
and
$k\geq 4$
and
 $q\equiv 3 ~\mathrm {(mod~ 4)}$
.
$q\equiv 3 ~\mathrm {(mod~ 4)}$
.
We recall that the
![]() $(2,3)$
-generation of
$(2,3)$
-generation of
![]() $\Omega _5(q)\cong \mathrm {PSp}_4(q)$
, when
$\Omega _5(q)\cong \mathrm {PSp}_4(q)$
, when
![]() $\gcd (q,6)=1$
, was proved in [Reference Cazzola and Di Martino2] (see also [Reference Pellegrini, Tamburini Bellani and Vsemirnov12]). Notice that the groups
$\gcd (q,6)=1$
, was proved in [Reference Cazzola and Di Martino2] (see also [Reference Pellegrini, Tamburini Bellani and Vsemirnov12]). Notice that the groups
![]() $\Omega _5(3^f)$
are not
$\Omega _5(3^f)$
are not
![]() $(2,3)$
-generated, but they are
$(2,3)$
-generated, but they are
![]() $(2,5)$
-generated (see [Reference King4]). In [Reference Pellegrini7], it was proved that the groups
$(2,5)$
-generated (see [Reference King4]). In [Reference Pellegrini7], it was proved that the groups
![]() $\Omega _7(q)$
are
$\Omega _7(q)$
are
![]() $(2,3)$
-generated for all odd q. As a consequence of all this, the constructive
$(2,3)$
-generated for all odd q. As a consequence of all this, the constructive
![]() $(2,3)$
-generation problem for the finite simple classical groups remains open only for the following orthogonal groups:
$(2,3)$
-generation problem for the finite simple classical groups remains open only for the following orthogonal groups:
-
(i)
 $\mathrm {P}\Omega _{2k}^\pm (q)$
with
$\mathrm {P}\Omega _{2k}^\pm (q)$
with
 $k\geq 5$
and q even;
$k\geq 5$
and q even; -
(ii)
 $\mathrm {P}\Omega _{10}^\pm (q)$
,
$\mathrm {P}\Omega _{10}^\pm (q)$
,
 $\mathrm {P}\Omega _{14}^\pm (q)$
, q odd;
$\mathrm {P}\Omega _{14}^\pm (q)$
, q odd; -
(iii)
 $\mathrm {P}\Omega _{4k}^-(q)$
with
$\mathrm {P}\Omega _{4k}^-(q)$
with
 $k\geq 3$
and q odd;
$k\geq 3$
and q odd; -
(iv)
 $\mathrm {P}\Omega _{4k+2}^+(q)$
with
$\mathrm {P}\Omega _{4k+2}^+(q)$
with
 $k\geq 4$
and
$k\geq 4$
and
 $q\equiv 3 ~\mathrm {(mod~ 4)}$
;
$q\equiv 3 ~\mathrm {(mod~ 4)}$
; -
(v)
 $\mathrm {P}\Omega _{4k+2}^-(q)$
with
$\mathrm {P}\Omega _{4k+2}^-(q)$
with
 $k\geq 4$
and
$k\geq 4$
and
 $q\equiv 1 ~\mathrm {(mod~ 4)}$
.
$q\equiv 1 ~\mathrm {(mod~ 4)}$
.
In our proof of Theorem 1.1, the cases
![]() $n\in \{9,11,13,17\}$
are dealt with in Section 3, where we use slightly different generators to make the proofs more efficient. For the general case, the generators are given in Section 4. The corresponding proofs are in Section 5 for
$n\in \{9,11,13,17\}$
are dealt with in Section 3, where we use slightly different generators to make the proofs more efficient. For the general case, the generators are given in Section 4. The corresponding proofs are in Section 5 for
![]() $n\in \{15, 18, 19\}$
or
$n\in \{15, 18, 19\}$
or
![]() $n\geq 21$
and in Section 6 for
$n\geq 21$
and in Section 6 for
![]() $n\in \{12, 16, 20\}$
.
$n\in \{12, 16, 20\}$
.
2 Preliminary results
Let
![]() $\mathbb {F}_q$
be the Galois field of order
$\mathbb {F}_q$
be the Galois field of order
![]() $q = p^f$
, a power of the prime
$q = p^f$
, a power of the prime
![]() $p>2$
, and let
$p>2$
, and let
![]() $\mathbb {F}$
be the algebraic closure of the field
$\mathbb {F}$
be the algebraic closure of the field
![]() $\mathbb {F}_p$
. We make
$\mathbb {F}_p$
. We make
![]() $\mathrm {GL}_n(\mathbb {F})$
act on the left on
$\mathrm {GL}_n(\mathbb {F})$
act on the left on
![]() $V=\mathbb {F}^n$
, whose canonical basis is
$V=\mathbb {F}^n$
, whose canonical basis is
![]() $\mathscr {C}=\{e_1, e_2, \ldots ,e_{n} \}$
.
$\mathscr {C}=\{e_1, e_2, \ldots ,e_{n} \}$
.
Up to isometry, there are two nondegenerate quadratic forms on
![]() $\mathbb {F}_q^n$
. If n is even, these two forms are not similar: we say that the quadratic form has sign
$\mathbb {F}_q^n$
. If n is even, these two forms are not similar: we say that the quadratic form has sign
![]() $+$
if the dimension of any maximal totally singular subspace is
$+$
if the dimension of any maximal totally singular subspace is
![]() ${n}/{2}$
; it has sign
${n}/{2}$
; it has sign
![]() $-$
if the dimension of such a space is
$-$
if the dimension of such a space is
![]() ${n}/{2}-1$
. The corresponding isometry groups are denoted by
${n}/{2}-1$
. The corresponding isometry groups are denoted by
![]() $\mathrm {O}_n^+(q)$
and
$\mathrm {O}_n^+(q)$
and
![]() $\mathrm {O}_n^-(q)$
. If n is odd, the two quadratic forms are similar. Hence, the corresponding isometry groups are isomorphic and are denoted by
$\mathrm {O}_n^-(q)$
. If n is odd, the two quadratic forms are similar. Hence, the corresponding isometry groups are isomorphic and are denoted by
![]() $\mathrm {O}^\circ _n(q)$
, or simply by
$\mathrm {O}^\circ _n(q)$
, or simply by
![]() $\mathrm {O}_n(q)$
. In short, we write
$\mathrm {O}_n(q)$
. In short, we write
![]() $\mathrm {O}^\epsilon _n(q)$
, where
$\mathrm {O}^\epsilon _n(q)$
, where
![]() $\epsilon =\circ $
if n is odd,
$\epsilon =\circ $
if n is odd,
![]() $\epsilon = +$
or
$\epsilon = +$
or
![]() $\epsilon = -$
if n is even.
$\epsilon = -$
if n is even.
If J is the Gram matrix of the symmetric bilinear form
![]() $\beta $
associated to a nondegenerate quadratic form Q on
$\beta $
associated to a nondegenerate quadratic form Q on
![]() $\mathbb {F}_q^n$
,
$\mathbb {F}_q^n$
,
In particular, since q is assumed to be odd, the form Q is determined by
![]() $\beta $
, that is, by J. When n is even, the isometry group of J is
$\beta $
, that is, by J. When n is even, the isometry group of J is
![]() $\mathrm {O}_n^+(q)$
if either
$\mathrm {O}_n^+(q)$
if either
![]() $\det (J)$
is a square in
$\det (J)$
is a square in
![]() $\mathbb {F}_q^*$
and
$\mathbb {F}_q^*$
and
![]() ${n(q-1)}/{4}$
is even, or
${n(q-1)}/{4}$
is even, or
![]() $\det (J)$
is a nonsquare and
$\det (J)$
is a nonsquare and
![]() ${n(q-1)}/{4}$
is odd; it is
${n(q-1)}/{4}$
is odd; it is
![]() $\mathrm {O}_n^-(q)$
otherwise (see [Reference Bray, Holt and Roney-Dougal1, Proposition 1.5.42]).
$\mathrm {O}_n^-(q)$
otherwise (see [Reference Bray, Holt and Roney-Dougal1, Proposition 1.5.42]).
The group
![]() $\Omega _n^\epsilon (q)$
is the derived subgroup of
$\Omega _n^\epsilon (q)$
is the derived subgroup of
![]() $\mathrm {O}_n^\epsilon (q)$
and has index
$\mathrm {O}_n^\epsilon (q)$
and has index
![]() $2$
in
$2$
in
![]() $\mathrm {SO}_n^\epsilon (q)$
, the subgroup of
$\mathrm {SO}_n^\epsilon (q)$
, the subgroup of
![]() $\mathrm {O}_n^\epsilon (q)$
consisting of matrices of determinant
$\mathrm {O}_n^\epsilon (q)$
consisting of matrices of determinant
![]() $1$
. Alternatively,
$1$
. Alternatively,
![]() $\Omega _n^\epsilon (q)$
consists of the elements in
$\Omega _n^\epsilon (q)$
consists of the elements in
![]() $\mathrm {SO}_n^\epsilon (q)$
with spinor norm in
$\mathrm {SO}_n^\epsilon (q)$
with spinor norm in
![]() $(\mathbb {F}_q^\ast )^2$
. We recall that the spinor norm
$(\mathbb {F}_q^\ast )^2$
. We recall that the spinor norm
![]() $\theta : \mathrm {O}_n^\epsilon (q) \to {\mathbb {F}_q^\ast }/{(\mathbb {F}_q^\ast )^2}$
is a homomorphism. For any nonsingular
$\theta : \mathrm {O}_n^\epsilon (q) \to {\mathbb {F}_q^\ast }/{(\mathbb {F}_q^\ast )^2}$
is a homomorphism. For any nonsingular
![]() $v \in \mathbb {F}_q^n$
, the reflection
$v \in \mathbb {F}_q^n$
, the reflection
![]() $r_v$
, of centre
$r_v$
, of centre
![]() $\langle v \rangle $
, acts as
$\langle v \rangle $
, acts as
![]() $w\mapsto w - Q(v)^{-1} \beta (w,v) v$
for all
$w\mapsto w - Q(v)^{-1} \beta (w,v) v$
for all
![]() $w \in V$
. Moreover,
$w \in V$
. Moreover,
![]() $\theta (r_v) = Q(v)(\mathbb {F}_q^\ast )^2$
(see [Reference Taylor15, pages 145, 163 and 164]).
$\theta (r_v) = Q(v)(\mathbb {F}_q^\ast )^2$
(see [Reference Taylor15, pages 145, 163 and 164]).
Given an eigenvalue
![]() $\lambda $
of a matrix
$\lambda $
of a matrix
![]() $g \in \mathrm {GL}_n(\mathbb {F})$
, write
$g \in \mathrm {GL}_n(\mathbb {F})$
, write
![]() $V_\lambda (g)$
for the corresponding eigenspace. The characteristic polynomial of g is denoted by
$V_\lambda (g)$
for the corresponding eigenspace. The characteristic polynomial of g is denoted by
![]() $\chi _g(t)$
. Let
$\chi _g(t)$
. Let
![]() $\omega \in \mathbb {F}$
be a primitive cube root of
$\omega \in \mathbb {F}$
be a primitive cube root of
![]() $1$
.
$1$
.
Lemma 2.1. Let H be a subgroup of
![]() $\mathrm {GL}_n(\mathbb {F})$
and U be a proper H-invariant subspace. Suppose that
$\mathrm {GL}_n(\mathbb {F})$
and U be a proper H-invariant subspace. Suppose that
![]() $g\in H$
has the eigenvalue
$g\in H$
has the eigenvalue
![]() $\lambda \in \mathbb {F}$
. If the restriction
$\lambda \in \mathbb {F}$
. If the restriction
![]() $g_{|U}$
does not have the eigenvalue
$g_{|U}$
does not have the eigenvalue
![]() $\lambda $
, then there exists an
$\lambda $
, then there exists an
![]() $H^{\mathsf {T}}$
-invariant subspace
$H^{\mathsf {T}}$
-invariant subspace
![]() $\overline {U}$
, with
$\overline {U}$
, with
![]() $\dim (\overline {U}) = n-\dim (U)$
, such that
$\dim (\overline {U}) = n-\dim (U)$
, such that
![]() $V_\lambda (g^{\mathsf {T}}) \leq \overline {U}$
.
$V_\lambda (g^{\mathsf {T}}) \leq \overline {U}$
.
Proof. There exists a nonsingular matrix P such that
 $$ \begin{align*}P^{-1} H P = \left\{\begin{pmatrix} A_h & B_h \\ 0 & C_h \end{pmatrix} \mid h\in H\right\},\quad P^{\mathsf{T}} H^{\mathsf{T}} P^{-\mathsf{T}} = \left\{\begin{pmatrix} A_h^{\mathsf{T}} & 0 \\[3pt] B_h^{\mathsf{T}} & C_h^{\mathsf{T}} \end{pmatrix} \mid h\in H \right\}.\end{align*} $$
$$ \begin{align*}P^{-1} H P = \left\{\begin{pmatrix} A_h & B_h \\ 0 & C_h \end{pmatrix} \mid h\in H\right\},\quad P^{\mathsf{T}} H^{\mathsf{T}} P^{-\mathsf{T}} = \left\{\begin{pmatrix} A_h^{\mathsf{T}} & 0 \\[3pt] B_h^{\mathsf{T}} & C_h^{\mathsf{T}} \end{pmatrix} \mid h\in H \right\}.\end{align*} $$
Set
![]() $A=A_g$
,
$A=A_g$
,
![]() $B=B_g$
,
$B=B_g$
,
![]() $C=C_g$
and
$C=C_g$
and
![]() $k=\dim (U)$
. Under our assumption,
$k=\dim (U)$
. Under our assumption,
![]() $A\in \mathrm {GL}_k(\mathbb {F})$
does not have the eigenvalue
$A\in \mathrm {GL}_k(\mathbb {F})$
does not have the eigenvalue
![]() $\lambda $
. Hence, the same is true for
$\lambda $
. Hence, the same is true for
![]() $A^{\mathsf {T}}$
. So, imposing
$A^{\mathsf {T}}$
. So, imposing
 $$ \begin{align*}\begin{pmatrix} A^{\mathsf{T}} & 0 \\ B^{\mathsf{T}} & C^{\mathsf{T}} \end{pmatrix} \begin{pmatrix} w \\ \overline{w}\end{pmatrix}= \begin{pmatrix} A^{\mathsf{T}} w \\ B^{\mathsf{T}} w + C^{\mathsf{T}} \overline{w}\end{pmatrix}= \begin{pmatrix} \lambda w \\ \lambda\overline{w} \end{pmatrix},\quad w \in \mathbb{F}^k, \; \overline{w} \in \mathbb{F}^{n-k},\end{align*} $$
$$ \begin{align*}\begin{pmatrix} A^{\mathsf{T}} & 0 \\ B^{\mathsf{T}} & C^{\mathsf{T}} \end{pmatrix} \begin{pmatrix} w \\ \overline{w}\end{pmatrix}= \begin{pmatrix} A^{\mathsf{T}} w \\ B^{\mathsf{T}} w + C^{\mathsf{T}} \overline{w}\end{pmatrix}= \begin{pmatrix} \lambda w \\ \lambda\overline{w} \end{pmatrix},\quad w \in \mathbb{F}^k, \; \overline{w} \in \mathbb{F}^{n-k},\end{align*} $$
we get
![]() $w = 0$
and
$w = 0$
and
 $$ \begin{align*}V_\lambda(P^{\mathsf{T}} g^{\mathsf{T}} P^{-\mathsf{T}}) =\left\{ \begin{pmatrix} 0 \\ \overline{w}\end{pmatrix}\mid C^{\mathsf{T}} \overline{w}= \lambda \overline{w}\right\}\leq \overline{E} =\langle e_i\mid k+1\leq i\leq n \rangle.\end{align*} $$
$$ \begin{align*}V_\lambda(P^{\mathsf{T}} g^{\mathsf{T}} P^{-\mathsf{T}}) =\left\{ \begin{pmatrix} 0 \\ \overline{w}\end{pmatrix}\mid C^{\mathsf{T}} \overline{w}= \lambda \overline{w}\right\}\leq \overline{E} =\langle e_i\mid k+1\leq i\leq n \rangle.\end{align*} $$
Set
![]() $\overline {U} = P^{-\mathsf {T}} \overline {E}$
. Since
$\overline {U} = P^{-\mathsf {T}} \overline {E}$
. Since
![]() $\overline {E}$
is invariant under
$\overline {E}$
is invariant under
![]() $P^{\mathsf {T}} H^{\mathsf {T}} P^{-\mathsf {T}}$
, we get that
$P^{\mathsf {T}} H^{\mathsf {T}} P^{-\mathsf {T}}$
, we get that
![]() $\overline {U}$
is
$\overline {U}$
is
![]() $H^{\mathsf {T}}$
-invariant. From
$H^{\mathsf {T}}$
-invariant. From
![]() $V_\lambda (g^{\mathsf {T}} ) = P^{-\mathsf {T}} V_\lambda (P^{\mathsf {T}} g^{\mathsf {T}} P^{-\mathsf {T}} )$
, it follows that
$V_\lambda (g^{\mathsf {T}} ) = P^{-\mathsf {T}} V_\lambda (P^{\mathsf {T}} g^{\mathsf {T}} P^{-\mathsf {T}} )$
, it follows that
![]() $V_\lambda (g^{\mathsf {T}} ) \leq \overline {U}$
.
$V_\lambda (g^{\mathsf {T}} ) \leq \overline {U}$
.
Corollary 2.2. Let H be a subgroup of
![]() $\mathrm {GL}_n(\mathbb {F})$
and U be a proper H-invariant subspace. Suppose that there exists
$\mathrm {GL}_n(\mathbb {F})$
and U be a proper H-invariant subspace. Suppose that there exists
![]() $J\in \mathrm {GL}_n(\mathbb {F})$
such that
$J\in \mathrm {GL}_n(\mathbb {F})$
such that
![]() $h^{\mathsf {T}} J h = J$
for all
$h^{\mathsf {T}} J h = J$
for all
![]() $h \in H$
. If
$h \in H$
. If
![]() $g\in H$
has the eigenvalue
$g\in H$
has the eigenvalue
![]() $\lambda \in \mathbb {F}$
, then
$\lambda \in \mathbb {F}$
, then
Also, if
![]() $g_{|U}$
does not have the eigenvalue
$g_{|U}$
does not have the eigenvalue
![]() $\lambda $
, then there exists an H-invariant subspace W, with
$\lambda $
, then there exists an H-invariant subspace W, with
![]() $\dim (W) = n-\dim (U)$
, such that
$\dim (W) = n-\dim (U)$
, such that
![]() $V_{\lambda ^{-1}}(g) \leq W$
.
$V_{\lambda ^{-1}}(g) \leq W$
.
In particular, for
![]() $\lambda =\lambda ^{-1}$
(that is,
$\lambda =\lambda ^{-1}$
(that is,
![]() $\lambda =\pm 1$
), we may assume that
$\lambda =\pm 1$
), we may assume that
![]() $g_{|U}$
has the eigenvalue
$g_{|U}$
has the eigenvalue
![]() $\lambda $
.
$\lambda $
.
Proof. From
![]() $g^{\mathsf {T}} J g =J$
, we get
$g^{\mathsf {T}} J g =J$
, we get
![]() $g(J^{-1} \overline {s}) =J^{-1} g^{-\mathsf {T}} \overline {s}=\lambda ^{-1} (J^{-1}\overline {s})$
for all
$g(J^{-1} \overline {s}) =J^{-1} g^{-\mathsf {T}} \overline {s}=\lambda ^{-1} (J^{-1}\overline {s})$
for all
![]() $\overline {s}\in V_{\lambda }(g^{\mathsf {T}})$
. It follows that
$\overline {s}\in V_{\lambda }(g^{\mathsf {T}})$
. It follows that
![]() $J^{-1} V_{\lambda }(g^{\mathsf {T}})\leq V_{\lambda ^{-1}}(g)$
. However, take
$J^{-1} V_{\lambda }(g^{\mathsf {T}})\leq V_{\lambda ^{-1}}(g)$
. However, take
![]() $v \in V_{\lambda ^{-1}}(g)$
. Then,
$v \in V_{\lambda ^{-1}}(g)$
. Then,
![]() $g^{\mathsf {T}} J v = J g^{-1} v =\lambda J v$
gives
$g^{\mathsf {T}} J v = J g^{-1} v =\lambda J v$
gives
![]() $Jv \in V_{\lambda }(g^{\mathsf {T}})$
, whence
$Jv \in V_{\lambda }(g^{\mathsf {T}})$
, whence
![]() $V_{\lambda ^{-1}}(g)\leq J^{-1} V_{\lambda }(g^{\mathsf {T}})$
.
$V_{\lambda ^{-1}}(g)\leq J^{-1} V_{\lambda }(g^{\mathsf {T}})$
.
If
![]() $g_{|U}$
does not have the eigenvalue
$g_{|U}$
does not have the eigenvalue
![]() $\lambda $
, we apply Lemma 2.1: so, there exists an
$\lambda $
, we apply Lemma 2.1: so, there exists an
![]() $H^{\mathsf {T}}$
-invariant subspace
$H^{\mathsf {T}}$
-invariant subspace
![]() $\overline {U}$
, with
$\overline {U}$
, with
![]() $\dim (\overline {U})=n-\dim (U)$
, such that
$\dim (\overline {U})=n-\dim (U)$
, such that
![]() $V_\lambda (g^{\mathsf {T}}) \leq \overline {U}$
. Set
$V_\lambda (g^{\mathsf {T}}) \leq \overline {U}$
. Set
![]() $W=J^{-1}\overline {U}$
. For any
$W=J^{-1}\overline {U}$
. For any
![]() $h \in H$
, we have
$h \in H$
, we have
![]() $h W = h (J^{-1}\overline {U})=J^{-1}h^{-\mathsf {T}}\overline {U} =J^{-1} \overline {U}=W$
. Hence, W is H-invariant and
$h W = h (J^{-1}\overline {U})=J^{-1}h^{-\mathsf {T}}\overline {U} =J^{-1} \overline {U}=W$
. Hence, W is H-invariant and
![]() $\dim (W)=\dim (\overline {U})=n-\dim (U)$
. Finally,
$\dim (W)=\dim (\overline {U})=n-\dim (U)$
. Finally,
![]() $V_{\lambda ^{-1}}(g) = J^{-1}V_\lambda (g^{\mathsf {T}})\leq J^{-1}\overline {U}=W$
.
$V_{\lambda ^{-1}}(g) = J^{-1}V_\lambda (g^{\mathsf {T}})\leq J^{-1}\overline {U}=W$
.
To prove our Theorem 1.1, we define two elements
![]() $x,y$
of respective orders
$x,y$
of respective orders
![]() $2$
and
$2$
and
![]() $3$
, where
$3$
, where
![]() $y\in \Omega _n^\epsilon (q)$
and x depends on some parameter
$y\in \Omega _n^\epsilon (q)$
and x depends on some parameter
![]() $a\in \mathbb {F}_q^*$
. Our aim is to find suitable conditions on a such that
$a\in \mathbb {F}_q^*$
. Our aim is to find suitable conditions on a such that
![]() $x\in \Omega _n^\epsilon (q)$
and the subgroup
$x\in \Omega _n^\epsilon (q)$
and the subgroup
![]() $H=\langle x,y\rangle $
is not contained in any maximal subgroup M of
$H=\langle x,y\rangle $
is not contained in any maximal subgroup M of
![]() $\Omega _n^\epsilon (q)$
.
$\Omega _n^\epsilon (q)$
.
The maximal subgroups of classical groups, described in [Reference Bray, Holt and Roney-Dougal1, Reference Kleidman and Liebeck5], belong to eight classes
![]() $\mathcal {C}_1,\mathcal {C}_2,\ldots , \mathcal {C}_8$
, and a further class
$\mathcal {C}_1,\mathcal {C}_2,\ldots , \mathcal {C}_8$
, and a further class
![]() $\mathcal {S}$
. Note that, for orthogonal groups, the class
$\mathcal {S}$
. Note that, for orthogonal groups, the class
![]() $\mathcal {C}_8$
is always empty. Those which are relevant in our results can be roughly described as follows (see [Reference Kleidman and Liebeck5, Table 1.2.A]):
$\mathcal {C}_8$
is always empty. Those which are relevant in our results can be roughly described as follows (see [Reference Kleidman and Liebeck5, Table 1.2.A]):
-
• groups that are reducible over
 $\mathbb {F}$
(classes
$\mathbb {F}$
(classes
 $\mathcal {C}_1$
and
$\mathcal {C}_1$
and
 $\mathcal {C}_3$
);
$\mathcal {C}_3$
); -
• imprimitive groups, that is, stabilizers of decompositions
 $\mathbb {F}_q^n=\oplus _{i=1}^t W_i$
, where
$\mathbb {F}_q^n=\oplus _{i=1}^t W_i$
, where
 $\dim (W_i)={n}/{t}$
(class
$\dim (W_i)={n}/{t}$
(class
 $\mathcal {C}_2$
). When
$\mathcal {C}_2$
). When
 $t=n$
, they are also called monomial;
$t=n$
, they are also called monomial; -
• stabilizers of subfields of
 $\mathbb {F}_q$
of prime index (class
$\mathbb {F}_q$
of prime index (class
 $\mathcal {C}_5$
). They are conjugate to subgroups of
$\mathcal {C}_5$
). They are conjugate to subgroups of
 $\mathrm {GL}_n(q_0)$
, where
$\mathrm {GL}_n(q_0)$
, where
 $q=q_0^r$
with r prime.
$q=q_0^r$
with r prime.
To understand these groups, it is also necessary to know the representations of classical groups in higher dimensions, where they may fix nondegenerate forms. In particular, we need (for instance, in Lemma 3.5) the representation
![]() $\psi : \mathrm {GL}_2(q)\to \mathrm {GL}_3(q)$
arising from the action of
$\psi : \mathrm {GL}_2(q)\to \mathrm {GL}_3(q)$
arising from the action of
![]() $\mathrm {GL}_2(q)$
on the space of homogeneous polynomials of degree
$\mathrm {GL}_2(q)$
on the space of homogeneous polynomials of degree
![]() $2$
in two variables over
$2$
in two variables over
![]() $\mathbb {F}_{q}$
, namely
$\mathbb {F}_{q}$
, namely
 $$ \begin{align} \psi\left(\begin{pmatrix} b_1 & b_2 \\ b_3 & b_4 \end{pmatrix}\right) = \begin{pmatrix} b_1^2 & b_1b_2 & b_2^2\\ 2b_1b_3 & b_1b_4+b_2b_3 & 2b_2b_4\\ b_3^2 & b_3b_4 & b_4^2 \end{pmatrix}. \end{align} $$
$$ \begin{align} \psi\left(\begin{pmatrix} b_1 & b_2 \\ b_3 & b_4 \end{pmatrix}\right) = \begin{pmatrix} b_1^2 & b_1b_2 & b_2^2\\ 2b_1b_3 & b_1b_4+b_2b_3 & 2b_2b_4\\ b_3^2 & b_3b_4 & b_4^2 \end{pmatrix}. \end{align} $$
Note that
![]() $\mathrm {Im}(\psi )$
preserves the symmetric form
$\mathrm {Im}(\psi )$
preserves the symmetric form
![]() $\bigg (\begin {smallmatrix} 0&0&1\\ 0&-1/2 &0\\ 1&0&0 \end {smallmatrix}\bigg )$
whenever
$\bigg (\begin {smallmatrix} 0&0&1\\ 0&-1/2 &0\\ 1&0&0 \end {smallmatrix}\bigg )$
whenever
![]() $b_1b_4 -b_2 b_3=\pm 1$
.
$b_1b_4 -b_2 b_3=\pm 1$
.
Finally, we recall some well-known facts (for example, see [Reference Kleidman and Liebeck5, page 185]). Let
![]() $\mathrm {Sym}(\ell )$
be the subgroup of
$\mathrm {Sym}(\ell )$
be the subgroup of
![]() $\mathrm {GL}_\ell (\mathbb {F})$
consisting of the permutation matrices. Clearly,
$\mathrm {GL}_\ell (\mathbb {F})$
consisting of the permutation matrices. Clearly,
![]() $\mathrm {Sym}(\ell )$
preserves the bilinear form defined by
$\mathrm {Sym}(\ell )$
preserves the bilinear form defined by
![]() $\mathrm {I}_\ell $
. Moreover, it fixes the vector
$\mathrm {I}_\ell $
. Moreover, it fixes the vector
![]() ${u=\sum \nolimits _{i=1}^\ell e_i}$
and the subspace
${u=\sum \nolimits _{i=1}^\ell e_i}$
and the subspace
![]() $u^\perp $
.
$u^\perp $
.
If
![]() $p\nmid \ell $
, then u is not isotropic, whence
$p\nmid \ell $
, then u is not isotropic, whence
![]() $\mathbb {F}^\ell = u^\perp \perp \langle u\rangle $
. The restriction of
$\mathbb {F}^\ell = u^\perp \perp \langle u\rangle $
. The restriction of
![]() $\mathrm {Sym}(\ell )$
to the subspace
$\mathrm {Sym}(\ell )$
to the subspace
![]() $u^\perp $
provides a representation of
$u^\perp $
provides a representation of
![]() $\mathrm {Sym}(\ell )$
of degree
$\mathrm {Sym}(\ell )$
of degree
![]() $\ell -1$
. The Jordan canonical form of any
$\ell -1$
. The Jordan canonical form of any
![]() $\sigma \in \mathrm {Sym}(\ell )$
is obtained from the Jordan form of
$\sigma \in \mathrm {Sym}(\ell )$
is obtained from the Jordan form of
![]() $\sigma _{|u^\perp }$
, adding a unique block
$\sigma _{|u^\perp }$
, adding a unique block
![]() $(\begin {smallmatrix} 1\end {smallmatrix})$
.
$(\begin {smallmatrix} 1\end {smallmatrix})$
.
If
![]() $p\mid \ell $
, then
$p\mid \ell $
, then
![]() $u\in u^\perp $
. Set
$u\in u^\perp $
. Set
![]() $\overline {W}=\langle e_1-e_{i+1}\mid 1\leq i \leq \ell -2\rangle $
. With respect to the decomposition
$\overline {W}=\langle e_1-e_{i+1}\mid 1\leq i \leq \ell -2\rangle $
. With respect to the decomposition
![]() $u^\perp =\overline {W}\oplus \langle u\rangle $
, every
$u^\perp =\overline {W}\oplus \langle u\rangle $
, every
![]() $\sigma \in \mathrm {Sym}(\ell )$
has matrix
$\sigma \in \mathrm {Sym}(\ell )$
has matrix
 $$ \begin{align*}\begin{pmatrix} \sigma_{|\overline W} & 0 \\[4pt] v_\sigma^{\mathsf{T}} & 1 \end{pmatrix},\quad \sigma_{|\overline W}\in \mathrm{GL}_{\ell-2}(p),\quad v_\sigma\in \mathbb{F}_p^{\ell-2}.\end{align*} $$
$$ \begin{align*}\begin{pmatrix} \sigma_{|\overline W} & 0 \\[4pt] v_\sigma^{\mathsf{T}} & 1 \end{pmatrix},\quad \sigma_{|\overline W}\in \mathrm{GL}_{\ell-2}(p),\quad v_\sigma\in \mathbb{F}_p^{\ell-2}.\end{align*} $$
The representation
![]() $\sigma \mapsto \sigma _{|\overline W}$
has degree
$\sigma \mapsto \sigma _{|\overline W}$
has degree
![]() $\ell -2$
. For any
$\ell -2$
. For any
![]() $\sigma $
of order not divisible by p, its Jordan form is obtained from that of
$\sigma $
of order not divisible by p, its Jordan form is obtained from that of
![]() $\sigma _{|\overline {W}}$
, adding a unique block
$\sigma _{|\overline {W}}$
, adding a unique block
![]() $\mathrm {I}_2$
.
$\mathrm {I}_2$
.
3 The case
 $n\in \{9,11, 13, 17\}$
$n\in \{9,11, 13, 17\}$
In this section, we take
![]() $J=\mathrm {diag}\bigg (\mathrm {I}_{n-3}, \bigg (\begin {smallmatrix} 0&0&1\\ 0&1&0\\ 1&0&0 \end {smallmatrix}\bigg )\bigg )$
of determinant
$J=\mathrm {diag}\bigg (\mathrm {I}_{n-3}, \bigg (\begin {smallmatrix} 0&0&1\\ 0&1&0\\ 1&0&0 \end {smallmatrix}\bigg )\bigg )$
of determinant
![]() $-1$
. For any
$-1$
. For any
![]() $a\in \mathbb {F}_q^*$
, we define four matrices
$a\in \mathbb {F}_q^*$
, we define four matrices
![]() $x_1,x_2,y_1,y_2 \in \mathrm {SL}_n(q)$
with
$x_1,x_2,y_1,y_2 \in \mathrm {SL}_n(q)$
with
![]() $x_i^2=y_i^3=\mathrm {I}_n$
as follows.
$x_i^2=y_i^3=\mathrm {I}_n$
as follows.
-
(x 1)
 $x_1$
acts on
$x_1$
acts on
 $\mathscr {C}=\{e_1,\ldots ,e_n\}$
as:
$\mathscr {C}=\{e_1,\ldots ,e_n\}$
as:-
• the identity if
 $n=9$
;
$n=9$
; -
• the permutation
 $(e_1,e_3)(e_2,e_4)$
if
$(e_1,e_3)(e_2,e_4)$
if
 $n=11$
;
$n=11$
; -
• the permutation
 $(e_1,e_2)(e_4,e_5)$
if
$(e_1,e_2)(e_4,e_5)$
if
 $n=13$
;
$n=13$
; -
• the permutation
 $(e_1,e_3)(e_2,e_4)(e_5,e_6)(e_8,e_9)$
if
$(e_1,e_3)(e_2,e_4)(e_5,e_6)(e_8,e_9)$
if
 $n=17$
.
$n=17$
.
-
-
(x 2)
 $x_2=\mathrm {diag}(\mathrm {I}_{n-9},\bar x)$
, where
$x_2=\mathrm {diag}(\mathrm {I}_{n-9},\bar x)$
, where
 $\bar x=\bar x(a)$
is as in Figure 1.
$\bar x=\bar x(a)$
is as in Figure 1.
Figure 1 Generators of
 $\Omega _9(q)$
.
$\Omega _9(q)$
. -
(y 1)
 $y_1$
acts on
$y_1$
acts on
 $\mathscr {C}$
as:
$\mathscr {C}$
as:-
• the identity if
 $n\in \{9,11\}$
;
$n\in \{9,11\}$
; -
• the permutation
 $(e_2,e_3,e_4)$
if
$(e_2,e_3,e_4)$
if
 $n=13$
;
$n=13$
; -
• the permutation
 $(e_3,e_4,e_5)(e_6,e_7,e_8)$
if
$(e_3,e_4,e_5)(e_6,e_7,e_8)$
if
 $n=17$
.
$n=17$
.
-
-
(y 2)
 $y_2=\mathrm {diag}(\mathrm {I}_{n-9},\bar y)$
, where
$y_2=\mathrm {diag}(\mathrm {I}_{n-9},\bar y)$
, where
 $\bar y$
is as in Figure 1.
$\bar y$
is as in Figure 1.
We can see
![]() $x_2$
as the product of an even number of transpositions and the matrix
$x_2$
as the product of an even number of transpositions and the matrix
![]() $\mathrm {diag}(\mathrm {I}_{n-3}, x_3)$
with
$\mathrm {diag}(\mathrm {I}_{n-3}, x_3)$
with
![]() $x_3 =\bigg (\begin {smallmatrix} 0& 0 & {2}/{a} \\ 0 & -1 & 0 \\ {a}/{2} & 0 & 0 \end {smallmatrix}\bigg )$
. Identifying
$x_3 =\bigg (\begin {smallmatrix} 0& 0 & {2}/{a} \\ 0 & -1 & 0 \\ {a}/{2} & 0 & 0 \end {smallmatrix}\bigg )$
. Identifying
![]() $\mathrm {Sym}(n-3)$
with the group of permutation matrices fixing
$\mathrm {Sym}(n-3)$
with the group of permutation matrices fixing
![]() $\{e_j \mid 1\leq j\leq n-3\}$
and acting as the identity on
$\{e_j \mid 1\leq j\leq n-3\}$
and acting as the identity on
![]() $\langle e_{n-2},e_{n-1},e_n\rangle $
, the first factor of
$\langle e_{n-2},e_{n-1},e_n\rangle $
, the first factor of
![]() $x_2$
viewed in
$x_2$
viewed in
![]() $\mathrm {Sym}(n-3)\times \mathrm {GL}_3(q)$
is in
$\mathrm {Sym}(n-3)\times \mathrm {GL}_3(q)$
is in
![]() $\mathrm {Alt}(n - 3) \leq \Omega _n(q)$
. In particular, it is an involution and the same applies to
$\mathrm {Alt}(n - 3) \leq \Omega _n(q)$
. In particular, it is an involution and the same applies to
![]() $x_3$
. Similarly, also
$x_3$
. Similarly, also
![]() $x_1$
is the product of an even number of transpositions, so is in
$x_1$
is the product of an even number of transpositions, so is in
![]() $\mathrm {Alt}(n - 3) \leq \Omega _n(q)$
. Moreover,
$\mathrm {Alt}(n - 3) \leq \Omega _n(q)$
. Moreover,
![]() $x_3\in \Omega _3(q)$
if and only if
$x_3\in \Omega _3(q)$
if and only if
![]() $-a\in (\mathbb {F}_q^\ast )^2$
. Indeed,
$-a\in (\mathbb {F}_q^\ast )^2$
. Indeed,
![]() $x_3$
is the product of the reflections with centres
$x_3$
is the product of the reflections with centres
![]() $\langle a e_{n-2}-2e_n\rangle $
and
$\langle a e_{n-2}-2e_n\rangle $
and
![]() $\langle e_{n-1}\rangle $
, whose spinor norms are, respectively,
$\langle e_{n-1}\rangle $
, whose spinor norms are, respectively,
![]() $-2a(\mathbb {F}_q^*)^2$
and
$-2a(\mathbb {F}_q^*)^2$
and
![]() $\tfrac 12(\mathbb {F}_q^*)^2$
.
$\tfrac 12(\mathbb {F}_q^*)^2$
.
Clearly,
![]() $y_1$
and
$y_1$
and
![]() $y_2$
have determinant
$y_2$
have determinant
![]() $1$
. Moreover,
$1$
. Moreover,
![]() $y_1 \in \mathrm {Alt}(n - 9)\leq \Omega _n(q)$
and
$y_1 \in \mathrm {Alt}(n - 9)\leq \Omega _n(q)$
and
![]() $y_2^{\mathsf {T}} J y_2=J$
. Since
$y_2^{\mathsf {T}} J y_2=J$
. Since
![]() $x_1x_2=x_2x_1$
and
$x_1x_2=x_2x_1$
and
![]() $y_1 y_2 = y_2y_1$
, we conclude that
$y_1 y_2 = y_2y_1$
, we conclude that
![]() $x:= x_1x_2$
and
$x:= x_1x_2$
and
![]() $y:= y_1y_2$
have respective orders
$y:= y_1y_2$
have respective orders
![]() $2$
and
$2$
and
![]() $3$
, and
$3$
, and
We also assume that
![]() $a\in \mathbb {F}_q^*$
is such that
$a\in \mathbb {F}_q^*$
is such that
![]() $\mathbb {F}_p[a]=\mathbb {F}_q$
.
$\mathbb {F}_p[a]=\mathbb {F}_q$
.
By direct computation, we see that the characteristic polynomial of
![]() $xy$
is
$xy$
is
In particular,
![]() $\mathrm {tr}(xy) = -(a + a^{-1})$
. Moreover, the minimal polynomial of
$\mathrm {tr}(xy) = -(a + a^{-1})$
. Moreover, the minimal polynomial of
![]() $xy$
is
$xy$
is
 $$ \begin{align*}\mathrm{min}_{xy}(t)= \begin{cases} (t + 1)(t^{n-2}-1) & \textrm{if } a=1,\\ (t + a)(t + a^{-1})(t^{n-2}-1) & \textrm{otherwise}. \end{cases}\end{align*} $$
$$ \begin{align*}\mathrm{min}_{xy}(t)= \begin{cases} (t + 1)(t^{n-2}-1) & \textrm{if } a=1,\\ (t + a)(t + a^{-1})(t^{n-2}-1) & \textrm{otherwise}. \end{cases}\end{align*} $$
If
![]() $a\neq 1$
, the minimal polynomial of
$a\neq 1$
, the minimal polynomial of
![]() $xy$
coincides with its characteristic polynomial. Hence, consideration of the canonical rational form of
$xy$
coincides with its characteristic polynomial. Hence, consideration of the canonical rational form of
![]() $xy$
when
$xy$
when
![]() $a\neq 1$
and direct computation when
$a\neq 1$
and direct computation when
![]() $a=1$
tell us that
$a=1$
tell us that
![]() $(xy)^{n-2}\neq \mathrm {I}_n$
has a fixed point space of dimension
$(xy)^{n-2}\neq \mathrm {I}_n$
has a fixed point space of dimension
![]() $n-2$
, namely it is a bireflection.
$n-2$
, namely it is a bireflection.
Lemma 3.1. For
![]() $1\leq j,k\leq n-3$
, there exists
$1\leq j,k\leq n-3$
, there exists
![]() $h\in H$
such that
$h\in H$
such that
![]() $h e_j=e_k$
.
$h e_j=e_k$
.
Proof. Clearly, it is enough to show that, for
![]() $k\leq n-3$
, there exists
$k\leq n-3$
, there exists
![]() $h\in H$
such that
$h\in H$
such that
![]() $he_1=e_k$
. Noting that
$he_1=e_k$
. Noting that
![]() $ye_1=e_2$
,
$ye_1=e_2$
,
![]() $ye_2=e_3$
,
$ye_2=e_3$
,
![]() $xe_3=e_4$
,
$xe_3=e_4$
,
![]() $ye_4=e_5$
for
$ye_4=e_5$
for
![]() $n=9$
,
$n=9$
,
![]() $xe_1=e_3$
,
$xe_1=e_3$
,
![]() ${ye_3=e_4}$
,
${ye_3=e_4}$
,
![]() $ye_4=e_5$
,
$ye_4=e_5$
,
![]() $xe_4=e_2$
for
$xe_4=e_2$
for
![]() $n\in \{11,17\}$
, and
$n\in \{11,17\}$
, and
![]() $xe_1=e_2$
,
$xe_1=e_2$
,
![]() $ye_2=e_3$
,
$ye_2=e_3$
,
![]() $ye_3=e_4\ xe_4=e_5$
for
$ye_3=e_4\ xe_4=e_5$
for
![]() $n=13$
, our claim is true for
$n=13$
, our claim is true for
![]() $k\leq 5$
.
$k\leq 5$
.
Now, let
![]() $5 \leq \ell \leq n - 3$
be the largest integer for which, for all
$5 \leq \ell \leq n - 3$
be the largest integer for which, for all
![]() $1\leq i\leq \ell $
, there exists
$1\leq i\leq \ell $
, there exists
![]() $h_i \in H$
such that
$h_i \in H$
such that
![]() $h_i e_1= e_i$
. If
$h_i e_1= e_i$
. If
![]() $\ell < n - 3$
, there exists
$\ell < n - 3$
, there exists
![]() $h \in \{x, y\}$
such that
$h \in \{x, y\}$
such that
![]() $he_\ell = e_{\ell +1}$
, which is a contradiction.
$he_\ell = e_{\ell +1}$
, which is a contradiction.
Lemma 3.2. Assume
![]() $a^2-a-1\neq 0$
if
$a^2-a-1\neq 0$
if
![]() $n=9$
,
$n=9$
,
![]() $(a-1)(a^3+2a^2+a+1)\neq 0$
if
$(a-1)(a^3+2a^2+a+1)\neq 0$
if
![]() $n=11$
and
$n=11$
and
![]() $a^4 + a^2 - a + 1\neq 0$
if
$a^4 + a^2 - a + 1\neq 0$
if
![]() $n=17$
. Then, the group H is absolutely irreducible.
$n=17$
. Then, the group H is absolutely irreducible.
Proof. Assume, for a contradiction, that U is a proper H-invariant subspace. Define
Under our hypotheses on a, for
![]() $n=9$
, we have
$n=9$
, we have
![]() $V_1(g_9)= \langle e_1\rangle $
. By Corollary 2.2, we may assume
$V_1(g_9)= \langle e_1\rangle $
. By Corollary 2.2, we may assume
![]() $e_1\in U$
and hence
$e_1\in U$
and hence
![]() $e_1,\ldots ,e_{n-3}\in U$
by Lemma 3.1. Similarly, for
$e_1,\ldots ,e_{n-3}\in U$
by Lemma 3.1. Similarly, for
![]() $n=11$
, we have
$n=11$
, we have
![]() $V_1(g_{11})= \langle e_3\rangle $
, for
$V_1(g_{11})= \langle e_3\rangle $
, for
![]() $n=13$
, we have
$n=13$
, we have
![]() $V_1(g_{13})= \langle e_2\rangle $
and for
$V_1(g_{13})= \langle e_2\rangle $
and for
![]() $n=17$
, we have
$n=17$
, we have
![]() $V_1(g_{17})= \langle e_6\rangle $
. In all these cases, as above, we may assume
$V_1(g_{17})= \langle e_6\rangle $
. In all these cases, as above, we may assume
![]() $e_1,\ldots ,e_{n-3}\in U$
. Noting that
$e_1,\ldots ,e_{n-3}\in U$
. Noting that
![]() $y e_{n-3}+e_{n-3} = -2 e_{n-2}$
,
$y e_{n-3}+e_{n-3} = -2 e_{n-2}$
,
![]() $y^2 e_{n-5} = e_{n-1}$
and
$y^2 e_{n-5} = e_{n-1}$
and
![]() $y^2 e_{n-2} = -\tfrac 12 e_n$
, we get the contradiction
$y^2 e_{n-2} = -\tfrac 12 e_n$
, we get the contradiction
![]() $U=V$
.
$U=V$
.
For the following result, we need the traces of
![]() $[x,y]^j$
,
$[x,y]^j$
,
![]() $j=1,2$
:
$j=1,2$
:
where
 $$ \begin{align*}\varsigma_n=\begin{cases} 1 & \textrm{if } n=9,\\ 0 & \textrm{otherwise} \end{cases} \quad \textrm{and} \quad \kappa_n=\begin{cases} 3 & \textrm{if } n=9,\\ 2 & \textrm{if } n=11,\\ 4 & \textrm{if } n=13,17. \end{cases} \end{align*} $$
$$ \begin{align*}\varsigma_n=\begin{cases} 1 & \textrm{if } n=9,\\ 0 & \textrm{otherwise} \end{cases} \quad \textrm{and} \quad \kappa_n=\begin{cases} 3 & \textrm{if } n=9,\\ 2 & \textrm{if } n=11,\\ 4 & \textrm{if } n=13,17. \end{cases} \end{align*} $$
Lemma 3.3. The group H is not contained in any maximal subgroup M in class
![]() $\mathcal {C}_5$
of
$\mathcal {C}_5$
of
![]() $\Omega _{n}(q)$
.
$\Omega _{n}(q)$
.
Proof. Suppose the contrary. By [Reference Bray, Holt and Roney-Dougal1, Tables 8.58 and 8.74] and [Reference Kleidman and Liebeck5, Proposition 4.5.8], we have either
![]() $M\cong \Omega _n(q_0)$
where
$M\cong \Omega _n(q_0)$
where
![]() $q=q_0^r$
and r is an odd prime, or
$q=q_0^r$
and r is an odd prime, or
![]() $M\cong \mathrm {SO}_n(q_0)$
where
$M\cong \mathrm {SO}_n(q_0)$
where
![]() $q=q_0^2$
. Thus, there exists
$q=q_0^2$
. Thus, there exists
![]() $g\in \mathrm {GL}_{n}(\mathbb {F})$
such that
$g\in \mathrm {GL}_{n}(\mathbb {F})$
such that
![]() $x^g=x_0$
,
$x^g=x_0$
,
![]() $y^g=y_0$
, with
$y^g=y_0$
, with
![]() $x_0, y_0\in \mathrm {GL}_{n}(q_0)$
. From
$x_0, y_0\in \mathrm {GL}_{n}(q_0)$
. From
![]() $\mathrm {tr}([x,y]^j)=\mathrm {tr}([x^g, y^g]^j )= \mathrm {tr}( [x_0,y_0]^j)$
,
$\mathrm {tr}([x,y]^j)=\mathrm {tr}([x^g, y^g]^j )= \mathrm {tr}( [x_0,y_0]^j)$
,
![]() $j=1,2$
, it follows that
$j=1,2$
, it follows that
![]() $4a+\kappa _n = (\mathrm {tr}([x,y])-\varsigma _n)^2-\mathrm {tr}([x,y]^2)\in \mathbb {F}_{q_0}$
, whence
$4a+\kappa _n = (\mathrm {tr}([x,y])-\varsigma _n)^2-\mathrm {tr}([x,y]^2)\in \mathbb {F}_{q_0}$
, whence
![]() $a \in \mathbb {F}_{q_0}$
. So,
$a \in \mathbb {F}_{q_0}$
. So,
![]() $\mathbb {F}_q=\mathbb {F}_p[a]\leq \mathbb {F}_{q_0}$
implies
$\mathbb {F}_q=\mathbb {F}_p[a]\leq \mathbb {F}_{q_0}$
implies
![]() ${q_0=q}$
.
${q_0=q}$
.
Lemma 3.4. Assume
![]() $a^2-a-1\neq 0$
for
$a^2-a-1\neq 0$
for
![]() $n=9$
. If H is absolutely irreducible, then H is not contained in any monomial subgroup of
$n=9$
. If H is absolutely irreducible, then H is not contained in any monomial subgroup of
![]() $\Omega _{n}(q)$
.
$\Omega _{n}(q)$
.
Proof. For the sake of contradiction, suppose that H is contained in a monomial subgroup
![]() $M\in \mathcal {C}_2$
of
$M\in \mathcal {C}_2$
of
![]() $\Omega _n(q)$
. In this case, we may assume
$\Omega _n(q)$
. In this case, we may assume
![]() $q=p$
and H acts monomially with respect to an orthonormal basis
$q=p$
and H acts monomially with respect to an orthonormal basis
![]() $\mathcal {B}=\{v_1,v_2,\ldots ,v_n\}$
, see [Reference Kleidman and Liebeck5, Proposition 4.2.15]. Moreover, by [Reference Bray, Holt and Roney-Dougal1, Tables 8.58 and 8.74] and [Reference Kleidman and Liebeck5, Proposition 4.5.8], the order of M divides
$\mathcal {B}=\{v_1,v_2,\ldots ,v_n\}$
, see [Reference Kleidman and Liebeck5, Proposition 4.2.15]. Moreover, by [Reference Bray, Holt and Roney-Dougal1, Tables 8.58 and 8.74] and [Reference Kleidman and Liebeck5, Proposition 4.5.8], the order of M divides
![]() $2^{n-1}|\mathrm {Sym}(n)|$
. In particular, any prime divisor
$2^{n-1}|\mathrm {Sym}(n)|$
. In particular, any prime divisor
![]() $\varrho $
of
$\varrho $
of
![]() $|H|$
should satisfy
$|H|$
should satisfy
![]() $\varrho \leq n$
. If we can show that
$\varrho \leq n$
. If we can show that
![]() $e_1\in \mathcal {B}$
, we easily get a contradiction. Indeed, from
$e_1\in \mathcal {B}$
, we easily get a contradiction. Indeed, from
![]() $e_1 \in \mathcal {B}$
, it follows that
$e_1 \in \mathcal {B}$
, it follows that
![]() $e_i \in \mathcal {B}$
for all
$e_i \in \mathcal {B}$
for all
![]() $1\leq i \leq n-3$
(see Lemma 3.1). Hence, we may assume
$1\leq i \leq n-3$
(see Lemma 3.1). Hence, we may assume
![]() ${v_i=e_i}$
for
${v_i=e_i}$
for
![]() ${1\leq i\leq n-3}$
. In particular,
${1\leq i\leq n-3}$
. In particular,
![]() $e_{n-3}\in \mathcal {B}$
. As
$e_{n-3}\in \mathcal {B}$
. As
![]() $ye_{n-3}= -2 e_{n-2}-e_{n-3}$
is not an element of
$ye_{n-3}= -2 e_{n-2}-e_{n-3}$
is not an element of
![]() $\langle e_i \mid 1\leq i \leq n-3\rangle $
,
$\langle e_i \mid 1\leq i \leq n-3\rangle $
,
![]() $ye_{n-3}$
should be orthogonal to
$ye_{n-3}$
should be orthogonal to
![]() $v_{n-3}$
obtaining the contradiction
$v_{n-3}$
obtaining the contradiction
![]() $v_{n-3}^{\mathsf {T}} J y e_{n-3} =e_{n-3}^{\mathsf {T}} J y e_{n-3}= -1\neq 0$
.
$v_{n-3}^{\mathsf {T}} J y e_{n-3} =e_{n-3}^{\mathsf {T}} J y e_{n-3}= -1\neq 0$
.
So, we now show that
![]() $e_1\in \mathcal {B}$
. To this purpose, note that if
$e_1\in \mathcal {B}$
. To this purpose, note that if
![]() $\mathrm {tr} (h)\neq 0$
, then h must fix at least one
$\mathrm {tr} (h)\neq 0$
, then h must fix at least one
![]() $\langle v_j\rangle $
. Moreover, given
$\langle v_j\rangle $
. Moreover, given
![]() $h\in H$
of order k,
$h\in H$
of order k,
![]() $h\langle v_j\rangle =\langle v_j\rangle $
implies
$h\langle v_j\rangle =\langle v_j\rangle $
implies
![]() $h v_j=\lambda v_j$
, with
$h v_j=\lambda v_j$
, with
![]() $\lambda =\pm 1$
. So, consider the permutation
$\lambda =\pm 1$
. So, consider the permutation
![]() $\zeta $
induced by h on the
$\zeta $
induced by h on the
![]() $\langle v_i\rangle $
. If
$\langle v_i\rangle $
. If
![]() $\zeta ^b$
acts as the identity on
$\zeta ^b$
acts as the identity on
![]() $\{\langle v_1\rangle ,\langle v_2\rangle , \ldots , \langle v_n\rangle \}$
for some
$\{\langle v_1\rangle ,\langle v_2\rangle , \ldots , \langle v_n\rangle \}$
for some
![]() $b\geq 1$
, then
$b\geq 1$
, then
![]() $h^b v_i = \pm v_i$
for every i. It follows that
$h^b v_i = \pm v_i$
for every i. It follows that
![]() $\zeta $
has order k or
$\zeta $
has order k or
![]() ${k}/{2}$
. In particular, if h has odd order, it permutes
${k}/{2}$
. In particular, if h has odd order, it permutes
![]() $\mathcal {B}$
and its cycle structure is determined by its rational canonical form. Also, if
$\mathcal {B}$
and its cycle structure is determined by its rational canonical form. Also, if
![]() $h\in H$
does not have the eigenvalue
$h\in H$
does not have the eigenvalue
![]() $-1$
, from
$-1$
, from
![]() $h\langle v_j\rangle =\langle v_j\rangle $
, we get
$h\langle v_j\rangle =\langle v_j\rangle $
, we get
![]() $hv_j=v_j$
. Clearly, this applies to
$hv_j=v_j$
. Clearly, this applies to
![]() $h=y$
. Since y has order
$h=y$
. Since y has order
![]() $3$
, setting
$3$
, setting
![]() $r=0$
if
$r=0$
if
![]() $n=9$
,
$n=9$
,
![]() $r=1$
if
$r=1$
if
![]() $n=13$
and
$n=13$
and
![]() $r=2$
if
$r=2$
if
![]() $n \in \{11,17\}$
, y fixes
$n \in \{11,17\}$
, y fixes
![]() $v_j$
for
$v_j$
for
![]() $1\leq j\leq r$
and permutes the remaining vectors
$1\leq j\leq r$
and permutes the remaining vectors
![]() $v_j$
in
$v_j$
in
![]() $({n-r})/{3}$
orbits of length
$({n-r})/{3}$
orbits of length
![]() $3$
.
$3$
.
Case
![]() $n=11,13,17$
. Call s the number of vectors
$n=11,13,17$
. Call s the number of vectors
![]() $u_j=e_j+ y e_j+y^2 e_j$
, with
$u_j=e_j+ y e_j+y^2 e_j$
, with
![]() $ye_j\neq e_j$
, fixed by y. Then, any
$ye_j\neq e_j$
, fixed by y. Then, any
![]() $v_1 \in V_1(y)$
can be written as
$v_1 \in V_1(y)$
can be written as
 $$ \begin{align*}v_1=\sum\limits_{i=1}^r \alpha_i e_i+ \sum\limits_{j=1}^s \beta_j u_j.\end{align*} $$
$$ \begin{align*}v_1=\sum\limits_{i=1}^r \alpha_i e_i+ \sum\limits_{j=1}^s \beta_j u_j.\end{align*} $$
Substituting
![]() $e_i$
by
$e_i$
by
![]() $\lambda _i e_i$
and
$\lambda _i e_i$
and
![]() $u_j$
by
$u_j$
by
![]() $\mu _j u_j$
if necessary, we may assume that all the coefficients
$\mu _j u_j$
if necessary, we may assume that all the coefficients
![]() $\alpha _i,\beta _j$
are in
$\alpha _i,\beta _j$
are in
![]() $\{0,1\}$
. Since y fixes
$\{0,1\}$
. Since y fixes
![]() $v_1$
, by the transitivity of H on the subspaces generated by the vectors of
$v_1$
, by the transitivity of H on the subspaces generated by the vectors of
![]() $\mathcal {B}$
, due to its irreducibility, we may also assume
$\mathcal {B}$
, due to its irreducibility, we may also assume
![]() $v_3=x v_1$
,
$v_3=x v_1$
,
![]() $v_4=yv_3$
,
$v_4=yv_3$
,
![]() $v_5 = y v_4$
and
$v_5 = y v_4$
and
![]() $v_6= x v_5$
. Imposing
$v_6= x v_5$
. Imposing
![]() $v_1^{\mathsf {T}} Jv_3=v_j^{\mathsf {T}} J v_6=0$
for all
$v_1^{\mathsf {T}} Jv_3=v_j^{\mathsf {T}} J v_6=0$
for all
![]() $j\in \{1,4,5\}$
, we get
$j\in \{1,4,5\}$
, we get
![]() $v_1\in \{e_1,\ldots ,e_r\}$
, unless
$v_1\in \{e_1,\ldots ,e_r\}$
, unless
![]() $n \in \{11,17\}$
,
$n \in \{11,17\}$
,
![]() $q=3$
and
$q=3$
and
![]() $a=-1$
. In these exceptional cases, by direct computation, the order of
$a=-1$
. In these exceptional cases, by direct computation, the order of
![]() $(xy)^2 x y^2$
is divisible by a prime
$(xy)^2 x y^2$
is divisible by a prime
![]() $\varrho \geq 41$
, which is a contradiction as
$\varrho \geq 41$
, which is a contradiction as
![]() $\varrho $
does not divide
$\varrho $
does not divide
![]() $|\mathrm {Sym}(n)|$
,
$|\mathrm {Sym}(n)|$
,
![]() $n\leq 17$
(see the beginning of the proof).
$n\leq 17$
(see the beginning of the proof).
Case
![]() $n=9$
. Take
$n=9$
. Take
![]() $h=[x,y]$
and suppose
$h=[x,y]$
and suppose
![]() $a^2-a-1\neq 0$
. Then
$a^2-a-1\neq 0$
. Then
![]() $V_1([x,y])=\langle e_1\rangle $
. We have
$V_1([x,y])=\langle e_1\rangle $
. We have
 $$ \begin{align*}\mathrm{tr} (h)=\frac{(a^2+1)^2}{a^2} \quad \textrm{and} \quad \chi_h(-1)= \frac{-8(a^2+a+1)^2}{a^2}.\end{align*} $$
$$ \begin{align*}\mathrm{tr} (h)=\frac{(a^2+1)^2}{a^2} \quad \textrm{and} \quad \chi_h(-1)= \frac{-8(a^2+a+1)^2}{a^2}.\end{align*} $$
It follows
![]() $e_1\in \mathcal {B}$
unless, possibly, when
$e_1\in \mathcal {B}$
unless, possibly, when
![]() $a^2+1=0$
or
$a^2+1=0$
or
![]() $a^2+a+1=0$
. As previously remarked, the order of any element of M, and hence a fortiori of H, if odd must belong to the set
$a^2+a+1=0$
. As previously remarked, the order of any element of M, and hence a fortiori of H, if odd must belong to the set
![]() $\{ 1, 3, 5, 7, 9, 15 \}$
, and if prime must belong to
$\{ 1, 3, 5, 7, 9, 15 \}$
, and if prime must belong to
![]() $\{2,3,5,7\}$
. Assume
$\{2,3,5,7\}$
. Assume
![]() $a^2+1=0$
. If
$a^2+1=0$
. If
![]() $p\neq 5$
, we may take
$p\neq 5$
, we may take
![]() $h=[x,y]^2$
, as
$h=[x,y]^2$
, as
![]() $V_1(h)=\langle e_1\rangle $
and
$V_1(h)=\langle e_1\rangle $
and
![]() $\mathrm {tr}(h)=-4a - 2\neq 0$
. If
$\mathrm {tr}(h)=-4a - 2\neq 0$
. If
![]() $q=5$
, then
$q=5$
, then
![]() $a=2$
and
$a=2$
and
![]() $[x,y]$
has order
$[x,y]$
has order
![]() $156=2^2\cdot 3 \cdot 13$
, which is a contradiction. So, assume
$156=2^2\cdot 3 \cdot 13$
, which is a contradiction. So, assume
![]() ${a^2+a+1=0}$
. If
${a^2+a+1=0}$
. If
![]() $p\neq 3$
, the permutation induced by
$p\neq 3$
, the permutation induced by
![]() $xy$
on the
$xy$
on the
![]() $\langle v_i\rangle $
has order divisible by
$\langle v_i\rangle $
has order divisible by
![]() $21$
, which is a contradiction. If
$21$
, which is a contradiction. If
![]() $q=3$
, then
$q=3$
, then
![]() $a=1$
and
$a=1$
and
![]() $[x,y]^3y$
has order
$[x,y]^3y$
has order
![]() $41$
, which is a contradiction.
$41$
, which is a contradiction.
Lemma 3.5. Assume
![]() $n=9$
. If the group H is absolutely irreducible, then it is neither contained in a maximal subgroup in class
$n=9$
. If the group H is absolutely irreducible, then it is neither contained in a maximal subgroup in class
![]() $\mathcal {C}_2$
of
$\mathcal {C}_2$
of
![]() $\Omega _9(q)$
nor contained in any maximal subgroup in class
$\Omega _9(q)$
nor contained in any maximal subgroup in class
![]() $\mathcal {C}_7$
.
$\mathcal {C}_7$
.
Proof. For the sake of contradiction, suppose that H is imprimitive. By Lemma 3.4, we may assume
![]() $H\leq M\cong \Omega _3(q)^3. 2^4. \mathrm {Sym}(3)$
, where M permutes a decomposition
$H\leq M\cong \Omega _3(q)^3. 2^4. \mathrm {Sym}(3)$
, where M permutes a decomposition
![]() ${\mathbb {F}_q^9 = W_1 \oplus W_2 \oplus W_3}$
, with
${\mathbb {F}_q^9 = W_1 \oplus W_2 \oplus W_3}$
, with
![]() $\dim (W_i)=3$
. Set
$\dim (W_i)=3$
. Set
![]() $h=(xy)^7$
and
$h=(xy)^7$
and
![]() $N=\Omega _3(q)^3$
. From
$N=\Omega _3(q)^3$
. From
![]() $\dim (V_1(h))=7$
, we get
$\dim (V_1(h))=7$
, we get
![]() $V_1(h)\cap W_i\neq \{0\}$
, whence
$V_1(h)\cap W_i\neq \{0\}$
, whence
![]() $hW_i=W_i$
for each
$hW_i=W_i$
for each
![]() $i=1,2,3$
. It follows that
$i=1,2,3$
. It follows that
![]() $(xy)^7 \in N$
. Since
$(xy)^7 \in N$
. Since
![]() $7$
is coprime to the index of N in M, we get
$7$
is coprime to the index of N in M, we get
![]() $xy \in N$
. Since y acts as a
$xy \in N$
. Since y acts as a
![]() $3$
-cycle on
$3$
-cycle on
![]() $\{W_1,W_2,W_3\}$
, it follows that the elements
$\{W_1,W_2,W_3\}$
, it follows that the elements
![]() $(xy)^iy$
,
$(xy)^iy$
,
![]() $1\leq i\leq 7$
, have trace equal to zero. Thus,
$1\leq i\leq 7$
, have trace equal to zero. Thus,
![]() $0=\mathrm {tr}(xy^2)=-(a+a^{-1})$
gives the condition
$0=\mathrm {tr}(xy^2)=-(a+a^{-1})$
gives the condition
![]() $a^2+1=0$
. In this case,
$a^2+1=0$
. In this case,
![]() $\mathrm {tr}((xy)^3y)=1$
, which is a contradiction.
$\mathrm {tr}((xy)^3y)=1$
, which is a contradiction.
Now, suppose that H is contained in a maximal subgroup M in class
![]() $\mathcal {C}_7$
of
$\mathcal {C}_7$
of
![]() $\Omega _n(q)$
. By [Reference Bray, Holt and Roney-Dougal1, Table 8.58],
$\Omega _n(q)$
. By [Reference Bray, Holt and Roney-Dougal1, Table 8.58],
![]() $M\cong \Omega _3(q)^2.[4]$
. Then,
$M\cong \Omega _3(q)^2.[4]$
. Then,
![]() $h=(xy)^7$
belongs to
$h=(xy)^7$
belongs to
![]() $\Omega _3(q)^2$
. Suppose first that
$\Omega _3(q)^2$
. Suppose first that
![]() $xy$
is semisimple. Up to conjugation,
$xy$
is semisimple. Up to conjugation,
![]() $h=\mathrm {diag}(\beta _1,1,\beta _1^{-1})\otimes \mathrm {diag}(\beta _2, 1, \beta _2^{-1})$
for some
$h=\mathrm {diag}(\beta _1,1,\beta _1^{-1})\otimes \mathrm {diag}(\beta _2, 1, \beta _2^{-1})$
for some
![]() $\beta _1,\beta _2 \in \mathbb {F}_q^*$
. In order that it has the eigenvalue
$\beta _1,\beta _2 \in \mathbb {F}_q^*$
. In order that it has the eigenvalue
![]() $1$
with multiplicity (at least)
$1$
with multiplicity (at least)
![]() $7$
, we need
$7$
, we need
![]() $\beta _1=\beta _2=1$
, which gives
$\beta _1=\beta _2=1$
, which gives
![]() $h=\mathrm {I}_9$
, which is a contradiction. Finally, assume that
$h=\mathrm {I}_9$
, which is a contradiction. Finally, assume that
![]() $xy$
has order divisible by p. Up to conjugation and because of (2.1),
$xy$
has order divisible by p. Up to conjugation and because of (2.1),
 $$ \begin{align*}h=\begin{pmatrix} 1 & 1 & 1 \\ 0 & 1 & 2 \\ 0 & 0 & 1 \end{pmatrix} \otimes \begin{pmatrix} \beta & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & \beta^{-1} \end{pmatrix}, \quad \beta\in \mathbb{F}_q^*.\end{align*} $$
$$ \begin{align*}h=\begin{pmatrix} 1 & 1 & 1 \\ 0 & 1 & 2 \\ 0 & 0 & 1 \end{pmatrix} \otimes \begin{pmatrix} \beta & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & \beta^{-1} \end{pmatrix}, \quad \beta\in \mathbb{F}_q^*.\end{align*} $$
Hence,
![]() $\chi _{h}(t)=(t-1)^3(t-\beta )^3(t-\beta ^{-1})^3$
. Since h is a bireflection (that is,
$\chi _{h}(t)=(t-1)^3(t-\beta )^3(t-\beta ^{-1})^3$
. Since h is a bireflection (that is,
![]() ${\dim (V_1(h))=7}$
), we must have
${\dim (V_1(h))=7}$
), we must have
![]() $\beta =1$
, in which case
$\beta =1$
, in which case
![]() $\dim (V_1(h))=3$
, which is a contradiction.
$\dim (V_1(h))=3$
, which is a contradiction.
Lemma 3.6. If H is absolutely irreducible, then the H-module
![]() $V=\mathbb {F}^{n}$
is not the deleted permutation module of degree
$V=\mathbb {F}^{n}$
is not the deleted permutation module of degree
![]() $\ell =n+1, n+2$
.
$\ell =n+1, n+2$
.
Proof. Assume the contrary. From what is seen at the end of Section 2, up to conjugation, we may assume
![]() $H\leq \mathrm {Sym}(\ell )\leq \mathrm {GL}_\ell (p)$
, with
$H\leq \mathrm {Sym}(\ell )\leq \mathrm {GL}_\ell (p)$
, with
![]() $\ell = n +1, n + 2$
.
$\ell = n +1, n + 2$
.
Case
![]() $\ell =n+1$
. Fix
$\ell =n+1$
. Fix
![]() $h \in H$
such that
$h \in H$
such that
![]() $\dim (V_1(h))=1$
and call
$\dim (V_1(h))=1$
and call
![]() $\zeta $
its preimage in
$\zeta $
its preimage in
![]() $\mathrm {Sym}(\ell )\leq \mathrm {GL}_\ell (p)$
. Then,
$\mathrm {Sym}(\ell )\leq \mathrm {GL}_\ell (p)$
. Then,
![]() $\zeta $
has at most two orbits. It follows that
$\zeta $
has at most two orbits. It follows that
![]() $\mathrm {tr}(\zeta )=0$
if
$\mathrm {tr}(\zeta )=0$
if
![]() $\zeta $
is an
$\zeta $
is an
![]() $\ell $
-cycle or the product of two cycles of length at least two. Otherwise,
$\ell $
-cycle or the product of two cycles of length at least two. Otherwise,
![]() $\mathrm {tr}(\zeta )=1$
and
$\mathrm {tr}(\zeta )=1$
and
![]() $\zeta $
is a cycle of length
$\zeta $
is a cycle of length
![]() $\ell -1$
. Note that
$\ell -1$
. Note that
![]() $\zeta $
and h have the same order.
$\zeta $
and h have the same order.
We may take
![]() $h=xy$
, as
$h=xy$
, as
![]() $\dim (V_1(xy))=1$
. Hence,
$\dim (V_1(xy))=1$
. Hence,
![]() $\mathrm {tr}(\zeta )-1=\mathrm {tr}(xy)=-(a+a^{-1})$
gives the following two cases: if
$\mathrm {tr}(\zeta )-1=\mathrm {tr}(xy)=-(a+a^{-1})$
gives the following two cases: if
![]() $\mathrm {tr}(\zeta )=0$
, then
$\mathrm {tr}(\zeta )=0$
, then
![]() $a^2-a+1=0$
; if
$a^2-a+1=0$
; if
![]() $\mathrm {tr}(\zeta )=1$
, then
$\mathrm {tr}(\zeta )=1$
, then
![]() $a^2+1=0$
. In the second case, the characteristic polynomial
$a^2+1=0$
. In the second case, the characteristic polynomial
![]() $\chi _{xy}(t)$
is divisible by
$\chi _{xy}(t)$
is divisible by
![]() $t^2+1$
, and then
$t^2+1$
, and then
![]() $xy$
has order divisible by
$xy$
has order divisible by
![]() $4$
. However,
$4$
. However,
![]() $\zeta $
has odd order n, being an n-cycle, which is a contradiction.
$\zeta $
has odd order n, being an n-cycle, which is a contradiction.
So, assume
![]() $a^2-a+1=0$
. In this case,
$a^2-a+1=0$
. In this case,
![]() $t^2+t+1$
divides
$t^2+t+1$
divides
![]() $\chi _{xy}(t)$
and hence the order of
$\chi _{xy}(t)$
and hence the order of
![]() $\zeta $
is divisible by
$\zeta $
is divisible by
![]() $3$
. Furthermore,
$3$
. Furthermore,
![]() $(xy)^{n-2}$
has order p when
$(xy)^{n-2}$
has order p when
![]() $n\in \{11,17\}$
. For
$n\in \{11,17\}$
. For
![]() $n=11$
, we get that the order of
$n=11$
, we get that the order of
![]() $\zeta $
is
$\zeta $
is
![]() $6$
,
$6$
,
![]() $9$
or
$9$
or
![]() $12$
, in contrast with
$12$
, in contrast with
![]() $(xy)^9$
of odd order p. For
$(xy)^9$
of odd order p. For
![]() $n=17$
, the order of
$n=17$
, the order of
![]() $\zeta $
is
$\zeta $
is
![]() $9$
,
$9$
,
![]() $12$
,
$12$
,
![]() $15$
or
$15$
or
![]() $18$
. However,
$18$
. However,
![]() $(xy)^9\neq \mathrm {I}_{17}$
and the other values are in contrast with
$(xy)^9\neq \mathrm {I}_{17}$
and the other values are in contrast with
![]() $(xy)^{15}$
of odd order p. For
$(xy)^{15}$
of odd order p. For
![]() $n\in \{9,13\}$
, we apply the previous argument to other elements h such that
$n\in \{9,13\}$
, we apply the previous argument to other elements h such that
![]() $\dim (V_1(h))=1$
. For
$\dim (V_1(h))=1$
. For
![]() $n=9$
, we take
$n=9$
, we take
![]() $h=[x,y]$
whose trace is equal to
$h=[x,y]$
whose trace is equal to
![]() $1$
, which is a contradiction. For
$1$
, which is a contradiction. For
![]() $n=13$
, we take
$n=13$
, we take
![]() $h= (xy^2)^2xy$
, which has trace equal to
$h= (xy^2)^2xy$
, which has trace equal to
![]() $3$
. Since
$3$
. Since
![]() $\mathrm {tr}(h)=\mathrm {tr}(\zeta )-1 \in \{-1,0\}$
, we get an absurdity unless
$\mathrm {tr}(h)=\mathrm {tr}(\zeta )-1 \in \{-1,0\}$
, we get an absurdity unless
![]() $p=3$
. However, in this case,
$p=3$
. However, in this case,
![]() $a=-1$
and
$a=-1$
and
![]() $h^8$
has order
$h^8$
has order
![]() $41$
, which is a contradiction as
$41$
, which is a contradiction as
![]() $h^8\in H\leq \mathrm {Sym}(14)$
.
$h^8\in H\leq \mathrm {Sym}(14)$
.
Case
![]() $\ell =n+2$
. In this case,
$\ell =n+2$
. In this case,
![]() $q \mid \ell $
, and hence we need to consider only the following cases: (a)
$q \mid \ell $
, and hence we need to consider only the following cases: (a)
![]() $(n,q)=(9,11)$
; (b)
$(n,q)=(9,11)$
; (b)
![]() $(n,q)=(11,13)$
; (c)
$(n,q)=(11,13)$
; (c)
![]() $(n,q)=(13,3)$
; (d)
$(n,q)=(13,3)$
; (d)
![]() $(n,q)=(13,5)$
; (e)
$(n,q)=(13,5)$
; (e)
![]() $(n,q)=(17,19)$
. Take
$(n,q)=(17,19)$
. Take
![]() $g=(xy)^3 (xy^2)^7$
in case (a);
$g=(xy)^3 (xy^2)^7$
in case (a);
![]() $g= xy (xy^2)^2$
in cases (b), (c) and (e); and
$g= xy (xy^2)^2$
in cases (b), (c) and (e); and
![]() $g= xy (xy^2)^3$
in case (d). By direct computation, in all these cases, the order of g is divisible by a prime
$g= xy (xy^2)^3$
in case (d). By direct computation, in all these cases, the order of g is divisible by a prime
![]() $\varrho \geq n+4$
, which is a contradiction as
$\varrho \geq n+4$
, which is a contradiction as
![]() $\varrho $
should divide
$\varrho $
should divide
![]() $|\mathrm {Sym}(n+2)|$
.
$|\mathrm {Sym}(n+2)|$
.
Theorem 3.7. Suppose
![]() $n \in \{9,11,13,17\}$
and let
$n \in \{9,11,13,17\}$
and let
![]() $a \in \mathbb {F}_q^*$
be such that:
$a \in \mathbb {F}_q^*$
be such that:
-
(i)
 $\mathbb {F}_p[a]=\mathbb {F}_q$
;
$\mathbb {F}_p[a]=\mathbb {F}_q$
; -
(ii)
 $ -a\in (\mathbb {F}_q^\ast )^2$
;
$ -a\in (\mathbb {F}_q^\ast )^2$
; -
(iii)
 $\begin {cases} a^2-a-1\neq 0 & \textrm { if } n=9; \\ (a-1)(a^3+2a^2+a+1)\neq 0 & \textrm { if } n=11; \\ a^4+a^2-a+1 \neq 0 & \textrm { if } n=17. \end {cases}$
$\begin {cases} a^2-a-1\neq 0 & \textrm { if } n=9; \\ (a-1)(a^3+2a^2+a+1)\neq 0 & \textrm { if } n=11; \\ a^4+a^2-a+1 \neq 0 & \textrm { if } n=17. \end {cases}$
Then,
![]() $H=\Omega _{n}(q)$
. In particular,
$H=\Omega _{n}(q)$
. In particular,
![]() $\Omega _{n}(q)$
is
$\Omega _{n}(q)$
is
![]() $(2,3)$
-generated for any odd q.
$(2,3)$
-generated for any odd q.
Proof. By condition (ii), H is a subgroup of
![]() $\Omega _{n}(q)$
. By condition (iii), Lemmas 3.2, 3.4 and 3.5, the group H is absolutely irreducible and is neither contained in a maximal subgroup in class
$\Omega _{n}(q)$
. By condition (iii), Lemmas 3.2, 3.4 and 3.5, the group H is absolutely irreducible and is neither contained in a maximal subgroup in class
![]() $\mathcal {C}_2$
of
$\mathcal {C}_2$
of
![]() $\Omega _n(q)$
nor contained in any maximal subgroup in class
$\Omega _n(q)$
nor contained in any maximal subgroup in class
![]() $\mathcal {C}_7$
. Since it contains the bireflection
$\mathcal {C}_7$
. Since it contains the bireflection
![]() $(xy)^{n-2}$
, we can apply [Reference Guralnick and Saxl3, Theorem 7.1] which, combined with condition (i) and Lemma 3.3, gives two possibilities: (a) H is an alternating or symmetric group of degree
$(xy)^{n-2}$
, we can apply [Reference Guralnick and Saxl3, Theorem 7.1] which, combined with condition (i) and Lemma 3.3, gives two possibilities: (a) H is an alternating or symmetric group of degree
![]() $\ell $
and
$\ell $
and
![]() $\mathbb {F}^n$
is the deleted permutation module of dimension
$\mathbb {F}^n$
is the deleted permutation module of dimension
![]() $\ell -1$
or
$\ell -1$
or
![]() $\ell -2$
; (b)
$\ell -2$
; (b)
![]() $H=\Omega _{n}(q)$
. Case (a) is excluded by Lemma 3.6: we conclude that
$H=\Omega _{n}(q)$
. Case (a) is excluded by Lemma 3.6: we conclude that
![]() $H=\Omega _{n}(q)$
.
$H=\Omega _{n}(q)$
.
Finally, we have to prove that there exists an element a satisfying all the requirements. If
![]() $q=p$
, take
$q=p$
, take
![]() $a=-1$
. Suppose now
$a=-1$
. Suppose now
![]() $q=p^f$
with
$q=p^f$
with
![]() $f\geq 2$
, and let
$f\geq 2$
, and let
![]() $\mathcal {N}(q)$
be the number of elements
$\mathcal {N}(q)$
be the number of elements
![]() $b\in \mathbb {F}_q^*$
such that
$b\in \mathbb {F}_q^*$
such that
![]() $\mathbb {F}_p[b]\neq \mathbb {F}_q$
. By [Reference Pellegrini, Tamburini Bellani and Vsemirnov12], we have
$\mathbb {F}_p[b]\neq \mathbb {F}_q$
. By [Reference Pellegrini, Tamburini Bellani and Vsemirnov12], we have
![]() $\mathcal {N}(q)\leq p({p^{\lfloor f/2 \rfloor }-1})/({p-1})$
, and hence it suffices to check when
$\mathcal {N}(q)\leq p({p^{\lfloor f/2 \rfloor }-1})/({p-1})$
, and hence it suffices to check when
![]() $({p^f-1})/{2} - p({p^{\lfloor f/2 \rfloor }-1})/({p-1})> 4$
. This condition is fulfilled unless
$({p^f-1})/{2} - p({p^{\lfloor f/2 \rfloor }-1})/({p-1})> 4$
. This condition is fulfilled unless
![]() $q=3^2$
. So, assume
$q=3^2$
. So, assume
![]() $q=9$
and take
$q=9$
and take
![]() $a\in \mathbb {F}_9^*$
whose minimal polynomial over
$a\in \mathbb {F}_9^*$
whose minimal polynomial over
![]() $\mathbb {F}_3$
is
$\mathbb {F}_3$
is
![]() $t^2+1$
. Then,
$t^2+1$
. Then,
![]() $\mathbb {F}_3[a]=\mathbb {F}_9$
and
$\mathbb {F}_3[a]=\mathbb {F}_9$
and
![]() $-a=(a+1)^2$
is a square.
$-a=(a+1)^2$
is a square.
4 Generators for
 $n\in \{12,15,16\}$
and for
$n\in \{12,15,16\}$
and for
 $n\geq 18$
$n\geq 18$
For
![]() $n\in \{12,15,16\}$
and for
$n\in \{12,15,16\}$
and for
![]() $n\geq 18$
, write
$n\geq 18$
, write
![]() $n=3m+9+r$
, with
$n=3m+9+r$
, with
![]() $m\geq 1$
and
$m\geq 1$
and
![]() ${r \in \{0,1,2\}}$
. Take the symmetric bilinear form corresponding to the Gram matrix
${r \in \{0,1,2\}}$
. Take the symmetric bilinear form corresponding to the Gram matrix
![]() ${J=\bigg (\begin {smallmatrix} \mathrm {I}_{n-8} & 0 & 0\\ 0 & 0 & \mathrm {I}_4 \\ 0 & \mathrm {I}_4 & 0 \end {smallmatrix}\bigg )}$
, having
${J=\bigg (\begin {smallmatrix} \mathrm {I}_{n-8} & 0 & 0\\ 0 & 0 & \mathrm {I}_4 \\ 0 & \mathrm {I}_4 & 0 \end {smallmatrix}\bigg )}$
, having
![]() $\det (J)=1$
. For any
$\det (J)=1$
. For any
![]() $a\in \mathbb {F}_q^*$
, we define four matrices
$a\in \mathbb {F}_q^*$
, we define four matrices
![]() $x_1,x_2,y_1,y_2$
of
$x_1,x_2,y_1,y_2$
of
![]() $\mathrm {GL}_n(q)$
as follows.
$\mathrm {GL}_n(q)$
as follows.
-
(x 1)
 $x_1$
acts on
$x_1$
acts on
 $\mathscr {C}$
as the product
$\mathscr {C}$
as the product
 $\nu _1\nu _2$
of the following two disjoint permutations: and
$\nu _1\nu _2$
of the following two disjoint permutations: and $$ \begin{align*}\nu_1=\begin{cases} \mathsf{id} & \textrm{if } r=0 \textrm{ and } n \textrm{ is odd},\\[-1pt] (e_1,e_2) & \textrm{if } r=0 \textrm{ and } n \textrm{ is even},\\[-1pt] (e_1,e_2) & \textrm{if } r=1 \textrm{ and } n \textrm{ is odd},\\[-1pt] (e_1,e_2)(e_3,e_6) & \textrm{if } r=1 \textrm{ and } n \textrm{ is even},\\[-1pt] (e_1,e_3)(e_2,e_4) & \textrm{if } r=2 \textrm{ and } n \textrm{ is odd},\\[-1pt] (e_1,e_3)(e_2,e_4)(e_7,e_{10}) & \textrm{if } r=2 \textrm{ and } n \textrm{ is even}, \end{cases}\end{align*} $$
$$ \begin{align*}\nu_1=\begin{cases} \mathsf{id} & \textrm{if } r=0 \textrm{ and } n \textrm{ is odd},\\[-1pt] (e_1,e_2) & \textrm{if } r=0 \textrm{ and } n \textrm{ is even},\\[-1pt] (e_1,e_2) & \textrm{if } r=1 \textrm{ and } n \textrm{ is odd},\\[-1pt] (e_1,e_2)(e_3,e_6) & \textrm{if } r=1 \textrm{ and } n \textrm{ is even},\\[-1pt] (e_1,e_3)(e_2,e_4) & \textrm{if } r=2 \textrm{ and } n \textrm{ is odd},\\[-1pt] (e_1,e_3)(e_2,e_4)(e_7,e_{10}) & \textrm{if } r=2 \textrm{ and } n \textrm{ is even}, \end{cases}\end{align*} $$
 $$ \begin{align*}\nu_2= \prod_{j=0}^{m-1} (e_{3j+r+3},e_{3j+r+4})=(e_{r+3},e_{r+4})(e_{r+6},e_{r+7})\cdots (e_{n-9},e_{n-8}).\end{align*} $$
$$ \begin{align*}\nu_2= \prod_{j=0}^{m-1} (e_{3j+r+3},e_{3j+r+4})=(e_{r+3},e_{r+4})(e_{r+6},e_{r+7})\cdots (e_{n-9},e_{n-8}).\end{align*} $$
-
(x 2)
 $x_2=\mathrm {diag}(\mathrm {I}_{n-9},\tilde x)$
, where
$x_2=\mathrm {diag}(\mathrm {I}_{n-9},\tilde x)$
, where
 $\tilde x=\tilde x(a)$
is as in Figure 2.
$\tilde x=\tilde x(a)$
is as in Figure 2.
Figure 2 Alternative generators of
 $\Omega _9(q)$
.
$\Omega _9(q)$
. -
(y 1)
 $y_1$
acts on
$y_1$
acts on
 $\mathscr {C}$
as the permutation
$\mathscr {C}$
as the permutation  $$ \begin{align*} \nu_3& = \prod\limits_{j=0}^{m-1} (e_{3j+r+1},e_{3j+r+2},e_{3j+r+3})\\[-2pt] & = (e_{r+1},e_{r+2},e_{r+3})(e_{r+4},e_{r+5},e_{r+6})\cdots (e_{n-11}, e_{n-10}, e_{n-9}). \end{align*} $$
$$ \begin{align*} \nu_3& = \prod\limits_{j=0}^{m-1} (e_{3j+r+1},e_{3j+r+2},e_{3j+r+3})\\[-2pt] & = (e_{r+1},e_{r+2},e_{r+3})(e_{r+4},e_{r+5},e_{r+6})\cdots (e_{n-11}, e_{n-10}, e_{n-9}). \end{align*} $$
-
(y 2)
 $y_2=\mathrm {diag}(\mathrm {I}_{n-9},\tilde y)$
, where
$y_2=\mathrm {diag}(\mathrm {I}_{n-9},\tilde y)$
, where
 $\tilde y$
is as in Figure 2.
$\tilde y$
is as in Figure 2.
Let us identify
![]() $\mathrm {Sym}(n-8)$
with the group of permutation matrices fixing the set
$\mathrm {Sym}(n-8)$
with the group of permutation matrices fixing the set
![]() $\{e_j \mid 1\leq j\leq n-8\}$
and acting as the identity on
$\{e_j \mid 1\leq j\leq n-8\}$
and acting as the identity on
![]() $\langle e_{n-7},e_{n-6},\ldots ,e_n\rangle $
. The matrix
$\langle e_{n-7},e_{n-6},\ldots ,e_n\rangle $
. The matrix
![]() $x_1$
is the product of N transpositions in
$x_1$
is the product of N transpositions in
![]() $\mathrm {Sym}(n-8)$
, where N is as follows:
$\mathrm {Sym}(n-8)$
, where N is as follows:
 $$ \begin{align*} \begin{array}{l|lll} & r=0 & r=1 & r=2 \\ \hline n\ \text{even} & N=m+1 & N=m+2 & N=m+3 \\ n\ \text{odd} & N=m & N=m+1 & N=m+2 \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{l|lll} & r=0 & r=1 & r=2 \\ \hline n\ \text{even} & N=m+1 & N=m+2 & N=m+3 \\ n\ \text{odd} & N=m & N=m+1 & N=m+2 \end{array} \end{align*} $$
Now, n is odd if and only if m and r have the same parity. It follows that N is always even, whence
![]() $x_1 \in \mathrm {Alt}(n-8)\leq \Omega _n^\epsilon (q)$
. In particular,
$x_1 \in \mathrm {Alt}(n-8)\leq \Omega _n^\epsilon (q)$
. In particular,
![]() $x_1$
is an involution and the same is easily verified for
$x_1$
is an involution and the same is easily verified for
![]() $x_2$
. To see that
$x_2$
. To see that
![]() $x_2 \in \Omega _n^\epsilon (q)$
, note that
$x_2 \in \Omega _n^\epsilon (q)$
, note that
![]() $\tilde x=\mathrm {diag} (1,h,h^{-\mathsf {T}})$
with
$\tilde x=\mathrm {diag} (1,h,h^{-\mathsf {T}})$
with
![]() $h\in \mathrm {SL}_4(q)$
. Since
$h\in \mathrm {SL}_4(q)$
. Since
![]() $\mathrm {diag} (1,g,g^{-\mathsf {T}})\in \mathrm {SO}_9(q)$
for each
$\mathrm {diag} (1,g,g^{-\mathsf {T}})\in \mathrm {SO}_9(q)$
for each
![]() $g\in \mathrm {GL}_4(q)$
, we conclude that
$g\in \mathrm {GL}_4(q)$
, we conclude that
![]() $\tilde x$
is in
$\tilde x$
is in
![]() $\Omega _9(q)$
.
$\Omega _9(q)$
.
Clearly,
![]() $y_1$
and
$y_1$
and
![]() $y_2$
have order
$y_2$
have order
![]() $3$
and determinant
$3$
and determinant
![]() $1$
. Moreover,
$1$
. Moreover,
![]() $y_1\in \mathrm {Alt}(n-9)\le \Omega _n^\epsilon (q)$
and
$y_1\in \mathrm {Alt}(n-9)\le \Omega _n^\epsilon (q)$
and
![]() $y_2^{\mathsf {T}} J y_2 =J$
. Since
$y_2^{\mathsf {T}} J y_2 =J$
. Since
![]() $x_1x_2=x_2x_1$
and
$x_1x_2=x_2x_1$
and
![]() $y_1y_2=y_2y_1$
, we conclude that
$y_1y_2=y_2y_1$
, we conclude that
![]() $x=x_1x_2$
and
$x=x_1x_2$
and
![]() $y=y_1y_2$
have respective orders
$y=y_1y_2$
have respective orders
![]() $2$
and
$2$
and
![]() $3$
, and that
$3$
, and that
We also assume that
![]() $a\in \mathbb {F}_q^*$
is such that
$a\in \mathbb {F}_q^*$
is such that
![]() $\mathbb {F}_p[a]=\mathbb {F}_q$
.
$\mathbb {F}_p[a]=\mathbb {F}_q$
.
When
![]() $n\neq 12$
, we can decompose
$n\neq 12$
, we can decompose
![]() $\mathbb {F}_q^{n}$
into the direct sum of the following
$\mathbb {F}_q^{n}$
into the direct sum of the following
![]() $[x,y]$
-invariant subspaces. Take
$[x,y]$
-invariant subspaces. Take
 $$ \begin{align*}\mathcal{A}=\begin{cases} \langle e_1, e_3, e_4 \rangle & \textrm{if } n=15,\\ \langle e_1, e_5 \rangle \oplus \langle e_2, e_4 \rangle & \textrm{if } n=16,\\ \langle e_1, e_2, e_4, e_5 \rangle \oplus \langle e_3, e_7, e_8 \rangle & \textrm{if } n=19,\\ \langle e_1, e_2, e_6, e_8 \rangle \oplus \langle e_3, e_4, e_5,e_9 \rangle & \textrm{if } n=20,\\ \langle e_1,e_2,e_3,e_4,e_5,e_6,e_8,e_9\rangle \oplus \langle e_7,e_{11},e_{12}\rangle & \textrm{if } n= 23. \end{cases} \end{align*} $$
$$ \begin{align*}\mathcal{A}=\begin{cases} \langle e_1, e_3, e_4 \rangle & \textrm{if } n=15,\\ \langle e_1, e_5 \rangle \oplus \langle e_2, e_4 \rangle & \textrm{if } n=16,\\ \langle e_1, e_2, e_4, e_5 \rangle \oplus \langle e_3, e_7, e_8 \rangle & \textrm{if } n=19,\\ \langle e_1, e_2, e_6, e_8 \rangle \oplus \langle e_3, e_4, e_5,e_9 \rangle & \textrm{if } n=20,\\ \langle e_1,e_2,e_3,e_4,e_5,e_6,e_8,e_9\rangle \oplus \langle e_7,e_{11},e_{12}\rangle & \textrm{if } n= 23. \end{cases} \end{align*} $$
Otherwise,
 $$ \begin{align*}\mathcal{A} = \begin{cases} \langle e_1, e_2, e_3, e_4, e_6, e_7\rangle & \textrm{if } r=0,\\ \langle e_1, e_2, e_4, e_5 \rangle \oplus \langle e_3, e_6, e_7, e_8, e_{10}, e_{11} \rangle & \textrm{if } r=1,\\ \langle e_1,e_2,e_3,e_4,e_5,e_6,e_8,e_9\rangle \oplus \langle e_7,e_{10},e_{11},e_{12},e_{14},e_{15}\rangle & \textrm{if } r=2. \end{cases}\end{align*} $$
$$ \begin{align*}\mathcal{A} = \begin{cases} \langle e_1, e_2, e_3, e_4, e_6, e_7\rangle & \textrm{if } r=0,\\ \langle e_1, e_2, e_4, e_5 \rangle \oplus \langle e_3, e_6, e_7, e_8, e_{10}, e_{11} \rangle & \textrm{if } r=1,\\ \langle e_1,e_2,e_3,e_4,e_5,e_6,e_8,e_9\rangle \oplus \langle e_7,e_{10},e_{11},e_{12},e_{14},e_{15}\rangle & \textrm{if } r=2. \end{cases}\end{align*} $$
Moreover,
 $$ \begin{align*} \mathcal{B}& = \textstyle\bigoplus\limits_{j=0}^{m-4-r} \langle e_{5+4r+3j}, e_{9+4r+3j}, e_{10+4r+3j}\rangle, \\ \mathcal{C} &= \langle e_{n-13}, e_{n-10}, e_{n-9}, e_{n-8}, e_{n-7}, e_{n-6}, e_{n-5}, e_{n-4}, e_{n-3}, e_{n-2}, e_{n-1}, e_n \rangle. \end{align*} $$
$$ \begin{align*} \mathcal{B}& = \textstyle\bigoplus\limits_{j=0}^{m-4-r} \langle e_{5+4r+3j}, e_{9+4r+3j}, e_{10+4r+3j}\rangle, \\ \mathcal{C} &= \langle e_{n-13}, e_{n-10}, e_{n-9}, e_{n-8}, e_{n-7}, e_{n-6}, e_{n-5}, e_{n-4}, e_{n-3}, e_{n-2}, e_{n-1}, e_n \rangle. \end{align*} $$
Lemma 4.1. Assume
![]() $n\neq 12$
. Then,
$n\neq 12$
. Then,
![]() $([x,y]_{|{\mathcal A}})^{24}=\mathrm {I}$
and
$([x,y]_{|{\mathcal A}})^{24}=\mathrm {I}$
and
![]() $([x,y]_{|\mathcal B})^3=\mathrm {I}$
.
$([x,y]_{|\mathcal B})^3=\mathrm {I}$
.
Proof. For
![]() $n \in \{15,16, 19,20, 23\}$
, the element
$n \in \{15,16, 19,20, 23\}$
, the element
![]() $[x,y]$
acts on
$[x,y]$
acts on
![]() $\mathcal {A}$
as the following permutation:
$\mathcal {A}$
as the following permutation:
 $$ \begin{align*}\begin{cases} (e_3,e_4) & \textrm{if } n =15,\\ (e_1,e_5)(e_2,e_4) & \textrm{if } n =16,\\ (e_1,e_5,e_4,e_2) (e_3,e_8,e_7) & \textrm{if } n =19,\\ (e_1, e_6, e_8, e_2)(e_3, e_4,e_9,e_5) & \textrm{if } n=20,\\ (e_1,e_6,e_5,e_3,e_4,e_9,e_8,e_2)(e_7,e_{12},e_{11}) & \textrm{if } n =23. \end{cases} \end{align*} $$
$$ \begin{align*}\begin{cases} (e_3,e_4) & \textrm{if } n =15,\\ (e_1,e_5)(e_2,e_4) & \textrm{if } n =16,\\ (e_1,e_5,e_4,e_2) (e_3,e_8,e_7) & \textrm{if } n =19,\\ (e_1, e_6, e_8, e_2)(e_3, e_4,e_9,e_5) & \textrm{if } n=20,\\ (e_1,e_6,e_5,e_3,e_4,e_9,e_8,e_2)(e_7,e_{12},e_{11}) & \textrm{if } n =23. \end{cases} \end{align*} $$
Otherwise, it acts on
![]() $\mathcal {A}$
as
$\mathcal {A}$
as
 $$ \begin{align*}\begin{cases} (e_1,e_4,e_3,e_2,e_7,e_6) & \textrm{if } n\equiv 0 ~\mathrm{(mod~ 6)},\\ (e_1,e_5,e_4,e_2) (e_3,e_8,e_7)(e_6,e_{11},e_{10}) & \textrm{if } n \equiv 1 ~\mathrm{(mod~ 6)},\\ (e_1, e_6, e_8, e_2)(e_3, e_4,e_9,e_5) (e_7,e_{12},e_{11},e_{10},e_{15},e_{14}) & \textrm{if } n\equiv 2~\mathrm{(mod~ 6)},\\ (e_2,e_7,e_6)(e_3,e_4) & \textrm{if } n\equiv 3~\mathrm{(mod~ 6)},\\ (e_1,e_5)(e_2,e_4)(e_3,e_8,e_7,e_6, e_{11},e_{10}) & \textrm{if } n \equiv 4 ~\mathrm{(mod~ 6)},\\ (e_1,e_6,e_5,e_3,e_4,e_9,e_8,e_2)(e_7,e_{12},e_{11})(e_{10}, e_{15}, e_{14}) & \textrm{if } n \equiv 5 ~\mathrm{(mod~ 6)}. \end{cases} \end{align*} $$
$$ \begin{align*}\begin{cases} (e_1,e_4,e_3,e_2,e_7,e_6) & \textrm{if } n\equiv 0 ~\mathrm{(mod~ 6)},\\ (e_1,e_5,e_4,e_2) (e_3,e_8,e_7)(e_6,e_{11},e_{10}) & \textrm{if } n \equiv 1 ~\mathrm{(mod~ 6)},\\ (e_1, e_6, e_8, e_2)(e_3, e_4,e_9,e_5) (e_7,e_{12},e_{11},e_{10},e_{15},e_{14}) & \textrm{if } n\equiv 2~\mathrm{(mod~ 6)},\\ (e_2,e_7,e_6)(e_3,e_4) & \textrm{if } n\equiv 3~\mathrm{(mod~ 6)},\\ (e_1,e_5)(e_2,e_4)(e_3,e_8,e_7,e_6, e_{11},e_{10}) & \textrm{if } n \equiv 4 ~\mathrm{(mod~ 6)},\\ (e_1,e_6,e_5,e_3,e_4,e_9,e_8,e_2)(e_7,e_{12},e_{11})(e_{10}, e_{15}, e_{14}) & \textrm{if } n \equiv 5 ~\mathrm{(mod~ 6)}. \end{cases} \end{align*} $$
Finally,
![]() $[x,y]$
acts on each summand of
$[x,y]$
acts on each summand of
![]() $\mathcal B$
as the cycle
$\mathcal B$
as the cycle
![]() $(e_{5+4r+3j}, e_{10+4r+3j}, e_{9+4r+3j} )$
.
$(e_{5+4r+3j}, e_{10+4r+3j}, e_{9+4r+3j} )$
.
By Lemma 4.1 and direct computations (in particular, for
![]() $n=12$
), the element
$n=12$
), the element
![]() ${\tau =[x,y]^{24}}$
has characteristic polynomial
${\tau =[x,y]^{24}}$
has characteristic polynomial
![]() $(t-1)^{n}$
. More precisely, setting
$(t-1)^{n}$
. More precisely, setting
 $$ \begin{align*}\vartheta_0= \begin{pmatrix} 1 & 0& -4a & 0& -32a^2 & -36a^2 & -8a& -56a^2\\ 0 & 1& -4a & 0& -28a^2& -32a^2 & -8a& -64a^2\\ 0 & 0& 1 & 0& 8a& 8a & 0& 16a\\ 0 & 0& -8a & 1& -72a^2& -64a^2 & -16a &-128a^2\\ 0& 0 & 0& 0 & 1& 0 & 0 & 0\\ 0& 0& 0& 0 & 0 & 1 & 0& 0\\ 0& 0& 0& 0 & 4a & 4a & 1& 8a\\ 0& 0 & 0& 0 & 0& 0 & 0& 1 \end{pmatrix}\end{align*} $$
$$ \begin{align*}\vartheta_0= \begin{pmatrix} 1 & 0& -4a & 0& -32a^2 & -36a^2 & -8a& -56a^2\\ 0 & 1& -4a & 0& -28a^2& -32a^2 & -8a& -64a^2\\ 0 & 0& 1 & 0& 8a& 8a & 0& 16a\\ 0 & 0& -8a & 1& -72a^2& -64a^2 & -16a &-128a^2\\ 0& 0 & 0& 0 & 1& 0 & 0 & 0\\ 0& 0& 0& 0 & 0 & 1 & 0& 0\\ 0& 0& 0& 0 & 4a & 4a & 1& 8a\\ 0& 0 & 0& 0 & 0& 0 & 0& 1 \end{pmatrix}\end{align*} $$
we have
![]() $\tau =\mathrm {diag}(\mathrm {I}_{n-8}, \vartheta )$
, where
$\tau =\mathrm {diag}(\mathrm {I}_{n-8}, \vartheta )$
, where
if
![]() $n\in \{12,16,20\}$
, and
$n\in \{12,16,20\}$
, and
![]() $\vartheta =\vartheta _0$
otherwise. Notice that the minimal polynomial of
$\vartheta =\vartheta _0$
otherwise. Notice that the minimal polynomial of
![]() $\vartheta $
is
$\vartheta $
is
![]() $(t-1)^3$
. It follows that
$(t-1)^3$
. It follows that
![]() $\tau $
is an element of order p fixing the
$\tau $
is an element of order p fixing the
![]() $9$
-dimensional subspace
$9$
-dimensional subspace
![]() $S_9=\langle e_{n-8},e_{n-7},\ldots ,e_n \rangle $
. Furthermore, the fixed point space of
$S_9=\langle e_{n-8},e_{n-7},\ldots ,e_n \rangle $
. Furthermore, the fixed point space of
![]() $\tau _{|S_9}$
has dimension
$\tau _{|S_9}$
has dimension
![]() $5$
, unless
$5$
, unless
![]() $n\in \{12,16,20\}$
and
$n\in \{12,16,20\}$
and
![]() $a^2= 3$
, in which case it has dimension
$a^2= 3$
, in which case it has dimension
![]() $7$
.
$7$
.
5 The case
 $n\in \{15, 18, 19\}$
or
$n\in \{15, 18, 19\}$
or
 $n\geq 21$
$n\geq 21$
The subspace
![]() $S_9$
is invariant under
$S_9$
is invariant under
![]() $K=\langle y, \tau \rangle $
: our first aim is to find conditions on
$K=\langle y, \tau \rangle $
: our first aim is to find conditions on
![]() $a\in \mathbb {F}_q^\ast $
so that
$a\in \mathbb {F}_q^\ast $
so that
![]() $K_{|S_9}=\Omega _9(q)$
. In the following, we identify
$K_{|S_9}=\Omega _9(q)$
. In the following, we identify
![]() $y,\tau $
with their restrictions to
$y,\tau $
with their restrictions to
![]() $S_9$
.
$S_9$
.
Lemma 5.1. The group
![]() $K_{|S_9}$
is absolutely irreducible.
$K_{|S_9}$
is absolutely irreducible.
Proof. We apply Corollary 2.2 to
![]() $g=[y, \tau ]$
and
$g=[y, \tau ]$
and
![]() $\lambda =1$
. So, we may assume that the eigenvector
$\lambda =1$
. So, we may assume that the eigenvector
![]() $s=e_{n-8} - e_{n-7}$
is contained in U. Take the matrices
$s=e_{n-8} - e_{n-7}$
is contained in U. Take the matrices
![]() $M_1,M_2$
, whose columns are the images of s under the following elements:
$M_1,M_2$
, whose columns are the images of s under the following elements:
 $$ \begin{align*}\begin{array}{rl} M_1: & \mathrm{I}_9,\; y, \; y^2, \; \tau y^2, \; \tau^2 y^2,\; y\tau y^2,\; y^2\tau y^2,\; y\tau^2 y^2,\; y^2\tau^2 y^2;\\ M_2: & \mathrm{I}_9,\; y, \; y^2, \; \tau y^2, \; \tau^2 y^2,\; y\tau y^2,\; y\tau^2 y^2,\; (\tau y^2)^2,\; \tau y^2\tau^2 y^2. \end{array}\end{align*} $$
$$ \begin{align*}\begin{array}{rl} M_1: & \mathrm{I}_9,\; y, \; y^2, \; \tau y^2, \; \tau^2 y^2,\; y\tau y^2,\; y^2\tau y^2,\; y\tau^2 y^2,\; y^2\tau^2 y^2;\\ M_2: & \mathrm{I}_9,\; y, \; y^2, \; \tau y^2, \; \tau^2 y^2,\; y\tau y^2,\; y\tau^2 y^2,\; (\tau y^2)^2,\; \tau y^2\tau^2 y^2. \end{array}\end{align*} $$
Then,
![]() $\det (M_1)= -2^{35} a^{10} (4 a^2+3)$
and
$\det (M_1)= -2^{35} a^{10} (4 a^2+3)$
and
![]() $\det (M_2)=-2^{35} a^{10} (28a^2 - 3)$
. Clearly, these two matrices cannot be both singular, whence
$\det (M_2)=-2^{35} a^{10} (28a^2 - 3)$
. Clearly, these two matrices cannot be both singular, whence
![]() $\dim (U)=9$
, which is a contradiction.
$\dim (U)=9$
, which is a contradiction.
Lemma 5.2. The group
![]() $K_{|S_9}$
is neither monomial nor contained in any maximal subgroup
$K_{|S_9}$
is neither monomial nor contained in any maximal subgroup
![]() $\mathrm {PSL}_2(8)$
,
$\mathrm {PSL}_2(8)$
,
![]() $\mathrm {PSL}_2(17)$
,
$\mathrm {PSL}_2(17)$
,
![]() $\mathrm {Alt}(10)$
,
$\mathrm {Alt}(10)$
,
![]() $\mathrm {Sym}(10)$
,
$\mathrm {Sym}(10)$
,
![]() $\mathrm {Sym}(11)$
in class
$\mathrm {Sym}(11)$
in class
![]() $\mathcal {S}$
of
$\mathcal {S}$
of
![]() $\Omega _9(q)$
.
$\Omega _9(q)$
.
Proof. Recall that
![]() $\tau $
is an element of order p. Considering the order of the maximal subgroups M described in the statement and the conditions on q given in [Reference Bray, Holt and Roney-Dougal1, Tables 8.58 and 8.59], we may reduce to the following cases:
$\tau $
is an element of order p. Considering the order of the maximal subgroups M described in the statement and the conditions on q given in [Reference Bray, Holt and Roney-Dougal1, Tables 8.58 and 8.59], we may reduce to the following cases:
-
(i)
 $M=2^8: \mathrm {Alt}(9)$
and
$M=2^8: \mathrm {Alt}(9)$
and
 $q\in \{3,5\}$
;
$q\in \{3,5\}$
; -
(ii)
 $M=2^8: \mathrm {Sym}(9)$
and
$M=2^8: \mathrm {Sym}(9)$
and
 $q=7$
;
$q=7$
; -
(iii)
 $M=\mathrm {Alt}(10)$
and
$M=\mathrm {Alt}(10)$
and
 $q \in \{3,7\}$
;
$q \in \{3,7\}$
; -
(iv)
 $M=\mathrm {PSL}_2(17)$
and
$M=\mathrm {PSL}_2(17)$
and
 $q=9$
;
$q=9$
; -
(v)
 $M=\mathrm {Sym}(11)$
and
$M=\mathrm {Sym}(11)$
and
 $q=11$
;
$q=11$
; -
(vi)
 $M=\mathrm {PSL}_2(8)$
and
$M=\mathrm {PSL}_2(8)$
and
 $q=27$
.
$q=27$
.
Now, we look for an element of H whose order does not divide
![]() $|M|$
. In particular, it suffices to find an element of H whose order is divisible by a prime
$|M|$
. In particular, it suffices to find an element of H whose order is divisible by a prime
![]() $\varrho>17$
in case (iv),
$\varrho>17$
in case (iv),
![]() $\varrho>11$
otherwise. Define
$\varrho>11$
otherwise. Define
![]() $g_j=y\tau ^j$
. If
$g_j=y\tau ^j$
. If
![]() $q\in \{3,9\}$
, then
$q\in \{3,9\}$
, then
![]() $g_1$
has order divisible by
$g_1$
has order divisible by
![]() $41$
. If
$41$
. If
![]() $q=5$
, then
$q=5$
, then
![]() $g_3$
has order divisible by a prime
$g_3$
has order divisible by a prime
![]() $\varrho \geq 13$
. If
$\varrho \geq 13$
. If
![]() $q=7$
, take
$q=7$
, take
![]() $j=2$
when
$j=2$
when
![]() $a=\pm 2$
, and
$a=\pm 2$
, and
![]() $j=3$
when
$j=3$
when
![]() $a\in \{\pm 1, \pm 3 \}$
. Then, the order of
$a\in \{\pm 1, \pm 3 \}$
. Then, the order of
![]() $g_j$
is divisible by a prime
$g_j$
is divisible by a prime
![]() $\varrho \geq 43$
. If
$\varrho \geq 43$
. If
![]() $q=11$
, take
$q=11$
, take
![]() $j=2$
if
$j=2$
if
![]() $a= \pm 5$
and
$a= \pm 5$
and
![]() $j=1$
otherwise. Then the order of
$j=1$
otherwise. Then the order of
![]() $g_j$
is divisible by a prime
$g_j$
is divisible by a prime
![]() $\varrho \geq 19$
. Finally, if
$\varrho \geq 19$
. Finally, if
![]() $q=27$
, then
$q=27$
, then
![]() $g_2$
has order divisible by
$g_2$
has order divisible by
![]() $37$
. In all these cases, we easily obtain a contradiction.
$37$
. In all these cases, we easily obtain a contradiction.
For the next lemma, we use the following traces of elements of
![]() $K_{|S_9}$
:
$K_{|S_9}$
:
Lemma 5.3. The group
![]() $K_{|S_9}$
is neither contained in a maximal subgroup in class
$K_{|S_9}$
is neither contained in a maximal subgroup in class
![]() $\mathcal {C}_2$
of
$\mathcal {C}_2$
of
![]() $\Omega _9(q)$
nor contained in any maximal subgroup in class
$\Omega _9(q)$
nor contained in any maximal subgroup in class
![]() $\mathcal {C}_7$
.
$\mathcal {C}_7$
.
Proof. By Lemma 5.2, the group
![]() $K_{|S_9}$
is not monomial. So, suppose that
$K_{|S_9}$
is not monomial. So, suppose that
![]() $K_{|S_9}$
preserves a nonsingular decomposition
$K_{|S_9}$
preserves a nonsingular decomposition
![]() $\mathbb {F}_q^9=W_1\oplus W_2\oplus W_3$
with
$\mathbb {F}_q^9=W_1\oplus W_2\oplus W_3$
with
![]() $\dim (W_i)=3$
. Clearly, for each
$\dim (W_i)=3$
. Clearly, for each
![]() $k\in K_{|S_9}$
, its cube fixes each
$k\in K_{|S_9}$
, its cube fixes each
![]() $W_i$
, preserving a nonsingular symmetric form. Thus, its eigenvalues are
$W_i$
, preserving a nonsingular symmetric form. Thus, its eigenvalues are
![]() $\pm 1, \alpha _i, \alpha _i^{-1}$
. It follows that
$\pm 1, \alpha _i, \alpha _i^{-1}$
. It follows that
![]() $k^3$
must have the eigenvalue
$k^3$
must have the eigenvalue
![]() $1$
with multiplicity at least
$1$
with multiplicity at least
![]() $3$
, or the eigenvalue
$3$
, or the eigenvalue
![]() $-1$
with multiplicity at least
$-1$
with multiplicity at least
![]() $2$
. Assume first
$2$
. Assume first
![]() $p=3$
. We have
$p=3$
. We have
![]() $\chi _{(y\tau )^3}(t)=(t-1)f(t)$
, where
$\chi _{(y\tau )^3}(t)=(t-1)f(t)$
, where
![]() $f(t)=t^8 + t^7 -(a^{12} +a^6 - 1) t^6 - (a^{12} - 1) t^5 - (a^6 - 1) t^4 -(a^{12} - 1) t^3 - (a^{12} + a^6 - 1) t^2 + t + 1$
. Then,
$f(t)=t^8 + t^7 -(a^{12} +a^6 - 1) t^6 - (a^{12} - 1) t^5 - (a^6 - 1) t^4 -(a^{12} - 1) t^3 - (a^{12} + a^6 - 1) t^2 + t + 1$
. Then,
![]() $f(1)=-a^{12}\neq 0$
and
$f(1)=-a^{12}\neq 0$
and
![]() $f(-1)=1$
, which is a contradiction. Next, assume
$f(-1)=1$
, which is a contradiction. Next, assume
![]() $p\neq 3$
. From
$p\neq 3$
. From
![]() $\mathrm {tr}(\tau )=9\neq 0$
, we get that
$\mathrm {tr}(\tau )=9\neq 0$
, we get that
![]() $\tau $
fixes each
$\tau $
fixes each
![]() $W_i$
. By the irreducibility of
$W_i$
. By the irreducibility of
![]() $K_{|S_9}$
, the element y acts on
$K_{|S_9}$
, the element y acts on
![]() $\{W_1,W_2,W_3\}$
as the
$\{W_1,W_2,W_3\}$
as the
![]() $3$
-cycle
$3$
-cycle
![]() $(W_1,W_2,W_3)$
. In this case, both
$(W_1,W_2,W_3)$
. In this case, both
![]() $(y\tau )^2$
and
$(y\tau )^2$
and
![]() $(y^2\tau )^2$
should have trace
$(y^2\tau )^2$
should have trace
![]() $0$
, in contrast with (5.1) which gives
$0$
, in contrast with (5.1) which gives
![]() $0=\mathrm {tr}((y^2\tau )^2)-\mathrm {tr}((y\tau )^2)=2^{12}a^4$
.
$0=\mathrm {tr}((y^2\tau )^2)-\mathrm {tr}((y\tau )^2)=2^{12}a^4$
.
Finally, suppose that
![]() $K_{|S_9}$
is contained in a maximal subgroup
$K_{|S_9}$
is contained in a maximal subgroup
![]() $M\cong \Omega _3(q)^2.[4]\in \mathcal {C}_7$
, and hence actually in
$M\cong \Omega _3(q)^2.[4]\in \mathcal {C}_7$
, and hence actually in
![]() $\Omega _3(q)^2$
. Up to conjugation, we may suppose
$\Omega _3(q)^2$
. Up to conjugation, we may suppose
![]() $\tau =\bigg (\begin {smallmatrix} 1 & 1 & 1 \\ 0 & 1 & 2 \\ 0 & 0 & 1 \end {smallmatrix}\bigg ) \otimes \bigg ( \begin {smallmatrix} 1 & 1 & 1 \\ 0 & 1 & 2 \\ 0 & 0 & 1 \end {smallmatrix}\bigg )$
. The dimensions of the fixed point space of this tensor product and of
$\tau =\bigg (\begin {smallmatrix} 1 & 1 & 1 \\ 0 & 1 & 2 \\ 0 & 0 & 1 \end {smallmatrix}\bigg ) \otimes \bigg ( \begin {smallmatrix} 1 & 1 & 1 \\ 0 & 1 & 2 \\ 0 & 0 & 1 \end {smallmatrix}\bigg )$
. The dimensions of the fixed point space of this tensor product and of
![]() $\tau $
are, respectively,
$\tau $
are, respectively,
![]() $3$
and
$3$
and
![]() $5$
, which is a contradiction.
$5$
, which is a contradiction.
Lemma 5.4. The group
![]() $K_{|S_9}$
is not contained in any maximal subgroup
$K_{|S_9}$
is not contained in any maximal subgroup
![]() $M\cong \mathrm {PSL}_2(q).2$
or
$M\cong \mathrm {PSL}_2(q).2$
or
![]() $M\cong \mathrm {PSL}_2(q^2).2$
in class
$M\cong \mathrm {PSL}_2(q^2).2$
in class
![]() $\mathcal {S}$
of
$\mathcal {S}$
of
![]() $\Omega _9(q)$
.
$\Omega _9(q)$
.
Proof. Suppose the contrary.
Case
![]() $M\cong \mathrm {PSL}_2(q).2$
. In this case, M arises from the representation
$M\cong \mathrm {PSL}_2(q).2$
. In this case, M arises from the representation
![]() $\Phi : \mathrm {GL}_2(q)\to \mathrm {GL}_9(q)$
obtained from the action of
$\Phi : \mathrm {GL}_2(q)\to \mathrm {GL}_9(q)$
obtained from the action of
![]() $\mathrm {GL}_2(q)$
on the space T of homogeneous polynomials of degree
$\mathrm {GL}_2(q)$
on the space T of homogeneous polynomials of degree
![]() $8$
in two variables
$8$
in two variables
![]() $t_1, t_2$
over
$t_1, t_2$
over
![]() $\mathbb {F}_q$
. Up to conjugation in
$\mathbb {F}_q$
. Up to conjugation in
![]() $\mathrm {GL}_2(q)$
, we may assume
$\mathrm {GL}_2(q)$
, we may assume
 $$ \begin{align*}\tau=\Phi(\mathrm{I}_2+E_{1,2})=\begin{cases} t_1 \mapsto t_1,\\ t_2 \mapsto t_1+t_2. \end{cases}\end{align*} $$
$$ \begin{align*}\tau=\Phi(\mathrm{I}_2+E_{1,2})=\begin{cases} t_1 \mapsto t_1,\\ t_2 \mapsto t_1+t_2. \end{cases}\end{align*} $$
Direct computation (with respect to the basis
![]() $t_1^8, t_1^7t_2, \ldots , t_2^8$
of T) gives that the fixed point space of this linear transformation is generated by
$t_1^8, t_1^7t_2, \ldots , t_2^8$
of T) gives that the fixed point space of this linear transformation is generated by
![]() $t_1^8$
. So, it has dimension
$t_1^8$
. So, it has dimension
![]() $1$
, which is a contradiction as
$1$
, which is a contradiction as
![]() $\tau $
has a fixed point space of dimension
$\tau $
has a fixed point space of dimension
![]() $5$
.
$5$
.
Case
![]() $M\cong \mathrm {PSL}_2(q^2).2$
. To understand M, start from the representation
$M\cong \mathrm {PSL}_2(q^2).2$
. To understand M, start from the representation
![]() $\psi :\mathrm {GL}_2(q^2)\to \mathrm {GL}_3(q^2)$
described in (2.1). Next, consider the subspace W of
$\psi :\mathrm {GL}_2(q^2)\to \mathrm {GL}_3(q^2)$
described in (2.1). Next, consider the subspace W of
![]() $\mathrm {Mat}_3(q^2)$
consisting of the matrices A such that
$\mathrm {Mat}_3(q^2)$
consisting of the matrices A such that
![]() $A^{\mathsf {T}}=(a_{i,j}^q)=A^\sigma $
. Clearly, W has dimension
$A^{\mathsf {T}}=(a_{i,j}^q)=A^\sigma $
. Clearly, W has dimension
![]() $9$
over
$9$
over
![]() $\mathbb {F}_q$
and we may consider the representation
$\mathbb {F}_q$
and we may consider the representation
![]() $\Phi : \mathrm {GL}_3(q^2)\to \mathrm {GL}_9(q)$
induced by
$\Phi : \mathrm {GL}_3(q^2)\to \mathrm {GL}_9(q)$
induced by
![]() $A\mapsto (\psi (g))^{\mathsf {T}} A (\psi (g))^\sigma $
for all
$A\mapsto (\psi (g))^{\mathsf {T}} A (\psi (g))^\sigma $
for all
![]() $g\in \mathrm {GL}_3(q^2)$
. The group M arises from this representation. Again, up to conjugation in
$g\in \mathrm {GL}_3(q^2)$
. The group M arises from this representation. Again, up to conjugation in
![]() $\mathrm {GL}_2(q^2)$
, we may suppose
$\mathrm {GL}_2(q^2)$
, we may suppose
![]() $\tau =\Phi (\psi (\mathrm {I}_2+E_{1,2}))=\Phi \bigg (\bigg (\begin {smallmatrix} 1 & 1 & 1 \\ 0 & 1 & 2 \\ 0 & 0 & 1 \end {smallmatrix}\bigg )\bigg )$
. Direct calculation gives that the fixed point space of
$\tau =\Phi (\psi (\mathrm {I}_2+E_{1,2}))=\Phi \bigg (\bigg (\begin {smallmatrix} 1 & 1 & 1 \\ 0 & 1 & 2 \\ 0 & 0 & 1 \end {smallmatrix}\bigg )\bigg )$
. Direct calculation gives that the fixed point space of
![]() $\Phi (\psi (\mathrm {I}_2+E_{1,2}))$
on
$\Phi (\psi (\mathrm {I}_2+E_{1,2}))$
on
![]() $W\leq \mathrm {Mat}_3(q^2)$
is generated by
$W\leq \mathrm {Mat}_3(q^2)$
is generated by
![]() $E_{2,2}, E_{3,3}, E_{2,3}+E_{3,2}$
. Thus, it has dimension
$E_{2,2}, E_{3,3}, E_{2,3}+E_{3,2}$
. Thus, it has dimension
![]() $3$
, which is again a contradiction as
$3$
, which is again a contradiction as
![]() $\tau $
has a fixed point space of dimension
$\tau $
has a fixed point space of dimension
![]() $5$
.
$5$
.
Proposition 5.5. Suppose that q is odd and
![]() $n\in \{ 15, 18,19 \}$
or
$n\in \{ 15, 18,19 \}$
or
![]() $n\geq 21$
. Let
$n\geq 21$
. Let
![]() $a \in \mathbb {F}_q^*$
be such that
$a \in \mathbb {F}_q^*$
be such that
![]() $\mathbb {F}_p[a]=\mathbb {F}_q$
. Then,
$\mathbb {F}_p[a]=\mathbb {F}_q$
. Then,
![]() $K_{|S_9}=\Omega _9(q)$
.
$K_{|S_9}=\Omega _9(q)$
.
Proof. By Lemmas 5.1 and 5.3,
![]() $K_{|S_9}$
is absolutely irreducible, and is neither contained in a maximal subgroup in class
$K_{|S_9}$
is absolutely irreducible, and is neither contained in a maximal subgroup in class
![]() $\mathcal {C}_2$
of
$\mathcal {C}_2$
of
![]() $\Omega _9(q)$
nor contained in any maximal subgroup in class
$\Omega _9(q)$
nor contained in any maximal subgroup in class
![]() $\mathcal {C}_7$
. Furthermore, by Lemmas 5.2 and 5.4, either
$\mathcal {C}_7$
. Furthermore, by Lemmas 5.2 and 5.4, either
![]() $K_{|S_9}=\Omega _9(q)$
or
$K_{|S_9}=\Omega _9(q)$
or
![]() $K_{|S_9}$
is contained in a maximal subgroup
$K_{|S_9}$
is contained in a maximal subgroup
![]() $M\in \{\Omega _9(q_0), \mathrm {SO}_9(q_0)\}$
in class
$M\in \{\Omega _9(q_0), \mathrm {SO}_9(q_0)\}$
in class
![]() $\mathcal {C}_5$
, where
$\mathcal {C}_5$
, where
![]() $q=q_0^r$
for some prime
$q=q_0^r$
for some prime
![]() $r\geq 2$
. Suppose there exists
$r\geq 2$
. Suppose there exists
![]() $g\in \mathrm {GL}_{9}(\mathbb {F})$
such that
$g\in \mathrm {GL}_{9}(\mathbb {F})$
such that
![]() $\tau ^g=\tau _0$
,
$\tau ^g=\tau _0$
,
![]() $y^g= y_0$
, with
$y^g= y_0$
, with
![]() $\tau _0,y_0\in \mathrm {GL}_{9}(q_0)$
. From
$\tau _0,y_0\in \mathrm {GL}_{9}(q_0)$
. From
![]() $ -2176 a^4 + 128 a^2 = \mathrm {tr}((y\tau )^2)= \mathrm {tr}((y^g\tau ^g)^2 )= \mathrm {tr}((y_0\tau _0)^2)$
, it follows that
$ -2176 a^4 + 128 a^2 = \mathrm {tr}((y\tau )^2)= \mathrm {tr}((y^g\tau ^g)^2 )= \mathrm {tr}((y_0\tau _0)^2)$
, it follows that
![]() $17 a^4- a^2 \in \mathbb {F}_{q_0}$
. Similarly, from
$17 a^4- a^2 \in \mathbb {F}_{q_0}$
. Similarly, from
![]() $\mathrm {tr}((y^2\tau )^2) = 1920 a^4 + 128 a^2$
, we obtain
$\mathrm {tr}((y^2\tau )^2) = 1920 a^4 + 128 a^2$
, we obtain
![]() $15 a^4+a^2 \in \mathbb {F}_{q_0}$
. It follows that
$15 a^4+a^2 \in \mathbb {F}_{q_0}$
. It follows that
![]() $32a^4\in \mathbb {F}_{q_0}$
and then
$32a^4\in \mathbb {F}_{q_0}$
and then
![]() $a^2 \in \mathbb {F}_{q_0}$
. Again, from
$a^2 \in \mathbb {F}_{q_0}$
. Again, from
![]() $\mathrm {tr}( y^2\tau ^2 (y\tau )^2)= -49\,152 a^6 + 16\,384 a^5 + 3840 a^4 + 256 a^2 \in \mathbb {F}_{q_0}$
, we get
$\mathrm {tr}( y^2\tau ^2 (y\tau )^2)= -49\,152 a^6 + 16\,384 a^5 + 3840 a^4 + 256 a^2 \in \mathbb {F}_{q_0}$
, we get
![]() $a\in \mathbb {F}_{q_0}$
. So,
$a\in \mathbb {F}_{q_0}$
. So,
![]() $\mathbb {F}_q=\mathbb {F}_p[a]\leq \mathbb {F}_{q_0}$
implies
$\mathbb {F}_q=\mathbb {F}_p[a]\leq \mathbb {F}_{q_0}$
implies
![]() $q_0=q$
, which is a contradiction. We conclude that
$q_0=q$
, which is a contradiction. We conclude that
![]() $K_{|S_9}=\Omega _9(q)$
.
$K_{|S_9}=\Omega _9(q)$
.
Define
![]() $E_0=S_0=\{0\}$
and, for
$E_0=S_0=\{0\}$
and, for
![]() $1\leq \ell \leq n$
,
$1\leq \ell \leq n$
,
Corollary 5.6. Suppose q odd and
![]() $n\in \{ 15, 18,19 \}$
or
$n\in \{ 15, 18,19 \}$
or
![]() $n\geq 21$
. Let
$n\geq 21$
. Let
![]() $a \in \mathbb {F}_q^*$
be such that
$a \in \mathbb {F}_q^*$
be such that
![]() $\mathbb {F}_p[a]=\mathbb {F}_q$
. Then:
$\mathbb {F}_p[a]=\mathbb {F}_q$
. Then:
-
(i)
 $H=\Omega _n (q)$
if n is odd;
$H=\Omega _n (q)$
if n is odd; -
(ii)
 $H=\Omega _n^+(q)$
if
$H=\Omega _n^+(q)$
if
 $q\equiv 1 ~\mathrm {(mod~ 4)}$
and n is even;
$q\equiv 1 ~\mathrm {(mod~ 4)}$
and n is even; -
(iii)
 $H=\Omega _n^+(q)$
if
$H=\Omega _n^+(q)$
if
 $q\equiv 3 ~\mathrm {(mod~ 4)}$
and
$q\equiv 3 ~\mathrm {(mod~ 4)}$
and
 $n\equiv 0 ~\mathrm {(mod~ 4)}$
;
$n\equiv 0 ~\mathrm {(mod~ 4)}$
; -
(iv)
 $H=\Omega _n^-(q)$
if
$H=\Omega _n^-(q)$
if
 $q\equiv 3 ~\mathrm {(mod~ 4)}$
and
$q\equiv 3 ~\mathrm {(mod~ 4)}$
and
 $n\equiv 2 ~\mathrm {(mod~ 4)}$
.
$n\equiv 2 ~\mathrm {(mod~ 4)}$
.
Proof. By [Reference Bray, Holt and Roney-Dougal1, Proposition 1.5.42(ii)], when n is even, we have
![]() $H\leq \Omega _n^+(q)$
or
$H\leq \Omega _n^+(q)$
or
![]() ${H\leq \Omega _n^-(q)}$
according as
${H\leq \Omega _n^-(q)}$
according as
![]() ${n(q-1)}/{4}$
is even or odd, respectively. Let
${n(q-1)}/{4}$
is even or odd, respectively. Let
![]() $\ell $
be maximal with respect to
$\ell $
be maximal with respect to
where
![]() $\epsilon \in \{\circ ,\pm \}$
. Noting that
$\epsilon \in \{\circ ,\pm \}$
. Noting that
![]() $K'=\mathrm {diag}(\mathrm {I}_{n-9}, \Omega _9(q))$
by the previous proposition, we have that
$K'=\mathrm {diag}(\mathrm {I}_{n-9}, \Omega _9(q))$
by the previous proposition, we have that
![]() $\ell $
is at least
$\ell $
is at least
![]() $9$
and we need to show that
$9$
and we need to show that
![]() $\ell =n$
. For the sake of contradiction, assume
$\ell =n$
. For the sake of contradiction, assume
![]() $9\leq \ell < n$
.
$9\leq \ell < n$
.
Suppose first that
![]() $(r,\ell )\not \in \{(2,n-2), (2,n-1) \}$
and
$(r,\ell )\not \in \{(2,n-2), (2,n-1) \}$
and
![]() $(r,\ell )\not \in \{(1,n-4),(2,n-8)\}$
when n is even. Then:
$(r,\ell )\not \in \{(1,n-4),(2,n-8)\}$
when n is even. Then:
-
(a) if
 $\ell \equiv 0 ~\mathrm {(mod~ 3)}$
, then x fixes the subspaces
$\ell \equiv 0 ~\mathrm {(mod~ 3)}$
, then x fixes the subspaces
 $S_{\ell -1}$
and
$S_{\ell -1}$
and
 $E_{n-\ell -1}$
, and acts as the transposition
$E_{n-\ell -1}$
, and acts as the transposition
 $(e_{n-\ell },e_{n-\ell +1})$
on
$(e_{n-\ell },e_{n-\ell +1})$
on
 $\langle e_{n-\ell }, e_{n-\ell +1} \rangle $
;
$\langle e_{n-\ell }, e_{n-\ell +1} \rangle $
; -
(b) if
 $\ell \equiv j ~\mathrm {(mod~ 3)}$
, with
$\ell \equiv j ~\mathrm {(mod~ 3)}$
, with
 $j=1,2$
, then y fixes the subspaces
$j=1,2$
, then y fixes the subspaces
 $S_{\ell -j}$
and
$S_{\ell -j}$
and
 $E_{n-\ell -3 +j}$
, and acts as
$E_{n-\ell -3 +j}$
, and acts as
 $(e_{n-\ell -2+j},e_{n-\ell -1+j}, e_{n-\ell +j})$
on
$(e_{n-\ell -2+j},e_{n-\ell -1+j}, e_{n-\ell +j})$
on
 $\langle e_{n-\ell -2+j},e_{n-\ell -1+j}, e_{n-\ell +j}\rangle $
.
$\langle e_{n-\ell -2+j},e_{n-\ell -1+j}, e_{n-\ell +j}\rangle $
.
Setting
![]() $g=x$
in case (a), and
$g=x$
in case (a), and
![]() $g=y$
in case (b), we claim that
$g=y$
in case (b), we claim that
![]() $K_{\ell +1}:=\langle K_\ell , K_{\ell }^g \rangle $
equals
$K_{\ell +1}:=\langle K_\ell , K_{\ell }^g \rangle $
equals
Noting that
![]() $g^{-1}S_\ell $
is obtained from
$g^{-1}S_\ell $
is obtained from
![]() $S_\ell $
by replacing
$S_\ell $
by replacing
![]() $e_{n-\ell +1}$
by
$e_{n-\ell +1}$
by
![]() $e_{n-\ell }$
, one gets
$e_{n-\ell }$
, one gets
![]() $\langle S_\ell , g^{-1} S_\ell \rangle = S_{\ell +1}$
. Thus,
$\langle S_\ell , g^{-1} S_\ell \rangle = S_{\ell +1}$
. Thus,
![]() $K_{\ell +1}$
fixes
$K_{\ell +1}$
fixes
![]() $S_{\ell +1}$
, induces the identity on
$S_{\ell +1}$
, induces the identity on
![]() $E_{n-\ell -1}$
and fixes the restriction of J to
$E_{n-\ell -1}$
and fixes the restriction of J to
![]() $S_{\ell +1}$
, of determinant
$S_{\ell +1}$
, of determinant
![]() $1$
. If follows that
$1$
. If follows that
![]() $K_{\ell +1}$
is contained in the group (5-2). Call
$K_{\ell +1}$
is contained in the group (5-2). Call
![]() $\rho $
the matrix in
$\rho $
the matrix in
![]() $\mathrm {GL}_n(q)$
which acts according to
$\mathrm {GL}_n(q)$
which acts according to
![]() $e_{n-\ell }\mapsto -e_{n-\ell }$
,
$e_{n-\ell }\mapsto -e_{n-\ell }$
,
![]() $e_{n-4}\mapsto -2e_n$
,
$e_{n-4}\mapsto -2e_n$
,
![]() $e_n\mapsto -\tfrac 12 e_{n-4}$
and fixes the remaining vectors
$e_n\mapsto -\tfrac 12 e_{n-4}$
and fixes the remaining vectors
![]() $e_i$
. Since
$e_i$
. Since
![]() $\rho $
has determinant
$\rho $
has determinant
![]() $1$
and spinor norm
$1$
and spinor norm
![]() $(\mathbb {F}_q^*)^2$
, it belongs to
$(\mathbb {F}_q^*)^2$
, it belongs to
![]() $K_\ell ^g$
, which induces
$K_\ell ^g$
, which induces
![]() $\Omega _{\ell }^\epsilon $
on
$\Omega _{\ell }^\epsilon $
on
![]() $g^{-1}S_\ell $
. Now,
$g^{-1}S_\ell $
. Now,
![]() $\langle \rho , K_\ell \rangle $
is the stabilizer in the group (5-2) of the nondegenerate subspace
$\langle \rho , K_\ell \rangle $
is the stabilizer in the group (5-2) of the nondegenerate subspace
![]() $\langle e_{n-\ell }\rangle $
. So, it is a maximal subgroup of the group (5-2). From
$\langle e_{n-\ell }\rangle $
. So, it is a maximal subgroup of the group (5-2). From
![]() $K_{\ell +1}\nleq \langle \rho , K_\ell \rangle $
, we get the final contradiction
$K_{\ell +1}\nleq \langle \rho , K_\ell \rangle $
, we get the final contradiction
![]() $K_{\ell +1}=\mathrm {diag}(\mathrm {I}_{n-\ell -1}, \Omega _{\ell +1}^{\overline {\epsilon }}(q))$
.
$K_{\ell +1}=\mathrm {diag}(\mathrm {I}_{n-\ell -1}, \Omega _{\ell +1}^{\overline {\epsilon }}(q))$
.
It remains to exclude the exceptional cases: in each of them, we get the same contradiction.
Case 1.
![]() $r=1$
,
$r=1$
,
![]() $\ell =n-4$
, n even. Let R be the stabilizer of
$\ell =n-4$
, n even. Let R be the stabilizer of
![]() $e_6$
in
$e_6$
in
![]() $K_{n-4}$
. Then,
$K_{n-4}$
. Then,
![]() $\langle R^x, K_{n-4}\rangle = K_{n-3}$
, as it fixes the vectors
$\langle R^x, K_{n-4}\rangle = K_{n-3}$
, as it fixes the vectors
![]() $e_1,e_2,e_3$
and the subspace
$e_1,e_2,e_3$
and the subspace
![]() $E_3^\perp $
, inducing
$E_3^\perp $
, inducing
![]() $\Omega _{n-3}(q)$
.
$\Omega _{n-3}(q)$
.
Case 2.
![]() $r=2$
,
$r=2$
,
![]() $\ell =n-8$
, n even. Let R be the stabilizer of
$\ell =n-8$
, n even. Let R be the stabilizer of
![]() $e_{10}$
in
$e_{10}$
in
![]() $K_{n-8}$
. Then,
$K_{n-8}$
. Then,
![]() $\langle R^x, K_{n-8}\rangle = K_{n-7}$
, as it fixes the vectors
$\langle R^x, K_{n-8}\rangle = K_{n-7}$
, as it fixes the vectors
![]() $e_1,e_2,\ldots ,e_7$
and the subspace
$e_1,e_2,\ldots ,e_7$
and the subspace
![]() $E_7^\perp $
, inducing
$E_7^\perp $
, inducing
![]() $\Omega _{n-7}(q)$
.
$\Omega _{n-7}(q)$
.
Case 3.
![]() $r=2$
,
$r=2$
,
![]() $\ell =n-2$
. Let R be the stabilizer of
$\ell =n-2$
. Let R be the stabilizer of
![]() $e_{3}$
in
$e_{3}$
in
![]() $K_{n-2}$
. Then,
$K_{n-2}$
. Then,
![]() $\langle R^x, K_{n-2}\rangle = K_{n-1}$
, as it fixes
$\langle R^x, K_{n-2}\rangle = K_{n-1}$
, as it fixes
![]() $e_1$
and
$e_1$
and
![]() $E_1^\perp $
, inducing
$E_1^\perp $
, inducing
![]() $\Omega ^{\overline \epsilon }_{n-1}(q)$
.
$\Omega ^{\overline \epsilon }_{n-1}(q)$
.
Case 4.
![]() $r=2$
,
$r=2$
,
![]() $\ell =n-1$
. Similar to the above cases.
$\ell =n-1$
. Similar to the above cases.
6 The case
 $n\in \{12, 16, 20\}$
$n\in \{12, 16, 20\}$
The values
![]() $n=12,16,20$
require some small adjustments with respect to the general case, described in Section 5. So, in the proof of the following results, we only give the necessary modifications.
$n=12,16,20$
require some small adjustments with respect to the general case, described in Section 5. So, in the proof of the following results, we only give the necessary modifications.
Lemma 6.1. Assume
![]() $a^2\neq 2,3$
. Then, the group
$a^2\neq 2,3$
. Then, the group
![]() $K_{|S_9}$
is absolutely irreducible.
$K_{|S_9}$
is absolutely irreducible.
Proof. We have
![]() $s=e_{n-8} - e_{n-7}$
by the hypothesis
$s=e_{n-8} - e_{n-7}$
by the hypothesis
![]() $a^2\neq 3$
. Now,
$a^2\neq 3$
. Now,
![]() $\det (M_1)=-2^{35} a^6 (a^2 - 2) (4 a^4-13 a^2+16) $
and
$\det (M_1)=-2^{35} a^6 (a^2 - 2) (4 a^4-13 a^2+16) $
and
![]() $\det (M_2)=-2^{35} a^6 (a^2 - 2) (28 a^4 - 83 a^2 - 16)$
. Since
$\det (M_2)=-2^{35} a^6 (a^2 - 2) (28 a^4 - 83 a^2 - 16)$
. Since
![]() $a^2\neq 2$
, the matrices
$a^2\neq 2$
, the matrices
![]() $M_1,M_2$
are both singular only if
$M_1,M_2$
are both singular only if
![]() $p=13$
and
$p=13$
and
![]() $a^2=3$
, which is excluded by hypothesis.
$a^2=3$
, which is excluded by hypothesis.
Lemma 6.2. The group
![]() $K_{|S_9}$
is neither monomial nor contained in any maximal subgroup
$K_{|S_9}$
is neither monomial nor contained in any maximal subgroup
![]() $\mathrm {PSL}_2(8)$
,
$\mathrm {PSL}_2(8)$
,
![]() $\mathrm {PSL}_2(17)$
,
$\mathrm {PSL}_2(17)$
,
![]() $\mathrm {Alt}(10)$
,
$\mathrm {Alt}(10)$
,
![]() $\mathrm {Sym}(10)$
,
$\mathrm {Sym}(10)$
,
![]() $\mathrm {Sym}(11)$
in class
$\mathrm {Sym}(11)$
in class
![]() $\mathcal {S}$
of
$\mathcal {S}$
of
![]() $\Omega _9(q)$
.
$\Omega _9(q)$
.
Proof. If
![]() $q\in \{3, 5, 11\}$
proceed as in the proof of Lemma 5.2. If
$q\in \{3, 5, 11\}$
proceed as in the proof of Lemma 5.2. If
![]() $q=7$
, take
$q=7$
, take
![]() $j=1$
if
$j=1$
if
![]() $a=\pm 1$
and
$a=\pm 1$
and
![]() $j=3$
if
$j=3$
if
![]() $a=\pm 2$
; take
$a=\pm 2$
; take
![]() $\tilde g=\tau ^2 y \tau y$
if
$\tilde g=\tau ^2 y \tau y$
if
![]() $a=\pm 3$
. Then, the order of
$a=\pm 3$
. Then, the order of
![]() $g_j$
and the order of
$g_j$
and the order of
![]() $\tilde g$
are divisible by a prime
$\tilde g$
are divisible by a prime
![]() $\varrho \geq 43$
. If
$\varrho \geq 43$
. If
![]() $q=9$
, then
$q=9$
, then
![]() $g_1$
has order divisible by
$g_1$
has order divisible by
![]() $13$
, a prime that does divide
$13$
, a prime that does divide
![]() $|\mathrm {PSL}_2(17)|$
; if
$|\mathrm {PSL}_2(17)|$
; if
![]() $q=27$
, then
$q=27$
, then
![]() $g_2$
has order divisible by a prime
$g_2$
has order divisible by a prime
![]() $\varrho \in \{13, 73\}$
.
$\varrho \in \{13, 73\}$
.
Lemma 6.3. Assume
![]() $a^2 \neq 3$
. The group
$a^2 \neq 3$
. The group
![]() $K_{|S_9}$
is neither contained in a maximal subgroup in class
$K_{|S_9}$
is neither contained in a maximal subgroup in class
![]() $\mathcal {C}_2$
of
$\mathcal {C}_2$
of
![]() $\Omega _9(q)$
nor contained in any maximal subgroup in class
$\Omega _9(q)$
nor contained in any maximal subgroup in class
![]() $\mathcal {C}_7$
.
$\mathcal {C}_7$
.
Proof. We proceed as in the proof of Lemma 5.3, describing only the necessary modifications to prove the primitivity of
![]() $K_{|S_9}$
. For
$K_{|S_9}$
. For
![]() $p=3$
, we have
$p=3$
, we have
![]() $\chi _{(y\tau )^3}(t)=(t-1)f(t)$
, where
$\chi _{(y\tau )^3}(t)=(t-1)f(t)$
, where
![]() $f(t)=t^8 -t^7 - (a^{12} - a^6 +1) t^6 - a^{12} t^5 + (a^6 -1) t^4 - a^{12} t^3 - (a^{12} - a^6 + 1) t^2 -t + 1$
. Also in this case,
$f(t)=t^8 -t^7 - (a^{12} - a^6 +1) t^6 - a^{12} t^5 + (a^6 -1) t^4 - a^{12} t^3 - (a^{12} - a^6 + 1) t^2 -t + 1$
. Also in this case,
![]() $f(1)=-a^{12}$
and
$f(1)=-a^{12}$
and
![]() $f(-1)=1$
. If
$f(-1)=1$
. If
![]() $p\neq 3$
, the product
$p\neq 3$
, the product
![]() $y\tau $
should have trace
$y\tau $
should have trace
![]() $0$
, in contrast with
$0$
, in contrast with
![]() $\mathrm {tr}(y\tau ) =-16$
.
$\mathrm {tr}(y\tau ) =-16$
.
Lemma 6.4. Assume
![]() $a^2 \neq 3$
. The group
$a^2 \neq 3$
. The group
![]() $K_{|S_9}$
is not contained in any maximal subgroup
$K_{|S_9}$
is not contained in any maximal subgroup
![]() $M\cong \mathrm {PSL}_2(q).2$
or
$M\cong \mathrm {PSL}_2(q).2$
or
![]() $M\cong \mathrm {PSL}_2(q^2).2$
in class
$M\cong \mathrm {PSL}_2(q^2).2$
in class
![]() $\mathcal {S}$
of
$\mathcal {S}$
of
![]() $\Omega _9(q)$
.
$\Omega _9(q)$
.
Proposition 6.5. Assume q odd and
![]() $n\in \{12,16,20\}$
. Let
$n\in \{12,16,20\}$
. Let
![]() $a \in \mathbb {F}_q^*$
be such that
$a \in \mathbb {F}_q^*$
be such that
![]() $\mathbb {F}_p[a^2]=\mathbb {F}_q$
with
$\mathbb {F}_p[a^2]=\mathbb {F}_q$
with
![]() $a^2\neq 2,3$
. Then
$a^2\neq 2,3$
. Then
![]() $K_{|S_9}=\Omega _9(q)$
.
$K_{|S_9}=\Omega _9(q)$
.
Proof. By Lemmas 6.1 and 6.3,
![]() $K_{|S_9}$
is absolutely irreducible and is neither contained in a maximal subgroup in class
$K_{|S_9}$
is absolutely irreducible and is neither contained in a maximal subgroup in class
![]() $\mathcal {C}_2$
of
$\mathcal {C}_2$
of
![]() $\Omega _9(q)$
nor contained in any maximal subgroup in class
$\Omega _9(q)$
nor contained in any maximal subgroup in class
![]() $\mathcal {C}_7$
. Furthermore, by Lemmas 6.2 and 6.4, either
$\mathcal {C}_7$
. Furthermore, by Lemmas 6.2 and 6.4, either
![]() $K_{|S_9}=\Omega _9(q)$
or
$K_{|S_9}=\Omega _9(q)$
or
![]() $K_{|S_9}$
is contained in a maximal subgroup
$K_{|S_9}$
is contained in a maximal subgroup
![]() $M\in \{\Omega _9(q_0), \mathrm {SO}_9(q_0)\}$
in class
$M\in \{\Omega _9(q_0), \mathrm {SO}_9(q_0)\}$
in class
![]() $\mathcal {C}_5$
, where
$\mathcal {C}_5$
, where
![]() $q=q_0^r$
for some prime
$q=q_0^r$
for some prime
![]() $r\geq 2$
. Suppose there exists
$r\geq 2$
. Suppose there exists
![]() $g\in \mathrm {GL}_{9}(\mathbb {F})$
such that
$g\in \mathrm {GL}_{9}(\mathbb {F})$
such that
![]() $\tau ^g=\tau _0$
,
$\tau ^g=\tau _0$
,
![]() $y^g= y_0$
, with
$y^g= y_0$
, with
![]() $\tau _0,y_0\in \mathrm {GL}_{9}(q_0)$
. From
$\tau _0,y_0\in \mathrm {GL}_{9}(q_0)$
. From
![]() $\mathrm {tr}((y\tau )^2)=-2176a^4 + 6784a^2 - 224$
and
$\mathrm {tr}((y\tau )^2)=-2176a^4 + 6784a^2 - 224$
and
![]() $\mathrm {tr}((y^2\tau )^2)=1920a^4 - 5504a^2 - 288$
, we get that
$\mathrm {tr}((y^2\tau )^2)=1920a^4 - 5504a^2 - 288$
, we get that
![]() $-17a^4+53a^2$
and
$-17a^4+53a^2$
and
![]() $15a^4-43a^2$
belong to
$15a^4-43a^2$
belong to
![]() $\mathbb {F}_{q_0}$
, whence
$\mathbb {F}_{q_0}$
, whence
![]() $64a^2\in \mathbb {F}_{q_0}$
. We conclude that
$64a^2\in \mathbb {F}_{q_0}$
. We conclude that
![]() $K_{|S_9}=\Omega _9(q)$
.
$K_{|S_9}=\Omega _9(q)$
.
Corollary 6.6. Assume q odd and
![]() $n\in \{12,16,20\}$
. Let
$n\in \{12,16,20\}$
. Let
![]() $a \in \mathbb {F}_q^*$
be such that
$a \in \mathbb {F}_q^*$
be such that
![]() ${\mathbb {F}_p[a^2]=\mathbb {F}_q}$
with
${\mathbb {F}_p[a^2]=\mathbb {F}_q}$
with
![]() $a^2\neq 2,3$
. Then
$a^2\neq 2,3$
. Then
![]() $H=\Omega _{n}^+(q)$
. In particular,
$H=\Omega _{n}^+(q)$
. In particular,
![]() $\Omega _n^+(q)$
is
$\Omega _n^+(q)$
is
![]() $(2,3)$
-generated.
$(2,3)$
-generated.
Proof. Since
![]() $K_{|S_9}=\Omega _9(q)$
, we can repeat the argument of Corollary 5.6, proving that
$K_{|S_9}=\Omega _9(q)$
, we can repeat the argument of Corollary 5.6, proving that
![]() $H=\Omega _{n}^+(q)$
. For the second part of the statement, we have to prove that there exists an element a satisfying all the hypotheses. If
$H=\Omega _{n}^+(q)$
. For the second part of the statement, we have to prove that there exists an element a satisfying all the hypotheses. If
![]() $q=p$
, take
$q=p$
, take
![]() $a=1$
. Suppose now
$a=1$
. Suppose now
![]() $q=p^f$
with
$q=p^f$
with
![]() $f\geq 2$
and let
$f\geq 2$
and let
![]() $\mathcal {N}(q)$
be the number of elements
$\mathcal {N}(q)$
be the number of elements
![]() $b\in \mathbb {F}_q^*$
such that
$b\in \mathbb {F}_q^*$
such that
![]() $\mathbb {F}_p[b^2]\neq \mathbb {F}_q$
. By [Reference Pellegrini, Tamburini Bellani and Vsemirnov12, Lemma 2.7], it suffices to check that the condition
$\mathbb {F}_p[b^2]\neq \mathbb {F}_q$
. By [Reference Pellegrini, Tamburini Bellani and Vsemirnov12, Lemma 2.7], it suffices to check that the condition
![]() $p^f - 2p ({p^{\lfloor f/2 \rfloor }-1})/({p-1})> 1$
is always fulfilled (the requirements
$p^f - 2p ({p^{\lfloor f/2 \rfloor }-1})/({p-1})> 1$
is always fulfilled (the requirements
![]() $a^2\neq 2,3$
can be dropped).
$a^2\neq 2,3$
can be dropped).
7 Conclusions
We can now prove our main result.
Proof of Theorem 1.1.
The
![]() $(2,3)$
-generation of
$(2,3)$
-generation of
![]() $\Omega _n(q)$
,
$\Omega _n(q)$
,
![]() $nq$
odd, follows from Theorem 3.7 when
$nq$
odd, follows from Theorem 3.7 when
![]() $n\in \{9,11,13,17\}$
and Corollary 5.6 for the other values of n. Due to Corollaries 5.6 and 6.6, we also proved the
$n\in \{9,11,13,17\}$
and Corollary 5.6 for the other values of n. Due to Corollaries 5.6 and 6.6, we also proved the
![]() $(2,3)$
-generation of the following even-dimensional orthogonal groups:
$(2,3)$
-generation of the following even-dimensional orthogonal groups:
![]() $\Omega _{2k}^+(q)$
, when
$\Omega _{2k}^+(q)$
, when
![]() $q\equiv 1 ~\mathrm {(mod~ 4)}$
and
$q\equiv 1 ~\mathrm {(mod~ 4)}$
and
![]() $k=6$
or
$k=6$
or
![]() $k\geq 8$
;
$k\geq 8$
;
![]() $\Omega _{4k}^+(q)$
, when
$\Omega _{4k}^+(q)$
, when
![]() $q\equiv 3~\mathrm {(mod~ 4)}$
and
$q\equiv 3~\mathrm {(mod~ 4)}$
and
![]() $k\geq 3$
;
$k\geq 3$
;
![]() $\Omega _{4k+2}^-(q)$
, when
$\Omega _{4k+2}^-(q)$
, when
![]() $q\equiv 3~\mathrm {(mod~ 4)}$
and
$q\equiv 3~\mathrm {(mod~ 4)}$
and
![]() $k\geq 4$
.
$k\geq 4$
.