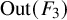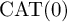Refine search
Actions for selected content:
150 results
A note on morphisms to wreath products
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 08 October 2025, pp. 1-28
-
- Article
- Export citation
Rigidity phenomena and the statistical properties of group actions on
 $\text {CAT}(0)$ cube complexes
$\text {CAT}(0)$ cube complexes
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 19 September 2025, e150
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The conjugacy ratio of abelian-by-cyclic groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 17 September 2025, pp. 1-24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quantitative ergodic theorems for actions of groups of polynomial growth
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 46 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 04 September 2025, pp. 128-181
- Print publication:
- January 2026
-
- Article
- Export citation
Higher incoherence of the automorphism groups of a free group
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 01 September 2025, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Posets arising from decompositions of objects in a monoidal category
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 July 2025, e123
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Thompson’s group T has quadratic Dehn function
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 08 July 2025, e109
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Hanna Neumann conjecture for graphs of free groups with cyclic edge groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 09 September 2025, pp. 1576-1614
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rotation groups virtually embed into right-angled rotation groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 16 June 2025, pp. 1-25
-
- Article
- Export citation
On Thompson groups for Ważewski dendrites
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 19 May 2025, pp. 189-231
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rigidity of mapping class groups MOD powers of twists
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 07 April 2025, pp. 1-71
-
- Article
- Export citation
A hyperbolic free-by-cyclic group determined by its finite quotients
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 04 April 2025, pp. 500-502
- Print publication:
- September 2025
-
- Article
- Export citation
The Klein bottle has stably unbounded homeomorphism group
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 04 April 2025, pp. 494-499
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tree-like graphings, wallings, and median graphings of equivalence relations
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 26 March 2025, e64
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Pride–Guba–Sapir exact sequence for the relation bimodule of an associative algebra
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 467-474
- Print publication:
- September 2025
-
- Article
- Export citation
Are free groups of different ranks bi-invariantly quasi-isometric?
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 26 February 2025, pp. 356-364
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The conjugacy problem for
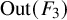 $\operatorname {Out}(F_3)$
$\operatorname {Out}(F_3)$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 13 February 2025, e41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Automorphisms of fine curve graphs for nonorientable surfaces
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 16 January 2025, pp. 232-244
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PROPER
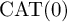 $\mathrm {CAT(0)}$ ACTIONS OF UNIPOTENT-FREE LINEAR GROUPS
$\mathrm {CAT(0)}$ ACTIONS OF UNIPOTENT-FREE LINEAR GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 07 January 2025, pp. 587-601
- Print publication:
- March 2025
-
- Article
- Export citation
Ideals of equations for elements in a free group and Stallings folding
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 19 December 2024, pp. 421-462
-
- Article
- Export citation