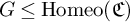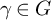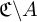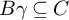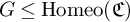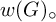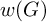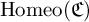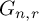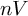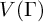1. Introduction
The papers [Reference Epstein13, Reference Higman17, Reference Ling22] provide conditions on a permutation group, or on a group of homeomorphisms, which imply simplicity of the commutator subgroup of that group. Two of the core conditions in those works are that the group is generated by elements with ‘small’ support (with differing definitions of the concept of small), and that the group acts nearly transitively (in the sense that given small sets can be sent into target small sets using elements which act as the identity off of some containing set which itself is ‘small enough’). Taken at a broad level of interpretation, one sees that these ideas also play a central role for the same result for large enough finite symmetric groups.
In this article, we explore some consequences of a similar set of conditions on groups of homeomorphisms of Cantor space
![]() $\mathfrak {C}$
, by which we mean any space homeomorphic to
$\mathfrak {C}$
, by which we mean any space homeomorphic to
![]() $\{0,1\}^\omega $
, the countably infinite product of the discrete space
$\{0,1\}^\omega $
, the countably infinite product of the discrete space
![]() $\{0,1\}$
with itself. The results here are new, but some of them bear comparison with results of Matui [Reference Matui28, Reference Matui29, Reference Matui30, Reference Matui32] and of Nekrashevych [Reference Nekrashevych35] for different (but related) families of groups.
$\{0,1\}$
with itself. The results here are new, but some of them bear comparison with results of Matui [Reference Matui28, Reference Matui29, Reference Matui30, Reference Matui32] and of Nekrashevych [Reference Nekrashevych35] for different (but related) families of groups.
A central new result is our Theorem 5.15: for a large family
![]() $\mathscr {K}^{\text {f.g.}}$
of finitely generated simple groups, each group in
$\mathscr {K}^{\text {f.g.}}$
of finitely generated simple groups, each group in
![]() $\mathscr {K}^{\text {f.g.}}$
is actually two-generated by torsion elements. We are unaware of a similar result in the literature. Note that this result applies to all of the known simple groups arising out of generalising the construction of the R. Thompson group V (e.g. the commutator subgroups of The Higman–Thompson groups
$\mathscr {K}^{\text {f.g.}}$
is actually two-generated by torsion elements. We are unaware of a similar result in the literature. Note that this result applies to all of the known simple groups arising out of generalising the construction of the R. Thompson group V (e.g. the commutator subgroups of The Higman–Thompson groups
![]() $G_{n,r}$
[Reference Higman17], the Brin-Thompson groups
$G_{n,r}$
[Reference Higman17], the Brin-Thompson groups
![]() $nV$
[Reference Brin6], the Röver group
$nV$
[Reference Brin6], the Röver group
![]() $V(\Gamma )$
[Reference Röver37], and many others of the ‘simple groups of dynamical origin’ of Nekrasheych [Reference Nekrashevych35]). Specifically, we believe this theorem provides the first proof that Röver’s group
$V(\Gamma )$
[Reference Röver37], and many others of the ‘simple groups of dynamical origin’ of Nekrasheych [Reference Nekrashevych35]). Specifically, we believe this theorem provides the first proof that Röver’s group
![]() $V(\Gamma )$
is two-generated. Finally, Belk and Zaremsky in [Reference Belk and Zaremsky3] employ Theorem 5.15 as part of their argument which gives a quasi-isometric embedding of any finitely generated group into a two-generated simple group.
$V(\Gamma )$
is two-generated. Finally, Belk and Zaremsky in [Reference Belk and Zaremsky3] employ Theorem 5.15 as part of their argument which gives a quasi-isometric embedding of any finitely generated group into a two-generated simple group.
We also derive dynamical conditions guaranteeing simplicity, and our conditions determine that the groups involved satisfy no laws, and indeed, the stronger condition that they are mixed identity free.
Part of our motivation has been the well known open question as to whether there are any finitely presented simple groups which are not two-generated (see [Reference Guba15] for finitely generated simple groups, with every two-generated subgroup being a free group). Thus, our results here exclude many natural candidate groups found within the setting of groups of homeomorphisms of Cantor space. Somewhat artificially, we observe the well known fact (see Proposition 6.3) that any countably infinite group can be realised as a group of homeomorphisms of Cantor space (although, the easy proof we give of this produces groups which do not satisfy our dynamical condition).
1.1. Freedom of action
In this paper, we follow the notational convention occurring in many papers on groups of homeomorphisms of a space, and, in particular, in many papers in the R. Thompson groups literature (see, e.g. [Reference Brin6]). Specifically, standard operators usually act on the left (such as ‘Homeo(
![]() $\cdot $
)’ and ‘supt(
$\cdot $
)’ and ‘supt(
![]() $\cdot $
)’, below), but group actions and created functions in the text will act on the right. For example, given an element
$\cdot $
)’, below), but group actions and created functions in the text will act on the right. For example, given an element
![]() $\gamma \in \operatorname {Homeo}(\mathfrak {C})$
, we denote by
$\gamma \in \operatorname {Homeo}(\mathfrak {C})$
, we denote by
![]() $\operatorname {supt}\!\left (\gamma \right )$
the support of
$\operatorname {supt}\!\left (\gamma \right )$
the support of
![]() $\gamma $
, that is, the set of all points which are actually moved by
$\gamma $
, that is, the set of all points which are actually moved by
![]() $\gamma $
:
$\gamma $
:
An example of this usage is that we also follow the convention established in the literature for verbal subgroups, where the sets
![]() $w[G]$
and
$w[G]$
and
![]() $w(G)$
(defined below in Section 1.2) are naturally thought of as examples of ‘left’ action notation. Two standard consequences of using right action notation are the following formulae:
$w(G)$
(defined below in Section 1.2) are naturally thought of as examples of ‘left’ action notation. Two standard consequences of using right action notation are the following formulae:
 $$ \begin{align*} h^g &:= g^{-1}hg; \textrm{ and }\\ [g,h] &:= g^{-1}h^{-1}gh = (h^{-1})^{g} \cdot h = g^{-1} \cdot g^h. \end{align*} $$
$$ \begin{align*} h^g &:= g^{-1}hg; \textrm{ and }\\ [g,h] &:= g^{-1}h^{-1}gh = (h^{-1})^{g} \cdot h = g^{-1} \cdot g^h. \end{align*} $$
Definition 1.1. We will say that a subset S of
![]() $\operatorname {Homeo}(\mathfrak {C})$
is vigorous if and only if for all
$\operatorname {Homeo}(\mathfrak {C})$
is vigorous if and only if for all
![]() $A,B,C$
clopen subsets of
$A,B,C$
clopen subsets of
![]() $\mathfrak {C}$
with B and C proper (nonempty) subsets of A, there exists
$\mathfrak {C}$
with B and C proper (nonempty) subsets of A, there exists
![]() $\gamma $
in S with
$\gamma $
in S with
![]() $\operatorname {supt}\!\left (\gamma \right ) \subseteq A$
and
$\operatorname {supt}\!\left (\gamma \right ) \subseteq A$
and
![]() $B\gamma \subseteq C$
.
$B\gamma \subseteq C$
.
Note that in the above definition, the requirement that
![]() $B, C$
be proper subsets of A cannot be removed. For example, in the case that
$B, C$
be proper subsets of A cannot be removed. For example, in the case that
![]() $C\subsetneq B=A = \mathfrak {C}$
, there is no
$C\subsetneq B=A = \mathfrak {C}$
, there is no
![]() $\gamma $
with
$\gamma $
with
![]() $B\gamma \subseteq C$
. Consequently, we cannot replace A with
$B\gamma \subseteq C$
. Consequently, we cannot replace A with
![]() $B \cup C$
.
$B \cup C$
.
We use the word vigorous because it is evocative of thoroughly mixing the Cantor set. The following lemma is immediate from the definition of vigorous.
Lemma 1.2. If F and G are subgroups of
![]() $\operatorname {Homeo}(\mathfrak {C})$
with F vigorous and contained in G, then G is also vigorous.
$\operatorname {Homeo}(\mathfrak {C})$
with F vigorous and contained in G, then G is also vigorous.
The reader can check that R. Thompson’s group
![]() $V_2$
is a vigorous group (see Section 2.1 for a definition of
$V_2$
is a vigorous group (see Section 2.1 for a definition of
![]() $V_2$
). Now, by Lemma 1.2, we see that Röver’s group [Reference Röver37] and the finitely generated simple overgroups of
$V_2$
). Now, by Lemma 1.2, we see that Röver’s group [Reference Röver37] and the finitely generated simple overgroups of
![]() $V_2$
constructed in [Reference Nekrashevych35] are vigorous as well.
$V_2$
constructed in [Reference Nekrashevych35] are vigorous as well.
1.2. The word is law
Let
![]() $F_j$
be a free group on symbols
$F_j$
be a free group on symbols
![]() $x_1$
, …,
$x_1$
, …,
![]() $x_j$
and G be a group with
$x_j$
and G be a group with
![]() $w = a_1a_2\dots a_m$
a word in the letters
$w = a_1a_2\dots a_m$
a word in the letters
![]() $\{x_1,\ldots ,x_j\}^{\pm 1}$
. Consider the function
$\{x_1,\ldots ,x_j\}^{\pm 1}$
. Consider the function
![]() $w:G^j\to G$
, defined by mapping the element
$w:G^j\to G$
, defined by mapping the element
![]() $(g_1,\ldots ,g_j)\in G^j$
to the element of G obtained by substituting
$(g_1,\ldots ,g_j)\in G^j$
to the element of G obtained by substituting
![]() $g_i$
for every occurrence of
$g_i$
for every occurrence of
![]() $x_i$
in w. If we set
$x_i$
in w. If we set
and
then, respectively, the set
![]() $w[G]$
is called the verbal subset for w and
$w[G]$
is called the verbal subset for w and
![]() $w(G)$
is the verbal subgroup for w.
$w(G)$
is the verbal subgroup for w.
It is immediate that verbal subgroups are characteristic, and a standard first example is given by taking
![]() $k = 2$
and
$k = 2$
and
![]() $w = x_1^{-1}x_2^{-1}x_1x_2$
, where
$w = x_1^{-1}x_2^{-1}x_1x_2$
, where
![]() $w(G)$
is then the commutator subgroup of G (see [Reference Magnus, Karrass and Solitar23] for more on verbal subgroups).
$w(G)$
is then the commutator subgroup of G (see [Reference Magnus, Karrass and Solitar23] for more on verbal subgroups).
We will denote the set of nonempty proper clopen subsets of
![]() $\mathfrak {C}$
by
$\mathfrak {C}$
by
![]() $K_{\mathfrak {C}}$
throughout. Note that
$K_{\mathfrak {C}}$
throughout. Note that
![]() $A\in K_{\mathfrak {C}}$
if and only if
$A\in K_{\mathfrak {C}}$
if and only if
![]() $\mathfrak {C}\backslash A\in K_{\mathfrak {C}}$
. If
$\mathfrak {C}\backslash A\in K_{\mathfrak {C}}$
. If
![]() $G\leq \operatorname {Homeo}(\mathfrak {C})$
and
$G\leq \operatorname {Homeo}(\mathfrak {C})$
and
![]() $A\in K_{\mathfrak {C}}$
, then we use
$A\in K_{\mathfrak {C}}$
, then we use
![]() $\operatorname {pstab}_G(A)$
to denote the elements in G which pointwise-stabilise the set A. For
$\operatorname {pstab}_G(A)$
to denote the elements in G which pointwise-stabilise the set A. For
![]() $G\leq \operatorname {Homeo}(\mathfrak {C})$
, we add a subscript
$G\leq \operatorname {Homeo}(\mathfrak {C})$
, we add a subscript
![]() $\circ $
to modify our verbal notations as follows:
$\circ $
to modify our verbal notations as follows:
Recall that a group G satisfies a law if there is a nontrivial freely reduced word w so that
![]() $w(\alpha _1,\alpha _2,\ldots ,\alpha _j)=1_G$
for any choice of
$w(\alpha _1,\alpha _2,\ldots ,\alpha _j)=1_G$
for any choice of
![]() $(\alpha _1,\alpha _2,\ldots ,\alpha _j)\in G^j$
. For example, abelian groups satisfy a law since
$(\alpha _1,\alpha _2,\ldots ,\alpha _j)\in G^j$
. For example, abelian groups satisfy a law since
![]() $w=x_1^{-1}x_2^{-1}x_1x_2$
evaluates to
$w=x_1^{-1}x_2^{-1}x_1x_2$
evaluates to
![]() $1_G$
for all choices of values for the variables
$1_G$
for all choices of values for the variables
![]() $x_1$
and
$x_1$
and
![]() $x_2$
. The law that is satisfied is typically stated as the equation in the variables
$x_2$
. The law that is satisfied is typically stated as the equation in the variables
![]() $x_1$
,
$x_1$
,
![]() $x_2$
,
$x_2$
,
![]() $\ldots $
,
$\ldots $
,
![]() $x_j$
that is satisfied for all choices of substituting group elements. That is,
$x_j$
that is satisfied for all choices of substituting group elements. That is,
![]() $w=1_G$
.
$w=1_G$
.
If a group satisfies no laws, we say it is lawless. Our first theorem is as follows.
Theorem 3.4. Let
![]() $G\leq \operatorname {Homeo}(\mathfrak {C})$
. If G is vigorous, then G is lawless.
$G\leq \operatorname {Homeo}(\mathfrak {C})$
. If G is vigorous, then G is lawless.
In fact, as pointed out by a helpful referee, a stronger theorem holds.
Let G be a group, and F a nontrivial free group. A mixed identity for G is
![]() $w\in G*F$
, such that
$w\in G*F$
, such that
![]() $1_G=(w)\phi $
for every homomorphism
$1_G=(w)\phi $
for every homomorphism
![]() $\phi : G*F\to G$
, such that
$\phi : G*F\to G$
, such that
![]() $\phi |_G$
is the identity. A mixed identity w is nontrivial if w is not the identity element of
$\phi |_G$
is the identity. A mixed identity w is nontrivial if w is not the identity element of
![]() $G*F$
. The group G is mixed identity free if it has no nontrivial mixed identity (see [Reference Anashin2, Reference Hull and Osin18] for more details).
$G*F$
. The group G is mixed identity free if it has no nontrivial mixed identity (see [Reference Anashin2, Reference Hull and Osin18] for more details).
Theorem 3.5. Let
![]() $G\leq \operatorname {Homeo}(\mathfrak {C})$
. If G is vigorous, then G is mixed identity free.
$G\leq \operatorname {Homeo}(\mathfrak {C})$
. If G is vigorous, then G is mixed identity free.
Definition 1.3. A subgroup G of
![]() $\operatorname {Homeo}(\mathfrak {C})$
is flawless if and only if G is equal to
$\operatorname {Homeo}(\mathfrak {C})$
is flawless if and only if G is equal to
![]() $w(G)_\circ $
for every nontrivial freely reduced word w.
$w(G)_\circ $
for every nontrivial freely reduced word w.
While it might seem that (outside of the trivial subgroup) flawless groups ought to be hard to discover among the subgroups of
![]() $\operatorname {Homeo}(\mathfrak {C})$
, in fact, many well known groups of homeomorphisms of Cantor space are flawless.
$\operatorname {Homeo}(\mathfrak {C})$
, in fact, many well known groups of homeomorphisms of Cantor space are flawless.
We now state a lemma where each result is immediate from the definition of flawless.
Lemma 1.4. Let
![]() $G\leq \operatorname {Homeo}(\mathfrak {C})$
be nontrivial and flawless. Then
$G\leq \operatorname {Homeo}(\mathfrak {C})$
be nontrivial and flawless. Then
-
1. G is lawless,
-
2. G is perfect,
-
3.
 $G=w(G)$
for any nontrivial freely reduced word w.
$G=w(G)$
for any nontrivial freely reduced word w.
Lemma 1.4 motivates our choice of the term flawless.
To state our next result, we will need several more definitions.
If
![]() $\gamma \in \operatorname {Homeo}(\mathfrak {C})$
fixes a proper clopen set A pointwise, then its support is contained in
$\gamma \in \operatorname {Homeo}(\mathfrak {C})$
fixes a proper clopen set A pointwise, then its support is contained in
![]() $\mathfrak {C}\backslash A$
. So the elements in
$\mathfrak {C}\backslash A$
. So the elements in
![]() $x[G]_\circ $
(that is,
$x[G]_\circ $
(that is,
![]() $w[G]_\circ $
with word
$w[G]_\circ $
with word
![]() $w=x$
) are precisely those homeomorphisms which admit a proper clopen set containing their support: we call these the elements of small support.
$w=x$
) are precisely those homeomorphisms which admit a proper clopen set containing their support: we call these the elements of small support.
Definition 1.5. A subgroup G of
![]() $\operatorname {Homeo}(\mathfrak {C})$
is generated by its elements of small support if and only if
$\operatorname {Homeo}(\mathfrak {C})$
is generated by its elements of small support if and only if
![]() $G=x(G)_\circ $
.
$G=x(G)_\circ $
.
1.3. (Approximately) full groups
The next definition is used in [Reference Lawson21].
Definition 1.6. We say a subgroup G of
![]() $\operatorname {Homeo}(\mathfrak {C})$
is full if and only if for all
$\operatorname {Homeo}(\mathfrak {C})$
is full if and only if for all
![]() $\gamma _1, \ldots , \gamma _n \in G$
and
$\gamma _1, \ldots , \gamma _n \in G$
and
![]() $D_1, D_2, \ldots , D_n$
clopen sets partitioning
$D_1, D_2, \ldots , D_n$
clopen sets partitioning
![]() $\mathfrak {C}$
so that
$\mathfrak {C}$
so that
![]() $D_1 \gamma _1, D_2\gamma _2,\ldots , D_n \gamma _n$
also partitions
$D_1 \gamma _1, D_2\gamma _2,\ldots , D_n \gamma _n$
also partitions
![]() $\mathfrak {C}$
, we have the union of partial functions
$\mathfrak {C}$
, we have the union of partial functions
is also in G.
The following is a weaker condition, which turns out to be natural in the context considered here.
Definition 1.7. We will say a subgroup G of
![]() $\operatorname {Homeo}(\mathfrak {C})$
is approximately full if and only if whenever
$\operatorname {Homeo}(\mathfrak {C})$
is approximately full if and only if whenever
![]() $\gamma _1, \ldots , \gamma _n\in G$
and
$\gamma _1, \ldots , \gamma _n\in G$
and
![]() $D_1, \ldots , D_n$
are clopen sets partitioning
$D_1, \ldots , D_n$
are clopen sets partitioning
![]() $\mathfrak {C}$
, such that
$\mathfrak {C}$
, such that
![]() $D_1 \gamma _1, D_2\gamma _2, \ldots , D_n \gamma _n$
also partitions
$D_1 \gamma _1, D_2\gamma _2, \ldots , D_n \gamma _n$
also partitions
![]() $\mathfrak {C}$
and
$\mathfrak {C}$
and
![]() $j\in \{1, \ldots , n\}$
, then there exists
$j\in \{1, \ldots , n\}$
, then there exists
![]() $\chi $
in G, such that
$\chi $
in G, such that
![]() $\chi $
extends
$\chi $
extends
![]() $\gamma _i|_{D_i}$
for each
$\gamma _i|_{D_i}$
for each
![]() $i \in \{1, \ldots , n\} \setminus \{j\}$
.
$i \in \{1, \ldots , n\} \setminus \{j\}$
.
Remark 1.8. For the curious reader, the commutator subgroup of the Higman–Thompson group
![]() $G_{3,1}$
is an example of a group of homeomorphisms of Cantor space which is approximately full but not full (the group
$G_{3,1}$
is an example of a group of homeomorphisms of Cantor space which is approximately full but not full (the group
![]() $G_{3,1}$
is commonly denoted by
$G_{3,1}$
is commonly denoted by
![]() $V_3$
following a notation introduced by Brown in [Reference Brown9]).
$V_3$
following a notation introduced by Brown in [Reference Brown9]).
We give a sketch argument here. We say that an element
![]() $f\in V_3$
is odd if there is
$f\in V_3$
is odd if there is
![]() $n\in \mathbb {N}$
, such that whenever
$n\in \mathbb {N}$
, such that whenever
![]() $p_1< \ldots < p_{k}\in \{0, 1, 2\}^*$
(in dictionary order) are such that every element of
$p_1< \ldots < p_{k}\in \{0, 1, 2\}^*$
(in dictionary order) are such that every element of
![]() $\{0,1, 2\}^{\mathbb {N}}$
has precisely one of
$\{0,1, 2\}^{\mathbb {N}}$
has precisely one of
![]() $p_1, \ldots , p_{k}$
as a prefix and
$p_1, \ldots , p_{k}$
as a prefix and
![]() $|p_1|, |p_2|, \ldots , |p_{k}|>n$
, it follows that the permutation
$|p_1|, |p_2|, \ldots , |p_{k}|>n$
, it follows that the permutation
![]() $\phi :\{1, \ldots , k\} \to \{ 1, \ldots , k\} $
defined by
$\phi :\{1, \ldots , k\} \to \{ 1, \ldots , k\} $
defined by
is odd. We define even analogously. It is routine to verify that every element of
![]() $V_3$
is either even or odd, but not both (here, we use the fact that 3 is odd). One can then verify that the commutator subgroup
$V_3$
is either even or odd, but not both (here, we use the fact that 3 is odd). One can then verify that the commutator subgroup
![]() $D(V_3)$
of
$D(V_3)$
of
![]() $V_3$
consists of precisely the even elements of
$V_3$
consists of precisely the even elements of
![]() $V_3$
. The full group of
$V_3$
. The full group of
![]() $D(V_3)$
is
$D(V_3)$
is
![]() $V_3$
, but
$V_3$
, but
![]() $D(V_3)$
is only approximately full (one can change an element from odd to even by modifying it on a small clopen set).
$D(V_3)$
is only approximately full (one can change an element from odd to even by modifying it on a small clopen set).
Theorem 4.9. Let G be a subgroup of
![]() $\operatorname {Homeo}(\mathfrak {C})$
.
$\operatorname {Homeo}(\mathfrak {C})$
.
-
1. If G is approximately full, then G is generated by its elements of small support.
-
2. If G is vigorous and generated by its elements of small support, then G is approximately full.
In particular, we have the following corollary.
Corollary 1.9. Let G be a vigorous subgroup of
![]() $\operatorname {Homeo}(\mathfrak {C})$
. Then, G is approximately full if and only if G is generated by its elements of small support.
$\operatorname {Homeo}(\mathfrak {C})$
. Then, G is approximately full if and only if G is generated by its elements of small support.
Our next result is on simplicity. Recall that a group is simple exactly if the normal closure of any nonidentity element is the whole group.
Theorem 4.18. Let G be a vigorous subgroup of
![]() $\operatorname {Homeo}(\mathfrak {C})$
. Then the following are equivalent
$\operatorname {Homeo}(\mathfrak {C})$
. Then the following are equivalent
-
1. G is simple,
-
2. G is flawless,
-
3.
 $G=w(G)_\circ $
with
$G=w(G)_\circ $
with
 $w=x_1^{-1}x_2^{-1}x_1x_2$
,
$w=x_1^{-1}x_2^{-1}x_1x_2$
, -
4. G is perfect and is generated by its elements of small support,
-
5. G is perfect and approximately full, and
-
6. G is the commutator subgroup of its own full group within
 $\operatorname {Homeo}(\mathfrak {C})$
.
$\operatorname {Homeo}(\mathfrak {C})$
.
The reader may recall that it is already known that point (6) implies point (1), above, when the full group of G is the full group of an essentially principle minimal étale groupoid
![]() $\mathscr {G}$
. This is a theorem of Matui in [Reference Matui31]. Indeed, Matui’s proof of that direction essentially holds up in our context, although, in general, our context is quite different. For example, our class of groups contains uncountable groups. The remaining parts of the theorem are new.
$\mathscr {G}$
. This is a theorem of Matui in [Reference Matui31]. Indeed, Matui’s proof of that direction essentially holds up in our context, although, in general, our context is quite different. For example, our class of groups contains uncountable groups. The remaining parts of the theorem are new.
1.4. On finitely generated vigorous simple groups
We next turn our attention to the class of vigorous simple subgroups of
![]() $\operatorname {Homeo}(\mathfrak {C})$
, and, in particular, to the subclass of those groups which are finitely generated.
$\operatorname {Homeo}(\mathfrak {C})$
, and, in particular, to the subclass of those groups which are finitely generated.
Theorem 5.15. Let
![]() $G \leq \operatorname {Homeo}(\mathfrak {C})$
be finitely generated simple and vigorous. Let
$G \leq \operatorname {Homeo}(\mathfrak {C})$
be finitely generated simple and vigorous. Let
![]() $n\in \mathbb {Z}$
be at least
$n\in \mathbb {Z}$
be at least
![]() $2$
. Then there exists
$2$
. Then there exists
![]() $\sigma $
and
$\sigma $
and
![]() $\zeta $
in G, such that
$\zeta $
in G, such that
![]() $\sigma $
is of finite order and
$\sigma $
is of finite order and
![]() $\zeta $
is of order n and
$\zeta $
is of order n and
![]() $\left \langle \sigma ,\zeta \right \rangle = G$
.
$\left \langle \sigma ,\zeta \right \rangle = G$
.
Remark 1.10. It follows that the Röver group
![]() $V(\Gamma )$
[Reference Röver37] is two-generated. Röver actually builds an infinite family of finitely presented simple groups, as Röver’s constructed groups are all overgroups of R. Thompson’s group
$V(\Gamma )$
[Reference Röver37] is two-generated. Röver actually builds an infinite family of finitely presented simple groups, as Röver’s constructed groups are all overgroups of R. Thompson’s group
![]() $V_2$
in
$V_2$
in
![]() $\operatorname {Homeo}(\mathfrak {C})$
are all vigorous. Thus, by Theorem 5.15, they are all two-generated by torsion elements.
$\operatorname {Homeo}(\mathfrak {C})$
are all vigorous. Thus, by Theorem 5.15, they are all two-generated by torsion elements.
Definition 1.11. We will write
![]() $\mathscr {K}$
for the family of subgroups of
$\mathscr {K}$
for the family of subgroups of
![]() $\operatorname {Homeo}(\mathfrak {C})$
which are simple and vigorous. We will write
$\operatorname {Homeo}(\mathfrak {C})$
which are simple and vigorous. We will write
![]() $\mathscr {K}^{\text {f.g.}}$
for the family of finitely generated groups in
$\mathscr {K}^{\text {f.g.}}$
for the family of finitely generated groups in
![]() $\mathscr {K}$
.
$\mathscr {K}$
.
1.5. An outline of what follows
The remainder of the paper can be loosely described as follows:
In Section 2, we give some background information on Cantor space and some well known groups of homeomorphisms of Cantor space which happen to be vigorous (i.e. the Higman–Thompson groups).
In Section 3, we explore properties of vigorous groups: namely, that they are lawless and indeed satisfy the stronger property of being mixed identity free. We also provide an example group that is vigorous, perfect, and lawless, but not simple (nor flawless).
In Section 4, we prove Theorems 4.9 and 4.18. This section has an initial part where we explore some dynamical properties of being vigorous, and two following subsections.
In Subsection 4.1, we introduce the further concept of strongly approximately full, and explore the relationships between the various versions of ‘full’, with or without the extra property of being vigorous. Here, we prove Theorem 4.9. We also touch on the interplay between a group being flexible (a concept which appears in many versions of Rubin’s spatial reconstruction theorem [Reference Rubin38]) and being vigorous. Specifically, we show that for a group of homeomorphisms of Cantor space, being flexible is a weaker property than being vigorous, but if the group is approximately full, then vigorous and flexible become equivalent properties.
In the following Section 4.2, we prove Theorem 4.18, which we recall states that for a vigorous group, many different conditions are equivalent (one of these is simplicity).
In Section 5, we explore properties of the groups in the classes
![]() $\mathscr {K}$
and
$\mathscr {K}$
and
![]() $\mathscr {K}^{\text {f.g.}}$
. We show that
$\mathscr {K}^{\text {f.g.}}$
. We show that
![]() $\mathscr {K}$
and
$\mathscr {K}$
and
![]() $\mathscr {K}^{\text {f.g.}}$
are closed under some natural constructions, and, of course, recall that
$\mathscr {K}^{\text {f.g.}}$
are closed under some natural constructions, and, of course, recall that
![]() $\mathscr {K}^{\text {f.g.}}$
contains some well known groups, such as all of the standard simple generalisations of R. Thompson’s group
$\mathscr {K}^{\text {f.g.}}$
contains some well known groups, such as all of the standard simple generalisations of R. Thompson’s group
![]() $V_2$
(e.g. the commutator subgroups
$V_2$
(e.g. the commutator subgroups
![]() $D(V_{n})$
of the Higman-Thompson groups
$D(V_{n})$
of the Higman-Thompson groups
![]() $V_{n}$
(note that
$V_{n}$
(note that
![]() $D(V_{n})=V_n$
when n is even, and
$D(V_{n})=V_n$
when n is even, and
![]() $D(V_{n})$
is an index two subgroup of
$D(V_{n})$
is an index two subgroup of
![]() $V_n$
when n is odd), the Röver group
$V_n$
when n is odd), the Röver group
![]() $V_\Gamma $
, the Brin-Thompson groups
$V_\Gamma $
, the Brin-Thompson groups
![]() $nV$
, and the finitely generated simple groups of dynamical origin of Nekrashevych [Reference Nekrashevych35]). Given a simple vigorous group G, we introduce a constructed ‘homology’ group
$nV$
, and the finitely generated simple groups of dynamical origin of Nekrashevych [Reference Nekrashevych35]). Given a simple vigorous group G, we introduce a constructed ‘homology’ group
![]() $\mathfrak {X}_{G}$
(following a model provided by Matui [Reference Matui29] which applies to our context), and we use properties of these induced groups to prove Theorem 5.15 that any groups in
$\mathfrak {X}_{G}$
(following a model provided by Matui [Reference Matui29] which applies to our context), and we use properties of these induced groups to prove Theorem 5.15 that any groups in
![]() $\mathscr {K}^{\text {f.g.}}$
are two-generated by torsion elements.
$\mathscr {K}^{\text {f.g.}}$
are two-generated by torsion elements.
In Section 6, we give a brief discussion of some directions for potential future work.
This paper contains parts of chapter 3 of the dissertation [Reference Hyde20]. The definitions of being flawless, vigorous, and approximately full are original to this work, though approximately full is similar to full as discussed in [Reference Lawson21, Reference Matui29, Reference Nekrashevych35]. As alluded to above, we use the word flawless because of its association with both perfection and lawlessness.
We emphasise that unlike the properties of being simple or perfect, the properties of being vigorous, flawless, full, and approximately full are dependent not just on the groups but also on their actions on
![]() $\mathfrak {C}$
.
$\mathfrak {C}$
.
2. On Cantor space
For natural
![]() $n>1$
, we give the set
$n>1$
, we give the set
![]() $\{0,1,\ldots , n-1\}$
the discrete topology and set
$\{0,1,\ldots , n-1\}$
the discrete topology and set
![]() $\mathfrak {C}_n:= \{0,1,\ldots ,n-1\}^\omega $
to which we give the product topology. Specifically, we have
$\mathfrak {C}_n:= \{0,1,\ldots ,n-1\}^\omega $
to which we give the product topology. Specifically, we have
For a given finite string
![]() $w=w_0w_1\ldots w_k$
(for some natural k), where each
$w=w_0w_1\ldots w_k$
(for some natural k), where each
![]() $w_i\in \{0,1,\ldots , n-1\}$
, the cone at w is the set
$w_i\in \{0,1,\ldots , n-1\}$
, the cone at w is the set
The standard basis for the topology of
![]() $\mathfrak {C}_n$
is then the full set of such cones, which we might call the basic open cones of
$\mathfrak {C}_n$
is then the full set of such cones, which we might call the basic open cones of
![]() $\mathfrak {C}_n$
.
$\mathfrak {C}_n$
.
Central to our point of view is Brouwer’s characterisation [Reference Brouwer8] of Cantor space as a nonempty, compact Hausdorff space, without isolated points, and having a countable basis consisting of clopen sets. From this view, we see that all of the spaces
![]() $\mathfrak {C}_n$
so defined are homeomorphic.
$\mathfrak {C}_n$
so defined are homeomorphic.
Now, for any given generic Cantor space
![]() $\mathfrak {C}$
( those which are not among the spaces
$\mathfrak {C}$
( those which are not among the spaces
![]() $\mathfrak {C}_n$
defined above), we will assume an implicit homeomorphism
$\mathfrak {C}_n$
defined above), we will assume an implicit homeomorphism
![]() $\phi $
to
$\phi $
to
![]() $\{0,1\}^\omega $
, which then provides an explicit basis of open sets for the topology of
$\{0,1\}^\omega $
, which then provides an explicit basis of open sets for the topology of
![]() $\mathfrak {C}$
. For the topology of
$\mathfrak {C}$
. For the topology of
![]() $\mathfrak {C}_n$
, we will use the basis as given above.
$\mathfrak {C}_n$
, we will use the basis as given above.
In the body of this paper, we will typically work with clopen sets, that is, sets which are both open and closed. In
![]() $\mathfrak {C}_n$
, these sets are precisely those sets which can be written as unions of finitely many basic open cones.
$\mathfrak {C}_n$
, these sets are precisely those sets which can be written as unions of finitely many basic open cones.
Mostly relevant for subsets of Cantor space, but perhaps appearing elsewhere below, we use the notation
![]() $\sqcup $
for unions of sets, where the sets appearing in the union are guaranteed to be disjoint from each other (and, particularly, only where it is easily clear from previous lines that the sets are disjoint). That is, the notation is meant as a helpful reminder that the sets are disjoint, and not as a claim to that effect. In the cases that the sets appearing in the union may not be disjoint, or where it is not intended that the reader already knows that they are disjoint, we use the usual
$\sqcup $
for unions of sets, where the sets appearing in the union are guaranteed to be disjoint from each other (and, particularly, only where it is easily clear from previous lines that the sets are disjoint). That is, the notation is meant as a helpful reminder that the sets are disjoint, and not as a claim to that effect. In the cases that the sets appearing in the union may not be disjoint, or where it is not intended that the reader already knows that they are disjoint, we use the usual
![]() $\cup $
notation.
$\cup $
notation.
2.1. The Higman–Thompson groups
 $V_n$
$V_n$
A family of groups that arise often in what follows are the Higman–Thompson groups
![]() $G_{n,1}$
from Higman’s book [Reference Higman17]. As alluded in the Introduction, we shall follow Brown’s notation from [Reference Brown9], where he uses
$G_{n,1}$
from Higman’s book [Reference Higman17]. As alluded in the Introduction, we shall follow Brown’s notation from [Reference Brown9], where he uses
![]() $V_n$
to represent the group
$V_n$
to represent the group
![]() $G_{n,1}$
. For a given natural
$G_{n,1}$
. For a given natural
![]() $n>1$
, the group
$n>1$
, the group
![]() $V_n$
is the group of homeomorphisms of
$V_n$
is the group of homeomorphisms of
![]() $\mathfrak {C}_n$
generated by the transpositions
$\mathfrak {C}_n$
generated by the transpositions
![]() $(\alpha \;\;\beta )$
, which are the homeomorphisms of
$(\alpha \;\;\beta )$
, which are the homeomorphisms of
![]() $\mathfrak {C}_n$
which transpose the points of
$\mathfrak {C}_n$
which transpose the points of
![]() $\mathfrak {C}_n$
with finite prefix
$\mathfrak {C}_n$
with finite prefix
![]() $\alpha $
with the corresponding points of
$\alpha $
with the corresponding points of
![]() $\mathfrak {C}_n$
with finite prefix
$\mathfrak {C}_n$
with finite prefix
![]() $\beta $
, and otherwise act as the identity. That is, if
$\beta $
, and otherwise act as the identity. That is, if
![]() $\alpha =\alpha _0\alpha _1\ldots \alpha _k$
, and
$\alpha =\alpha _0\alpha _1\ldots \alpha _k$
, and
![]() $\beta =\beta _0\beta _1\ldots \beta _j$
are finite nonempty strings of symbols over the set
$\beta =\beta _0\beta _1\ldots \beta _j$
are finite nonempty strings of symbols over the set
![]() $\{0,1,\ldots ,n-1\}$
(which plays the role of an alphabet), such that neither
$\{0,1,\ldots ,n-1\}$
(which plays the role of an alphabet), such that neither
![]() $\alpha $
nor
$\alpha $
nor
![]() $\beta $
is a prefix of the other, then for all
$\beta $
is a prefix of the other, then for all
![]() $\vec {z}\in \mathfrak {C}_n$
, we have
$\vec {z}\in \mathfrak {C}_n$
, we have
 $$\begin{align*}\vec{z}\cdot(\alpha\;\;\beta)= \left\{ \begin{array}{@{}ll} \vec{z} &\textrm{ if } \vec{z}\not\in \alpha\mathfrak{C}_{n}\sqcup\beta\mathfrak{C}_{n}\\ \beta_0\beta_1\ldots\beta_j z_{k+1}z_{k+2}\ldots & \textrm{ if } \vec{z} = \alpha_0\alpha_1\ldots\alpha_k z_{k+1}z_{k+2}\ldots\in \alpha\mathfrak{C}_{n}\\ \alpha_0\alpha_1\ldots\alpha_k z_{j+1}z_{j+2}\ldots &\textrm{ if } \vec{z}=\beta_1\beta_1\ldots \beta_j z_{j+1}z_{j+2}\ldots\in\beta\mathfrak{C}_{n}. \end{array} \right. \end{align*}$$
$$\begin{align*}\vec{z}\cdot(\alpha\;\;\beta)= \left\{ \begin{array}{@{}ll} \vec{z} &\textrm{ if } \vec{z}\not\in \alpha\mathfrak{C}_{n}\sqcup\beta\mathfrak{C}_{n}\\ \beta_0\beta_1\ldots\beta_j z_{k+1}z_{k+2}\ldots & \textrm{ if } \vec{z} = \alpha_0\alpha_1\ldots\alpha_k z_{k+1}z_{k+2}\ldots\in \alpha\mathfrak{C}_{n}\\ \alpha_0\alpha_1\ldots\alpha_k z_{j+1}z_{j+2}\ldots &\textrm{ if } \vec{z}=\beta_1\beta_1\ldots \beta_j z_{j+1}z_{j+2}\ldots\in\beta\mathfrak{C}_{n}. \end{array} \right. \end{align*}$$
The group
![]() $V_n$
then consists of those homeomorphisms of
$V_n$
then consists of those homeomorphisms of
![]() $\mathfrak {C}_n$
which can be thought of as finitary ‘prefix-exchange’ maps. The paper [Reference Bleak, Cameron, Maissel, Navas and Olukoya4] contains a corresponding definition of the groups
$\mathfrak {C}_n$
which can be thought of as finitary ‘prefix-exchange’ maps. The paper [Reference Bleak, Cameron, Maissel, Navas and Olukoya4] contains a corresponding definition of the groups
![]() $G_{n,r}$
using alphabets, strings, prefix maps, etc., while Higman in [Reference Higman17] gave the initial definitions as groups of automorphisms of particular algebras. We note in passing that
$G_{n,r}$
using alphabets, strings, prefix maps, etc., while Higman in [Reference Higman17] gave the initial definitions as groups of automorphisms of particular algebras. We note in passing that
![]() $V_n$
is a dense subgroup of
$V_n$
is a dense subgroup of
![]() $\operatorname {Homeo}(\mathfrak {C}_n)$
. For each
$\operatorname {Homeo}(\mathfrak {C}_n)$
. For each
![]() $n>1$
, the group
$n>1$
, the group
![]() $V_n$
has a simple commutator subgroup
$V_n$
has a simple commutator subgroup
![]() $D(V_n)$
, and this is the whole group if n is even, or an index two subgroup if n is odd. The groups
$D(V_n)$
, and this is the whole group if n is even, or an index two subgroup if n is odd. The groups
![]() $V_n$
are finitely presented. Thompson introduced
$V_n$
are finitely presented. Thompson introduced
![]() $V:= V_2$
and a related group T as the first examples of infinite, finitely presented simple groups in 1965 (see [Reference Thompson40], and see [Reference Bleak and Quick5] for a presentation of
$V:= V_2$
and a related group T as the first examples of infinite, finitely presented simple groups in 1965 (see [Reference Thompson40], and see [Reference Bleak and Quick5] for a presentation of
![]() $V_2$
using this generating set).
$V_2$
using this generating set).
We state the following result at the full level of generality of the Higman–Thompson groups
![]() $G_{n,r}$
, though we shall only prove it for the groups
$G_{n,r}$
, though we shall only prove it for the groups
![]() $V_n$
(the informed reader will see that the proof easily generalises to the broader context).
$V_n$
(the informed reader will see that the proof easily generalises to the broader context).
Lemma 2.1. The Higman–Thompson groups
![]() $G_{n,r}$
are vigorous.
$G_{n,r}$
are vigorous.
Proof. Let
![]() $n>1$
be an integer, and consider
$n>1$
be an integer, and consider
![]() $V_n$
acting on
$V_n$
acting on
![]() $\mathfrak {C}_{n}$
.
$\mathfrak {C}_{n}$
.
Let A, B, C be nonempty clopen sets in
![]() $\mathfrak {C}_{n}$
so that B and C are proper subsets of A.
$\mathfrak {C}_{n}$
so that B and C are proper subsets of A.
Let
![]() $u_1, u_2,\ldots ,u_k\in \{0,1,\ldots ,n-1\}^*$
be so that
$u_1, u_2,\ldots ,u_k\in \{0,1,\ldots ,n-1\}^*$
be so that
![]() $B=u_1\mathfrak {C}_n\sqcup u_2\mathfrak {C}_n\sqcup \cdots \sqcup u_k\mathfrak {C}_n$
(that is, these cones are pairwise disjoint and form a partition of B: note that such a decomposition exists as B is compact and open, and the cones of
$B=u_1\mathfrak {C}_n\sqcup u_2\mathfrak {C}_n\sqcup \cdots \sqcup u_k\mathfrak {C}_n$
(that is, these cones are pairwise disjoint and form a partition of B: note that such a decomposition exists as B is compact and open, and the cones of
![]() $\mathfrak {C}_n$
form a basis for its topology). Further, let
$\mathfrak {C}_n$
form a basis for its topology). Further, let
![]() $v_1,v_2,v_3\in \{0,1,\ldots ,n-1\}^*$
so that
$v_1,v_2,v_3\in \{0,1,\ldots ,n-1\}^*$
so that
![]() $v_1\mathfrak {C}_n\cap v_2\mathfrak {C}_n=\emptyset $
,
$v_1\mathfrak {C}_n\cap v_2\mathfrak {C}_n=\emptyset $
,
![]() $v_1\mathfrak {C}_n\subseteq A\backslash B$
,
$v_1\mathfrak {C}_n\subseteq A\backslash B$
,
![]() $v_2\mathfrak {C}_n\subset A\backslash C$
, and
$v_2\mathfrak {C}_n\subset A\backslash C$
, and
![]() $v_3\mathfrak {C}_n\subseteq C$
. Define the elements
$v_3\mathfrak {C}_n\subseteq C$
. Define the elements
![]() $\gamma _1, \gamma _2, \gamma _3$
in
$\gamma _1, \gamma _2, \gamma _3$
in
![]() $V_n$
as follows:
$V_n$
as follows:
 $$ \begin{align*} \gamma_1&=(u_1\;\;v_1u_1)(u_2\;\;v_1u_2)\cdots (u_k\;\;v_1u_k)\\ \gamma_2&=(v_1u_1\;\;v_2u_1)(v_1u_2\;\;v_2u_2)\cdots (v_1u_k\;\;v_2u_k)\\ \gamma_3&=(v_2u_1\;\;v_3u_1)(v_2u_2\;\;v_3u_2)\cdots (v_2u_k\;\;v_3u_k) .\end{align*} $$
$$ \begin{align*} \gamma_1&=(u_1\;\;v_1u_1)(u_2\;\;v_1u_2)\cdots (u_k\;\;v_1u_k)\\ \gamma_2&=(v_1u_1\;\;v_2u_1)(v_1u_2\;\;v_2u_2)\cdots (v_1u_k\;\;v_2u_k)\\ \gamma_3&=(v_2u_1\;\;v_3u_1)(v_2u_2\;\;v_3u_2)\cdots (v_2u_k\;\;v_3u_k) .\end{align*} $$
It now follows that the composition
![]() $\gamma _1\gamma _2\gamma _3$
moves B into C, with the action fully supported in A.
$\gamma _1\gamma _2\gamma _3$
moves B into C, with the action fully supported in A.
Note that we built this element as a product of sets of (disjoint support) transpositions in three stages, as it could be the case that
![]() $C\subset B$
, for instance, and so we cannot just transpose any cone in B to one in C without possibly creating an ill-defined map (transpositions are only defined for a pair of disjoint cones).
$C\subset B$
, for instance, and so we cannot just transpose any cone in B to one in C without possibly creating an ill-defined map (transpositions are only defined for a pair of disjoint cones).
Unless we are discussing some explicit example group (such as within Example 3.6), from this point forward, we will generally operate in the setting of a Cantor space
![]() $\mathfrak {C}$
, without needing to explicitly reference the details of the construction of the clopen subsets of
$\mathfrak {C}$
, without needing to explicitly reference the details of the construction of the clopen subsets of
![]() $\mathfrak {C}$
.
$\mathfrak {C}$
.
3. Exploring identities for vigorous groups
In this section, we explore some properties of vigorous groups. In particular, we show that they admit non-abelian free subgroups, and hence are lawless. We go further and show that they have the much stronger property of being mixed identity free, and also that the property of being vigorous is inherited by overgroups. We close by giving an example of a perfect vigorous group which is not simple (and, in particular, is not flawless).
Recall that we denote the set of nonempty proper clopen subsets of
![]() $\mathfrak {C}$
by
$\mathfrak {C}$
by
![]() $K_{\mathfrak {C}}$
throughout.
$K_{\mathfrak {C}}$
throughout.
Lemma 3.1. Let
![]() $G\leq \operatorname {Homeo}(\mathfrak {C})$
be vigorous, and let
$G\leq \operatorname {Homeo}(\mathfrak {C})$
be vigorous, and let
![]() $\{A,B,C\}\subset K_{\mathfrak {C}}$
be a partition of
$\{A,B,C\}\subset K_{\mathfrak {C}}$
be a partition of
![]() $\mathfrak {C}$
into three disjoint proper clopen subsets. Then there is
$\mathfrak {C}$
into three disjoint proper clopen subsets. Then there is
![]() $\gamma \in \operatorname {pstab}_G(A)$
, so that for all
$\gamma \in \operatorname {pstab}_G(A)$
, so that for all
![]() $n\in \mathbb {Z}\backslash \{0\}$
, we have
$n\in \mathbb {Z}\backslash \{0\}$
, we have
![]() $B\gamma ^n\subseteq C$
.
$B\gamma ^n\subseteq C$
.
Proof. Let A, B, and C be in
![]() $K_{\mathfrak {C}}$
be such that
$K_{\mathfrak {C}}$
be such that
![]() $\{A,B,C\}$
is a partition of
$\{A,B,C\}$
is a partition of
![]() $\mathfrak {C}$
. Let
$\mathfrak {C}$
. Let
![]() $D, E\in K_{\mathfrak {C}}$
be such that
$D, E\in K_{\mathfrak {C}}$
be such that
![]() $\{D, E\}$
is a partition of C. Let
$\{D, E\}$
is a partition of C. Let
![]() $\gamma \in \operatorname {pstab}(A)$
be such that
$\gamma \in \operatorname {pstab}(A)$
be such that
![]() $(B \sqcup E)\gamma \subseteq E$
. The element
$(B \sqcup E)\gamma \subseteq E$
. The element
![]() $\gamma $
is as required.
$\gamma $
is as required.
The following is a version of the Ping-Pong lemma similar to that appearing in [Reference de la Harpe12] as the Table-Tennis Lemma.
Lemma 3.2 (Ping-Pong lemma)
Let G be a group acting on a set X, and let
![]() $\Gamma _1$
,
$\Gamma _1$
,
![]() $\Gamma _2$
be two subgroups of G. Let
$\Gamma _2$
be two subgroups of G. Let
![]() $\Gamma $
be the subgroup of G generated by
$\Gamma $
be the subgroup of G generated by
![]() $\Gamma _1$
and
$\Gamma _1$
and
![]() $\Gamma _2$
; assume that
$\Gamma _2$
; assume that
![]() $\Gamma _1$
contains at least three elements and
$\Gamma _1$
contains at least three elements and
![]() $\Gamma _2$
contains at least two elements. Assume that there exists two nonempty subsets
$\Gamma _2$
contains at least two elements. Assume that there exists two nonempty subsets
![]() $X_1$
,
$X_1$
,
![]() $X_2$
in X, with
$X_2$
in X, with
![]() $X_2$
not included in
$X_2$
not included in
![]() $X_1$
, such that
$X_1$
, such that
 $$ \begin{align*} (X_2)\gamma\subseteq X_1 \textrm{ for all } \gamma\in\Gamma_1\backslash \{1_\Gamma\},\\ (X_1)\gamma\subseteq X_2 \textrm{ for all } \gamma\in\Gamma_2\backslash \{1_\Gamma\}. \end{align*} $$
$$ \begin{align*} (X_2)\gamma\subseteq X_1 \textrm{ for all } \gamma\in\Gamma_1\backslash \{1_\Gamma\},\\ (X_1)\gamma\subseteq X_2 \textrm{ for all } \gamma\in\Gamma_2\backslash \{1_\Gamma\}. \end{align*} $$
Then
![]() $\Gamma $
is isomorphic to the free product
$\Gamma $
is isomorphic to the free product
![]() $\Gamma _1*\Gamma _2$
.
$\Gamma _1*\Gamma _2$
.
We will now prove vigorous groups have non-abelian free subgroups through an application of the Ping-Pong lemma.
Theorem 3.3. Let
![]() $G \leq \operatorname {Homeo}(\mathfrak {C})$
be a vigorous group, and let A be in
$G \leq \operatorname {Homeo}(\mathfrak {C})$
be a vigorous group, and let A be in
![]() $K_{\mathfrak {C}}$
. Then a free group of rank
$K_{\mathfrak {C}}$
. Then a free group of rank
![]() $2$
embeds in
$2$
embeds in
![]() $\operatorname {pstab}_G(A)$
.
$\operatorname {pstab}_G(A)$
.
Proof. Let B, C be in
![]() $K_{\mathfrak {C}}$
, such that
$K_{\mathfrak {C}}$
, such that
![]() $\{A,B,C\}$
is a partition of
$\{A,B,C\}$
is a partition of
![]() $\mathfrak {C}$
.
$\mathfrak {C}$
.
By Lemma 3.1, let
![]() $\gamma \in \operatorname {pstab}(A)$
be such that for all
$\gamma \in \operatorname {pstab}(A)$
be such that for all
![]() $n\neq 0$
, we have
$n\neq 0$
, we have
![]() $(C)\gamma ^n \subseteq B$
. By Lemma 3.1 again, let
$(C)\gamma ^n \subseteq B$
. By Lemma 3.1 again, let
![]() $\tau \in \operatorname {pstab}(A)$
be such that for all
$\tau \in \operatorname {pstab}(A)$
be such that for all
![]() $n\neq 0$
, we have
$n\neq 0$
, we have
![]() $(B)\tau ^n \subseteq C$
.
$(B)\tau ^n \subseteq C$
.
The last two sentences allow us to apply the Ping-Pong lemma with
![]() $X:= B \sqcup C $
,
$X:= B \sqcup C $
,
![]() $\Gamma _1:=\left \langle \gamma \right \rangle $
,
$\Gamma _1:=\left \langle \gamma \right \rangle $
,
![]() $\Gamma _2:=\left \langle \tau \right \rangle $
,
$\Gamma _2:=\left \langle \tau \right \rangle $
,
![]() $X_1:=B$
, and
$X_1:=B$
, and
![]() $X_2:=C$
, to conclude that
$X_2:=C$
, to conclude that
![]() $\left \langle \tau , \gamma \right \rangle $
is a free group of rank
$\left \langle \tau , \gamma \right \rangle $
is a free group of rank
![]() $2$
.
$2$
.
Theorem 3.3 above gives the following immediate corollary, as the free group of rank
![]() $2$
is lawless and lawlessness is inherited by overgroups.
$2$
is lawless and lawlessness is inherited by overgroups.
Theorem 3.4. Let
![]() $G\leq \operatorname {Homeo}(\mathfrak {C})$
. If G is vigorous, then G is lawless.
$G\leq \operatorname {Homeo}(\mathfrak {C})$
. If G is vigorous, then G is lawless.
We now prove an extension provided by a helpful anonymous referee, that if G is vigorous, then it is mixed-identity free.
Theorem 3.5. Let
![]() $G\leq \operatorname {Homeo}(\mathfrak {C})$
. If G is vigorous, then G is mixed identity free.
$G\leq \operatorname {Homeo}(\mathfrak {C})$
. If G is vigorous, then G is mixed identity free.
Proof. Note that by Remark 5.1 of [Reference Hull and Osin18], we only need to show the case where
![]() $F=\mathbb {Z}$
in the general definition of mixed identity free. Let
$F=\mathbb {Z}$
in the general definition of mixed identity free. Let
![]() $w(x) \in (G * \langle x\rangle ) \backslash \{1\}$
, we must find
$w(x) \in (G * \langle x\rangle ) \backslash \{1\}$
, we must find
![]() $\gamma $
$\gamma $
![]() $\in $
G, such that
$\in $
G, such that
![]() $w(\gamma ) \neq 1$
. By conjugating w, we may assume
$w(\gamma ) \neq 1$
. By conjugating w, we may assume
![]() $w = x^{n_1} g_1x^{n_2} g_2 \dots x^{n_k} g_k$
, where all the
$w = x^{n_1} g_1x^{n_2} g_2 \dots x^{n_k} g_k$
, where all the
![]() $n_i \in \mathbb {Z} \backslash \{0\}$
and
$n_i \in \mathbb {Z} \backslash \{0\}$
and
![]() $g_i\neq 1$
. We then find pairwise disjoint proper clopen sets
$g_i\neq 1$
. We then find pairwise disjoint proper clopen sets
![]() $U_i, V_i$
, such that
$U_i, V_i$
, such that
![]() $U_ig_i = V_i$
with
$U_ig_i = V_i$
with
![]() $X \backslash {\sqcup }_{i=1}^{k} (U_i {\sqcup } V_i)\neq \varnothing $
. Let
$X \backslash {\sqcup }_{i=1}^{k} (U_i {\sqcup } V_i)\neq \varnothing $
. Let
![]() $V_0$
be a nonempty clopen subset of
$V_0$
be a nonempty clopen subset of
![]() $X \backslash {\sqcup }_{i=1}^{k} (U_i {\sqcup } V_i)$
. Using Lemma 3.1, we find for
$X \backslash {\sqcup }_{i=1}^{k} (U_i {\sqcup } V_i)$
. Using Lemma 3.1, we find for
![]() $i = 1, \ldots , k$
an element
$i = 1, \ldots , k$
an element
![]() ${\gamma }_i {\in } G $
supported on
${\gamma }_i {\in } G $
supported on
![]() $V_{i-1} {\sqcup } U_i$
, such that
$V_{i-1} {\sqcup } U_i$
, such that
![]() $V_{i-1}{\gamma _i}^{n_i} {\subseteq } U_i$
. By construction, the elements
$V_{i-1}{\gamma _i}^{n_i} {\subseteq } U_i$
. By construction, the elements
![]() $\gamma _1, \ldots , {\gamma }_k$
have disjoint supports. Let
$\gamma _1, \ldots , {\gamma }_k$
have disjoint supports. Let
![]() $g=\gamma _1 \ldots {\gamma }_k$
. It is then straightforward to check that
$g=\gamma _1 \ldots {\gamma }_k$
. It is then straightforward to check that
![]() $(V_0)(w(g)) \subseteq V_k$
, in particular,
$(V_0)(w(g)) \subseteq V_k$
, in particular,
![]() $w(g)\neq 1$
as wanted.
$w(g)\neq 1$
as wanted.
Noting that the verbal subgroups of non-abelian free groups are not typically the whole group, and that we can realise non-abelian free groups in
![]() $\operatorname {Homeo}(\mathfrak {C})$
(and, indeed, any countable group, see Corollary 6.4), we see that there are lawless subgroups of
$\operatorname {Homeo}(\mathfrak {C})$
(and, indeed, any countable group, see Corollary 6.4), we see that there are lawless subgroups of
![]() $\operatorname {Homeo}(\mathfrak {C})$
which are not flawless.
$\operatorname {Homeo}(\mathfrak {C})$
which are not flawless.
The example below is of a perfect and vigorous subgroup of
![]() $\operatorname {Homeo}(\mathfrak {C})$
, which is therefore lawless but not flawless.
$\operatorname {Homeo}(\mathfrak {C})$
, which is therefore lawless but not flawless.
Example 3.6. If
![]() $\gamma \in A_6$
and
$\gamma \in A_6$
and
![]() $l_1l_2l_3\dots $
is in
$l_1l_2l_3\dots $
is in
![]() $\{0,1,2,3,4,5\}^\omega $
, then set
$\{0,1,2,3,4,5\}^\omega $
, then set
and further set
![]() $\dot {A}_6$
as the copy of the alternating group
$\dot {A}_6$
as the copy of the alternating group
![]() $A_6$
in the group
$A_6$
in the group
![]() $\operatorname {Homeo}({\{0,1,2,3,4,5\}^\omega })$
generated by these functions
$\operatorname {Homeo}({\{0,1,2,3,4,5\}^\omega })$
generated by these functions
![]() $\dot {\gamma }$
.
$\dot {\gamma }$
.
As
![]() $V_6$
is vigorous by Lemma 2.1, we have by Lemma 1.2 that the group
$V_6$
is vigorous by Lemma 2.1, we have by Lemma 1.2 that the group
![]() $\left \langle V_6 \cup \dot {A}_6 \right \rangle $
is also vigorous. The group
$\left \langle V_6 \cup \dot {A}_6 \right \rangle $
is also vigorous. The group
![]() $\left \langle V_6 \cup \dot {A}_6 \right \rangle $
is perfect, since both
$\left \langle V_6 \cup \dot {A}_6 \right \rangle $
is perfect, since both
![]() $V_6$
and
$V_6$
and
![]() $\dot {A}_6$
are perfect. The group
$\dot {A}_6$
are perfect. The group
![]() $\left \langle V_6 \cup \dot {A}_6 \right \rangle $
is not simple because
$\left \langle V_6 \cup \dot {A}_6 \right \rangle $
is not simple because
![]() $V_6$
is a normal subgroup. The group
$V_6$
is a normal subgroup. The group
![]() $\left \langle V_6 \cup \dot {A}_6 \right \rangle $
is therefore not flawless by Theorem 4.18.
$\left \langle V_6 \cup \dot {A}_6 \right \rangle $
is therefore not flawless by Theorem 4.18.
4. On being vigorous
In this section, we prove Theorems 4.9 and 4.18. We begin by exploring some initial consequences of being vigorous.
Lemma 4.1. If G is a subgroup of
![]() $\operatorname {Homeo}(\mathfrak {C})$
and w is a word, then
$\operatorname {Homeo}(\mathfrak {C})$
and w is a word, then
![]() $w(G)_\circ \unlhd G$
.
$w(G)_\circ \unlhd G$
.
Proof. Let w be a word in the letters
![]() $x_1, x_2, \ldots , x_j$
. If
$x_1, x_2, \ldots , x_j$
. If
![]() $g_1,g_2, \ldots g_j , \in G$
are supported on
$g_1,g_2, \ldots g_j , \in G$
are supported on
![]() $A\in K_{\mathfrak {C}}$
with
$A\in K_{\mathfrak {C}}$
with
![]() $w(g_1,g_2, \ldots , g_j)\neq 1_G$
and
$w(g_1,g_2, \ldots , g_j)\neq 1_G$
and
![]() $h\in G$
, then
$h\in G$
, then
![]() $g_1^h,g_2^h, \ldots , g_j^h$
are supported on
$g_1^h,g_2^h, \ldots , g_j^h$
are supported on
![]() $Ah$
and
$Ah$
and
In particular,
![]() $w[G]_\circ $
is closed under conjugation, so the group it generates is normal.
$w[G]_\circ $
is closed under conjugation, so the group it generates is normal.
Lemma 4.2. Let
![]() $\gamma \in \operatorname {Homeo}(\mathfrak {C})$
be nontrivial. There exists a nonempty clopen subset Y of
$\gamma \in \operatorname {Homeo}(\mathfrak {C})$
be nontrivial. There exists a nonempty clopen subset Y of
![]() $\mathfrak {C}$
with
$\mathfrak {C}$
with
![]() $Y\gamma $
disjoint from Y.
$Y\gamma $
disjoint from Y.
Proof. Let
![]() $x\in \operatorname {supt}\!\left (\gamma \right )$
. As
$x\in \operatorname {supt}\!\left (\gamma \right )$
. As
![]() $\operatorname {supt}\!\left (\gamma \right )$
is open, there are nonempty disjoint clopen subsets
$\operatorname {supt}\!\left (\gamma \right )$
is open, there are nonempty disjoint clopen subsets
![]() $A, B$
of
$A, B$
of
![]() $\operatorname {supt}\!\left (\gamma \right )$
containing x and
$\operatorname {supt}\!\left (\gamma \right )$
containing x and
![]() $(x)\gamma $
, respectively. Let
$(x)\gamma $
, respectively. Let
![]() $A'= A\cap (B)\gamma ^{-1}$
. Note
$A'= A\cap (B)\gamma ^{-1}$
. Note
![]() $A'$
is a clopen neighbourhood of x. Then
$A'$
is a clopen neighbourhood of x. Then
![]() $(A')\gamma \subseteq B$
which is disjoint from A (and hence
$(A')\gamma \subseteq B$
which is disjoint from A (and hence
![]() $A'$
).
$A'$
).
Lemma 4.3. Let G be a vigorous subgroup of
![]() $\operatorname {Homeo}(\mathfrak {C})$
. Let U be in
$\operatorname {Homeo}(\mathfrak {C})$
. Let U be in
![]() $K_{\mathfrak {C}}$
. Then
$K_{\mathfrak {C}}$
. Then
generates
![]() $\operatorname {pstab}_G(\mathfrak {C}\backslash U)$
.
$\operatorname {pstab}_G(\mathfrak {C}\backslash U)$
.
Proof. Let
![]() $\eta $
in G be wholly supported on
$\eta $
in G be wholly supported on
![]() $U.$
We will find
$U.$
We will find
![]() $\mu $
and
$\mu $
and
![]() $\nu $
in
$\nu $
in
![]() $S_{G,U}$
, such that
$S_{G,U}$
, such that
![]() $\mu \nu = \eta .$
Let
$\mu \nu = \eta .$
Let
![]() $P \in K_{\mathfrak {C}}$
be such that
$P \in K_{\mathfrak {C}}$
be such that
![]() $P\eta ^{-1} \cup P$
is a proper subset of
$P\eta ^{-1} \cup P$
is a proper subset of
![]() $U.$
Let
$U.$
Let
![]() $Q \in K_{\mathfrak {C}}$
be a proper subset of
$Q \in K_{\mathfrak {C}}$
be a proper subset of
![]() $\mathfrak {C} \backslash U$
.
$\mathfrak {C} \backslash U$
.
Since G is vigorous, we may find
![]() $\phi \in G$
with support in
$\phi \in G$
with support in
![]() $P\sqcup (\mathfrak {C} \backslash U)$
, such that
$P\sqcup (\mathfrak {C} \backslash U)$
, such that
![]() $(P \sqcup Q)\phi \subseteq P$
. Set
$(P \sqcup Q)\phi \subseteq P$
. Set
![]() $\nu := \eta ^\phi $
. It follows that
$\nu := \eta ^\phi $
. It follows that
![]() $\nu $
is wholly supported on
$\nu $
is wholly supported on
![]() $U \backslash (Q\phi )$
, a proper clopen subset of U.
$U \backslash (Q\phi )$
, a proper clopen subset of U.
The homeomorphisms
![]() $\nu $
and
$\nu $
and
![]() $\eta $
must agree off
$\eta $
must agree off
![]() $\operatorname {supt}\!\left (\phi \right )\eta ^{-1} \cup \operatorname {supt}\!\left (\phi \right )$
. Note that
$\operatorname {supt}\!\left (\phi \right )\eta ^{-1} \cup \operatorname {supt}\!\left (\phi \right )$
. Note that
![]() $\operatorname {supt}\!\left (\phi \right )\eta ^{-1} \cup \operatorname {supt}\!\left (\phi \right ) \subseteq (P\eta ^{-1} \cup P)\sqcup (\mathfrak {C} \setminus U)$
. It follows that
$\operatorname {supt}\!\left (\phi \right )\eta ^{-1} \cup \operatorname {supt}\!\left (\phi \right ) \subseteq (P\eta ^{-1} \cup P)\sqcup (\mathfrak {C} \setminus U)$
. It follows that
![]() $\mu := \eta \nu ^{-1}$
is wholly supported on
$\mu := \eta \nu ^{-1}$
is wholly supported on
![]() $(P\eta ^{-1} \cup P)\sqcup (\mathfrak {C} \setminus U)$
. However,
$(P\eta ^{-1} \cup P)\sqcup (\mathfrak {C} \setminus U)$
. However,
![]() $\operatorname {supt}\!\left (\eta \right )\subseteq {U}$
and
$\operatorname {supt}\!\left (\eta \right )\subseteq {U}$
and
![]() $\operatorname {supt}\!\left (\nu \right ) \subseteq U \setminus (Q\phi ) \subseteq U$
. Therefore,
$\operatorname {supt}\!\left (\nu \right ) \subseteq U \setminus (Q\phi ) \subseteq U$
. Therefore,
![]() $\operatorname {supt}\!\left (\mu \right )=\operatorname {supt}\!\left (\eta \nu ^{-1}\right )\subseteq (P\eta ^{-1} \cup P)$
, a proper clopen subset of U.
$\operatorname {supt}\!\left (\mu \right )=\operatorname {supt}\!\left (\eta \nu ^{-1}\right )\subseteq (P\eta ^{-1} \cup P)$
, a proper clopen subset of U.
Lemma 4.4. Let
![]() $G\leq \operatorname {Homeo}(\mathfrak {C})$
be a vigorous group generated by its elements of small support. Suppose there are disjoint sets
$G\leq \operatorname {Homeo}(\mathfrak {C})$
be a vigorous group generated by its elements of small support. Suppose there are disjoint sets
![]() $B,C,D\in K_{\mathfrak {C}}$
partitioning
$B,C,D\in K_{\mathfrak {C}}$
partitioning
![]() $\mathfrak {C}$
. Then
$\mathfrak {C}$
. Then
![]() $G=\left \langle \operatorname {pstab}_G(C)\cup \operatorname {pstab}_G(D) \right \rangle $
.
$G=\left \langle \operatorname {pstab}_G(C)\cup \operatorname {pstab}_G(D) \right \rangle $
.
Proof. Let
![]() $L\in K_{\mathfrak {C}}$
, and suppose
$L\in K_{\mathfrak {C}}$
, and suppose
![]() $\eta \in \operatorname {pstab}_G(L)$
. We will write
$\eta \in \operatorname {pstab}_G(L)$
. We will write
![]() $\eta $
as a product of elements of
$\eta $
as a product of elements of
![]() $\operatorname {pstab}_G(C)$
and
$\operatorname {pstab}_G(C)$
and
![]() $\operatorname {pstab}_G(D)$
.
$\operatorname {pstab}_G(D)$
.
By the symmetry of context of C and D, we may assume without meaningful loss of generality that
![]() $L\cap (B\sqcup C)$
is not empty (and is also proper and clopen).
$L\cap (B\sqcup C)$
is not empty (and is also proper and clopen).
As G is vigorous, there is
![]() $\mu \in \operatorname {pstab}_G(D)$
, wholly supported on
$\mu \in \operatorname {pstab}_G(D)$
, wholly supported on
![]() $(B \sqcup C)$
, with
$(B \sqcup C)$
, with
![]() $C\mu ^{-1}\subseteq L\cap (B\sqcup C)$
.
$C\mu ^{-1}\subseteq L\cap (B\sqcup C)$
.
Consider
![]() $\nu := \eta ^{\mu }$
. Observe that
$\nu := \eta ^{\mu }$
. Observe that
In particular, we see that
![]() $\nu \in \operatorname {pstab}_G(C)$
.
$\nu \in \operatorname {pstab}_G(C)$
.
We have found
![]() $\eta =\mu \nu \mu ^{-1}$
, a decomposition of
$\eta =\mu \nu \mu ^{-1}$
, a decomposition of
![]() $\eta $
as a product of elements from the sets
$\eta $
as a product of elements from the sets
![]() $\operatorname {pstab}_G(C)$
and
$\operatorname {pstab}_G(C)$
and
![]() $\operatorname {pstab}_G(D)$
, as desired.
$\operatorname {pstab}_G(D)$
, as desired.
Lemma 4.5. Let G be a vigorous subgroup of
![]() $\operatorname {Homeo}(\mathfrak {C})$
. Let A be in
$\operatorname {Homeo}(\mathfrak {C})$
. Let A be in
![]() $K_{\mathfrak {C}}$
, and let C and D be clopen subsets of
$K_{\mathfrak {C}}$
, and let C and D be clopen subsets of
![]() $\mathfrak {C}$
with A, C, and D pairwise disjoint and with
$\mathfrak {C}$
with A, C, and D pairwise disjoint and with
![]() $A\sqcup C\sqcup D\neq \mathfrak {C}$
. Then,
$A\sqcup C\sqcup D\neq \mathfrak {C}$
. Then,
Proof. Let
![]() $B := \mathfrak {C} \backslash (A \sqcup C \sqcup D)$
. Observe that the group
$B := \mathfrak {C} \backslash (A \sqcup C \sqcup D)$
. Observe that the group
![]() $\operatorname {pstab}_{G}(A)$
acts vigorously on the Cantor space
$\operatorname {pstab}_{G}(A)$
acts vigorously on the Cantor space
![]() $\mathfrak {C}\backslash A$
. By Lemma 4.3, we have that
$\mathfrak {C}\backslash A$
. By Lemma 4.3, we have that
![]() $\operatorname {pstab}_{G}(A)$
is generated by its elements of small support (those with support contained in a proper and clopen subset of
$\operatorname {pstab}_{G}(A)$
is generated by its elements of small support (those with support contained in a proper and clopen subset of
![]() $\mathfrak {C}\backslash A$
). The result then follows from Lemma 4.4.
$\mathfrak {C}\backslash A$
). The result then follows from Lemma 4.4.
The following lemma is useful in the proof of both of the theorems in this section. In the statement below, note that even though the image of
![]() $\varepsilon $
is not all of
$\varepsilon $
is not all of
![]() $\mathfrak {C}$
, the function f is still a well-defined and injective homomorphism of groups.
$\mathfrak {C}$
, the function f is still a well-defined and injective homomorphism of groups.
Lemma 4.6. Let G be a vigorous subgroup of
![]() $\operatorname {Homeo}(\mathfrak {C})$
generated by its elements of small support. Let B, C, and D in
$\operatorname {Homeo}(\mathfrak {C})$
generated by its elements of small support. Let B, C, and D in
![]() $K_{\mathfrak {C}}$
be such that
$K_{\mathfrak {C}}$
be such that
![]() $\{B,C,D\}$
is a partition of
$\{B,C,D\}$
is a partition of
![]() $\mathfrak {C}$
. Let
$\mathfrak {C}$
. Let
![]() $\delta \in \operatorname {pstab}_G(D)$
be such that
$\delta \in \operatorname {pstab}_G(D)$
be such that
![]() $B\delta \subsetneq B$
. Let
$B\delta \subsetneq B$
. Let
![]() $\varepsilon :\mathfrak {C} \longrightarrow \mathfrak {C}$
be the injective function agreeing with
$\varepsilon :\mathfrak {C} \longrightarrow \mathfrak {C}$
be the injective function agreeing with
![]() $\delta $
on B and pointwise stabilising
$\delta $
on B and pointwise stabilising
![]() $C \sqcup D$
.
$C \sqcup D$
.
Let
![]() $f:\operatorname {Homeo}(\mathfrak {C}) \longrightarrow \operatorname {Homeo}(\mathfrak {C})$
be the function that takes
$f:\operatorname {Homeo}(\mathfrak {C}) \longrightarrow \operatorname {Homeo}(\mathfrak {C})$
be the function that takes
![]() $\gamma \in \operatorname {Homeo}(\mathfrak {C})$
to the element of
$\gamma \in \operatorname {Homeo}(\mathfrak {C})$
to the element of
![]() $\operatorname {Homeo}(\mathfrak {C})$
which agrees with
$\operatorname {Homeo}(\mathfrak {C})$
which agrees with
![]() $\varepsilon ^{-1}\gamma \varepsilon $
on
$\varepsilon ^{-1}\gamma \varepsilon $
on
![]() $\mathfrak {C} \varepsilon $
and fixes the rest of
$\mathfrak {C} \varepsilon $
and fixes the rest of
![]() $\mathfrak {C}$
pointwise. Then
$\mathfrak {C}$
pointwise. Then
![]() $f|_G$
is an isomorphism from G to
$f|_G$
is an isomorphism from G to
![]() $\operatorname {pstab}_G(\mathfrak {C} \setminus \mathfrak {C}\varepsilon )$
.
$\operatorname {pstab}_G(\mathfrak {C} \setminus \mathfrak {C}\varepsilon )$
.
Proof. Set
![]() $H:= \operatorname {pstab}_G(\mathfrak {C} \setminus \mathfrak {C}\varepsilon )$
and
$H:= \operatorname {pstab}_G(\mathfrak {C} \setminus \mathfrak {C}\varepsilon )$
and
One can think of f as a restriction and corestriction of conjugation by a homeomorphism
![]() $\hat {\varepsilon }$
which is an extension of
$\hat {\varepsilon }$
which is an extension of
![]() $\varepsilon $
to a larger Cantor space. Consequently, f is a group monomorphism. It remains to show
$\varepsilon $
to a larger Cantor space. Consequently, f is a group monomorphism. It remains to show
![]() $(G)f = H$
.
$(G)f = H$
.
As G is vigorous, it follows from Lemma 4.3 that
![]() $\left \langle S_{G,\mathfrak {C}\varepsilon } \right \rangle = \operatorname {pstab}_G(\mathfrak {C} \setminus \mathfrak {C}\varepsilon )=H$
.
$\left \langle S_{G,\mathfrak {C}\varepsilon } \right \rangle = \operatorname {pstab}_G(\mathfrak {C} \setminus \mathfrak {C}\varepsilon )=H$
.
Note that
![]() $B\varepsilon $
is a nonempty clopen set properly contained in B. Set
$B\varepsilon $
is a nonempty clopen set properly contained in B. Set
![]() $A:= B\setminus (B\varepsilon )$
, which is therefore another proper clopen subset of B. Observe further that
$A:= B\setminus (B\varepsilon )$
, which is therefore another proper clopen subset of B. Observe further that
![]() $ \mathfrak {C}\varepsilon = B\varepsilon \sqcup C \sqcup D$
, with complement in
$ \mathfrak {C}\varepsilon = B\varepsilon \sqcup C \sqcup D$
, with complement in
![]() $\mathfrak {C}$
being A. In particular,
$\mathfrak {C}$
being A. In particular,
![]() $\operatorname {pstab}_G(A)=H$
.
$\operatorname {pstab}_G(A)=H$
.
Using Lemma 4.5, where the sets A, C, and D in this proof are used in the same way as their namesakes in Lemma 4.5, we obtain that
By Lemma 4.4, we observe that
![]() $G=\left \langle \operatorname {pstab}_G(C)\cup \operatorname {pstab}_G(D) \right \rangle $
. It follows that
$G=\left \langle \operatorname {pstab}_G(C)\cup \operatorname {pstab}_G(D) \right \rangle $
. It follows that
![]() $(G)f=\left \langle \operatorname {pstab}_G(C)f\cup \operatorname {pstab}_G(D)f \right \rangle $
.
$(G)f=\left \langle \operatorname {pstab}_G(C)f\cup \operatorname {pstab}_G(D)f \right \rangle $
.
Rename
![]() $\delta $
as
$\delta $
as
![]() $\delta _D$
(as it stabilises D pointwise). As G is vigorous, there is
$\delta _D$
(as it stabilises D pointwise). As G is vigorous, there is
![]() $\theta $
with support contained in
$\theta $
with support contained in
![]() $C\sqcup D$
so that
$C\sqcup D$
so that
![]() $C\theta ^{-1}\subseteq D$
. Set
$C\theta ^{-1}\subseteq D$
. Set
![]() $\delta _C:=\delta _D^\theta $
, observing that
$\delta _C:=\delta _D^\theta $
, observing that
![]() $\delta _C|_B=\delta _D|_B=\varepsilon |_B$
and that
$\delta _C|_B=\delta _D|_B=\varepsilon |_B$
and that
![]() $\delta _C$
has support contained in
$\delta _C$
has support contained in
![]() $B\sqcup D$
(and thus it stabilises C pointwise).
$B\sqcup D$
(and thus it stabilises C pointwise).
We claim that for all
![]() $\gamma \in \operatorname {pstab}_G(C)$
, we have
$\gamma \in \operatorname {pstab}_G(C)$
, we have
![]() $(\gamma )f = \delta _D^{-1} \gamma \delta _D$
. Indeed, for any
$(\gamma )f = \delta _D^{-1} \gamma \delta _D$
. Indeed, for any
![]() $p \in \mathfrak {C}$
,
$p \in \mathfrak {C}$
,
-
- If
 $p\in A$
, then
$p\in A$
, then
 $p\delta _D^{-1} \in C$
, so
$p\delta _D^{-1} \in C$
, so
 $p\delta _D^{-1}\gamma \delta _D = p = p\,(\gamma )f$
.
$p\delta _D^{-1}\gamma \delta _D = p = p\,(\gamma )f$
. -
- If
 $p\in C$
, then again,
$p\in C$
, then again,
 $p\delta _D^{-1} \in C$
, so
$p\delta _D^{-1} \in C$
, so
 $p\delta _D^{-1}\gamma \delta _D = p = p\varepsilon ^{-1} \gamma \varepsilon $
since
$p\delta _D^{-1}\gamma \delta _D = p = p\varepsilon ^{-1} \gamma \varepsilon $
since
 $\varepsilon $
is the identity on C, so by the definition of f,
$\varepsilon $
is the identity on C, so by the definition of f,
 $p\,(\gamma )f = p\delta _D^{-1}\gamma \delta _D$
.
$p\,(\gamma )f = p\delta _D^{-1}\gamma \delta _D$
. -
- If
 $p \in B\varepsilon \sqcup D$
, then as
$p \in B\varepsilon \sqcup D$
, then as
 $B\varepsilon \sqcup D = (B \sqcup D)\varepsilon = (B \sqcup D)\delta _D$
, we have
$B\varepsilon \sqcup D = (B \sqcup D)\varepsilon = (B \sqcup D)\delta _D$
, we have
 $p\delta _D^{-1} \gamma \delta _D = p\varepsilon ^{-1}\gamma \varepsilon = p\,(\gamma )f$
as
$p\delta _D^{-1} \gamma \delta _D = p\varepsilon ^{-1}\gamma \varepsilon = p\,(\gamma )f$
as
 $\delta _D$
and
$\delta _D$
and
 $\varepsilon $
agree on
$\varepsilon $
agree on
 $B \sqcup D$
,
$B \sqcup D$
,
Similarly, for all
![]() $\gamma \in \operatorname {pstab}_G(D)$
, we have
$\gamma \in \operatorname {pstab}_G(D)$
, we have
![]() $(\gamma )f = \delta _C^{-1} \gamma \delta _C$
.
$(\gamma )f = \delta _C^{-1} \gamma \delta _C$
.
We have now shown
 $$ \begin{align*} (G) f &= \left\langle \operatorname{pstab}_G(C)f\cup \operatorname{pstab}_G(D)f \right\rangle \\ &= \left\langle \operatorname{pstab}_G(C)^{\delta_D}\cup\operatorname{pstab}_G(D)^{\delta_C} \right\rangle\\ &= \left\langle \operatorname{pstab}_G(C \cup A)\cup\operatorname{pstab}_G(D \cup A) \right\rangle\\ &= \operatorname{pstab}_G(A)\\ &= H.\\[-39pt] \end{align*} $$
$$ \begin{align*} (G) f &= \left\langle \operatorname{pstab}_G(C)f\cup \operatorname{pstab}_G(D)f \right\rangle \\ &= \left\langle \operatorname{pstab}_G(C)^{\delta_D}\cup\operatorname{pstab}_G(D)^{\delta_C} \right\rangle\\ &= \left\langle \operatorname{pstab}_G(C \cup A)\cup\operatorname{pstab}_G(D \cup A) \right\rangle\\ &= \operatorname{pstab}_G(A)\\ &= H.\\[-39pt] \end{align*} $$
4.1. Variants of full
In this subsection, we prove Theorem 4.9 and Lemma 4.11. These results explore interactions between variants of the concept of full, and what more can be deduced from being vigorous in the presence of variants of being full.
Recall the definitions of full and approximately full from Definitions 1.6 and 1.7. Here, we offer yet another variant.
Definition 4.7. We will say a subgroup G of
![]() $\operatorname {Homeo}(\mathfrak {C})$
is strongly approximately full if and only if, for any
$\operatorname {Homeo}(\mathfrak {C})$
is strongly approximately full if and only if, for any
![]() $D,R\in K_{\mathfrak {C}}$
,
$D,R\in K_{\mathfrak {C}}$
,
![]() $\gamma _1, \ldots , \gamma _n\in G$
and clopen sets
$\gamma _1, \ldots , \gamma _n\in G$
and clopen sets
![]() $D_1, \ldots , D_n$
partitioning D, such that the clopen sets
$D_1, \ldots , D_n$
partitioning D, such that the clopen sets
![]() $D_1\gamma _1, \ldots , D_n\gamma _n$
partition R, there exists
$D_1\gamma _1, \ldots , D_n\gamma _n$
partition R, there exists
![]() $\chi $
in G, such that
$\chi $
in G, such that
![]() $\chi $
extends
$\chi $
extends
![]() $\gamma _i|_{D_i}$
for all
$\gamma _i|_{D_i}$
for all
![]() $1\leq i\leq n$
.
$1\leq i\leq n$
.
Remark 4.8. Note that strongly approximately full subgroups of
![]() $\operatorname {Homeo}(\mathfrak {C})$
are also approximately full. To appease the reader’s certain curiosity, we show in the next paragraph that the full group of the group generated by the full shift is not strongly approximately full. In particular, not all full groups are strongly approximately full.
$\operatorname {Homeo}(\mathfrak {C})$
are also approximately full. To appease the reader’s certain curiosity, we show in the next paragraph that the full group of the group generated by the full shift is not strongly approximately full. In particular, not all full groups are strongly approximately full.
Consider elements of
![]() $\{0,1\}^{\mathbb {Z}}$
as biinfinite words. Let
$\{0,1\}^{\mathbb {Z}}$
as biinfinite words. Let
![]() $f:\{0,1\}^{\mathbb {Z}} \to \{0,1\}^{\mathbb {Z}}$
be the partial map which applies the full shift to those words that have a
$f:\{0,1\}^{\mathbb {Z}} \to \{0,1\}^{\mathbb {Z}}$
be the partial map which applies the full shift to those words that have a
![]() $0$
in the
$0$
in the
![]() $0^{th}$
coordinate (to obtain those words that have a
$0^{th}$
coordinate (to obtain those words that have a
![]() $0$
in the
$0$
in the
![]() $1^{st}$
coordinate) and which pointwise fixes the set
$1^{st}$
coordinate) and which pointwise fixes the set
![]() $S_{11}$
of those points with a
$S_{11}$
of those points with a
![]() $1$
in both the
$1$
in both the
![]() $0^{th}$
and
$0^{th}$
and
![]() $1^{st}$
coordinates.
$1^{st}$
coordinates.
Any homeomorphism of
![]() $\{0, 1\}^{\mathbb {Z}}$
extending f must map the remaining domain set (those words with
$\{0, 1\}^{\mathbb {Z}}$
extending f must map the remaining domain set (those words with
![]() $1$
in the
$1$
in the
![]() $0^{th}$
coordinate and
$0^{th}$
coordinate and
![]() $0$
in the
$0$
in the
![]() $1^{st}$
coordinate) to the remaining codomain set (those words with
$1^{st}$
coordinate) to the remaining codomain set (those words with
![]() $0$
in the
$0$
in the
![]() $0^{th}$
coordinate and
$0^{th}$
coordinate and
![]() $1$
in the
$1$
in the
![]() $1^{st}$
coordinate). In particular, if such an extension is in the full group of the shift, then the element of
$1^{st}$
coordinate). In particular, if such an extension is in the full group of the shift, then the element of
![]() $\{0,1\}^{\mathbb {Z}}$
which is
$\{0,1\}^{\mathbb {Z}}$
which is
![]() $0$
on precisely the positive coordinates (and
$0$
on precisely the positive coordinates (and
![]() $1$
in all other coordinates) must be mapped to a word with
$1$
in all other coordinates) must be mapped to a word with
![]() $0$
in the
$0$
in the
![]() $0^{th}$
position and
$0^{th}$
position and
![]() $1$
in the
$1$
in the
![]() $1^{st}$
position by a power of the full shift, which is impossible.
$1^{st}$
position by a power of the full shift, which is impossible.
We can now give the proof of Theorem 4.9. In the proof of the second part below, we, in fact, show that vigorous subgroups of
![]() $\operatorname {Homeo}(\mathfrak {C})$
generated by their elements of small support are strongly approximately full, which is stronger than the stated result (see the corollary).
$\operatorname {Homeo}(\mathfrak {C})$
generated by their elements of small support are strongly approximately full, which is stronger than the stated result (see the corollary).
Theorem 4.9. Let G be a subgroup of
![]() $\operatorname {Homeo}(\mathfrak {C})$
.
$\operatorname {Homeo}(\mathfrak {C})$
.
-
1. If G is approximately full, then G is generated by its elements of small support.
-
2. If G is vigorous and generated by its elements of small support, then G is approximately full.
Proof. First, assume that G is approximately full.
Let
![]() $\gamma $
be a nonidentity element of G. We will find
$\gamma $
be a nonidentity element of G. We will find
![]() $\alpha , \beta \in G$
of small support such that
$\alpha , \beta \in G$
of small support such that
![]() $\alpha \beta = \gamma $
.
$\alpha \beta = \gamma $
.
Let
![]() $A\in K_{\mathfrak {C}}$
be such that
$A\in K_{\mathfrak {C}}$
be such that
![]() $A\gamma ^{-1} \cap A = \varnothing $
and
$A\gamma ^{-1} \cap A = \varnothing $
and
![]() $(A\gamma ^{-1} \sqcup A) \neq \mathfrak {C}$
. Let
$(A\gamma ^{-1} \sqcup A) \neq \mathfrak {C}$
. Let
![]() $(\gamma _1, \gamma _2, \gamma _3) = (\gamma , \gamma ^{-1}, 1_G)$
, where
$(\gamma _1, \gamma _2, \gamma _3) = (\gamma , \gamma ^{-1}, 1_G)$
, where
![]() $1_G$
represents the identity of G. Set
$1_G$
represents the identity of G. Set
![]() $D_1 := A\gamma ^{-1}$
and
$D_1 := A\gamma ^{-1}$
and
![]() $D_{2} := A$
and
$D_{2} := A$
and
![]() $D_{3} := \mathfrak {C} \setminus (A\gamma ^{-1} \sqcup A)$
. Since G is approximately full, we may find
$D_{3} := \mathfrak {C} \setminus (A\gamma ^{-1} \sqcup A)$
. Since G is approximately full, we may find
![]() $\beta $
in G, such that
$\beta $
in G, such that
![]() $\beta $
agrees with
$\beta $
agrees with
![]() $\gamma $
on
$\gamma $
on
![]() $D_{1}=A\gamma ^{-1}$
and agrees with
$D_{1}=A\gamma ^{-1}$
and agrees with
![]() $1_G$
on
$1_G$
on
![]() $D_{3}=\mathfrak {C} \setminus (A\gamma ^{-1} \sqcup A)$
. Set
$D_{3}=\mathfrak {C} \setminus (A\gamma ^{-1} \sqcup A)$
. Set
![]() $\alpha := \gamma \beta ^{-1}$
.
$\alpha := \gamma \beta ^{-1}$
.
Note firstly that
![]() $\gamma $
was arbitrary (nonidentity) in G. Also,
$\gamma $
was arbitrary (nonidentity) in G. Also,
![]() $\alpha $
pointwise stabilises the clopen set
$\alpha $
pointwise stabilises the clopen set
![]() $A\gamma ^{-1}$
, while
$A\gamma ^{-1}$
, while
![]() $\beta $
pointwise stabilises the clopen set
$\beta $
pointwise stabilises the clopen set
![]() $D_3$
. Finally, as
$D_3$
. Finally, as
![]() $\gamma =\alpha \beta $
, we have point (1).
$\gamma =\alpha \beta $
, we have point (1).
Now, assume that G is vigorous and is generated by its elements of small support. We will show that G is strongly approximately full, from which it follows that G is approximately full.
Let D and R be in
![]() $K_{\mathfrak {C}}$
. Let
$K_{\mathfrak {C}}$
. Let
![]() $\gamma _1, \ldots , \gamma _n\in G$
, and let
$\gamma _1, \ldots , \gamma _n\in G$
, and let
![]() $D_1,\ldots ,D_n$
be a partition of D into clopen sets, such that
$D_1,\ldots ,D_n$
be a partition of D into clopen sets, such that
![]() $D_1 \gamma _1, \ldots , D_n\gamma _n$
forms a partition of R. Set the notation, for each
$D_1 \gamma _1, \ldots , D_n\gamma _n$
forms a partition of R. Set the notation, for each
![]() $1\leq i\leq n$
,
$1\leq i\leq n$
,
![]() $R_i:= D_i\gamma _i$
.
$R_i:= D_i\gamma _i$
.
Let
![]() $S,T\in K_{\mathfrak {C}}$
be disjoint and such that
$S,T\in K_{\mathfrak {C}}$
be disjoint and such that
![]() $S\subsetneq \mathfrak {C} \setminus D$
,
$S\subsetneq \mathfrak {C} \setminus D$
,
![]() $T\subsetneq \mathfrak {C}\setminus R$
,
$T\subsetneq \mathfrak {C}\setminus R$
,
![]() $(R\cup S\cup T)\subsetneq \mathfrak {C}$
, and
$(R\cup S\cup T)\subsetneq \mathfrak {C}$
, and
![]() $D\cup S\cup T\subsetneq \mathfrak {C}$
(it is easy to check that such a pair of sets, S and T with the desired properties, exists). As G is vigorous, there is
$D\cup S\cup T\subsetneq \mathfrak {C}$
(it is easy to check that such a pair of sets, S and T with the desired properties, exists). As G is vigorous, there is
![]() $\tau $
in G with support contained in
$\tau $
in G with support contained in
![]() $R\cup S\cup T$
so that
$R\cup S\cup T$
so that
![]() $R\tau \subseteq S$
.
$R\tau \subseteq S$
.
We will find
![]() $\chi \in G$
, such that
$\chi \in G$
, such that
![]() $\chi $
extends
$\chi $
extends
![]() $(\gamma _i\tau )|_{D_i}$
for each
$(\gamma _i\tau )|_{D_i}$
for each
![]() $1\leq i \leq n$
. This is sufficient because then
$1\leq i \leq n$
. This is sufficient because then
![]() $\chi \tau ^{-1}$
will extend
$\chi \tau ^{-1}$
will extend
![]() $\gamma _i|_{D_i}$
for each
$\gamma _i|_{D_i}$
for each
![]() $1\leq i\leq n$
.
$1\leq i\leq n$
.
By construction,
![]() $D\sqcup S\subsetneq \mathfrak {C}$
. Choose
$D\sqcup S\subsetneq \mathfrak {C}$
. Choose
![]() $E\in K_{\mathfrak {C}}$
, a proper clopen subset of
$E\in K_{\mathfrak {C}}$
, a proper clopen subset of
![]() $\mathfrak {C}\setminus (D\sqcup S)$
, noting that
$\mathfrak {C}\setminus (D\sqcup S)$
, noting that
![]() $(D\sqcup R\tau )\cap E=\varnothing $
and
$(D\sqcup R\tau )\cap E=\varnothing $
and
![]() $D\sqcup S\sqcup E \subsetneq \mathfrak {C}$
.
$D\sqcup S\sqcup E \subsetneq \mathfrak {C}$
.
Let
![]() $i\in \{1, \ldots , n\}$
. Set
$i\in \{1, \ldots , n\}$
. Set
![]() $I_i:= D_i\sqcup R_i\tau $
. Set
$I_i:= D_i\sqcup R_i\tau $
. Set
![]() $K_i = I_i\sqcup E$
.
$K_i = I_i\sqcup E$
.
Since G is generated by its elements of small support, by Lemma 4.6, there is a clopen set
![]() $J_i$
with
$J_i$
with
![]() $I_i\subsetneq J_i\subsetneq K_i$
and an isomorphism
$I_i\subsetneq J_i\subsetneq K_i$
and an isomorphism
![]() $f_i:G\to \operatorname {pstab}_G(\mathfrak {C}\setminus J_i)$
so that we have
$f_i:G\to \operatorname {pstab}_G(\mathfrak {C}\setminus J_i)$
so that we have
![]() $(\gamma _i\tau ) f_i$
agrees with
$(\gamma _i\tau ) f_i$
agrees with
![]() $\gamma _i\tau $
on the set
$\gamma _i\tau $
on the set
![]() $I_i\cap (I_{i}\tau ^{-1}\gamma _i^{-1})$
. Observe that
$I_i\cap (I_{i}\tau ^{-1}\gamma _i^{-1})$
. Observe that
![]() $D_i\subseteq I_i\cap (I_{i}\tau ^{-1}\gamma _i^{-1})$
. Further observe that
$D_i\subseteq I_i\cap (I_{i}\tau ^{-1}\gamma _i^{-1})$
. Further observe that
![]() $(\gamma _i \tau )f_i$
acts as the identity on the complement of
$(\gamma _i \tau )f_i$
acts as the identity on the complement of
![]() $K_i$
, since
$K_i$
, since
![]() $J_i\subsetneq K_i$
. In particular,
$J_i\subsetneq K_i$
. In particular,
![]() $(\gamma _i \tau )f_i$
fixes
$(\gamma _i \tau )f_i$
fixes
![]() $(D\sqcup R\tau )\setminus (D_i\sqcup R_i\tau )$
pointwise.
$(D\sqcup R\tau )\setminus (D_i\sqcup R_i\tau )$
pointwise.
For each
![]() $i\in \{1, \ldots , n\}$
, set
$i\in \{1, \ldots , n\}$
, set
![]() $\chi _i:=(\gamma _i\tau )f_i$
.
$\chi _i:=(\gamma _i\tau )f_i$
.
Let
![]() $\chi := \chi _1\chi _2\ldots \chi _n$
. The element
$\chi := \chi _1\chi _2\ldots \chi _n$
. The element
![]() $\chi $
obtained has the property that, for each i,
$\chi $
obtained has the property that, for each i,
![]() $\chi |_{D_i}=(\gamma _i\tau )|_{D_i}$
, as desired.
$\chi |_{D_i}=(\gamma _i\tau )|_{D_i}$
, as desired.
Corollary 4.10. Let G be a vigorous approximately full subgroup of
![]() $\operatorname {Homeo}(\mathfrak {C})$
. Then G is strongly approximately full. In particular, for vigorous subgroups of
$\operatorname {Homeo}(\mathfrak {C})$
. Then G is strongly approximately full. In particular, for vigorous subgroups of
![]() $\operatorname {Homeo}(\mathfrak {C})$
approximately full and strongly approximately full are equivalent.
$\operatorname {Homeo}(\mathfrak {C})$
approximately full and strongly approximately full are equivalent.
Proof. By the first point of Theorem 4.9, we have that G is generated by its elements of small support. When proving the second part of Theorem 4.9, we, in fact, showed that if G is vigorous and generated by its elements of small support, then G is strongly approximately full. It follows that our group G is strongly approximately full.
In the proof that (1)
![]() $\Rightarrow $
(6) within the proof of Theorem 4.18 that we shall give in the next subsection, we use the concept of a flexible group. A group
$\Rightarrow $
(6) within the proof of Theorem 4.18 that we shall give in the next subsection, we use the concept of a flexible group. A group
![]() $G\leq \operatorname {Homeo}(\mathfrak {C})$
is flexible if given U,
$G\leq \operatorname {Homeo}(\mathfrak {C})$
is flexible if given U,
![]() $V\in K_{\mathfrak {C}}$
, there is a group element
$V\in K_{\mathfrak {C}}$
, there is a group element
![]() $\gamma \in G$
so that
$\gamma \in G$
so that
![]() $U\gamma \subseteq V$
. We observe in Lemma 4.11 below that being flexible is a weaker property for a group to have than being vigorous, but we also show that in the presence of approximately full, the concepts are equivalent.
$U\gamma \subseteq V$
. We observe in Lemma 4.11 below that being flexible is a weaker property for a group to have than being vigorous, but we also show that in the presence of approximately full, the concepts are equivalent.
Lemma 4.11. Let
![]() $G\leq \operatorname {Homeo}(\mathfrak {C})$
be such that G is approximately full. Then G is flexible if and only if G is vigorous.
$G\leq \operatorname {Homeo}(\mathfrak {C})$
be such that G is approximately full. Then G is flexible if and only if G is vigorous.
Proof. Let
![]() $G\leq \operatorname {Homeo}(\mathfrak {C})$
.
$G\leq \operatorname {Homeo}(\mathfrak {C})$
.
If G is vigorous, it follows that G is flexible. This follows because being vigorous allows one to move clopen sets into each other while restricting the set of other points being moved, while being flexible simply allows one to move clopen sets into each other.
Let us now suppose that G is approximately full and flexible. Let A, B, and
![]() $C\in K_{\mathfrak {C}}$
with B and C proper subsets of A. We will show there is some
$C\in K_{\mathfrak {C}}$
with B and C proper subsets of A. We will show there is some
![]() $\gamma \in G$
so that
$\gamma \in G$
so that
![]() $B\gamma \subseteq C$
with the support of
$B\gamma \subseteq C$
with the support of
![]() $\gamma $
fully contained in A.
$\gamma $
fully contained in A.
Choose
![]() $D\subseteq C$
with
$D\subseteq C$
with
![]() $B\cup D$
, a proper clopen subset of A.
$B\cup D$
, a proper clopen subset of A.
As G is flexible, there is
![]() $\rho \in G$
so that
$\rho \in G$
so that
![]() $B\rho \subseteq A\backslash (B\cup D)$
. Consider the partition
$B\rho \subseteq A\backslash (B\cup D)$
. Consider the partition
![]() $X_1 = \{B, B\rho , \mathfrak {C}\backslash (B\rho \cup B)\}$
of Cantor space into proper clopen sets. Let us nominate these sets as
$X_1 = \{B, B\rho , \mathfrak {C}\backslash (B\rho \cup B)\}$
of Cantor space into proper clopen sets. Let us nominate these sets as
![]() $U_1:= B, U_2:= B\rho $
, and
$U_1:= B, U_2:= B\rho $
, and
![]() $U_3:= \mathfrak {C}\backslash (B\rho \cup B)$
. Set
$U_3:= \mathfrak {C}\backslash (B\rho \cup B)$
. Set
![]() $\theta _1 := \rho $
,
$\theta _1 := \rho $
,
![]() $\theta _2 := \rho ^{-1}$
, and
$\theta _2 := \rho ^{-1}$
, and
![]() $\theta _3:= 1_G$
(where
$\theta _3:= 1_G$
(where
![]() $1_G$
is the identity element in G). The set
$1_G$
is the identity element in G). The set
![]() $X_1$
corresponds to both the domain and range partitions appearing in the definition of approximately full, while the elements
$X_1$
corresponds to both the domain and range partitions appearing in the definition of approximately full, while the elements
![]() $\theta _1$
,
$\theta _1$
,
![]() $\theta _2$
, and
$\theta _2$
, and
![]() $\theta _3$
are corresponding to the group elements which, respectively, take
$\theta _3$
are corresponding to the group elements which, respectively, take
![]() $U_1$
to
$U_1$
to
![]() $U_2$
, then
$U_2$
, then
![]() $U_2$
to
$U_2$
to
![]() $U_1$
, and finally
$U_1$
, and finally
![]() $U_3$
to
$U_3$
to
![]() $U_3$
. Since G is approximately full, there is
$U_3$
. Since G is approximately full, there is
![]() $\chi _1\in G$
which agrees with
$\chi _1\in G$
which agrees with
![]() $\theta _1$
on
$\theta _1$
on
![]() $U_1$
and
$U_1$
and
![]() $\theta _3$
on
$\theta _3$
on
![]() $U_3$
. We note that
$U_3$
. We note that
![]() $B\chi _1\subseteq A\backslash (B\cup D)$
and
$B\chi _1\subseteq A\backslash (B\cup D)$
and
![]() $\chi _1$
acts as the identity over
$\chi _1$
acts as the identity over
![]() $\mathfrak {C}\backslash (B\rho \cup B)$
, and specifically, on the complement of A.
$\mathfrak {C}\backslash (B\rho \cup B)$
, and specifically, on the complement of A.
By an entirely similar argument, we can find a
![]() $\chi _2\in G$
which takes
$\chi _2\in G$
which takes
![]() $A\backslash (B\cup D)$
into D while pointwise fixing the complement of A. The composition
$A\backslash (B\cup D)$
into D while pointwise fixing the complement of A. The composition
![]() $\gamma =\chi _1\chi _2$
acts as the identity on the complement of A and
$\gamma =\chi _1\chi _2$
acts as the identity on the complement of A and
![]() $B\gamma \subseteq D\subseteq C$
. In particular, G is vigorous.
$B\gamma \subseteq D\subseteq C$
. In particular, G is vigorous.
4.2. Equivalent conditions
In this subsection, we give the proof of Theorem 4.18.
We begin with more lemmata concerning vigorous subgroups of
![]() $\operatorname {Homeo}(\mathfrak {C})$
.
$\operatorname {Homeo}(\mathfrak {C})$
.
Lemma 4.12. Let G be a vigorous subgroup of
![]() $\operatorname {Homeo}(\mathfrak {C})$
generated by its own set of elements of small support. Let I and K in
$\operatorname {Homeo}(\mathfrak {C})$
generated by its own set of elements of small support. Let I and K in
![]() $K_{\mathfrak {C}}$
be such that
$K_{\mathfrak {C}}$
be such that
![]() $I \subsetneq K$
. Then there exists
$I \subsetneq K$
. Then there exists
![]() $J \in K_{\mathfrak {C}}$
and an isomorphism
$J \in K_{\mathfrak {C}}$
and an isomorphism
![]() $f:G \longrightarrow \operatorname {pstab}_G(\mathfrak {C} \setminus J)$
, such that
$f:G \longrightarrow \operatorname {pstab}_G(\mathfrak {C} \setminus J)$
, such that
![]() $I \subsetneq J \subsetneq K$
and for each
$I \subsetneq J \subsetneq K$
and for each
![]() $\gamma \in G$
the homeomorphism
$\gamma \in G$
the homeomorphism
![]() $(\gamma ) f$
agrees with
$(\gamma ) f$
agrees with
![]() $\gamma $
on
$\gamma $
on
![]() $I\gamma ^{-1} \cap I$
.
$I\gamma ^{-1} \cap I$
.
Proof. Our strategy is to first find sets B, C, and D and a group element
![]() $\delta $
as in Lemma 4.6. We then determine the clopen set J with
$\delta $
as in Lemma 4.6. We then determine the clopen set J with
![]() $I\subsetneq J \subsetneq K$
so that the
$I\subsetneq J \subsetneq K$
so that the
![]() $\delta $
-induced isomorphism f has
$\delta $
-induced isomorphism f has
![]() $f:G \longrightarrow \operatorname {pstab}_G(\mathfrak {C} \setminus J)$
. Finally, for each
$f:G \longrightarrow \operatorname {pstab}_G(\mathfrak {C} \setminus J)$
. Finally, for each
![]() $\gamma \in G$
and
$\gamma \in G$
and
![]() $p\in I\cap I{\gamma ^{-1}}$
, we verify that
$p\in I\cap I{\gamma ^{-1}}$
, we verify that
![]() $p\gamma f = p \gamma $
.
$p\gamma f = p \gamma $
.
Let
![]() $L,L' \in K_{\mathfrak {C}}$
be such that
$L,L' \in K_{\mathfrak {C}}$
be such that
![]() $L' \subsetneq L \subsetneq K \setminus I$
.
$L' \subsetneq L \subsetneq K \setminus I$
.
We set
![]() $D:= I$
and
$D:= I$
and
![]() $B := L \sqcup (\mathfrak {C} \setminus K)$
. Note
$B := L \sqcup (\mathfrak {C} \setminus K)$
. Note
![]() $B\cap D = \emptyset $
. This allows us to determine C as the complement of B and D in
$B\cap D = \emptyset $
. This allows us to determine C as the complement of B and D in
![]() $\mathfrak {C}$
. That is,
$\mathfrak {C}$
. That is,
![]() $C:= \mathfrak {C}\setminus (B\sqcup D)$
. Observe as well that as
$C:= \mathfrak {C}\setminus (B\sqcup D)$
. Observe as well that as
![]() $L'\subsetneq L \subsetneq B$
, we have L and
$L'\subsetneq L \subsetneq B$
, we have L and
![]() $L'$
are each disjoint from
$L'$
are each disjoint from
![]() $C\sqcup D$
.
$C\sqcup D$
.
Since G is vigorous, we may find
![]() $\delta \in \operatorname {pstab}_G(I)$
so that
$\delta \in \operatorname {pstab}_G(I)$
so that
![]() $B\delta \subseteq L'$
.
$B\delta \subseteq L'$
.
Set
![]() $A:= B \setminus B\delta $
and
$A:= B \setminus B\delta $
and
![]() $J:= \mathfrak {C} \setminus A$
. Note that
$J:= \mathfrak {C} \setminus A$
. Note that
That is,
![]() $J\subsetneq K$
. Further note that as
$J\subsetneq K$
. Further note that as
![]() $D=I$
and C is not empty, we have
$D=I$
and C is not empty, we have
![]() $I\subsetneq J$
, and we conclude that
$I\subsetneq J$
, and we conclude that
![]() $I\subsetneq J \subsetneq K$
.
$I\subsetneq J \subsetneq K$
.
We are now in the context of Lemma 4.6. Let f be the induced homomorphism from
![]() $\operatorname {Homeo}(\mathfrak {C})$
to
$\operatorname {Homeo}(\mathfrak {C})$
to
![]() $\operatorname {Homeo}(\mathfrak {C})$
which restricts to an isomorphism from G to
$\operatorname {Homeo}(\mathfrak {C})$
which restricts to an isomorphism from G to
![]() $\operatorname {pstab}_G(A)$
.
$\operatorname {pstab}_G(A)$
.
Recall there is a monic function
![]() $\varepsilon :\mathfrak {C}\to \mathfrak {C}$
which acts as the identity on C and D, and acts as
$\varepsilon :\mathfrak {C}\to \mathfrak {C}$
which acts as the identity on C and D, and acts as
![]() $\delta $
on B, and where
$\delta $
on B, and where
![]() $\gamma f = \gamma ^{\varepsilon }$
on J (note that
$\gamma f = \gamma ^{\varepsilon }$
on J (note that
![]() $\gamma f$
acts as the identity off J).
$\gamma f$
acts as the identity off J).
Now, for all points
![]() $p\in I\cap I{\gamma ^{-1}}$
, we can compute
$p\in I\cap I{\gamma ^{-1}}$
, we can compute
![]() $p \gamma f$
. Specifically,
$p \gamma f$
. Specifically,
![]() $p\gamma f= p\varepsilon ^{-1}\gamma \varepsilon = p\gamma \varepsilon $
since
$p\gamma f= p\varepsilon ^{-1}\gamma \varepsilon = p\gamma \varepsilon $
since
![]() $\varepsilon $
acts as the identity in
$\varepsilon $
acts as the identity in
![]() $I\cap I\gamma ^{-1}\subseteq D$
. As
$I\cap I\gamma ^{-1}\subseteq D$
. As
![]() $p\in I\gamma ^{-1}$
, we see that
$p\in I\gamma ^{-1}$
, we see that
![]() $p\gamma =z\in I = D$
so we can further compute
$p\gamma =z\in I = D$
so we can further compute
![]() $p\gamma f=p\gamma \varepsilon =z\varepsilon =z$
. Thus,
$p\gamma f=p\gamma \varepsilon =z\varepsilon =z$
. Thus,
![]() $\gamma f$
and
$\gamma f$
and
![]() $\gamma $
agree over
$\gamma $
agree over
![]() $I\cap I\gamma ^{-1}$
.
$I\cap I\gamma ^{-1}$
.
Lemma 4.13. Suppose that G is vigorous, N is a nontrivial normal subgroup of G,
![]() $A\in K_{\mathfrak {C}}$
, and
$A\in K_{\mathfrak {C}}$
, and
![]() $\delta \in G$
is supported on A. There is some
$\delta \in G$
is supported on A. There is some
![]() $\gamma \in N$
, such that
$\gamma \in N$
, such that
![]() $\gamma |_A=\delta |_A$
.
$\gamma |_A=\delta |_A$
.
Proof. Let
![]() $k\in N\backslash \{1_N\}$
. Let
$k\in N\backslash \{1_N\}$
. Let
![]() $B\in K_{\mathfrak {C}}$
be such that
$B\in K_{\mathfrak {C}}$
be such that
![]() $(B)k\cap B = \varnothing $
.
$(B)k\cap B = \varnothing $
.
Let
![]() $l\in G$
be such that
$l\in G$
be such that
![]() $(A)l\subseteq H$
, so
$(A)l\subseteq H$
, so
![]() $A\subseteq (H)l^{-1}$
. It follows that
$A\subseteq (H)l^{-1}$
. It follows that
![]() $k^{l^{-1}}\in N$
, and
$k^{l^{-1}}\in N$
, and
![]() $(A)k^{l^{-1}}\cap A = \varnothing $
. Finally, we have
$(A)k^{l^{-1}}\cap A = \varnothing $
. Finally, we have
agrees with
![]() $\delta $
on A as required.
$\delta $
on A as required.
Lemma 4.14. If G is vigorous and N is a nontrivial normal subgroup of G, then N is vigorous.
Proof. Suppose that
![]() $A,B,C$
are clopen subsets of
$A,B,C$
are clopen subsets of
![]() $\mathfrak {C}$
with B and C proper (nonempty) subsets of A. We need only show that there exists
$\mathfrak {C}$
with B and C proper (nonempty) subsets of A. We need only show that there exists
![]() $\gamma $
in N with
$\gamma $
in N with
![]() $\operatorname {supt}\!\left (\gamma \right ) \subseteq A$
and
$\operatorname {supt}\!\left (\gamma \right ) \subseteq A$
and
![]() $B\gamma \subseteq C$
. Let
$B\gamma \subseteq C$
. Let
![]() $D, E\in K_{\mathfrak {C}}$
be such that
$D, E\in K_{\mathfrak {C}}$
be such that
![]() $A=B\sqcup D\sqcup E$
. Without loss of generality, assume that
$A=B\sqcup D\sqcup E$
. Without loss of generality, assume that
![]() $C\cap (B\sqcup D) \neq \varnothing $
. Define
$C\cap (B\sqcup D) \neq \varnothing $
. Define
![]() $A':=B\sqcup D$
and
$A':=B\sqcup D$
and
![]() $C':=C\cap A'$
.
$C':=C\cap A'$
.
As G is vigorous, there is some
![]() $\delta \in G$
supported on
$\delta \in G$
supported on
![]() $A'$
with
$A'$
with
![]() $(B)\delta \subseteq C'$
(if
$(B)\delta \subseteq C'$
(if
![]() $C'=A'$
, then the identity function does this).
$C'=A'$
, then the identity function does this).
By Lemma 4.13, there is some
![]() $\gamma \in N$
, such that
$\gamma \in N$
, such that
![]() $\gamma |_{\mathfrak {C}\backslash E}=\delta |_{\mathfrak {C}\backslash E}$
. So
$\gamma |_{\mathfrak {C}\backslash E}=\delta |_{\mathfrak {C}\backslash E}$
. So
![]() $B\gamma =B\delta \subseteq C'\subseteq C$
, and
$B\gamma =B\delta \subseteq C'\subseteq C$
, and
![]() $\gamma $
is supported on A as required.
$\gamma $
is supported on A as required.
The following lemma is proven following the outline of the proof of the first part of Theorem 4.9.
Recall that a subgroup G of
![]() $\operatorname {Homeo}(\mathfrak {C})$
is approximately full if and only if whenever
$\operatorname {Homeo}(\mathfrak {C})$
is approximately full if and only if whenever
![]() $\gamma _1, \ldots , \gamma _n\in G$
, and
$\gamma _1, \ldots , \gamma _n\in G$
, and
![]() $D_1, \ldots , D_n$
are clopen sets partitioning
$D_1, \ldots , D_n$
are clopen sets partitioning
![]() $\mathfrak {C}$
, such that
$\mathfrak {C}$
, such that
![]() $D_1 \gamma _1, \ldots , D_n \gamma _n$
also partitions
$D_1 \gamma _1, \ldots , D_n \gamma _n$
also partitions
![]() $\mathfrak {C}$
and
$\mathfrak {C}$
and
![]() $j\in \{1, \ldots , n\}$
, then there exists
$j\in \{1, \ldots , n\}$
, then there exists
![]() $\chi $
in G, such that
$\chi $
in G, such that
![]() $\chi $
extends
$\chi $
extends
![]() $\gamma _i|_{D_i}$
for each
$\gamma _i|_{D_i}$
for each
![]() $i \in \{1, \ldots , n\} \setminus \{j\}$
.
$i \in \{1, \ldots , n\} \setminus \{j\}$
.
Lemma 4.15. Let G be vigorous and approximately full. If N is a nontrivial normal subgroup of G, then N is vigorous and approximately full. Moreover, every element of N can be expressed as a product of two elements of N with small support.
Proof. By Lemma 4.14, N is vigorous. By Theorem 4.9, G generated by its elements of small support, and we need only show that every element of N can be expressed as a product of two elements of N with small support.
Let
![]() $\gamma $
be a nonidentity element of N. We will find
$\gamma $
be a nonidentity element of N. We will find
![]() $\alpha , \beta \in N$
with small support, such that
$\alpha , \beta \in N$
with small support, such that
![]() $\alpha \beta = \gamma $
.
$\alpha \beta = \gamma $
.
Let
![]() $A\in K_{\mathfrak {C}}$
be such that
$A\in K_{\mathfrak {C}}$
be such that
![]() $A\gamma ^{-1} \cap A = \varnothing $
and
$A\gamma ^{-1} \cap A = \varnothing $
and
![]() $(A\gamma ^{-1} \sqcup A) \neq \mathfrak {C}$
. Let
$(A\gamma ^{-1} \sqcup A) \neq \mathfrak {C}$
. Let
![]() $(\gamma _1, \gamma _2, \gamma _3) = (\gamma , \gamma ^{-1}, 1_G)$
, where
$(\gamma _1, \gamma _2, \gamma _3) = (\gamma , \gamma ^{-1}, 1_G)$
, where
![]() $1_G$
represents the identity of G. Set
$1_G$
represents the identity of G. Set
![]() $D_1 := A\gamma ^{-1}$
and
$D_1 := A\gamma ^{-1}$
and
![]() $D_{2} := A$
and
$D_{2} := A$
and
![]() $D_{3} := \mathfrak {C} \setminus (A\gamma ^{-1} \sqcup A)$
. Since G is approximately full, we may find
$D_{3} := \mathfrak {C} \setminus (A\gamma ^{-1} \sqcup A)$
. Since G is approximately full, we may find
![]() $\delta $
in G, such that
$\delta $
in G, such that
![]() $\delta $
agrees with
$\delta $
agrees with
![]() $\gamma $
on
$\gamma $
on
![]() $D_{1}=A\gamma ^{-1}$
and agrees with
$D_{1}=A\gamma ^{-1}$
and agrees with
![]() $1_G$
on
$1_G$
on
![]() $D_{3}=\mathfrak {C} \setminus (A\gamma ^{-1} \sqcup A)$
.
$D_{3}=\mathfrak {C} \setminus (A\gamma ^{-1} \sqcup A)$
.
Note that
![]() $\delta \in \operatorname {pstab}_G(D_3)$
. Let B be a proper clopen subset of
$\delta \in \operatorname {pstab}_G(D_3)$
. Let B be a proper clopen subset of
![]() $D_3$
. By Lemma 4.13, there is
$D_3$
. By Lemma 4.13, there is
![]() $\beta \in N$
, such that
$\beta \in N$
, such that
![]() $\beta |_{B\cup D_1 \cup D_2}=\delta |_{B\cup D_1 \cup D_2}$
. Set
$\beta |_{B\cup D_1 \cup D_2}=\delta |_{B\cup D_1 \cup D_2}$
. Set
![]() $\alpha := \gamma \beta ^{-1}$
.
$\alpha := \gamma \beta ^{-1}$
.
Note firstly that
![]() $\gamma $
was an arbitrary (nonidentity) element of N. Also,
$\gamma $
was an arbitrary (nonidentity) element of N. Also,
![]() $\alpha $
pointwise stabilises the clopen set
$\alpha $
pointwise stabilises the clopen set
![]() $A\gamma ^{-1}$
, while
$A\gamma ^{-1}$
, while
![]() $\beta $
pointwise stabilises the clopen set
$\beta $
pointwise stabilises the clopen set
![]() $B $
. So
$B $
. So
![]() $\gamma $
is a product of elements of small support in N as required.
$\gamma $
is a product of elements of small support in N as required.
Below, working towards Lemma 4.17, we essentially follow Matui’s proof of his Theorem 4.16 of [Reference Matui31] but in our context. The core result is that the commutator subgroup of an approximately full vigorous group is simple, but we write it slightly differently to capture a chain of natural constructions.
Lemma 4.16. Suppose that G is vigorous and approximately full. If
![]() $N \unlhd D(G)$
, then
$N \unlhd D(G)$
, then
![]() $N \unlhd G$
.
$N \unlhd G$
.
Proof. This proof is similar to that of Theorem 4.15 from [Reference Matui31] but is included for completeness and due to the need to translate the proof to our context.
Let
![]() $\alpha \in G$
and
$\alpha \in G$
and
![]() $\tau \in N$
. We show that
$\tau \in N$
. We show that
![]() $\tau ^{\alpha } \in N$
. We may assume that
$\tau ^{\alpha } \in N$
. We may assume that
![]() $\alpha $
and
$\alpha $
and
![]() $\tau $
have small support as, by Lemma 4.15, both G and N are generated by their elements of small support. As G is vigorous, there exists
$\tau $
have small support as, by Lemma 4.15, both G and N are generated by their elements of small support. As G is vigorous, there exists
![]() $\sigma \in G$
, such that
$\sigma \in G$
, such that
![]() $(\operatorname {supt}\!\left (\alpha \right ))\sigma \cap \operatorname {supt}\!\left (\tau \right ) = \varnothing $
. Then
$(\operatorname {supt}\!\left (\alpha \right ))\sigma \cap \operatorname {supt}\!\left (\tau \right ) = \varnothing $
. Then
Lemma 4.17. The commutator subgroup
![]() $D(G)$
of a vigorous, approximately full group G is vigorous, approximately full, and simple.
$D(G)$
of a vigorous, approximately full group G is vigorous, approximately full, and simple.
Proof. The nonsimplicity parts are handled by Lemma 4.15. The simplicity proof is taken directly from [Reference Matui31] Theorem 4.16 but is included for completeness and due to the need to slightly translate the proof to our context.
Let N be a nontrivial normal subgroup of
![]() $D(G)$
. Let
$D(G)$
. Let
![]() $\tau \in N \backslash \{1\}$
. There exists a nonempty clopen set
$\tau \in N \backslash \{1\}$
. There exists a nonempty clopen set
![]() $A \subseteq \mathfrak {C}$
, such that
$A \subseteq \mathfrak {C}$
, such that
![]() $A \cap (A)\tau = \varnothing $
. We would like to show that
$A \cap (A)\tau = \varnothing $
. We would like to show that
![]() $[\alpha , \beta ]$
is in N for any
$[\alpha , \beta ]$
is in N for any
![]() $\alpha , \beta \in G$
.
$\alpha , \beta \in G$
.
First, we assume
![]() $\alpha ,\beta $
have small support. As G is vigorous, we can find
$\alpha ,\beta $
have small support. As G is vigorous, we can find
![]() $\gamma \in G$
, such that
$\gamma \in G$
, such that
![]() $(\operatorname {supt}\!\left (\alpha \right ))\gamma \cap \operatorname {supt}\!\left (\beta \right ) = \varnothing $
and
$(\operatorname {supt}\!\left (\alpha \right ))\gamma \cap \operatorname {supt}\!\left (\beta \right ) = \varnothing $
and
![]() $\operatorname {supt}\!\left (\alpha \right )\cup \operatorname {supt}\!\left (\gamma \right )$
is not dense. There exists
$\operatorname {supt}\!\left (\alpha \right )\cup \operatorname {supt}\!\left (\gamma \right )$
is not dense. There exists
![]() $\sigma \in G$
, such that
$\sigma \in G$
, such that
![]() $(\operatorname {supt}\!\left (\alpha \right ) \cup \operatorname {supt}\!\left (\gamma \right ))\sigma \subseteq A$
. By Lemma 4.16,
$(\operatorname {supt}\!\left (\alpha \right ) \cup \operatorname {supt}\!\left (\gamma \right ))\sigma \subseteq A$
. By Lemma 4.16,
![]() $\tilde {\tau } = \tau ^\sigma \in N$
.
$\tilde {\tau } = \tau ^\sigma \in N$
.
By the construction of
![]() $\tilde {\tau }$
,
$\tilde {\tau }$
,
![]() $(\operatorname {supt}\!\left (\alpha \right ) \cup \operatorname {supt}\!\left (\gamma \right )) \cap (\operatorname {supt}\!\left (\alpha \right ) \cup \operatorname {supt}\!\left (\gamma \right ))\tilde {\tau } = \varnothing $
. Hence,
$(\operatorname {supt}\!\left (\alpha \right ) \cup \operatorname {supt}\!\left (\gamma \right )) \cap (\operatorname {supt}\!\left (\alpha \right ) \cup \operatorname {supt}\!\left (\gamma \right ))\tilde {\tau } = \varnothing $
. Hence,
![]() $\tilde {\gamma } = (\gamma ^{-1})^{\tilde {\tau }}\gamma =[\tilde {\tau },\gamma ]$
agrees with
$\tilde {\gamma } = (\gamma ^{-1})^{\tilde {\tau }}\gamma =[\tilde {\tau },\gamma ]$
agrees with
![]() $\gamma $
on
$\gamma $
on
![]() $(\operatorname {supt}\!\left (\alpha \right ) \cup \operatorname {supt}\!\left (\gamma \right ))$
. In particular, it satisfies
$(\operatorname {supt}\!\left (\alpha \right ) \cup \operatorname {supt}\!\left (\gamma \right ))$
. In particular, it satisfies
![]() $(\operatorname {supt}\!\left (\alpha \right ))\tilde {\gamma } \cap \operatorname {supt}\!\left (\beta \right ) = \varnothing $
. It follows that
$(\operatorname {supt}\!\left (\alpha \right ))\tilde {\gamma } \cap \operatorname {supt}\!\left (\beta \right ) = \varnothing $
. It follows that
![]() $ \alpha ^{ \tilde {\gamma }}$
commutes with
$ \alpha ^{ \tilde {\gamma }}$
commutes with
![]() $\beta $
and
$\beta $
and
![]() $\beta ^{-1}$
. Moreover, by Lemma 4.16,
$\beta ^{-1}$
. Moreover, by Lemma 4.16,
![]() $\tilde {\gamma }$
is in N, too. Therefore
$\tilde {\gamma }$
is in N, too. Therefore
Next, we show
![]() $[\alpha , \beta ] \in N$
when only
$[\alpha , \beta ] \in N$
when only
![]() $\beta $
is assumed to have small support. By Lemma 4.15, we can find
$\beta $
is assumed to have small support. By Lemma 4.15, we can find
![]() $\alpha _1, \alpha _2, \beta _1, \beta _2 \in G$
with small support, such that
$\alpha _1, \alpha _2, \beta _1, \beta _2 \in G$
with small support, such that
![]() $\alpha = \alpha _1 \alpha _2$
and
$\alpha = \alpha _1 \alpha _2$
and
![]() $\beta =\beta _1\beta _2$
. By the proof above,
$\beta =\beta _1\beta _2$
. By the proof above,
![]() $[\alpha _1, \beta ]$
and
$[\alpha _1, \beta ]$
and
![]() $[\alpha _2, \beta ]$
are in N. Note that
$[\alpha _2, \beta ]$
are in N. Note that
and similarly
So from Lemma 4.16, we have
![]() $[\alpha , \beta ]\in N$
as required.
$[\alpha , \beta ]\in N$
as required.
Theorem 4.18. Let G be a vigorous subgroup of
![]() $\operatorname {Homeo}(\mathfrak {C})$
. Then the following are equivalent
$\operatorname {Homeo}(\mathfrak {C})$
. Then the following are equivalent
-
1. G is simple,
-
2. G is flawless,
-
3.
 $G=w(G)_\circ $
with
$G=w(G)_\circ $
with
 $w=x_1^{-1}x_2^{-1}x_1x_2$
,
$w=x_1^{-1}x_2^{-1}x_1x_2$
, -
4. G is perfect and is generated by its elements of small support,
-
5. G is perfect and approximately full, and
-
6. G is the commutator subgroup of its own full group within
 $\operatorname {Homeo}(\mathfrak {C})$
.
$\operatorname {Homeo}(\mathfrak {C})$
.
Proof. (1)
![]() $\Rightarrow $
(2)
$\Rightarrow $
(2)
Let w be a nontrivial freely reduced word. By Lemma 4.1,
![]() $w(G)_\circ $
is normal in G. Theorem 3.3 gives that
$w(G)_\circ $
is normal in G. Theorem 3.3 gives that
![]() $w(G)_\circ $
contains a nonidentity element of G, so
$w(G)_\circ $
contains a nonidentity element of G, so
![]() $w(G)_\circ $
is a nontrivial normal subgroup of G which must therefore be G by simplicity.
$w(G)_\circ $
is a nontrivial normal subgroup of G which must therefore be G by simplicity.
(2)
![]() $\Rightarrow $
(3)
$\Rightarrow $
(3)
By inspection, the property of being
![]() $flawless{}$
is stronger than Condition (3).
$flawless{}$
is stronger than Condition (3).
(3)
![]() $\Rightarrow $
(4)
$\Rightarrow $
(4)
The group G is perfect because it is generated by a subset of the set of commutators. Noting that the complement of a proper clopen set is a proper clopen set, we see that
![]() $\left \{ [\alpha ,\beta ] \hspace {1mm} \middle | \hspace {1mm} \alpha ,\beta \in G,\exists K\in K_{\mathfrak {C}}\,,\text { such that}\, \operatorname {supt}\!\left ([\alpha ,\beta ]\right )\subseteq K \right \}$
is equivalent to the set
$\left \{ [\alpha ,\beta ] \hspace {1mm} \middle | \hspace {1mm} \alpha ,\beta \in G,\exists K\in K_{\mathfrak {C}}\,,\text { such that}\, \operatorname {supt}\!\left ([\alpha ,\beta ]\right )\subseteq K \right \}$
is equivalent to the set
![]() $\left \{ [\alpha ,\beta ] \in \operatorname {pstab}_G(A) \hspace {1mm} \middle | \hspace {1mm} \alpha ,\beta \in G, A \in K_{\mathfrak {C}} \right \}$
. Therefore, this last set generates G and is a subset of the set of elements of small support.
$\left \{ [\alpha ,\beta ] \in \operatorname {pstab}_G(A) \hspace {1mm} \middle | \hspace {1mm} \alpha ,\beta \in G, A \in K_{\mathfrak {C}} \right \}$
. Therefore, this last set generates G and is a subset of the set of elements of small support.
(4)
![]() $\Leftrightarrow $
(5)
$\Leftrightarrow $
(5)
This follows immediately from Corollary 1.9.
(5)
![]() $\Rightarrow $
(1)
$\Rightarrow $
(1)
This follows from Lemma 4.17.
(6)
![]() $\Rightarrow $
(1)
$\Rightarrow $
(1)
This follows from Lemma 4.17.
(1)
![]() $\Rightarrow $
(6) This direction was established by Belk and Matucci in an independent project. Upon hearing of this work, they graciously suggested its inclusion here.
$\Rightarrow $
(6) This direction was established by Belk and Matucci in an independent project. Upon hearing of this work, they graciously suggested its inclusion here.
Let us now suppose that G is simple and H is the full group of G in
![]() $\operatorname {Homeo}(\mathfrak {C})$
. As G is vigorous, G satisfies all of the Conditions (1)–(5). We now argue that G is the commutator subgroup of its own full group within
$\operatorname {Homeo}(\mathfrak {C})$
. As G is vigorous, G satisfies all of the Conditions (1)–(5). We now argue that G is the commutator subgroup of its own full group within
![]() $\operatorname {Homeo}(\mathfrak {C})$
.
$\operatorname {Homeo}(\mathfrak {C})$
.
Since G is perfect and a subgroup of the full group of G, it follows that G must be a subgroup of the commutator subgroup of the full group of G. Recalling as before that Matui in [Reference Matui31] shows that the commutator subgroup of a full vigorous (flexible) group of homeomorphisms of Cantor space is simple, it is sufficient to show that G is normal in the commutator subgroup of the full group of G. We will now show that G is normal in the full group of G.
Since G is generated by its elements of small support, we only need to show that the elements of small support in G are closed under conjugation by elements of the full group of G.
Let
![]() $\gamma $
now represent an element of small support in G, which is supported inside a particular clopen set
$\gamma $
now represent an element of small support in G, which is supported inside a particular clopen set
![]() $U\in K_{\mathfrak {C}}$
. Let
$U\in K_{\mathfrak {C}}$
. Let
![]() $\sigma $
be a (nonidentity) element of the full group H. Then, by definition, there is a positive integer k and partitions
$\sigma $
be a (nonidentity) element of the full group H. Then, by definition, there is a positive integer k and partitions
![]() $D:= \{D_1,D_2,\ldots , D_k\}$
and
$D:= \{D_1,D_2,\ldots , D_k\}$
and
![]() $R:=\{R_1,R_2,\ldots ,R_k\}$
of
$R:=\{R_1,R_2,\ldots ,R_k\}$
of
![]() $\mathfrak {C}$
, together with a set of elements
$\mathfrak {C}$
, together with a set of elements
![]() $\{\sigma _1,\sigma _2,\ldots ,\sigma _k\}\subsetneq G$
so that for each index i, we have
$\{\sigma _1,\sigma _2,\ldots ,\sigma _k\}\subsetneq G$
so that for each index i, we have
![]() $\sigma $
agrees with
$\sigma $
agrees with
![]() $\sigma _i$
over
$\sigma _i$
over
![]() $D_i$
and
$D_i$
and
![]() $D_i\sigma = R_i$
. Further, there is an index j so that
$D_i\sigma = R_i$
. Further, there is an index j so that
![]() $D_j\not \subseteq \operatorname {supt}\!\left (\gamma \right )$
. We can now choose
$D_j\not \subseteq \operatorname {supt}\!\left (\gamma \right )$
. We can now choose
![]() $E_j,F_j\in K_{\mathfrak {C}}$
so that
$E_j,F_j\in K_{\mathfrak {C}}$
so that
![]() $E_j\cap F_j=\varnothing $
,
$E_j\cap F_j=\varnothing $
,
![]() $E_j\cup F_j = D_j$
, and
$E_j\cup F_j = D_j$
, and
![]() $F_j\cap \operatorname {supt}\!\left (\gamma \right )=\varnothing $
.
$F_j\cap \operatorname {supt}\!\left (\gamma \right )=\varnothing $
.
Now the sets
and
are partitions of
![]() $\mathfrak {C}$
into clopen sets, and further, we have that
$\mathfrak {C}$
into clopen sets, and further, we have that
![]() $\sigma $
agrees with
$\sigma $
agrees with
![]() $\sigma _i$
over each
$\sigma _i$
over each
![]() $D_i$
, for any index i, and particularly,
$D_i$
, for any index i, and particularly,
![]() $\sigma $
agrees with
$\sigma $
agrees with
![]() $\sigma _i$
over each of the sets
$\sigma _i$
over each of the sets
![]() $E_j$
and
$E_j$
and
![]() $F_j$
. Thus, we have a system as per the definition of approximately full groups, as each
$F_j$
. Thus, we have a system as per the definition of approximately full groups, as each
![]() $\sigma _i\in G$
.
$\sigma _i\in G$
.
Now, we note that the union of these restricted elements is
![]() $\sigma $
, but we can find an element
$\sigma $
, but we can find an element
![]() $\chi \in G$
which agrees with all of these restricted elements over all of the parts of the domain partition
$\chi \in G$
which agrees with all of these restricted elements over all of the parts of the domain partition
![]() $D'$
except
$D'$
except
![]() $F_j$
. It follows that (as
$F_j$
. It follows that (as
![]() $\gamma $
acts as the identity over
$\gamma $
acts as the identity over
![]() $F_j$
)
$F_j$
)
![]() $\gamma ^\sigma = \gamma ^{\chi }$
, but this last element is an element of G.
$\gamma ^\sigma = \gamma ^{\chi }$
, but this last element is an element of G.
As
![]() $\gamma $
was an arbitrary element of small support in G, and as
$\gamma $
was an arbitrary element of small support in G, and as
![]() $\sigma $
was an arbitrary (nonidentity) element of H, we see that the set of elements of small support in G is not only a generating set for G, but this set is also a union of conjugacy classes of H. Consequently, G is normal in H, as desired.
$\sigma $
was an arbitrary (nonidentity) element of H, we see that the set of elements of small support in G is not only a generating set for G, but this set is also a union of conjugacy classes of H. Consequently, G is normal in H, as desired.
We note that there exist full subgroups of
![]() $\operatorname {Homeo}(\mathfrak {C})$
which are not simple. For example, the Higman–Thompson group
$\operatorname {Homeo}(\mathfrak {C})$
which are not simple. For example, the Higman–Thompson group
![]() $V_3$
.
$V_3$
.
5. Exploring simple vigorous groups
Recall
![]() $\mathscr {K}$
is the family of simple vigorous subgroups of
$\mathscr {K}$
is the family of simple vigorous subgroups of
![]() $\operatorname {Homeo}(\mathfrak {C})$
. In the first subsection, we show this is a rather large family.
$\operatorname {Homeo}(\mathfrak {C})$
. In the first subsection, we show this is a rather large family.
Further recall that
![]() $\mathscr {K}^{\text {f.g.}}$
is the subfamily of
$\mathscr {K}^{\text {f.g.}}$
is the subfamily of
![]() $\mathscr {K}$
consisting of the finitely generated simple vigorous subgroups of
$\mathscr {K}$
consisting of the finitely generated simple vigorous subgroups of
![]() $\operatorname {Homeo}(\mathfrak {C})$
. From Lemma 1.2 and the fact that the commutator subgroups of the Higman–Thompson groups
$\operatorname {Homeo}(\mathfrak {C})$
. From Lemma 1.2 and the fact that the commutator subgroups of the Higman–Thompson groups
![]() $V_k$
are vigorous, finitely presented, and simple, we obtain, for instance, that the (now called) simple Röver-Nekrashevych groups of [Reference Nekrashevych35] are all in
$V_k$
are vigorous, finitely presented, and simple, we obtain, for instance, that the (now called) simple Röver-Nekrashevych groups of [Reference Nekrashevych35] are all in
![]() $\mathscr {K}^{\text {f.g.}}$
. It is also easy to verify that the Brin–Thompson groups
$\mathscr {K}^{\text {f.g.}}$
. It is also easy to verify that the Brin–Thompson groups
![]() $nV$
are vigorous, so as these are finitely presented [Reference Brin6, Reference Brin7, Reference Hennig and Matucci16], they are in
$nV$
are vigorous, so as these are finitely presented [Reference Brin6, Reference Brin7, Reference Hennig and Matucci16], they are in
![]() $\mathscr {K}^{\text {f.g.}}$
as well. In the second subsection, we prove Theorem 5.15 that all of these groups are two-generated by torsion elements.
$\mathscr {K}^{\text {f.g.}}$
as well. In the second subsection, we prove Theorem 5.15 that all of these groups are two-generated by torsion elements.
5.1. Exploring the classes
 $\mathscr {K}$
and
$\mathscr {K}$
and
 $\mathscr {K}^{\text {f.g.}}$
$\mathscr {K}^{\text {f.g.}}$
Having given some examples previously of groups in
![]() $\mathscr {K}^{\text {f.g.}}$
(e.g. Thompson’s group
$\mathscr {K}^{\text {f.g.}}$
(e.g. Thompson’s group
![]() $V_2$
and Röver’s group
$V_2$
and Röver’s group
![]() $V(\Gamma $
)), we will now show that
$V(\Gamma $
)), we will now show that
![]() $\mathscr {K}$
and
$\mathscr {K}$
and
![]() $\mathscr {K}^{\text {f.g.}}$
are closed under various natural constructions to allow for more groups in
$\mathscr {K}^{\text {f.g.}}$
are closed under various natural constructions to allow for more groups in
![]() $\mathscr {K}$
and
$\mathscr {K}$
and
![]() $\mathscr {K}^{\text {f.g.}}$
to be easily constructed.
$\mathscr {K}^{\text {f.g.}}$
to be easily constructed.
For D a nonempty subset of
![]() $\mathfrak {C}$
, we will say that a subgroup
$\mathfrak {C}$
, we will say that a subgroup
![]() $G\leq \operatorname {Homeo}(\mathfrak {C})$
is vigorous over D if for any nonempty clopen subset A of D and nonempty proper clopen subsets B and C of A, there exists
$G\leq \operatorname {Homeo}(\mathfrak {C})$
is vigorous over D if for any nonempty clopen subset A of D and nonempty proper clopen subsets B and C of A, there exists
![]() $\gamma \in G$
with support contained in A, such that
$\gamma \in G$
with support contained in A, such that
![]() $B\gamma \subseteq C$
. We will write
$B\gamma \subseteq C$
. We will write
![]() $\mathscr {K}_{D}$
for the family of simple subgroups of
$\mathscr {K}_{D}$
for the family of simple subgroups of
![]() $\operatorname {Homeo}(\mathfrak {C})$
whose elements are with support contained in D and where these groups are vigorous over D. We will write
$\operatorname {Homeo}(\mathfrak {C})$
whose elements are with support contained in D and where these groups are vigorous over D. We will write
![]() $\mathscr {K}^{\text {f.g.}}_{D}$
for the family of finitely generated groups in
$\mathscr {K}^{\text {f.g.}}_{D}$
for the family of finitely generated groups in
![]() $\mathscr {K}_{D}$
.
$\mathscr {K}_{D}$
.
Remark 5.1. Let C and D be nonempty clopen subsets of
![]() $\mathfrak {C}$
, and let
$\mathfrak {C}$
, and let
![]() $\lambda :C \longrightarrow D$
be a homeomorphism. The homeomorphism
$\lambda :C \longrightarrow D$
be a homeomorphism. The homeomorphism
![]() $\lambda $
induces an isomorphism from
$\lambda $
induces an isomorphism from
![]() $\operatorname {pstab}_{\operatorname {Homeo}(\mathfrak {C})}(\mathfrak {C} \setminus C)$
to
$\operatorname {pstab}_{\operatorname {Homeo}(\mathfrak {C})}(\mathfrak {C} \setminus C)$
to
![]() $\operatorname {pstab}_{\operatorname {Homeo}(\mathfrak {C})}(\mathfrak {C} \setminus D)$
. This isomorphism induces a correspondence between groups in
$\operatorname {pstab}_{\operatorname {Homeo}(\mathfrak {C})}(\mathfrak {C} \setminus D)$
. This isomorphism induces a correspondence between groups in
![]() $\mathscr {K}_{C}$
and groups in
$\mathscr {K}_{C}$
and groups in
![]() $\mathscr {K}_{D}$
and a correspondence between groups in
$\mathscr {K}_{D}$
and a correspondence between groups in
![]() $\mathscr {K}^{\text {f.g.}}_{C}$
and groups in
$\mathscr {K}^{\text {f.g.}}_{C}$
and groups in
![]() $\mathscr {K}^{\text {f.g.}}_{D}$
. Note that C and D could be equal to
$\mathscr {K}^{\text {f.g.}}_{D}$
. Note that C and D could be equal to
![]() $\mathfrak {C}$
.
$\mathfrak {C}$
.
The above remark is both an easy observation and a useful tool for constructing groups trivially in
![]() $\mathscr {K}$
or
$\mathscr {K}$
or
![]() $\mathscr {K}^{\text {f.g.}}$
and, when combined with the propositions below, groups nontrivially in
$\mathscr {K}^{\text {f.g.}}$
and, when combined with the propositions below, groups nontrivially in
![]() $\mathscr {K}$
or
$\mathscr {K}$
or
![]() $\mathscr {K}^{\text {f.g.}}$
.
$\mathscr {K}^{\text {f.g.}}$
.
Proposition 5.2. Let U and V in
![]() $K_{\mathfrak {C}}$
be such that
$K_{\mathfrak {C}}$
be such that
![]() $U \cap V$
is nonempty. If G is in
$U \cap V$
is nonempty. If G is in
![]() $\mathscr {K}_{U}$
and H is in
$\mathscr {K}_{U}$
and H is in
![]() $\mathscr {K}_{V}$
, then
$\mathscr {K}_{V}$
, then
![]() $\left \langle G \cup H \right \rangle $
is in
$\left \langle G \cup H \right \rangle $
is in
![]() $\mathscr {K}_{U \cup V}$
. If, furthermore, G is in
$\mathscr {K}_{U \cup V}$
. If, furthermore, G is in
![]() $\mathscr {K}^{\text {f.g.}}_{U}$
and H is in
$\mathscr {K}^{\text {f.g.}}_{U}$
and H is in
![]() $\mathscr {K}^{\text {f.g.}}_{V}$
, then
$\mathscr {K}^{\text {f.g.}}_{V}$
, then
![]() $\left \langle G \cup H \right \rangle $
is in
$\left \langle G \cup H \right \rangle $
is in
![]() $\mathscr {K}^{\text {f.g.}}_{U \cup V}$
.
$\mathscr {K}^{\text {f.g.}}_{U \cup V}$
.
Proof. Let A be a nonempty clopen subset of
![]() $U \cup V$
, and let B and C be nonempty proper subsets of A.
$U \cup V$
, and let B and C be nonempty proper subsets of A.
Let
![]() $D \subseteq A \setminus B$
not be a superset of C. Since
$D \subseteq A \setminus B$
not be a superset of C. Since
![]() $D \subsetneq A \subseteq U \cup V$
, at least one of
$D \subsetneq A \subseteq U \cup V$
, at least one of
![]() $D \cap U$
and
$D \cap U$
and
![]() $D \cap V$
are nonempty. By symmetry, we may assume that
$D \cap V$
are nonempty. By symmetry, we may assume that
![]() $D \cap U$
is nonempty. Let
$D \cap U$
is nonempty. Let
![]() $\lambda \in G$
be such that
$\lambda \in G$
be such that
![]() $(U \setminus V)\lambda \subseteq D$
. Note that
$(U \setminus V)\lambda \subseteq D$
. Note that
![]() $V\lambda \supseteq (U \cup V) \setminus D$
$V\lambda \supseteq (U \cup V) \setminus D$
By Remark 5.1, the group
![]() $H^\lambda $
is in
$H^\lambda $
is in
![]() $\mathscr {K}_{V\lambda }$
. Since B and
$\mathscr {K}_{V\lambda }$
. Since B and
![]() $C \setminus D$
are nonempty proper subsets of
$C \setminus D$
are nonempty proper subsets of
![]() $A \setminus D \subseteq V\delta \cap A$
, there exist
$A \setminus D \subseteq V\delta \cap A$
, there exist
![]() $\gamma \in \operatorname {pstab}_{H^\lambda }(\mathfrak {C} \setminus A)$
, such that
$\gamma \in \operatorname {pstab}_{H^\lambda }(\mathfrak {C} \setminus A)$
, such that
![]() $B\gamma \subseteq C \setminus D$
as desired.
$B\gamma \subseteq C \setminus D$
as desired.
For the remainder of the argument, note that Theorem 4.18 holds for groups wholly supported on an element
![]() $D\in K_{\mathfrak {C}}$
(by replacing ‘vigorous’ with ‘vigorous over D’), as such sets D are themselves homeomorphic to Cantor space.
$D\in K_{\mathfrak {C}}$
(by replacing ‘vigorous’ with ‘vigorous over D’), as such sets D are themselves homeomorphic to Cantor space.
Now we will show that
![]() $\left \langle G \cup H \right \rangle $
is simple. By Theorem 4.18, the groups G and H are flawless. Also by Theorem 4.18, it is sufficient to show that
$\left \langle G \cup H \right \rangle $
is simple. By Theorem 4.18, the groups G and H are flawless. Also by Theorem 4.18, it is sufficient to show that
![]() $\left \langle G \cup H \right \rangle $
is flawless, as we have just proved that the group
$\left \langle G \cup H \right \rangle $
is flawless, as we have just proved that the group
![]() $\langle G\cup H\rangle $
is vigorous over
$\langle G\cup H\rangle $
is vigorous over
![]() $U\cup V$
. Since for any nontrivial freely reduced word w we have
$U\cup V$
. Since for any nontrivial freely reduced word w we have
![]() $\langle G\cup H\rangle =\langle w[G]_\circ \cup w[H]_\circ \rangle $
, we see that
$\langle G\cup H\rangle =\langle w[G]_\circ \cup w[H]_\circ \rangle $
, we see that
![]() $\langle G\cup H\rangle $
is also flawless, and we are done.
$\langle G\cup H\rangle $
is also flawless, and we are done.
If G and H are finitely generated, then it is immediate that
![]() $\left \langle G \cup H \right \rangle $
is also finitely generated.
$\left \langle G \cup H \right \rangle $
is also finitely generated.
The next lemma is used both in the next proposition and in Theorem 5.15. Observe that it follows immediately from Lemma 4.5 and Remark 5.1.
Lemma 5.3. Let U and V in
![]() $K_{\mathfrak {C}}$
be such that
$K_{\mathfrak {C}}$
be such that
![]() $U \cap V$
is nonempty. If G pointwise stabilises
$U \cap V$
is nonempty. If G pointwise stabilises
![]() $\mathfrak {C}\backslash (U \cup V)$
, and is generated by its elements which are supported on a proper clopen subset of
$\mathfrak {C}\backslash (U \cup V)$
, and is generated by its elements which are supported on a proper clopen subset of
![]() $U \cup V$
, and G is vigorous over
$U \cup V$
, and G is vigorous over
![]() $U\cup V$
, then
$U\cup V$
, then
Proposition 5.4. Let K be in
![]() $K_{\mathfrak {C}}$
. If G is in
$K_{\mathfrak {C}}$
. If G is in
![]() $\mathscr {K}$
, then the group
$\mathscr {K}$
, then the group
![]() $\operatorname {pstab}_G(\mathfrak {C} \setminus K)$
is in
$\operatorname {pstab}_G(\mathfrak {C} \setminus K)$
is in
![]() $\mathscr {K}_{K}$
. If G is in
$\mathscr {K}_{K}$
. If G is in
![]() $\mathscr {K}^{\text {f.g.}}$
, then the group
$\mathscr {K}^{\text {f.g.}}$
, then the group
![]() $\operatorname {pstab}_G(\mathfrak {C} \setminus K)$
is in
$\operatorname {pstab}_G(\mathfrak {C} \setminus K)$
is in
![]() $\mathscr {K}^{\text {f.g.}}_{K}$
.
$\mathscr {K}^{\text {f.g.}}_{K}$
.
Proof. Let
![]() $I_1 \in K_{\mathfrak {C}}$
and
$I_1 \in K_{\mathfrak {C}}$
and
![]() $I_2 \in K_{\mathfrak {C}}$
be such that
$I_2 \in K_{\mathfrak {C}}$
be such that
![]() $I_1 \cap I_2$
is nonempty,
$I_1 \cap I_2$
is nonempty,
![]() $I_1\not \subseteq I_2$
,
$I_1\not \subseteq I_2$
,
![]() $I_2\not \subseteq I_1$
, and
$I_2\not \subseteq I_1$
, and
![]() $I_1 \cup I_2 = K$
.
$I_1 \cup I_2 = K$
.
By Lemma 4.12, there exists
![]() $J_1$
and
$J_1$
and
![]() $J_2$
in
$J_2$
in
![]() $K_{\mathfrak {C}}$
, such that
$K_{\mathfrak {C}}$
, such that
![]() $I_1 \subsetneq J_1 \subsetneq K$
and
$I_1 \subsetneq J_1 \subsetneq K$
and
![]() $I_2 \subsetneq J_2 \subsetneq K$
and both
$I_2 \subsetneq J_2 \subsetneq K$
and both
![]() $\operatorname {pstab}_G(\mathfrak {C} \setminus J_1)$
and
$\operatorname {pstab}_G(\mathfrak {C} \setminus J_1)$
and
![]() $\operatorname {pstab}_G(\mathfrak {C} \setminus J_2)$
are isomorphic to G. The groups
$\operatorname {pstab}_G(\mathfrak {C} \setminus J_2)$
are isomorphic to G. The groups
![]() $\operatorname {pstab}_G(\mathfrak {C} \setminus J_1)$
and
$\operatorname {pstab}_G(\mathfrak {C} \setminus J_1)$
and
![]() $\operatorname {pstab}_G(\mathfrak {C} \setminus J_2)$
are therefore simple. Since G is vigorous, the group
$\operatorname {pstab}_G(\mathfrak {C} \setminus J_2)$
are therefore simple. Since G is vigorous, the group
![]() $\operatorname {pstab}_G(\mathfrak {C} \setminus J_1)$
is in
$\operatorname {pstab}_G(\mathfrak {C} \setminus J_1)$
is in
![]() $\mathscr {K}_{J_1}$
. Similarly, the group
$\mathscr {K}_{J_1}$
. Similarly, the group
![]() $\operatorname {pstab}_G(\mathfrak {C} \setminus J_2)$
is in
$\operatorname {pstab}_G(\mathfrak {C} \setminus J_2)$
is in
![]() $\mathscr {K}_{J_2}$
. By Proposition 5.2, the group
$\mathscr {K}_{J_2}$
. By Proposition 5.2, the group
![]() $\left \langle \operatorname {pstab}_G(\mathfrak {C} \setminus J_1) \cup \operatorname {pstab}_G(\mathfrak {C} \setminus J_2) \right \rangle $
is in
$\left \langle \operatorname {pstab}_G(\mathfrak {C} \setminus J_1) \cup \operatorname {pstab}_G(\mathfrak {C} \setminus J_2) \right \rangle $
is in
![]() $\mathscr {K}_{K}$
.
$\mathscr {K}_{K}$
.
Similarly, if G is finitely generated, then as
![]() $\left \langle \operatorname {pstab}_G(\mathfrak {C} \setminus J_1) \cup \operatorname {pstab}_G(\mathfrak {C} \setminus J_2) \right \rangle $
is generated by two isomorphic copies of G, then the group
$\left \langle \operatorname {pstab}_G(\mathfrak {C} \setminus J_1) \cup \operatorname {pstab}_G(\mathfrak {C} \setminus J_2) \right \rangle $
is generated by two isomorphic copies of G, then the group
![]() $\left \langle \operatorname {pstab}_G(\mathfrak {C} \setminus J_1) \cup \operatorname {pstab}_G(\mathfrak {C} \setminus J_2) \right \rangle $
is finitely generated and is in
$\left \langle \operatorname {pstab}_G(\mathfrak {C} \setminus J_1) \cup \operatorname {pstab}_G(\mathfrak {C} \setminus J_2) \right \rangle $
is finitely generated and is in
![]() $\mathscr {K}^{\text {f.g.}}_{K}$
.
$\mathscr {K}^{\text {f.g.}}_{K}$
.
It remains to show that
![]() $\left \langle \operatorname {pstab}_G(\mathfrak {C} \setminus J_1) \cup \operatorname {pstab}_G(\mathfrak {C} \setminus J_2) \right \rangle = \operatorname {pstab}_G(\mathfrak {C}\backslash K)$
.
$\left \langle \operatorname {pstab}_G(\mathfrak {C} \setminus J_1) \cup \operatorname {pstab}_G(\mathfrak {C} \setminus J_2) \right \rangle = \operatorname {pstab}_G(\mathfrak {C}\backslash K)$
.
As G is vigorous, we see that
![]() $H=\operatorname {pstab}_G(\mathfrak {C}\backslash K)$
is vigorous over K. By Lemma 4.3, we have that H is generated by those of its elements which are supported on proper clopen subsets of K. We apply Lemma 5.3 using
$H=\operatorname {pstab}_G(\mathfrak {C}\backslash K)$
is vigorous over K. By Lemma 4.3, we have that H is generated by those of its elements which are supported on proper clopen subsets of K. We apply Lemma 5.3 using
![]() $J_1$
and
$J_1$
and
![]() $J_2$
as U and V, respectively, and noting that
$J_2$
as U and V, respectively, and noting that
 $$\begin{align*}&\operatorname{pstab}_{G}(\mathfrak{C}\backslash J_1)=\operatorname{pstab}_{H}(K\backslash J_1)=\operatorname{pstab}_{H}(J_2\backslash J_1)\\&\kern100pt\mathrm{and} \\ &\operatorname{pstab}_{G}(\mathfrak{C}\backslash J_2)=\operatorname{pstab}_{H}(K\backslash J_2)=\operatorname{pstab}_{H}(J_1\backslash J_2) \end{align*}$$
$$\begin{align*}&\operatorname{pstab}_{G}(\mathfrak{C}\backslash J_1)=\operatorname{pstab}_{H}(K\backslash J_1)=\operatorname{pstab}_{H}(J_2\backslash J_1)\\&\kern100pt\mathrm{and} \\ &\operatorname{pstab}_{G}(\mathfrak{C}\backslash J_2)=\operatorname{pstab}_{H}(K\backslash J_2)=\operatorname{pstab}_{H}(J_1\backslash J_2) \end{align*}$$
hold to conclude that
![]() $H=\langle \operatorname {pstab}_{H}(J_1\backslash J_2)\cup \operatorname {pstab}_{H}(J_2\backslash J_1)\rangle $
as desired.
$H=\langle \operatorname {pstab}_{H}(J_1\backslash J_2)\cup \operatorname {pstab}_{H}(J_2\backslash J_1)\rangle $
as desired.
Proposition 5.5. Let G be in
![]() $\mathscr {K}$
. Let D be in
$\mathscr {K}$
. Let D be in
![]() $K_{\mathfrak {C}}$
. Let
$K_{\mathfrak {C}}$
. Let
![]() $\gamma \in G$
be such that
$\gamma \in G$
be such that
![]() $D\gamma \cap D$
is empty and
$D\gamma \cap D$
is empty and
![]() $D\gamma \cup D$
is a proper subset of
$D\gamma \cup D$
is a proper subset of
![]() $\mathfrak {C}$
. Let
$\mathfrak {C}$
. Let
![]() $\delta $
be in
$\delta $
be in
![]() $\operatorname {pstab}_{\operatorname {Homeo}(\mathfrak {C})}(\mathfrak {C} \setminus D)$
. Let H be the group
$\operatorname {pstab}_{\operatorname {Homeo}(\mathfrak {C})}(\mathfrak {C} \setminus D)$
. Let H be the group
![]() $\left \langle G \cup \{[\delta ,\gamma ]\} \right \rangle $
. Then H is also in
$\left \langle G \cup \{[\delta ,\gamma ]\} \right \rangle $
. Then H is also in
![]() $\mathscr {K}$
. If, further, G is in
$\mathscr {K}$
. If, further, G is in
![]() $\mathscr {K}^{\text {f.g.}}$
, then H is also in
$\mathscr {K}^{\text {f.g.}}$
, then H is also in
![]() $\mathscr {K}^{\text {f.g.}}$
.
$\mathscr {K}^{\text {f.g.}}$
.
Proof. The group H is
![]() $vigorous{}$
because it contains G. If the group G is finitely generated, then the group H is also finitely generated. It remains to show that H is simple.
$vigorous{}$
because it contains G. If the group G is finitely generated, then the group H is also finitely generated. It remains to show that H is simple.
Let T be equal to the union
Note that as
![]() $[\delta ,\gamma ]$
fixes
$[\delta ,\gamma ]$
fixes
![]() $\mathfrak {C} \backslash (D\cup D\gamma )$
, we have
$\mathfrak {C} \backslash (D\cup D\gamma )$
, we have
![]() $[\delta ,\gamma ]\in T$
.
$[\delta ,\gamma ]\in T$
.
Since G is generated by
![]() $T \cap G$
and
$T \cap G$
and
![]() $[\delta ,\gamma ]$
is in T, it follows that H is generated by T. Therefore, by Theorem 4.18, it is sufficient to show that H is perfect.
$[\delta ,\gamma ]$
is in T, it follows that H is generated by T. Therefore, by Theorem 4.18, it is sufficient to show that H is perfect.
By Theorem 4.18, the group G is perfect, so it is sufficient to show that
![]() $[\delta ,\gamma ]$
is a commutator of elements of H (we cannot use
$[\delta ,\gamma ]$
is a commutator of elements of H (we cannot use
![]() $\delta $
and
$\delta $
and
![]() $\gamma $
because
$\gamma $
because
![]() $\delta $
may not be in H).
$\delta $
may not be in H).
Let A and B in
![]() $K_{\mathfrak {C}}$
be disjoint subsets of
$K_{\mathfrak {C}}$
be disjoint subsets of
![]() $\mathfrak {C} \setminus (D\gamma \cup D)$
. By Theorem 4.9, the group H is approximately full, so we may find
$\mathfrak {C} \setminus (D\gamma \cup D)$
. By Theorem 4.9, the group H is approximately full, so we may find
![]() $\mu $
and
$\mu $
and
![]() $\nu $
in H, such that
$\nu $
in H, such that
![]() $\mu $
agrees with
$\mu $
agrees with
![]() $\delta $
on D and is wholly supported on
$\delta $
on D and is wholly supported on
![]() $D \cup A$
(for this, we can actually take
$D \cup A$
(for this, we can actually take
![]() $\mu =[\gamma ,\delta ]$
, which agrees with
$\mu =[\gamma ,\delta ]$
, which agrees with
![]() $\delta $
on D) and so that
$\delta $
on D) and so that
![]() $\nu $
agrees with
$\nu $
agrees with
![]() $\gamma $
on D and is wholly supported on
$\gamma $
on D and is wholly supported on
![]() $D\gamma \cup D \cup B$
(for this latter construction, we can use the approximately full property taking
$D\gamma \cup D \cup B$
(for this latter construction, we can use the approximately full property taking
![]() $\nu $
so that
$\nu $
so that
![]() $\nu $
agrees with
$\nu $
agrees with
![]() $\gamma ^{-1}$
on
$\gamma ^{-1}$
on
![]() $D\gamma $
to construct our element). Now
$D\gamma $
to construct our element). Now
![]() $[\mu ,\nu ] = [\delta ,\gamma ]$
.
$[\mu ,\nu ] = [\delta ,\gamma ]$
.
Corollary 5.6. All the groups in
![]() $\mathscr {K}^{\text {f.g.}}$
are semigroup two-generated. This includes
$\mathscr {K}^{\text {f.g.}}$
are semigroup two-generated. This includes
![]() $V_2$
and any group that may be constructed from
$V_2$
and any group that may be constructed from
![]() $V_2$
using the constructions described in Remark 5.1and Propositions 5.2, 5.4, and 5.5.
$V_2$
using the constructions described in Remark 5.1and Propositions 5.2, 5.4, and 5.5.
Proof. This follows immediately from Theorem 5.15.
Recall in Example 3.6, we construct a nonsimple overgroup in
![]() $\operatorname {Homeo}(\mathfrak {C})$
of the Higman–Thompson group
$\operatorname {Homeo}(\mathfrak {C})$
of the Higman–Thompson group
![]() $V_6$
. Consequently, neither
$V_6$
. Consequently, neither
![]() $\mathscr {K}$
nor
$\mathscr {K}$
nor
![]() $\mathscr {K}^{\text {f.g.}}$
are closed under taking overgroups in
$\mathscr {K}^{\text {f.g.}}$
are closed under taking overgroups in
![]() $\operatorname {Homeo}(\mathfrak {C})$
.
$\operatorname {Homeo}(\mathfrak {C})$
.
5.2. Two-generation of groups in
 $\mathscr {K}^{\text {f.g.}}$
$\mathscr {K}^{\text {f.g.}}$
In this section, we will prove Theorem 5.15.
As has been mentioned above, the groups we are exploring bear some comparison with the full groups explored by Matui and others (see, e.g. [Reference Matsumoto25, Reference Matsumoto and Matui26, Reference Matui28, Reference Matui29, Reference Matui30]). Matui’s full groups are generally built from almost finite or purely infinite étale groupoids and act naturally on the groupoids’ unit spaces (which is a Cantor space in many cases of interest). However, the groups we consider need not be full, instead, they are vigorous and approximately full. Meanwhile, Matui’s groups need not be vigorous but often act with minimal actions. In particular, neither of these classes contains the other. In general, our class of groups corresponds most closely with the case where Matui is analysing full groups over an étale groupoid of purely infinite type, and some similar statements can be made (see, e.g. Lemma 4.14 and Theorem 4.16 [Reference Matui30], which are close to our Lemmas 4.15 and 4.17, respectively).
Continuing this theme, in what follows, we build an abelian group
![]() $(\mathfrak {X}_{G},+)$
corresponding to Matui’s
$(\mathfrak {X}_{G},+)$
corresponding to Matui’s
![]() $0$
-th homology group of [Reference Matui29], which, in turn, is based on Crainic and Moerdijk’s homology theory for étale groupoids (see [Reference Crainic and Moerdijk11]). Indeed, there have been many related constructions since [Reference Matui29] (for example, see [Reference Lawson21, Reference Matsumoto25, Reference Matsumoto and Matui26, Reference Bon27, Reference Matui30, Reference Matui31, Reference Nawata33, Reference Nekrashevych35]).
$0$
-th homology group of [Reference Matui29], which, in turn, is based on Crainic and Moerdijk’s homology theory for étale groupoids (see [Reference Crainic and Moerdijk11]). Indeed, there have been many related constructions since [Reference Matui29] (for example, see [Reference Lawson21, Reference Matsumoto25, Reference Matsumoto and Matui26, Reference Bon27, Reference Matui30, Reference Matui31, Reference Nawata33, Reference Nekrashevych35]).
In our case, we use our group
![]() $(\mathfrak {X}_{G},+)$
to help us to understand how to assemble torsion elements which have some prescribed dynamics (see Lemmas 5.12 and 5.13) in approximately full groups.
$(\mathfrak {X}_{G},+)$
to help us to understand how to assemble torsion elements which have some prescribed dynamics (see Lemmas 5.12 and 5.13) in approximately full groups.
5.2.1. Homology
Our proof that a finitely generated vigorous simple group is actually two-generated uses our constructed group
![]() $(\mathfrak {X}_{G},+)$
. An older proof, using only elementary arguments (but this path is more complicated), can be found in [Reference Hyde20].
$(\mathfrak {X}_{G},+)$
. An older proof, using only elementary arguments (but this path is more complicated), can be found in [Reference Hyde20].
Definition 5.7. Let
![]() $G \leq \operatorname {Homeo}(\mathfrak {C})$
be approximately full and vigorous. For B in
$G \leq \operatorname {Homeo}(\mathfrak {C})$
be approximately full and vigorous. For B in
![]() $K_{\mathfrak {C}}$
, we will use
$K_{\mathfrak {C}}$
, we will use
![]() $[B]_{G}$
to denote the set
$[B]_{G}$
to denote the set
![]() $\left \{ B\gamma \hspace {1mm} \middle | \hspace {1mm} \gamma \in G \right \}$
. We will use
$\left \{ B\gamma \hspace {1mm} \middle | \hspace {1mm} \gamma \in G \right \}$
. We will use
![]() $\mathfrak {X}_{G}$
to denote the set
$\mathfrak {X}_{G}$
to denote the set
![]() $\left \{ [C]_{G} \hspace {1mm} \middle | \hspace {1mm} C \in K_{\mathfrak {C}} \right \}$
. For
$\left \{ [C]_{G} \hspace {1mm} \middle | \hspace {1mm} C \in K_{\mathfrak {C}} \right \}$
. For
![]() $U, V\in K_{\mathfrak {C}}$
, define
$U, V\in K_{\mathfrak {C}}$
, define
![]() $[U]_{G}+[V]_{G}:= [U\mu \sqcup V\nu ]_{G}$
, where
$[U]_{G}+[V]_{G}:= [U\mu \sqcup V\nu ]_{G}$
, where
![]() $\mu , \nu \in G$
are so that
$\mu , \nu \in G$
are so that
![]() $U\mu \cap V\nu =\varnothing $
and
$U\mu \cap V\nu =\varnothing $
and
![]() $U\mu \sqcup V\nu \neq \mathfrak {C}$
. In the next proposition, we prove this operation is well-defined.
$U\mu \sqcup V\nu \neq \mathfrak {C}$
. In the next proposition, we prove this operation is well-defined.
Proposition 5.8. Let
![]() $G \leq \operatorname {Homeo}(\mathfrak {C})$
be approximately full and vigorous. The operation
$G \leq \operatorname {Homeo}(\mathfrak {C})$
be approximately full and vigorous. The operation
![]() $+$
defined in 5.7 is well-defined, and when equipped with this operation,
$+$
defined in 5.7 is well-defined, and when equipped with this operation,
![]() $\mathfrak {X}_{G}$
is a commutative group.
$\mathfrak {X}_{G}$
is a commutative group.
Proof. We first show that the operation
![]() $+$
is well-defined.
$+$
is well-defined.
Let
![]() $U, V\in K_{\mathfrak {C}}$
, we will show
$U, V\in K_{\mathfrak {C}}$
, we will show
![]() $[U\mu _1 \sqcup V\nu _1]_{G} = [U\mu _2 \sqcup V\nu _2]_{G}$
for any
$[U\mu _1 \sqcup V\nu _1]_{G} = [U\mu _2 \sqcup V\nu _2]_{G}$
for any
![]() $\mu _1,\mu _2,\nu _1,\nu _2\in G$
with
$\mu _1,\mu _2,\nu _1,\nu _2\in G$
with
![]() $U\mu _i\cap V\nu _i=\varnothing $
and
$U\mu _i\cap V\nu _i=\varnothing $
and
![]() $U\mu _i\sqcup V\nu _i\neq \mathfrak {C}$
for
$U\mu _i\sqcup V\nu _i\neq \mathfrak {C}$
for
![]() $i\in \{1,2\}$
.
$i\in \{1,2\}$
.
Let
![]() $\mu _1$
,
$\mu _1$
,
![]() $\mu _2$
,
$\mu _2$
,
![]() $\nu _1$
,
$\nu _1$
,
![]() $\nu _2\in G$
so that
$\nu _2\in G$
so that
![]() $U\mu _i\cap V\nu _i=\varnothing $
and
$U\mu _i\cap V\nu _i=\varnothing $
and
![]() $U\mu _i\sqcup V\nu _i\neq \mathfrak {C}$
for
$U\mu _i\sqcup V\nu _i\neq \mathfrak {C}$
for
![]() $i\in \{1,2\}$
.
$i\in \{1,2\}$
.
We first prove a simplified case where the four sets
![]() $U\mu _1$
,
$U\mu _1$
,
![]() $U\mu _2$
,
$U\mu _2$
,
![]() $V\nu _1$
, and
$V\nu _1$
, and
![]() $V\nu _2$
are pairwise disjoint and where the union of these four sets is not all of Cantor space.
$V\nu _2$
are pairwise disjoint and where the union of these four sets is not all of Cantor space.
Set
![]() $C:= \mathfrak {C}\backslash (U\mu _1\sqcup U\mu _2\sqcup V\nu _1\sqcup V\nu _2)$
, and consider
$C:= \mathfrak {C}\backslash (U\mu _1\sqcup U\mu _2\sqcup V\nu _1\sqcup V\nu _2)$
, and consider
![]() $\mathcal {D}:= \{U\mu _1,U\mu _2,V\nu _1,V\nu _2, C\}$
, a partition of
$\mathcal {D}:= \{U\mu _1,U\mu _2,V\nu _1,V\nu _2, C\}$
, a partition of
![]() $\mathfrak {C}$
into five proper clopen sets.
$\mathfrak {C}$
into five proper clopen sets.
Consider
![]() $\gamma _1, \gamma _2, \gamma _3, \gamma _4, \gamma _5\in G$
taken as
$\gamma _1, \gamma _2, \gamma _3, \gamma _4, \gamma _5\in G$
taken as
![]() $\gamma _1=\mu _1^{-1}\mu _2$
,
$\gamma _1=\mu _1^{-1}\mu _2$
,
![]() $\gamma _2=\nu _1^{-1}\nu _2$
,
$\gamma _2=\nu _1^{-1}\nu _2$
,
![]() $\gamma _3=\gamma _1^{-1}$
,
$\gamma _3=\gamma _1^{-1}$
,
![]() $\gamma _4=\gamma _2^{-1}$
and
$\gamma _4=\gamma _2^{-1}$
and
![]() $\gamma _5=1_G$
, the identity of G. As G is approximately full, there is
$\gamma _5=1_G$
, the identity of G. As G is approximately full, there is
![]() $\gamma \in G$
which agrees with
$\gamma \in G$
which agrees with
![]() $\gamma _1$
over
$\gamma _1$
over
![]() $U\mu _1$
, with
$U\mu _1$
, with
![]() $\gamma _2$
over
$\gamma _2$
over
![]() $V\nu _1$
, with
$V\nu _1$
, with
![]() $\gamma _3$
over
$\gamma _3$
over
![]() $U\mu _2$
, and with
$U\mu _2$
, and with
![]() $\gamma _4$
over
$\gamma _4$
over
![]() $V\nu _2$
. In particular,
$V\nu _2$
. In particular,
![]() $(U\mu _1\sqcup V\nu _1)\gamma =(U\mu _2\sqcup V\nu _2)$
, and therefore
$(U\mu _1\sqcup V\nu _1)\gamma =(U\mu _2\sqcup V\nu _2)$
, and therefore
![]() $[U\mu _1\sqcup V\nu _1]_{G}=[U\mu _2\sqcup V\nu _2]_{G}$
in this case.
$[U\mu _1\sqcup V\nu _1]_{G}=[U\mu _2\sqcup V\nu _2]_{G}$
in this case.
Now let us drop the two assumptions that the four sets
![]() $U\mu _1$
,
$U\mu _1$
,
![]() $U\mu _2$
,
$U\mu _2$
,
![]() $V\nu _1$
, and
$V\nu _1$
, and
![]() $V\nu _2$
are pairwise disjoint and that the union of these four sets is not all of Cantor space. Set
$V\nu _2$
are pairwise disjoint and that the union of these four sets is not all of Cantor space. Set
![]() $E:=\mathfrak {C}\backslash (U\mu _1\sqcup V\nu _1)$
and
$E:=\mathfrak {C}\backslash (U\mu _1\sqcup V\nu _1)$
and
![]() $F:= \mathfrak {C}\backslash (U\mu _2\sqcup V\nu _2)$
. Choose
$F:= \mathfrak {C}\backslash (U\mu _2\sqcup V\nu _2)$
. Choose
![]() $E'\subseteq E$
and
$E'\subseteq E$
and
![]() $F'\subseteq F$
proper clopen subsets of E and F, respectively, so that the following properties hold:
$F'\subseteq F$
proper clopen subsets of E and F, respectively, so that the following properties hold:
-
1.
 $E\backslash E'\neq \varnothing $
,
$E\backslash E'\neq \varnothing $
, -
2.
 $F\backslash F'\neq \varnothing $
,
$F\backslash F'\neq \varnothing $
, -
3.
 $E'\cap F' = \varnothing $
, and
$E'\cap F' = \varnothing $
, and -
4.
 $E'\sqcup F'\neq \mathfrak {C}$
$E'\sqcup F'\neq \mathfrak {C}$
observing we can find these sets even if
![]() $E\cap F\neq \varnothing $
.
$E\cap F\neq \varnothing $
.
Now, as G is vigorous, there are group elements
![]() $\theta _1, \theta _2\in G$
so that
$\theta _1, \theta _2\in G$
so that
![]() $(U\mu _1\sqcup V\nu _1)\theta _1\subseteq E'$
while
$(U\mu _1\sqcup V\nu _1)\theta _1\subseteq E'$
while
![]() $(U\mu _2\sqcup V\nu _2)\theta _2\subseteq F'$
.
$(U\mu _2\sqcup V\nu _2)\theta _2\subseteq F'$
.
By the definition of the sets
![]() $[A]_{G}$
for
$[A]_{G}$
for
![]() $A\in K_{\mathfrak {C}}$
, we see that
$A\in K_{\mathfrak {C}}$
, we see that
![]() $[U\mu _1\sqcup V\nu _1]_{G}=[(U\mu _1\sqcup V\nu _1)\theta _1]_{G}$
and
$[U\mu _1\sqcup V\nu _1]_{G}=[(U\mu _1\sqcup V\nu _1)\theta _1]_{G}$
and
![]() $[U\mu _2\sqcup V\nu _2]_{G}=[(U\mu _2\sqcup V\nu _2)\theta _2]_{G}$
. However, we have that the four sets
$[U\mu _2\sqcup V\nu _2]_{G}=[(U\mu _2\sqcup V\nu _2)\theta _2]_{G}$
. However, we have that the four sets
![]() $U\mu _1\theta _1, V\nu _1\theta _1, U\mu _2\theta _2, V\nu _2\theta _2$
are pairwise disjoint and have union not all of
$U\mu _1\theta _1, V\nu _1\theta _1, U\mu _2\theta _2, V\nu _2\theta _2$
are pairwise disjoint and have union not all of
![]() $\mathfrak {C}$
(as they are contained in
$\mathfrak {C}$
(as they are contained in
![]() $E'\sqcup F'$
). Thus, it follows from our result in the simplified case that
$E'\sqcup F'$
). Thus, it follows from our result in the simplified case that
![]() $[U\mu _1\theta _1\sqcup V\nu _1\theta _1]_{G}=[U\mu _2\theta _2\sqcup V\nu _2\theta _2]_{G}$
. In particular,
$[U\mu _1\theta _1\sqcup V\nu _1\theta _1]_{G}=[U\mu _2\theta _2\sqcup V\nu _2\theta _2]_{G}$
. In particular,
![]() $+$
is well-defined.
$+$
is well-defined.
Now we show that the operation
![]() $+$
is associative. Let X, Y,
$+$
is associative. Let X, Y,
![]() $Z\in K_{\mathfrak {C}}$
. We will show that
$Z\in K_{\mathfrak {C}}$
. We will show that
![]() $([X]_{G} + [Y]_{G}) + [Z]_{G} = [X]_{G} + ([Y]_{G} + [Z]_{G})$
. As G is vigorous, we may find
$([X]_{G} + [Y]_{G}) + [Z]_{G} = [X]_{G} + ([Y]_{G} + [Z]_{G})$
. As G is vigorous, we may find
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
in G so that
$\beta $
in G so that
![]() $X\alpha $
,
$X\alpha $
,
![]() $Y\beta $
, and Z are disjoint and where
$Y\beta $
, and Z are disjoint and where
![]() $X\alpha \cup Y\beta \cup Z\neq \mathfrak {C}$
. Now
$X\alpha \cup Y\beta \cup Z\neq \mathfrak {C}$
. Now
 $$ \begin{align*} ([X]_{G} + [Y]_{G}) + [Z]_{G} & = ([X\alpha]_{G} + [Y\beta]_{G}) + [Z]_{G} \\[1.2pt] & = ([X\alpha \sqcup Y\beta]_{G}) + [Z]_{G} \\[1.2pt] & = [X\alpha \sqcup Y\beta \sqcup Z]_{G} \\[1.2pt] & = ([X\alpha]_{G} + [Y\beta \sqcup Z]_{G}) \\[1.2pt] & = [X\alpha]_{G} + ([Y\beta]_{G} + [Z]_{G}) \\[1.2pt] & = [X]_{G} + ([Y]_{G} + [Z]_{G}) \end{align*} $$
$$ \begin{align*} ([X]_{G} + [Y]_{G}) + [Z]_{G} & = ([X\alpha]_{G} + [Y\beta]_{G}) + [Z]_{G} \\[1.2pt] & = ([X\alpha \sqcup Y\beta]_{G}) + [Z]_{G} \\[1.2pt] & = [X\alpha \sqcup Y\beta \sqcup Z]_{G} \\[1.2pt] & = ([X\alpha]_{G} + [Y\beta \sqcup Z]_{G}) \\[1.2pt] & = [X\alpha]_{G} + ([Y\beta]_{G} + [Z]_{G}) \\[1.2pt] & = [X]_{G} + ([Y]_{G} + [Z]_{G}) \end{align*} $$
as desired.
Since the unions are commutative, it follows that the operation
![]() $+$
is commutative. It remains to show that
$+$
is commutative. It remains to show that
![]() $\mathfrak {X}_{G}$
under the operation of
$\mathfrak {X}_{G}$
under the operation of
![]() $+$
forms a group.
$+$
forms a group.
Let A and
![]() $C\in K_{\mathfrak {C}}$
. It is sufficient to find
$C\in K_{\mathfrak {C}}$
. It is sufficient to find
![]() $B \in K_{\mathfrak {C}}$
, such that
$B \in K_{\mathfrak {C}}$
, such that
![]() $[A]_{G} + [B]_{G} = [C]_{G}$
.
$[A]_{G} + [B]_{G} = [C]_{G}$
.
Since G is vigorous, we may find
![]() $\beta $
in G, such that
$\beta $
in G, such that
![]() $A\beta \subsetneq C$
. Let B be equal to
$A\beta \subsetneq C$
. Let B be equal to
![]() $C \setminus A\beta $
. Now
$C \setminus A\beta $
. Now
![]() $[A]_{G} + [B]_{G} = [A\beta \sqcup B]_{G} = [C]_{G}$
as desired.
$[A]_{G} + [B]_{G} = [A\beta \sqcup B]_{G} = [C]_{G}$
as desired.
Below, we use
![]() $[\varnothing ]_{G}$
to denote the set
$[\varnothing ]_{G}$
to denote the set
![]() $\left \{ A\gamma \setminus A \hspace {1mm} \middle | \hspace {1mm} A \in K_{\mathfrak {C}} \textrm { and } \gamma \in G \textrm { and } A\subsetneq A\gamma \right \}$
and use
$\left \{ A\gamma \setminus A \hspace {1mm} \middle | \hspace {1mm} A \in K_{\mathfrak {C}} \textrm { and } \gamma \in G \textrm { and } A\subsetneq A\gamma \right \}$
and use
![]() $[\mathfrak {C}]_{G}$
to denote the set
$[\mathfrak {C}]_{G}$
to denote the set
![]() $\left \{ \mathfrak {C} \setminus A \hspace {1mm} \middle | \hspace {1mm} A \in [\varnothing ]_{G} \right \}$
. We have the following lemma.
$\left \{ \mathfrak {C} \setminus A \hspace {1mm} \middle | \hspace {1mm} A \in [\varnothing ]_{G} \right \}$
. We have the following lemma.
Lemma 5.9. Let
![]() $G \leq \operatorname {Homeo}(\mathfrak {C})$
be approximately full and vigorous. We have the following.
$G \leq \operatorname {Homeo}(\mathfrak {C})$
be approximately full and vigorous. We have the following.
-
1. The set
 $[\varnothing ]_{G}$
is an element of
$[\varnothing ]_{G}$
is an element of
 $\mathfrak {X}_{G}$
, and for all
$\mathfrak {X}_{G}$
, and for all
 $A\in K_{\mathfrak {C}}$
, we have
$A\in K_{\mathfrak {C}}$
, we have
 $[A]_{G}+[\varnothing ]_{G}=[A]_{G}$
.
$[A]_{G}+[\varnothing ]_{G}=[A]_{G}$
. -
2. Let
 $A\in K_{\mathfrak {C}}$
,
$A\in K_{\mathfrak {C}}$
,-
(a) if
 $\alpha ,\beta \in G$
so that
$\alpha ,\beta \in G$
so that
 $A\subsetneq A\alpha $
and
$A\subsetneq A\alpha $
and
 $A\beta \subsetneq A\alpha \backslash A$
, then
$A\beta \subsetneq A\alpha \backslash A$
, then
 $[A\alpha \backslash (A\sqcup A\beta )]_{G}$
is the inverse of
$[A\alpha \backslash (A\sqcup A\beta )]_{G}$
is the inverse of
 $[A]_{G}$
, and
$[A]_{G}$
, and -
(b)
 $[A]_{G}+[\mathfrak {C}\backslash A]_{G}=[\mathfrak {C}]_{G}$
.
$[A]_{G}+[\mathfrak {C}\backslash A]_{G}=[\mathfrak {C}]_{G}$
.
-
Proof. Let
![]() $A, B\in K_{\mathfrak {C}}$
and
$A, B\in K_{\mathfrak {C}}$
and
![]() $\alpha , \beta \in G$
so that
$\alpha , \beta \in G$
so that
![]() $A\subsetneq A\alpha $
and
$A\subsetneq A\alpha $
and
![]() $B\subsetneq B\beta $
.
$B\subsetneq B\beta $
.
It is the case that
![]() $[A\alpha \backslash A]_{G}+[A]_{G}= [A\alpha ]_{G}=[A]_{G}$
, so
$[A\alpha \backslash A]_{G}+[A]_{G}= [A\alpha ]_{G}=[A]_{G}$
, so
![]() $[A\alpha \backslash A]_{G}$
is the identity for the group
$[A\alpha \backslash A]_{G}$
is the identity for the group
![]() $\mathfrak {X}_{G}$
. Similarly,
$\mathfrak {X}_{G}$
. Similarly,
![]() $[B\beta \backslash B]_{G}$
is also the identity of
$[B\beta \backslash B]_{G}$
is also the identity of
![]() $\mathfrak {X}_{G}$
, so we have
$\mathfrak {X}_{G}$
, so we have
![]() $[A\alpha \backslash A]_{G}=[B\beta \backslash B]_{G}$
. In particular, there is
$[A\alpha \backslash A]_{G}=[B\beta \backslash B]_{G}$
. In particular, there is
![]() $\gamma \in G$
so that
$\gamma \in G$
so that
![]() $(A\alpha \backslash A)\gamma = (B\beta \backslash B)$
. From this, it follows that
$(A\alpha \backslash A)\gamma = (B\beta \backslash B)$
. From this, it follows that
![]() $[\varnothing ]_{G}\subseteq (A\alpha \backslash A)G=[A\alpha \backslash A]_{G}$
.
$[\varnothing ]_{G}\subseteq (A\alpha \backslash A)G=[A\alpha \backslash A]_{G}$
.
Observing that for any
![]() $C\in K_{\mathfrak {C}}$
and
$C\in K_{\mathfrak {C}}$
and
![]() $\delta ,\rho \in G$
with
$\delta ,\rho \in G$
with
![]() $C\subsetneq C\rho $
we have
$C\subsetneq C\rho $
we have
![]() $(C\rho \backslash C)\cdot \delta = (C\delta )\rho ^\delta \backslash C\delta $
, we see that
$(C\rho \backslash C)\cdot \delta = (C\delta )\rho ^\delta \backslash C\delta $
, we see that
![]() $[\varnothing ]_{G}\supseteq (A\alpha \backslash A)G=[A\alpha \backslash A]_{G}$
. It now follows that
$[\varnothing ]_{G}\supseteq (A\alpha \backslash A)G=[A\alpha \backslash A]_{G}$
. It now follows that
![]() $[\varnothing ]_{G}=[A\alpha \backslash A]_{G}$
, and so
$[\varnothing ]_{G}=[A\alpha \backslash A]_{G}$
, and so
![]() $[\varnothing ]_{G}$
is an element of
$[\varnothing ]_{G}$
is an element of
![]() $\mathfrak {X}_{G}$
and, in particular, it is the identity under
$\mathfrak {X}_{G}$
and, in particular, it is the identity under
![]() $+$
.
$+$
.
In passing, we note that the argument above shows that the set
![]() $[\mathfrak {C}]_{G}$
is a group element, as the orbit of the complement of a proper clopen set is the orbit of a proper clopen set.
$[\mathfrak {C}]_{G}$
is a group element, as the orbit of the complement of a proper clopen set is the orbit of a proper clopen set.
For point (2a), we recall from the last paragraph of the proof of Proposition 5.8 that if
![]() $A,C\in K_{\mathfrak {C}}$
, then choosing any
$A,C\in K_{\mathfrak {C}}$
, then choosing any
![]() $\beta $
so that
$\beta $
so that
![]() $A\beta \subsetneq C$
, we obtain the formula
$A\beta \subsetneq C$
, we obtain the formula
![]() $[A]_{G}+[C\backslash A\beta ]_{G}=[C]_{G}$
. Therefore, if we consider some
$[A]_{G}+[C\backslash A\beta ]_{G}=[C]_{G}$
. Therefore, if we consider some
![]() $\alpha \in G$
so that
$\alpha \in G$
so that
![]() $A\subsetneq A\alpha $
, then
$A\subsetneq A\alpha $
, then
![]() $(A\alpha \backslash A)\in K_{\mathfrak {C}}$
and
$(A\alpha \backslash A)\in K_{\mathfrak {C}}$
and
![]() $[\varnothing ]_{G} = [A\alpha \backslash A]_{G}$
. Thus, setting
$[\varnothing ]_{G} = [A\alpha \backslash A]_{G}$
. Thus, setting
![]() $C:= A\alpha \backslash A$
in our formula and choosing
$C:= A\alpha \backslash A$
in our formula and choosing
![]() $\beta \in G$
so that
$\beta \in G$
so that
![]() $A\beta \subsetneq C$
, then we obtain the desired result for the inverse of
$A\beta \subsetneq C$
, then we obtain the desired result for the inverse of
![]() $[A]_{G}$
.
$[A]_{G}$
.
Point (2b) follows easily as well. Let
![]() $A\in K_{\mathfrak {C}}$
, and choose some
$A\in K_{\mathfrak {C}}$
, and choose some
![]() $\gamma $
so that
$\gamma $
so that
![]() $A\gamma \subsetneq A$
. It then follows that
$A\gamma \subsetneq A$
. It then follows that
![]() $[A]_{G}+[\mathfrak {C}\backslash A]_{G}= [A\gamma ]_{G} +[\mathfrak {C}\backslash A]_{G} = [A\gamma \sqcup \mathfrak {C}\backslash A]_{G}= [\mathfrak {C}\backslash (A\backslash A\gamma )]_{G}$
. But
$[A]_{G}+[\mathfrak {C}\backslash A]_{G}= [A\gamma ]_{G} +[\mathfrak {C}\backslash A]_{G} = [A\gamma \sqcup \mathfrak {C}\backslash A]_{G}= [\mathfrak {C}\backslash (A\backslash A\gamma )]_{G}$
. But
![]() $[A\backslash A\gamma ]_{G}=[\varnothing ]_{G}$
, so
$[A\backslash A\gamma ]_{G}=[\varnothing ]_{G}$
, so
![]() $[\mathfrak {C}\backslash (A\backslash A\gamma )]_{G}=[\mathfrak {C}]_{G}$
by the definition of
$[\mathfrak {C}\backslash (A\backslash A\gamma )]_{G}=[\mathfrak {C}]_{G}$
by the definition of
![]() $[\mathfrak {C}]_{G}$
, and so we have our desired result.
$[\mathfrak {C}]_{G}$
, and so we have our desired result.
The reader may check the following.
Remark 5.10. A vigorous and approximately full group G is dense in
![]() $\operatorname {Homeo}(\mathfrak {C})$
if and only if
$\operatorname {Homeo}(\mathfrak {C})$
if and only if
![]() $\mathfrak {X}_{G}$
is trivial.
$\mathfrak {X}_{G}$
is trivial.
5.2.2. Four Lemmas towards Theorem 5.15
The following lemma is a well-known and useful purely algebraic statement about finitely generated subgroups of groups.
Lemma 5.11. If
![]() $F \leq G$
are groups, F is finitely generated, and Y is a generating set for G, then there exists a finite subset
$F \leq G$
are groups, F is finitely generated, and Y is a generating set for G, then there exists a finite subset
![]() $Y_0$
of Y with
$Y_0$
of Y with
![]() $\left \langle Y_0 \right \rangle \geq F$
.
$\left \langle Y_0 \right \rangle \geq F$
.
Proof. This is left as an exercise for the reader.
We prove the next lemma to allow us to embed finite alternating groups in any group in
![]() $\mathscr {K}$
in a natural way.
$\mathscr {K}$
in a natural way.
We say an element of x of
![]() $\mathfrak {X}_{G}$
is even if there exists y in
$\mathfrak {X}_{G}$
is even if there exists y in
![]() $\mathfrak {X}_{G}$
, such that
$\mathfrak {X}_{G}$
, such that
![]() $x = y + y$
.
$x = y + y$
.
Lemma 5.12. Let
![]() $G \leq \operatorname {Homeo}(\mathfrak {C})$
be vigorous and approximately full. Let C be in
$G \leq \operatorname {Homeo}(\mathfrak {C})$
be vigorous and approximately full. Let C be in
![]() $K_{\mathfrak {C}}$
, and let
$K_{\mathfrak {C}}$
, and let
![]() $\Gamma $
a finite subset of G be such that if
$\Gamma $
a finite subset of G be such that if
![]() $\gamma _1, \gamma _2\in \Gamma $
are distinct, then
$\gamma _1, \gamma _2\in \Gamma $
are distinct, then
![]() $C\gamma _1$
and
$C\gamma _1$
and
![]() $C\gamma _2$
are disjoint.
$C\gamma _2$
are disjoint.
Let
![]() $\pi $
be a permutation of the set
$\pi $
be a permutation of the set
![]() $\Gamma $
. Let
$\Gamma $
. Let
![]() $\delta \in \operatorname {Homeo}(\mathfrak {C})$
be such that for each
$\delta \in \operatorname {Homeo}(\mathfrak {C})$
be such that for each
![]() $\gamma \in \Gamma $
, the homeomorphism
$\gamma \in \Gamma $
, the homeomorphism
![]() $\delta $
agrees with
$\delta $
agrees with
![]() $\gamma ^{-1} (\gamma \cdot \pi )$
on
$\gamma ^{-1} (\gamma \cdot \pi )$
on
![]() $C\gamma $
and has support contained in
$C\gamma $
and has support contained in
![]() $\bigcup \limits _{\gamma \in \Gamma } C\gamma $
. If
$\bigcup \limits _{\gamma \in \Gamma } C\gamma $
. If
![]() $[C]_{G}$
is an even element of
$[C]_{G}$
is an even element of
![]() $\mathfrak {X}_{G}$
or
$\mathfrak {X}_{G}$
or
![]() $\pi $
is an even permutation, then
$\pi $
is an even permutation, then
![]() $\delta $
is in G.
$\delta $
is in G.
Proof. First, assume that
![]() $\pi $
is an even permutation.
$\pi $
is an even permutation.
We may assume
![]() $|\Gamma | \geq 3$
because the alternating group on
$|\Gamma | \geq 3$
because the alternating group on
![]() $\Gamma $
is trivial if
$\Gamma $
is trivial if
![]() $|\Gamma |<3$
. If
$|\Gamma |<3$
. If
![]() $|\Gamma |\geq 3$
, then the embedded copy of the alternating group on
$|\Gamma |\geq 3$
, then the embedded copy of the alternating group on
![]() $\Gamma $
is generated by its embedded
$\Gamma $
is generated by its embedded
![]() $3$
-cycles, so we only need to address the case where
$3$
-cycles, so we only need to address the case where
![]() $\Gamma = \{\alpha ,\beta ,\gamma \}$
, a set of size
$\Gamma = \{\alpha ,\beta ,\gamma \}$
, a set of size
![]() $3$
, and where we further assume that
$3$
, and where we further assume that
![]() $\pi $
is the 3-cycle
$\pi $
is the 3-cycle
![]() $(\alpha \ \beta \ \gamma )$
.
$(\alpha \ \beta \ \gamma )$
.
First, we assume
![]() $(C\alpha ) \cup (C\beta ) \cup (C\gamma ) \subsetneq \mathfrak {C}$
.
$(C\alpha ) \cup (C\beta ) \cup (C\gamma ) \subsetneq \mathfrak {C}$
.
Let U and V in
![]() $K_{\mathfrak {C}}$
be disjoint so that U and V are also disjoint from
$K_{\mathfrak {C}}$
be disjoint so that U and V are also disjoint from
![]() $(C\alpha ) \cup (C\beta ) \cup (C\gamma )$
. Let
$(C\alpha ) \cup (C\beta ) \cup (C\gamma )$
. Let
![]() $\mu \in \operatorname {pstab}_G(\mathfrak {C} \setminus ((C\alpha ) \cup (C\beta ) \cup V))$
be such that
$\mu \in \operatorname {pstab}_G(\mathfrak {C} \setminus ((C\alpha ) \cup (C\beta ) \cup V))$
be such that
![]() $\mu $
agrees with
$\mu $
agrees with
![]() $\alpha ^{-1}\beta $
on
$\alpha ^{-1}\beta $
on
![]() $C\alpha $
and
$C\alpha $
and
![]() $\beta ^{-1}\alpha $
on
$\beta ^{-1}\alpha $
on
![]() $C\beta $
. Let
$C\beta $
. Let
![]() $\nu \in \operatorname {pstab}_G(\mathfrak {C} \setminus ((C\beta ) \cup (C\gamma ) \cup U))$
be such that
$\nu \in \operatorname {pstab}_G(\mathfrak {C} \setminus ((C\beta ) \cup (C\gamma ) \cup U))$
be such that
![]() $\nu $
agrees with
$\nu $
agrees with
![]() $\beta ^{-1}\gamma $
on
$\beta ^{-1}\gamma $
on
![]() $C\beta $
and
$C\beta $
and
![]() $\gamma ^{-1}\beta $
on
$\gamma ^{-1}\beta $
on
![]() $C\gamma $
.
$C\gamma $
.
By inspection, the commutator
![]() $[\mu ,\nu ]$
has support contained in
$[\mu ,\nu ]$
has support contained in
![]() $(C\alpha ) \cup (C\beta ) \cup (C\gamma )$
and agrees with
$(C\alpha ) \cup (C\beta ) \cup (C\gamma )$
and agrees with
![]() $\alpha ^{-1}\beta $
on
$\alpha ^{-1}\beta $
on
![]() $C\alpha $
and agrees with
$C\alpha $
and agrees with
![]() $\beta ^{-1}\gamma $
on
$\beta ^{-1}\gamma $
on
![]() $C\beta $
and agrees with
$C\beta $
and agrees with
![]() $\gamma ^{-1}\alpha $
on
$\gamma ^{-1}\alpha $
on
![]() $C\gamma $
as desired.
$C\gamma $
as desired.
Now, assume
![]() $(C\alpha ) \cup (C\beta ) \cup (C\gamma ) =\mathfrak {C}$
. Let
$(C\alpha ) \cup (C\beta ) \cup (C\gamma ) =\mathfrak {C}$
. Let
![]() $D \in K_{\mathfrak {C}}$
be a proper subset of C.
$D \in K_{\mathfrak {C}}$
be a proper subset of C.
Let
![]() $\sigma \in \operatorname {Homeo}(\mathfrak {C})$
be the homeomorphism of
$\sigma \in \operatorname {Homeo}(\mathfrak {C})$
be the homeomorphism of
![]() $\mathfrak {C}$
with support equal to
$\mathfrak {C}$
with support equal to
![]() $(D\alpha ) \cup (D\beta ) \cup (D\gamma )$
which agrees with
$(D\alpha ) \cup (D\beta ) \cup (D\gamma )$
which agrees with
![]() $\alpha ^{-1}\beta $
on
$\alpha ^{-1}\beta $
on
![]() $D\alpha $
and agrees with
$D\alpha $
and agrees with
![]() $\beta ^{-1}\gamma $
on
$\beta ^{-1}\gamma $
on
![]() $D\beta $
and agrees with
$D\beta $
and agrees with
![]() $\gamma ^{-1}\alpha $
on
$\gamma ^{-1}\alpha $
on
![]() $D\gamma $
. Let
$D\gamma $
. Let
![]() $\rho \in \operatorname {Homeo}(\mathfrak {C})$
be the homeomorphism of
$\rho \in \operatorname {Homeo}(\mathfrak {C})$
be the homeomorphism of
![]() $\mathfrak {C}$
with support equal to
$\mathfrak {C}$
with support equal to
![]() $((C \setminus D)\alpha ) \cup ((C \setminus D)\beta ) \cup ((C \setminus D)\gamma )$
which agrees with
$((C \setminus D)\alpha ) \cup ((C \setminus D)\beta ) \cup ((C \setminus D)\gamma )$
which agrees with
![]() $\alpha ^{-1}\beta $
on
$\alpha ^{-1}\beta $
on
![]() $(C \setminus D)\alpha $
and agrees with
$(C \setminus D)\alpha $
and agrees with
![]() $\beta ^{-1}\gamma $
on
$\beta ^{-1}\gamma $
on
![]() $(C \setminus D)\beta $
and agrees with
$(C \setminus D)\beta $
and agrees with
![]() $\gamma ^{-1}\alpha $
on
$\gamma ^{-1}\alpha $
on
![]() $(C \setminus D)\gamma $
.
$(C \setminus D)\gamma $
.
By the first case,
![]() $\sigma $
and
$\sigma $
and
![]() $\rho $
are both in G. The product
$\rho $
are both in G. The product
![]() $\sigma \rho $
is as desired, and the case where
$\sigma \rho $
is as desired, and the case where
![]() $\pi $
is an even permutation is complete.
$\pi $
is an even permutation is complete.
If
![]() $[C]_{G}$
is even, then we may find a nonempty proper clopen subset
$[C]_{G}$
is even, then we may find a nonempty proper clopen subset
![]() $C_0$
of
$C_0$
of
![]() $\mathfrak {C}$
, such that
$\mathfrak {C}$
, such that
![]() $[C_0]_{G} + [C_0]_{G} = [C]_{G}$
. We may assume that by the definition of
$[C_0]_{G} + [C_0]_{G} = [C]_{G}$
. We may assume that by the definition of
![]() $[C]_{G}$
and of our ‘
$[C]_{G}$
and of our ‘
![]() $+$
’ operator that
$+$
’ operator that
![]() $C_0$
is a nonempty proper subset of C, and, in particular, we may find
$C_0$
is a nonempty proper subset of C, and, in particular, we may find
![]() $\tau $
in G, such that
$\tau $
in G, such that
![]() $C_0\tau = C \setminus C_0$
.
$C_0\tau = C \setminus C_0$
.
Let
![]() $\Gamma _0$
be the set
$\Gamma _0$
be the set
![]() $\Gamma \cup \left \{ \tau \gamma \hspace {1mm} \middle | \hspace {1mm} \gamma \in \Gamma \right \}$
. Let
$\Gamma \cup \left \{ \tau \gamma \hspace {1mm} \middle | \hspace {1mm} \gamma \in \Gamma \right \}$
. Let
![]() $\pi _0$
be the permutation of
$\pi _0$
be the permutation of
![]() $\Gamma _0$
, such that
$\Gamma _0$
, such that
![]() $\gamma \cdot \pi _0 = \gamma \cdot \pi $
and
$\gamma \cdot \pi _0 = \gamma \cdot \pi $
and
![]() $\tau \gamma \cdot \pi _0 = \tau (\gamma \cdot \pi )$
.
$\tau \gamma \cdot \pi _0 = \tau (\gamma \cdot \pi )$
.
Now the sets
![]() $\{C_0\gamma _0\}_{\gamma _0 \in \Gamma _0}$
are pairwise disjoint and
$\{C_0\gamma _0\}_{\gamma _0 \in \Gamma _0}$
are pairwise disjoint and
![]() $\pi _0$
is an even permutation of
$\pi _0$
is an even permutation of
![]() $\Gamma _0$
. By applying the case for even permutations, we find the desired homeomorphism.
$\Gamma _0$
. By applying the case for even permutations, we find the desired homeomorphism.
Lemma 5.13. Let
![]() $G \leq \operatorname {Homeo}(\mathfrak {C})$
be approximately full and vigorous. Let T be a nonempty finite set, and let f be a map from T to
$G \leq \operatorname {Homeo}(\mathfrak {C})$
be approximately full and vigorous. Let T be a nonempty finite set, and let f be a map from T to
![]() $\mathfrak {X}_{G}$
. There exists a partition
$\mathfrak {X}_{G}$
. There exists a partition
![]() $\{C_t \in (t)f\}_{t \in T}$
of
$\{C_t \in (t)f\}_{t \in T}$
of
![]() $\mathfrak {C}$
exactly if
$\mathfrak {C}$
exactly if
![]() $\sum \limits _{t \in T} ((t)f) = [\mathfrak {C}]_{G}$
.
$\sum \limits _{t \in T} ((t)f) = [\mathfrak {C}]_{G}$
.
Proof. It follows immediately from Lemma 5.9 that if such a partition exists, then
![]() $\sum \limits _{t \in T} ((t)f) = [\mathfrak {C}]_{G}$
.
$\sum \limits _{t \in T} ((t)f) = [\mathfrak {C}]_{G}$
.
Given such a set T, we will construct such a partition. First put a total order on T. Let l be the greatest element of T. If
![]() $C_t$
has been assigned for each
$C_t$
has been assigned for each
![]() $t < q$
for some
$t < q$
for some
![]() $q \in T \setminus \{l\}$
and
$q \in T \setminus \{l\}$
and
![]() $C_q$
has not been assigned, then let
$C_q$
has not been assigned, then let
![]() $C_q$
be an element of
$C_q$
be an element of
![]() $(q)f$
and a nonempty proper subset
$(q)f$
and a nonempty proper subset
![]() $\mathfrak {C} \setminus \bigsqcup \limits _{t < q}C_t$
. If
$\mathfrak {C} \setminus \bigsqcup \limits _{t < q}C_t$
. If
![]() $C_t$
has been defined for each
$C_t$
has been defined for each
![]() $t \in T \setminus \{l\}$
, then let
$t \in T \setminus \{l\}$
, then let
![]() $C_l$
be the set
$C_l$
be the set
![]() $\mathfrak {C} \setminus \bigsqcup \limits _{t \in T \setminus \{l\}} C_t$
. The set
$\mathfrak {C} \setminus \bigsqcup \limits _{t \in T \setminus \{l\}} C_t$
. The set
![]() $C_l$
is in
$C_l$
is in
![]() $(q)f$
by Lemma 5.9.
$(q)f$
by Lemma 5.9.
Lemmas 5.12 and 5.13 combine powerfully to construct bespoke (torsion) elements in G. The first of these roughly says we can find elements of G which induce ‘even permutations’ of a partition of
![]() $\mathfrak {C}$
into proper clopen sets by focusing on elements of the partition with the same homology type in
$\mathfrak {C}$
into proper clopen sets by focusing on elements of the partition with the same homology type in
![]() $\mathfrak {X}_{G}$
, while the second informs us of the existence of partitions where the parts satisfy algebraic conditions measured by
$\mathfrak {X}_{G}$
, while the second informs us of the existence of partitions where the parts satisfy algebraic conditions measured by
![]() $\mathfrak {X}_{G}$
. We will see a powerful use of this synergy in the proof of Theorem 5.15.
$\mathfrak {X}_{G}$
. We will see a powerful use of this synergy in the proof of Theorem 5.15.
The final lemma is a technical lemma which we apply in the proof of Theorem 5.15. In this lemma, we use a closed real interval with integer bounds to represent the integers between and including those bounds. For example,
![]() $[3,6] = \{3,4,5,6\}$
in the notation below.
$[3,6] = \{3,4,5,6\}$
in the notation below.
Lemma 5.14. For each positive integer j and
![]() $i \in [1, j]$
, the set
$i \in [1, j]$
, the set
is equal to
![]() $\{0\}$
.
$\{0\}$
.
Proof. Note that
![]() $0$
is an element of this set. Let z be an arbitrary element of this intersection. We show that
$0$
is an element of this set. Let z be an arbitrary element of this intersection. We show that
![]() $z=0$
.
$z=0$
.
Suppose that
![]() $z=xu-i=yv-i(j+1)$
, where
$z=xu-i=yv-i(j+1)$
, where
![]() $x,y \in [1,j]$
,
$x,y \in [1,j]$
,
![]() $u,v\in \{1,j+1\}$
. It follows that
$u,v\in \{1,j+1\}$
. It follows that
![]() $x-i\equiv y-i$
mod j, so
$x-i\equiv y-i$
mod j, so
![]() $x=y$
and
$x=y$
and
![]() $u<v$
. It follows that
$u<v$
. It follows that
![]() $u=1$
and
$u=1$
and
![]() $v=j+1$
. Therefore,
$v=j+1$
. Therefore,
![]() $z=x-i=x(j+1)-i(j+1)$
and so
$z=x-i=x(j+1)-i(j+1)$
and so
![]() $ij=xj$
and
$ij=xj$
and
![]() $x=i$
. Finally,
$x=i$
. Finally,
![]() $z=i-i=0$
as required.
$z=i-i=0$
as required.
Theorem 5.15. Let
![]() $G \leq \operatorname {Homeo}(\mathfrak {C})$
be finitely generated simple and vigorous. Let
$G \leq \operatorname {Homeo}(\mathfrak {C})$
be finitely generated simple and vigorous. Let
![]() $n\in \mathbb {Z}$
be at least
$n\in \mathbb {Z}$
be at least
![]() $2$
. Then there exists
$2$
. Then there exists
![]() $\sigma $
and
$\sigma $
and
![]() $\zeta $
in G, such that
$\zeta $
in G, such that
![]() $\sigma $
is of finite order and
$\sigma $
is of finite order and
![]() $\zeta $
is of order n and
$\zeta $
is of order n and
![]() $\left \langle \sigma ,\zeta \right \rangle = G$
.
$\left \langle \sigma ,\zeta \right \rangle = G$
.
Proof. Let
![]() $C \in K_{\mathfrak {C}}$
be such that
$C \in K_{\mathfrak {C}}$
be such that
![]() $[C]_{G} = [\mathfrak {C}]_{G}$
. Let
$[C]_{G} = [\mathfrak {C}]_{G}$
. Let
![]() $D \in K_{\mathfrak {C}}$
be a proper subset of
$D \in K_{\mathfrak {C}}$
be a proper subset of
![]() $\mathfrak {C} \setminus C$
, such that
$\mathfrak {C} \setminus C$
, such that
![]() $[D]_{G} = -2[C]_{G}$
.
$[D]_{G} = -2[C]_{G}$
.
By Proposition 5.4, the group
![]() $\operatorname {pstab}_G(\mathfrak {C} \setminus (C \sqcup D))$
is in
$\operatorname {pstab}_G(\mathfrak {C} \setminus (C \sqcup D))$
is in
![]() $\mathscr {K}^{\text {f.g.}}_{C \sqcup D}$
. Now set
$\mathscr {K}^{\text {f.g.}}_{C \sqcup D}$
. Now set
By Lemma 5.12, arbitrarily large finite alternating groups embed in
![]() $\operatorname {pstab}_G(\mathfrak {C} \setminus (C \sqcup D))$
, therefore, P must be nonempty.
$\operatorname {pstab}_G(\mathfrak {C} \setminus (C \sqcup D))$
, therefore, P must be nonempty.
Since
![]() $\operatorname {pstab}_G(\mathfrak {C} \setminus (C \sqcup D))$
is simple and the set P is closed under conjugation by elements of
$\operatorname {pstab}_G(\mathfrak {C} \setminus (C \sqcup D))$
is simple and the set P is closed under conjugation by elements of
![]() $\operatorname {pstab}_G(\mathfrak {C} \setminus (C \sqcup D))$
, it follows that P generates
$\operatorname {pstab}_G(\mathfrak {C} \setminus (C \sqcup D))$
, it follows that P generates
![]() $\operatorname {pstab}_G(\mathfrak {C} \setminus (C \sqcup D))$
. Let
$\operatorname {pstab}_G(\mathfrak {C} \setminus (C \sqcup D))$
. Let
![]() $Q := \left \{ [\alpha ,\beta ] \hspace {1mm} \middle | \hspace {1mm} \alpha ,\beta \in P \right \}$
. The group
$Q := \left \{ [\alpha ,\beta ] \hspace {1mm} \middle | \hspace {1mm} \alpha ,\beta \in P \right \}$
. The group
![]() $\operatorname {pstab}_G(\mathfrak {C} \setminus (C \sqcup D))$
is infinite and simple and, therefore, not commutative. Consequently, there must be nonidentity elements of Q.
$\operatorname {pstab}_G(\mathfrak {C} \setminus (C \sqcup D))$
is infinite and simple and, therefore, not commutative. Consequently, there must be nonidentity elements of Q.
Since
![]() $\operatorname {pstab}_G(\mathfrak {C} \setminus (C \sqcup D))$
is simple and the set Q is closed under conjugation, the set Q must generate
$\operatorname {pstab}_G(\mathfrak {C} \setminus (C \sqcup D))$
is simple and the set Q is closed under conjugation, the set Q must generate
![]() $\operatorname {pstab}_G(\mathfrak {C} \setminus (C \sqcup D))$
.
$\operatorname {pstab}_G(\mathfrak {C} \setminus (C \sqcup D))$
.
By Lemma 5.11, there exists a j and elements
![]() $\{\psi _i\}_{0\leq i < j} \subseteq \operatorname {pstab}_G(\mathfrak {C} \setminus (C \sqcup D))$
and
$\{\psi _i\}_{0\leq i < j} \subseteq \operatorname {pstab}_G(\mathfrak {C} \setminus (C \sqcup D))$
and
![]() $\{\omega _i\}_{0 \leq i < j} \subseteq \operatorname {pstab}_G(\mathfrak {C} \setminus (C \sqcup D))$
of order n, such that the set
$\{\omega _i\}_{0 \leq i < j} \subseteq \operatorname {pstab}_G(\mathfrak {C} \setminus (C \sqcup D))$
of order n, such that the set
![]() $\{[\psi _i,\omega _i]\}_{0 \leq i < j}$
generates
$\{[\psi _i,\omega _i]\}_{0 \leq i < j}$
generates
![]() $\operatorname {pstab}_G(\mathfrak {C} \setminus (C \sqcup D))$
.
$\operatorname {pstab}_G(\mathfrak {C} \setminus (C \sqcup D))$
.
Let
![]() $x \in \mathbb {N}$
be at least
$x \in \mathbb {N}$
be at least
![]() $2j(j+1)$
.
$2j(j+1)$
.
By Lemma 5.13, we may choose a partition P of
![]() $\mathfrak {C}$
into proper clopen sets so that
$\mathfrak {C}$
into proper clopen sets so that
![]() $|P|=3x+1$
, and where P itself admits a partition as
$|P|=3x+1$
, and where P itself admits a partition as
![]() $X\sqcup Y$
so that
$X\sqcup Y$
so that
-
1.
 $X\subseteq [C]_G$
,
$X\subseteq [C]_G$
, -
2.
 $Y\subseteq [D]_G$
,
$Y\subseteq [D]_G$
, -
3.
 $|X| = 2x+1$
, and
$|X| = 2x+1$
, and -
4.
 $|Y|=x$
$|Y|=x$
(for example, let
![]() $T= \{1, \ldots , 2x+1\}\sqcup \{-1, \ldots , -x\}$
and let
$T= \{1, \ldots , 2x+1\}\sqcup \{-1, \ldots , -x\}$
and let
![]() $f:T\to \mathfrak {X}_{G}$
be the function mapping the positive values to
$f:T\to \mathfrak {X}_{G}$
be the function mapping the positive values to
![]() $[C]_{G}\in \mathfrak {X}_{G}$
and the negative values to
$[C]_{G}\in \mathfrak {X}_{G}$
and the negative values to
![]() $[D]_{G}\in \mathfrak {X}_{G}$
). We may further assume that
$[D]_{G}\in \mathfrak {X}_{G}$
). We may further assume that
![]() $C \in X$
and
$C \in X$
and
![]() $D \in Y$
.
$D \in Y$
.
By Lemma 5.12, there exists
![]() $\tau \in \operatorname {pstab}_G(\mathfrak {C} \setminus \bigsqcup X)$
of order
$\tau \in \operatorname {pstab}_G(\mathfrak {C} \setminus \bigsqcup X)$
of order
![]() $2x+1$
respecting X, such that the induced action of
$2x+1$
respecting X, such that the induced action of
![]() $\tau $
on X has only one orbit (i.e. a
$\tau $
on X has only one orbit (i.e. a
![]() $2x+1$
-cycle over the elements of X). Since
$2x+1$
-cycle over the elements of X). Since
![]() $[D]_{G}$
is even, we may apply Lemma 5.12 to find
$[D]_{G}$
is even, we may apply Lemma 5.12 to find
![]() $\pi \in \operatorname {pstab}_G(\mathfrak {C} \setminus \bigsqcup Y)$
of order x respecting Y, such that the induced action of
$\pi \in \operatorname {pstab}_G(\mathfrak {C} \setminus \bigsqcup Y)$
of order x respecting Y, such that the induced action of
![]() $\pi $
on Y has only one orbit.
$\pi $
on Y has only one orbit.
Let
![]() $\sigma := \pi \tau $
. The order of
$\sigma := \pi \tau $
. The order of
![]() $\sigma $
is the least common multiple of
$\sigma $
is the least common multiple of
![]() $2x+1$
and x, which is
$2x+1$
and x, which is
![]() $2x^2+x$
as
$2x^2+x$
as
![]() $2x+1$
and x are coprime. In particular, the order of
$2x+1$
and x are coprime. In particular, the order of
![]() $\sigma $
is finite.
$\sigma $
is finite.
Let R be the graph with vertex set
![]() $\left \{ (C \sqcup D)\sigma ^k \hspace {1mm} \middle | \hspace {1mm} k \in \mathbb {Z} \right \}$
and an edge between two vertices if they properly intersect. Note that R is a finite graph. Since
$\left \{ (C \sqcup D)\sigma ^k \hspace {1mm} \middle | \hspace {1mm} k \in \mathbb {Z} \right \}$
and an edge between two vertices if they properly intersect. Note that R is a finite graph. Since
![]() $2x+1$
and x are coprime, the graph R is connected. Since R is connected and
$2x+1$
and x are coprime, the graph R is connected. Since R is connected and
![]() $\bigcup \limits _{k \in \mathbb {Z}}(C \sqcup D)\sigma ^k = \mathfrak {C}$
, it follows from repetitive application of Lemma 5.3 that the set
$\bigcup \limits _{k \in \mathbb {Z}}(C \sqcup D)\sigma ^k = \mathfrak {C}$
, it follows from repetitive application of Lemma 5.3 that the set
![]() $\{\sigma \} \sqcup \operatorname {pstab}_G(\mathfrak {C} \setminus (C \sqcup D))$
generates G.
$\{\sigma \} \sqcup \operatorname {pstab}_G(\mathfrak {C} \setminus (C \sqcup D))$
generates G.
Therefore, it is sufficient to find
![]() $\zeta \in G$
of order n, such that
$\zeta \in G$
of order n, such that
![]() $\left \langle \sigma ,\zeta \right \rangle \supseteq \{[\psi _i,\omega _i]\}_{0 \leq i < j}$
. By the choice of x, it follows that the supports of the elements in the set
$\left \langle \sigma ,\zeta \right \rangle \supseteq \{[\psi _i,\omega _i]\}_{0 \leq i < j}$
. By the choice of x, it follows that the supports of the elements in the set
are disjoint, so the product of all of them is well-defined even without an order specified. Let
![]() $\zeta $
be equal to this product, which has order n.
$\zeta $
be equal to this product, which has order n.
We will show for each
![]() $1 \leq k \leq j$
, the commutator
$1 \leq k \leq j$
, the commutator
![]() $\left [\zeta ^{\left (\sigma ^{-k}\right )},\zeta ^{\left (\sigma ^{-k(j+1)}\right )}\right ]$
is equal to the commutator
$\left [\zeta ^{\left (\sigma ^{-k}\right )},\zeta ^{\left (\sigma ^{-k(j+1)}\right )}\right ]$
is equal to the commutator
![]() $[\psi _k,\omega _k]$
. This is sufficient to complete the proof.
$[\psi _k,\omega _k]$
. This is sufficient to complete the proof.
Let
![]() $1 \leq k \leq j$
be given. Note
$1 \leq k \leq j$
be given. Note
 $$ \begin{align*} \operatorname{supt}\!\left(\zeta\right) & = \bigsqcup\limits_{1\leq i \leq j} \operatorname{supt}\!\left(\psi_i^{\left(\sigma^i\right)}\right) \sqcup \bigsqcup\limits_{1\leq i \leq j}\operatorname{supt}\!\left(\omega_i^{\left(\sigma^{i(j+1)}\right)}\right) \\ & = \bigsqcup\limits_{1\leq i \leq j} (C \sqcup D) \sigma^i \sqcup (C \sqcup D) \sigma^{i(j+1)}. \end{align*} $$
$$ \begin{align*} \operatorname{supt}\!\left(\zeta\right) & = \bigsqcup\limits_{1\leq i \leq j} \operatorname{supt}\!\left(\psi_i^{\left(\sigma^i\right)}\right) \sqcup \bigsqcup\limits_{1\leq i \leq j}\operatorname{supt}\!\left(\omega_i^{\left(\sigma^{i(j+1)}\right)}\right) \\ & = \bigsqcup\limits_{1\leq i \leq j} (C \sqcup D) \sigma^i \sqcup (C \sqcup D) \sigma^{i(j+1)}. \end{align*} $$
Now
![]() $\operatorname {supt}\!\left (\zeta ^{\left (\sigma ^{-k}\right )}\right ) \cap \operatorname {supt}\!\left (\zeta ^{\left (\sigma ^{-k(j+1)}\right )}\right )$
is equal to the intersection of
$\operatorname {supt}\!\left (\zeta ^{\left (\sigma ^{-k}\right )}\right ) \cap \operatorname {supt}\!\left (\zeta ^{\left (\sigma ^{-k(j+1)}\right )}\right )$
is equal to the intersection of
 $$\begin{align*}\left(\bigsqcup\limits_{1\leq i \leq j} (C \sqcup D) \sigma^i \sqcup (C \sqcup D) \sigma^{i(j+1)}\right)^{\left(\sigma^{-k}\right)}\end{align*}$$
$$\begin{align*}\left(\bigsqcup\limits_{1\leq i \leq j} (C \sqcup D) \sigma^i \sqcup (C \sqcup D) \sigma^{i(j+1)}\right)^{\left(\sigma^{-k}\right)}\end{align*}$$
and
 $$\begin{align*}\left(\bigsqcup\limits_{1\leq i \leq j} (C \sqcup D) \sigma^i \sqcup (C \sqcup D) \sigma^{i(j+1)}\right)^{\left(\sigma^{-k(j+1)}\right)},\end{align*}$$
$$\begin{align*}\left(\bigsqcup\limits_{1\leq i \leq j} (C \sqcup D) \sigma^i \sqcup (C \sqcup D) \sigma^{i(j+1)}\right)^{\left(\sigma^{-k(j+1)}\right)},\end{align*}$$
which, by Lemma 5.14, is equal to
![]() $C \sqcup D$
. Here, note we are relying on the fact that x is at least
$C \sqcup D$
. Here, note we are relying on the fact that x is at least
![]() $2j(j+1)$
. It only remains to note that
$2j(j+1)$
. It only remains to note that
![]() $\left [\zeta ^{\left (\sigma ^{-k}\right )},\zeta ^{\left (\sigma ^{-k(j+1)}\right )}\right ]$
agrees with
$\left [\zeta ^{\left (\sigma ^{-k}\right )},\zeta ^{\left (\sigma ^{-k(j+1)}\right )}\right ]$
agrees with
![]() $[\psi _k,\omega _k]$
on
$[\psi _k,\omega _k]$
on
![]() $C \sqcup D$
.
$C \sqcup D$
.
Corollary 5.16. If G is in
![]() $\mathscr {K}^{\text {f.g.}}$
, then G is two-generated as a semigroup.
$\mathscr {K}^{\text {f.g.}}$
, then G is two-generated as a semigroup.
Proof. This follows immediately from Theorem 5.15.
Example 5.17. The group
![]() $V_2$
is a simple vigorous and finitely generated subgroup of
$V_2$
is a simple vigorous and finitely generated subgroup of
![]() $\operatorname {Homeo}(\mathfrak {C})$
, so Theorem 5.15 applies and
$\operatorname {Homeo}(\mathfrak {C})$
, so Theorem 5.15 applies and
![]() $V_2$
is two-generated.
$V_2$
is two-generated.
We note that Mason shows in [Reference Mason24] that
![]() $V_2$
is two-generated, while later, Bleak and Quick in [Reference Bleak and Quick5] find elements they denote as u,
$V_2$
is two-generated, while later, Bleak and Quick in [Reference Bleak and Quick5] find elements they denote as u,
![]() $v\in V_2$
so that
$v\in V_2$
so that
![]() $V_2=\langle u,v\rangle $
, where
$V_2=\langle u,v\rangle $
, where
![]() $|u|=6$
and
$|u|=6$
and
![]() $|v|=3$
. It is immediate from Theorem 5.15 that
$|v|=3$
. It is immediate from Theorem 5.15 that
![]() $V_2$
admits two torsion elements
$V_2$
admits two torsion elements
![]() $\sigma $
,
$\sigma $
,
![]() $\zeta $
with
$\zeta $
with
![]() $V_2=\langle \sigma ,\zeta \rangle $
, where
$V_2=\langle \sigma ,\zeta \rangle $
, where
![]() $|\zeta |=2$
. Mark Sapir, in a personal communication with the first author (2016), asked whether
$|\zeta |=2$
. Mark Sapir, in a personal communication with the first author (2016), asked whether
![]() $V_2$
is a quotient of PSL
$V_2$
is a quotient of PSL
![]() $_2(\mathbb {Z})\cong C_3*C_2$
(so, in particular, can
$_2(\mathbb {Z})\cong C_3*C_2$
(so, in particular, can
![]() $\sigma $
and
$\sigma $
and
![]() $\zeta $
as above be found with
$\zeta $
as above be found with
![]() $|\sigma |=3$
).
$|\sigma |=3$
).
Example 5.18. Similar to the above, the simple Röver-Nekrashevych groups of [Reference Nekrashevych34] are all two-generated, being finite-index (yet still vigorous) simple subgroups of specific finitely generated overgroups of the groups
![]() $V_n$
(see [Reference Nekrashevych34, Reference Röver37, Reference Skipper, Witzel and Zaremsky39] for more on these groups).
$V_n$
(see [Reference Nekrashevych34, Reference Röver37, Reference Skipper, Witzel and Zaremsky39] for more on these groups).
Example 5.19. In our final example, after [Reference Hennig and Matucci16], it was known that
![]() $nV$
admitted a presentation with
$nV$
admitted a presentation with
![]() $2n+4$
generators. Quick shows in [Reference Quick36] that for all n, the group
$2n+4$
generators. Quick shows in [Reference Quick36] that for all n, the group
![]() $nV$
admits a finite presentation with two generators (matching our result here but also providing explicitly the generators).
$nV$
admits a finite presentation with two generators (matching our result here but also providing explicitly the generators).
6. Conclusion
Question 6.1. Does there exist a finitely presented simple group that is not two-generated?
Question 6.1 is well-known and has been partially answered by the Classification of Finite Simple Groups from which it follows that if there are finitely presented simple groups which are not two-generated, then they must be infinite. There are examples of simple groups which are finitely generated but not two-generated as shown by Guba in [Reference Guba15], and there are certainly examples of finitely presented nontwo-generated groups, and examples of finitely presented simple groups, so there are no obstructions to any proper subset of the demands of the question.
Epstein in [Reference Epstein13] provides three axioms under which a group of homeomorphisms of a space will be simple (or at least, will have a simple commutator subgroup). One of these is that there is a countable basis of open sets upon which the group acts transitively, another subsumes the property that the group is generated by elements which are with support contained in these basic open sets. These properties seem not far from the properties we have used in this paper to find two element generating sets for finitely generated groups of homeomorphisms of the Cantor set.
For this reason, it may be an interesting project for the future to try to adapt the argument of the main theorem of this paper to the context of Epstein’s axioms, [Reference Epstein13] and thus investigate the following question.
Question 6.2. If G is a finitely generated simple group of homeomorphisms which satisfies Epstein’s axioms, must G actually be two-generated?
The following result is well-known. Note that the proof we give does not result in a vigorous group.
Proposition 6.3. The group
![]() $Sym(\mathbb {N})$
embeds in
$Sym(\mathbb {N})$
embeds in
![]() $\operatorname {Homeo}(\mathfrak {C})$
.
$\operatorname {Homeo}(\mathfrak {C})$
.
Proof. For this proof, we will think of elements of
![]() $\mathfrak {C}$
as infinite words over
$\mathfrak {C}$
as infinite words over
![]() $\{0,1\}$
. Let g be in
$\{0,1\}$
. Let g be in
![]() $Sym(\mathbb {N})$
, and let x be in
$Sym(\mathbb {N})$
, and let x be in
![]() $\mathfrak {C}$
. If x contains only the letter
$\mathfrak {C}$
. If x contains only the letter
![]() $0$
, then let g fix x. If the first
$0$
, then let g fix x. If the first
![]() $1$
of x is the
$1$
of x is the
![]() $(n+1)$
th digit of x, then remove the first n digits (all of which will be
$(n+1)$
th digit of x, then remove the first n digits (all of which will be
![]() $0$
) and replace them with a word of length
$0$
) and replace them with a word of length
![]() $ng$
containing only the letter
$ng$
containing only the letter
![]() $0$
and define
$0$
and define
![]() $xg$
to be the result. Extend this principle to define the action of
$xg$
to be the result. Extend this principle to define the action of
![]() $Sym(\mathbb {N})$
on the Cantor set. By inspection,
$Sym(\mathbb {N})$
on the Cantor set. By inspection,
![]() $Sym(\mathbb {N})$
now acts faithfully as desired.
$Sym(\mathbb {N})$
now acts faithfully as desired.
The following corollary is immediate from Cayley’s theorem.
Corollary 6.4. All countably infinite groups embed in
![]() $\operatorname {Homeo}(\mathfrak {C})$
.
$\operatorname {Homeo}(\mathfrak {C})$
.
From the above, one might hope to achieve vigorous realisations of all finitely presented simple groups and thus show that all finitely presented simple groups are two-generated. However, this fails as follows.
Proposition 6.5. Every vigorous simple group has torsion elements.
Proof. A vigorous simple group G, by Theorem 4.18, is the commutator subgroup of its own full group. Any such full group would admit torsion elements of small support, and by commutating one of these with an element moving that support fully off of itself, we obtain a nontrivial torsion element in G.
In particular, the Burger-Mozes torsion-free finitely presented simple groups [Reference Burger and Mozes10] admit no vigorous realisation in
![]() $\operatorname {Homeo}(\mathfrak {C})$
.
$\operatorname {Homeo}(\mathfrak {C})$
.
We remain interested in generalisations of the work in this paper from Cantor spaces to other spaces of interest (such as manifolds). In such context, a natural generalisation of our concept of vigorous could be as follows.
Definition 6.6. Let X be a topological space. Let
![]() $H\leq \operatorname {Homeo}(X)$
. We will say that a subset G of H is vigorous with respect to H if and only if for all
$H\leq \operatorname {Homeo}(X)$
. We will say that a subset G of H is vigorous with respect to H if and only if for all
![]() $A,B,C$
open nonempty subsets of X so that
$A,B,C$
open nonempty subsets of X so that
![]() $\overline {B}$
and
$\overline {B}$
and
![]() $\overline {C}$
are proper subsets of A where there exists h in H with
$\overline {C}$
are proper subsets of A where there exists h in H with
![]() $\operatorname {supt}\!\left (h\right ) \subseteq A$
so that
$\operatorname {supt}\!\left (h\right ) \subseteq A$
so that
![]() $\overline {B}h \subseteq C$
, there is
$\overline {B}h \subseteq C$
, there is
![]() $g\in G$
with
$g\in G$
with
![]() $\operatorname {supt}\!\left (g\right )\subseteq A$
so that
$\operatorname {supt}\!\left (g\right )\subseteq A$
so that
![]() $\overline {B}g\subseteq C$
.
$\overline {B}g\subseteq C$
.
If
![]() $X=\mathfrak {C}$
and
$X=\mathfrak {C}$
and
![]() $H=\operatorname {Homeo}(\mathfrak {C})$
, then a group G being vigorous with respect to H implies G is vigorous. The generality of the definition above allows us to suppose that by restricting attention to less capable groups than
$H=\operatorname {Homeo}(\mathfrak {C})$
, then a group G being vigorous with respect to H implies G is vigorous. The generality of the definition above allows us to suppose that by restricting attention to less capable groups than
![]() $\operatorname {Homeo}(X)$
, we can still obtain interesting generation results. For example, if X had a measure, and if H were the measure preserving subgroup of
$\operatorname {Homeo}(X)$
, we can still obtain interesting generation results. For example, if X had a measure, and if H were the measure preserving subgroup of
![]() $\operatorname {Homeo}(X)$
, then an obstacle to a proof approach analogous to that of Theorem 5.15 is that we frequently map clopen sets into proper subsets of themselves. Such maps are unlikely to respect the ambient measure.
$\operatorname {Homeo}(X)$
, then an obstacle to a proof approach analogous to that of Theorem 5.15 is that we frequently map clopen sets into proper subsets of themselves. Such maps are unlikely to respect the ambient measure.
This leads us to the following question.
Question 6.7. For which space-group pairs
![]() $(X,H)$
is it the case that if
$(X,H)$
is it the case that if
![]() $G\leq \operatorname {Homeo}(X)$
is finitely generated, simple and vigorous with respect to H then G is two-generated?
$G\leq \operatorname {Homeo}(X)$
is finitely generated, simple and vigorous with respect to H then G is two-generated?
The following two questions are, in part, motivated by similar considerations for a family
![]() $\mathscr {F}$
of groups inspired by the theory of universal sequences [Reference Galvin14, Reference Hyde, Jonušas, Mitchell and Péresse19] and described below.
$\mathscr {F}$
of groups inspired by the theory of universal sequences [Reference Galvin14, Reference Hyde, Jonušas, Mitchell and Péresse19] and described below.
Firstly, let
![]() $\mathscr {L}$
be the family of those two-generated groups H, such that for any group G in
$\mathscr {L}$
be the family of those two-generated groups H, such that for any group G in
![]() $\mathscr {K}^{\text {f.g.}}$
, there exists an epimorphism from H to G.
$\mathscr {K}^{\text {f.g.}}$
, there exists an epimorphism from H to G.
Note that by Theorem 5.15,
![]() $\mathscr {L}$
contains
$\mathscr {L}$
contains
![]() $C * \mathbb {Z}$
for all nontrivial cyclic groups C.
$C * \mathbb {Z}$
for all nontrivial cyclic groups C.
Question 6.8. What more can be said about the family
![]() $\mathscr {L}$
?
$\mathscr {L}$
?
Let
![]() $F_{\mathbb {N}}$
denote the free group of countably infinite rank. Let
$F_{\mathbb {N}}$
denote the free group of countably infinite rank. Let
![]() $\mathscr {F}$
be the family of those two-generated groups G, such that there exists a homomorphism
$\mathscr {F}$
be the family of those two-generated groups G, such that there exists a homomorphism
![]() $\phi :F_{\mathbb {N}} \to G$
, such that for any homomorphism
$\phi :F_{\mathbb {N}} \to G$
, such that for any homomorphism
![]() $\psi :F_{\mathbb {N}} \to \operatorname {Sym}\left ({\mathbb {N}}\right )$
, there exists a homomorphism
$\psi :F_{\mathbb {N}} \to \operatorname {Sym}\left ({\mathbb {N}}\right )$
, there exists a homomorphism
![]() $\rho :G \to \operatorname {Sym}\left ({\mathbb {N}}\right )$
, such that
$\rho :G \to \operatorname {Sym}\left ({\mathbb {N}}\right )$
, such that
![]() $\phi \rho = \psi $
.
$\phi \rho = \psi $
.
Clearly groups in
![]() $\mathscr {L}$
or
$\mathscr {L}$
or
![]() $\mathscr {F}$
must be lawless, have exponential growth, and have uncountably many normal subgroups.
$\mathscr {F}$
must be lawless, have exponential growth, and have uncountably many normal subgroups.
Galvin effectively shows in the proof of Theorem 4.3 of [Reference Galvin14] that for any
![]() $i\geq 3$
and even
$i\geq 3$
and even
![]() $j\geq 4$
, the group
$j\geq 4$
, the group
![]() $C_i*C_j$
is in
$C_i*C_j$
is in
![]() $\mathscr {F}$
, which motivates the following question.
$\mathscr {F}$
, which motivates the following question.
Question 6.9. Are there elements of
![]() $\mathscr {K}^{\text {f.g.}}$
which are not quotients of
$\mathscr {K}^{\text {f.g.}}$
which are not quotients of
![]() $C_2*C_3$
?
$C_2*C_3$
?
The families
![]() $\mathscr {L}$
and
$\mathscr {L}$
and
![]() $\mathscr {F}$
both arise as being compatible with finite generation in uncountably many ways corresponding to groups that are infinite versions of finite symmetric groups.
$\mathscr {F}$
both arise as being compatible with finite generation in uncountably many ways corresponding to groups that are infinite versions of finite symmetric groups.
Acknowledgements
We are grateful for various conversations on this topic with Jim Belk, Martin Kassabov, Mark Lawson, Francesco Matucci, Volodymyr Nekrashevych, Martyn Quick, and Nik Ruškuc. We are also grateful for suggestions from our anonymous referees which have improved some of the results and much of the writing in this paper. The first author is also grateful for support from EPSRC grant EP/R032866/1.
Competing interest
The authors have no competing interest to declare.