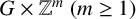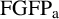1 Introduction
For a group G, the rank of G, denoted
![]() $\mathrm {rk}(G)$
, is the minimal number of generators of G and
$\mathrm {rk}(G)$
, is the minimal number of generators of G and
![]() $\mathrm {Aut}(G)$
denotes the group of all automorphisms of G. For an endomorphism
$\mathrm {Aut}(G)$
denotes the group of all automorphisms of G. For an endomorphism
![]() $\phi $
of G, the fixed subgroup of
$\phi $
of G, the fixed subgroup of
![]() $\phi $
is
$\phi $
is
The study of fixed subgroups goes back to Dyer and Scott in 1975. In [Reference Dyer and Scott7], they proved that for a finite order automorphism
![]() $\phi $
of a free group
$\phi $
of a free group
![]() $F_n$
of rank n, the rank of
$F_n$
of rank n, the rank of
![]() $\mathrm {Fix}\phi $
is not greater than n. Moreover, Scott conjectured that
$\mathrm {Fix}\phi $
is not greater than n. Moreover, Scott conjectured that
![]() $\mathrm {rk}(\mathrm {Fix}\phi )\leq n$
for any
$\mathrm {rk}(\mathrm {Fix}\phi )\leq n$
for any
![]() $\phi \in \mathrm {Aut}(F_n)$
. Scott’s conjecture was resolved by Bestvina and Handel [Reference Bestvina and Handel2] in 1988, and extended to all endomorphisms by Imrich and Turner [Reference Imrich and Turner11] almost simultaneously. For every endomorphism
$\phi \in \mathrm {Aut}(F_n)$
. Scott’s conjecture was resolved by Bestvina and Handel [Reference Bestvina and Handel2] in 1988, and extended to all endomorphisms by Imrich and Turner [Reference Imrich and Turner11] almost simultaneously. For every endomorphism
![]() $\phi $
of a surface group G (that is, the fundamental group of a closed surface), the same bound
$\phi $
of a surface group G (that is, the fundamental group of a closed surface), the same bound
![]() $\mathrm {rk}(\mathrm {Fix}\phi )\leq \mathrm {rk}(G)$
also holds [Reference Jiang, Wang and Zhang13]. The study of fixed subgroups of various groups and related topics, such as the Nielsen fixed point theory, has produced many interesting results (see [Reference Ciobanu and Logan6, Reference Jaikin-Zapirain12, Reference Roy and Ventura23, Reference Zhang and Zhao29–Reference Zhang and Zhao31]).
$\mathrm {rk}(\mathrm {Fix}\phi )\leq \mathrm {rk}(G)$
also holds [Reference Jiang, Wang and Zhang13]. The study of fixed subgroups of various groups and related topics, such as the Nielsen fixed point theory, has produced many interesting results (see [Reference Ciobanu and Logan6, Reference Jaikin-Zapirain12, Reference Roy and Ventura23, Reference Zhang and Zhao29–Reference Zhang and Zhao31]).
More generally, we say that a group G has the finitely generated fixed subgroup property of automorphisms (
![]() $\mathrm {FGFP_a}$
), if the fixed subgroup
$\mathrm {FGFP_a}$
), if the fixed subgroup
![]() $\mathrm {Fix}\phi $
is finitely generated for every automorphism
$\mathrm {Fix}\phi $
is finitely generated for every automorphism
![]() $\phi \in \mathrm {Aut}(G)$
. Note that if a group G has
$\phi \in \mathrm {Aut}(G)$
. Note that if a group G has
![]() $\mathrm {FGFP_a}$
, it must itself be finitely generated. In addition to free groups and surface groups mentioned above, many types of groups had been proven to have
$\mathrm {FGFP_a}$
, it must itself be finitely generated. In addition to free groups and surface groups mentioned above, many types of groups had been proven to have
![]() $\mathrm {FGFP_a}$
, such as Gromov hyperbolic groups [Reference Neumann20, Reference Paulin21, Reference Shor24] and limit groups [Reference Minasyan and Osin18]. The
$\mathrm {FGFP_a}$
, such as Gromov hyperbolic groups [Reference Neumann20, Reference Paulin21, Reference Shor24] and limit groups [Reference Minasyan and Osin18]. The
![]() $\mathrm {FGFP_a}$
property is preserved under taking free products [Reference Lei and Zhang15], but not under taking direct products [Reference Zhang, Ventura and Wu28]. For example, the free group
$\mathrm {FGFP_a}$
property is preserved under taking free products [Reference Lei and Zhang15], but not under taking direct products [Reference Zhang, Ventura and Wu28]. For example, the free group
![]() $F_2$
and
$F_2$
and
![]() $\mathbb Z$
both have
$\mathbb Z$
both have
![]() $\mathrm {FGFP_a}$
, but their direct product
$\mathrm {FGFP_a}$
, but their direct product
![]() $F_2\times \mathbb Z$
does not.
$F_2\times \mathbb Z$
does not.
Example 1.1. Let
![]() $\phi $
be the automorphism of
$\phi $
be the automorphism of
![]() $F_2\times \mathbb Z=\langle a, b\rangle \times \langle t \rangle $
defined by
$F_2\times \mathbb Z=\langle a, b\rangle \times \langle t \rangle $
defined by
![]() $\phi (a)=at$
,
$\phi (a)=at$
,
![]() $\phi (b)=b$
and
$\phi (b)=b$
and
![]() $\phi (t)=t$
. An element u is in
$\phi (t)=t$
. An element u is in
![]() $\mathrm {Fix}\phi $
if and only if the total a exponent in u is zero. Then the fixed subgroup
$\mathrm {Fix}\phi $
if and only if the total a exponent in u is zero. Then the fixed subgroup
![]() $\mathrm {Fix}\phi \cong F_{\aleph _{0}}\times \mathbb Z$
is not finitely generated (it is generated by the set
$\mathrm {Fix}\phi \cong F_{\aleph _{0}}\times \mathbb Z$
is not finitely generated (it is generated by the set
![]() $\{ t, a^iba^{-i}\mid i\in \mathbb Z\}$
).
$\{ t, a^iba^{-i}\mid i\in \mathbb Z\}$
).
In this note, we will investigate the following question.
Question 1.2. For a group G, when does
![]() $G\times \mathbb {Z}^m\ (m\geq 1)$
have
$G\times \mathbb {Z}^m\ (m\geq 1)$
have
![]() $\mathrm {FGFP_a}$
?
$\mathrm {FGFP_a}$
?
We provide some partial answers (see Theorems 3.1, 3.7 and 3.11) by using the BNS-invariant.
2 Preliminaries
2.1 BNS-invariant
The BNS-invariant, introduced in 1987 by Bieri et al. [Reference Bieri, Neumann and Strebel3], is a geometric invariant of finitely generated groups inspired by the work of Thurston [Reference Thurston27]. It determines whether the kernel of a homomorphism from a group to an abelian group is finitely generated or not. Generally, the BNS-invariant is hard to compute. It was described for some families of groups like RAAGs [Reference Meier and Vanwyk17], limit groups [Reference Kochloukova14] and some other groups. Bieri and Renz [Reference Bieri and Renz4] introduced the higher dimension BNS-invariant to get more information on the kernel.
Definition 2.1. Let G be a finitely generated group with a finite generating set
![]() $X\subset G$
,
$X\subset G$
,
![]() $n=\mathrm {rk}(H^1(G; \mathbb Z))$
the torsion-free rank of the abelianisation of G, and
$n=\mathrm {rk}(H^1(G; \mathbb Z))$
the torsion-free rank of the abelianisation of G, and
![]() $S(G)=(\mathrm {Hom}(G,\mathbb {R})-{0})/\mathbb {R}_{+}$
the character sphere which is an
$S(G)=(\mathrm {Hom}(G,\mathbb {R})-{0})/\mathbb {R}_{+}$
the character sphere which is an
![]() $(n-1)$
-sphere. Note that an element of
$(n-1)$
-sphere. Note that an element of
![]() $S(G)$
is an equivalence class
$S(G)$
is an equivalence class
![]() $[\chi ]=\{r\chi \mid r\in \mathbb {R}_+\}$
. Denote by
$[\chi ]=\{r\chi \mid r\in \mathbb {R}_+\}$
. Denote by
![]() $\Gamma =\Gamma (G,X)$
the Cayley graph of G with respect to X. The first
$\Gamma =\Gamma (G,X)$
the Cayley graph of G with respect to X. The first
![]() $\Sigma $
-invariant (or
$\Sigma $
-invariant (or
![]() $BNS$
-invariant) of G is
$BNS$
-invariant) of G is
where
![]() $\Gamma _{\chi }$
is the subgraph of
$\Gamma _{\chi }$
is the subgraph of
![]() $\Gamma $
whose vertices are the elements
$\Gamma $
whose vertices are the elements
![]() $g\in G$
with
$g\in G$
with
![]() $\chi (g)\geq 0$
and whose edges are the edges of
$\chi (g)\geq 0$
and whose edges are the edges of
![]() $\Gamma $
which connect two such vertices.
$\Gamma $
which connect two such vertices.
A nontrivial homomorphism
![]() $\chi : G \to \mathbb R$
with discrete (and hence infinite cyclic) image is said to be a discrete or rank one homomorphism. It represents a rational point of
$\chi : G \to \mathbb R$
with discrete (and hence infinite cyclic) image is said to be a discrete or rank one homomorphism. It represents a rational point of
![]() $S(G)$
. The set of rational points,
$S(G)$
. The set of rational points,
is dense in
![]() $S(G$
).
$S(G$
).
For later use, we present the main results of the paper [Reference Bieri, Neumann and Strebel3].
Theorem 2.2 (Bieri, Neumann and Strebel).
Let G be a finitely generated group.
-
(1) Let N be a normal subgroup of G with
 $G/N$
abelian. Then N is finitely generated if and only if
$G/N$
abelian. Then N is finitely generated if and only if
 $S(G, N):=\{[\chi ]\in S(G) \mid \chi (N)=0\}\subset \Sigma ^1(G)$
. In particular,
$S(G, N):=\{[\chi ]\in S(G) \mid \chi (N)=0\}\subset \Sigma ^1(G)$
. In particular,
 $\Sigma ^1(G)=S(G)$
if and only if the derived subgroup
$\Sigma ^1(G)=S(G)$
if and only if the derived subgroup
 $[G,G]$
is finitely generated.
$[G,G]$
is finitely generated. -
(2) Let
 $\phi : G \rightarrow \mathbb {Z}$
be a nontrivial homomorphism. Then
$\phi : G \rightarrow \mathbb {Z}$
be a nontrivial homomorphism. Then
 $\ker \phi $
is finitely generated if and only if
$\ker \phi $
is finitely generated if and only if
 $\{\phi , -\phi \} \subset \Sigma ^1(G)$
. In particular,
$\{\phi , -\phi \} \subset \Sigma ^1(G)$
. In particular,
 $S\mathbb Q(G)\subset \Sigma ^1(G)$
if and only if
$S\mathbb Q(G)\subset \Sigma ^1(G)$
if and only if
 $\ker \phi $
is finitely generated for every homomorphism
$\ker \phi $
is finitely generated for every homomorphism
 $\phi : G \rightarrow \mathbb {Z}$
.
$\phi : G \rightarrow \mathbb {Z}$
.
2.2 Automorphism
A centreless group G is one in which the centre
![]() $C(G)$
is trivial.
$C(G)$
is trivial.
Proposition 2.3. If G is a centreless group, then every automorphism
![]() $\phi : G\times \mathbb Z^m\rightarrow G\times \mathbb Z^m\ (m\geq 1)$
has the form:
$\phi : G\times \mathbb Z^m\rightarrow G\times \mathbb Z^m\ (m\geq 1)$
has the form:
where
![]() $\psi :G\rightarrow G$
and
$\psi :G\rightarrow G$
and
![]() $\mathcal L: \mathbb Z^m\to \mathbb Z^m$
are automorphisms and
$\mathcal L: \mathbb Z^m\to \mathbb Z^m$
are automorphisms and
![]() $\alpha :G\rightarrow \mathbb Z^m$
is a homomorphism.
$\alpha :G\rightarrow \mathbb Z^m$
is a homomorphism.
Proof. Since G is a centreless group, the centre
Note that an automorphism preserves the centre, so
![]() $\phi (1\times \mathbb Z^m)=1\times \mathbb Z^m$
and
$\phi (1\times \mathbb Z^m)=1\times \mathbb Z^m$
and
![]() $\phi (1,v)=(1, \mathcal {L}v)$
for
$\phi (1,v)=(1, \mathcal {L}v)$
for
![]() $\mathcal {L}$
an invertible matrix. Therefore, we can suppose
$\mathcal {L}$
an invertible matrix. Therefore, we can suppose
The endomorphism
![]() $\psi :G\rightarrow G$
is clearly surjective, so it remains to show that it is also injective. Indeed, for any
$\psi :G\rightarrow G$
is clearly surjective, so it remains to show that it is also injective. Indeed, for any
![]() $g\in \ker \psi $
,
$g\in \ker \psi $
,
Now
![]() $(g,0)\in 1 \times \mathbb Z^m$
implies
$(g,0)\in 1 \times \mathbb Z^m$
implies
![]() $g=1$
and hence
$g=1$
and hence
![]() $\psi :G\rightarrow G$
is an automorphism.
$\psi :G\rightarrow G$
is an automorphism.
3 Main results
In this section, we study the necessary and sufficient conditions for Question 1.2 to have a positive answer.
3.1 Necessary condition
Theorem 3.1. For a group G:
-
(1) if
 $G\times \mathbb {Z}$
has
$G\times \mathbb {Z}$
has
 $\mathrm {FGFP_a}$
, then G has
$\mathrm {FGFP_a}$
, then G has
 $\mathrm {FGFP_a}$
and
$\mathrm {FGFP_a}$
and
 $S\mathbb Q(G)\subset \Sigma ^1(G)$
, or equivalently, every homomorphism
$S\mathbb Q(G)\subset \Sigma ^1(G)$
, or equivalently, every homomorphism
 $\alpha : G\to \mathbb Z$
has finitely generated kernel;
$\alpha : G\to \mathbb Z$
has finitely generated kernel; -
(2) if
 $G\times \mathbb {Z}^m$
has
$G\times \mathbb {Z}^m$
has
 $\mathrm {FGFP_a}$
for some
$\mathrm {FGFP_a}$
for some
 $m\geq \mathrm {rk}(H^1(G;\mathbb Z))$
, then
$m\geq \mathrm {rk}(H^1(G;\mathbb Z))$
, then
 $G\times \mathbb {Z}^n$
has
$G\times \mathbb {Z}^n$
has
 $\mathrm {FGFP_a}$
for every n with
$\mathrm {FGFP_a}$
for every n with
 $0\leq n\leq m$
, and
$0\leq n\leq m$
, and
 $\Sigma ^1(G)=S(G)$
, or equivalently, its derived subgroup
$\Sigma ^1(G)=S(G)$
, or equivalently, its derived subgroup
 $[G,G]$
is finitely generated.
$[G,G]$
is finitely generated.
Proof. (1) First, we assume that G does not have
![]() $\mathrm {FGFP_a}$
, that is, there is an automorphism
$\mathrm {FGFP_a}$
, that is, there is an automorphism
![]() $\psi $
of G, such that
$\psi $
of G, such that
![]() $\mathrm {Fix}\psi $
is not finitely generated. Consider the automorphism
$\mathrm {Fix}\psi $
is not finitely generated. Consider the automorphism
![]() $\phi :G\times \mathbb Z \to G\times \mathbb Z$
given by
$\phi :G\times \mathbb Z \to G\times \mathbb Z$
given by
Its fixed subgroup,
![]() $\mathrm {Fix}\phi =\mathrm {Fix}\psi \times \mathbb Z$
, is not finitely generated, contradicting the hypothesis that
$\mathrm {Fix}\phi =\mathrm {Fix}\psi \times \mathbb Z$
, is not finitely generated, contradicting the hypothesis that
![]() $G\times \mathbb Z$
has
$G\times \mathbb Z$
has
![]() $\mathrm {FGFP_a}$
.
$\mathrm {FGFP_a}$
.
Now we assume
![]() $S\mathbb Q(G)\not \subset \Sigma ^1(G)$
, or equivalently by Theorem 2.2, there is a nontrivial homomorphism
$S\mathbb Q(G)\not \subset \Sigma ^1(G)$
, or equivalently by Theorem 2.2, there is a nontrivial homomorphism
![]() $\alpha : G\to \mathbb Z$
such that
$\alpha : G\to \mathbb Z$
such that
![]() $\ker \alpha $
is not finitely generated. Let
$\ker \alpha $
is not finitely generated. Let
![]() $\phi :G\times \mathbb Z \to G\times \mathbb Z$
be given by
$\phi :G\times \mathbb Z \to G\times \mathbb Z$
be given by
Then
![]() $\phi $
is an automorphism whose inverse is
$\phi $
is an automorphism whose inverse is
![]() $\phi ^{-1}(g,n)=(g, n-\alpha (g))$
. It is easy to see that
$\phi ^{-1}(g,n)=(g, n-\alpha (g))$
. It is easy to see that
![]() $\mathrm {Fix}\phi =\ker \alpha \times \mathbb {Z}$
is not finitely generated, also contradicting the hypothesis that
$\mathrm {Fix}\phi =\ker \alpha \times \mathbb {Z}$
is not finitely generated, also contradicting the hypothesis that
![]() $G\times \mathbb Z$
has
$G\times \mathbb Z$
has
![]() $\mathrm {FGFP_a}$
.
$\mathrm {FGFP_a}$
.
(2) If
![]() $G\times \mathbb {Z}^m$
has
$G\times \mathbb {Z}^m$
has
![]() $\mathrm {FGFP_a}$
for some
$\mathrm {FGFP_a}$
for some
![]() $m\geq \mathrm {rk}(H^1(G;\mathbb Z))$
, then
$m\geq \mathrm {rk}(H^1(G;\mathbb Z))$
, then
![]() $G\times \mathbb {Z}^n$
has
$G\times \mathbb {Z}^n$
has
![]() $\mathrm {FGFP_a}$
for every n with
$\mathrm {FGFP_a}$
for every n with
![]() $0\leq n\leq m$
. This follows directly from proof (1) because
$0\leq n\leq m$
. This follows directly from proof (1) because
![]() $G\times \mathbb Z^m=(G\times \mathbb Z^{m-1})\times \mathbb Z$
.
$G\times \mathbb Z^m=(G\times \mathbb Z^{m-1})\times \mathbb Z$
.
Now we assume that
![]() $[G,G]$
is not finitely generated. Then Theorem 2.2 implies
$[G,G]$
is not finitely generated. Then Theorem 2.2 implies
![]() $\Sigma ^1(G)\neq S(G)$
and there is a nontrivial homomorphism
$\Sigma ^1(G)\neq S(G)$
and there is a nontrivial homomorphism
![]() $\alpha : G\to \mathbb R$
such that
$\alpha : G\to \mathbb R$
such that
![]() $\ker \alpha $
is not finitely generated. Note that the image of
$\ker \alpha $
is not finitely generated. Note that the image of
![]() $\alpha $
is an abelian group
$\alpha $
is an abelian group
![]() $\mathbb Z^n$
with
$\mathbb Z^n$
with
![]() $n\leq \mathrm {rk}(H^1(G;\mathbb Z))$
. So
$n\leq \mathrm {rk}(H^1(G;\mathbb Z))$
. So
![]() $\alpha $
can be viewed as a homomorphism
$\alpha $
can be viewed as a homomorphism
![]() $\alpha : G\to \mathbb Z^n$
, and the automorphism
$\alpha : G\to \mathbb Z^n$
, and the automorphism
has fixed subgroup
![]() $\mathrm {Fix}\phi =\ker \alpha \times \mathbb {Z}^n$
which is not finitely generated, contradicting the hypothesis that
$\mathrm {Fix}\phi =\ker \alpha \times \mathbb {Z}^n$
which is not finitely generated, contradicting the hypothesis that
![]() $G\times \mathbb Z^n$
has
$G\times \mathbb Z^n$
has
![]() $\mathrm {FGFP_a}$
.
$\mathrm {FGFP_a}$
.
Remark 3.2. Spahn and Zaremsky [Reference Spahn and Zaremsky26] showed that every kernel of a map from the group
![]() $F_{2,3}$
to
$F_{2,3}$
to
![]() $\mathbb Z$
is finitely generated, but there exist maps from
$\mathbb Z$
is finitely generated, but there exist maps from
![]() $F_{2,3}$
to
$F_{2,3}$
to
![]() $\mathbb Z^2$
whose kernels are not finitely generated. For the definition of
$\mathbb Z^2$
whose kernels are not finitely generated. For the definition of
![]() $F_{2,3}$
and more details, see [Reference Spahn and Zaremsky26].
$F_{2,3}$
and more details, see [Reference Spahn and Zaremsky26].
Example 3.3. Let G be a nonabelian limit group. Then
![]() $G\times \mathbb {Z}$
(and hence
$G\times \mathbb {Z}$
(and hence
![]() $G\times \mathbb Z^m\ (m\geq 1)$
) does not have
$G\times \mathbb Z^m\ (m\geq 1)$
) does not have
![]() $\mathrm {FGFP_a}$
. Indeed, Kochloukova [Reference Kochloukova14] proved that the BNS-invariant of a nonabelian limit group is the empty set. Note that the sphere
$\mathrm {FGFP_a}$
. Indeed, Kochloukova [Reference Kochloukova14] proved that the BNS-invariant of a nonabelian limit group is the empty set. Note that the sphere
![]() $S(G)$
is not empty, so
$S(G)$
is not empty, so
![]() $S\mathbb Q(G)\not \subset \Sigma ^1(G)$
. By Theorem 3.1,
$S\mathbb Q(G)\not \subset \Sigma ^1(G)$
. By Theorem 3.1,
![]() $G\times \mathbb {Z}$
does not have
$G\times \mathbb {Z}$
does not have
![]() $\mathrm {FGFP_a}$
.
$\mathrm {FGFP_a}$
.
3.2 Sufficient condition
To give sufficient conditions for Question 1.2 to have a positive answer, we need to introduce the Howson and weakly Howson properties.
Definition 3.4. A group G is said to have the Howson property if the intersection
![]() $H\cap K$
of any two finitely generated subgroups
$H\cap K$
of any two finitely generated subgroups
![]() $H, K<G$
is again finitely generated; G is said to have the weakly Howson property, if in addition, one of H and K is normal in G.
$H, K<G$
is again finitely generated; G is said to have the weakly Howson property, if in addition, one of H and K is normal in G.
Note that a group with the Howson property necessarily has the weakly Howson property and simple groups clearly have the weakly Howson property. Free groups and surface groups both have the Howson property [Reference Howson10]. More concretely, for a free or surface group G,
which was conjectured by Hanna Neumann in 1957, and proved independently by Friedman [Reference Friedman8] and Mineyev [Reference Mineyev19] in 2011 for free groups and by Antolín and Jaikin-Zapirain [Reference Antolín and Jaikin-Zapirain1] in 2022 for surface groups.
Lemma 3.5. (Some basic properties of the weakly Howson property).
-
(1)
 $F_2\times \mathbb Z$
does not have the weakly Howson property, and hence does not have the Howson property;
$F_2\times \mathbb Z$
does not have the weakly Howson property, and hence does not have the Howson property; -
(2) the Howson property is heritable (that is, if a group has the Howson property, then each subgroup of it does), and hence any group containing a subgroup isomorphic to
 $F_2\times \mathbb Z$
does not have the Howson property;
$F_2\times \mathbb Z$
does not have the Howson property; -
(3) Thompson’s group V has the weakly Howson property but does not have the Howson property;
-
(4) the weakly Howson property is not heritable.
Proof. (1) Let
![]() $F_2\times \mathbb Z=\langle a, b\rangle \times \langle t \rangle $
and let
$F_2\times \mathbb Z=\langle a, b\rangle \times \langle t \rangle $
and let
![]() $K=\langle a, bt\rangle $
be a finitely generated subgroup. Then
$K=\langle a, bt\rangle $
be a finitely generated subgroup. Then
![]() $F_2=\langle a, b\rangle $
is normal in
$F_2=\langle a, b\rangle $
is normal in
![]() $F_2\times \mathbb Z$
, and
$F_2\times \mathbb Z$
, and
![]() $F_2\cap K=\langle b^nab^{-n}\mid n\in \mathbb Z\rangle $
is the normal closure of a in
$F_2\cap K=\langle b^nab^{-n}\mid n\in \mathbb Z\rangle $
is the normal closure of a in
![]() $F_2$
and hence not finitely generated. Therefore,
$F_2$
and hence not finitely generated. Therefore,
![]() $F_2\times \mathbb Z$
does not have the weakly Howson property (and hence does not have the Howson property).
$F_2\times \mathbb Z$
does not have the weakly Howson property (and hence does not have the Howson property).
(2) The Howson property is clearly heritable. So any group with a subgroup isomorphic to
![]() $F_2\times \mathbb Z$
does not have the Howson property. For example, the special linear group
$F_2\times \mathbb Z$
does not have the Howson property. For example, the special linear group
![]() $\mbox {SL}(n, \mathbb Z) ~( n\geq 4)$
contains a subgroup isomorphic to
$\mbox {SL}(n, \mathbb Z) ~( n\geq 4)$
contains a subgroup isomorphic to
![]() $F_2\times \mathbb Z$
and does not have the Howson property. Moreover, by the virtually fibred theorem of 3-manifolds, every hyperbolic 3-manifold of finite volume is finitely covered by a surface bundle over the circle. So the fundamental group of every hyperbolic 3-manifold of finite volume does not have the Howson property [Reference Soma25].
$F_2\times \mathbb Z$
and does not have the Howson property. Moreover, by the virtually fibred theorem of 3-manifolds, every hyperbolic 3-manifold of finite volume is finitely covered by a surface bundle over the circle. So the fundamental group of every hyperbolic 3-manifold of finite volume does not have the Howson property [Reference Soma25].
(3) Note that Thompson’s group V is a finitely presented infinite simple group, so it has the weakly Howson property. Moreover, Thompson’s group V contains a remarkable variety of subgroups, such as finitely generated free groups, finitely generated abelian groups and Houghton’s groups. The class of subgroups of V is closed under direct products and restricted wreath products with finite or infinite cyclic top group [Reference Higman9]. In particular, V contains
![]() $F_2\times \mathbb Z$
as a subgroup and hence V does not have the Howson property.
$F_2\times \mathbb Z$
as a subgroup and hence V does not have the Howson property.
(4) This clearly follows from item (3).
Lemma 3.6. Let G be a finitely generated group,
![]() $H<G$
a finite index subgroup and
$H<G$
a finite index subgroup and
![]() $K<G$
a finitely generated subgroup. Then
$K<G$
a finitely generated subgroup. Then
![]() $H\cap K$
is finitely generated.
$H\cap K$
is finitely generated.
Proof. It is easy to see that
![]() $H\cap K$
has finite index in K. Since K is finitely generated,
$H\cap K$
has finite index in K. Since K is finitely generated,
![]() $H\cap K$
is also finitely generated.
$H\cap K$
is also finitely generated.
Theorem 3.7. Let G be a centreless group with the weakly Howson property. Then:
-
(1)
 $G\times \mathbb {Z}$
has
$G\times \mathbb {Z}$
has
 $\mathrm {FGFP_a}$
if and only if G has
$\mathrm {FGFP_a}$
if and only if G has
 $\mathrm {FGFP_a}$
and
$\mathrm {FGFP_a}$
and
 $S\mathbb Q(G)\subset \Sigma ^1(G)$
, or equivalently, every homomorphism
$S\mathbb Q(G)\subset \Sigma ^1(G)$
, or equivalently, every homomorphism
 $\alpha : G\to \mathbb Z$
has finitely generated kernel;
$\alpha : G\to \mathbb Z$
has finitely generated kernel; -
(2)
 $G\times \mathbb {Z}^m$
has
$G\times \mathbb {Z}^m$
has
 $\mathrm {FGFP_a}$
for every
$\mathrm {FGFP_a}$
for every
 $m\geq 1$
if and only if G has
$m\geq 1$
if and only if G has
 $\mathrm {FGFP_a}$
and
$\mathrm {FGFP_a}$
and
 $\Sigma ^1(G)=S(G)$
, or equivalently, the derived subgroup
$\Sigma ^1(G)=S(G)$
, or equivalently, the derived subgroup
 $[G,G]$
is finitely generated.
$[G,G]$
is finitely generated.
Proof. The ‘only if’ part clearly follows from Theorem 3.1. For the ‘if’ part, note that G is centreless, so by Proposition 2.3, every automorphism
![]() $\phi $
of
$\phi $
of
![]() $G\times \mathbb {Z}^m\ (m\geq 1)$
has the form
$G\times \mathbb {Z}^m\ (m\geq 1)$
has the form
where
![]() $\psi \in \mathrm {Aut}(G)$
,
$\psi \in \mathrm {Aut}(G)$
,
![]() $\alpha \in \mathrm {Hom}(G,\mathbb {Z}^m)$
and
$\alpha \in \mathrm {Hom}(G,\mathbb {Z}^m)$
and
![]() $\mathcal {L}\in \mathrm {Aut}(\mathbb Z^m).$
This gives the fixed subgroup
$\mathcal {L}\in \mathrm {Aut}(\mathbb Z^m).$
This gives the fixed subgroup
We now prove the ‘if’ part for the two statements in the theorem.
(1) In this case,
![]() $m=1$
and
$m=1$
and
![]() $\mathcal {L}=\pm \mathrm {Id}$
. Since G has
$\mathcal {L}=\pm \mathrm {Id}$
. Since G has
![]() $\mathrm {FGFP_a}$
and
$\mathrm {FGFP_a}$
and
![]() $S\mathbb Q(G)\subset \Sigma ^1(G)$
,
$S\mathbb Q(G)\subset \Sigma ^1(G)$
,
![]() $\mathrm {Fix}\psi $
and
$\mathrm {Fix}\psi $
and
![]() $\ker \alpha $
are both finitely generated for every homomorphism
$\ker \alpha $
are both finitely generated for every homomorphism
![]() $\alpha : G\to \mathbb Z$
by Theorem 2.2. When
$\alpha : G\to \mathbb Z$
by Theorem 2.2. When
![]() $\mathcal {L}=\mathrm {Id}$
,
$\mathcal {L}=\mathrm {Id}$
,
and
![]() $\mathrm {Fix}\phi $
is finitely generated by the weakly Howson property of G. When
$\mathrm {Fix}\phi $
is finitely generated by the weakly Howson property of G. When
![]() $\mathcal {L}=-\mathrm {Id}$
, the fixed subgroup is
$\mathcal {L}=-\mathrm {Id}$
, the fixed subgroup is
 $$ \begin{align*} \mathrm{Fix}\phi&=\{(g, n)\mid \psi(g)=g, ~\alpha(g)-n=n\}\nonumber\\ &=\{(g, n)\mid g\in \mathrm{Fix}\psi\cap\alpha^{-1}(2\mathbb{Z}), ~n=\alpha(g)/2\}\nonumber\\ &\cong\mathrm{Fix}\psi\cap \alpha^{-1}(2\mathbb{Z}).\nonumber \end{align*} $$
$$ \begin{align*} \mathrm{Fix}\phi&=\{(g, n)\mid \psi(g)=g, ~\alpha(g)-n=n\}\nonumber\\ &=\{(g, n)\mid g\in \mathrm{Fix}\psi\cap\alpha^{-1}(2\mathbb{Z}), ~n=\alpha(g)/2\}\nonumber\\ &\cong\mathrm{Fix}\psi\cap \alpha^{-1}(2\mathbb{Z}).\nonumber \end{align*} $$
Actually, the weakly Howson property adds nothing in this case, because
![]() $\alpha ^{-1}(2\mathbb {Z})<G$
is a subgroup of index
$\alpha ^{-1}(2\mathbb {Z})<G$
is a subgroup of index
![]() $\leq 2$
and
$\leq 2$
and
![]() $\mathrm {Fix}\phi $
is finitely generated by Lemma 3.6. In both cases,
$\mathrm {Fix}\phi $
is finitely generated by Lemma 3.6. In both cases,
![]() $G\times \mathbb Z$
has
$G\times \mathbb Z$
has
![]() $\mathrm {FGFP_a}$
and item (1) holds.
$\mathrm {FGFP_a}$
and item (1) holds.
(2) To prove
![]() $ G\times \mathbb Z^m$
has
$ G\times \mathbb Z^m$
has
![]() $\mathrm {FGFP_a}$
for every
$\mathrm {FGFP_a}$
for every
![]() $m\geq 1$
, let us consider the projection
$m\geq 1$
, let us consider the projection
Then, by (3.1), we have the natural short exact sequence
where
for some
![]() $s\leq m$
, and
$s\leq m$
, and
is a normal subgroup of
![]() $\mathrm {Fix}\psi $
.
$\mathrm {Fix}\psi $
.
By the above exact sequence, to prove that
![]() $\mathrm {Fix}\phi $
is finitely generated, it suffices to prove that
$\mathrm {Fix}\phi $
is finitely generated, it suffices to prove that
![]() $p(\mathrm {Fix}\phi )$
is finitely generated. Indeed, note that
$p(\mathrm {Fix}\phi )$
is finitely generated. Indeed, note that
![]() $\Sigma ^1(G)=S(G)$
, and
$\Sigma ^1(G)=S(G)$
, and
![]() $G/\alpha ^{-1}((\mathrm {Id}-\mathcal {L})\mathbb {Z}^m)$
is a quotient of
$G/\alpha ^{-1}((\mathrm {Id}-\mathcal {L})\mathbb {Z}^m)$
is a quotient of
![]() $\alpha (G)$
and hence abelian. So by Theorem 2.2,
$\alpha (G)$
and hence abelian. So by Theorem 2.2,
![]() $\alpha ^{-1}((\mathrm {Id}-\mathcal {L})\mathbb {Z}^m)$
is a finitely generated normal subgroup of G. Moreover, since G has
$\alpha ^{-1}((\mathrm {Id}-\mathcal {L})\mathbb {Z}^m)$
is a finitely generated normal subgroup of G. Moreover, since G has
![]() $\mathrm {FGFP_a}$
, both G and
$\mathrm {FGFP_a}$
, both G and
![]() $\mathrm {Fix}\psi $
are finitely generated. By the weakly Howson property of G,
$\mathrm {Fix}\psi $
are finitely generated. By the weakly Howson property of G,
![]() $p(\mathrm {Fix}\phi )$
is again finitely generated.
$p(\mathrm {Fix}\phi )$
is again finitely generated.
Therefore,
![]() $\mathrm {Fix}\phi $
is finitely generated and hence
$\mathrm {Fix}\phi $
is finitely generated and hence
![]() $G\times \mathbb {Z}^m\ (m\geq 1)$
has
$G\times \mathbb {Z}^m\ (m\geq 1)$
has
![]() $\mathrm {FGFP_a}$
.
$\mathrm {FGFP_a}$
.
For an arbitrary group G, it seems too difficult to guarantee that G has both the (weakly) Howson and
![]() $\mathrm {FGFP_a}$
properties and that
$\mathrm {FGFP_a}$
properties and that
![]() $[G, G]$
is finitely generated, unless G is slender, that is, every subgroup of G is finitely generated. For example, all finite groups and all finitely generated nilpotent groups are slender. Note that nilpotent groups have nontrivial centres.
$[G, G]$
is finitely generated, unless G is slender, that is, every subgroup of G is finitely generated. For example, all finite groups and all finitely generated nilpotent groups are slender. Note that nilpotent groups have nontrivial centres.
Hyperbolic groups have
![]() $\mathrm {FGFP_a}$
and nonelementary hyperbolic groups are centreless. However, for a hyperbolic group G, we do not necessarily have the Howson property and
$\mathrm {FGFP_a}$
and nonelementary hyperbolic groups are centreless. However, for a hyperbolic group G, we do not necessarily have the Howson property and
![]() $[G,G]$
finitely generated. For example, every nonsolvable surface group is hyperbolic and has the Howson property, but its derived subgroup is not finitely generated.
$[G,G]$
finitely generated. For example, every nonsolvable surface group is hyperbolic and has the Howson property, but its derived subgroup is not finitely generated.
Every finitely generated nonabelian simple group G (for example, Thompson’s group V) is centreless, with
![]() $[G, G]$
finitely generated and satisfies the weakly Howson property, but currently, little is known about the fixed subgroups.
$[G, G]$
finitely generated and satisfies the weakly Howson property, but currently, little is known about the fixed subgroups.
Question 3.8. Is there a centreless, infinite group G with
![]() $[G, G]$
finitely generated and satisfying the (weakly) Howson and
$[G, G]$
finitely generated and satisfying the (weakly) Howson and
![]() $\mathrm {FGFP_a}$
properties?
$\mathrm {FGFP_a}$
properties?
3.3 Nontrivial example
For a hyperbolic 3-manifold M, Soma [Reference Soma25] showed that the fundamental group
![]() $\pi _1(M)$
has the Howson property if and only if M has infinite volume. Although the fundamental group
$\pi _1(M)$
has the Howson property if and only if M has infinite volume. Although the fundamental group
![]() $G=\pi _1(M)$
of a hyperbolic 3-manifold M with infinite volume has the Howson property, it never has a finitely generated derived subgroup
$G=\pi _1(M)$
of a hyperbolic 3-manifold M with infinite volume has the Howson property, it never has a finitely generated derived subgroup
![]() $[G, G]$
unless G is nilpotent. In fact, assume there is a hyperbolic 3-manifold M with infinite volume and with fundamental group having finitely generated derived subgroup
$[G, G]$
unless G is nilpotent. In fact, assume there is a hyperbolic 3-manifold M with infinite volume and with fundamental group having finitely generated derived subgroup
![]() $[G, G]$
. Moreover, assume that M is not the solid torus and not homotopic to a closed surface. For such a hyperbolic 3-manifold M, we know one component of
$[G, G]$
. Moreover, assume that M is not the solid torus and not homotopic to a closed surface. For such a hyperbolic 3-manifold M, we know one component of
![]() $\partial M$
has genus at least two, so the first homology group of M is infinite. Let N be the infinite regular cover of M with fundamental group
$\partial M$
has genus at least two, so the first homology group of M is infinite. Let N be the infinite regular cover of M with fundamental group
![]() $\pi _1(N)=[G, G]$
. We may deform the hyperbolic structure on M so that it is geometrically finite and has no cusps. By Thurston’s theorem [Reference Canary and Johannson5], the hyperbolic structure on N is also geometrically finite. Since
$\pi _1(N)=[G, G]$
. We may deform the hyperbolic structure on M so that it is geometrically finite and has no cusps. By Thurston’s theorem [Reference Canary and Johannson5], the hyperbolic structure on N is also geometrically finite. Since
![]() $[G, G]$
is a normal subgroup of G, the groups have the same limit set. Let C be the convex hull of the limit set. Then the convex core of N is
$[G, G]$
is a normal subgroup of G, the groups have the same limit set. Let C be the convex hull of the limit set. Then the convex core of N is
![]() $C/[G, G]$
and the convex core of M is
$C/[G, G]$
and the convex core of M is
![]() $C/G$
. Both have nonzero finite volume since N and M are geometrically finite. However,
$C/G$
. Both have nonzero finite volume since N and M are geometrically finite. However,
![]() $C/[G, G]$
is an infinite cover of
$C/[G, G]$
is an infinite cover of
![]() $C/G$
, which is a contradiction.
$C/G$
, which is a contradiction.
In the case of M having finite volume, Lin and Wang [Reference Lin and Wang16] studied the fixed subgroups of automorphisms of
![]() $\pi _1(M)$
and obtained the following result.
$\pi _1(M)$
and obtained the following result.
Theorem 3.9 [Reference Lin and Wang16, Theorem 1.6].
Suppose
![]() $G=\pi _1(M)$
, where M is an orientable hyperbolic
$G=\pi _1(M)$
, where M is an orientable hyperbolic
![]() $3$
-manifold with finite volume and
$3$
-manifold with finite volume and
![]() $\phi $
is an automorphism of G. Then
$\phi $
is an automorphism of G. Then
![]() $\mathrm {Fix}\phi $
is either the whole group G, or the trivial group 1, or
$\mathrm {Fix}\phi $
is either the whole group G, or the trivial group 1, or
![]() $\mathbb {Z}$
, or
$\mathbb {Z}$
, or
![]() $\mathbb {Z}\times \mathbb {Z}$
, or a surface group
$\mathbb {Z}\times \mathbb {Z}$
, or a surface group
![]() $\pi _1(S)$
, where S can be orientable or not and closed or not. More precisely:
$\pi _1(S)$
, where S can be orientable or not and closed or not. More precisely:
-
(1) if
 $\phi $
is induced by an orientation-preserving isometry, then:
$\phi $
is induced by an orientation-preserving isometry, then:-
(a)
 $\mathrm {Fix}\phi $
is either
$\mathrm {Fix}\phi $
is either
 $\mathbb {Z}$
or
$\mathbb {Z}$
or
 $\mathbb {Z}\times \mathbb {Z}$
or G or 1;
$\mathbb {Z}\times \mathbb {Z}$
or G or 1; -
(b) moreover, if M is closed, then
 $\mathrm {Fix}\phi $
is either
$\mathrm {Fix}\phi $
is either
 $\mathbb {Z}$
or G;
$\mathbb {Z}$
or G;
-
-
(2) if
 $\phi $
is induced by an orientation-reversing isometry f, then:
$\phi $
is induced by an orientation-reversing isometry f, then:-
(a) if
 $\phi ^2\neq \mathrm {id}$
,
$\phi ^2\neq \mathrm {id}$
,
 $\mathrm {Fix}\phi $
is either
$\mathrm {Fix}\phi $
is either
 $\mathbb {Z}$
or 1;
$\mathbb {Z}$
or 1; -
(b) if
 $\phi ^2= \mathrm {id}$
,
$\phi ^2= \mathrm {id}$
,
 $\mathrm {Fix}\phi $
is either 1 or the surface group
$\mathrm {Fix}\phi $
is either 1 or the surface group
 $\pi _1(S)$
, where S is an embedded surface in M that is pointwise fixed by f.
$\pi _1(S)$
, where S is an embedded surface in M that is pointwise fixed by f.
-
Note that in [Reference Lin and Wang16], a 3-manifold M is hyperbolic if M is orientable, compact and the interior of M admits a complete hyperbolic structure of finite volume (so that M is either closed or has a boundary consisting of a union of tori).
Proposition 3.10. Let
![]() $G=\pi _1(M)$
for M an orientable hyperbolic
$G=\pi _1(M)$
for M an orientable hyperbolic
![]() $3$
-manifold with finite volume and without an involution. Then for any automorphism
$3$
-manifold with finite volume and without an involution. Then for any automorphism
![]() $\phi $
of G, the fixed subgroup
$\phi $
of G, the fixed subgroup
![]() $\mathrm {Fix}\phi $
is inert in G, that is,
$\mathrm {Fix}\phi $
is inert in G, that is,
![]() $\mathrm {rk}(H\cap \mathrm {Fix}\phi )\leq \mathrm {rk}(H)$
for any finitely generated subgroup
$\mathrm {rk}(H\cap \mathrm {Fix}\phi )\leq \mathrm {rk}(H)$
for any finitely generated subgroup
![]() $H<G$
.
$H<G$
.
Proof. Since M has no involution, we have
![]() $\phi ^2\neq \mathrm {id}$
for any automorphism
$\phi ^2\neq \mathrm {id}$
for any automorphism
![]() $\phi $
of
$\phi $
of
![]() ${G=\pi _1(M)}$
, by Mostow’s rigidity theorem. Then by Theorem 3.9, the fixed subgroup
${G=\pi _1(M)}$
, by Mostow’s rigidity theorem. Then by Theorem 3.9, the fixed subgroup
![]() $\mathrm {Fix}\phi $
is either 1,
$\mathrm {Fix}\phi $
is either 1,
![]() $\mathbb Z$
,
$\mathbb Z$
,
![]() $\mathbb {Z}\times \mathbb {Z}$
or the whole group G, and the proposition follows.
$\mathbb {Z}\times \mathbb {Z}$
or the whole group G, and the proposition follows.
To get nontrivial examples, we remove the weakly Howson property from the conditions in Theorem 3.7.
Theorem 3.11. The group
![]() $G\times \mathbb {Z}^m$
has
$G\times \mathbb {Z}^m$
has
![]() $\mathrm {FGFP_a}$
for every
$\mathrm {FGFP_a}$
for every
![]() $m\geq 1$
if G is one of the following types:
$m\geq 1$
if G is one of the following types:
-
(1) a slender group (for example, a finite group or a finitely generated nilpotent group);
-
(2)
 $G=\pi _1(M)$
where M is a closed orientable hyperbolic 3-manifold with finite first homology group
$G=\pi _1(M)$
where M is a closed orientable hyperbolic 3-manifold with finite first homology group
 $H_1(M)$
and with the isometry group
$H_1(M)$
and with the isometry group
 $\mathrm {Isom}(M)$
of odd order.
$\mathrm {Isom}(M)$
of odd order.
Proof. (1) Let G be a slender group, that is, every subgroup of G is finitely generated. Then
![]() $G\times \mathbb Z^m$
is again slender, and hence it has
$G\times \mathbb Z^m$
is again slender, and hence it has
![]() $\mathrm {FGFP_a}$
. Indeed, for any subgroup
$\mathrm {FGFP_a}$
. Indeed, for any subgroup
![]() $H<G\times \mathbb Z^m$
, we have a short exact sequence
$H<G\times \mathbb Z^m$
, we have a short exact sequence
where p is the natural projection
![]() $G\times \mathbb Z^m\to \mathbb Z^m$
with
$G\times \mathbb Z^m\to \mathbb Z^m$
with
![]() $\ker (p)=G$
. Then,
$\ker (p)=G$
. Then,
![]() $H\cap \ker (p)$
is a subgroup of the slender group G and hence it is finitely generated. So H is also finitely generated.
$H\cap \ker (p)$
is a subgroup of the slender group G and hence it is finitely generated. So H is also finitely generated.
(2) Since M is a closed orientable hyperbolic 3-manifold,
![]() $G=\pi _1(M)$
is a centreless, finitely generated Gromov hyperbolic group, and hence, G has
$G=\pi _1(M)$
is a centreless, finitely generated Gromov hyperbolic group, and hence, G has
![]() $\mathrm {FGFP_a}$
. Moreover,
$\mathrm {FGFP_a}$
. Moreover,
![]() $H_1(M)$
finite implies that the derived subgroup
$H_1(M)$
finite implies that the derived subgroup
![]() $[G, G]$
is of finite index in the finitely generated group G and hence it is again finitely generated. Note that the weakly Howson property in the proof of Theorem 3.7(2) is only used to ensure that
$[G, G]$
is of finite index in the finitely generated group G and hence it is again finitely generated. Note that the weakly Howson property in the proof of Theorem 3.7(2) is only used to ensure that
in (3.2) is finitely generated. However, now, since
![]() $\mathrm {Isom}(M)$
is of odd order, M has no involution. By Proposition 3.10, the fixed subgroup
$\mathrm {Isom}(M)$
is of odd order, M has no involution. By Proposition 3.10, the fixed subgroup
![]() $\mathrm {Fix}\psi $
is inert in G for every automorphism
$\mathrm {Fix}\psi $
is inert in G for every automorphism
![]() $\psi :G\to G$
. So
$\psi :G\to G$
. So
that is,
![]() $\mathrm {Fix}\psi \cap \alpha ^{-1}((\mathrm {Id}-\mathcal {L})\mathbb {Z}^m)$
is finitely generated.
$\mathrm {Fix}\psi \cap \alpha ^{-1}((\mathrm {Id}-\mathcal {L})\mathbb {Z}^m)$
is finitely generated.
In conclusion, we can show that
![]() $G\times \mathbb {Z}^m$
has
$G\times \mathbb {Z}^m$
has
![]() $\mathrm {FGFP_a}$
, by the same argument as in the proof of Theorem 3.7(2), without using the weakly Howson property.
$\mathrm {FGFP_a}$
, by the same argument as in the proof of Theorem 3.7(2), without using the weakly Howson property.
There are many closed hyperbolic 3-manifolds such that their fundamental groups satisfy condition (2) of Theorem 3.11.
Example 3.12. Let M be the 3-manifold
![]() $\mathbb {S}^3-9_{32}$
and
$\mathbb {S}^3-9_{32}$
and
![]() $M_{p,q}$
be the Dehn filling from M along the slope
$M_{p,q}$
be the Dehn filling from M along the slope
![]() $p \mathcal {M}+q\mathcal {L}$
. Here,
$p \mathcal {M}+q\mathcal {L}$
. Here,
![]() $9_{32}$
is the knot in Rolfsen’s list [Reference Rolfsen22], and
$9_{32}$
is the knot in Rolfsen’s list [Reference Rolfsen22], and
![]() $(\mathcal {M},\mathcal {L})$
is the canonical meridian-longitude system of the cusp of M. So
$(\mathcal {M},\mathcal {L})$
is the canonical meridian-longitude system of the cusp of M. So
![]() $H_{1}(M)= \mathbb {Z}_{p}$
. From Snappy, we know that
$H_{1}(M)= \mathbb {Z}_{p}$
. From Snappy, we know that
![]() $\mathbb {S}^3-9_{32}$
is hyperbolic with trivial isometry group. When p, q are large enough,
$\mathbb {S}^3-9_{32}$
is hyperbolic with trivial isometry group. When p, q are large enough,
![]() $M_{p,q}$
is a closed hyperbolic 3-manifold by Thurston’s hyperbolic Dehn surgery theorem. The proof of Thurston’s hyperbolic Dehn surgery theorem also implies the Dehn filling has a very short geodesic core when p, q are large. So any isometry of
$M_{p,q}$
is a closed hyperbolic 3-manifold by Thurston’s hyperbolic Dehn surgery theorem. The proof of Thurston’s hyperbolic Dehn surgery theorem also implies the Dehn filling has a very short geodesic core when p, q are large. So any isometry of
![]() $M_{p,q}$
will preserve the core of the Dehn filling, and hence will preserve M, that is, it will be isotopic to the identity. In summary, when p, q are large enough,
$M_{p,q}$
will preserve the core of the Dehn filling, and hence will preserve M, that is, it will be isotopic to the identity. In summary, when p, q are large enough,
![]() $M_{p,q}$
is a closed hyperbolic 3-manifold with trivial isometry group and finite first homology group. So its fundamental group satisfies condition (2) of Theorem 3.11.
$M_{p,q}$
is a closed hyperbolic 3-manifold with trivial isometry group and finite first homology group. So its fundamental group satisfies condition (2) of Theorem 3.11.
Finally, inspired by Theorem 3.11, we may wonder whether the assumption ‘centreless and with the weakly Howson property’ in Theorem 3.7 can be removed or not.
Question 3.13. Does
![]() $G\times \mathbb Z$
have
$G\times \mathbb Z$
have
![]() $\mathrm {FGFP_a}$
if the group G has
$\mathrm {FGFP_a}$
if the group G has
![]() $\mathrm {FGFP_a}$
and the derived subgroup
$\mathrm {FGFP_a}$
and the derived subgroup
![]() $[G, G]$
is finitely generated?
$[G, G]$
is finitely generated?
Acknowledgements
The authors would like to thank Luis Mendonça for pointing out an error in the first version of this note and for providing Remark 3.2. The authors also thank Enric Ventura for his helpful comments, which led us to more general results for
![]() $G\times \mathbb Z^m$
instead of
$G\times \mathbb Z^m$
instead of
![]() $G\times \mathbb Z$
. Furthermore, the authors thank the anonymous referee very much for valuable and detailed comments which helped to greatly improve our original manuscript, especially for inspiring us to introduce the concept of the weakly Howson property in Theorem 3.7.
$G\times \mathbb Z$
. Furthermore, the authors thank the anonymous referee very much for valuable and detailed comments which helped to greatly improve our original manuscript, especially for inspiring us to introduce the concept of the weakly Howson property in Theorem 3.7.