No CrossRef data available.
Article contents
PROPER 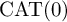 $\mathrm {CAT(0)}$ ACTIONS OF UNIPOTENT-FREE LINEAR GROUPS
$\mathrm {CAT(0)}$ ACTIONS OF UNIPOTENT-FREE LINEAR GROUPS
Published online by Cambridge University Press: 07 January 2025
Abstract
Let 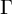 $\Gamma $ be a finitely generated group of matrices over
$\Gamma $ be a finitely generated group of matrices over 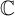 $\mathbb {C}$. We construct an isometric action of
$\mathbb {C}$. We construct an isometric action of 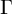 $\Gamma $ on a complete
$\Gamma $ on a complete 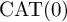 $\mathrm {CAT}(0)$ space such that the restriction of this action to any subgroup of
$\mathrm {CAT}(0)$ space such that the restriction of this action to any subgroup of 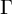 $\Gamma $ containing no nontrivial unipotent elements is well behaved. As an application, we show that if M is a graph manifold that does not admit a nonpositively curved Riemannian metric, then any finite-dimensional
$\Gamma $ containing no nontrivial unipotent elements is well behaved. As an application, we show that if M is a graph manifold that does not admit a nonpositively curved Riemannian metric, then any finite-dimensional 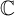 $\mathbb {C}$-linear representation of
$\mathbb {C}$-linear representation of 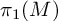 $\pi _1(M)$ maps a nontrivial element of
$\pi _1(M)$ maps a nontrivial element of 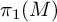 $\pi _1(M)$ to a unipotent matrix. In particular, the fundamental groups of such 3-manifolds do not admit any faithful finite-dimensional unitary representations.
$\pi _1(M)$ to a unipotent matrix. In particular, the fundamental groups of such 3-manifolds do not admit any faithful finite-dimensional unitary representations.
MSC classification
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 24 , Issue 2 , March 2025 , pp. 587 - 601
- Copyright
- © The Author(s), 2025. Published by Cambridge University Press
Footnotes
The author was partially supported by the National Science Centre, Poland UMO-2018/30/M/ST1/00668


