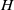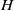1. Introduction
Let
![]() $\Gamma$
be a finite simplicial graph with vertex set
$\Gamma$
be a finite simplicial graph with vertex set
![]() $\mathrm{V}(\Gamma )$
and edge set
$\mathrm{V}(\Gamma )$
and edge set
![]() $\mathrm{E}(\Gamma )$
. The associated right-angled Artin group (RAAG), denoted by
$\mathrm{E}(\Gamma )$
. The associated right-angled Artin group (RAAG), denoted by
![]() $\mathrm{A}_\Gamma$
, is generated by
$\mathrm{A}_\Gamma$
, is generated by
![]() $\mathrm{V}(\Gamma )$
, and two generators
$\mathrm{V}(\Gamma )$
, and two generators
![]() $v$
and
$v$
and
![]() $w$
commute whenever they are connected by an edge. A common question in group theory is: when does a group split as an amalgamated product or an HNN extension over a subgroup? For RAAGs, the splittings over infinite cyclic subgroups and abelian subgroups were characterized by Clay [Reference Clay3] and by Groves and Hull [Reference Groves and Hull6], respectively. Recently, Hull [Reference Hull7] generalized the splittings of RAAGs over abelian subgroups to non-abelian subgroups.
$w$
commute whenever they are connected by an edge. A common question in group theory is: when does a group split as an amalgamated product or an HNN extension over a subgroup? For RAAGs, the splittings over infinite cyclic subgroups and abelian subgroups were characterized by Clay [Reference Clay3] and by Groves and Hull [Reference Groves and Hull6], respectively. Recently, Hull [Reference Hull7] generalized the splittings of RAAGs over abelian subgroups to non-abelian subgroups.
Let
![]() $\phi \colon \mathrm{A}_\Gamma \to \mathbb{Z}$
be a homomorphism that sends all the generators to
$\phi \colon \mathrm{A}_\Gamma \to \mathbb{Z}$
be a homomorphism that sends all the generators to
![]() $1$
. The kernel of
$1$
. The kernel of
![]() $\phi$
is called the Bestvina–Brady group and is denoted by
$\phi$
is called the Bestvina–Brady group and is denoted by
![]() $\mathrm{BB}_\Gamma$
. We only focus on finitely presented Bestvina–Brady groups, which is equivalent to saying that the flag complexes on the defining graphs are simply connected [Reference Bestvina and Brady1]. The author in [Reference Chang2] characterized the splittings of finitely presented Bestvina–Brady groups over abelian subgroups. In this note, we prove a result for the splittings of finitely presented Bestvina–Brady groups over non-abelian subgroups.
$\mathrm{BB}_\Gamma$
. We only focus on finitely presented Bestvina–Brady groups, which is equivalent to saying that the flag complexes on the defining graphs are simply connected [Reference Bestvina and Brady1]. The author in [Reference Chang2] characterized the splittings of finitely presented Bestvina–Brady groups over abelian subgroups. In this note, we prove a result for the splittings of finitely presented Bestvina–Brady groups over non-abelian subgroups.
Theorem 1.1.
Let
![]() $\Gamma$
be a finite simplicial graph with no cut vertices and whose associated flag complex is simply connected. Suppose that
$\Gamma$
be a finite simplicial graph with no cut vertices and whose associated flag complex is simply connected. Suppose that
![]() $\mathrm{BB}_\Gamma$
splits as an amalgamated product over a subgroup
$\mathrm{BB}_\Gamma$
splits as an amalgamated product over a subgroup
![]() $H$
. Then
$H$
. Then
![]() $\Gamma$
contains an induced subgraph
$\Gamma$
contains an induced subgraph
![]() $\Lambda$
that separates
$\Lambda$
that separates
![]() $\Gamma$
and
$\Gamma$
and
![]() $\mathrm{BB}_{\Lambda }$
is contained in a conjugate of
$\mathrm{BB}_{\Lambda }$
is contained in a conjugate of
![]() $H$
.
$H$
.
In other words, Theorem1.1 says that if
![]() $\mathrm{BB}_\Gamma$
acts on a tree which is not a line, then there is an induced subgraph
$\mathrm{BB}_\Gamma$
acts on a tree which is not a line, then there is an induced subgraph
![]() $\Lambda$
of
$\Lambda$
of
![]() $\Gamma$
such that
$\Gamma$
such that
![]() $\Lambda$
separates
$\Lambda$
separates
![]() $\Gamma$
and
$\Gamma$
and
![]() $\mathrm{BB}_\Lambda$
fixes an edge of
$\mathrm{BB}_\Lambda$
fixes an edge of
![]() $T$
.
$T$
.
If
![]() $\Gamma$
contains an induced subgraph
$\Gamma$
contains an induced subgraph
![]() $\Lambda$
such that
$\Lambda$
such that
![]() $\Gamma \setminus \Lambda$
has more than one connected component, then
$\Gamma \setminus \Lambda$
has more than one connected component, then
![]() $\mathrm{A}_\Gamma$
splits over
$\mathrm{A}_\Gamma$
splits over
![]() $\mathrm{A}_\Lambda$
and
$\mathrm{A}_\Lambda$
and
![]() $\mathrm{BB}_\Gamma$
splits over
$\mathrm{BB}_\Gamma$
splits over
![]() $\mathrm{BB}_\Lambda$
. In the language of Bass–Serre Theory, all the vertex groups and edge groups of this splitting for
$\mathrm{BB}_\Lambda$
. In the language of Bass–Serre Theory, all the vertex groups and edge groups of this splitting for
![]() $\mathrm{A}_\Gamma$
are finitely presented, but this is not always the case for the corresponding splitting for
$\mathrm{A}_\Gamma$
are finitely presented, but this is not always the case for the corresponding splitting for
![]() $\mathrm{BB}_\Gamma$
; see Example 3.3. We remark that
$\mathrm{BB}_\Gamma$
; see Example 3.3. We remark that
![]() $\Gamma$
contains a cut vertex if and only if
$\Gamma$
contains a cut vertex if and only if
![]() $\mathrm{BB}_\Gamma$
splits as a free product.
$\mathrm{BB}_\Gamma$
splits as a free product.
The proof of Theorem1.1 uses basic facts about groups acting on trees, and the idea of the proof is similar to those in [Reference Groves and Hull6], [Reference Chang2], and [Reference Hull7].

Figure 1. A directed triangle.
2. Preliminaries
2.1. Bestvina–Brady groups
Let
![]() $\Gamma$
be a finite simplicial graph. The main result in [Reference Bestvina and Brady1] states that
$\Gamma$
be a finite simplicial graph. The main result in [Reference Bestvina and Brady1] states that
![]() $\Gamma$
is connected if and only if
$\Gamma$
is connected if and only if
![]() $\mathrm{BB}_{\Gamma }$
is finitely generated, and that the flag complex on
$\mathrm{BB}_{\Gamma }$
is finitely generated, and that the flag complex on
![]() $\Gamma$
is simply connected if and only if
$\Gamma$
is simply connected if and only if
![]() $\mathrm{BB}_{\Gamma }$
is finitely presented. In the latter situation, Dicks and Leary found an explicit presentation:
$\mathrm{BB}_{\Gamma }$
is finitely presented. In the latter situation, Dicks and Leary found an explicit presentation:
Theorem 2.1. ([Reference Dicks and Leary5, Corollary 3]) Let
![]() $\Gamma$
be a finite simplicial directed graph. If the flag complex on
$\Gamma$
be a finite simplicial directed graph. If the flag complex on
![]() $\Gamma$
is simply connected, then
$\Gamma$
is simply connected, then
![]() $\mathrm{BB}_\Gamma$
is generated by all the directed edges of
$\mathrm{BB}_\Gamma$
is generated by all the directed edges of
![]() $\Gamma$
, and the relators are of the form
$\Gamma$
, and the relators are of the form
![]() $ee^{-1}$
, where
$ee^{-1}$
, where
![]() $e^{-1}$
denotes the edge
$e^{-1}$
denotes the edge
![]() $e$
with the opposite orientation, and
$e$
with the opposite orientation, and
![]() $ef=g=fe$
, where
$ef=g=fe$
, where
![]() $e$
,
$e$
,
![]() $f$
, and
$f$
, and
![]() $g$
form a directed triangle; see Figure 1
.
$g$
form a directed triangle; see Figure 1
.
2.2. Group acting on trees
Let
![]() $G$
be a group acting on a tree
$G$
be a group acting on a tree
![]() $T$
without inversions. We always assume that actions are minimal and nontrivial. An element
$T$
without inversions. We always assume that actions are minimal and nontrivial. An element
![]() $g\in G$
is called elliptic if it fixes a point in
$g\in G$
is called elliptic if it fixes a point in
![]() $T$
; otherwise, it is called hyperbolic. When
$T$
; otherwise, it is called hyperbolic. When
![]() $g\in G$
is elliptic, the set of points fixed by
$g\in G$
is elliptic, the set of points fixed by
![]() $g$
is a subtree of
$g$
is a subtree of
![]() $T$
and is denoted by
$T$
and is denoted by
![]() $\mathrm{Fix}(g)$
. When
$\mathrm{Fix}(g)$
. When
![]() $g\in G$
is hyperbolic, it fixes a line in
$g\in G$
is hyperbolic, it fixes a line in
![]() $T$
on which it acts by translation. This line is called the axis of
$T$
on which it acts by translation. This line is called the axis of
![]() $g$
and is denoted by
$g$
and is denoted by
![]() $\mathrm{Axis}(g)$
.
$\mathrm{Axis}(g)$
.
Lemma 2.2. ([Reference Culler and Vogtmann4, Lemma 1.1, Corollary 1.5], [Reference Groves and Hull6, Lemma 1.1]) Let
![]() $G$
be a group acting on a tree, and let
$G$
be a group acting on a tree, and let
![]() $g$
and
$g$
and
![]() $h$
be commuting elements in
$h$
be commuting elements in
![]() $G$
.
$G$
.
-
(1) If
 $h$
is hyperbolic, then
$h$
is hyperbolic, then
 $\mathrm{Axis}(h)\subseteq \mathrm{Fix}(g)$
.
$\mathrm{Axis}(h)\subseteq \mathrm{Fix}(g)$
. -
(2) If both
 $g$
and
$g$
and
 $h$
are hyperbolic, then
$h$
are hyperbolic, then
 $\mathrm{Axis}(g)=\mathrm{Axis}(h)$
.
$\mathrm{Axis}(g)=\mathrm{Axis}(h)$
. -
(3) If both
 $g$
and
$g$
and
 $h$
are elliptic, then
$h$
are elliptic, then
 $\mathrm{Fix}(g)\cap \mathrm{Fix}(h)\neq \emptyset$
.
$\mathrm{Fix}(g)\cap \mathrm{Fix}(h)\neq \emptyset$
.
3. Proof of Theorem 1.1
Throughout this section, we identify edges of a graph with elements in the associated Bestvina–Brady group.
Definition 3.1. Let
![]() $\Gamma$
be a finite simplicial graph. A triangle path
$\Gamma$
be a finite simplicial graph. A triangle path
![]() $P_\Delta$
between two distinct edges
$P_\Delta$
between two distinct edges
![]() $e$
and
$e$
and
![]() $f$
in
$f$
in
![]() $\Gamma$
is a sequence of triangles
$\Gamma$
is a sequence of triangles
![]() $\Delta _1,\dots, \Delta _n$
such that
$\Delta _1,\dots, \Delta _n$
such that
-
• the edges
 $e$
and
$e$
and
 $f$
are contained in
$f$
are contained in
 $\Delta _1$
and
$\Delta _1$
and
 $\Delta _n$
, respectively;
$\Delta _n$
, respectively; -
• the triangles
 $\Delta _i$
and
$\Delta _i$
and
 $\Delta _{i+1}$
share a unique edge for each
$\Delta _{i+1}$
share a unique edge for each
 $i=1,\dots, n-1$
;
$i=1,\dots, n-1$
; -
• the triangles
 $\Delta _i$
and
$\Delta _i$
and
 $\Delta _j$
do not share a common edge if
$\Delta _j$
do not share a common edge if
 $j\neq i-1$
or
$j\neq i-1$
or
 $j\neq i+1$
.
$j\neq i+1$
.
The edge shared by
![]() $\Delta _i$
and
$\Delta _i$
and
![]() $\Delta _{i+1}$
is called an intermediate edge.
$\Delta _{i+1}$
is called an intermediate edge.
Two examples of triangle paths and their intermediate edges are given in Figure 2. Notice that triangle paths between two edges may not be unique, and all the triangles in a triangle path can share a common vertex.

Figure 2. Two triangle paths and their intermediate edges (red edges). The graph on the right illustrates that all the triangles in a triangle path share a common vertex.
Recall that a subgraph
![]() $\Lambda$
of
$\Lambda$
of
![]() $\Gamma$
separates two vertices (or two edges) if these two vertices (or edges) lie in different connected components of
$\Gamma$
separates two vertices (or two edges) if these two vertices (or edges) lie in different connected components of
![]() $\Gamma \setminus \Lambda$
.
$\Gamma \setminus \Lambda$
.
Lemma 3.2.
Let
![]() $\Gamma$
be a finite simplicial graph without cut vertices and whose associated flag complex is simply connected. Let
$\Gamma$
be a finite simplicial graph without cut vertices and whose associated flag complex is simply connected. Let
![]() $\Lambda$
be an induced subgraph of
$\Lambda$
be an induced subgraph of
![]() $\Gamma$
. If every triangle path between
$\Gamma$
. If every triangle path between
![]() $e_1$
and
$e_1$
and
![]() $e_2$
in
$e_2$
in
![]() $E(\Gamma )$
has an intermediate edge in
$E(\Gamma )$
has an intermediate edge in
![]() $E(\Lambda )$
, then
$E(\Lambda )$
, then
![]() $\Lambda$
separates
$\Lambda$
separates
![]() $e_1$
from
$e_1$
from
![]() $e_2$
.
$e_2$
.
Proof. Since
![]() $\Gamma$
has no cut vertices and the associated flag complex is simply connected, every edge of
$\Gamma$
has no cut vertices and the associated flag complex is simply connected, every edge of
![]() $\Gamma$
is contained in a triangle, and there is a triangle path between any two edges in
$\Gamma$
is contained in a triangle, and there is a triangle path between any two edges in
![]() $\Gamma$
. Let
$\Gamma$
. Let
![]() $e_1=(u_1,v_1)$
and
$e_1=(u_1,v_1)$
and
![]() $e_2=(u_2,v_2)$
. Suppose that
$e_2=(u_2,v_2)$
. Suppose that
![]() $\Lambda$
does not separate
$\Lambda$
does not separate
![]() $e_1$
from
$e_1$
from
![]() $e_2$
. Then, without loss of generality, there is an edge path
$e_2$
. Then, without loss of generality, there is an edge path
![]() $p$
between the vertices
$p$
between the vertices
![]() $u_1$
and
$u_1$
and
![]() $u_2$
. This edge path
$u_2$
. This edge path
![]() $p$
is contained in some triangle path
$p$
is contained in some triangle path
![]() $P_\Delta$
between
$P_\Delta$
between
![]() $e_1$
and
$e_1$
and
![]() $e_2$
, and therefore, every vertex of
$e_2$
, and therefore, every vertex of
![]() $p$
, possibly except for the two end vertices, is a vertex of an intermediate edge of
$p$
, possibly except for the two end vertices, is a vertex of an intermediate edge of
![]() $P_\Delta$
. Since
$P_\Delta$
. Since
![]() $\Lambda$
contains an intermediate edge of
$\Lambda$
contains an intermediate edge of
![]() $P_\Delta$
, removing
$P_\Delta$
, removing
![]() $\Lambda$
will disconnect the path
$\Lambda$
will disconnect the path
![]() $p$
. Thus, the path
$p$
. Thus, the path
![]() $p$
cannot exist. Hence, the subgraph
$p$
cannot exist. Hence, the subgraph
![]() $\Lambda$
separates
$\Lambda$
separates
![]() $e_1$
from
$e_1$
from
![]() $e_2$
.
$e_2$
.
We now prove the main theorem.
Proof of Theorem 1.1
. Let
![]() $\mathrm{BB}_\Gamma$
act on a tree
$\mathrm{BB}_\Gamma$
act on a tree
![]() $T$
, and let
$T$
, and let
![]() $e_h\in \mathrm{E}(\Gamma )$
be hyperbolic. Since
$e_h\in \mathrm{E}(\Gamma )$
be hyperbolic. Since
![]() $\mathrm{BB}_\Gamma$
splits as an amalgamated product, the tree
$\mathrm{BB}_\Gamma$
splits as an amalgamated product, the tree
![]() $T$
is not a path. Let
$T$
is not a path. Let
![]() $\Lambda$
be the induced subgraph of
$\Lambda$
be the induced subgraph of
![]() $\Gamma$
such that
$\Gamma$
such that
![]() $\mathrm{E}(\Lambda )$
consists of all the elliptic edges of
$\mathrm{E}(\Lambda )$
consists of all the elliptic edges of
![]() $\Gamma$
that fix
$\Gamma$
that fix
![]() $\mathrm{Axis}(e_h)$
pointwise. Let
$\mathrm{Axis}(e_h)$
pointwise. Let
![]() $e$
be an edge of
$e$
be an edge of
![]() $\mathrm{Axis}(e_h)$
. Then
$\mathrm{Axis}(e_h)$
. Then
![]() $\mathrm{BB}_\Lambda$
fixes
$\mathrm{BB}_\Lambda$
fixes
![]() $e$
and is contained in a conjugate of
$e$
and is contained in a conjugate of
![]() $H$
.
$H$
.
We now show that
![]() $\Lambda$
separates
$\Lambda$
separates
![]() $\Gamma$
. We claim that there is an edge
$\Gamma$
. We claim that there is an edge
![]() $f\in \mathrm{E}(\Gamma )\setminus \mathrm{E}(\Lambda )$
such that every triangle path between
$f\in \mathrm{E}(\Gamma )\setminus \mathrm{E}(\Lambda )$
such that every triangle path between
![]() $e_h$
and
$e_h$
and
![]() $f$
has an intermediate edge in
$f$
has an intermediate edge in
![]() $\mathrm{E}(\Lambda )$
. Suppose to the contrary that for every edge
$\mathrm{E}(\Lambda )$
. Suppose to the contrary that for every edge
![]() $f'$
in
$f'$
in
![]() $\mathrm{E}(\Gamma )\setminus \mathrm{E}(\Lambda )$
, there is a triangle path
$\mathrm{E}(\Gamma )\setminus \mathrm{E}(\Lambda )$
, there is a triangle path
![]() $P_\Delta =\lbrace \Delta _1,\dots, \Delta _n\rbrace$
between
$P_\Delta =\lbrace \Delta _1,\dots, \Delta _n\rbrace$
between
![]() $e_h$
and
$e_h$
and
![]() $f'$
such that none of its intermediate edges is in
$f'$
such that none of its intermediate edges is in
![]() $\mathrm{E}(\Lambda )$
. Denote by
$\mathrm{E}(\Lambda )$
. Denote by
![]() $\{f_1,\dots, f_{n-1}\}$
the set of intermediate edges of
$\{f_1,\dots, f_{n-1}\}$
the set of intermediate edges of
![]() $P_\Delta$
, where
$P_\Delta$
, where
![]() $f_i$
is the edge shared by
$f_i$
is the edge shared by
![]() $\Delta _i$
and
$\Delta _i$
and
![]() $\Delta _{i+1}$
. Since
$\Delta _{i+1}$
. Since
![]() $e_h$
and
$e_h$
and
![]() $f_1$
are contained in
$f_1$
are contained in
![]() $\Delta _1$
, they are commuting elements. Since
$\Delta _1$
, they are commuting elements. Since
![]() $e_h$
is hyperbolic, the element
$e_h$
is hyperbolic, the element
![]() $f_1$
is also hyperbolic. Otherwise, it follows from Lemma 2.2 (1) that
$f_1$
is also hyperbolic. Otherwise, it follows from Lemma 2.2 (1) that
![]() $f_1\in \mathrm{E}(\Lambda )$
. Therefore, Lemma 2.2 (2) implies
$f_1\in \mathrm{E}(\Lambda )$
. Therefore, Lemma 2.2 (2) implies
![]() $\mathrm{Axis}(e_h)=\mathrm{Axis}(f_1)$
. Similarly, since
$\mathrm{Axis}(e_h)=\mathrm{Axis}(f_1)$
. Similarly, since
![]() $f_1$
is hyperbolic and commuting with
$f_1$
is hyperbolic and commuting with
![]() $f_2$
, the element
$f_2$
, the element
![]() $f_2$
is also hyperbolic and has the axis
$f_2$
is also hyperbolic and has the axis
![]() $\mathrm{Axis}(f_2)=\mathrm{Axis}(f_1)$
. Continuing with the same argument, we have that the edges
$\mathrm{Axis}(f_2)=\mathrm{Axis}(f_1)$
. Continuing with the same argument, we have that the edges
![]() $e_h,f_1,\dots, f_{n-1},f'$
are all hyperbolic with the same axis
$e_h,f_1,\dots, f_{n-1},f'$
are all hyperbolic with the same axis
![]() $\mathrm{Axis}(e_h)$
. Now, every edge in
$\mathrm{Axis}(e_h)$
. Now, every edge in
![]() $\mathrm{E}(\Gamma )\setminus \mathrm{E}(\Lambda )$
is hyperbolic and has the axis
$\mathrm{E}(\Gamma )\setminus \mathrm{E}(\Lambda )$
is hyperbolic and has the axis
![]() $\mathrm{Axis}(e_h)$
, which is fixed by
$\mathrm{Axis}(e_h)$
, which is fixed by
![]() $\mathrm{E}(\Lambda )$
pointwise. Thus, the set
$\mathrm{E}(\Lambda )$
pointwise. Thus, the set
![]() $\mathrm{E}(\Gamma )$
fixes
$\mathrm{E}(\Gamma )$
fixes
![]() $\mathrm{Axis}(e_h)$
, contradicting the fact that
$\mathrm{Axis}(e_h)$
, contradicting the fact that
![]() $T$
is not a path. This proves the claim. Therefore, the subgraph
$T$
is not a path. This proves the claim. Therefore, the subgraph
![]() $\Lambda$
separates
$\Lambda$
separates
![]() $e_h$
from
$e_h$
from
![]() $f$
by Lemma 3.2.
$f$
by Lemma 3.2.
Next, suppose that every edge of
![]() $\Gamma$
is elliptic. Since the action of
$\Gamma$
is elliptic. Since the action of
![]() $\mathrm{BB}_\Gamma$
on
$\mathrm{BB}_\Gamma$
on
![]() $T$
has no global fixed points, it follows from [Reference Serre8, p.64, Corollary 2] that there are two edges
$T$
has no global fixed points, it follows from [Reference Serre8, p.64, Corollary 2] that there are two edges
![]() $e_{\alpha }$
and
$e_{\alpha }$
and
![]() $e_{\beta }$
in
$e_{\beta }$
in
![]() $\mathrm{E}(\Gamma )$
such that the intersection
$\mathrm{E}(\Gamma )$
such that the intersection
![]() $\mathrm{Fix}(e_{\alpha })\cap \mathrm{Fix}(e_{\beta })$
is empty. Let
$\mathrm{Fix}(e_{\alpha })\cap \mathrm{Fix}(e_{\beta })$
is empty. Let
![]() $L$
be the geodesic in
$L$
be the geodesic in
![]() $T$
between
$T$
between
![]() $\mathrm{Fix}(e_{\alpha })$
and
$\mathrm{Fix}(e_{\alpha })$
and
![]() $\mathrm{Fix}(e_{\beta })$
, and let
$\mathrm{Fix}(e_{\beta })$
, and let
![]() $e$
be an edge of
$e$
be an edge of
![]() $L$
. Let
$L$
. Let
![]() $\Lambda$
be an induced subgraph of
$\Lambda$
be an induced subgraph of
![]() $\Gamma$
such that every edge of
$\Gamma$
such that every edge of
![]() $\Lambda$
fixes
$\Lambda$
fixes
![]() $e$
. Then,
$e$
. Then,
![]() $\mathrm{BB}_\Lambda$
fixes
$\mathrm{BB}_\Lambda$
fixes
![]() $e$
and is contained in a conjugate of
$e$
and is contained in a conjugate of
![]() $H$
. We now show that
$H$
. We now show that
![]() $\Lambda$
separates
$\Lambda$
separates
![]() $\Gamma$
. Let
$\Gamma$
. Let
![]() $P_\Delta =\lbrace \Delta _1,\dots, \Delta _n\rbrace$
be a triangle path between
$P_\Delta =\lbrace \Delta _1,\dots, \Delta _n\rbrace$
be a triangle path between
![]() $e_\alpha$
and
$e_\alpha$
and
![]() $e_\beta$
. Denote by
$e_\beta$
. Denote by
![]() $\{f_1,\dots, f_{n-1}\}$
the set of intermediate edges of
$\{f_1,\dots, f_{n-1}\}$
the set of intermediate edges of
![]() $P_\Delta$
, where
$P_\Delta$
, where
![]() $f_i$
is the edge shared by
$f_i$
is the edge shared by
![]() $\Delta _i$
and
$\Delta _i$
and
![]() $\Delta _{i+1}$
. For convenience, we write
$\Delta _{i+1}$
. For convenience, we write
![]() $f_0=e_\alpha$
and
$f_0=e_\alpha$
and
![]() $f_n=e_\beta$
. Since
$f_n=e_\beta$
. Since
![]() $f_i$
and
$f_i$
and
![]() $f_{i+1}$
are contained in the triangle
$f_{i+1}$
are contained in the triangle
![]() $\Delta _{i+1}$
, they are commuting elliptic elements. It follows from Lemma 2.2 (3) that the intersection
$\Delta _{i+1}$
, they are commuting elliptic elements. It follows from Lemma 2.2 (3) that the intersection
![]() $\mathrm{Fix}(f_i)\cap \mathrm{Fix}(f_{i+1})$
is nonempty for
$\mathrm{Fix}(f_i)\cap \mathrm{Fix}(f_{i+1})$
is nonempty for
![]() $i=0,\dots, n-1$
. Thus, there is a path
$i=0,\dots, n-1$
. Thus, there is a path
![]() $L'$
in
$L'$
in
![]() $T$
from
$T$
from
![]() $\mathrm{Fix}(f_0)=\mathrm{Fix}(e_{\alpha })$
to
$\mathrm{Fix}(f_0)=\mathrm{Fix}(e_{\alpha })$
to
![]() $\mathrm{Fix}(f_{n})=\mathrm{Fix}(e_{\beta })$
lying entirely in
$\mathrm{Fix}(f_{n})=\mathrm{Fix}(e_{\beta })$
lying entirely in
![]() $\bigcup ^{n}_{i=0}\mathrm{Fix}(f_i)$
. Since
$\bigcup ^{n}_{i=0}\mathrm{Fix}(f_i)$
. Since
![]() $T$
is a tree, we have
$T$
is a tree, we have
![]() $L'=L$
. Then the edge
$L'=L$
. Then the edge
![]() $e$
belongs to
$e$
belongs to
![]() $\mathrm{Fix}(f_i)$
for some
$\mathrm{Fix}(f_i)$
for some
![]() $i$
. That is, there is an intermediate edge
$i$
. That is, there is an intermediate edge
![]() $f_i$
of
$f_i$
of
![]() $P_\Delta$
that belongs to
$P_\Delta$
that belongs to
![]() $\mathrm{E}(\Lambda )$
. Since the choice of the triangle path
$\mathrm{E}(\Lambda )$
. Since the choice of the triangle path
![]() $P_\Delta$
between
$P_\Delta$
between
![]() $e_\alpha$
and
$e_\alpha$
and
![]() $e_\beta$
is arbitrary, the subgraph
$e_\beta$
is arbitrary, the subgraph
![]() $\Lambda$
separates
$\Lambda$
separates
![]() $e_\alpha$
from
$e_\alpha$
from
![]() $e_\beta$
by Lemma 3.2.
$e_\beta$
by Lemma 3.2.

Figure 3. A splitting of a finitely presented Bestvina–Brady group over a finitely generated but not finitely presented subgroup.
We end this section with one example.
Example 3.3.
Let
![]() $\Gamma$
be the graph shown in Figure 3
. Let
$\Gamma$
be the graph shown in Figure 3
. Let
![]() $W$
be the set of vertices that are adjacent to either
$W$
be the set of vertices that are adjacent to either
![]() $u$
or
$u$
or
![]() $v$
but different from
$v$
but different from
![]() $u$
and
$u$
and
![]() $v$
. Let
$v$
. Let
![]() $\Lambda$
,
$\Lambda$
,
![]() $\Gamma _1$
, and
$\Gamma _1$
, and
![]() $\Gamma _2$
be the induced graphs on
$\Gamma _2$
be the induced graphs on
![]() $W$
,
$W$
,
![]() $\mathrm{V}(\Gamma )\setminus \lbrace u,v\rbrace$
, and
$\mathrm{V}(\Gamma )\setminus \lbrace u,v\rbrace$
, and
![]() $W\cup \lbrace u,v\rbrace$
, respectively. Then
$W\cup \lbrace u,v\rbrace$
, respectively. Then
![]() $\Lambda$
is an induced separating subgraph of
$\Lambda$
is an induced separating subgraph of
![]() $\Gamma$
and
$\Gamma$
and
![]() $\mathrm{BB}_\Gamma \cong \mathrm{BB}_{\Gamma _1}\ast _{\mathrm{BB}_{\Lambda }}\mathrm{BB}_{\Gamma _2}$
. However, the groups
$\mathrm{BB}_\Gamma \cong \mathrm{BB}_{\Gamma _1}\ast _{\mathrm{BB}_{\Lambda }}\mathrm{BB}_{\Gamma _2}$
. However, the groups
![]() $\mathrm{BB}_\Gamma$
and
$\mathrm{BB}_\Gamma$
and
![]() $\mathrm{BB}_{\Gamma _2}$
are finitely presented, while
$\mathrm{BB}_{\Gamma _2}$
are finitely presented, while
![]() $\mathrm{BB}_{\Gamma _1}$
and
$\mathrm{BB}_{\Gamma _1}$
and
![]() $\mathrm{BB}_{\Lambda }$
are finitely generated but not finitely presented.
$\mathrm{BB}_{\Lambda }$
are finitely generated but not finitely presented.
Acknowledgements
The author thanks Lorenzo Ruffoni for his encouragement and helpful discussions. The author thanks the referee for the constructive comments and suggestions.