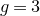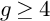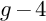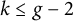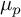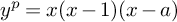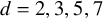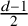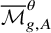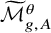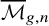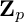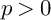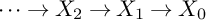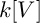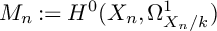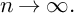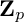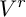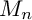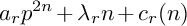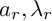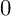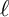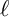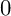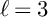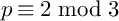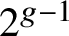Refine search
Actions for selected content:
37 results
On (2,2)-decomposable genus 4 Jacobians
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 12 September 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Rank of the Normal Functions of the Ceresa and Gross–Schoen Cycles
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 08 September 2025, e141
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Abelian varieties with no power isogenous to a Jacobian
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 6 / June 2025
- Published online by Cambridge University Press:
- 30 October 2025, pp. 1404-1457
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rationality and arithmetic of the moduli of abelian varieties
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SOME CASES OF OORT’S CONJECTURE ABOUT NEWTON POLYGONS OF CURVES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 257 / March 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 93-103
- Print publication:
- March 2025
-
- Article
- Export citation
Non-torsion algebraic cycles on the Jacobians of Fermat quotients
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 22 November 2024, pp. 60-72
- Print publication:
- March 2025
-
- Article
- Export citation
ARBITRARILY LARGE p-TORSION IN TATE-SHAFAREVICH GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 12 November 2024, pp. 481-502
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stability conditions for line bundles on nodal curves
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 28 October 2024, e87
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cyclic coverings of genus
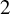 $2$ curves of Sophie Germain type
$2$ curves of Sophie Germain type
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 21 May 2024, e64
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mirror symmetry and Hitchin system on Deligne–Mumford curves: Strominger–Yau–Zaslow duality
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 06 May 2024, pp. 1488-1545
- Print publication:
- October 2025
-
- Article
- Export citation
Smooth Compactifications of the Abel-Jacobi Section
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 04 October 2023, e88
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Integral Fourier transforms and the integral Hodge conjecture for one-cycles on abelian varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 15 May 2023, pp. 1188-1213
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
IWASAWA THEORY FOR p-TORSION CLASS GROUP SCHEMES IN CHARACTERISTIC p
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 250 / June 2023
- Published online by Cambridge University Press:
- 22 November 2022, pp. 298-351
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The logarithmic Picard group and its tropicalization
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 7 / July 2022
- Published online by Cambridge University Press:
- 09 September 2022, pp. 1477-1562
- Print publication:
- July 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE BOUNDARY OF THE p-RANK
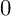 $0$ STRATUM OF THE MODULI SPACE OF CYCLIC COVERS OF THE PROJECTIVE LINE
$0$ STRATUM OF THE MODULI SPACE OF CYCLIC COVERS OF THE PROJECTIVE LINE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 248 / December 2022
- Published online by Cambridge University Press:
- 30 May 2022, pp. 865-887
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Kirchhoff’s theorem for Prym varieties
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 16 February 2022, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Infinitesimal structure of the pluricanonical double ramification locus
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 14 September 2021, pp. 2280-2337
- Print publication:
- October 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rational points and derived equivalence
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 1036-1050
- Print publication:
- May 2021
-
- Article
- Export citation
A support theorem for Hilbert schemes of planar curves, II
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 28 April 2021, pp. 835-882
- Print publication:
- April 2021
-
- Article
- Export citation
EXTENDING THE DOUBLE RAMIFICATION CYCLE BY RESOLVING THE ABEL-JACOBI MAP
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 20 May 2019, pp. 331-359
- Print publication:
- January 2021
-
- Article
-
- You have access
- Open access
- Export citation