No CrossRef data available.
Article contents
SOME CASES OF OORT’S CONJECTURE ABOUT NEWTON POLYGONS OF CURVES
Part of:
Arithmetic algebraic geometry
Zeta and $L$-functions: analytic theory
Arithmetic problems. Diophantine geometry
Curves
Published online by Cambridge University Press: 02 December 2024
Abstract
This paper contains a method to prove the existence of smooth curves in positive characteristic whose Jacobians have unusual Newton polygons. Using this method, I give a new proof that there exist supersingular curves of genus  $4$ in every prime characteristic. More generally, the main result of the paper is that, for every
$4$ in every prime characteristic. More generally, the main result of the paper is that, for every 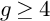 $g \geq 4$ and prime p, every Newton polygon whose p-rank is at least
$g \geq 4$ and prime p, every Newton polygon whose p-rank is at least 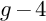 $g-4$ occurs for a smooth curve of genus g in characteristic p. In addition, this method resolves some cases of Oort’s conjecture about Newton polygons of curves.
$g-4$ occurs for a smooth curve of genus g in characteristic p. In addition, this method resolves some cases of Oort’s conjecture about Newton polygons of curves.
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Foundation Nagoya Mathematical Journal
References
Achter, J. D. and Pries, R., “Generic Newton polygons for curves of given p-rank” in Algebraic curves and finite fields, Radon Series on Computational and Applied Mathematics, Vol. 16, De Gruyter, Berlin, 2014, pp. 1–21. MR3287680Google Scholar
Bosch, S., Lütkebohmert, W. and Raynaud, M., Néron models, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], Vol. 21, Springer-Verlag, Berlin, 1990. MR1045822 (91i:14034)CrossRefGoogle Scholar
Chai, C.-L. and Oort, F.,
Monodromy and irreducibility of leaves
, Ann. Math. (2) 173 (2011), no. 3, 1359–1396. MR2800716CrossRefGoogle Scholar
de Jong, A. J. and Oort, F.,
Purity of the stratification by Newton polygons
, J. Amer. Math. Soc. 13 (2000), no. 1, 209–241. MR1703336CrossRefGoogle Scholar
Faber, C. and van der Geer, G.,
Complete subvarieties of moduli spaces and the Prym map
, J. Reine Angew. Math. 573 (2004), 117–137. MR2084584Google Scholar
Harashita, S., Supersingular abelian varieties and curves, and their moduli spaces, with a remark on the dimension of the moduli of supersingular curves of genus 4, Theory and Applications of Supersingular Curves and Supersingular Abelian Varieties, RIMS Kôkyûroku Bessatsu, Vol. B90, Research Institute for Mathematical Sciences, Kyoto, 2022, pp. 1–16. MR4521510Google Scholar
Kudo, M., Harashita, S. and Senda, H.,
The existence of supersingular curves of genus 4 in arbitrary characteristic
, Res. Number Theory 6 (2020), no. 4, Paper No. 44, 17 pp. MR4170348CrossRefGoogle Scholar
Li, W., Mantovan, E., Pries, R. and Tang, Y.,
Newton polygons arising from special families of cyclic covers of the projective line
, Res. Number Theory 5 (2019), no. 1, Paper No. 12, 31 pp. MR3897613CrossRefGoogle Scholar
Li, W., Mantovan, E., Pries, R. and Tang, Y., “Newton polygons of cyclic covers of the projective line branched at three points” in Research directions in number theory—Women in Numbers IV, Association for Women in Mathematics Series, Vol. 19, Springer, Cham, [2019] ©2019, pp. 115–132. MR4069381Google Scholar
Li, K.-Z. and Oort, F., Moduli of supersingular abelian varieties, Lecture Notes in Mathematics, Vol. 1680, Springer-Verlag, Berlin, 1998.CrossRefGoogle Scholar
Manin, J. I.,
Theory of commutative formal groups over fields of finite characteristic
, Uspehi Mat. Nauk 18 (1963), no. 6 (114), 3–90. MR0157972Google Scholar
Oort, F., “Hyperelliptic supersingular curves” in Arithmetic algebraic geometry (Texel, 1989), Progress in Mathematics, Vol. 89, Birkhäuser Boston, Boston, MA, 1991, pp. 247–284. MR1085262CrossRefGoogle Scholar
Oort, F., “Newton polygon strata in the moduli space of abelian varieties” in Moduli of abelian varieties (Texel Island, 1999), Progress in Mathematics, Vol. 195, Birkhäuser, Basel, 2001, pp. 417–440. MR1827028CrossRefGoogle Scholar
Oort, F., Abelian varieties isogenous to a Jacobian (Cornelissen, G. and Oort, F., eds.), Problems from the Workshop on Automorphisms of Curves, Vol. 113 2005, pp. 129–177. MR2168985 (2006d:14027)Google Scholar
Oort, F., “Newton polygons and p-divisible groups: a conjecture by Grothendieck” in Automorphic forms. I, Astérisque, Vol. 298, 2005, Société Mathématique de France, Paris, pp. 255–269. MR2141704Google Scholar
Pries, R., “Current results on Newton polygons of curves” in Open problems in arithmetic algebraic geometry, Advanced Lectures in Mathematics, Vol. 46, International Press, Somerville, MA, 2019, pp. 179–207. MR3971184Google Scholar
Vistoli, A.,
Intersection theory on algebraic stacks and on their moduli spaces
, Invent. Math. 97 (1989), no. 3, 613–670. MR1005008 (90k:14004)CrossRefGoogle Scholar


