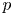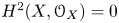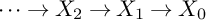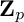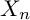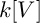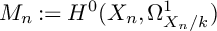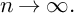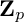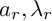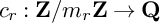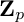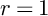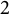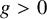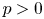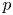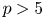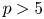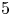Refine search
Actions for selected content:
38 results
On proper splinters in positive characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 16 December 2025, pp. 2493-2544
- Print publication:
- October 2025
-
- Article
- Export citation
ON THE SINGULARITIES OF QUOTIENTS BY 1-FOLIATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 261 / 2026
- Published online by Cambridge University Press:
- 30 June 2025, e6
- Print publication:
- 2026
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NON-LOG LIFTABLE LOG DEL PEZZO SURFACES OF RANK ONE IN CHARACTERISTIC FIVE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 259 / September 2025
- Published online by Cambridge University Press:
- 10 February 2025, pp. 399-422
- Print publication:
- September 2025
-
- Article
- Export citation
Positivity, plethysm and hyperbolicity of Siegel varieties in positive characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 17 June 2025, pp. 257-304
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The isotrivial case in the Mordell-Lang conjecture for semiabelian varieties defined over fields of positive characteristic
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 13 January 2025, pp. 461-476
- Print publication:
- June 2025
-
- Article
- Export citation
On the properness of the moduli space of stable surfaces over
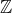 $\mathbb{Z}$[1/30]
$\mathbb{Z}$[1/30]
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bounding geometrically integral del Pezzo surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 14 October 2024, e81
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Bezrukavnikov–Kaledin quantization of symplectic varieties in characteristic p
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 05 January 2024, pp. 411-450
- Print publication:
- February 2024
-
- Article
- Export citation
THE MORDELL–LANG CONJECTURE FOR SEMIABELIAN VARIETIES DEFINED OVER FIELDS OF POSITIVE CHARACTERISTIC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 08 September 2023, pp. 254-264
- Print publication:
- April 2024
-
- Article
- Export citation
Zariski dense orbits for regular self-maps of split semiabelian varieties in positive characteristic
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 3 / November 2023
- Published online by Cambridge University Press:
- 02 May 2023, pp. 479-519
- Print publication:
- November 2023
-
- Article
- Export citation
Integration questions in separably good characteristics
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 890-932
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SEMIAMPLENESS FOR CALABI–YAU SURFACES IN POSITIVE AND MIXED CHARACTERISTIC
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 250 / June 2023
- Published online by Cambridge University Press:
- 28 November 2022, pp. 365-384
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
IWASAWA THEORY FOR p-TORSION CLASS GROUP SCHEMES IN CHARACTERISTIC p
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 250 / June 2023
- Published online by Cambridge University Press:
- 22 November 2022, pp. 298-351
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Torsion codimension
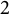 $2$ cycles on supersingular abelian varieties
$2$ cycles on supersingular abelian varieties
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 23 June 2022, pp. 458-466
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Curves of maximal moduli on K3 surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 08 June 2022, e36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Perfect points on curves of genus 1 and consequences for supersingular K3 surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 5 / May 2022
- Published online by Cambridge University Press:
- 22 July 2022, pp. 1052-1083
- Print publication:
- May 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Reductions of abelian surfaces over global function fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 4 / April 2022
- Published online by Cambridge University Press:
- 16 June 2022, pp. 893-950
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Kawamata–Viehweg vanishing theorem for log del Pezzo surfaces in positive characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 4 / April 2022
- Published online by Cambridge University Press:
- 13 June 2022, pp. 750-763
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Positivity of Hodge bundles of abelian varieties over some function fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 03 August 2021, pp. 1964-2000
- Print publication:
- September 2021
-
- Article
- Export citation
UNIRATIONALITY AND GEOMETRIC UNIRATIONALITY FOR HYPERSURFACES IN POSITIVE CHARACTERISTICS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 08 March 2021, pp. 1831-1847
- Print publication:
- September 2022
-
- Article
- Export citation