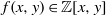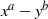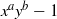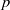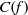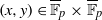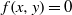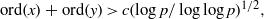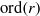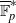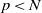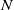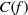Refine search
Actions for selected content:
27 results
LINEAR SYSTEMS OF GEOMETRICALLY IRREDUCIBLE PLANE CUBICS OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 27 February 2025, pp. 303-311
- Print publication:
- October 2025
-
- Article
- Export citation
SOME CASES OF OORT’S CONJECTURE ABOUT NEWTON POLYGONS OF CURVES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 257 / March 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 93-103
- Print publication:
- March 2025
-
- Article
- Export citation
TANGENT-FILLING PLANE CURVES OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 02 May 2023, pp. 301-315
- Print publication:
- April 2024
-
- Article
- Export citation
Nearly sharp Lang–Weil bounds for a hypersurface
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 18 October 2022, pp. 654-664
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SMOOTHNESS IN PENCILS OF HYPERSURFACES OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 25 August 2022, pp. 85-94
- Print publication:
- February 2023
-
- Article
- Export citation
Corrections to “Value sets of sparse polynomials”
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 02 November 2021, pp. 1071-1073
- Print publication:
- December 2022
-
- Article
- Export citation
Average-case complexity of the Euclidean algorithm with a fixed polynomial over a finite field
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 06 July 2021, pp. 166-183
-
- Article
- Export citation
CHARACTERISTIC POLYNOMIALS OF SIMPLE ORDINARY ABELIAN VARIETIES OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 19 February 2021, pp. 391-397
- Print publication:
- December 2021
-
- Article
- Export citation
ON SEMIGROUP ORBITS OF POLYNOMIALS AND MULTIPLICATIVE ORDERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 20 February 2020, pp. 365-373
- Print publication:
- December 2020
-
- Article
- Export citation
Value Sets of Sparse Polynomials
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 24 September 2019, pp. 187-196
- Print publication:
- March 2020
-
- Article
-
- You have access
- Export citation
TWISTED GALOIS STRATIFICATION
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 222 / Issue 1 / June 2016
- Published online by Cambridge University Press:
- 13 May 2016, pp. 1-60
- Print publication:
- June 2016
-
- Article
-
- You have access
- HTML
- Export citation
ON THE NUMBER OF RATIONAL POINTS ON PRYM VARIETIES OVER FINITE FIELDS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 55-68
- Print publication:
- January 2016
-
- Article
-
- You have access
- Export citation
La conjecture de Tate entière pour les cubiques de dimension quatre
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 2 / February 2015
- Published online by Cambridge University Press:
- 16 October 2014, pp. 253-264
- Print publication:
- February 2015
-
- Article
- Export citation
The Fixed Point Locus of the Verschiebung on ℳX(2, 0) for Genus-2 Curves X in Charateristic 2
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 2 / 14 June 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 439-448
- Print publication:
- 14 June 2014
-
- Article
-
- You have access
- Export citation
The Lang–Weil Estimate for Cubic Hypersurfaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 3 / 01 September 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 500-502
- Print publication:
- 01 September 2013
-
- Article
-
- You have access
- Export citation
On lower bounds for the Ihara constants
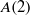 $A(2)$ and
$A(2)$ and 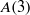 $A(3)$
$A(3)$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 7 / July 2013
- Published online by Cambridge University Press:
- 03 May 2013, pp. 1108-1128
- Print publication:
- July 2013
-
- Article
- Export citation
Automorphisms of Drinfeld half-spaces over a finite field
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 7 / July 2013
- Published online by Cambridge University Press:
- 26 April 2013, pp. 1211-1224
- Print publication:
- July 2013
-
- Article
- Export citation
Cycles de codimension 2 et H3 non ramifié pour les variétés sur les corps finis
-
- Journal:
- Journal of K-Theory / Volume 11 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 04 February 2013, pp. 1-53
- Print publication:
- February 2013
-
- Article
- Export citation
ELEMENTS OF LARGE ORDER IN PRIME FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 1 / August 2013
- Published online by Cambridge University Press:
- 16 October 2012, pp. 169-176
- Print publication:
- August 2013
-
- Article
-
- You have access
- Export citation
On the discrete logarithm problem in elliptic curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 15 October 2010, pp. 75-104
- Print publication:
- January 2011
-
- Article
-
- You have access
- Export citation





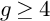
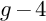
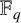
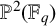
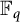
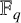
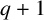
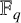
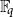
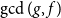
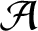
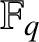
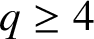
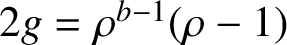
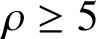
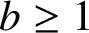
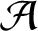
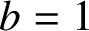
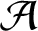
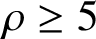
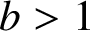
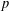
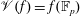
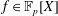
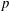
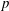
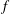
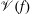
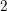
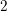

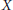

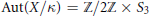
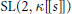
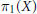
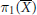
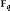
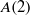
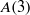
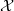
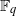
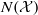
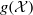
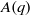
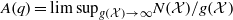
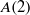
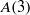
 . We discuss the unramified cohomology group
. We discuss the unramified cohomology group