Article contents
Average-case complexity of the Euclidean algorithm with a fixed polynomial over a finite field
Part of:
Arithmetic problems. Diophantine geometry
General field theory
Algorithms - Computer Science
Published online by Cambridge University Press: 06 July 2021
Abstract
We analyse the behaviour of the Euclidean algorithm applied to pairs (g,f) of univariate nonconstant polynomials over a finite field 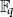 $\mathbb{F}_{q}$ of q elements when the highest degree polynomial g is fixed. Considering all the elements f of fixed degree, we establish asymptotically optimal bounds in terms of q for the number of elements f that are relatively prime with g and for the average degree of
$\mathbb{F}_{q}$ of q elements when the highest degree polynomial g is fixed. Considering all the elements f of fixed degree, we establish asymptotically optimal bounds in terms of q for the number of elements f that are relatively prime with g and for the average degree of 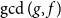 $\gcd(g,f)$. We also exhibit asymptotically optimal bounds for the average-case complexity of the Euclidean algorithm applied to pairs (g,f) as above.
$\gcd(g,f)$. We also exhibit asymptotically optimal bounds for the average-case complexity of the Euclidean algorithm applied to pairs (g,f) as above.
Keywords
MSC classification
Information
- Type
- Paper
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
Footnotes
†
The authors were partially supported by the grants PIP CONICET 11220130100598 and PIO CONICET-UNGS 14420140100027
References
Basu, S., Pollack, R. and Roy, M.-F. (2006) Algorithms in Real Algebraic Geometry, 2nd ed. Algorithms Comput. Math., Vol. 10, Springer.CrossRefGoogle Scholar
Berthé, V., Nakada, H., Natsui, R. and Vallée, B. (2014) Fine costs for Euclid’s algorithm on polynomials and Farey maps. Adv. Appl. Math. 54 27–65.CrossRefGoogle Scholar
Cafure, A. and Matera, G. (2006) Improved explicit estimates on the number of solutions of equations over a finite field. Finite Fields Appl. 12 155–185.CrossRefGoogle Scholar
Flajolet, P. and Sedgewick, R. (2009) Analytic Combinatorics. Cambridge University Press.CrossRefGoogle Scholar
von zur Gathen, J. and Gerhard, J. (1999) Modern Computer Algebra. Cambridge University Press.Google Scholar
Graham, R., Knuth, D. and Patashnik, O.(1994) Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Addison–Wesley.Google Scholar
Heintz, J. (1983) Definability and fast quantifier elimination in algebraically closed fields. Theoret. Comput. Sci. 24 239–277.CrossRefGoogle Scholar
Heydtmann, A. and Jensen, J. (2000) On the equivalence of the Berlekamp–Massey and the Euclidean algorithms for decoding. IEEE Trans. Inform. Theory 46 2614–2624.Google Scholar
Knuth, D. E. (1981) The Art of Computer Programming II: Semi–Numerical Algorithms, Vol. 2. Addison-Wesley.Google Scholar
Lascoux, A. (2003)
Symmetric Functions and Combinatorial Operators on Polynomials. CBMS Reg. Conf. Ser. Math., Vol. 99, American Mathematical Society.Google Scholar
Lhote, L. and Vallée, B. (2008) Gaussian laws for the main parameters of the Euclid algorithms. Algorithmica 50 497–554.CrossRefGoogle Scholar
Ma, K. and von zur Gathen, J. (1990) Analysis of Euclidean algorithms for polynomials over finite fields. J. Symb. Comput. 9 429–455.CrossRefGoogle Scholar
Norton, G. (1989) Precise analyses of the right- and left-shift greatest common divisor algorithms for GF(q)[x]. SIAM J. Comput. 18 608–624.CrossRefGoogle Scholar
- 1
- Cited by


