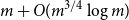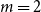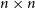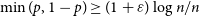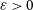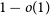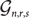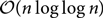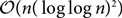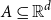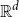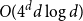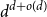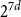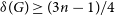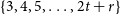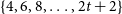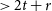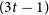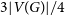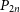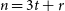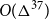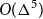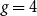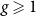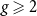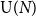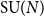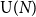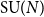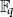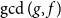Contents
Paper
Card guessing with partial feedback
- Part of:
-
- Published online by Cambridge University Press:
- 15 June 2021, pp. 1-20
-
- Article
- Export citation
Singularity of sparse random matrices: simple proofs
- Part of:
-
- Published online by Cambridge University Press:
- 15 June 2021, pp. 21-28
-
- Article
- Export citation
Spanning trees in random regular uniform hypergraphs
- Part of:
-
- Published online by Cambridge University Press:
- 26 May 2021, pp. 29-53
-
- Article
- Export citation
Concentration functions and entropy bounds for discrete log-concave distributions
- Part of:
-
- Published online by Cambridge University Press:
- 27 May 2021, pp. 54-72
-
- Article
- Export citation
The power of two choices for random walks
- Part of:
-
- Published online by Cambridge University Press:
- 28 May 2021, pp. 73-100
-
- Article
-
- You have access
- Open access
- Export citation
On convex holes in d-dimensional point sets
- Part of:
-
- Published online by Cambridge University Press:
- 18 June 2021, pp. 101-108
-
- Article
- Export citation
Monochromatic paths and cycles in 2-edge-coloured graphs with large minimum degree
- Part of:
-
- Published online by Cambridge University Press:
- 14 June 2021, pp. 109-122
-
- Article
- Export citation
Clustered 3-colouring graphs of bounded degree
- Part of:
-
- Published online by Cambridge University Press:
- 18 June 2021, pp. 123-135
-
- Article
- Export citation
Triangle-free subgraphs with large fractional chromatic number
- Part of:
-
- Published online by Cambridge University Press:
- 29 June 2021, pp. 136-143
-
- Article
- Export citation
Large N behaviour of the two-dimensional Yang–Mills partition function
- Part of:
-
- Published online by Cambridge University Press:
- 30 June 2021, pp. 144-165
-
- Article
- Export citation
Average-case complexity of the Euclidean algorithm with a fixed polynomial over a finite field
- Part of:
-
- Published online by Cambridge University Press:
- 06 July 2021, pp. 166-183
-
- Article
- Export citation