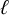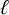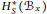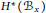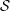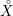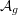Refine search
Actions for selected content:
25 results
On the formal Peterson subalgebra and its dual
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 07 August 2025, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Kappa classes on KSBA spaces
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Integral equivariant cohomology of affine Grassmannians
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 08 February 2024, pp. 727-741
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Noninjectivity of the cycle class map in continuous
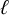 $\ell $-adic cohomology
$\ell $-adic cohomology
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 01 February 2023, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the cohomology of reciprocity sheaves
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 30 August 2022, e72
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Corrigendum to ‘Endoscopy for Hecke categories, character sheaves and representations’
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 9 / 2021
- Published online by Cambridge University Press:
- 30 November 2021, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ENDOSCOPY FOR HECKE CATEGORIES, CHARACTER SHEAVES AND REPRESENTATIONS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 28 May 2020, e12
-
- Article
-
- You have access
- Open access
- Export citation
Relative Equivariant Motives and Modules
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 08 November 2019, pp. 131-159
- Print publication:
- February 2021
-
- Article
- Export citation
PARABOLIC KAZHDAN–LUSZTIG BASIS, SCHUBERT CLASSES, AND EQUIVARIANT ORIENTED COHOMOLOGY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 11 February 2019, pp. 1889-1929
- Print publication:
- November 2020
-
- Article
- Export citation
On two cohomological Hall algebras
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 1581-1607
- Print publication:
- June 2020
-
- Article
- Export citation
SYMMETRIC OPERADS IN ABSTRACT SYMMETRIC SPECTRA
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 4 / July 2019
- Published online by Cambridge University Press:
- 25 May 2018, pp. 707-758
- Print publication:
- July 2019
-
- Article
- Export citation
RELATIVE CYCLES WITH MODULI AND REGULATOR MAPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 6 / November 2019
- Published online by Cambridge University Press:
- 02 November 2017, pp. 1233-1293
- Print publication:
- November 2019
-
- Article
- Export citation
Springer's Weyl Group Representation via Localization
-
- Journal:
- Canadian Mathematical Bulletin / Volume 60 / Issue 3 / 01 September 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 478-483
- Print publication:
- 01 September 2017
-
- Article
-
- You have access
- Export citation
Goresky–Pardon lifts of Chern classes and associated Tate extensions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 7 / July 2017
- Published online by Cambridge University Press:
- 03 May 2017, pp. 1349-1371
- Print publication:
- July 2017
-
- Article
- Export citation
An approach to intersection theory on singular varieties using motivic complexes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 11 / November 2016
- Published online by Cambridge University Press:
- 08 November 2016, pp. 2371-2404
- Print publication:
- November 2016
-
- Article
- Export citation
Perverse, Hodge and motivic realizations of étale motives
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 6 / June 2016
- Published online by Cambridge University Press:
- 26 February 2016, pp. 1237-1285
- Print publication:
- June 2016
-
- Article
- Export citation
Projectivity in Algebraic Cobordism
-
- Journal:
- Canadian Journal of Mathematics / Volume 67 / Issue 3 / 01 June 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 639-653
- Print publication:
- 01 June 2015
-
- Article
-
- You have access
- Export citation
Mixed motivic sheaves (and weights for them) exist if ‘ordinary’ mixed motives do
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 5 / May 2015
- Published online by Cambridge University Press:
- 09 January 2015, pp. 917-956
- Print publication:
- May 2015
-
- Article
- Export citation
KAROUBI’S RELATIVE CHERN CHARACTER, THE RIGID SYNTOMIC REGULATOR, AND THE BLOCH–KATO EXPONENTIAL MAP
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 20 August 2014, e20
-
- Article
-
- You have access
- Open access
- Export citation
ON THE FORMAL AFFINE HECKE ALGEBRA
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 4 / October 2015
- Published online by Cambridge University Press:
- 09 June 2014, pp. 837-855
- Print publication:
- October 2015
-
- Article
- Export citation

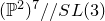
 .
.