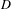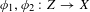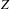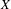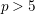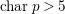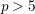Refine search
Actions for selected content:
15 results
Covering gonality of symmetric products of curves and Cayley–Bacharach condition on Grassmannians
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 January 2025, e13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A bound of the number of weighted blow-ups to compute the minimal log discrepancy for smooth 3-folds
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 08 March 2024, pp. 495-515
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Angehrn-Siu-Helmke’s method applied to abelian varieties
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 11 May 2023, e38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The existence of the Kähler–Ricci soliton degeneration
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 10 March 2023, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On birationally trivial families and adjoint quadrics
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 3 / August 2022
- Published online by Cambridge University Press:
- 04 July 2022, pp. 587-617
-
- Article
- Export citation
The construction problem for Hodge numbers modulo an integer in positive characteristic
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 09 November 2020, e45
-
- Article
-
- You have access
- Open access
- Export citation
INVARIANT HYPERSURFACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 17 August 2020, pp. 713-739
- Print publication:
- March 2022
-
- Article
- Export citation
Some remarks on the volume of log varieties
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 18 December 2019, pp. 314-322
-
- Article
- Export citation
FINITENESS OF LOG MINIMAL MODELS AND NEF CURVES ON
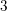 $3$-FOLDS IN CHARACTERISTIC
$3$-FOLDS IN CHARACTERISTIC 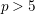 $p>5$
$p>5$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 239 / September 2020
- Published online by Cambridge University Press:
- 10 September 2018, pp. 76-109
- Print publication:
- September 2020
-
- Article
-
- You have access
- HTML
- Export citation
AFFINE GEOMETRY OF STRATA OF DIFFERENTIALS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 6 / November 2019
- Published online by Cambridge University Press:
- 26 October 2017, pp. 1331-1340
- Print publication:
- November 2019
-
- Article
- Export citation
b-Stability and Blow-Ups
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 57 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 23 December 2013, pp. 125-137
-
- Article
-
- You have access
- Export citation
Quantitative extensions of pluricanonical forms and closed positive currents
-
- Journal:
- Nagoya Mathematical Journal / Volume 205 / March 2012
- Published online by Cambridge University Press:
- 11 January 2016, pp. 25-65
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
Equivalences and stratified flops
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 09 November 2011, pp. 185-208
- Print publication:
- January 2012
-
- Article
-
- You have access
- Export citation
The Effective Cone of the Kontsevich Moduli Space
-
- Journal:
- Canadian Mathematical Bulletin / Volume 51 / Issue 4 / 01 December 2008
- Published online by Cambridge University Press:
- 20 November 2018, pp. 519-534
- Print publication:
- 01 December 2008
-
- Article
-
- You have access
- Export citation
The nef cone of toroidal compactifications of ${\cal A}_4$
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 88 / Issue 3 / May 2004
- Published online by Cambridge University Press:
- 14 April 2004, pp. 659-704
- Print publication:
- May 2004
-
- Article
- Export citation