Article contents
AFFINE GEOMETRY OF STRATA OF DIFFERENTIALS
Published online by Cambridge University Press: 26 October 2017
Abstract
Affine varieties among all algebraic varieties have simple structures. For example, an affine variety does not contain any complete algebraic curve. In this paper, we study affine-related properties of strata of 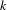 $k$-differentials on smooth curves which parameterize sections of the
$k$-differentials on smooth curves which parameterize sections of the 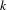 $k$th power of the canonical line bundle with prescribed orders of zeros and poles. We show that if there is a prescribed pole of order at least
$k$th power of the canonical line bundle with prescribed orders of zeros and poles. We show that if there is a prescribed pole of order at least 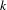 $k$, then the corresponding stratum does not contain any complete curve. Moreover, we explore the amusing question whether affine invariant manifolds arising from Teichmüller dynamics are affine varieties, and confirm the answer for Teichmüller curves, Hurwitz spaces of torus coverings, hyperelliptic strata as well as some low genus strata.
$k$, then the corresponding stratum does not contain any complete curve. Moreover, we explore the amusing question whether affine invariant manifolds arising from Teichmüller dynamics are affine varieties, and confirm the answer for Teichmüller curves, Hurwitz spaces of torus coverings, hyperelliptic strata as well as some low genus strata.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 18 , Issue 6 , November 2019 , pp. 1331 - 1340
- Copyright
- © Cambridge University Press 2017
Footnotes
The author is partially supported by NSF CAREER Award DMS-1350396.
References
- 7
- Cited by

