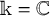Throughout this paper, we work over an algebraically closed field
![]() of characteristic
of characteristic
![]() $0$
.
$0$
.
1 Introduction
A Kähler–Einstein metric is arguably ‘the most canonical’ metric that one can find on a Fano variety. However, not every Fano variety admits a Kähler–Einstein metric. So it is natural to ask what kind of structure one should look for on a general Fano variety. In fact, there are several candidates. In this note, we will study one structure, namely the Kähler–Ricci soliton. This kind of metric has been investigated in many previous works. While not every Fano variety itself admits a Kähler–Ricci soliton, it is expected that any Fano variety has a unique degeneration to one with a Kähler–Ricci soliton (see, e.g., [Reference TianTia97, Section 9]).
For a smooth Fano manifold X, the approach of using Kähler–Ricci flow to study Kähler–Ricci solitons has been intensively studied in complex geometry literature and leads to the solution of the Hamilton–Tian conjecture (see [Reference Tian and ZhangTZ16, Reference BamlerBam18, Reference Chen and WangCW20]), which says that the Gromov–Hausdorff limit
![]() $X_{\infty }$
of X under the Kähler–Ricci flow admits a Kähler–Ricci soliton. What is more relevant to us is that in [Reference Chen, Sun and WangCSW18] it is shown that
$X_{\infty }$
of X under the Kähler–Ricci flow admits a Kähler–Ricci soliton. What is more relevant to us is that in [Reference Chen, Sun and WangCSW18] it is shown that
![]() $X_{\infty }$
can be realized as a (two-step) degeneration of X, and in [Reference Dervan and SzékelyhidiDS20] that the first degeneration minimizes the H-functional among all possible
$X_{\infty }$
can be realized as a (two-step) degeneration of X, and in [Reference Dervan and SzékelyhidiDS20] that the first degeneration minimizes the H-functional among all possible
![]() $\mathbb {R}$
-degenerations (note that our sign on H is opposite to the one in [Reference Dervan and SzékelyhidiDS20]).
$\mathbb {R}$
-degenerations (note that our sign on H is opposite to the one in [Reference Dervan and SzékelyhidiDS20]).
In this paper, we will pursue a purely algebraic study of the above degeneration process by studying the geometry of the minimizer of the non-Archimedean type functional
![]() $\mathbf {H}^{\mathrm {NA}}$
, which in particular can be applied to a general (possibly singular) log Fano pair
$\mathbf {H}^{\mathrm {NA}}$
, which in particular can be applied to a general (possibly singular) log Fano pair
![]() $(X,\Delta )$
. Such algebraic study, including developing the non-Archimedean theory of the
$(X,\Delta )$
. Such algebraic study, including developing the non-Archimedean theory of the
![]() $\mathbf {H}^{\mathrm {NA}}$
-functional, was initiated in [Reference Han and LiHL20b]. There it is shown the uniqueness of the above degeneration process. Our first main theorem of this paper is the existence of such a degeneration for general log Fano pairs. It can be considered to be an algebraic version of the Hamilton–Tian conjecture, though there is no metric involved. More precisely, we have the following result.
$\mathbf {H}^{\mathrm {NA}}$
-functional, was initiated in [Reference Han and LiHL20b]. There it is shown the uniqueness of the above degeneration process. Our first main theorem of this paper is the existence of such a degeneration for general log Fano pairs. It can be considered to be an algebraic version of the Hamilton–Tian conjecture, though there is no metric involved. More precisely, we have the following result.
Theorem 1.1. Let
![]() $(X,\Delta )$
be a log Fano pair. Then it admits a two-step degeneration to a K-polystable triple
$(X,\Delta )$
be a log Fano pair. Then it admits a two-step degeneration to a K-polystable triple
![]() $(Y,\Delta _Y,\xi _Y)$
, which is indeed reduced uniformly Ding stable. In particular, it admits a Kähler–Ricci soliton if
$(Y,\Delta _Y,\xi _Y)$
, which is indeed reduced uniformly Ding stable. In particular, it admits a Kähler–Ricci soliton if
![]() .
.
In the above theorem,
![]() $\xi _Y=0$
if and only if
$\xi _Y=0$
if and only if
![]() $(X,\Delta )$
is K-semistable. The proof of Theorem 1.1 will be separated into two parts, contained, respectively, in Theorems 1.2 and 1.3.
$(X,\Delta )$
is K-semistable. The proof of Theorem 1.1 will be separated into two parts, contained, respectively, in Theorems 1.2 and 1.3.
By [Reference Han and LiHL20b, Theorem 1.3], it is already known that any K-semistable triple
![]() $(X_0,\Delta _0,\xi )$
admits a unique K-polystable degeneration
$(X_0,\Delta _0,\xi )$
admits a unique K-polystable degeneration
![]() $(Y,\Delta _Y,\xi _Y)$
(whose proof is based on [Reference Li, Wang and XuLWX21]). Therefore, it suffices to establish the first-step degeneration which degenerates
$(Y,\Delta _Y,\xi _Y)$
(whose proof is based on [Reference Li, Wang and XuLWX21]). Therefore, it suffices to establish the first-step degeneration which degenerates
![]() $(X,\Delta )$
to a K-semistable triple
$(X,\Delta )$
to a K-semistable triple
![]() $(X_0,\Delta _0,\xi )$
. To construct such a degeneration, we follow [Reference Han and LiHL20b] and study the valuation which computes
$(X_0,\Delta _0,\xi )$
. To construct such a degeneration, we follow [Reference Han and LiHL20b] and study the valuation which computes
![]() $h(X,\Delta )$
(i.e., the minimizer of the
$h(X,\Delta )$
(i.e., the minimizer of the
![]() $\tilde {\beta }$
). As a result, we prove the following statement, which establishes the first half of Theorem 1.1 and gives an affirmative answer to [Reference Han and LiHL20b, Conjecture 4.10].
$\tilde {\beta }$
). As a result, we prove the following statement, which establishes the first half of Theorem 1.1 and gives an affirmative answer to [Reference Han and LiHL20b, Conjecture 4.10].
Theorem 1.2. Let
![]() $(X,\Delta )$
be a log Fano pair. Let r be a positive integer such that
$(X,\Delta )$
be a log Fano pair. Let r be a positive integer such that
![]() $r(K_X+\Delta )$
is Cartier. Then
$r(K_X+\Delta )$
is Cartier. Then
![]() $(X,\Delta )$
has a unique valuation v computing
$(X,\Delta )$
has a unique valuation v computing
![]() $h(X,\Delta )$
.
$h(X,\Delta )$
.
Moreover, the associated graded ring
![]() $\mathrm {gr}_v R$
for
$\mathrm {gr}_v R$
for
![]() $R=\bigoplus _{m\in \mathbb {N}} H^0(-mr(K_X+\Delta ))$
is finitely generated, whose
$R=\bigoplus _{m\in \mathbb {N}} H^0(-mr(K_X+\Delta ))$
is finitely generated, whose
![]() $\mathrm {Proj}$
together with the degeneration of
$\mathrm {Proj}$
together with the degeneration of
![]() $\Delta $
and the induced vector
$\Delta $
and the induced vector
![]() $\xi _v$
yields the first-step degeneration to a K-semistable triple
$\xi _v$
yields the first-step degeneration to a K-semistable triple
![]() $(X_0,\Delta _0,\xi _v)$
.
$(X_0,\Delta _0,\xi _v)$
.
It was shown in [Reference Han and LiHL20b] that the uniqueness statement in the above theorem follows from the finite generation of the
![]() $\mathrm {gr}_v R$
. In this note, we first establish stronger convexity results for various non-Archimedean functionals (see Theorem 3.7). Then we will obtain uniqueness as a consequence, without using finite generation.
$\mathrm {gr}_v R$
. In this note, we first establish stronger convexity results for various non-Archimedean functionals (see Theorem 3.7). Then we will obtain uniqueness as a consequence, without using finite generation.
The second step to proving Theorem 1.1 is to establish the following Yau–Tian–Donaldson (YTD) conjecture for Kähler–Ricci solitons.
Theorem 1.3 (YTD Conjecture for Kähler-Ricci Solitons).
A triple
![]() $(X,\Delta ,\xi )$
is K-polystable if and only if it is reduced uniformly Ding stable. In particular, when
$(X,\Delta ,\xi )$
is K-polystable if and only if it is reduced uniformly Ding stable. In particular, when
![]() ,
,
![]() $(X,\Delta ,\xi )$
admits a Kähler–Ricci soliton if and only if it is K-polystable.
$(X,\Delta ,\xi )$
admits a Kähler–Ricci soliton if and only if it is K-polystable.
In fact, in [Reference Han and LiHL20], it is proven that the reduced uniform Ding stability of
![]() $(X,\Delta ,\xi )$
is equivalent to the existence of a Kähler–Ricci soliton, by using variational methods. Here, we verify that reduced uniform Ding stability is equivalent to K-polystability. When X is smooth and
$(X,\Delta ,\xi )$
is equivalent to the existence of a Kähler–Ricci soliton, by using variational methods. Here, we verify that reduced uniform Ding stability is equivalent to K-polystability. When X is smooth and
![]() $\Delta =0$
, the second part of Theorem 1.3 is proved in [Reference Datar and SzékelyhidiDS16, Reference Chen, Sun and WangCSW18].
$\Delta =0$
, the second part of Theorem 1.3 is proved in [Reference Datar and SzékelyhidiDS16, Reference Chen, Sun and WangCSW18].
Remark 1.4. As we already mentioned, when X is smooth, the Cheeger–Colding–Tian theory can be used to establish Theorem 1.1, Theorem 1.2 and Theorem 1.3. In fact, one can obtain the optimal degeneration from the study of the Hamilton–Tian conjecture on the long time behavior of Kähler–Ricci flows on X. See [Reference Datar and SzékelyhidiDS16, Reference Tian and ZhangTZ16, Reference BamlerBam18, Reference Chen and WangCW20, Reference Chen, Sun and WangCSW18]. However, it seems to us it is hard to extend these types of arguments to the more general (possibly singular) case.
Recent work of Han and Li builds an algebraic framework for studying the two-step degeneration process. Specifically, in [Reference Han and LiHL20b], they developed the non-Archimedean theory for the
![]() $\mathbf {H}^{\mathrm {NA}}$
-functional (based on the H-function(al) defined in [Reference Tian, Zhang, Zhang and ZhuTZZZ13, Reference HeHe16]) and interpret the existence of the optimal degeneration, which is essentially equivalent to Theorem 1.2, in terms of geometric properties of the minimizer of the
$\mathbf {H}^{\mathrm {NA}}$
-functional (based on the H-function(al) defined in [Reference Tian, Zhang, Zhang and ZhuTZZZ13, Reference HeHe16]) and interpret the existence of the optimal degeneration, which is essentially equivalent to Theorem 1.2, in terms of geometric properties of the minimizer of the
![]() $\tilde {\beta }_{X,\Delta }$
-function, which is a variant of the
$\tilde {\beta }_{X,\Delta }$
-function, which is a variant of the
![]() $\mathbf {H}^{\mathrm {NA}}$
-functional but defined on
$\mathbf {H}^{\mathrm {NA}}$
-functional but defined on
![]() $\mathrm { Val}_X^{\circ }\cup \{v_{\mathrm {triv}}\}$
.
$\mathrm { Val}_X^{\circ }\cup \{v_{\mathrm {triv}}\}$
.
From the algebro-geometric viewpoint, the study of
![]() $\tilde {\beta }_{X,\Delta }$
in [Reference Han and LiHL20b] is entirely parallel to the study of the stability threshold of a log Fano pair or in the local setting the normalized volume function of a Kawamata log terminal (klt) singularity. Therefore, it is natural to apply the arguments in the former problems to the current case. Indeed, [Reference Han and LiHL20b] has made significant progress in carrying out this study, and the main remaining step is the finite generation of the graded ring induced by minimizers of various functions, for example,
$\tilde {\beta }_{X,\Delta }$
in [Reference Han and LiHL20b] is entirely parallel to the study of the stability threshold of a log Fano pair or in the local setting the normalized volume function of a Kawamata log terminal (klt) singularity. Therefore, it is natural to apply the arguments in the former problems to the current case. Indeed, [Reference Han and LiHL20b] has made significant progress in carrying out this study, and the main remaining step is the finite generation of the graded ring induced by minimizers of various functions, for example,
![]() $\tilde {\beta }_{X,\Delta }$
and
$\tilde {\beta }_{X,\Delta }$
and
![]() $\delta _g(X,\Delta ,\xi )$
.
$\delta _g(X,\Delta ,\xi )$
.
In [Reference Liu, Xu and ZhuangLXZ22], the finite generation of the associated graded ring for the valuation computing the stability threshold is solved. In this note, we solve the finite generation in Theorem 1.2 and Theorem 1.3 by a similar method. We also give a more straightforward argument of the uniqueness without using the finite generation (which is needed in [Reference Han and LiHL20b]) but by establishing convexity of various functionals based on the arguments in [Reference Xu and ZhuangXZ21].
We will also investigate a moduli approach to study general log Fano pairs with fixed h-invariant.
Theorem 1.5 (=Theorem 6.1).
For a fixed dimension n, volume V, a positive integer N and a constant
![]() $h_0$
, families of n-dimensional log Fano pairs
$h_0$
, families of n-dimensional log Fano pairs
![]() $(X,\Delta )$
with
$(X,\Delta )$
with
![]() $(-K_X-\Delta )^n=V$
,
$(-K_X-\Delta )^n=V$
,
![]() $N\Delta $
integral and
$N\Delta $
integral and
![]() $h(X,\Delta )\ge h_0$
are parameterized by an Artin stack
$h(X,\Delta )\ge h_0$
are parameterized by an Artin stack
![]() $\mathcal {M}^{\mathrm {Fano}}_{n,V,N,h^+_0}$
of finite type.
$\mathcal {M}^{\mathrm {Fano}}_{n,V,N,h^+_0}$
of finite type.
In the upcoming work, we aim to show that there is a finite type Artin stack
![]() $\mathcal {M}^{\mathrm { Kss}}_{n,V,N,h_0}$
which parametrizes families of n-dimensional K-semistable triples
$\mathcal {M}^{\mathrm { Kss}}_{n,V,N,h_0}$
which parametrizes families of n-dimensional K-semistable triples
![]() $(X,\Delta ,\xi )$
with
$(X,\Delta ,\xi )$
with
![]() $(-K_X-\Delta )^n=V$
,
$(-K_X-\Delta )^n=V$
,
![]() $N\Delta $
integral and
$N\Delta $
integral and
![]() $h(\xi )=h_0$
. Moreover,
$h(\xi )=h_0$
. Moreover,
![]() $\mathcal {M}^{\mathrm {Kss}}_{n,V,N,h_0}$
admits a proper good moduli space
$\mathcal {M}^{\mathrm {Kss}}_{n,V,N,h_0}$
admits a proper good moduli space
![]() ${M}^{\mathrm {Kps}}_{n,V,N,h_0}$
. Then we will study the two-step degeneration from a moduli theoretic viewpoint.
${M}^{\mathrm {Kps}}_{n,V,N,h_0}$
. Then we will study the two-step degeneration from a moduli theoretic viewpoint.
1.1 Outline of the proof
In recent years, there have been two functions on the space of valuations which have been intensively studied in algebraic geometry. The first one is the function
![]() $\frac {A_{X,\Delta }(\cdot )}{S(\cdot )}$
of a log Fano pair
$\frac {A_{X,\Delta }(\cdot )}{S(\cdot )}$
of a log Fano pair
![]() $(X,\Delta )$
, and the second one is the normalized volume function on a klt singularity
$(X,\Delta )$
, and the second one is the normalized volume function on a klt singularity
![]() $x\in (X,\Delta )$
. Many of their fundamental properties were proved in a sequence of works. The general framework for the proofs of the theorems in this paper is largely parallel to the previous works on the study of these two functions, especially the first one.
$x\in (X,\Delta )$
. Many of their fundamental properties were proved in a sequence of works. The general framework for the proofs of the theorems in this paper is largely parallel to the previous works on the study of these two functions, especially the first one.
Step 1: The first step is to show the strict convexity of the
![]() $\mathbf {H}^{\mathrm {NA}}$
-functional. For any pair of filtrations
$\mathbf {H}^{\mathrm {NA}}$
-functional. For any pair of filtrations
![]() ${\mathcal {F}}_0$
and
${\mathcal {F}}_0$
and
![]() ${\mathcal {F}}_1$
, there is a natural family
${\mathcal {F}}_1$
, there is a natural family
![]() $({\mathcal {F}}_t)_{t\in [0,1]}$
of filtrations connecting them called the geodesic (see Section 3.1.2). To study it, we define a measure
$({\mathcal {F}}_t)_{t\in [0,1]}$
of filtrations connecting them called the geodesic (see Section 3.1.2). To study it, we define a measure
![]() $\mathrm {DH}_{{\mathcal {F}}_0,{\mathcal {F}}_1}$
over
$\mathrm {DH}_{{\mathcal {F}}_0,{\mathcal {F}}_1}$
over
![]() $\mathbb {R}^2$
(called the compatible Duistermaat–Heckman measure) that encodes
$\mathbb {R}^2$
(called the compatible Duistermaat–Heckman measure) that encodes
![]() $\mathrm {DH}_{{\mathcal {F}}_t}$
for
$\mathrm {DH}_{{\mathcal {F}}_t}$
for
![]() $t\in [0,1]$
(see Section 3.1.3). Then convexity results for various functionals, for example,
$t\in [0,1]$
(see Section 3.1.3). Then convexity results for various functionals, for example,
![]() $\mathbf {E}^{\mathrm {NA}}$
and
$\mathbf {E}^{\mathrm {NA}}$
and
![]() $\widetilde {S}$
along geodesics can be proved by doing integration over this measure. And for
$\widetilde {S}$
along geodesics can be proved by doing integration over this measure. And for
![]() $\mathbf {L}^{\mathrm {NA}}$
, the convexity is proved by interpreting it as the log canonical slope
$\mathbf {L}^{\mathrm {NA}}$
, the convexity is proved by interpreting it as the log canonical slope
![]() $\mu $
and then applying results from [Reference Xu and ZhuangXZ21] to compare log canonical thresholds. As a result, this yields the convexity of
$\mu $
and then applying results from [Reference Xu and ZhuangXZ21] to compare log canonical thresholds. As a result, this yields the convexity of
![]() $\mathbf {D}^{\mathrm {NA}}$
and the strict convexity of
$\mathbf {D}^{\mathrm {NA}}$
and the strict convexity of
![]() $\mathbf {H}^{\mathrm {NA}}$
along geodesics (analogous results in the Archimedean setting were proved in [Reference BerndtssonBer15]). The latter will imply the uniqueness of the minimizer.
$\mathbf {H}^{\mathrm {NA}}$
along geodesics (analogous results in the Archimedean setting were proved in [Reference BerndtssonBer15]). The latter will imply the uniqueness of the minimizer.
Step 2: To prove Theorem 1.3, we will take a similar strategy to the solution of the usual YTD conjecture for log Fano pairs. First, we will extend the usual definition of the S-invariant function to the weighted setting with respect to a quasi-monomial valuation
![]() $v_0$
(see Section 4.1) and then we can define the corresponding
$v_0$
(see Section 4.1) and then we can define the corresponding
![]() $\delta (X,\Delta ,v_0)$
.
$\delta (X,\Delta ,v_0)$
.
We are first interested in the special case when
![]() $v_0$
is a valuation coming from a vector field
$v_0$
is a valuation coming from a vector field
![]() $\xi $
induced by a torus action. In this case, as seen in [Reference Han and LiHL20b], many criteria for testing the the K-semistability or (reduced) uniformly K-stability of a pair
$\xi $
induced by a torus action. In this case, as seen in [Reference Han and LiHL20b], many criteria for testing the the K-semistability or (reduced) uniformly K-stability of a pair
![]() $(X,\Delta )$
can be extended in to the setting of triples
$(X,\Delta )$
can be extended in to the setting of triples
![]() $(X,\Delta ,\xi )$
. In particular, we extend results from [Reference LiLi22] and [Reference Xu and ZhuangXZ20, Appendix] to this setting in Sections 4.2 and 4.3.
$(X,\Delta ,\xi )$
. In particular, we extend results from [Reference LiLi22] and [Reference Xu and ZhuangXZ20, Appendix] to this setting in Sections 4.2 and 4.3.
In a similar but slightly different setting, we consider the minimizer
![]() $v_0$
of the nonhomogeneous function
$v_0$
of the nonhomogeneous function
![]() $\tilde {\beta }_{X,\Delta }$
, and we show it computes
$\tilde {\beta }_{X,\Delta }$
, and we show it computes
![]() $\delta (X,\Delta ,v_0)$
for the weight function
$\delta (X,\Delta ,v_0)$
for the weight function
![]() $g=e^{-x}$
. See Section 5.1.
$g=e^{-x}$
. See Section 5.1.
Step 3: In the last step, we will show in the above two cases
![]() $v_0$
is a monomial log canonical (lc) place of a special
$v_0$
is a monomial log canonical (lc) place of a special
![]() $\mathbb {Q}$
-complement (in the sense of [Reference Liu, Xu and ZhuangLXZ22, Definition 3.3]) constructed from a weighted basis type divisor. Then we can apply the finite generation result in [Reference Liu, Xu and ZhuangLXZ22] to show the associated graded ring of
$\mathbb {Q}$
-complement (in the sense of [Reference Liu, Xu and ZhuangLXZ22, Definition 3.3]) constructed from a weighted basis type divisor. Then we can apply the finite generation result in [Reference Liu, Xu and ZhuangLXZ22] to show the associated graded ring of
![]() $v_0$
is finitely generated (see Corollary 5.7 and 5.8). This completes the proof of Theorem 1.2 and 1.3.
$v_0$
is finitely generated (see Corollary 5.7 and 5.8). This completes the proof of Theorem 1.2 and 1.3.
Finally, to prove Theorem 1.5, that is, to verify
![]() $\mathcal {M}^{\mathrm {Fano}}_{n,V,N,h^{+}_0}$
is an Artin stack of finite type, we first need to show that the set of all n-dimensional log Fano pairs
$\mathcal {M}^{\mathrm {Fano}}_{n,V,N,h^{+}_0}$
is an Artin stack of finite type, we first need to show that the set of all n-dimensional log Fano pairs
![]() $(X,\Delta )$
with
$(X,\Delta )$
with
![]() $(-K_X-\Delta )^n=V$
,
$(-K_X-\Delta )^n=V$
,
![]() $N\Delta $
integral and
$N\Delta $
integral and
![]() $h(X,\Delta )\ge h_0$
is bounded, and then we conclude by showing, for any
$h(X,\Delta )\ge h_0$
is bounded, and then we conclude by showing, for any
![]() $\mathbb {Q}$
-Gorenstein family of
$\mathbb {Q}$
-Gorenstein family of
![]() $(X,\Delta )\to B$
over a finite type base B, the function
$(X,\Delta )\to B$
over a finite type base B, the function
![]() $B\ni t \mapsto h(X_t, \Delta _t)$
is constructible and lower semicontinuous.
$B\ni t \mapsto h(X_t, \Delta _t)$
is constructible and lower semicontinuous.
2 Preliminaries
Notation and Conventions: We follow the standard notation as in [Reference Kollár and MoriKM98, Reference KollárKol13, Reference LazarsfeldLaz04].
A variety is a separated integral scheme of finite type over
![]() . A pair
. A pair
![]() $(X,\Delta )$
consists of a normal variety X and an effective
$(X,\Delta )$
consists of a normal variety X and an effective
![]() ${\mathbb {Q}}$
-divisor
${\mathbb {Q}}$
-divisor
![]() $\Delta $
on X such that
$\Delta $
on X such that
![]() $K_X+\Delta $
is
$K_X+\Delta $
is
![]() ${\mathbb {Q}}$
-Cartier. A pair
${\mathbb {Q}}$
-Cartier. A pair
![]() $(X,\Delta )$
is called log Fano if X is projective,
$(X,\Delta )$
is called log Fano if X is projective,
![]() $(X,\Delta )$
is klt and
$(X,\Delta )$
is klt and
![]() $-K_X-\Delta $
is ample. A log smooth model
$-K_X-\Delta $
is ample. A log smooth model
![]() $(Y,E)$
of a pair
$(Y,E)$
of a pair
![]() $(X,\Delta )$
consists of a projective birational morphism
$(X,\Delta )$
consists of a projective birational morphism
![]() $\pi \colon Y\to X$
and a reduced divisor E on Y such that
$\pi \colon Y\to X$
and a reduced divisor E on Y such that
![]() $(Y,\mathrm {Supp}(E+\mathrm {Ex}(\pi )+\pi _*^{-1}\Delta ))$
has simple normal crossing support.
$(Y,\mathrm {Supp}(E+\mathrm {Ex}(\pi )+\pi _*^{-1}\Delta ))$
has simple normal crossing support.
Let X be a normal variety. We denote by
![]() $\mathrm {Val}_X$
the space of real valuations
$\mathrm {Val}_X$
the space of real valuations
![]() $K(X)^{\times } \to \mathbb {R} $
centered on X whose restriction over the ground field
$K(X)^{\times } \to \mathbb {R} $
centered on X whose restriction over the ground field
![]() is trivial. We endow
is trivial. We endow
![]() $\mathrm { Val}_X$
with the weak topology. We denote the trivial valuation on X by
$\mathrm { Val}_X$
with the weak topology. We denote the trivial valuation on X by
![]() $v_{\mathrm {triv}}$
.
$v_{\mathrm {triv}}$
.
For the definitions of divisorial valuations, quasi-monomial valuations and log discrepancy of valuations; see, for example, [Reference Jonsson and MustaţăJM12, Reference Li, Liu and XuLLX20, Reference XuXu20].
Definition 2.1. Let
![]() $(X,\Delta )$
be a pair. We denote by
$(X,\Delta )$
be a pair. We denote by
If
![]() $(X, \Delta )$
admits a torus
$(X, \Delta )$
admits a torus
![]() $\mathbb {T}$
-action, then we denote by
$\mathbb {T}$
-action, then we denote by
![]() $\mathrm {Val}_X^{\mathbb {T}}$
the subset of
$\mathrm {Val}_X^{\mathbb {T}}$
the subset of
![]() $\mathrm {Val}_X$
consisting of all
$\mathrm {Val}_X$
consisting of all
![]() $\mathbb {T}$
-invariant valuations, and let
$\mathbb {T}$
-invariant valuations, and let
![]() $\mathrm { Val}_X^{\mathbb {T},\circ }:=\mathrm {Val}_X^{\circ }\cap \mathrm {Val}_X^{\mathbb {T}}$
.
$\mathrm { Val}_X^{\mathbb {T},\circ }:=\mathrm {Val}_X^{\circ }\cap \mathrm {Val}_X^{\mathbb {T}}$
.
2.1 Filtrations
Let
![]() $(X,\Delta )$
be an n-dimensional log Fano pair. Fix
$(X,\Delta )$
be an n-dimensional log Fano pair. Fix
![]() $r>0$
so that
$r>0$
so that
![]() $L:=-r(K_X+\Delta )$
is an ample Cartier divisor. We write
$L:=-r(K_X+\Delta )$
is an ample Cartier divisor. We write
for the section ring of L and
![]() $N_m := \dim R_m$
.
$N_m := \dim R_m$
.
Definition 2.2. A filtration
![]() ${\mathcal {F}}$
of R is a collection of vector subspaces
${\mathcal {F}}$
of R is a collection of vector subspaces
![]() ${\mathcal {F}}^{\lambda } R_m \subset R_m$
for each
${\mathcal {F}}^{\lambda } R_m \subset R_m$
for each
![]() $\lambda \in \mathbb {R}$
and
$\lambda \in \mathbb {R}$
and
![]() $m \in \mathbb {N}$
satisfying
$m \in \mathbb {N}$
satisfying
-
(F1)
 ${\mathcal {F}}^{\lambda } R_m \subset {\mathcal {F}}^{\lambda '} R_m$
for
${\mathcal {F}}^{\lambda } R_m \subset {\mathcal {F}}^{\lambda '} R_m$
for
 $\lambda \geq \lambda '$
;
$\lambda \geq \lambda '$
; -
(F2)
 ${\mathcal {F}}^{\lambda } R_m = \bigcap _{\lambda ' <\lambda } {\mathcal {F}}^{\lambda '} R_m$
;
${\mathcal {F}}^{\lambda } R_m = \bigcap _{\lambda ' <\lambda } {\mathcal {F}}^{\lambda '} R_m$
; -
(F3)
 ${\mathcal {F}}^{\lambda } R_m = R_m$
for
${\mathcal {F}}^{\lambda } R_m = R_m$
for
 $\lambda \ll 0$
and
$\lambda \ll 0$
and
 ${\mathcal {F}}^{\lambda } R_m=0$
for
${\mathcal {F}}^{\lambda } R_m=0$
for
 $\lambda \gg 0$
;
$\lambda \gg 0$
; -
(F4)
 ${\mathcal {F}}^{\lambda } R_m \cdot {\mathcal {F}}^{\lambda '} R_{m'} \subset {\mathcal {F}}^{\lambda +\lambda '} R_{m+m'}$
.
${\mathcal {F}}^{\lambda } R_m \cdot {\mathcal {F}}^{\lambda '} R_{m'} \subset {\mathcal {F}}^{\lambda +\lambda '} R_{m+m'}$
.
A filtration
![]() ${\mathcal {F}}$
is a
${\mathcal {F}}$
is a
![]() $\mathbb {Z}$
-filtration if
$\mathbb {Z}$
-filtration if
![]() ${\mathcal {F}}^{\lceil \lambda \rceil } R_m= {\mathcal {F}}^{\lambda } R_m$
for all
${\mathcal {F}}^{\lceil \lambda \rceil } R_m= {\mathcal {F}}^{\lambda } R_m$
for all
![]() $\lambda \in \mathbb {R}$
and
$\lambda \in \mathbb {R}$
and
![]() $m \in \mathbb {N}$
. A filtration is finitely generated if the associated graded
$m \in \mathbb {N}$
. A filtration is finitely generated if the associated graded
![]() -algebra
-algebra
![]() $\mathrm {gr}_{\mathcal {F}} R:=\bigoplus _{(m,\lambda ) \in \mathbb {N}\times \mathbb {R}} \mathrm { gr}_{{\mathcal {F}}}^{\lambda } R_m $
, where
$\mathrm {gr}_{\mathcal {F}} R:=\bigoplus _{(m,\lambda ) \in \mathbb {N}\times \mathbb {R}} \mathrm { gr}_{{\mathcal {F}}}^{\lambda } R_m $
, where
![]() $\mathrm {gr}_{{\mathcal {F}}}^{\lambda } R_m = {\mathcal {F}}^{\lambda } R_m / (\cup _{\mu> \lambda } {\mathcal {F}}^{\mu } R_m)$
, is finitely generated.
$\mathrm {gr}_{{\mathcal {F}}}^{\lambda } R_m = {\mathcal {F}}^{\lambda } R_m / (\cup _{\mu> \lambda } {\mathcal {F}}^{\mu } R_m)$
, is finitely generated.
The translation of
![]() ${\mathcal {F}}$
by
${\mathcal {F}}$
by
![]() $c\in \mathbb {R}$
is the filtration defined by
$c\in \mathbb {R}$
is the filtration defined by
![]() ${\mathcal {G}}^{\lambda } R_m : = {\mathcal {F}}^{\lambda -mrc} R_m$
. The scaling by
${\mathcal {G}}^{\lambda } R_m : = {\mathcal {F}}^{\lambda -mrc} R_m$
. The scaling by
![]() $a\in \mathbb {R}_{>0}$
is the filtration defined by
$a\in \mathbb {R}_{>0}$
is the filtration defined by
![]() $\mathcal {H}^{\lambda } R_m := {\mathcal {F}}^{\lambda /a}R_m$
.
$\mathcal {H}^{\lambda } R_m := {\mathcal {F}}^{\lambda /a}R_m$
.
A filtration
![]() ${\mathcal {F}}$
is linearly bounded if there exists
${\mathcal {F}}$
is linearly bounded if there exists
![]() $C>0$
so that
$C>0$
so that
![]() ${\mathcal {F}}^{mC} R_m =0$
for all
${\mathcal {F}}^{mC} R_m =0$
for all
![]() $m>0$
. Note that there always exists
$m>0$
. Note that there always exists
![]() $C>0$
so that
$C>0$
so that
![]() ${\mathcal {F}}^{-mC}R_m=R_m$
for all
${\mathcal {F}}^{-mC}R_m=R_m$
for all
![]() $m>0$
by the finite generation of R combined with (F3) and (F4).
$m>0$
by the finite generation of R combined with (F3) and (F4).
For an element
![]() $s\in R_m\setminus \{0\}$
, we set
$s\in R_m\setminus \{0\}$
, we set
![]() $\mathrm {ord}_{{\mathcal {F}}}(s): = \max \{ \lambda \in \mathbb {R} \, \vert \, s\in {\mathcal {F}}^{\lambda } R_m \} $
. We set
$\mathrm {ord}_{{\mathcal {F}}}(s): = \max \{ \lambda \in \mathbb {R} \, \vert \, s\in {\mathcal {F}}^{\lambda } R_m \} $
. We set
![]() $\mathrm {ord}_{{\mathcal {F}}}(0)=+\infty $
by convention. A basis
$\mathrm {ord}_{{\mathcal {F}}}(0)=+\infty $
by convention. A basis
![]() $(s_1,\ldots , s_{N_m})$
of
$(s_1,\ldots , s_{N_m})$
of
![]() $R_m$
is said to be compatible with
$R_m$
is said to be compatible with
![]() ${\mathcal {F}}$
if
${\mathcal {F}}$
if
![]() ${\mathcal {F}}^{\lambda } R_m = \mathrm {span} \langle s_j \, \vert \, \mathrm {ord}_{{\mathcal {F}}}(s_j) \geq \lambda \rangle $
for each
${\mathcal {F}}^{\lambda } R_m = \mathrm {span} \langle s_j \, \vert \, \mathrm {ord}_{{\mathcal {F}}}(s_j) \geq \lambda \rangle $
for each
![]() $\lambda \in \mathbb {R}$
.
$\lambda \in \mathbb {R}$
.
Example 2.1. The following filtrations play an important role in this paper.
-
1. Given
 $v\in \mathrm {Val}_X$
, there is an induced filtration
$v\in \mathrm {Val}_X$
, there is an induced filtration
 ${\mathcal {F}}_v$
of R defined by When
${\mathcal {F}}_v$
of R defined by When $$\begin{align*}{\mathcal{F}}_v^{\lambda} R_m : = {\{ s \in R_m \, \vert \, v(s) \geq \lambda \}}.\end{align*}$$
$$\begin{align*}{\mathcal{F}}_v^{\lambda} R_m : = {\{ s \in R_m \, \vert \, v(s) \geq \lambda \}}.\end{align*}$$
 $A_{X,\Delta }(v)<+\infty $
,
$A_{X,\Delta }(v)<+\infty $
,
 ${\mathcal {F}}_v$
is linearly bounded [Reference Blum and JonssonBJ20, Lemma 3.1].
${\mathcal {F}}_v$
is linearly bounded [Reference Blum and JonssonBJ20, Lemma 3.1].
-
2. Similarly, any effective
 ${\mathbb {Q}}$
-divisor G on X induces a filtration
${\mathbb {Q}}$
-divisor G on X induces a filtration
 ${\mathcal {F}}_G$
of R by setting
${\mathcal {F}}_G$
of R by setting  $$\begin{align*}{\mathcal{F}}_G^{\lambda} R_m := \{s\in R_m \, \vert \, \{s=0\}\geq \lambda G\}. \end{align*}$$
$$\begin{align*}{\mathcal{F}}_G^{\lambda} R_m := \{s\in R_m \, \vert \, \{s=0\}\geq \lambda G\}. \end{align*}$$
-
3. A test configuration
 $({\mathcal {X}},{\mathcal {L}})$
of
$({\mathcal {X}},{\mathcal {L}})$
of
 $(X,L)$
induces a finitely generated
$(X,L)$
induces a finitely generated
 $\mathbb {Z}$
-filtration of R. See [Reference Boucksom, Hisamoto and JonssonBHJ17, Section 2.5] for details.
$\mathbb {Z}$
-filtration of R. See [Reference Boucksom, Hisamoto and JonssonBHJ17, Section 2.5] for details.
2.1.1 Successive minima
Given a basis
![]() $(s_1,\ldots , s_{N_m})$
of
$(s_1,\ldots , s_{N_m})$
of
![]() $R_m$
compatible with
$R_m$
compatible with
![]() ${\mathcal {F}}$
, the numbers
${\mathcal {F}}$
, the numbers
are called the successive minima of
![]() ${\mathcal {F}}$
along R. Since
${\mathcal {F}}$
along R. Since
![]() $\frac {d}{d\lambda } \dim {\mathcal {F}}^{\lambda } R_m = -\sum _{j} \delta _{\lambda _j^{(m)}}$
the values
$\frac {d}{d\lambda } \dim {\mathcal {F}}^{\lambda } R_m = -\sum _{j} \delta _{\lambda _j^{(m)}}$
the values
![]() $(\lambda _j^{(m)})_j$
are independent of the choice of compatible basis up to reordering. We write
$(\lambda _j^{(m)})_j$
are independent of the choice of compatible basis up to reordering. We write
![]() $\lambda _{\max }^{(m)}= \max \{ \lambda \in \mathbb {R} \, \vert \, {\mathcal {F}}^{\lambda } R_m \neq 0 \}$
and set
$\lambda _{\max }^{(m)}= \max \{ \lambda \in \mathbb {R} \, \vert \, {\mathcal {F}}^{\lambda } R_m \neq 0 \}$
and set
![]() $\lambda _{\max } : = \sup _{m\geq 1} \frac {\lambda _{\max }^{(m)} }{mr}$
.
$\lambda _{\max } : = \sup _{m\geq 1} \frac {\lambda _{\max }^{(m)} }{mr}$
.
2.1.2 Graded linear series
A graded linear series
![]() $V_{\bullet }= (V_m)_{m \in \mathbb {N}}$
of L is a collection of vector subspaces
$V_{\bullet }= (V_m)_{m \in \mathbb {N}}$
of L is a collection of vector subspaces
![]() $V_m \subset R_m$
satisfying
$V_m \subset R_m$
satisfying
![]() $V_{m} \cdot V_{m'} \subset V_{m+m'}$
. The volume of
$V_{m} \cdot V_{m'} \subset V_{m+m'}$
. The volume of
![]() $V_{\bullet }$
is the value
$V_{\bullet }$
is the value
Given a filtration
![]() ${\mathcal {F}} $
of R and
${\mathcal {F}} $
of R and
![]() $s\in \mathbb {R}$
, we define a graded linear series
$s\in \mathbb {R}$
, we define a graded linear series
![]() $V_{\bullet }^{(s)} $
by setting
$V_{\bullet }^{(s)} $
by setting
![]() $V_{m}^{(s)} := {\mathcal {F}}^{mr s } R_m$
. When the choice of filtration is not clear from context, we will denote it by
$V_{m}^{(s)} := {\mathcal {F}}^{mr s } R_m$
. When the choice of filtration is not clear from context, we will denote it by
![]() $V_{\bullet }^{{\mathcal {F}},(s)}$
.
$V_{\bullet }^{{\mathcal {F}},(s)}$
.
The following result is a consequence of [Reference Boucksom and ChenBC11]. See [Reference Boucksom, Hisamoto and JonssonBHJ17, Theorem 5.2].
Proposition 2.3. Let
![]() ${\mathcal {F}}$
be a linearly bounded filtration of R.
${\mathcal {F}}$
be a linearly bounded filtration of R.
-
(i) For each
 $s< \lambda _{\max }$
,
$s< \lambda _{\max }$
,
 $\mathrm {vol}(V_{\bullet }^{(s)})$
is a limit.
$\mathrm {vol}(V_{\bullet }^{(s)})$
is a limit. -
(ii) The function
 $s\mapsto \mathrm {vol}(V_{\bullet } ^{(s)})^{1/n}$
is concave on
$s\mapsto \mathrm {vol}(V_{\bullet } ^{(s)})^{1/n}$
is concave on
 $(-\infty , \lambda _{\max })$
and vanishes on
$(-\infty , \lambda _{\max })$
and vanishes on
 $(\lambda _{\max }, \infty )$
(hence, it is continuous away from
$(\lambda _{\max }, \infty )$
(hence, it is continuous away from
 $s=\lambda _{\max }$
).
$s=\lambda _{\max }$
).
2.1.3 Base ideals
Given a linearly bounded filtration
![]() ${\mathcal {F}} $
of R, we set
${\mathcal {F}} $
of R, we set
which is the base ideal of the linear series
![]() ${\mathcal {F}}^{\lambda } R_m $
. Note that
${\mathcal {F}}^{\lambda } R_m $
. Note that
![]() $I_{m,\lambda } \cdot I_{m',\lambda '} \subset I_{m+m',\lambda +\lambda '}$
.
$I_{m,\lambda } \cdot I_{m',\lambda '} \subset I_{m+m',\lambda +\lambda '}$
.
For each
![]() $\lambda \in \mathbb {R}$
, we write
$\lambda \in \mathbb {R}$
, we write
![]() $I_{\bullet }^{(\lambda )}$
for the graded sequence of ideals on X defined by setting
$I_{\bullet }^{(\lambda )}$
for the graded sequence of ideals on X defined by setting
![]() $I_{m}^{(\lambda )}: = I_{m,\lambda mr}$
. For each
$I_{m}^{(\lambda )}: = I_{m,\lambda mr}$
. For each
![]() $m \in \mathbb {Z}_{>0}$
, we set
$m \in \mathbb {Z}_{>0}$
, we set
Note that
![]() $ t^{ \lceil \lambda _{\max }^{(m)} \rceil } \cdot {\mathcal {I}}_{m} \subset {\mathcal {O}}_{X_{ \mathbb {A}^1}}$
since
$ t^{ \lceil \lambda _{\max }^{(m)} \rceil } \cdot {\mathcal {I}}_{m} \subset {\mathcal {O}}_{X_{ \mathbb {A}^1}}$
since
![]() $I_{m,i}=0$
for
$I_{m,i}=0$
for
![]() $i> \lambda _{\max }^{(m)}$
. Therefore,
$i> \lambda _{\max }^{(m)}$
. Therefore,
![]() ${\mathcal {I}}_m$
is a fractional ideal on
${\mathcal {I}}_m$
is a fractional ideal on
![]() $X_{ \mathbb {A}^1} := X\times \mathbb {A}^1$
.
$X_{ \mathbb {A}^1} := X\times \mathbb {A}^1$
.
2.1.4 Duistermaat–Heckman measure
Given a linearly bounded filtration
![]() ${\mathcal {F}}$
of R and an integer
${\mathcal {F}}$
of R and an integer
![]() $m>0$
, we consider the probability measure on
$m>0$
, we consider the probability measure on
![]() $\mathbb {R}$
defined by
$\mathbb {R}$
defined by
 $$\begin{align*}\nu_m^{{\mathcal{F}}} : = \frac{1}{N_m} \sum _{i=1}^{N_m} \delta_{(mr)^{-1} \lambda_{i}^{(m)}} = - \frac{ d}{d \lambda} \frac{ \dim {\mathcal{F}}^{mr\lambda} R_m}{N_m}. \end{align*}$$
$$\begin{align*}\nu_m^{{\mathcal{F}}} : = \frac{1}{N_m} \sum _{i=1}^{N_m} \delta_{(mr)^{-1} \lambda_{i}^{(m)}} = - \frac{ d}{d \lambda} \frac{ \dim {\mathcal{F}}^{mr\lambda} R_m}{N_m}. \end{align*}$$
By [Reference Boucksom and ChenBC11] (see [Reference Boucksom, Hisamoto and JonssonBHJ17, §5.1]),
![]() $\nu _m^{\mathcal {F}}$
converges weakly as
$\nu _m^{\mathcal {F}}$
converges weakly as
![]() $m\to \infty $
to the probability measure
$m\to \infty $
to the probability measure
 $$\begin{align*}\mathrm{DH}_{\mathcal{F}} := - \frac{d}{d \lambda} \frac{ \mathrm{vol}( V_{\bullet}^{(\lambda)}) }{L^n}. \end{align*}$$
$$\begin{align*}\mathrm{DH}_{\mathcal{F}} := - \frac{d}{d \lambda} \frac{ \mathrm{vol}( V_{\bullet}^{(\lambda)}) }{L^n}. \end{align*}$$
The measure satisfies
![]() $\mathrm {supp}(\mathrm {DH}_{{\mathcal {F}}}) = [{\lambda }_{\min }, \lambda _{\max }]$
, where
$\mathrm {supp}(\mathrm {DH}_{{\mathcal {F}}}) = [{\lambda }_{\min }, \lambda _{\max }]$
, where
and
![]() $\lambda _{\max }$
is as defined previously.
$\lambda _{\max }$
is as defined previously.
The following statement is an extension of [Reference Boucksom, Hisamoto and JonssonBHJ17, Lemma 5.13] from divisorial valuations to valuations with finite log discrepancy.
Lemma 2.4. If
![]() $v\in \mathrm {Val}_{X}$
and
$v\in \mathrm {Val}_{X}$
and
![]() $A_{X,\Delta }(v)< +\infty $
, then
$A_{X,\Delta }(v)< +\infty $
, then
![]() ${\lambda }_{\min }({\mathcal {F}}_v)=0$
.
${\lambda }_{\min }({\mathcal {F}}_v)=0$
.
Proof. It is clear that
![]() $\lambda _{\min }({\mathcal {F}}_v)\geq 0$
since
$\lambda _{\min }({\mathcal {F}}_v)\geq 0$
since
![]() ${\mathcal {F}}_v^{\lambda } R =R$
for
${\mathcal {F}}_v^{\lambda } R =R$
for
![]() $\lambda \leq 0$
. For the reverse inequality, fix a log resolution
$\lambda \leq 0$
. For the reverse inequality, fix a log resolution
![]() $Y\to X$
of
$Y\to X$
of
![]() $(X,\Delta )$
and let
$(X,\Delta )$
and let
![]() $\xi :=c_{Y}(v)$
be the center of v on Y. Note that
$\xi :=c_{Y}(v)$
be the center of v on Y. Note that
![]() $ A_{Y,0}(v)$
is finite since
$ A_{Y,0}(v)$
is finite since
![]() $A_{X,\Delta }(v)<+\infty $
by assumption. An Izumi type inequality [Reference Jonsson and MustaţăJM12, Proposition 5.10] implies
$A_{X,\Delta }(v)<+\infty $
by assumption. An Izumi type inequality [Reference Jonsson and MustaţăJM12, Proposition 5.10] implies
where
![]() $c:= A_{Y,0}(v)>0$
, and, hence,
$c:= A_{Y,0}(v)>0$
, and, hence,
![]() $ {\mathcal {F}}_v^{\lambda } \subset {\mathcal {F}}_{c \cdot \mathrm { ord}_{\xi }}^{\lambda } R $
for all
$ {\mathcal {F}}_v^{\lambda } \subset {\mathcal {F}}_{c \cdot \mathrm { ord}_{\xi }}^{\lambda } R $
for all
![]() $\lambda \in \mathbb {R}$
. Therefore,
$\lambda \in \mathbb {R}$
. Therefore,
![]() $\lambda _{\min }({\mathcal {F}}_v) \leq \lambda _{\min }({\mathcal {F}}_{c \cdot \mathrm {ord}_{\xi }}) = 0$
, where the equality holds by [Reference Boucksom, Hisamoto and JonssonBHJ17, Lemma 5.13], since
$\lambda _{\min }({\mathcal {F}}_v) \leq \lambda _{\min }({\mathcal {F}}_{c \cdot \mathrm {ord}_{\xi }}) = 0$
, where the equality holds by [Reference Boucksom, Hisamoto and JonssonBHJ17, Lemma 5.13], since
![]() $c\cdot \mathrm { ord}_{\xi }$
is a divisorial valuation.
$c\cdot \mathrm { ord}_{\xi }$
is a divisorial valuation.
2.2 Non-Archimedean functionals
2.2.1 Energy functional
Following [Reference Boucksom, Hisamoto and JonssonBHJ17], the Monge–Ampère energy of
![]() ${\mathcal {F}}$
is given by
${\mathcal {F}}$
is given by
which is the barycenter of
![]() $\mathrm {DH}_{{\mathcal {F}}}$
. When
$\mathrm {DH}_{{\mathcal {F}}}$
. When
![]() ${\mathcal {F}}={\mathcal {F}}_v$
for a valuation
${\mathcal {F}}={\mathcal {F}}_v$
for a valuation
![]() $v\in \mathrm {Val}_X$
with
$v\in \mathrm {Val}_X$
with
![]() $A_{X,\Delta }(v)<\infty $
,
$A_{X,\Delta }(v)<\infty $
,
![]() $\mathbf {E}^{\mathrm {NA}}({\mathcal {F}}_v)=S(v)$
and
$\mathbf {E}^{\mathrm {NA}}({\mathcal {F}}_v)=S(v)$
and
![]() $\lambda _{\max }({\mathcal {F}}_v) = T(v)$
, where
$\lambda _{\max }({\mathcal {F}}_v) = T(v)$
, where
![]() $S(\cdot )$
and
$S(\cdot )$
and
![]() $T(\cdot )$
are the expected and maximal vanishing order appearing in [Reference Blum and JonssonBJ20].
$T(\cdot )$
are the expected and maximal vanishing order appearing in [Reference Blum and JonssonBJ20].
2.2.2 Ding-functional
The Ding invariant of a linearly bounded filtration
![]() ${\mathcal {F}}$
is defined by
${\mathcal {F}}$
is defined by
where
![]() $\mathbf {L}^{\mathrm {NA}}({\mathcal {F}}) = \lim _{m\to \infty } \mathrm { lct}(X_{\mathbb {A}^1},\Delta _{\mathbb {A}^1}, {\mathcal {I}}_{m}^{\frac {1}{mr}}; (t) )-1$
and
$\mathbf {L}^{\mathrm {NA}}({\mathcal {F}}) = \lim _{m\to \infty } \mathrm { lct}(X_{\mathbb {A}^1},\Delta _{\mathbb {A}^1}, {\mathcal {I}}_{m}^{\frac {1}{mr}}; (t) )-1$
and
This invariant was introduced in [Reference BermanBer16] for test configurations and [Reference Boucksom, Hisamoto and JonssonBHJ17, Reference FujitaFuj19] for general filtrations.
2.2.3
 $\mathbf {H}^{\mathrm {NA}}$
-functional
$\mathbf {H}^{\mathrm {NA}}$
-functional
Following [Reference Han and LiHL20b], for a linearly bounded filtration
![]() ${\mathcal {F}}$
we set
${\mathcal {F}}$
we set
where
![]() $\mathbf {L}^{\mathrm {NA}}({\mathcal {F}})$
is defined above and
$\mathbf {L}^{\mathrm {NA}}({\mathcal {F}})$
is defined above and
![]() $\widetilde {S}({\mathcal {F}}): = - \log \int _{\mathbb {R}} e^{- \lambda } \, \mathrm {DH}_{{\mathcal {F}}}(d \lambda )$
. This invariant was introduced in [Reference Tian, Zhang, Zhang and ZhuTZZZ13] for holomorphic vector fields and then extended to
$\widetilde {S}({\mathcal {F}}): = - \log \int _{\mathbb {R}} e^{- \lambda } \, \mathrm {DH}_{{\mathcal {F}}}(d \lambda )$
. This invariant was introduced in [Reference Tian, Zhang, Zhang and ZhuTZZZ13] for holomorphic vector fields and then extended to
![]() $\mathbb {R}$
-test configurations in [Reference Dervan and SzékelyhidiDS20] and linearly bounded filtrations in [Reference Han and LiHL20b]. We set
$\mathbb {R}$
-test configurations in [Reference Dervan and SzékelyhidiDS20] and linearly bounded filtrations in [Reference Han and LiHL20b]. We set
where the infimum runs through all linearly bounded filtrations of
![]() ${\mathcal {F}}$
. By [Reference Han and LiHL20b, Corollary 4.7],
${\mathcal {F}}$
. By [Reference Han and LiHL20b, Corollary 4.7],
![]() $h(X,\Delta )\leq 0$
and equality holds iff
$h(X,\Delta )\leq 0$
and equality holds iff
![]() $(X,\Delta )$
is K-semistable.
$(X,\Delta )$
is K-semistable.
For a valuation
![]() $v\in \mathrm {Val}_X^{\circ } \cup \{ v_{\mathrm {triv}} \}$
, we define
$v\in \mathrm {Val}_X^{\circ } \cup \{ v_{\mathrm {triv}} \}$
, we define
where
![]() $\widetilde {S}(v)=\widetilde {S}({\mathcal {F}}_v)$
. Note that
$\widetilde {S}(v)=\widetilde {S}({\mathcal {F}}_v)$
. Note that
![]() $\tilde {\beta }_{X,\Delta }(v_{\mathrm {triv}})=0$
. By [Reference Han and LiHL20b, Theorem 1.5],
$\tilde {\beta }_{X,\Delta }(v_{\mathrm {triv}})=0$
. By [Reference Han and LiHL20b, Theorem 1.5],
We say that
![]() $v\in \mathrm {Val}_X^{\circ }\cup \{v_{\mathrm {triv}}\}$
computes
$v\in \mathrm {Val}_X^{\circ }\cup \{v_{\mathrm {triv}}\}$
computes
![]() $h(X,\Delta )$
if it achieves the above infimum. By [Reference Han and LiHL20b, Theorem 4.9], there always exists a quasi-monomial valuation computing
$h(X,\Delta )$
if it achieves the above infimum. By [Reference Han and LiHL20b, Theorem 4.9], there always exists a quasi-monomial valuation computing
![]() $h(X,\Delta )$
.
$h(X,\Delta )$
.
3 Convexity and uniqueness
In this section, we will obtain the uniqueness of the valuation computing
![]() $h(X,\Delta )$
. In [Reference Han and LiHL20b], this was proved to follow from the finite generation, that is, Theorem 1.2. In this section, instead of using the finite generation, we will take the approach of establishing more general convexity results. In fact, for two filtrations
$h(X,\Delta )$
. In [Reference Han and LiHL20b], this was proved to follow from the finite generation, that is, Theorem 1.2. In this section, instead of using the finite generation, we will take the approach of establishing more general convexity results. In fact, for two filtrations
![]() ${\mathcal {F}}_0$
and
${\mathcal {F}}_0$
and
![]() ${\mathcal {F}}_1$
, we consider a segment in the space of filtrations
${\mathcal {F}}_1$
, we consider a segment in the space of filtrations
![]() $({\mathcal {F}}_t)_{t\in [0,1]}$
, which we call the geodesic between the two filtrations. We then introduce a probability measure on
$({\mathcal {F}}_t)_{t\in [0,1]}$
, which we call the geodesic between the two filtrations. We then introduce a probability measure on
![]() $\mathbb {R}^2$
that encodes
$\mathbb {R}^2$
that encodes
![]() $\mathrm {DH}_{{\mathcal {F}}_t}$
for
$\mathrm {DH}_{{\mathcal {F}}_t}$
for
![]() $t\in [0,1]$
. This will allow us to deduce the convexity of a number of functionals which take the form of integrating over the Duistermaat–Heckman measure (DH). For
$t\in [0,1]$
. This will allow us to deduce the convexity of a number of functionals which take the form of integrating over the Duistermaat–Heckman measure (DH). For
![]() $\mathbf {L}^{\mathrm {NA}}$
, the proof of its convexity uses the ideas from [Reference Xu and ZhuangXZ21] in the local setting.
$\mathbf {L}^{\mathrm {NA}}$
, the proof of its convexity uses the ideas from [Reference Xu and ZhuangXZ21] in the local setting.
Throughout,
![]() $(X,\Delta )$
is a log Fano pair,
$(X,\Delta )$
is a log Fano pair,
![]() $r>0$
a rational number so that
$r>0$
a rational number so that
![]() $L:=-r(K_X+\Delta )$
is a Cartier divisor, and
$L:=-r(K_X+\Delta )$
is a Cartier divisor, and
![]() $R:=R(X,L)$
.
$R:=R(X,L)$
.
3.1 Geodesics and DH measures
Fix two linearly bounded filtrations
![]() ${\mathcal {F}}_0$
and
${\mathcal {F}}_0$
and
![]() ${\mathcal {F}}_1$
of R. For each integer
${\mathcal {F}}_1$
of R. For each integer
![]() $m>0$
, choose a basis
$m>0$
, choose a basis
![]() $(s_1,\ldots , s_{N_m})$
of
$(s_1,\ldots , s_{N_m})$
of
![]() $R_m$
that is compatible with both
$R_m$
that is compatible with both
![]() ${\mathcal {F}}_0$
and
${\mathcal {F}}_0$
and
![]() ${\mathcal {F}}_1$
simultaneously; see [Reference Abban and ZhuangAZ22, Lemma 3.1] or [Reference Boucksom and ErikssonBE21, Proposition 1.14] for the existence of such a basis. For
${\mathcal {F}}_1$
simultaneously; see [Reference Abban and ZhuangAZ22, Lemma 3.1] or [Reference Boucksom and ErikssonBE21, Proposition 1.14] for the existence of such a basis. For
![]() $1\leq i \leq N_m$
, we set
$1\leq i \leq N_m$
, we set
The pairs
![]() $(\lambda _{i}^{0,(m)}, \lambda _{i}^{1,(m)})$
are unique up to reordering. For example, this follows from the observation that
$(\lambda _{i}^{0,(m)}, \lambda _{i}^{1,(m)})$
are unique up to reordering. For example, this follows from the observation that
![]() $-\frac {\partial ^2 }{\partial x \partial y} \dim ( {\mathcal {F}}_0^{x}R_m \cap {\mathcal {F}}_1^y R_m) = \sum _{i} \delta _{ \lambda _i^{0,(m)}, \lambda _{i}^{1,(m)}}$
. The above basis and notation will be used in the constructions below.
$-\frac {\partial ^2 }{\partial x \partial y} \dim ( {\mathcal {F}}_0^{x}R_m \cap {\mathcal {F}}_1^y R_m) = \sum _{i} \delta _{ \lambda _i^{0,(m)}, \lambda _{i}^{1,(m)}}$
. The above basis and notation will be used in the constructions below.
3.1.1 Relative limit measure
For each integer
![]() $m>0$
, we define a probability measure on
$m>0$
, we define a probability measure on
![]() $\mathbb {R}$
by
$\mathbb {R}$
by
 $$\begin{align*}\nu_m^{{\mathcal{F}}_0,{\mathcal{F}}_1} : = \frac{1}{N_m} \sum_{i=1}^{N_m} \delta_{(mr)^{-1} ( \lambda^{0,(m)}_{i} - \lambda^{1,(m)}_{i})} .\end{align*}$$
$$\begin{align*}\nu_m^{{\mathcal{F}}_0,{\mathcal{F}}_1} : = \frac{1}{N_m} \sum_{i=1}^{N_m} \delta_{(mr)^{-1} ( \lambda^{0,(m)}_{i} - \lambda^{1,(m)}_{i})} .\end{align*}$$
It was proven in [Reference Chen and MacleanCM15] that
![]() $\nu _m^{{\mathcal {F}}_0,{\mathcal {F}}_1} $
converges weakly as
$\nu _m^{{\mathcal {F}}_0,{\mathcal {F}}_1} $
converges weakly as
![]() $m\to \infty $
to a compactly supported probability measure that we denote by
$m\to \infty $
to a compactly supported probability measure that we denote by
![]() $\mathrm { RLM}_{{\mathcal {F}}_0,{\mathcal {F}}_1}$
. See [Reference Boucksom and JonssonBJ21, Theorem 3.3] for the statement and proof written in our setting.
$\mathrm { RLM}_{{\mathcal {F}}_0,{\mathcal {F}}_1}$
. See [Reference Boucksom and JonssonBJ21, Theorem 3.3] for the statement and proof written in our setting.
The
![]() $L^1$
-distance [Reference Boucksom and JonssonBJ21, Section 3.4] between
$L^1$
-distance [Reference Boucksom and JonssonBJ21, Section 3.4] between
![]() ${\mathcal {F}}_0$
and
${\mathcal {F}}_0$
and
![]() ${\mathcal {F}}_1$
is defined by
${\mathcal {F}}_1$
is defined by
We say
![]() ${\mathcal {F}}_0$
and
${\mathcal {F}}_0$
and
![]() ${\mathcal {F}}_1$
are equivalent if
${\mathcal {F}}_1$
are equivalent if
![]() $d_1({\mathcal {F}}_0,{\mathcal {F}}_1)=0$
.
$d_1({\mathcal {F}}_0,{\mathcal {F}}_1)=0$
.
Proposition 3.1 [Reference Boucksom and JonssonBJ21, Corollary 3.13].
If
![]() ${\mathcal {F}}_0$
and
${\mathcal {F}}_0$
and
![]() ${\mathcal {F}}_1$
are equivalent, then
${\mathcal {F}}_1$
are equivalent, then
![]() $\mathrm {DH}_{{\mathcal {F}}_0}= \mathrm { DH}_{{\mathcal {F}}_1}$
.
$\mathrm {DH}_{{\mathcal {F}}_0}= \mathrm { DH}_{{\mathcal {F}}_1}$
.
3.1.2 Geodesics
Let
![]() ${\mathcal {F}}_0 $
and
${\mathcal {F}}_0 $
and
![]() ${\mathcal {F}}_1 $
be linearly bounded filtrations of R. For
${\mathcal {F}}_1 $
be linearly bounded filtrations of R. For
![]() $t\in (0,1)$
, we define a filtration
$t\in (0,1)$
, we define a filtration
![]() ${\mathcal {F}}_t$
of R by setting
${\mathcal {F}}_t$
of R by setting
 $$ \begin{align} {\mathcal{F}}^{\lambda}_t R_m : = \sum_{\mu(1-t)+\nu t \ge \lambda} {\mathcal{F}}_0^{\mu} {\mathcal{F}}_m \cap {\mathcal{F}}_1^{\nu} R_m. \end{align} $$
$$ \begin{align} {\mathcal{F}}^{\lambda}_t R_m : = \sum_{\mu(1-t)+\nu t \ge \lambda} {\mathcal{F}}_0^{\mu} {\mathcal{F}}_m \cap {\mathcal{F}}_1^{\nu} R_m. \end{align} $$
It is straightforward to check that
![]() ${\mathcal {F}}_t $
is a filtration of R and is linearly bounded. We will call
${\mathcal {F}}_t $
is a filtration of R and is linearly bounded. We will call
![]() $({\mathcal {F}}_{t})_{t\in [0,1]}$
the geodesic connecting
$({\mathcal {F}}_{t})_{t\in [0,1]}$
the geodesic connecting
![]() ${\mathcal {F}}_0$
and
${\mathcal {F}}_0$
and
![]() ${\mathcal {F}}_1$
.
${\mathcal {F}}_1$
.
An alternative way to describe
![]() ${\mathcal {F}}_t$
is in terms of the basis
${\mathcal {F}}_t$
is in terms of the basis
![]() $(s_{1},\ldots , s_{N_m})$
of
$(s_{1},\ldots , s_{N_m})$
of
![]() $R_m$
fixed earlier. Indeed, since
$R_m$
fixed earlier. Indeed, since
![]() ${\mathcal {F}}_0^{\mu } R_m \cap {\mathcal {F}}_1^{\nu } R_m = \mathrm {span} \langle s_{i} \, \vert \, \lambda ^{0,(m)}_{i} \geq \mu \text { and } \lambda ^{1,(m)}_{i} \geq \nu \rangle $
, it follows that
${\mathcal {F}}_0^{\mu } R_m \cap {\mathcal {F}}_1^{\nu } R_m = \mathrm {span} \langle s_{i} \, \vert \, \lambda ^{0,(m)}_{i} \geq \mu \text { and } \lambda ^{1,(m)}_{i} \geq \nu \rangle $
, it follows that
Therefore, the basis
![]() $(s_{1},\ldots , s_{N_m})$
is compatible with
$(s_{1},\ldots , s_{N_m})$
is compatible with
![]() ${\mathcal {F}}_t$
and
${\mathcal {F}}_t$
and
![]() $\mathrm {ord}_{{\mathcal {F}}_t}(s_{i}) = (1-t) {\lambda }_{i}^{0,(m)} + t {\lambda }_{i}^{1,(m)}$
. As a consequence of this observation,
$\mathrm {ord}_{{\mathcal {F}}_t}(s_{i}) = (1-t) {\lambda }_{i}^{0,(m)} + t {\lambda }_{i}^{1,(m)}$
. As a consequence of this observation,
 $$ \begin{align} \nu_{m}^{{\mathcal{F}}_t} = \frac{1}{N_m} \sum_{i=1} \delta_{(mr)^{-1} ( \lambda^{0,(m)}_{i}(1-t) + \lambda^{1,(m)}_{i} t)}. \end{align} $$
$$ \begin{align} \nu_{m}^{{\mathcal{F}}_t} = \frac{1}{N_m} \sum_{i=1} \delta_{(mr)^{-1} ( \lambda^{0,(m)}_{i}(1-t) + \lambda^{1,(m)}_{i} t)}. \end{align} $$
In the following section, will analyze a measure on
![]() $\mathbb {R}^2$
that encodes equation (3.2) for each
$\mathbb {R}^2$
that encodes equation (3.2) for each
![]() $t\in [0,1]$
.
$t\in [0,1]$
.
Remark 3.2. In the language of graded norms, the definition of
![]() $({\mathcal {F}}_t)_{t\in [0,1]}$
appears in the work of Reboulet in a more general setting and plays a key role in his theory of geodesics in the space of non-Archimedean metrics on a line bundle [Reference RebouletReb22].
$({\mathcal {F}}_t)_{t\in [0,1]}$
appears in the work of Reboulet in a more general setting and plays a key role in his theory of geodesics in the space of non-Archimedean metrics on a line bundle [Reference RebouletReb22].
3.1.3 Duistermaat—Heckman measures
For each
![]() $m>0$
, we consider the probability measure on
$m>0$
, we consider the probability measure on
![]() $\mathbb {R}^2$
defined by
$\mathbb {R}^2$
defined by
 $$\begin{align*}\boldsymbol{\nu}_m: = \frac{1}{N_m} \sum_{i=1}^{N_m}\delta_{ ( (mr)^{-1}\lambda^{0,(m)}_{i} , (mr)^{-1}\lambda^{1,(m)}_{i} )} = \frac{ \partial^2}{ \partial x \partial y } \frac{ \dim ({\mathcal{F}}_0^{mrx} R_m \cap {\mathcal{F}}_1^{mry} R_m)}{N_m}. \end{align*}$$
$$\begin{align*}\boldsymbol{\nu}_m: = \frac{1}{N_m} \sum_{i=1}^{N_m}\delta_{ ( (mr)^{-1}\lambda^{0,(m)}_{i} , (mr)^{-1}\lambda^{1,(m)}_{i} )} = \frac{ \partial^2}{ \partial x \partial y } \frac{ \dim ({\mathcal{F}}_0^{mrx} R_m \cap {\mathcal{F}}_1^{mry} R_m)}{N_m}. \end{align*}$$
Since
![]() ${\mathcal {F}}_0$
and
${\mathcal {F}}_0$
and
![]() ${\mathcal {F}}_1$
are assumed to be linearly bounded, we may fix
${\mathcal {F}}_1$
are assumed to be linearly bounded, we may fix
![]() $C>0$
so that
$C>0$
so that
![]() ${\mathcal {F}}_i^{Cmr}R_m = 0$
and
${\mathcal {F}}_i^{Cmr}R_m = 0$
and
![]() ${\mathcal {F}}_i^{-Cmr} R_m = R_m$
for both
${\mathcal {F}}_i^{-Cmr} R_m = R_m$
for both
![]() $i=0,1$
. Hence,
$i=0,1$
. Hence,
![]() $\mathrm {supp}(\boldsymbol {\nu }_m)$
is contained in the bounded set
$\mathrm {supp}(\boldsymbol {\nu }_m)$
is contained in the bounded set
![]() $[-C,C]\times [-C,C]$
.
$[-C,C]\times [-C,C]$
.
Theorem 3.3. The sequence
![]() $\boldsymbol {\nu }_m$
converges weakly as
$\boldsymbol {\nu }_m$
converges weakly as
![]() $m\to \infty $
to the compactly supported probability measure
$m\to \infty $
to the compactly supported probability measure
 $$\begin{align*}\mathrm{DH}_{{\mathcal{F}}_0,{\mathcal{F}}_1}:= \frac{ \partial^2}{ \partial x \partial y} \frac{ \mathrm{vol} (W_{\bullet}^{(x,y)})}{L^n}, \end{align*}$$
$$\begin{align*}\mathrm{DH}_{{\mathcal{F}}_0,{\mathcal{F}}_1}:= \frac{ \partial^2}{ \partial x \partial y} \frac{ \mathrm{vol} (W_{\bullet}^{(x,y)})}{L^n}, \end{align*}$$
where
![]() $W_{\bullet }^{(x,y)}$
is the graded linear series defined by
$W_{\bullet }^{(x,y)}$
is the graded linear series defined by
![]() $W_{m}^{(x,y)} = {\mathcal {F}}_0^{mrx} R_m \cap {\mathcal {F}}_1^{mry} R_m$
.
$W_{m}^{(x,y)} = {\mathcal {F}}_0^{mrx} R_m \cap {\mathcal {F}}_1^{mry} R_m$
.
We will call
![]() $\mathrm {DH}_{{\mathcal {F}}_0,{\mathcal {F}}_1}$
the compatible DH measure of the two filtrations. The use of the measure is that it encodes
$\mathrm {DH}_{{\mathcal {F}}_0,{\mathcal {F}}_1}$
the compatible DH measure of the two filtrations. The use of the measure is that it encodes
![]() $\mathrm {DH}_{{\mathcal {F}}_t}$
for
$\mathrm {DH}_{{\mathcal {F}}_t}$
for
![]() $t\in [0,1]$
, as well as
$t\in [0,1]$
, as well as
![]() $\mathrm {RLM}_{{\mathcal {F}}_0,{\mathcal {F}}_1}$
(see Proposition 3.6).
$\mathrm {RLM}_{{\mathcal {F}}_0,{\mathcal {F}}_1}$
(see Proposition 3.6).
To prove Theorem 3.3, we analyze the following functions
![]() $\mathbb {R}^2\to [0,1]$
that are nonincreasing in both variables:
$\mathbb {R}^2\to [0,1]$
that are nonincreasing in both variables:
 $$\begin{align*}f_m(x,y) = \frac{\dim ( W_{m}^{(x,y)} )} {N_m} \quad \text{ and } \quad f(x,y) :=\limsup_{m\to \infty} f_m(x,y)= \frac{\mathrm{vol}(W_{\bullet}^{(x,y)})}{(L^n)}, \end{align*}$$
$$\begin{align*}f_m(x,y) = \frac{\dim ( W_{m}^{(x,y)} )} {N_m} \quad \text{ and } \quad f(x,y) :=\limsup_{m\to \infty} f_m(x,y)= \frac{\mathrm{vol}(W_{\bullet}^{(x,y)})}{(L^n)}, \end{align*}$$
as well as the locus
![]() $P = \overline {\bigcup _{m\geq 1} P_m}$
where
$P = \overline {\bigcup _{m\geq 1} P_m}$
where
![]() $P_{m} = \mathrm {Supp}(f_m)$
.
$P_{m} = \mathrm {Supp}(f_m)$
.
Proposition 3.4. The set P is convex and
![]() $\mathrm {Int}(P) = \cup _m \mathrm {Int}(P_m)$
$\mathrm {Int}(P) = \cup _m \mathrm {Int}(P_m)$
Proof. Using property (F4) of a filtration, it follows that
Indeed, if
![]() $(x,y) \in c m P_{m}$
and
$(x,y) \in c m P_{m}$
and
![]() $(x',y') \in d q P_{q}$
, then there exist nonzero sections
$(x',y') \in d q P_{q}$
, then there exist nonzero sections
Hence,
which implies
![]() $(x+x',y+y') \in ( mc+qd) P_{mc+qd}$
as desired. Now, equation (3.3) implies: if
$(x+x',y+y') \in ( mc+qd) P_{mc+qd}$
as desired. Now, equation (3.3) implies: if
![]() $p,q \in \cup _m P_m$
and
$p,q \in \cup _m P_m$
and
![]() $t\in [0,1]\cap \mathbb {Q}$
, then
$t\in [0,1]\cap \mathbb {Q}$
, then
![]() $p(1-t)+tq \in \cup _m P_m$
. Therefore, the closure of
$p(1-t)+tq \in \cup _m P_m$
. Therefore, the closure of
![]() $\cup _{m} P_m$
is convex.
$\cup _{m} P_m$
is convex.
To show
![]() $\mathrm {Int}(P) = \cup _m \mathrm {Int}(P_m)$
, first note that the inclusion
$\mathrm {Int}(P) = \cup _m \mathrm {Int}(P_m)$
, first note that the inclusion
![]() $\supset $
clearly holds. To see
$\supset $
clearly holds. To see
![]() $\subset $
holds, fix
$\subset $
holds, fix
![]() $(a,b) \in \mathrm {Int}(P)$
. Since
$(a,b) \in \mathrm {Int}(P)$
. Since
![]() $\mathrm {Int}(P)$
is open, we may choose
$\mathrm {Int}(P)$
is open, we may choose
![]() $\epsilon>0$
so that
$\epsilon>0$
so that
![]() $(a+\epsilon , b+\epsilon ) \in \mathrm {Int}(P)$
. Since P is the closure of
$(a+\epsilon , b+\epsilon ) \in \mathrm {Int}(P)$
. Since P is the closure of
![]() $\cup _m P_m$
and
$\cup _m P_m$
and
![]() $(a+\epsilon ,b+\epsilon ) \in P$
, there exists
$(a+\epsilon ,b+\epsilon ) \in P$
, there exists
![]() $(x,y) \in \cup _m P_m$
so that
$(x,y) \in \cup _m P_m$
so that
![]() $ a<x$
and
$ a<x$
and
![]() $b<y$
. Using that each
$b<y$
. Using that each
![]() $f_m$
is
$f_m$
is
![]() $\geq 0$
and nonincreasing in both variables, the latter implies
$\geq 0$
and nonincreasing in both variables, the latter implies
![]() $(a,b) \in \cup _m \mathrm {Int}(P_m)$
as desired.
$(a,b) \in \cup _m \mathrm {Int}(P_m)$
as desired.
Proposition 3.5. On the locus
![]() $\mathbb {R}^2 \setminus \partial P$
,
$\mathbb {R}^2 \setminus \partial P$
,
![]() $f=\lim _{m\to \infty } f_m$
and f is continuous.
$f=\lim _{m\to \infty } f_m$
and f is continuous.
Proof. The statement clearly holds on
![]() $\mathbb {R}^2 \setminus P$
since
$\mathbb {R}^2 \setminus P$
since
![]() $f_m$
and f are both zero on that locus. It remains to verify the statement on
$f_m$
and f are both zero on that locus. It remains to verify the statement on
![]() $\mathrm {Int}(P)$
.
$\mathrm {Int}(P)$
.
Fix
![]() $(a,b) \in \mathrm {Int}(P)$
. Let
$(a,b) \in \mathrm {Int}(P)$
. Let
![]() ${\mathcal {G}}$
denote the filtration of R defined by
${\mathcal {G}}$
denote the filtration of R defined by
which is linearly bounded since both
![]() ${\mathcal {F}}_0$
and
${\mathcal {F}}_0$
and
![]() ${\mathcal {F}}_1$
are linearly bounded. Let
${\mathcal {F}}_1$
are linearly bounded. Let
![]() $ V_m^{{\mathcal {G}},(t)}$
and
$ V_m^{{\mathcal {G}},(t)}$
and
![]() $V_{\bullet }^{{\mathcal {G}},(t)}$
be defined as in Section 2.1.2. If we set
$V_{\bullet }^{{\mathcal {G}},(t)}$
be defined as in Section 2.1.2. If we set
 $$\begin{align*}g_m(t) =\frac{ \dim V_m^{{\mathcal{G}},(t)}}{ N_m} \quad \text{ and } \quad g(t)= \limsup_{m\to \infty }\frac{ \mathrm{vol}( V_{\bullet}^{{\mathcal{G}},(t)})}{(L^n)} ,\end{align*}$$
$$\begin{align*}g_m(t) =\frac{ \dim V_m^{{\mathcal{G}},(t)}}{ N_m} \quad \text{ and } \quad g(t)= \limsup_{m\to \infty }\frac{ \mathrm{vol}( V_{\bullet}^{{\mathcal{G}},(t)})}{(L^n)} ,\end{align*}$$
then
![]() $g_m(t) = f_m(a+t,b+t)$
and
$g_m(t) = f_m(a+t,b+t)$
and
![]() $g(t) = f(a+t,b+t)$
since
$g(t) = f(a+t,b+t)$
since
![]() $V_{m}^{{\mathcal {G}},(t)}= W_m^{(a+t,b+t)}$
. Note that, for
$V_{m}^{{\mathcal {G}},(t)}= W_m^{(a+t,b+t)}$
. Note that, for
![]() $t< \lambda _{\max }({\mathcal {G}})$
,
$t< \lambda _{\max }({\mathcal {G}})$
,
![]() $g(t)=\lim _{m\to \infty } g_m(t)$
exists and g is continuous at t by Proposition 2.3.
$g(t)=\lim _{m\to \infty } g_m(t)$
exists and g is continuous at t by Proposition 2.3.
We claim that
![]() $\lambda _{\max }({\mathcal {G}})>0$
. Indeed, using that
$\lambda _{\max }({\mathcal {G}})>0$
. Indeed, using that
![]() $g_m(t) = f_m(a+t,b+t)$
, we see
$g_m(t) = f_m(a+t,b+t)$
, we see
Since
![]() $(a,b) \in \mathrm {Int}(P)$
, Proposition 3.4 implies there exists
$(a,b) \in \mathrm {Int}(P)$
, Proposition 3.4 implies there exists
![]() $m'>0$
so that
$m'>0$
so that
![]() $(a,b) \in \mathrm {Int}(P_{m'})$
. Therefore,
$(a,b) \in \mathrm {Int}(P_{m'})$
. Therefore,
![]() $\lambda _{\max }^{(m')}({\mathcal {G}})>0$
and, hence,
$\lambda _{\max }^{(m')}({\mathcal {G}})>0$
and, hence,
![]() $\lambda _{\max }({\mathcal {G}})>0$
as desired.
$\lambda _{\max }({\mathcal {G}})>0$
as desired.
Using the above claim, we see that
![]() $\lim _{m\to \infty } f_m(a,b)=f(a,b)$
, and
$\lim _{m\to \infty } f_m(a,b)=f(a,b)$
, and
![]() $f(a+t, b+t)$
is continuous at
$f(a+t, b+t)$
is continuous at
![]() $t=0$
. Since f is nonincreasing in both variables, the latter implies that f is continuous at
$t=0$
. Since f is nonincreasing in both variables, the latter implies that f is continuous at
![]() $(a,b)$
.
$(a,b)$
.
Theorem 3.3 is now an easy consequence of the previous propositions.
Proof of Theorem 3.3.
As
![]() $m\to \infty $
,
$m\to \infty $
,
![]() $f_m$
converge pointwise to f away from a set of measure zero by by Propositions 3.4 and 3.5. Since
$f_m$
converge pointwise to f away from a set of measure zero by by Propositions 3.4 and 3.5. Since
![]() $0\leq f_m \leq 1$
, the dominated converges theorem implies
$0\leq f_m \leq 1$
, the dominated converges theorem implies
![]() $f_m \to f$
in
$f_m \to f$
in
![]() $L_{\mathrm {loc}}^{1}(\mathbb {R}^2)$
. Therefore,
$L_{\mathrm {loc}}^{1}(\mathbb {R}^2)$
. Therefore,
![]() $f_m\to f$
as distributions and, hence,
$f_m\to f$
as distributions and, hence,
![]() $\boldsymbol {\nu }_m=\frac {\partial ^2}{\partial x \partial y} f_m \to \frac {\partial ^2}{ \partial x \, \partial y} f$
as distributions, as well. Since each distribution
$\boldsymbol {\nu }_m=\frac {\partial ^2}{\partial x \partial y} f_m \to \frac {\partial ^2}{ \partial x \, \partial y} f$
as distributions, as well. Since each distribution
![]() $\boldsymbol {\nu }_m$
is a measure, [Reference HörmanderHor03, Theorem 2.1.9] implies
$\boldsymbol {\nu }_m$
is a measure, [Reference HörmanderHor03, Theorem 2.1.9] implies
![]() $\mathrm {DH}_{{\mathcal {F}}_0,{\mathcal {F}}_1}:=\frac {\partial ^2}{ \partial x \, \partial y} f$
is a measure and
$\mathrm {DH}_{{\mathcal {F}}_0,{\mathcal {F}}_1}:=\frac {\partial ^2}{ \partial x \, \partial y} f$
is a measure and
![]() $\boldsymbol {\nu }_m \overset {\mathrm {weak}}{\longrightarrow }\mathrm {DH}_{{\mathcal {F}}_0,{\mathcal {F}}_1}$
as measures. Furthermore, the measure
$\boldsymbol {\nu }_m \overset {\mathrm {weak}}{\longrightarrow }\mathrm {DH}_{{\mathcal {F}}_0,{\mathcal {F}}_1}$
as measures. Furthermore, the measure
![]() $\mathrm {DH}_{{\mathcal {F}}_0,{\mathcal {F}}_1}$
is a compactly supported probability measure since it is a weak limit of probability measures with uniformly bounded support.
$\mathrm {DH}_{{\mathcal {F}}_0,{\mathcal {F}}_1}$
is a compactly supported probability measure since it is a weak limit of probability measures with uniformly bounded support.
Proposition 3.6. Fix
![]() $t\in [0,1]$
,
$t\in [0,1]$
,
![]() $c\in \mathbb {R}_{>0}$
, and
$c\in \mathbb {R}_{>0}$
, and
![]() $d\in \mathbb {R}$
. Consider the maps
$d\in \mathbb {R}$
. Consider the maps
![]() $p,q:\mathbb {R}^2 \to \mathbb {R}$
defined by
$p,q:\mathbb {R}^2 \to \mathbb {R}$
defined by
![]() $p(x,y)= (1-t)x+ty$
and
$p(x,y)= (1-t)x+ty$
and
![]() $q(x,y) = x-c(y+d)$
. The following hold:
$q(x,y) = x-c(y+d)$
. The following hold:
-
1.
 $p_*(\mathrm {DH}_{{\mathcal {F}}_0,{\mathcal {F}}_1}) = \mathrm {DH}_{{\mathcal {F}}_t}$
, and
$p_*(\mathrm {DH}_{{\mathcal {F}}_0,{\mathcal {F}}_1}) = \mathrm {DH}_{{\mathcal {F}}_t}$
, and -
2.
 $q_*(\mathrm {DH}_{{\mathcal {F}}_0,{\mathcal {F}}_1}) = \mathrm { RLM}_{{\mathcal {F}}_0,{\mathcal {G}}}$
, where
$q_*(\mathrm {DH}_{{\mathcal {F}}_0,{\mathcal {F}}_1}) = \mathrm { RLM}_{{\mathcal {F}}_0,{\mathcal {G}}}$
, where
 ${\mathcal {G}}$
is filtration given by
${\mathcal {G}}$
is filtration given by
 ${\mathcal {G}}^{\lambda } R_m:={\mathcal {F}}_1^{(\lambda -dmr)/c} R_m$
.
${\mathcal {G}}^{\lambda } R_m:={\mathcal {F}}_1^{(\lambda -dmr)/c} R_m$
.
Proof. Observe that
![]() $p_*(\boldsymbol {\nu }_m) = \nu _m^{{\mathcal {F}}_t} $
and
$p_*(\boldsymbol {\nu }_m) = \nu _m^{{\mathcal {F}}_t} $
and
![]() $q_*(\boldsymbol {\nu }_m) = \boldsymbol {\nu }_m^{{\mathcal {F}}_0,{\mathcal {G}}}$
. Therefore,
$q_*(\boldsymbol {\nu }_m) = \boldsymbol {\nu }_m^{{\mathcal {F}}_0,{\mathcal {G}}}$
. Therefore,
![]() $p_*(\boldsymbol {\nu }_m) \overset { \mathrm {weak}}{ \longrightarrow } \mathrm {DH}_{{\mathcal {F}}_t}$
and
$p_*(\boldsymbol {\nu }_m) \overset { \mathrm {weak}}{ \longrightarrow } \mathrm {DH}_{{\mathcal {F}}_t}$
and
![]() $q_*(\boldsymbol {\nu }_m)\overset { \mathrm {weak}}{ \longrightarrow } \mathrm {RLM}_{{\mathcal {F}}_0,{\mathcal {G}}}$
. By Theorem 3.3 and the continuity of p and q, we also have
$q_*(\boldsymbol {\nu }_m)\overset { \mathrm {weak}}{ \longrightarrow } \mathrm {RLM}_{{\mathcal {F}}_0,{\mathcal {G}}}$
. By Theorem 3.3 and the continuity of p and q, we also have
![]() $p_*(\boldsymbol {\nu }_m) \overset { \mathrm {weak}}{ \longrightarrow } p_*(\mathrm { DH}_{{\mathcal {F}}_0,{\mathcal {F}}_1})$
and
$p_*(\boldsymbol {\nu }_m) \overset { \mathrm {weak}}{ \longrightarrow } p_*(\mathrm { DH}_{{\mathcal {F}}_0,{\mathcal {F}}_1})$
and
![]() $q_*(\boldsymbol {\nu }_m)\overset { \mathrm {weak}}{ \longrightarrow } q_*(\mathrm { DH}_{{\mathcal {F}}_0,{\mathcal {F}}_1})$
. Since weak limits of measure on
$q_*(\boldsymbol {\nu }_m)\overset { \mathrm {weak}}{ \longrightarrow } q_*(\mathrm { DH}_{{\mathcal {F}}_0,{\mathcal {F}}_1})$
. Since weak limits of measure on
![]() $\mathbb {R}^2$
are unique, the result follows.
$\mathbb {R}^2$
are unique, the result follows.
3.2 Convexity
In this section, we prove the following result on the convexity of the non-Archimedean Ding and H-functionals.
Theorem 3.7. Let
![]() ${\mathcal {F}}_0$
and
${\mathcal {F}}_0$
and
![]() ${\mathcal {F}}_1$
be linearly bounded filtrations of R and
${\mathcal {F}}_1$
be linearly bounded filtrations of R and
![]() $({\mathcal {F}}_t)_{t\in [0,1]}$
be the geodesic connecting them. For
$({\mathcal {F}}_t)_{t\in [0,1]}$
be the geodesic connecting them. For
![]() $t\in (0,1)$
, the following hold:
$t\in (0,1)$
, the following hold:
-
1.
 $\mathbf {D}^{\mathrm {NA}}({\mathcal {F}}_t)\leq (1-t) \mathbf {D}^{\mathrm {NA}}({\mathcal {F}}_0) +t \mathbf {D}^{\mathrm {NA}}({\mathcal {F}}_1)$
;
$\mathbf {D}^{\mathrm {NA}}({\mathcal {F}}_t)\leq (1-t) \mathbf {D}^{\mathrm {NA}}({\mathcal {F}}_0) +t \mathbf {D}^{\mathrm {NA}}({\mathcal {F}}_1)$
; -
2.
 $\mathbf {H}^{\mathrm {NA}}({\mathcal {F}}_t) \leq (1-t) \mathbf {H}^{\mathrm {NA}}({\mathcal {F}}_0) + t \mathbf {H}^{\mathrm {NA}}({\mathcal {F}}_1)$
.
$\mathbf {H}^{\mathrm {NA}}({\mathcal {F}}_t) \leq (1-t) \mathbf {H}^{\mathrm {NA}}({\mathcal {F}}_0) + t \mathbf {H}^{\mathrm {NA}}({\mathcal {F}}_1)$
.
Furthermore, the inequality in (ii) is strict unless there exists
![]() $d\in \mathbb {R}$
so that
$d\in \mathbb {R}$
so that
![]() $d_{1}({\mathcal {F}}_0,{\mathcal {G}})=0$
, where
$d_{1}({\mathcal {F}}_0,{\mathcal {G}})=0$
, where
![]() ${\mathcal {G}}$
is the filtration defined by
${\mathcal {G}}$
is the filtration defined by
![]() ${\mathcal {G}}^{\lambda } R_m := {\mathcal {F}}_1^{\lambda -dmr}R_m$
.
${\mathcal {G}}^{\lambda } R_m := {\mathcal {F}}_1^{\lambda -dmr}R_m$
.
The result is an algebraic analogue of a theorem of Berndtsson on the convexity of the Ding-functional along geodesics in the space of Kähler potentials [Reference BerndtssonBer15]. In forthcoming work, Reboulet shows that Theorem 3.7 can in fact be deduced from Berndtsson’s convexity result when X is smooth [Reference RebouletReb21]. The proof below is self-contained and purely algebraic.
To prove Theorem 3.7, we first show the convexity of
![]() $\mathbf {L}^{\mathrm {NA}}$
along geodesics. For this, we first compare
$\mathbf {L}^{\mathrm {NA}}$
along geodesics. For this, we first compare
![]() $\mathbf {L}^{\mathrm {NA}}$
with the log canonical slope of a filtration
$\mathbf {L}^{\mathrm {NA}}$
with the log canonical slope of a filtration
![]() ${\mathcal {F}}$
, defined as (c.f. [Reference Xu and ZhuangXZ20, Definition 1.3 and Lemma 4.13])
${\mathcal {F}}$
, defined as (c.f. [Reference Xu and ZhuangXZ20, Definition 1.3 and Lemma 4.13])
 $$\begin{align*}\mu({\mathcal{F}}) := \mu_{X,\Delta}({\mathcal{F}}) := \sup \left\{s\in\mathbb{R}\,|\,\mathrm{ lct}(X,\Delta;I^{(s)}_{\bullet})\ge \frac{1}{r}\right\} = \sup \left\{s\in\mathbb{R}\,|\,\mathrm{ lct}(X,\Delta;I^{(s)}_{\bullet})> \frac{1}{r}\right\}. \end{align*}$$
$$\begin{align*}\mu({\mathcal{F}}) := \mu_{X,\Delta}({\mathcal{F}}) := \sup \left\{s\in\mathbb{R}\,|\,\mathrm{ lct}(X,\Delta;I^{(s)}_{\bullet})\ge \frac{1}{r}\right\} = \sup \left\{s\in\mathbb{R}\,|\,\mathrm{ lct}(X,\Delta;I^{(s)}_{\bullet})> \frac{1}{r}\right\}. \end{align*}$$
Lemma 3.8. For any linearly bounded filtration
![]() ${\mathcal {F}}$
of R we have
${\mathcal {F}}$
of R we have
![]() $\mu ({\mathcal {F}})=\mathbf {L}^{\mathrm {NA}}({\mathcal {F}})$
, and there exists some valuation
$\mu ({\mathcal {F}})=\mathbf {L}^{\mathrm {NA}}({\mathcal {F}})$
, and there exists some valuation
![]() $v\in \mathrm { Val}_X^{\circ }\cup \{v_{\mathrm {triv}}\}$
such that
$v\in \mathrm { Val}_X^{\circ }\cup \{v_{\mathrm {triv}}\}$
such that
for all
![]() $\lambda \in \mathbb {R}$
. Moreover, if
$\lambda \in \mathbb {R}$
. Moreover, if
![]() ${\mathcal {F}}$
is a finitely generated
${\mathcal {F}}$
is a finitely generated
![]() $\mathbb {Z}$
-filtration and
$\mathbb {Z}$
-filtration and
![]() $\mathbf {L}^{\mathrm {NA}}({\mathcal {F}})<\lambda _{\max }({\mathcal {F}})$
, then v can be chosen to be a divisorial lc place of some
$\mathbf {L}^{\mathrm {NA}}({\mathcal {F}})<\lambda _{\max }({\mathcal {F}})$
, then v can be chosen to be a divisorial lc place of some
![]() ${\mathbb {Q}}$
-complement.
${\mathbb {Q}}$
-complement.
Recall that a valuation v is said to be an lc place of some
![]() ${\mathbb {Q}}$
-complement if there exists some effective
${\mathbb {Q}}$
-complement if there exists some effective
![]() ${\mathbb {Q}}$
-divisor
${\mathbb {Q}}$
-divisor
![]() $\Gamma \sim _{\mathbb {Q}} -(K_X+\Delta )$
such that
$\Gamma \sim _{\mathbb {Q}} -(K_X+\Delta )$
such that
![]() $(X,\Delta +\Gamma )$
is lc and
$(X,\Delta +\Gamma )$
is lc and
![]() $A_{X,\Delta +\Gamma }(v)=0$
.
$A_{X,\Delta +\Gamma }(v)=0$
.
Proof. By [Reference Xu and ZhuangXZ20, Theorem 4.3], we already have
![]() $\mu ({\mathcal {F}})\ge \mathbf {L}^{\mathrm {NA}}({\mathcal {F}})$
, thus it suffices to show
$\mu ({\mathcal {F}})\ge \mathbf {L}^{\mathrm {NA}}({\mathcal {F}})$
, thus it suffices to show
![]() $\mu ({\mathcal {F}})\le \mathbf {L}^{\mathrm {NA}}({\mathcal {F}})$
. By [Reference Jonsson and MustaţăJM12, Theorem 7.3],
$\mu ({\mathcal {F}})\le \mathbf {L}^{\mathrm {NA}}({\mathcal {F}})$
. By [Reference Jonsson and MustaţăJM12, Theorem 7.3],
![]() $\mathrm { lct}(X_{\mathbb {A}^1},\Delta _{\mathbb {A}^1}+{\mathcal {I}}_{\bullet }^{\frac {1}{r}}; (t))=\mathbf {L}^{\mathrm {NA}}({\mathcal {F}})+1$
is computed by some
$\mathrm { lct}(X_{\mathbb {A}^1},\Delta _{\mathbb {A}^1}+{\mathcal {I}}_{\bullet }^{\frac {1}{r}}; (t))=\mathbf {L}^{\mathrm {NA}}({\mathcal {F}})+1$
is computed by some
![]() $\mathbb {G}_m$
-invariant valuation
$\mathbb {G}_m$
-invariant valuation
![]() $w\in \mathrm {Val}_{X\times \mathbb {A}^1}^{\circ }$
(the
$w\in \mathrm {Val}_{X\times \mathbb {A}^1}^{\circ }$
(the
![]() $\mathbb {G}_m$
-equivariant version is not proved in [Reference Jonsson and MustaţăJM12] but is not hard to achieve from the proof). By [Reference Boucksom, Hisamoto and JonssonBHJ17, Lemma 4.2], up to rescaling w is the Gauss extension of a valuation
$\mathbb {G}_m$
-equivariant version is not proved in [Reference Jonsson and MustaţăJM12] but is not hard to achieve from the proof). By [Reference Boucksom, Hisamoto and JonssonBHJ17, Lemma 4.2], up to rescaling w is the Gauss extension of a valuation
![]() $v\in \mathrm { Val}_X^{\circ }\cup \{v_{\mathrm {triv}}\}$
, that is,
$v\in \mathrm { Val}_X^{\circ }\cup \{v_{\mathrm {triv}}\}$
, that is,
![]() $w(ft^i)=v(f)+i$
for any
$w(ft^i)=v(f)+i$
for any
![]() $0\neq f\in K(X)$
and
$0\neq f\in K(X)$
and
![]() $i\in \mathbb {Z}$
. Since w computes the lct and
$i\in \mathbb {Z}$
. Since w computes the lct and
![]() $w(t)=1$
, we have
$w(t)=1$
, we have
Thus,
![]() $A_{X,\Delta }(v)-\mathbf {L}^{\mathrm {NA}}({\mathcal {F}})=w({\mathcal {I}}_{\bullet }^{\frac {1}{r}})\le w({\mathcal {I}}_m^{\frac {1}{mr}})\le \frac {v(I_{m,i})-i}{mr}$
for all
$A_{X,\Delta }(v)-\mathbf {L}^{\mathrm {NA}}({\mathcal {F}})=w({\mathcal {I}}_{\bullet }^{\frac {1}{r}})\le w({\mathcal {I}}_m^{\frac {1}{mr}})\le \frac {v(I_{m,i})-i}{mr}$
for all
![]() $m\in \mathbb {N}$
and
$m\in \mathbb {N}$
and
![]() $i\in \mathbb {Z}$
. It follows that
$i\in \mathbb {Z}$
. It follows that
for all
![]() $\lambda \in \mathbb {R}$
. In particular,
$\lambda \in \mathbb {R}$
. In particular,
![]() $\mathrm {lct}(X,\Delta ;I_{\bullet }^{(\lambda )})<r^{-1}$
for any
$\mathrm {lct}(X,\Delta ;I_{\bullet }^{(\lambda )})<r^{-1}$
for any
![]() $\lambda>\mathbf {L}^{\mathrm {NA}}({\mathcal {F}})$
. By the definition of log canonical slope, this implies
$\lambda>\mathbf {L}^{\mathrm {NA}}({\mathcal {F}})$
. By the definition of log canonical slope, this implies
![]() $\mu ({\mathcal {F}})\le \mathbf {L}^{\mathrm {NA}}({\mathcal {F}})$
and proves the first part of the lemma.
$\mu ({\mathcal {F}})\le \mathbf {L}^{\mathrm {NA}}({\mathcal {F}})$
and proves the first part of the lemma.
If
![]() ${\mathcal {F}}$
is finitely generated, then
${\mathcal {F}}$
is finitely generated, then
![]() ${\mathcal {I}}_{pm}={\mathcal {I}}_m^p$
for any sufficiently divisible
${\mathcal {I}}_{pm}={\mathcal {I}}_m^p$
for any sufficiently divisible
![]() $m,p\in \mathbb {N}$
and thus w can be chosen as a divisorial valuation. Since
$m,p\in \mathbb {N}$
and thus w can be chosen as a divisorial valuation. Since
![]() $\mathbf {L}^{\mathrm {NA}}({\mathcal {F}})<\lambda _{\max }({\mathcal {F}})$
, the valuation v cannot be the trivial one, otherwise equation (3.4) becomes
$\mathbf {L}^{\mathrm {NA}}({\mathcal {F}})<\lambda _{\max }({\mathcal {F}})$
, the valuation v cannot be the trivial one, otherwise equation (3.4) becomes
![]() $\lambda \le \mathbf {L}^{\mathrm {NA}}({\mathcal {F}})$
for all
$\lambda \le \mathbf {L}^{\mathrm {NA}}({\mathcal {F}})$
for all
![]() $\lambda < \lambda _{\max }({\mathcal {F}})$
and therefore
$\lambda < \lambda _{\max }({\mathcal {F}})$
and therefore
![]() $\lambda _{\max }({\mathcal {F}})\le \mathbf {L}^{\mathrm {NA}}({\mathcal {F}})$
, a contradiction. By [Reference Boucksom, Hisamoto and JonssonBHJ17, Lemma 4.1], we know that v is divisorial. Let
$\lambda _{\max }({\mathcal {F}})\le \mathbf {L}^{\mathrm {NA}}({\mathcal {F}})$
, a contradiction. By [Reference Boucksom, Hisamoto and JonssonBHJ17, Lemma 4.1], we know that v is divisorial. Let
![]() ${\mathfrak {a}}_m=I_{m,\mu mr}$
. Again,
${\mathfrak {a}}_m=I_{m,\mu mr}$
. Again,
![]() ${\mathfrak {a}}_{pm}={\mathfrak {a}}_m^p$
for any sufficiently divisible
${\mathfrak {a}}_{pm}={\mathfrak {a}}_m^p$
for any sufficiently divisible
![]() $m,p\in \mathbb {N}$
as
$m,p\in \mathbb {N}$
as
![]() ${\mathcal {F}}$
is finitely generated. By equation (3.4), we have
${\mathcal {F}}$
is finitely generated. By equation (3.4), we have
![]() $r^{-1}v({\mathfrak {a}}_{\bullet })\ge A_{X,\Delta }(v)$
; thus, from the definition of log canonical slope, we see that v necessarily computes
$r^{-1}v({\mathfrak {a}}_{\bullet })\ge A_{X,\Delta }(v)$
; thus, from the definition of log canonical slope, we see that v necessarily computes
for sufficiently divisible m and general
![]() $s\in {\mathcal {F}}^{\mu mr} R_m$
. As
$s\in {\mathcal {F}}^{\mu mr} R_m$
. As
![]() $K_X+\Delta +\frac {1}{mr}\{s=0\}\sim _{\mathbb {Q}} 0$
, this easily implies that v is an lc place of some
$K_X+\Delta +\frac {1}{mr}\{s=0\}\sim _{\mathbb {Q}} 0$
, this easily implies that v is an lc place of some
![]() ${\mathbb {Q}}$
-complement.
${\mathbb {Q}}$
-complement.
Remark 3.9. From the above proof, it is clear that if the filtration
![]() ${\mathcal {F}}$
is
${\mathcal {F}}$
is
![]() $\mathbb {T}$
-equivariant for some torus
$\mathbb {T}$
-equivariant for some torus
![]() $\mathbb {T}<\operatorname {Aut}(X,\Delta )$
, then the valuation v can be chosen to be
$\mathbb {T}<\operatorname {Aut}(X,\Delta )$
, then the valuation v can be chosen to be
![]() $\mathbb {T}$
-invariant as well.
$\mathbb {T}$
-invariant as well.
Remark 3.10. Lemma 3.8 immediately implies that
![]() $\beta ({\mathcal {F}})=\mathbf {D}^{\mathrm {NA}}({\mathcal {F}})$
(see [Reference Xu and ZhuangXZ20, Definition 4.1] for the definition
$\beta ({\mathcal {F}})=\mathbf {D}^{\mathrm {NA}}({\mathcal {F}})$
(see [Reference Xu and ZhuangXZ20, Definition 4.1] for the definition
![]() $\beta ({\mathcal {F}})$
) for any linearly bounded multiplicative filtration
$\beta ({\mathcal {F}})$
) for any linearly bounded multiplicative filtration
![]() ${\mathcal {F}}$
.
${\mathcal {F}}$
.
Corollary 3.11. For any
![]() $v\in \mathrm {Val}_X^{\circ }$
, we have
$v\in \mathrm {Val}_X^{\circ }$
, we have
![]() $\mathbf {L}^{\mathrm {NA}}({\mathcal {F}}_v)\le A_{X,\Delta }(v)$
and
$\mathbf {L}^{\mathrm {NA}}({\mathcal {F}}_v)\le A_{X,\Delta }(v)$
and
![]() $\mathbf {H}^{\mathrm {NA}}({\mathcal {F}}_v)\le \tilde {\beta }_{X,\Delta }(v)$
.
$\mathbf {H}^{\mathrm {NA}}({\mathcal {F}}_v)\le \tilde {\beta }_{X,\Delta }(v)$
.
Proof. It is not hard to see from the definition that
![]() $\mu ({\mathcal {F}}_v)\le A_{X,\Delta }(v)$
(c.f. [Reference Xu and ZhuangXZ20, Proposition 4.2]), thus the first inequality follows from Lemma 3.8. The second inequality follows from the first and the definition of
$\mu ({\mathcal {F}}_v)\le A_{X,\Delta }(v)$
(c.f. [Reference Xu and ZhuangXZ20, Proposition 4.2]), thus the first inequality follows from Lemma 3.8. The second inequality follows from the first and the definition of
![]() $\mathbf {H}^{\mathrm {NA}}$
and
$\mathbf {H}^{\mathrm {NA}}$
and
![]() $\tilde {\beta }$
.
$\tilde {\beta }$
.
Given the equality
![]() $\mathbf {L}^{\mathrm {NA}}({\mathcal {F}})=\mu ({\mathcal {F}})$
(see Lemma 3.8), we can establish the convexity of
$\mathbf {L}^{\mathrm {NA}}({\mathcal {F}})=\mu ({\mathcal {F}})$
(see Lemma 3.8), we can establish the convexity of
![]() $\mathbf {L}^{\mathrm {NA}}$
using [Reference Xu and ZhuangXZ21].
$\mathbf {L}^{\mathrm {NA}}$
using [Reference Xu and ZhuangXZ21].
Proposition 3.12. Let
![]() ${\mathcal {F}}_0$
and
${\mathcal {F}}_0$
and
![]() ${\mathcal {F}}_1$
be linearly bounded filtrations of R and
${\mathcal {F}}_1$
be linearly bounded filtrations of R and
![]() $({\mathcal {F}}_t)_{t\in [0,1]}$
be the geodesic connecting them. For
$({\mathcal {F}}_t)_{t\in [0,1]}$
be the geodesic connecting them. For
![]() $t\in (0,1)$
,
$t\in (0,1)$
,
![]() $\mathbf {L}^{\mathrm {NA}}({\mathcal {F}}_t) \leq (1-t) \mathbf {L}^{\mathrm {NA}}({\mathcal {F}}_0) + t \mathbf {L}^{\mathrm {NA}}({\mathcal {F}}_1)$
.
$\mathbf {L}^{\mathrm {NA}}({\mathcal {F}}_t) \leq (1-t) \mathbf {L}^{\mathrm {NA}}({\mathcal {F}}_0) + t \mathbf {L}^{\mathrm {NA}}({\mathcal {F}}_1)$
.
Proof. It is not hard to see that the statement is unaffected by translation of the filtrations. Thus, by Lemma 3.8, we may assume that, after shifting the filtrations, there exists valuations
![]() $v_0, v_1$
on X with
$v_0, v_1$
on X with
![]() $A_{X,\Delta }(v_i)<\infty $
such that
$A_{X,\Delta }(v_i)<\infty $
such that
![]() $\mathbf {L}^{\mathrm {NA}}({\mathcal {F}}_i)=\mu ({\mathcal {F}}_i)=A_{X,\Delta }(v_i)$
and
$\mathbf {L}^{\mathrm {NA}}({\mathcal {F}}_i)=\mu ({\mathcal {F}}_i)=A_{X,\Delta }(v_i)$
and
![]() $v_i(I_{{\mathcal {F}}_i,\bullet }^{(\lambda )})\ge r\lambda $
for all
$v_i(I_{{\mathcal {F}}_i,\bullet }^{(\lambda )})\ge r\lambda $
for all
![]() $\lambda \in \mathbb {R}$
and
$\lambda \in \mathbb {R}$
and
![]() $i=0,1$
. In particular,
$i=0,1$
. In particular,
![]() ${\mathcal {F}}_i^{\lambda } R\subseteq {\mathcal {F}}_{v_i}^{\lambda } R$
for all
${\mathcal {F}}_i^{\lambda } R\subseteq {\mathcal {F}}_{v_i}^{\lambda } R$
for all
![]() $\lambda \in \mathbb {R}$
.
$\lambda \in \mathbb {R}$
.
Let
![]() $(Y=\mathrm {Spec}(R),\Gamma )$
denote the affine cone over
$(Y=\mathrm {Spec}(R),\Gamma )$
denote the affine cone over
![]() $(X,\Delta )$
with respect to the polarization
$(X,\Delta )$
with respect to the polarization
![]() $L=-r(K_X+\Delta )$
. Let
$L=-r(K_X+\Delta )$
. Let
![]() $w_i$
be the
$w_i$
be the
![]() $\mathbb {G}_m$
-invariant valuation on Y given by
$\mathbb {G}_m$
-invariant valuation on Y given by
![]() $w_i(s)=mr+v_i(s)$
for
$w_i(s)=mr+v_i(s)$
for
![]() $s\in R_m$
(informally
$s\in R_m$
(informally
![]() $w_i=r\cdot \mathrm {ord}_o+v_i$
). Let
$w_i=r\cdot \mathrm {ord}_o+v_i$
). Let
![]() ${\mathfrak {b}}_{t,\bullet }$
be the graded sequence of ideals on Y defined by
${\mathfrak {b}}_{t,\bullet }$
be the graded sequence of ideals on Y defined by
 $$\begin{align*}{\mathfrak{b}}_{t,m}={\mathfrak{a}}_{\bullet}((1-t)w_0)\boxplus {\mathfrak{a}}_{\bullet}(tw_1):=\sum_{i=0}^m {\mathfrak{a}}_{m-i}((1-t)w_0)\cap {\mathfrak{a}}_i(tw_1). \end{align*}$$
$$\begin{align*}{\mathfrak{b}}_{t,m}={\mathfrak{a}}_{\bullet}((1-t)w_0)\boxplus {\mathfrak{a}}_{\bullet}(tw_1):=\sum_{i=0}^m {\mathfrak{a}}_{m-i}((1-t)w_0)\cap {\mathfrak{a}}_i(tw_1). \end{align*}$$
In other words,
![]() ${\mathfrak {b}}_{t,m}$
is generated by those
${\mathfrak {b}}_{t,m}$
is generated by those
![]() $s\in R$
with
$s\in R$
with
![]() $\lfloor (1-t)w_0(s) \rfloor + \lfloor tw_1(s) \rfloor \ge m$
. For any
$\lfloor (1-t)w_0(s) \rfloor + \lfloor tw_1(s) \rfloor \ge m$
. For any
![]() $k\in \mathbb {Z}$
and any
$k\in \mathbb {Z}$
and any
![]() $s\in {\mathcal {F}}_t^{k+2} R_m$
, we have
$s\in {\mathcal {F}}_t^{k+2} R_m$
, we have
![]() $(1-t)w_0(s)+tw_1(s)\ge mr+k+2$
by equation (3.1). It follows that s is a section of
$(1-t)w_0(s)+tw_1(s)\ge mr+k+2$
by equation (3.1). It follows that s is a section of
![]() ${\mathfrak {b}}_{t,mr+k}$
(for if
${\mathfrak {b}}_{t,mr+k}$
(for if
![]() $a+b\ge k+2$
then
$a+b\ge k+2$
then
![]() $\lfloor a \rfloor +\lfloor b \rfloor \ge k$
). Therefore, elements in
$\lfloor a \rfloor +\lfloor b \rfloor \ge k$
). Therefore, elements in
![]() ${\mathcal {F}}_t^{k+2} R_m$
yield sections of
${\mathcal {F}}_t^{k+2} R_m$
yield sections of
![]() ${\mathfrak {b}}_{t,mr+k}$
on Y for any
${\mathfrak {b}}_{t,mr+k}$
on Y for any
![]() $k\in \mathbb {Z}$
. By [Reference Xu and ZhuangXZ21, Theorem 3.11], we have
$k\in \mathbb {Z}$
. By [Reference Xu and ZhuangXZ21, Theorem 3.11], we have
 $$ \begin{align*} \mathrm{lct}({\mathfrak{b}}_{t,\bullet}) & \le \mathrm{lct}({\mathfrak{a}}_{\bullet}((1-t)w_0))+\mathrm{lct}({\mathfrak{a}}_{\bullet}(tw_1)) \le (1-t)A_{Y,\Gamma}(w_0)+tA_{Y,\Gamma}(w_1) \\ & = 1+(1-t)A_{X,\Delta}(v_0)+tA_{X,\Delta}(v_1) = 1+(1-t) \mathbf{L}^{\mathrm{NA}}({\mathcal{F}}_0) + t \mathbf{L}^{\mathrm{NA}}({\mathcal{F}}_1). \end{align*} $$
$$ \begin{align*} \mathrm{lct}({\mathfrak{b}}_{t,\bullet}) & \le \mathrm{lct}({\mathfrak{a}}_{\bullet}((1-t)w_0))+\mathrm{lct}({\mathfrak{a}}_{\bullet}(tw_1)) \le (1-t)A_{Y,\Gamma}(w_0)+tA_{Y,\Gamma}(w_1) \\ & = 1+(1-t)A_{X,\Delta}(v_0)+tA_{X,\Delta}(v_1) = 1+(1-t) \mathbf{L}^{\mathrm{NA}}({\mathcal{F}}_0) + t \mathbf{L}^{\mathrm{NA}}({\mathcal{F}}_1). \end{align*} $$
Thus, for any rational
![]() $c>(1-t) \mathbf {L}^{\mathrm {NA}}({\mathcal {F}}_0) + t \mathbf {L}^{\mathrm {NA}}({\mathcal {F}}_1)$
and any
$c>(1-t) \mathbf {L}^{\mathrm {NA}}({\mathcal {F}}_0) + t \mathbf {L}^{\mathrm {NA}}({\mathcal {F}}_1)$
and any
![]() $s\in {\mathcal {F}}^{cmr+2}_t R_m$
(where m is sufficiently divisible), as it yields a section of
$s\in {\mathcal {F}}^{cmr+2}_t R_m$
(where m is sufficiently divisible), as it yields a section of
![]() ${\mathfrak {b}}_{t,(1+c)mr}$
on Y, the pair
${\mathfrak {b}}_{t,(1+c)mr}$
on Y, the pair
![]() $(Y,\Gamma +\frac {1}{mr}\{s=0\})$
is not lc. Using [Reference KollárKol13, Lemma 3.1(5)], it follows that the base
$(Y,\Gamma +\frac {1}{mr}\{s=0\})$
is not lc. Using [Reference KollárKol13, Lemma 3.1(5)], it follows that the base
![]() $(X,\Delta +\frac {1}{mr}\{s=0\})$
is not lc for any
$(X,\Delta +\frac {1}{mr}\{s=0\})$
is not lc for any
![]() $m\in \mathbb {N}$
and any
$m\in \mathbb {N}$
and any
![]() $s\in {\mathcal {F}}^{cmr+2}_t R_m$
. By the definition of log canonical slope, this implies that
$s\in {\mathcal {F}}^{cmr+2}_t R_m$
. By the definition of log canonical slope, this implies that
![]() $\mu ({\mathcal {F}}_t)\le c$
. By Lemma 3.8 and the fact that
$\mu ({\mathcal {F}}_t)\le c$
. By Lemma 3.8 and the fact that
![]() $c>(1-t) \mathbf {L}^{\mathrm {NA}}({\mathcal {F}}_0) + t \mathbf {L}^{\mathrm {NA}}({\mathcal {F}}_1)$
was arbitrary, the result follows.
$c>(1-t) \mathbf {L}^{\mathrm {NA}}({\mathcal {F}}_0) + t \mathbf {L}^{\mathrm {NA}}({\mathcal {F}}_1)$
was arbitrary, the result follows.
Using the measure
![]() $\mathrm {DH}_{{\mathcal {F}}_0,{\mathcal {F}}_1}$
constructed in Section 3.1.3, we next describe the behavior of the Monge–Ampère Energy and
$\mathrm {DH}_{{\mathcal {F}}_0,{\mathcal {F}}_1}$
constructed in Section 3.1.3, we next describe the behavior of the Monge–Ampère Energy and
![]() $\widetilde {S}$
functionals along the geodesic.
$\widetilde {S}$
functionals along the geodesic.
Proposition 3.13. For
![]() $t\in [0,1]$
,
$t\in [0,1]$
,
![]() $\mathbf {E}^{\mathrm {NA}}({\mathcal {F}}_t) = (1-t) \mathbf {E}^{\mathrm {NA}}({\mathcal {F}}_0) + t \mathbf {E}^{\mathrm {NA}}({\mathcal {F}}_1)$
.
$\mathbf {E}^{\mathrm {NA}}({\mathcal {F}}_t) = (1-t) \mathbf {E}^{\mathrm {NA}}({\mathcal {F}}_0) + t \mathbf {E}^{\mathrm {NA}}({\mathcal {F}}_1)$
.
Proof. Set
![]() $\boldsymbol {\nu }:= \mathrm {DH}_{{\mathcal {F}}_0,{\mathcal {F}}_1}$
. We compute
$\boldsymbol {\nu }:= \mathrm {DH}_{{\mathcal {F}}_0,{\mathcal {F}}_1}$
. We compute
where the second equality is by Proposition 3.6. From this, the result follows.
Proposition 3.14. For
![]() $t\in (0,1)$
,
$t\in (0,1)$
,
![]() $\widetilde {S}({\mathcal {F}}_t) \geq (1-t) \widetilde {S}({\mathcal {F}}_0) + t \widetilde {S}({\mathcal {F}}_1)$
. Furthermore, the inequality is strict unless there exists
$\widetilde {S}({\mathcal {F}}_t) \geq (1-t) \widetilde {S}({\mathcal {F}}_0) + t \widetilde {S}({\mathcal {F}}_1)$
. Furthermore, the inequality is strict unless there exists
![]() $d\in \mathbb {R}$
so that
$d\in \mathbb {R}$
so that
![]() $d_1({\mathcal {F}}_0, {\mathcal {G}})= 0$
, where
$d_1({\mathcal {F}}_0, {\mathcal {G}})= 0$
, where
![]() ${\mathcal {G}}$
is the filtration defined by
${\mathcal {G}}$
is the filtration defined by
![]() ${\mathcal {G}}^{\lambda } R_m : = {\mathcal {G}}^{\lambda -mrd} R_m$
.
${\mathcal {G}}^{\lambda } R_m : = {\mathcal {G}}^{\lambda -mrd} R_m$
.
Proof. Set
![]() $\boldsymbol {\nu }: = \mathrm {DH}_{{\mathcal {F}}_0,{\mathcal {F}}_1}$
,
$\boldsymbol {\nu }: = \mathrm {DH}_{{\mathcal {F}}_0,{\mathcal {F}}_1}$
,
![]() $f(x,y): = e^{-x}$
, and
$f(x,y): = e^{-x}$
, and
![]() $g(x,y) := e^{-y}$
. For
$g(x,y) := e^{-y}$
. For
![]() $t\in [0,1]$
,
$t\in [0,1]$
,
where the second equality is by Proposition 3.6. Hölder’s inequality implies
 $$ \begin{align*} -\log \lVert f^{1-t} g^{t} \rVert_{1,\boldsymbol{\nu}} \geq - \log \left( \lVert f \rVert_{1,\boldsymbol{\nu}}^{1-t} \lVert g \rVert_{1,\boldsymbol{\nu}}^t \right) &= - (1-t) \log \lVert f \rVert_{1,\boldsymbol{\nu}} - t \log \lVert g \rVert_{1,\boldsymbol{\nu}}\\ & = (1-t) \widetilde{S}({\mathcal{F}}_0) + t \widetilde{S}({\mathcal{F}}_1) \end{align*} $$
$$ \begin{align*} -\log \lVert f^{1-t} g^{t} \rVert_{1,\boldsymbol{\nu}} \geq - \log \left( \lVert f \rVert_{1,\boldsymbol{\nu}}^{1-t} \lVert g \rVert_{1,\boldsymbol{\nu}}^t \right) &= - (1-t) \log \lVert f \rVert_{1,\boldsymbol{\nu}} - t \log \lVert g \rVert_{1,\boldsymbol{\nu}}\\ & = (1-t) \widetilde{S}({\mathcal{F}}_0) + t \widetilde{S}({\mathcal{F}}_1) \end{align*} $$
Furthermore, the inequality is strict unless (i)
![]() $f=0$
or
$f=0$
or
![]() $g=0 \ \boldsymbol {\nu }$
-a.e. or (ii) there exists
$g=0 \ \boldsymbol {\nu }$
-a.e. or (ii) there exists
![]() $c>0$
so that
$c>0$
so that
![]() $f- c g =0 \ \boldsymbol {\nu }$
-a.e.
$f- c g =0 \ \boldsymbol {\nu }$
-a.e.
Condition (i) cannot occur since f and g are
![]() $>0$
. Condition (ii) is equivalent to saying
$>0$
. Condition (ii) is equivalent to saying
![]() $x-y-d=0 \ \boldsymbol {\nu }$
-a.e., where
$x-y-d=0 \ \boldsymbol {\nu }$
-a.e., where
![]() $d: = -\ln (c)$
. Now, if we write
$d: = -\ln (c)$
. Now, if we write
![]() ${\mathcal {G}}$
for the filtration of R defined by
${\mathcal {G}}$
for the filtration of R defined by
![]() ${\mathcal {G}}^{\lambda } R_m : = {\mathcal {F}}_1^{\lambda -mrd}R_m$
, then
${\mathcal {G}}^{\lambda } R_m : = {\mathcal {F}}_1^{\lambda -mrd}R_m$
, then
where the second is by Proposition 3.6. Therefore, (ii) holds iff
![]() $d_{1}({\mathcal {F}},{\mathcal {G}})=0$
.
$d_{1}({\mathcal {F}},{\mathcal {G}})=0$
.
3.3 Uniqueness of valuations computing
 $h(X,\Delta )$
$h(X,\Delta )$
As a consequence of the convexity results in the previous section, we prove that the minimizer of
![]() $\mathbf {H}^{\mathrm {NA}}$
is unique.
$\mathbf {H}^{\mathrm {NA}}$
is unique.
Theorem 3.15. Assume v and w are valuations in
![]() $\mathrm {Val}_X^{\circ }\cup \{v_{\mathrm {triv}}\}$
. If
$\mathrm {Val}_X^{\circ }\cup \{v_{\mathrm {triv}}\}$
. If
![]() $v,w$
both compute
$v,w$
both compute
![]() $h(X,\Delta )$
, then
$h(X,\Delta )$
, then
![]() $v=w$
.
$v=w$
.
In [Reference Han and LiHL20b], the previous theorem was shown under the assumption that there exists a special
![]() $\mathbb {R}$
-test configuration computing
$\mathbb {R}$
-test configuration computing
![]() $h(X,\Delta )$
. The latter assumption will be verified in Corollary 5.7.
$h(X,\Delta )$
. The latter assumption will be verified in Corollary 5.7.
Proof. Consider the geodesic
![]() $({\mathcal {F}}_t)_{t\in [0,1]}$
connecting
$({\mathcal {F}}_t)_{t\in [0,1]}$
connecting
![]() ${\mathcal {F}}_0 : = {\mathcal {F}}_v$
and
${\mathcal {F}}_0 : = {\mathcal {F}}_v$
and
![]() ${\mathcal {F}}_1 :={\mathcal {F}}_w$
. For
${\mathcal {F}}_1 :={\mathcal {F}}_w$
. For
![]() $t\in (0,1)$
,
$t\in (0,1)$
,
where first inequality is Theorem 3.7 and the second Corollary 3.11. Since
![]() $h(X,\Delta ) \leq \mathbf {H}^{\mathrm {NA}}({\mathcal {F}}_t)$
, the first inequality cannot be strict. Therefore, Theorem 3.7 further implies there exists
$h(X,\Delta ) \leq \mathbf {H}^{\mathrm {NA}}({\mathcal {F}}_t)$
, the first inequality cannot be strict. Therefore, Theorem 3.7 further implies there exists
![]() $d\in \mathbb {R}$
so that
$d\in \mathbb {R}$
so that
![]() $d_{1}({\mathcal {F}}_0,{\mathcal {G}})=0$
, where
$d_{1}({\mathcal {F}}_0,{\mathcal {G}})=0$
, where
![]() ${\mathcal {G}}^{\lambda } R_m : = {\mathcal {F}}_1^{\lambda -mrd} R_m$
.
${\mathcal {G}}^{\lambda } R_m : = {\mathcal {F}}_1^{\lambda -mrd} R_m$
.
Next, note that
![]() $d=0$
, since
$d=0$
, since
where first and last inequality is by Lemma 2.4 and the second by Proposition 3.1. Therefore,
![]() $d_{1}({\mathcal {F}}_0,{\mathcal {F}}_1)=0$
. By Lemma 3.16, we conclude
$d_{1}({\mathcal {F}}_0,{\mathcal {F}}_1)=0$
. By Lemma 3.16, we conclude
![]() $v=w$
.
$v=w$
.
Lemma 3.16 [Reference Han and LiHL20b, Proposition 2.27].
Assume v and w are valuations in
![]() $\mathrm {Val}_X^{\circ }\cup \{v_{\mathrm {triv}}\}$
. If
$\mathrm {Val}_X^{\circ }\cup \{v_{\mathrm {triv}}\}$
. If
![]() ${\mathcal {F}}_v$
and
${\mathcal {F}}_v$
and
![]() ${\mathcal {F}}_w$
are equivalent, then
${\mathcal {F}}_w$
are equivalent, then
![]() $v=w$
.
$v=w$
.
This result was first proved in [Reference Han and LiHL20b] using the machinery of non-Archimedean metrics from [Reference Boucksom and JonssonBJ21]. For the sake of completeness, we give a proof which only uses the terminology introduced in this paper.
Proof. It is enough to show
![]() $v(f)=w(f)$
for all
$v(f)=w(f)$
for all
![]() $f\in R_m$
and
$f\in R_m$
and
![]() $m \in \mathbb {N}$
. Indeed, for any
$m \in \mathbb {N}$
. Indeed, for any
![]() $\lambda \in \mathbb {R}$
, we may choose some integer
$\lambda \in \mathbb {R}$
, we may choose some integer
![]() $m\gg 0$
such that
$m\gg 0$
such that
![]() $ {\mathcal {O}}_X(mL)\otimes {\mathfrak {a}}_{\lambda } (v)$
is globally generated, where
$ {\mathcal {O}}_X(mL)\otimes {\mathfrak {a}}_{\lambda } (v)$
is globally generated, where
![]() ${\mathfrak {a}}_{\lambda } (v):=\{f\in {\mathcal {O}}_X\,\vert \,v(f)\ge \lambda \}$
denotes the valuation ideal. If
${\mathfrak {a}}_{\lambda } (v):=\{f\in {\mathcal {O}}_X\,\vert \,v(f)\ge \lambda \}$
denotes the valuation ideal. If
![]() $v(f)=w(f)$
for all
$v(f)=w(f)$
for all
![]() $f\in H^0(X, {\mathcal {O}}_X(mL) \otimes {\mathfrak {a}}_{\lambda } (v))\subseteq R_m$
, then
$f\in H^0(X, {\mathcal {O}}_X(mL) \otimes {\mathfrak {a}}_{\lambda } (v))\subseteq R_m$
, then
![]() ${\mathfrak {a}}_{\lambda } (v)\subseteq {\mathfrak {a}}_{\lambda } (w)$
. Switching the role of v and w gives the reverse containment. Thus,
${\mathfrak {a}}_{\lambda } (v)\subseteq {\mathfrak {a}}_{\lambda } (w)$
. Switching the role of v and w gives the reverse containment. Thus,
![]() ${\mathfrak {a}}_{\lambda } (v) = {\mathfrak {a}}_{\lambda } (w)$
for all
${\mathfrak {a}}_{\lambda } (v) = {\mathfrak {a}}_{\lambda } (w)$
for all
![]() $\lambda \in \mathbb {R}$
, and, hence,
$\lambda \in \mathbb {R}$
, and, hence,
![]() $v=w$
.
$v=w$
.
Suppose now that
![]() $a=v(f)\neq w(f)=b$
for some
$a=v(f)\neq w(f)=b$
for some
![]() $f\in R_m$
. Without loss of generality, we may assume
$f\in R_m$
. Without loss of generality, we may assume
![]() $a>b$
. Let
$a>b$
. Let
![]() $\lambda =\lambda _{\max }({\mathcal {F}}_w)$
. Fix some
$\lambda =\lambda _{\max }({\mathcal {F}}_w)$
. Fix some
![]() $\varepsilon \in (0,a-b)$
, and let p be a sufficiently large integer such that
$\varepsilon \in (0,a-b)$
, and let p be a sufficiently large integer such that
![]() $\lambda r\le (a-b-\varepsilon )p$
. Consider the subspace
$\lambda r\le (a-b-\varepsilon )p$
. Consider the subspace
![]() $V_k:=f^{kp} \cdot R_k\subseteq {\mathcal {F}}_v^{akp} R_{k(mp+1)}$
. For any
$V_k:=f^{kp} \cdot R_k\subseteq {\mathcal {F}}_v^{akp} R_{k(mp+1)}$
. For any
![]() $g\in V_k$
, we have
$g\in V_k$
, we have
![]() $w(g)\le bkp+k\lambda r\le (a-\varepsilon )kp$
by our choice of p. Thus, for any basis
$w(g)\le bkp+k\lambda r\le (a-\varepsilon )kp$
by our choice of p. Thus, for any basis
![]() $(s_1,\cdots ,s_N)$
of
$(s_1,\cdots ,s_N)$
of
![]() $R_{k(mp+1)}$
that is compatible with both
$R_{k(mp+1)}$
that is compatible with both
![]() ${\mathcal {F}}_v$
and
${\mathcal {F}}_v$
and
![]() ${\mathcal {F}}_w$
, the part that spans
${\mathcal {F}}_w$
, the part that spans
![]() ${\mathcal {F}}_v^{akp} R_{k(mp+1)}$
contains at least
${\mathcal {F}}_v^{akp} R_{k(mp+1)}$
contains at least
![]() $\dim V_k = \dim R_k$
elements
$\dim V_k = \dim R_k$
elements
![]() $s_i$
with
$s_i$
with
![]() $w(s_i)\le (a-\varepsilon )kp$
. In particular for these
$w(s_i)\le (a-\varepsilon )kp$
. In particular for these
![]() $s_i$
, we have
$s_i$
, we have
![]() $v(s_i)-w(s_i)\ge \varepsilon kp$
. It follows that
$v(s_i)-w(s_i)\ge \varepsilon kp$
. It follows that
 $$\begin{align*}\int_{\mathbb{R}} |\lambda| \mathrm{d} \nu_{k(mp+1)}^{{\mathcal{F}}_v,{\mathcal{F}}_w}\ge \frac{\frac{\varepsilon p}{(mp+1)r}\cdot \dim R_k}{\dim R_{k(mp+1)}} \end{align*}$$
$$\begin{align*}\int_{\mathbb{R}} |\lambda| \mathrm{d} \nu_{k(mp+1)}^{{\mathcal{F}}_v,{\mathcal{F}}_w}\ge \frac{\frac{\varepsilon p}{(mp+1)r}\cdot \dim R_k}{\dim R_{k(mp+1)}} \end{align*}$$
for all
![]() $k\gg 0$
. Letting
$k\gg 0$
. Letting
![]() $k\to \infty $
, we get
$k\to \infty $
, we get
![]() $d_1({\mathcal {F}}_v,{\mathcal {F}}_w)>0$
, contradicting our assumption. Thus, we must have
$d_1({\mathcal {F}}_v,{\mathcal {F}}_w)>0$
, contradicting our assumption. Thus, we must have
![]() $v(f)=w(f)$
for all
$v(f)=w(f)$
for all
![]() $m\in \mathbb {N}$
and all
$m\in \mathbb {N}$
and all
![]() $f\in R_m$
and therefore
$f\in R_m$
and therefore
![]() $v=w$
.
$v=w$
.
Corollary 3.17. Let
![]() $(X,\Delta )$
be a log Fano pair, there is a unique valuation computing
$(X,\Delta )$
be a log Fano pair, there is a unique valuation computing
![]() $h(X,\Delta )$
in
$h(X,\Delta )$
in
![]() $\mathrm { Val}_X^{\circ }\cup \{v_{\mathrm {triv}}\}$
and it is quasi-monomial.
$\mathrm { Val}_X^{\circ }\cup \{v_{\mathrm {triv}}\}$
and it is quasi-monomial.
Proof. By [Reference Han and LiHL20b, Corollary 4.9], there is a quasi-monomial valuation
![]() $v\in \mathrm {Val}_X^{\circ } \cup \{v_{\mathrm {triv}}\}$
computing
$v\in \mathrm {Val}_X^{\circ } \cup \{v_{\mathrm {triv}}\}$
computing
![]() $h(X,\Delta )$
. The uniqueness is by Theorem 3.15.
$h(X,\Delta )$
. The uniqueness is by Theorem 3.15.
4 Weighted stability
In this section, we provide a common ground to study the stability of both Kähler–Ricci solitons and triples
![]() $(X,\Delta ,v_0)$
(where
$(X,\Delta ,v_0)$
(where
![]() $v_0$
is the unique minimizer of
$v_0$
is the unique minimizer of
![]() $\tilde {\beta }$
from the previous section) in a suitably weighted sense. The results will be applied in the next section to study the finite generation property for various minimizers.
$\tilde {\beta }$
from the previous section) in a suitably weighted sense. The results will be applied in the next section to study the finite generation property for various minimizers.
4.1 Weighted
 $\delta $
-invariants
$\delta $
-invariants
We first introduce a weighted version of the stability threshold and then generalize results from [Reference Blum and JonssonBJ20] to this setting (see also [Reference Rubinstein, Tian and ZhangRTZ21, Section 6]).
Definition 4.1. Let
![]() $v_0\in \mathrm {Val}_X$
be a quasi-monomial valuation and
$v_0\in \mathrm {Val}_X$
be a quasi-monomial valuation and
![]() $g\colon \mathbb {R}\to \mathbb {R}_+$
a continuous function. A g-weighted
$g\colon \mathbb {R}\to \mathbb {R}_+$
a continuous function. A g-weighted
![]() $(m,v_0)$
-basis type divisor is a divisor of the form
$(m,v_0)$
-basis type divisor is a divisor of the form
 $$\begin{align*}D=\frac{1}{mrQ_m} \sum_{i=1}^{N_m} g\left(\frac{v_0 (s_i)}{mr}\right)\cdot \{s_i=0\}, \end{align*}$$
$$\begin{align*}D=\frac{1}{mrQ_m} \sum_{i=1}^{N_m} g\left(\frac{v_0 (s_i)}{mr}\right)\cdot \{s_i=0\}, \end{align*}$$
where
![]() $(s_1, \cdots , s_{N_m})$
is a basis of
$(s_1, \cdots , s_{N_m})$
is a basis of
![]() $R_m$
that is compatible with
$R_m$
that is compatible with
![]() $v_0$
and
$v_0$
and
![]() $Q_m=\sum _{i=1}^{N_m} g\left (\frac {v_0(s_i)}{mr}\right )$
. Note that
$Q_m=\sum _{i=1}^{N_m} g\left (\frac {v_0(s_i)}{mr}\right )$
. Note that
![]() $D\in |-K_X-\Delta |_{\mathbb {R}}$
. We say D is compatible with a filtration
$D\in |-K_X-\Delta |_{\mathbb {R}}$
. We say D is compatible with a filtration
![]() ${\mathcal {F}}$
on R if the basis
${\mathcal {F}}$
on R if the basis
![]() $(s_1,\cdots ,s_{N_m})$
is compatible with
$(s_1,\cdots ,s_{N_m})$
is compatible with
![]() ${\mathcal {F}}$
. In particular, we say D is compatible with a valuation
${\mathcal {F}}$
. In particular, we say D is compatible with a valuation
![]() $v\in \mathrm {Val}_X^{\circ }$
(resp. an effective
$v\in \mathrm {Val}_X^{\circ }$
(resp. an effective
![]() ${\mathbb {Q}}$
-divisor G on X) if it is compatible with the induced filtration
${\mathbb {Q}}$
-divisor G on X) if it is compatible with the induced filtration
![]() ${\mathcal {F}}_v$
(resp.
${\mathcal {F}}_v$
(resp.
![]() ${\mathcal {F}}_G$
).
${\mathcal {F}}_G$
).
For any linearly bounded filtration
![]() ${\mathcal {F}}$
on R, let
${\mathcal {F}}$
on R, let
![]() $\boldsymbol {\nu }_m$
and
$\boldsymbol {\nu }_m$
and
![]() $\boldsymbol {\nu }=\mathrm { DH}_{{\mathcal {F}}_{v_0},{\mathcal {F}}}=\lim _{m\to \infty } \boldsymbol {\nu }_m$
denote the measures on
$\boldsymbol {\nu }=\mathrm { DH}_{{\mathcal {F}}_{v_0},{\mathcal {F}}}=\lim _{m\to \infty } \boldsymbol {\nu }_m$
denote the measures on
![]() $\mathbb {R}^2$
associated to
$\mathbb {R}^2$
associated to
![]() ${\mathcal {F}}_{v_0}$
and
${\mathcal {F}}_{v_0}$
and
![]() ${\mathcal {F}}$
as constructed in Section 3.1.3. We set
${\mathcal {F}}$
as constructed in Section 3.1.3. We set
 $$\begin{align*}S_{g,m}(v_0;{\mathcal{F}}):=\frac{\int_{\mathbb{R}^2} g(x)y \mathrm{d} \boldsymbol{\nu}_m}{\int_{\mathbb{R}^2} g(x) \mathrm{d} \boldsymbol{\nu}_m} \quad \text{and}\quad S_g(v_0;{\mathcal{F}}):=\lim_{m\to\infty} S_{g,m}(v_0;{\mathcal{F}})=\frac{\int_{\mathbb{R}^2} g(x)y \mathrm{d} \boldsymbol{\nu}}{\int_{\mathbb{R}^2} g(x) \mathrm{d} \boldsymbol{\nu}}. \end{align*}$$
$$\begin{align*}S_{g,m}(v_0;{\mathcal{F}}):=\frac{\int_{\mathbb{R}^2} g(x)y \mathrm{d} \boldsymbol{\nu}_m}{\int_{\mathbb{R}^2} g(x) \mathrm{d} \boldsymbol{\nu}_m} \quad \text{and}\quad S_g(v_0;{\mathcal{F}}):=\lim_{m\to\infty} S_{g,m}(v_0;{\mathcal{F}})=\frac{\int_{\mathbb{R}^2} g(x)y \mathrm{d} \boldsymbol{\nu}}{\int_{\mathbb{R}^2} g(x) \mathrm{d} \boldsymbol{\nu}}. \end{align*}$$
It is clear that
 $$\begin{align*}S_{g,m}(v_0;{\mathcal{F}}) = \frac{1}{mrQ_m}\sum_{i=1}^{N_m} g\left(\frac{v_0 (s_i)}{mr}\right)\cdot \mathrm{ ord}_{\mathcal{F}}(s_i) \end{align*}$$
$$\begin{align*}S_{g,m}(v_0;{\mathcal{F}}) = \frac{1}{mrQ_m}\sum_{i=1}^{N_m} g\left(\frac{v_0 (s_i)}{mr}\right)\cdot \mathrm{ ord}_{\mathcal{F}}(s_i) \end{align*}$$
for any basis
![]() $(s_1,\cdots ,s_{N_m})$
that is compatible with both
$(s_1,\cdots ,s_{N_m})$
that is compatible with both
![]() $v_0$
and
$v_0$
and
![]() ${\mathcal {F}}$
.
${\mathcal {F}}$
.
Lemma 4.2. For any
![]() $\varepsilon>0$
, there exists a positive integer
$\varepsilon>0$
, there exists a positive integer
![]() $m_0=m_0(\varepsilon )$
such that
$m_0=m_0(\varepsilon )$
such that
for any linearly bounded filtration
![]() ${\mathcal {F}}$
of R satisfying
${\mathcal {F}}$
of R satisfying
![]() ${\mathcal {F}}^0 R=R$
and any
${\mathcal {F}}^0 R=R$
and any
![]() $m\geq m_0$
.
$m\geq m_0$
.
This follows from essentially the same argument as [Reference Blum and JonssonBJ20, Corollary 2.10] except we need to use an Okounkov body that is induced by a suitable valuation.
Definition 4.3. Let
![]() $w\colon K(X)^{\times } \to \mathbb {Z}^n$
be a valuation with values in the group
$w\colon K(X)^{\times } \to \mathbb {Z}^n$
be a valuation with values in the group
![]() $\mathbb {Z}^n$
(equipped with some total ordering). Following [Reference Kaveh and KhovanskiiKK12], we say that w is faithful if its image equals
$\mathbb {Z}^n$
(equipped with some total ordering). Following [Reference Kaveh and KhovanskiiKK12], we say that w is faithful if its image equals
![]() $\mathbb {Z}^n$
; we say that w has one-dimensional leaves if
$\mathbb {Z}^n$
; we say that w has one-dimensional leaves if
![]() $\dim \hat {V}_{\alpha } \le 1$
for every
$\dim \hat {V}_{\alpha } \le 1$
for every
![]() $\alpha \in \mathbb {Z}^n$
, where
$\alpha \in \mathbb {Z}^n$
, where
![]() $\hat {V}_{\alpha }:=\{f\in K(X)\,\vert \,w(f)\ge \alpha \}/\{f\in K(X)\,\vert \,w(f)> \alpha \}$
. Finally, we say that w is a good valuation if it is faithful, has one-dimensional leaves and
$\hat {V}_{\alpha }:=\{f\in K(X)\,\vert \,w(f)\ge \alpha \}/\{f\in K(X)\,\vert \,w(f)> \alpha \}$
. Finally, we say that w is a good valuation if it is faithful, has one-dimensional leaves and
![]() $n=\dim X$
.
$n=\dim X$
.
Lemma 4.4. Let
![]() $v_0$
be a quasi-monomial valuation on X. Then there exists a good valuation
$v_0$
be a quasi-monomial valuation on X. Then there exists a good valuation
![]() $w_0\colon K(X)^{\times } \to \mathbb {Z}^n$
and
$w_0\colon K(X)^{\times } \to \mathbb {Z}^n$
and
![]() $u_0\in \mathbb {R}^n_{\ge 0}$
such that
$u_0\in \mathbb {R}^n_{\ge 0}$
such that
Proof. Let r be the rational rank of
![]() $v_0$
. Since
$v_0$
. Since
![]() $v_0$
is quasi-monomial, there exists a log resolution
$v_0$
is quasi-monomial, there exists a log resolution
![]() $\pi \colon Y\to X$
, a regular system of parameters
$\pi \colon Y\to X$
, a regular system of parameters
![]() $y_1,\ldots , y_r$
at a point
$y_1,\ldots , y_r$
at a point
![]() $\eta \in Y$
, and
$\eta \in Y$
, and
![]() $\alpha \in \mathbb {R}^r_+$
such that
$\alpha \in \mathbb {R}^r_+$
such that
![]() $v_0=v_{\alpha }$
. Let
$v_0=v_{\alpha }$
. Let
![]() $W=C_Y(v_0)$
. Possibly after further blowups, we may choose a flag
$W=C_Y(v_0)$
. Possibly after further blowups, we may choose a flag
![]() $W_{\bullet }\colon W=W_0\supseteq \cdots \supseteq W_{n-r}=\{\text {point}\}$
of smooth subvarieties such that each
$W_{\bullet }\colon W=W_0\supseteq \cdots \supseteq W_{n-r}=\{\text {point}\}$
of smooth subvarieties such that each
![]() $W_{i+1}$
is a divisor in
$W_{i+1}$
is a divisor in
![]() $W_i$
. Let
$W_i$
. Let
![]() $\nu =\nu _{W_{\bullet }}\colon K(W)^{\times } \to \mathbb {Z}^{n-r}$
be the induced valuation as in [Reference Lazarsfeld and MustaţăLM09]. Any nonzero
$\nu =\nu _{W_{\bullet }}\colon K(W)^{\times } \to \mathbb {Z}^{n-r}$
be the induced valuation as in [Reference Lazarsfeld and MustaţăLM09]. Any nonzero
![]() $f\in {\mathcal {O}}_{Y,W}$
can be written as
$f\in {\mathcal {O}}_{Y,W}$
can be written as
![]() $f=c_{\beta } y^{\beta } +f_1$
for some (uniquely determined)
$f=c_{\beta } y^{\beta } +f_1$
for some (uniquely determined)
![]() $\beta \in \mathbb {N}^r$
and
$\beta \in \mathbb {N}^r$
and
![]() $c_{\beta },f_1\in {\mathcal {O}}_{Y,W}$
such that
$c_{\beta },f_1\in {\mathcal {O}}_{Y,W}$
such that
![]() $\langle \alpha ,\beta \rangle =v_0(f)$
and
$\langle \alpha ,\beta \rangle =v_0(f)$
and
![]() $v_0(f_1)>v_0(f)$
. Moreover,
$v_0(f_1)>v_0(f)$
. Moreover,
![]() $0\neq \bar {c}_{\beta } \in K(W)$
is well defined and does not depend on the choice of
$0\neq \bar {c}_{\beta } \in K(W)$
is well defined and does not depend on the choice of
![]() $c_{\beta }$
. Now, consider the valuation
$c_{\beta }$
. Now, consider the valuation
![]() $w_0\colon K(X)^{\times } \to \mathbb {Z}^n$
given by setting
$w_0\colon K(X)^{\times } \to \mathbb {Z}^n$
given by setting
![]() $w_0(f)=(\beta ,\nu (\bar {c}_{\beta }))$
for
$w_0(f)=(\beta ,\nu (\bar {c}_{\beta }))$
for
![]() $f\in {\mathcal {O}}_{Y,W}$
. It is not hard to check from the construction that
$f\in {\mathcal {O}}_{Y,W}$
. It is not hard to check from the construction that
![]() $w_0$
is faithful and has one-dimensional leaves. Clearly,
$w_0$
is faithful and has one-dimensional leaves. Clearly,
![]() $v_0(f)=\langle (\alpha ,0,\cdots ,0),w_0(f)\rangle $
. Thus,
$v_0(f)=\langle (\alpha ,0,\cdots ,0),w_0(f)\rangle $
. Thus,
![]() $w_0$
is the good valuation we want.
$w_0$
is the good valuation we want.
Proof of Lemma 4.2.
Since the argument is very similar to those in [Reference Blum and JonssonBJ20], we only sketch the proof. By Lemma 4.4, there exists some good valuation
![]() $w_0\colon K(X)\to \mathbb {Z}^n$
and some
$w_0\colon K(X)\to \mathbb {Z}^n$
and some
![]() $u_0\in \mathbb {R}^n_{\ge 0}$
such that
$u_0\in \mathbb {R}^n_{\ge 0}$
such that
![]() $v_0(f)=\langle u_0,w_0(f) \rangle $
. Let
$v_0(f)=\langle u_0,w_0(f) \rangle $
. Let
![]() $\Sigma \subseteq \mathbb {R}^n$
be the corresponding Okounkov body (see [Reference Kaveh and KhovanskiiKK12]), that is, the closed convex hull of
$\Sigma \subseteq \mathbb {R}^n$
be the corresponding Okounkov body (see [Reference Kaveh and KhovanskiiKK12]), that is, the closed convex hull of
![]() $\bigcup _{m\geq 1}\{\frac {w_0(s)}{mr}\,\vert \,s\in R_m\setminus \{0\}\}$
. We regard the function g also as a positive function on
$\bigcup _{m\geq 1}\{\frac {w_0(s)}{mr}\,\vert \,s\in R_m\setminus \{0\}\}$
. We regard the function g also as a positive function on
![]() $\Sigma $
by
$\Sigma $
by
![]() $g(\alpha )=g(\langle u_0,\alpha \rangle )$
. Let
$g(\alpha )=g(\langle u_0,\alpha \rangle )$
. Let
![]() $\rho $
denote the Lebesgue measure on
$\rho $
denote the Lebesgue measure on
![]() $\Sigma $
and
$\Sigma $
and
![]() $\rho _m$
the atomic probability measure supported on
$\rho _m$
the atomic probability measure supported on
![]() $\Sigma \cap \frac {1}{m} \mathbb {Z}^n$
as defined in [Reference Blum and JonssonBJ20, Section 2.2]. Note that
$\Sigma \cap \frac {1}{m} \mathbb {Z}^n$
as defined in [Reference Blum and JonssonBJ20, Section 2.2]. Note that
![]() $\lim _{m\to \infty }\rho _m=\rho $
in the weak topology of measures (see [Reference Blum and JonssonBJ20, Theorem 2.1]). Using the argument of [Reference Blum and JonssonBJ20, Lemma 2.2] and the uniform continuity of g on
$\lim _{m\to \infty }\rho _m=\rho $
in the weak topology of measures (see [Reference Blum and JonssonBJ20, Theorem 2.1]). Using the argument of [Reference Blum and JonssonBJ20, Lemma 2.2] and the uniform continuity of g on
![]() $\Sigma $
, we see that for each
$\Sigma $
, we see that for each
![]() $\varepsilon>0$
there exists
$\varepsilon>0$
there exists
![]() $m_0=m_0(\varepsilon )$
such that
$m_0=m_0(\varepsilon )$
such that
for every
![]() $m\ge m_0$
and every concave function
$m\ge m_0$
and every concave function
![]() $f\colon \Sigma \to \mathbb {R}$
satisfying
$f\colon \Sigma \to \mathbb {R}$
satisfying
![]() $0\le f\le 1$
. We may then apply the proof of [Reference Blum and JonssonBJ20, Corollary 2.10] to the concave transform of
$0\le f\le 1$
. We may then apply the proof of [Reference Blum and JonssonBJ20, Corollary 2.10] to the concave transform of
![]() ${\mathcal {F}}$
and conclude that (after possibly enlarging
${\mathcal {F}}$
and conclude that (after possibly enlarging
![]() $m_0$
)
$m_0$
)
![]() $S_{g,m}(v_0;{\mathcal {F}})\le (1+\varepsilon )S_g(v_0;{\mathcal {F}})$
for all linearly bounded filtrations
$S_{g,m}(v_0;{\mathcal {F}})\le (1+\varepsilon )S_g(v_0;{\mathcal {F}})$
for all linearly bounded filtrations
![]() ${\mathcal {F}}$
and all
${\mathcal {F}}$
and all
![]() $m\ge m_0$
.
$m\ge m_0$
.
When
![]() ${\mathcal {F}}$
is the filtration induced by some valuation
${\mathcal {F}}$
is the filtration induced by some valuation
![]() $v\in \mathrm {Val}_X^{\circ }$
(resp. effective divisor
$v\in \mathrm {Val}_X^{\circ }$
(resp. effective divisor
![]() $G\neq 0$
on X), we will simply write
$G\neq 0$
on X), we will simply write
![]() $S_g(v_0;v)$
(resp.
$S_g(v_0;v)$
(resp.
![]() $S_g(v_0;G)$
) for
$S_g(v_0;G)$
) for
![]() $S_{g}(v_0,{\mathcal {F}})$
. Let
$S_{g}(v_0,{\mathcal {F}})$
. Let
![]() $\mathbb {T}=\mathbb {G}_m^s<\operatorname {Aut}(X,\Delta )$
be a torus subgroup of the automorphism group (we allow
$\mathbb {T}=\mathbb {G}_m^s<\operatorname {Aut}(X,\Delta )$
be a torus subgroup of the automorphism group (we allow
![]() $\mathbb {T}=\{1\}$
). For any quasi-monomial valuation
$\mathbb {T}=\{1\}$
). For any quasi-monomial valuation
![]() $v_0\in \mathrm {Val}_X^{\mathbb {T},\circ }$
we set
$v_0\in \mathrm {Val}_X^{\mathbb {T},\circ }$
we set
 $$\begin{align*}\delta_{g,\mathbb{T}} (X,\Delta,v_0): = \inf_{v\in \mathrm{Val}_X^{\mathbb{T},\circ}} \frac{A_{X,\Delta}(v)}{S_g(v_0;v)}. \end{align*}$$
$$\begin{align*}\delta_{g,\mathbb{T}} (X,\Delta,v_0): = \inf_{v\in \mathrm{Val}_X^{\mathbb{T},\circ}} \frac{A_{X,\Delta}(v)}{S_g(v_0;v)}. \end{align*}$$
We say that
![]() $v\in \mathrm {Val}_X^{\mathbb {T},\circ }$
computes
$v\in \mathrm {Val}_X^{\mathbb {T},\circ }$
computes
![]() $\delta _{g,\mathbb {T}}(X,\Delta ,v_0)$
if it achieves the above infimum. For each positive integer m, we also set
$\delta _{g,\mathbb {T}}(X,\Delta ,v_0)$
if it achieves the above infimum. For each positive integer m, we also set
When
![]() $\mathbb {T}=\{1\}$
, we will suppress the subscript
$\mathbb {T}=\{1\}$
, we will suppress the subscript
![]() $\mathbb {T}$
and write
$\mathbb {T}$
and write
![]() $\delta _g(X,\Delta ,v_0)$
and
$\delta _g(X,\Delta ,v_0)$
and
![]() $\delta _{g,m}(X,\Delta ,v_0)$
.
$\delta _{g,m}(X,\Delta ,v_0)$
.
Lemma 4.5. In the above setup, we have
Proof. It is not hard to check from the definition that
and in fact
![]() $S_{g,m}(v_0;v)=v(D)$
for any g-weighted
$S_{g,m}(v_0;v)=v(D)$
for any g-weighted
![]() $(m,v_0)$
-basis type divisor D that’s also compatible with v. Moreover, when
$(m,v_0)$
-basis type divisor D that’s also compatible with v. Moreover, when
![]() $v_0,v\in \mathrm {Val}_X^{\mathbb {T},\circ }$
, such a divisor D can be chosen to be
$v_0,v\in \mathrm {Val}_X^{\mathbb {T},\circ }$
, such a divisor D can be chosen to be
![]() $\mathbb {T}$
-invariant by choosing compatible basis in each component of the weight decomposition under the torus action. Hence,
$\mathbb {T}$
-invariant by choosing compatible basis in each component of the weight decomposition under the torus action. Hence,
 $$ \begin{align} \delta_{g,\mathbb{T},m}(X,\Delta,v_0) =\inf_{v\in\mathrm{Val}_X^{\mathbb{T},\circ}} \frac{A_{X,\Delta}(v)}{S_{g,m}(v_0;v)}. \end{align} $$
$$ \begin{align} \delta_{g,\mathbb{T},m}(X,\Delta,v_0) =\inf_{v\in\mathrm{Val}_X^{\mathbb{T},\circ}} \frac{A_{X,\Delta}(v)}{S_{g,m}(v_0;v)}. \end{align} $$
Combined with Lemma 4.2, the argument in the proof of [Reference Blum and JonssonBJ20, Theorem 4.4] then yields
![]() $\delta _{g,\mathbb {T}}(X,\Delta ,v_0)=\lim _{m\to \infty }\delta _{g,\mathbb {T},m}(X,\Delta ,v_0)$
.
$\delta _{g,\mathbb {T}}(X,\Delta ,v_0)=\lim _{m\to \infty }\delta _{g,\mathbb {T},m}(X,\Delta ,v_0)$
.
4.2 Reduced uniform stability
In this section, we define stability notions for triples
![]() $(X,\Delta ,v_0)$
where
$(X,\Delta ,v_0)$
where
![]() $(X,\Delta )$
is a log Fano pair,
$(X,\Delta )$
is a log Fano pair,
![]() $v_0$
is a quasi-monomial valuation on X, and
$v_0$
is a quasi-monomial valuation on X, and
![]() $g\colon \mathbb {R}\to \mathbb {R}_+$
is a continuous function.
$g\colon \mathbb {R}\to \mathbb {R}_+$
is a continuous function.
We first define the weighted version of the non-Archimedean functional. For any linearly bounded filtration on R, we set
 $$ \begin{align*} \mathbf{D}^{\mathrm{NA}}_g({\mathcal{F}}) & := \mathbf{L}^{\mathrm{NA}}({\mathcal{F}}) - S_g(v_0;{\mathcal{F}}),\\ \mathbf{J}^{\mathrm{NA}}_g({\mathcal{F}}) & := \lambda_{\max}({\mathcal{F}})-S_g(v_0;{\mathcal{F}}). \end{align*} $$
$$ \begin{align*} \mathbf{D}^{\mathrm{NA}}_g({\mathcal{F}}) & := \mathbf{L}^{\mathrm{NA}}({\mathcal{F}}) - S_g(v_0;{\mathcal{F}}),\\ \mathbf{J}^{\mathrm{NA}}_g({\mathcal{F}}) & := \lambda_{\max}({\mathcal{F}})-S_g(v_0;{\mathcal{F}}). \end{align*} $$
Note that
![]() $\mathbf {J}^{\mathrm {NA}}_g({\mathcal {F}})\geq 0$
. We also set
$\mathbf {J}^{\mathrm {NA}}_g({\mathcal {F}})\geq 0$
. We also set
![]() $\mathbf {E}^{\mathrm {NA}}_g({\mathcal {F}}):=S_g(v_0;{\mathcal {F}})$
. If
$\mathbf {E}^{\mathrm {NA}}_g({\mathcal {F}}):=S_g(v_0;{\mathcal {F}})$
. If
![]() $({\mathcal {X}},\Delta _{{\mathcal {X}}};{\mathcal {L}})$
is a normal test configuration of
$({\mathcal {X}},\Delta _{{\mathcal {X}}};{\mathcal {L}})$
is a normal test configuration of
![]() $(X,\Delta )$
, then we set
$(X,\Delta )$
, then we set
![]() $\mathbf {D}^{\mathrm {NA}}_g({\mathcal {X}},\Delta _{{\mathcal {X}}};{\mathcal {L}}):= \mathbf {D}^{\mathrm {NA}}_g ({\mathcal {F}}_{({\mathcal {X}},\Delta ;{\mathcal {L}})})$
and
$\mathbf {D}^{\mathrm {NA}}_g({\mathcal {X}},\Delta _{{\mathcal {X}}};{\mathcal {L}}):= \mathbf {D}^{\mathrm {NA}}_g ({\mathcal {F}}_{({\mathcal {X}},\Delta ;{\mathcal {L}})})$
and
![]() $\mathbf {J}^{\mathrm {NA}}_g({\mathcal {X}},\Delta ;{\mathcal {L}}):= \mathbf {J}^{\mathrm {NA}}_g ({\mathcal {F}}_{({\mathcal {X}},\Delta _{{\mathcal {X}}};{\mathcal {L}})})$
. Denote by
$\mathbf {J}^{\mathrm {NA}}_g({\mathcal {X}},\Delta ;{\mathcal {L}}):= \mathbf {J}^{\mathrm {NA}}_g ({\mathcal {F}}_{({\mathcal {X}},\Delta _{{\mathcal {X}}};{\mathcal {L}})})$
. Denote by
![]() $\operatorname {Aut}(X,\Delta ,v_0)$
the subgroup of
$\operatorname {Aut}(X,\Delta ,v_0)$
the subgroup of
![]() $\operatorname {Aut}(X,\Delta )$
that leaves the valuation
$\operatorname {Aut}(X,\Delta )$
that leaves the valuation
![]() $v_0$
invariant, and let
$v_0$
invariant, and let
![]() $\mathbb {T}<\operatorname {Aut}(X,\Delta ,v_0)$
be a torus subgroup.
$\mathbb {T}<\operatorname {Aut}(X,\Delta ,v_0)$
be a torus subgroup.
Definition 4.6. We say that the triple
![]() $(X,\Delta ,v_0)$
is
$(X,\Delta ,v_0)$
is
![]() $\mathbb {T}$
-equivariantly g-Ding semistable (or simply g-Ding semistable when
$\mathbb {T}$
-equivariantly g-Ding semistable (or simply g-Ding semistable when
![]() $\mathbb {T}=\{1\}$
) if
$\mathbb {T}=\{1\}$
) if
![]() $\mathbf {D}^{\mathrm {NA}}_g({\mathcal {X}},\Delta ;{\mathcal {L}})\ge 0$
for all
$\mathbf {D}^{\mathrm {NA}}_g({\mathcal {X}},\Delta ;{\mathcal {L}})\ge 0$
for all
![]() $\mathbb {T}$
-equivariant normal test configurations
$\mathbb {T}$
-equivariant normal test configurations
![]() $({\mathcal {X}},\Delta ;{\mathcal {L}})$
of
$({\mathcal {X}},\Delta ;{\mathcal {L}})$
of
![]() $(X,\Delta )$
.
$(X,\Delta )$
.
Denote by
![]() $M:=\mathrm {Hom}(\mathbb {T},\mathbb {G}_m)$
the weight lattice and
$M:=\mathrm {Hom}(\mathbb {T},\mathbb {G}_m)$
the weight lattice and
![]() $N:=\mathrm { Hom}(\mathbb {G}_m,\mathbb {T})$
the co-weight lattice. Then there is a weight decomposition
$N:=\mathrm { Hom}(\mathbb {G}_m,\mathbb {T})$
the co-weight lattice. Then there is a weight decomposition
![]() $R_m=\oplus _{\alpha \in M} R_{m,\alpha }$
. Recall that, for any
$R_m=\oplus _{\alpha \in M} R_{m,\alpha }$
. Recall that, for any
![]() $\mathbb {T}$
-equivariant filtration
$\mathbb {T}$
-equivariant filtration
![]() ${\mathcal {F}}$
and each
${\mathcal {F}}$
and each
![]() $\eta \in N_{\mathbb {R}}$
, there is an
$\eta \in N_{\mathbb {R}}$
, there is an
![]() $\eta $
-twist
$\eta $
-twist
![]() ${\mathcal {F}}_{\eta }$
of
${\mathcal {F}}_{\eta }$
of
![]() ${\mathcal {F}}$
given by
${\mathcal {F}}$
given by
Set
![]() $\mathrm {Fut}_g (\eta ) := \mathbf {E}^{\mathrm {NA}}_g ({\mathcal {F}}) - \mathbf {E}^{\mathrm {NA}}_g ({\mathcal {F}}_{\eta })$
. It is not hard to see from the definition that
$\mathrm {Fut}_g (\eta ) := \mathbf {E}^{\mathrm {NA}}_g ({\mathcal {F}}) - \mathbf {E}^{\mathrm {NA}}_g ({\mathcal {F}}_{\eta })$
. It is not hard to see from the definition that
![]() $\mathrm {Fut}_g$
does not depend on the choice of the filtration
$\mathrm {Fut}_g$
does not depend on the choice of the filtration
![]() ${\mathcal {F}}$
and is linear on
${\mathcal {F}}$
and is linear on
![]() $N_{\mathbb {R}}$
. We define the reduced
$N_{\mathbb {R}}$
. We define the reduced
![]() $\mathbf {J}^{\mathrm {NA}}_g$
-norm of
$\mathbf {J}^{\mathrm {NA}}_g$
-norm of
![]() ${\mathcal {F}}$
as
${\mathcal {F}}$
as
Definition 4.7. We say a triple
![]() $(X,\Delta ,v_0)$
is reduced uniformly g-Ding stable if there exists a maximal torus
$(X,\Delta ,v_0)$
is reduced uniformly g-Ding stable if there exists a maximal torus
![]() $\mathbb {T}<\operatorname {Aut}(X,\Delta ,v_0)$
and some
$\mathbb {T}<\operatorname {Aut}(X,\Delta ,v_0)$
and some
![]() $\varepsilon>0$
such that
$\varepsilon>0$
such that
for all
![]() $\mathbb {T}$
-equivariant normal test configurations
$\mathbb {T}$
-equivariant normal test configurations
![]() $({\mathcal {X}},\Delta _{{\mathcal {X}}};{\mathcal {L}})$
of
$({\mathcal {X}},\Delta _{{\mathcal {X}}};{\mathcal {L}})$
of
![]() $(X,\Delta )$
.
$(X,\Delta )$
.
Note that the above definition is independent of the choice of
![]() $\mathbb {T}$
since any two maximal tori are conjugate.
$\mathbb {T}$
since any two maximal tori are conjugate.
Lemma 4.8. Let
![]() $\mathbb {T}<\operatorname {Aut}(X,\Delta ,v_0)$
be a torus. Assume that
$\mathbb {T}<\operatorname {Aut}(X,\Delta ,v_0)$
be a torus. Assume that
![]() $\mathbf {D}^{\mathrm {NA}}_g\ge 0$
for any product test configurations that is induced by a one parameter subgroup of
$\mathbf {D}^{\mathrm {NA}}_g\ge 0$
for any product test configurations that is induced by a one parameter subgroup of
![]() $\mathbb {T}$
. Then
$\mathbb {T}$
. Then
![]() $\mathrm {Fut}_g\equiv 0$
on
$\mathrm {Fut}_g\equiv 0$
on
![]() $N_{\mathbb {R}}$
.
$N_{\mathbb {R}}$
.
Proof. Let
![]() ${\mathcal {F}}$
be the trivial filtration of R. By Lemma 3.8 and [Reference Xu and ZhuangXZ20, Lemma A.6], we have
${\mathcal {F}}$
be the trivial filtration of R. By Lemma 3.8 and [Reference Xu and ZhuangXZ20, Lemma A.6], we have
![]() $\mathbf {L}^{\mathrm {NA}}({\mathcal {F}})=\mathbf {L}^{\mathrm {NA}}({\mathcal {F}}_{\eta })$
for any
$\mathbf {L}^{\mathrm {NA}}({\mathcal {F}})=\mathbf {L}^{\mathrm {NA}}({\mathcal {F}}_{\eta })$
for any
![]() $\eta \in N_{\mathbb {R}}$
. Thus,
$\eta \in N_{\mathbb {R}}$
. Thus,
![]() $\mathbf {D}^{\mathrm {NA}}_g({\mathcal {F}}_{\eta })=\mathbf {D}^{\mathrm {NA}}_g({\mathcal {F}})+\mathrm {Fut}_g(\eta )=\mathrm { Fut}_g(\eta )$
. By assumption,
$\mathbf {D}^{\mathrm {NA}}_g({\mathcal {F}}_{\eta })=\mathbf {D}^{\mathrm {NA}}_g({\mathcal {F}})+\mathrm {Fut}_g(\eta )=\mathrm { Fut}_g(\eta )$
. By assumption,
![]() $\mathbf {D}^{\mathrm {NA}}_g({\mathcal {F}}_{\eta })\ge 0$
for any
$\mathbf {D}^{\mathrm {NA}}_g({\mathcal {F}}_{\eta })\ge 0$
for any
![]() $\eta \in N$
. By linearity,
$\eta \in N$
. By linearity,
![]() $\mathrm {Fut}_g\equiv 0$
on N and, hence, the same holds on
$\mathrm {Fut}_g\equiv 0$
on N and, hence, the same holds on
![]() $N_{\mathbb {R}}$
.
$N_{\mathbb {R}}$
.
We are most interested in the case
![]() $v_0=\mathrm {wt}_{\xi }$
for some torus
$v_0=\mathrm {wt}_{\xi }$
for some torus
![]() $\mathbb {T}<\operatorname {Aut}(X,\Delta )$
and some
$\mathbb {T}<\operatorname {Aut}(X,\Delta )$
and some
![]() $\xi \in N_{\mathbb {R}}$
. In this case, we write
$\xi \in N_{\mathbb {R}}$
. In this case, we write
![]() $(X,\Delta ,\xi )$
instead of
$(X,\Delta ,\xi )$
instead of
![]() $(X,\Delta ,\mathrm {wt}_{\xi })$
. We note that while
$(X,\Delta ,\mathrm {wt}_{\xi })$
. We note that while
![]() $\mathbb {T}$
is not explicitly written out in the notion
$\mathbb {T}$
is not explicitly written out in the notion
![]() $(X,\Delta ,\xi )$
, it is indeed part of the data.
$(X,\Delta ,\xi )$
, it is indeed part of the data.
Theorem 4.9 [Reference Han and LiHL20].
Let
![]() $(X,\Delta ,\xi )$
be a triple over
$(X,\Delta ,\xi )$
be a triple over
![]() . Then it admits a Kähler–Ricci g-soliton if and only if it is reduced uniformly g-Ding stable.
. Then it admits a Kähler–Ricci g-soliton if and only if it is reduced uniformly g-Ding stable.
Definition 4.10. Let
![]() $(X,\Delta ,\xi )$
be a triple. We say that
$(X,\Delta ,\xi )$
be a triple. We say that
![]() $(X,\Delta ,\xi )$
is g-Ding semistable if it is
$(X,\Delta ,\xi )$
is g-Ding semistable if it is
![]() $\mathbb {T}$
-equivariantly g-Ding semistable. We say that
$\mathbb {T}$
-equivariantly g-Ding semistable. We say that
![]() $(X,\Delta ,\xi )$
is g-Ding polystable if it is g-Ding semistable and
$(X,\Delta ,\xi )$
is g-Ding polystable if it is g-Ding semistable and
![]() $\mathbf {D}^{\mathrm {NA}}_g({\mathcal {X}},\Delta _{{\mathcal {X}}};{\mathcal {L}})= 0$
for a weakly special
$\mathbf {D}^{\mathrm {NA}}_g({\mathcal {X}},\Delta _{{\mathcal {X}}};{\mathcal {L}})= 0$
for a weakly special
![]() $\mathbb {T}$
-equivariant test configuration
$\mathbb {T}$
-equivariant test configuration
![]() $({\mathcal {X}},\Delta _{{\mathcal {X}}};{\mathcal {L}})$
only if it is a product test configuration.
$({\mathcal {X}},\Delta _{{\mathcal {X}}};{\mathcal {L}})$
only if it is a product test configuration.
We say that
![]() $(X,\Delta ,\xi )$
is K-semistable (resp. K-polystable, or reduced uniformly Ding stable) if it is g-Ding semistable (resp. g-Ding polystable, or reduced uniformly g-Ding stable) for
$(X,\Delta ,\xi )$
is K-semistable (resp. K-polystable, or reduced uniformly Ding stable) if it is g-Ding semistable (resp. g-Ding polystable, or reduced uniformly g-Ding stable) for
![]() $g(x)=e^{-x}$
.
$g(x)=e^{-x}$
.
Remark 4.11. The above definition of K-polystability agrees with the notion in [Reference Berman and NyströmBWN14] when
![]() $\mathbb {T}$
is the torus of smallest dimension such that
$\mathbb {T}$
is the torus of smallest dimension such that
![]() $\xi \in N_{\mathbb {R}}$
; see [Reference Han and LiHL20b, Remark 2.47]. Note that K-polystability of Kähler–Ricci solitons is proved in [Reference Berman and NyströmBWN14, Theorem 1.5]. Later, we will see that the definition indeed does not depend on the choice of
$\xi \in N_{\mathbb {R}}$
; see [Reference Han and LiHL20b, Remark 2.47]. Note that K-polystability of Kähler–Ricci solitons is proved in [Reference Berman and NyströmBWN14, Theorem 1.5]. Later, we will see that the definition indeed does not depend on the choice of
![]() $\mathbb {T}$
(see Remark 5.10).
$\mathbb {T}$
(see Remark 5.10).
The following is the main result of this subsection.
Lemma 4.12. Let
![]() $v_0$
be a quasi-monomial valuation on X, and let
$v_0$
be a quasi-monomial valuation on X, and let
![]() $\mathbb {T}<\operatorname {Aut}(X,\Delta ,v_0)$
be a torus. Let
$\mathbb {T}<\operatorname {Aut}(X,\Delta ,v_0)$
be a torus. Let
![]() $g\colon \mathbb {R}\to \mathbb {R}_+$
be a continuous function and
$g\colon \mathbb {R}\to \mathbb {R}_+$
be a continuous function and
![]() $c\in [0,1)$
. Then the following are equivalent:
$c\in [0,1)$
. Then the following are equivalent:
-
1.
 $\mathbf {D}^{\mathrm {NA}}_g({\mathcal {X}},\Delta _{{\mathcal {X}}};{\mathcal {L}})\geq c\cdot \mathbf {J}^{\mathrm {NA}}_{g,\mathbb {T}} ({\mathcal {X}},\Delta _{{\mathcal {X}}};{\mathcal {L}})$
for any
$\mathbf {D}^{\mathrm {NA}}_g({\mathcal {X}},\Delta _{{\mathcal {X}}};{\mathcal {L}})\geq c\cdot \mathbf {J}^{\mathrm {NA}}_{g,\mathbb {T}} ({\mathcal {X}},\Delta _{{\mathcal {X}}};{\mathcal {L}})$
for any
 $\mathbb {T}$
-equivariant normal test configuration
$\mathbb {T}$
-equivariant normal test configuration
 $({\mathcal {X}},\Delta _{{\mathcal {X}}};{\mathcal {L}})$
of
$({\mathcal {X}},\Delta _{{\mathcal {X}}};{\mathcal {L}})$
of
 $(X,\Delta )$
.
$(X,\Delta )$
. -
2.
 $\mathbf {D}^{\mathrm {NA}}_g({\mathcal {X}},\Delta _{{\mathcal {X}}};{\mathcal {L}})\geq c\cdot \mathbf {J}^{\mathrm {NA}}_{g,\mathbb {T}} ({\mathcal {X}},\Delta _{{\mathcal {X}}};{\mathcal {L}})$
for any
$\mathbf {D}^{\mathrm {NA}}_g({\mathcal {X}},\Delta _{{\mathcal {X}}};{\mathcal {L}})\geq c\cdot \mathbf {J}^{\mathrm {NA}}_{g,\mathbb {T}} ({\mathcal {X}},\Delta _{{\mathcal {X}}};{\mathcal {L}})$
for any
 $\mathbb {T}$
-equivariant weakly special test configuration
$\mathbb {T}$
-equivariant weakly special test configuration
 $({\mathcal {X}},\Delta _{{\mathcal {X}}};{\mathcal {L}})$
of
$({\mathcal {X}},\Delta _{{\mathcal {X}}};{\mathcal {L}})$
of
 $(X,\Delta )$
.
$(X,\Delta )$
. -
3.
 $\mathbf {D}^{\mathrm {NA}}_g({\mathcal {F}}_v) \ge c \cdot \mathbf {J}^{\mathrm {NA}}_{g,\mathbb {T}}({\mathcal {F}}_v)$
for any divisorial valuation
$\mathbf {D}^{\mathrm {NA}}_g({\mathcal {F}}_v) \ge c \cdot \mathbf {J}^{\mathrm {NA}}_{g,\mathbb {T}}({\mathcal {F}}_v)$
for any divisorial valuation
 $v\in \mathrm { Val}_X^{\mathbb {T},\circ }$
that is an lc place of a
$v\in \mathrm { Val}_X^{\mathbb {T},\circ }$
that is an lc place of a
 ${\mathbb {Q}}$
-complement.
${\mathbb {Q}}$
-complement.
Proof. When
![]() $v_0=\mathrm {wt}_{\xi }$
this is treated in [Reference Han and LiHL20, Section 7] using [Reference Li and XuLX14]. Here, we present a proof that is independent of [Reference Li and XuLX14]. It is clear that (1) implies (2). By [Reference Blum, Liu and XuBLX22, Theorem A.2], (2) implies (3). Thus, it remains to show (3) implies (1). To see this, let
$v_0=\mathrm {wt}_{\xi }$
this is treated in [Reference Han and LiHL20, Section 7] using [Reference Li and XuLX14]. Here, we present a proof that is independent of [Reference Li and XuLX14]. It is clear that (1) implies (2). By [Reference Blum, Liu and XuBLX22, Theorem A.2], (2) implies (3). Thus, it remains to show (3) implies (1). To see this, let
![]() ${\mathcal {F}}$
be a finitely generated
${\mathcal {F}}$
be a finitely generated
![]() $\mathbb {T}$
-equivariant
$\mathbb {T}$
-equivariant
![]() $\mathbb {Z}$
-filtration of R. If
$\mathbb {Z}$
-filtration of R. If
![]() $\mathbf {L}^{\mathrm {NA}}({\mathcal {F}})\ge \lambda _{\max }({\mathcal {F}})$
, then we already have
$\mathbf {L}^{\mathrm {NA}}({\mathcal {F}})\ge \lambda _{\max }({\mathcal {F}})$
, then we already have
![]() $\mathbf {D}^{\mathrm {NA}}_g({\mathcal {F}})\ge \mathbf {J}^{\mathrm {NA}}_g({\mathcal {F}})\ge \mathbf {J}^{\mathrm {NA}}_{g,\mathbb {T}}({\mathcal {F}})$
. Thus, to prove (1) we may assume that
$\mathbf {D}^{\mathrm {NA}}_g({\mathcal {F}})\ge \mathbf {J}^{\mathrm {NA}}_g({\mathcal {F}})\ge \mathbf {J}^{\mathrm {NA}}_{g,\mathbb {T}}({\mathcal {F}})$
. Thus, to prove (1) we may assume that
![]() $\mathbf {L}^{\mathrm {NA}}({\mathcal {F}})<\lambda _{\max }({\mathcal {F}})$
. By the second part of Lemma 3.8 and Remark 3.9, there exists some divisorial lc place of a
$\mathbf {L}^{\mathrm {NA}}({\mathcal {F}})<\lambda _{\max }({\mathcal {F}})$
. By the second part of Lemma 3.8 and Remark 3.9, there exists some divisorial lc place of a
![]() ${\mathbb {Q}}$
-complement
${\mathbb {Q}}$
-complement
![]() $v\in \mathrm {Val}_X^{\mathbb {T},\circ }$
such that
$v\in \mathrm {Val}_X^{\mathbb {T},\circ }$
such that
for all
![]() $\lambda \in \mathbb {R}$
. Since
$\lambda \in \mathbb {R}$
. Since
![]() $\mathbf {D}^{\mathrm {NA}}_g({\mathcal {F}})$
and
$\mathbf {D}^{\mathrm {NA}}_g({\mathcal {F}})$
and
![]() $\mathbf {J}^{\mathrm {NA}}_{g,\mathbb {T}}({\mathcal {F}})$
are both translation invariant, we may shift
$\mathbf {J}^{\mathrm {NA}}_{g,\mathbb {T}}({\mathcal {F}})$
are both translation invariant, we may shift
![]() ${\mathcal {F}}$
so that
${\mathcal {F}}$
so that
![]() $\mathbf {L}^{\mathrm {NA}}({\mathcal {F}})=A_{X,\Delta }(v)$
. The above inequality then becomes
$\mathbf {L}^{\mathrm {NA}}({\mathcal {F}})=A_{X,\Delta }(v)$
. The above inequality then becomes
![]() $v(I^{(\lambda )}_{\bullet })\ge \lambda r$
and therefore
$v(I^{(\lambda )}_{\bullet })\ge \lambda r$
and therefore
![]() ${\mathcal {F}}^{\lambda } R\subseteq {\mathcal {F}}_v^{\lambda } R$
for all
${\mathcal {F}}^{\lambda } R\subseteq {\mathcal {F}}_v^{\lambda } R$
for all
![]() $\lambda \in \mathbb {R}$
.
$\lambda \in \mathbb {R}$
.
Let
![]() $\eta \in N_{\mathbb {R}}$
, and let
$\eta \in N_{\mathbb {R}}$
, and let
![]() ${\mathcal {G}}$
be the
${\mathcal {G}}$
be the
![]() $\eta $
-twist of
$\eta $
-twist of
![]() ${\mathcal {F}}_v$
. Then we also have
${\mathcal {F}}_v$
. Then we also have
![]() ${\mathcal {F}}_{\eta }^{\lambda } R\subseteq {\mathcal {G}}^{\lambda } R$
for all
${\mathcal {F}}_{\eta }^{\lambda } R\subseteq {\mathcal {G}}^{\lambda } R$
for all
![]() $\lambda $
, and this clearly implies
$\lambda $
, and this clearly implies
Since
![]() $\mathbf {L}^{\mathrm {NA}}({\mathcal {F}})=A_{X,\Delta }(v)\ge \mathbf {L}^{\mathrm {NA}}({\mathcal {F}}_v)$
by Corollary 3.11, we also get
$\mathbf {L}^{\mathrm {NA}}({\mathcal {F}})=A_{X,\Delta }(v)\ge \mathbf {L}^{\mathrm {NA}}({\mathcal {F}}_v)$
by Corollary 3.11, we also get
![]() $\mathbf {L}^{\mathrm {NA}}({\mathcal {F}}_{\eta })\ge \mathbf {L}^{\mathrm {NA}}({\mathcal {G}})$
by Lemma 3.8 and [Reference Xu and ZhuangXZ20, Lemma A.6]. Note that by Lemma 4.8, [Reference Blum, Liu and XuBLX22, Theorem A.2] and (3) we have
$\mathbf {L}^{\mathrm {NA}}({\mathcal {F}}_{\eta })\ge \mathbf {L}^{\mathrm {NA}}({\mathcal {G}})$
by Lemma 3.8 and [Reference Xu and ZhuangXZ20, Lemma A.6]. Note that by Lemma 4.8, [Reference Blum, Liu and XuBLX22, Theorem A.2] and (3) we have
![]() $\mathrm {Fut}_g\equiv 0$
on
$\mathrm {Fut}_g\equiv 0$
on
![]() $N_{\mathbb {R}}$
, thus
$N_{\mathbb {R}}$
, thus
![]() $\mathbf {D}^{\mathrm {NA}}_g({\mathcal {F}}_{\eta })=\mathbf {D}^{\mathrm {NA}}_g({\mathcal {F}})$
and
$\mathbf {D}^{\mathrm {NA}}_g({\mathcal {F}}_{\eta })=\mathbf {D}^{\mathrm {NA}}_g({\mathcal {F}})$
and
![]() $\mathbf {D}^{\mathrm {NA}}_g({\mathcal {G}})=\mathbf {D}^{\mathrm {NA}}_g({\mathcal {F}}_v)$
.
$\mathbf {D}^{\mathrm {NA}}_g({\mathcal {G}})=\mathbf {D}^{\mathrm {NA}}_g({\mathcal {F}}_v)$
.
Since
we then obtain
 $$ \begin{align*} \mathbf{D}^{\mathrm{NA}}_g({\mathcal{F}}) - c\cdot \mathbf{J}^{\mathrm{NA}}_{g,\mathbb{T}}({\mathcal{F}}) & \ge \mathbf{D}^{\mathrm{NA}}_g({\mathcal{F}}_{\eta}) - c \cdot \mathbf{J}^{\mathrm{NA}}_g({\mathcal{F}}_{\eta}) \\ & \ge \mathbf{D}^{\mathrm{NA}}_g({\mathcal{G}}) - c \cdot \mathbf{J}^{\mathrm{NA}}_g({\mathcal{G}}) = \mathbf{D}^{\mathrm{NA}}_g({\mathcal{F}}_v) - c \cdot \mathbf{J}^{\mathrm{NA}}_g({\mathcal{G}}). \end{align*} $$
$$ \begin{align*} \mathbf{D}^{\mathrm{NA}}_g({\mathcal{F}}) - c\cdot \mathbf{J}^{\mathrm{NA}}_{g,\mathbb{T}}({\mathcal{F}}) & \ge \mathbf{D}^{\mathrm{NA}}_g({\mathcal{F}}_{\eta}) - c \cdot \mathbf{J}^{\mathrm{NA}}_g({\mathcal{F}}_{\eta}) \\ & \ge \mathbf{D}^{\mathrm{NA}}_g({\mathcal{G}}) - c \cdot \mathbf{J}^{\mathrm{NA}}_g({\mathcal{G}}) = \mathbf{D}^{\mathrm{NA}}_g({\mathcal{F}}_v) - c \cdot \mathbf{J}^{\mathrm{NA}}_g({\mathcal{G}}). \end{align*} $$
As
![]() $\eta \in N_{\mathbb {R}}$
is arbitrary, this gives
$\eta \in N_{\mathbb {R}}$
is arbitrary, this gives
By (3), the right-hand side is
![]() $\ge 0$
. Thus, the same is true for the left-hand side. Since
$\ge 0$
. Thus, the same is true for the left-hand side. Since
![]() ${\mathcal {F}}$
is arbitrary, this proves that (3) implies (1).
${\mathcal {F}}$
is arbitrary, this proves that (3) implies (1).
We get the following generalized version of Fujita–Li valuative criterion [Reference FujitaFuj19, Reference LiLi17] which treat the case
![]() $g=1$
(see also [Reference Han and LiHL20, Theorem 5.18]).
$g=1$
(see also [Reference Han and LiHL20, Theorem 5.18]).
Corollary 4.13. A triple
![]() $(X,\Delta ,v_0)$
is
$(X,\Delta ,v_0)$
is
![]() $\mathbb {T}$
-equivariantly g-Ding semistable if and only if
$\mathbb {T}$
-equivariantly g-Ding semistable if and only if
![]() $\delta _{g,\mathbb {T}}(X,\Delta ,v_0)\ge 1$
.
$\delta _{g,\mathbb {T}}(X,\Delta ,v_0)\ge 1$
.
Proof. Assume that
![]() $(X,\Delta ,v_0)$
is
$(X,\Delta ,v_0)$
is
![]() $\mathbb {T}$
-equivariantly g-Ding semistable. If
$\mathbb {T}$
-equivariantly g-Ding semistable. If
![]() $\delta :=\delta _{g,\mathbb {T}}(X,\Delta ,v_0) < 1$
, then we may choose some
$\delta :=\delta _{g,\mathbb {T}}(X,\Delta ,v_0) < 1$
, then we may choose some
![]() $\varepsilon>0$
such that
$\varepsilon>0$
such that
![]() $(1+\varepsilon )^2 \delta <1$
. Let
$(1+\varepsilon )^2 \delta <1$
. Let
![]() $m\gg 0$
be such that
$m\gg 0$
be such that
![]() $\delta _m:=\delta _{g,\mathbb {T},m}(X,\Delta ,v_0)<(1+\varepsilon )\delta $
. By Lemma 4.2, we may also assume that
$\delta _m:=\delta _{g,\mathbb {T},m}(X,\Delta ,v_0)<(1+\varepsilon )\delta $
. By Lemma 4.2, we may also assume that
![]() $S_{g,m}(v_0;v)\le (1+\varepsilon )S_g(v_0;v)$
for any
$S_{g,m}(v_0;v)\le (1+\varepsilon )S_g(v_0;v)$
for any
![]() $v\in \mathrm {Val}_X^{\circ }$
. By definition,
$v\in \mathrm {Val}_X^{\circ }$
. By definition,
![]() $\delta _m=\mathrm {lct}(X,\Delta ;D)$
for some
$\delta _m=\mathrm {lct}(X,\Delta ;D)$
for some
![]() $\mathbb {T}$
-invariant g-weighted
$\mathbb {T}$
-invariant g-weighted
![]() $(m,v_0)$
-basis type divisor D. Thus, if w is a
$(m,v_0)$
-basis type divisor D. Thus, if w is a
![]() $\mathbb {T}$
-invariant divisorial valuation that computes the lct, we would have
$\mathbb {T}$
-invariant divisorial valuation that computes the lct, we would have
On the other hand, since
![]() $\delta _m<1$
, we know that
$\delta _m<1$
, we know that
![]() $-(K_X+\Delta +\delta _m D)$
is ample, thus
$-(K_X+\Delta +\delta _m D)$
is ample, thus
![]() $\mathrm {gr}_w R$
is finitely generated by [Reference Birkar, Cascini, Hacon and McKernanBCHM10, Corollary 1.4.3]. In other words, w induces a
$\mathrm {gr}_w R$
is finitely generated by [Reference Birkar, Cascini, Hacon and McKernanBCHM10, Corollary 1.4.3]. In other words, w induces a
![]() $\mathbb {T}$
-equivariant test configuration of
$\mathbb {T}$
-equivariant test configuration of
![]() $(X,\Delta )$
. As
$(X,\Delta )$
. As
![]() $(X,\Delta ,v_0)$
is
$(X,\Delta ,v_0)$
is
![]() $\mathbb {T}$
-equivariantly g-Ding semistable, Corollary 3.11 gives
$\mathbb {T}$
-equivariantly g-Ding semistable, Corollary 3.11 gives
![]() $A_{X,\Delta }(w) - S_g(v_0;w)\ge \mathbf {D}^{\mathrm {NA}}_{g}({\mathcal {F}}_w) \geq 0$
, a contradiction. Therefore,
$A_{X,\Delta }(w) - S_g(v_0;w)\ge \mathbf {D}^{\mathrm {NA}}_{g}({\mathcal {F}}_w) \geq 0$
, a contradiction. Therefore,
![]() $\delta _{g,\mathbb {T}}(X,\Delta ,v_0)\ge 1$
when
$\delta _{g,\mathbb {T}}(X,\Delta ,v_0)\ge 1$
when
![]() $(X,\Delta ,v_0)$
is
$(X,\Delta ,v_0)$
is
![]() $\mathbb {T}$
-equivariantly g-Ding semistable.
$\mathbb {T}$
-equivariantly g-Ding semistable.
Conversely, if
![]() $\delta _{g,\mathbb {T}}(X,\Delta ,v_0)\ge 1$
, then for any
$\delta _{g,\mathbb {T}}(X,\Delta ,v_0)\ge 1$
, then for any
![]() $v\in \mathrm { Val}_X^{\mathbb {T},\circ }$
we have
$v\in \mathrm { Val}_X^{\mathbb {T},\circ }$
we have
![]() $A_{X,\Delta }(v)\ge S_g(v_0;v)$
. If v is an lc place of a
$A_{X,\Delta }(v)\ge S_g(v_0;v)$
. If v is an lc place of a
![]() ${\mathbb {Q}}$
-complement, then we also have
${\mathbb {Q}}$
-complement, then we also have
![]() $\mathbf {L}^{\mathrm {NA}}({\mathcal {F}}_v)=A_{X,\Delta }(v)$
(c.f. [Reference Xu and ZhuangXZ20, Proposition 4.2]). Thus,
$\mathbf {L}^{\mathrm {NA}}({\mathcal {F}}_v)=A_{X,\Delta }(v)$
(c.f. [Reference Xu and ZhuangXZ20, Proposition 4.2]). Thus,
![]() $\mathbf {D}^{\mathrm {NA}}_g({\mathcal {F}}_v)\ge 0$
for any
$\mathbf {D}^{\mathrm {NA}}_g({\mathcal {F}}_v)\ge 0$
for any
![]() $v\in \mathrm {Val}_X^{\mathbb {T},\circ }$
that is an lc place of a
$v\in \mathrm {Val}_X^{\mathbb {T},\circ }$
that is an lc place of a
![]() ${\mathbb {Q}}$
-complement. By Lemma 4.12 (with
${\mathbb {Q}}$
-complement. By Lemma 4.12 (with
![]() $c=0$
), this implies that
$c=0$
), this implies that
![]() $(X,\Delta ,v_0)$
is
$(X,\Delta ,v_0)$
is
![]() $\mathbb {T}$
-equivariantly g-Ding semistable.
$\mathbb {T}$
-equivariantly g-Ding semistable.
4.3 Existence of minimizer
Throughout this section, let
![]() $\mathbb {T}<\operatorname {Aut}(X,\Delta )$
be a torus and let
$\mathbb {T}<\operatorname {Aut}(X,\Delta )$
be a torus and let
![]() $\xi \in N_{\mathbb {R}}$
. We aim to prove the following statement.
$\xi \in N_{\mathbb {R}}$
. We aim to prove the following statement.
Proposition 4.14. Assume that
![]() $(X,\Delta ,\xi )$
is g-Ding semistable but not reduced uniformly g-Ding stable. Then there exists a
$(X,\Delta ,\xi )$
is g-Ding semistable but not reduced uniformly g-Ding stable. Then there exists a
![]() $\mathbb {T}$
-invariant quasi-monomial valuation v that is not of the form
$\mathbb {T}$
-invariant quasi-monomial valuation v that is not of the form
![]() $\mathrm {wt}_{\eta }$
for any
$\mathrm {wt}_{\eta }$
for any
![]() $\eta \in N_{\mathbb {R}}$
such that
$\eta \in N_{\mathbb {R}}$
such that
![]() $1=\delta _g (X,\Delta ,\xi )(:=\delta _{g,\mathbb {T}} (X,\Delta ,\mathrm {wt}_{\xi }))$
is computed by v.
$1=\delta _g (X,\Delta ,\xi )(:=\delta _{g,\mathbb {T}} (X,\Delta ,\mathrm {wt}_{\xi }))$
is computed by v.
Proof. The argument is very similar to those in [Reference Xu and ZhuangXZ20, Appendix], so we only give a sketch. First, note that the assumption remains true if we enlarge the torus
![]() $\mathbb {T}$
, and clearly if the conclusion holds for a maximal torus containing
$\mathbb {T}$
, and clearly if the conclusion holds for a maximal torus containing
![]() $\mathbb {T}$
, then it also holds for
$\mathbb {T}$
, then it also holds for
![]() $\mathbb {T}$
. Thus, we may assume that
$\mathbb {T}$
. Thus, we may assume that
![]() $\mathbb {T}$
is a maximal torus.
$\mathbb {T}$
is a maximal torus.
By Lemma 4.12 and [Reference Blum, Liu and XuBLX22, Theorem 3.5], we know that there exist some integer
![]() $N>0$
and a sequence of divisorial lc places of N-complements
$N>0$
and a sequence of divisorial lc places of N-complements
![]() $v_i\in \mathrm { Val}_X^{\mathbb {T},\circ }$
(not of the form
$v_i\in \mathrm { Val}_X^{\mathbb {T},\circ }$
(not of the form
![]() $\mathrm {wt}_{\eta }$
) such that
$\mathrm {wt}_{\eta }$
) such that
 $$\begin{align*}\lim_{i\to\infty} \frac{\mathbf{D}^{\mathrm{NA}}_g({\mathcal{F}}_{v_i})}{\mathbf{J}^{\mathrm{NA}}_{g,\mathbb{T}}({\mathcal{F}}_{v_i})} = 0. \end{align*}$$
$$\begin{align*}\lim_{i\to\infty} \frac{\mathbf{D}^{\mathrm{NA}}_g({\mathcal{F}}_{v_i})}{\mathbf{J}^{\mathrm{NA}}_{g,\mathbb{T}}({\mathcal{F}}_{v_i})} = 0. \end{align*}$$
By the constructibility result [Reference Xu and ZhuangXZ20, Lemma A.11] and arguing as in the proof of [Reference Xu and ZhuangXZ20, Theorem A.5], we may assume that the
![]() $v_i$
’s are lc places of the same
$v_i$
’s are lc places of the same
![]() ${\mathbb {Q}}$
-complement and after rescaling
${\mathbb {Q}}$
-complement and after rescaling
![]() $v=\lim _i v_i\in \mathrm {Val}_X^{\mathbb {T},\circ }$
exists and
$v=\lim _i v_i\in \mathrm {Val}_X^{\mathbb {T},\circ }$
exists and
![]() $v\neq \mathrm {wt}_{\eta }$
for any
$v\neq \mathrm {wt}_{\eta }$
for any
![]() $\eta \in N_{\mathbb {R}}$
. By the following Lemma 4.15, we have
$\eta \in N_{\mathbb {R}}$
. By the following Lemma 4.15, we have
![]() $\lim _i S_g(v_0;v_i) = S_g(v_0;v)$
. Since
$\lim _i S_g(v_0;v_i) = S_g(v_0;v)$
. Since
![]() $v_i$
are lc places of
$v_i$
are lc places of
![]() ${\mathbb {Q}}$
-complements, it follows from Lemma 3.8 that
${\mathbb {Q}}$
-complements, it follows from Lemma 3.8 that
![]() $\mathbf {L}^{\mathrm {NA}}({\mathcal {F}}_{v_i})=A_{X,\Delta }(v_i)$
and thus
$\mathbf {L}^{\mathrm {NA}}({\mathcal {F}}_{v_i})=A_{X,\Delta }(v_i)$
and thus
![]() $\lim _i \mathbf {D}^{\mathrm {NA}}_g({\mathcal {F}}_{v_i}) = \mathbf {D}^{\mathrm {NA}}_g({\mathcal {F}}_{v})$
. Since the function
$\lim _i \mathbf {D}^{\mathrm {NA}}_g({\mathcal {F}}_{v_i}) = \mathbf {D}^{\mathrm {NA}}_g({\mathcal {F}}_{v})$
. Since the function
![]() $v\mapsto \lambda _{\max }({\mathcal {F}}_v)=T_{X,\Delta }(v)$
is also continuous on
$v\mapsto \lambda _{\max }({\mathcal {F}}_v)=T_{X,\Delta }(v)$
is also continuous on
![]() $\mathrm {QM}(Y,E)$
by [Reference Blum, Liu and XuBLX22, Proposition 2.4], we get
$\mathrm {QM}(Y,E)$
by [Reference Blum, Liu and XuBLX22, Proposition 2.4], we get
![]() $\lim _i \mathbf {J}^{\mathrm {NA}}_g({\mathcal {F}}_{v_i}) = \mathbf {J}^{\mathrm {NA}}_g({\mathcal {F}}_{v})$
as well. Thus,
$\lim _i \mathbf {J}^{\mathrm {NA}}_g({\mathcal {F}}_{v_i}) = \mathbf {J}^{\mathrm {NA}}_g({\mathcal {F}}_{v})$
as well. Thus,
 $$\begin{align*}\frac{\mathbf{D}^{\mathrm{NA}}_g({\mathcal{F}}_v)}{\mathbf{J}^{\mathrm{NA}}_{g,\mathbb{T}}({\mathcal{F}}_v)} = \lim_{i\to\infty} \frac{\mathbf{D}^{\mathrm{NA}}_g({\mathcal{F}}_{v_i})}{\mathbf{J}^{\mathrm{NA}}_{g,\mathbb{T}}({\mathcal{F}}_{v_i})}= 0, \end{align*}$$
$$\begin{align*}\frac{\mathbf{D}^{\mathrm{NA}}_g({\mathcal{F}}_v)}{\mathbf{J}^{\mathrm{NA}}_{g,\mathbb{T}}({\mathcal{F}}_v)} = \lim_{i\to\infty} \frac{\mathbf{D}^{\mathrm{NA}}_g({\mathcal{F}}_{v_i})}{\mathbf{J}^{\mathrm{NA}}_{g,\mathbb{T}}({\mathcal{F}}_{v_i})}= 0, \end{align*}$$
which implies
![]() $\mathbf {D}^{\mathrm {NA}}_g({\mathcal {F}}_v)=A_{X,\Delta }(v)-S_g(v_0;v)=0$
. Since
$\mathbf {D}^{\mathrm {NA}}_g({\mathcal {F}}_v)=A_{X,\Delta }(v)-S_g(v_0;v)=0$
. Since
![]() $\delta _g(X,\Delta ,\xi )\ge 1$
by Corollary 4.13, we see that
$\delta _g(X,\Delta ,\xi )\ge 1$
by Corollary 4.13, we see that
![]() $\delta _g(X,\Delta ,\xi ) = 1$
and v computes
$\delta _g(X,\Delta ,\xi ) = 1$
and v computes
![]() $\delta _g (X,\Delta ,\xi )$
.
$\delta _g (X,\Delta ,\xi )$
.
We have used the following statement in the above proof.
Lemma 4.15. Let
![]() $Y\to X$
be a proper birational map with Y regular and
$Y\to X$
be a proper birational map with Y regular and
![]() $E:= \sum _{i=1}^d E_i$
a reduced simple normal crossing divisor on Y. Then the function
$E:= \sum _{i=1}^d E_i$
a reduced simple normal crossing divisor on Y. Then the function
![]() $S_{g}(v_0;\, \cdot \, )$
is continuous on
$S_{g}(v_0;\, \cdot \, )$
is continuous on
![]() $\mathrm {QM}(Y,E)$
.
$\mathrm {QM}(Y,E)$
.
We will deduce the result from the continuity of
![]() $S(\cdot )$
on
$S(\cdot )$
on
![]() $\mathrm {QM}(Y,E)$
shown in [Reference Blum, Liu and XuBLX22].
$\mathrm {QM}(Y,E)$
shown in [Reference Blum, Liu and XuBLX22].
Proof. Fix a point
![]() $\eta \in \mathrm {Supp}(E)$
and local coordinates
$\eta \in \mathrm {Supp}(E)$
and local coordinates
![]() $y_1,\ldots , y_r \in {\mathcal {O}}_{Y,\eta }$
so that each
$y_1,\ldots , y_r \in {\mathcal {O}}_{Y,\eta }$
so that each
![]() $y_j$
cuts out an irreducible component of E at
$y_j$
cuts out an irreducible component of E at
![]() $\eta $
. For
$\eta $
. For
![]() $\alpha =( \alpha _1,\ldots , \alpha _r)\in \mathbb {R}_{\geq 0}^{r}$
, write
$\alpha =( \alpha _1,\ldots , \alpha _r)\in \mathbb {R}_{\geq 0}^{r}$
, write
![]() $v_{\alpha }\in \mathrm {Val}_X$
for the associated quasi-monomial valuation satisfying
$v_{\alpha }\in \mathrm {Val}_X$
for the associated quasi-monomial valuation satisfying
![]() $v_{\alpha }(y_j) = \alpha _j$
.
$v_{\alpha }(y_j) = \alpha _j$
.
To prove the continuity of
![]() $S_g(v_0;\, \cdot \, )$
on
$S_g(v_0;\, \cdot \, )$
on
![]() $\mathbb {R}_{\geq 0}^r$
, fix a convergent sequence
$\mathbb {R}_{\geq 0}^r$
, fix a convergent sequence
![]() $\alpha ^{i}$
in
$\alpha ^{i}$
in
![]() $\mathbb {R}_{\geq 0}^{r}$
and set
$\mathbb {R}_{\geq 0}^{r}$
and set
![]() $ \alpha : = \lim _i \alpha ^{i}$
. We aim to show
$ \alpha : = \lim _i \alpha ^{i}$
. We aim to show
![]() $\lim _i S_g(v_0;v_i) = S_g(v_0;v)$
, where
$\lim _i S_g(v_0;v_i) = S_g(v_0;v)$
, where
![]() $v_i: = v_{\alpha ^i}$
and
$v_i: = v_{\alpha ^i}$
and
![]() $v : = v_{\alpha }$
.
$v : = v_{\alpha }$
.
First, note that
![]() $S_g(v_0;c w)= cS_g(v_0;w) $
for all
$S_g(v_0;c w)= cS_g(v_0;w) $
for all
![]() $w\in \mathrm {Val}_X^{\circ }$
and
$w\in \mathrm {Val}_X^{\circ }$
and
![]() $c\in \mathbb {R}_{>0}$
. Therefore, after rescaling the
$c\in \mathbb {R}_{>0}$
. Therefore, after rescaling the
![]() $\alpha ^i$
and removing finitely many terms, we may assume the sequence
$\alpha ^i$
and removing finitely many terms, we may assume the sequence
![]() $(\alpha ^i)$
is nonincreasing. Hence,
$(\alpha ^i)$
is nonincreasing. Hence,
![]() $v_i \geq v_{i+1} \geq v$
for all i. Next, consider the Okounkov body
$v_i \geq v_{i+1} \geq v$
for all i. Next, consider the Okounkov body
![]() $\Sigma \subset \mathbb {R}^n$
induced by the good valuation form Lemma 4.4. Write
$\Sigma \subset \mathbb {R}^n$
induced by the good valuation form Lemma 4.4. Write
![]() $G_i$
and G for the concave functions
$G_i$
and G for the concave functions
![]() $\Sigma \to \mathbb {R}_{\geq 0}$
induced by the filtrations
$\Sigma \to \mathbb {R}_{\geq 0}$
induced by the filtrations
![]() ${\mathcal {F}}_{v}$
and
${\mathcal {F}}_{v}$
and
![]() ${\mathcal {F}}_{v_i}$
(see [Reference Blum and JonssonBJ20, Section 2.5]) and set
${\mathcal {F}}_{v_i}$
(see [Reference Blum and JonssonBJ20, Section 2.5]) and set
![]() $\mathrm {vol}_g(\Sigma )= \int _{\Sigma } g\, \mathrm {d} \rho $
. Note that
$\mathrm {vol}_g(\Sigma )= \int _{\Sigma } g\, \mathrm {d} \rho $
. Note that
 $$ \begin{align} |S_g(v_0;v_i) - S_g(v_0;v) | = \left| \frac{1}{ \mathrm{vol}_g (\Sigma) } \int_{\Sigma }g G_i \, \mathrm{d} \rho - \frac{1}{ \mathrm{vol}_g (\Sigma) } \int_{\Sigma } g G \, \mathrm{d} \rho \right | = \frac{1}{\mathrm{vol}_g(\Sigma)} \int_{\Sigma} g |G_i-G| \, \mathrm{d} \rho ,\end{align} $$
$$ \begin{align} |S_g(v_0;v_i) - S_g(v_0;v) | = \left| \frac{1}{ \mathrm{vol}_g (\Sigma) } \int_{\Sigma }g G_i \, \mathrm{d} \rho - \frac{1}{ \mathrm{vol}_g (\Sigma) } \int_{\Sigma } g G \, \mathrm{d} \rho \right | = \frac{1}{\mathrm{vol}_g(\Sigma)} \int_{\Sigma} g |G_i-G| \, \mathrm{d} \rho ,\end{align} $$
where the second equality uses that
![]() $G_i\leq G$
. Using that
$G_i\leq G$
. Using that
![]() $\lim _i S_1(v_0; v_i) = S_{1}(v_0;v)$
by [Reference Blum, Liu and XuBLX22, Proposition 2.4] and equation (4.3), we see
$\lim _i S_1(v_0; v_i) = S_{1}(v_0;v)$
by [Reference Blum, Liu and XuBLX22, Proposition 2.4] and equation (4.3), we see
![]() $(G_i)$
converges to G a.e. Therefore, the dominated convergence theorem implies
$(G_i)$
converges to G a.e. Therefore, the dominated convergence theorem implies
which completes the proof.
5 Finite generation
5.1 A valuative criterion for
 $\tilde {\beta }_{X,\Delta }$
-minimizers
$\tilde {\beta }_{X,\Delta }$
-minimizers
In this section, we give a valuative criterion for valuations computing h-invariant inspired by [Reference Xu and ZhuangXZ21] in terms of weighted stability thresholds. Let us recall that in Corollary 3.17, we know the valuation computing
![]() $h(X,\Delta )$
is quasi-monomial. Thus, we can apply the construction in Section 4.1. We use the following notation: for any quasi-monomial
$h(X,\Delta )$
is quasi-monomial. Thus, we can apply the construction in Section 4.1. We use the following notation: for any quasi-monomial
![]() $v_0$
and
$v_0$
and
![]() $v\in \mathrm {Val}_X^{\circ }$
, let
$v\in \mathrm {Val}_X^{\circ }$
, let
![]() $\widetilde {S}(v_0;v):=S_g(v_0;v)$
, where
$\widetilde {S}(v_0;v):=S_g(v_0;v)$
, where
![]() $g(x)=e^{-x}$
. By [Reference Han and LiHL20b] and Theorem 3.15, the unique valuation computing
$g(x)=e^{-x}$
. By [Reference Han and LiHL20b] and Theorem 3.15, the unique valuation computing
![]() $h(X,\Delta )$
is trivial if and only if
$h(X,\Delta )$
is trivial if and only if
![]() $(X,\Delta )$
is K-semistable. Hence, throughout this subsection, we assume that
$(X,\Delta )$
is K-semistable. Hence, throughout this subsection, we assume that
![]() $(X,\Delta )$
is K-unstable, that is,
$(X,\Delta )$
is K-unstable, that is,
![]() $h(X,\Delta )<0$
.
$h(X,\Delta )<0$
.
Theorem 5.1. A quasi-monomial valuation
![]() $v_0\in \mathrm {Val}_{X}^{\circ }$
computes
$v_0\in \mathrm {Val}_{X}^{\circ }$
computes
![]() $h(X,\Delta )$
if and only if
$h(X,\Delta )$
if and only if
![]() $A_{X,\Delta }(v)\geq \widetilde {S}(v_0;v)$
for any valuation
$A_{X,\Delta }(v)\geq \widetilde {S}(v_0;v)$
for any valuation
![]() $v\in \mathrm {Val}_X^{\circ }$
and
$v\in \mathrm {Val}_X^{\circ }$
and
![]() $A_{X,\Delta }(v_0)=\widetilde {S}(v_0;v_0)$
.
$A_{X,\Delta }(v_0)=\widetilde {S}(v_0;v_0)$
.
Proof. We first show the ‘if’ part. It suffices to show that
![]() $\tilde {\beta }_{X,\Delta }(v) \geq \tilde {\beta }_{X,\Delta }(v_0)$
for any valuation
$\tilde {\beta }_{X,\Delta }(v) \geq \tilde {\beta }_{X,\Delta }(v_0)$
for any valuation
![]() $v\in \mathrm {Val}_X^{\circ }$
. Let
$v\in \mathrm {Val}_X^{\circ }$
. Let
![]() ${\mathcal {F}}_0:={\mathcal {F}}_{v_0}$
and
${\mathcal {F}}_0:={\mathcal {F}}_{v_0}$
and
![]() ${\mathcal {F}}_1:={\mathcal {F}}_{v}$
. Let
${\mathcal {F}}_1:={\mathcal {F}}_{v}$
. Let
![]() $\boldsymbol {\nu }$
denote the compatible measure of
$\boldsymbol {\nu }$
denote the compatible measure of
![]() ${\mathcal {F}}_0$
and
${\mathcal {F}}_0$
and
![]() ${\mathcal {F}}_1$
from Section 3.1.3. From the definitions, we know that
${\mathcal {F}}_1$
from Section 3.1.3. From the definitions, we know that
 $$ \begin{align} \widetilde{S}(v_0;v_0)=\frac{\int_{\mathbb{R}^2} x e^{-x} d\boldsymbol{\nu}}{\int_{\mathbb{R}^2} e^{-x} d\boldsymbol{\nu}}, \quad \textrm{and}\quad \widetilde{S}(v_0;v)=\frac{\int_{\mathbb{R}^2} y e^{-x} d\boldsymbol{\nu}}{\int_{\mathbb{R}^2} e^{-x} d\boldsymbol{\nu}}. \end{align} $$
$$ \begin{align} \widetilde{S}(v_0;v_0)=\frac{\int_{\mathbb{R}^2} x e^{-x} d\boldsymbol{\nu}}{\int_{\mathbb{R}^2} e^{-x} d\boldsymbol{\nu}}, \quad \textrm{and}\quad \widetilde{S}(v_0;v)=\frac{\int_{\mathbb{R}^2} y e^{-x} d\boldsymbol{\nu}}{\int_{\mathbb{R}^2} e^{-x} d\boldsymbol{\nu}}. \end{align} $$
Consider the following function
![]() $f:[0,1]\to \mathbb {R}$
given by
$f:[0,1]\to \mathbb {R}$
given by
It is clear that
![]() $f(0)=\tilde {\beta }_{X,\Delta }(v_0)$
and
$f(0)=\tilde {\beta }_{X,\Delta }(v_0)$
and
![]() $f(1)=\tilde {\beta }_{X,\Delta }(v)$
. By Hölder’s inequality as in the proof of Proposition 3.14, we know that
$f(1)=\tilde {\beta }_{X,\Delta }(v)$
. By Hölder’s inequality as in the proof of Proposition 3.14, we know that
![]() $f(t)$
is convex in t. Moreover, we have
$f(t)$
is convex in t. Moreover, we have
 $$ \begin{align*} f'(0) & = A_{X,\Delta}(v) - A_{X,\Delta}(v_0) + \frac{\int_{\mathbb{R}^2} (x-y)e^{-x} d\boldsymbol{\nu}}{\int_{\mathbb{R}^2} e^{-x} d\boldsymbol{\nu}}\\ & = (A_{X,\Delta}(v)- \widetilde{S}(v_0;v)) - (A_{X,\Delta}(v_0)-\widetilde{S}(v_0;v_0)) \geq 0. \end{align*} $$
$$ \begin{align*} f'(0) & = A_{X,\Delta}(v) - A_{X,\Delta}(v_0) + \frac{\int_{\mathbb{R}^2} (x-y)e^{-x} d\boldsymbol{\nu}}{\int_{\mathbb{R}^2} e^{-x} d\boldsymbol{\nu}}\\ & = (A_{X,\Delta}(v)- \widetilde{S}(v_0;v)) - (A_{X,\Delta}(v_0)-\widetilde{S}(v_0;v_0)) \geq 0. \end{align*} $$
Thus,
![]() $f(1)\geq f(0)$
and the ‘if’ part is proved.
$f(1)\geq f(0)$
and the ‘if’ part is proved.
Next, we show the ‘only if’ part. Let
![]() $({\mathcal {F}}_t)_{t\in [0,1]}$
be the geodesic of filtrations connecting
$({\mathcal {F}}_t)_{t\in [0,1]}$
be the geodesic of filtrations connecting
![]() ${\mathcal {F}}_0$
and
${\mathcal {F}}_0$
and
![]() ${\mathcal {F}}_1$
. Since
${\mathcal {F}}_1$
. Since
![]() $v_0$
computes
$v_0$
computes
![]() $h(X,\Delta )$
, we know that
$h(X,\Delta )$
, we know that
![]() $\mathbf {H}^{\mathrm {NA}}({\mathcal {F}}_t)\geq \mathbf {H}^{\mathrm {NA}}({\mathcal {F}}_0)=f(0)$
for any
$\mathbf {H}^{\mathrm {NA}}({\mathcal {F}}_t)\geq \mathbf {H}^{\mathrm {NA}}({\mathcal {F}}_0)=f(0)$
for any
![]() $t\in [0,1]$
. Recall that
$t\in [0,1]$
. Recall that
By Proposition 3.12 and Corollary 3.11, we obtain
Hence, we have
![]() $\mathbf {H}^{\mathrm {NA}}({\mathcal {F}}_t)\leq f(t)$
which implies that
$\mathbf {H}^{\mathrm {NA}}({\mathcal {F}}_t)\leq f(t)$
which implies that
![]() $f(t)\ge f(0)$
for all
$f(t)\ge f(0)$
for all
![]() $t\in [0,1]$
and thus
$t\in [0,1]$
and thus
![]() $f'(0)\geq 0$
, that is,
$f'(0)\geq 0$
, that is,
Since
![]() $v\in \mathrm {Val}_{X}^{\circ }$
is arbitrary, the above inequality remains true if we replace v by
$v\in \mathrm {Val}_{X}^{\circ }$
is arbitrary, the above inequality remains true if we replace v by
![]() $\lambda v$
for any
$\lambda v$
for any
![]() $\lambda \in \mathbb {R}_{>0}$
, that is,
$\lambda \in \mathbb {R}_{>0}$
, that is,
Thus, we have
![]() $A_{X,\Delta }(v) \geq \widetilde {S}(v_0;v)$
for any
$A_{X,\Delta }(v) \geq \widetilde {S}(v_0;v)$
for any
![]() $v\in \mathrm {Val}_X^{\circ }$
and
$v\in \mathrm {Val}_X^{\circ }$
and
![]() $A_{X,\Delta }(v_0)\leq \widetilde {S}(v_0;v_0)$
, which implies that
$A_{X,\Delta }(v_0)\leq \widetilde {S}(v_0;v_0)$
, which implies that
![]() $A_{X,\Delta }(v_0)= \widetilde {S}(v_0;v_0)$
. This finishes the proof.
$A_{X,\Delta }(v_0)= \widetilde {S}(v_0;v_0)$
. This finishes the proof.
The previous theorem immediately implies the following corollary.
Corollary 5.2. Let
![]() $g(x)=e^{-x}$
, and let
$g(x)=e^{-x}$
, and let
![]() $v_0\in \mathrm {Val}_X^{\circ }$
be the valuation computing
$v_0\in \mathrm {Val}_X^{\circ }$
be the valuation computing
![]() $h(X,\Delta )$
. Then
$h(X,\Delta )$
. Then
![]() $\delta _g(X,\Delta ,v_0)=1$
and is computed by
$\delta _g(X,\Delta ,v_0)=1$
and is computed by
![]() $v_0$
.
$v_0$
.
5.2
 $\delta _g$
-minimizers
$\delta _g$
-minimizers
In this section, we fix a continuous function
![]() $g\colon \mathbb {R}\to \mathbb {R}_{>0}$
, a torus
$g\colon \mathbb {R}\to \mathbb {R}_{>0}$
, a torus
![]() $\mathbb {T}<\operatorname {Aut}(X,\Delta )$
and a quasi-monomial valuation
$\mathbb {T}<\operatorname {Aut}(X,\Delta )$
and a quasi-monomial valuation
![]() $v_0\in \mathrm {Val}_X^{\mathbb {T},\circ }$
. Let
$v_0\in \mathrm {Val}_X^{\mathbb {T},\circ }$
. Let
![]() $N=\mathrm {Hom}(\mathbb {G}_m,\mathbb {T})$
and
$N=\mathrm {Hom}(\mathbb {G}_m,\mathbb {T})$
and
![]() $N_{\mathbb {R}}=N\otimes _{\mathbb {Z}} \mathbb {R}$
as before.
$N_{\mathbb {R}}=N\otimes _{\mathbb {Z}} \mathbb {R}$
as before.
Question 5.3. Assume that
![]() $\delta _{g,\mathbb {T}}(X,\Delta ,v_0)\le 1$
. Let
$\delta _{g,\mathbb {T}}(X,\Delta ,v_0)\le 1$
. Let
![]() $v\in \mathrm {Val}_X^{\mathbb {T},\circ }$
be a valuation that computes
$v\in \mathrm {Val}_X^{\mathbb {T},\circ }$
be a valuation that computes
![]() $\delta _{g,\mathbb {T}}(X,\Delta ,v_0)$
. Is the associated graded ring
$\delta _{g,\mathbb {T}}(X,\Delta ,v_0)$
. Is the associated graded ring
![]() $\mathrm {gr}_v R:=\mathrm {gr}_{{\mathcal {F}}_v} R$
finitely generated?
$\mathrm {gr}_v R:=\mathrm {gr}_{{\mathcal {F}}_v} R$
finitely generated?
We give an affirmative answer in two special cases, which is enough for our applications.
Theorem 5.4. Let
![]() $v\in \mathrm {Val}_X^{\mathbb {T},\circ }$
be a quasi-monomial valuation that computes
$v\in \mathrm {Val}_X^{\mathbb {T},\circ }$
be a quasi-monomial valuation that computes
![]() $\delta _{g,\mathbb {T}}(X,\Delta ,v_0)$
. Assume that
$\delta _{g,\mathbb {T}}(X,\Delta ,v_0)$
. Assume that
![]() $\delta _{g,\mathbb {T}}(X,\Delta ,v_0)\le 1$
and that
$\delta _{g,\mathbb {T}}(X,\Delta ,v_0)\le 1$
and that
![]() $v=(v_0)_{\xi }$
or
$v=(v_0)_{\xi }$
or
![]() $v_0=\mathrm {wt}_{\xi }$
for some
$v_0=\mathrm {wt}_{\xi }$
for some
![]() $\xi \in N_{\mathbb {R}}$
. Then
$\xi \in N_{\mathbb {R}}$
. Then
![]() $\mathrm {gr}_v R$
is finitely generated.
$\mathrm {gr}_v R$
is finitely generated.
For the proof, we first recall a statement that can be extracted from the proof of [Reference Liu, Xu and ZhuangLXZ22, Lemma 3.1].
Lemma 5.5. Let v be a quasi-monomial valuation on X. Assume that there exists a sequence of
![]() ${\mathbb {Q}}$
-divisors
${\mathbb {Q}}$
-divisors
![]() $D_m \ (m\in \mathbb {N})$
such that
$D_m \ (m\in \mathbb {N})$
such that
![]() $(X,\Delta +D_m)$
is lc and
$(X,\Delta +D_m)$
is lc and
![]() $-(K_X+\Delta +D_m)$
is semiample for all m and that
$-(K_X+\Delta +D_m)$
is semiample for all m and that
![]() $\lim _{m\to \infty } v(D_m)=A_{X,\Delta }(v)$
. Then v is an lc place of
$\lim _{m\to \infty } v(D_m)=A_{X,\Delta }(v)$
. Then v is an lc place of
![]() $(X,\Delta +\Gamma )$
for some
$(X,\Delta +\Gamma )$
for some
![]() ${\mathbb {Q}}$
-complement
${\mathbb {Q}}$
-complement
![]() $\Gamma $
of
$\Gamma $
of
![]() $(X,\Delta )$
.
$(X,\Delta )$
.
Proof. We only sketch the proof since the argument is almost the same as in [Reference Liu, Xu and ZhuangLXZ22, Lemma 3.1]. After rescaling, we assume that
![]() $A_{X,\Delta }(v)=1$
. Since v is quasi-monomial, we have
$A_{X,\Delta }(v)=1$
. Since v is quasi-monomial, we have
![]() $v\in \mathrm {QM}(Y,E)$
for some log smooth model
$v\in \mathrm {QM}(Y,E)$
for some log smooth model
![]() $(Y,E)\to (X,\Delta )$
. Let
$(Y,E)\to (X,\Delta )$
. Let
![]() ${\mathfrak {a}}_m = {\mathfrak {a}}_m(v)$
(
${\mathfrak {a}}_m = {\mathfrak {a}}_m(v)$
(
![]() $m\in \mathbb {N}$
) be the valuation ideals. By the proof of [Reference Liu, Xu and ZhuangLXZ22, (3.1)] (which only uses the fact that v is quasi-monomial), we know that, for any
$m\in \mathbb {N}$
) be the valuation ideals. By the proof of [Reference Liu, Xu and ZhuangLXZ22, (3.1)] (which only uses the fact that v is quasi-monomial), we know that, for any
![]() $\varepsilon \in (0,1)$
, there exists
$\varepsilon \in (0,1)$
, there exists
![]() $\varepsilon _0>0$
and divisorial valuations
$\varepsilon _0>0$
and divisorial valuations
![]() $v_i=\mathrm { ord}_{F_i}\in \mathrm {QM}(Y,E)$
(
$v_i=\mathrm { ord}_{F_i}\in \mathrm {QM}(Y,E)$
(
![]() $i=1,\cdots ,r$
) such that v is in the convex hull of
$i=1,\cdots ,r$
) such that v is in the convex hull of
![]() $v_1,\cdots ,v_r$
and
$v_1,\cdots ,v_r$
and
![]() $A_{X,\Delta +{\mathfrak {a}}_{\bullet }^{1-\varepsilon _0}}(F_i)<\varepsilon $
for all i. By assumption, we have
$A_{X,\Delta +{\mathfrak {a}}_{\bullet }^{1-\varepsilon _0}}(F_i)<\varepsilon $
for all i. By assumption, we have
![]() $v(D_m)>1-\varepsilon _0$
for sufficiently large m and for such m we obtain
$v(D_m)>1-\varepsilon _0$
for sufficiently large m and for such m we obtain
By [Reference Birkar, Cascini, Hacon and McKernanBCHM10, Corollary 1.4.3], we get a
![]() ${\mathbb {Q}}$
-factorial birational model
${\mathbb {Q}}$
-factorial birational model
![]() $p\colon \widetilde {X}\to X$
that extracts exactly the divisors
$p\colon \widetilde {X}\to X$
that extracts exactly the divisors
![]() $F_i$
. By assumption, all
$F_i$
. By assumption, all
![]() $(X,\Delta +D_m)$
(
$(X,\Delta +D_m)$
(
![]() $m\in \mathbb {N}$
) have
$m\in \mathbb {N}$
) have
![]() ${\mathbb {Q}}$
-complements. Together with equation (5.2), this implies that
${\mathbb {Q}}$
-complements. Together with equation (5.2), this implies that
![]() $(\widetilde {X},p_*^{-1}\Delta +(1-\varepsilon )\sum _{i=1}^r F_i)$
has
$(\widetilde {X},p_*^{-1}\Delta +(1-\varepsilon )\sum _{i=1}^r F_i)$
has
![]() ${\mathbb {Q}}$
-complements as well. Using [Reference Liu, Xu and ZhuangLXZ22, Lemma 3.2], we conclude that
${\mathbb {Q}}$
-complements as well. Using [Reference Liu, Xu and ZhuangLXZ22, Lemma 3.2], we conclude that
![]() ${\mathbb {Q}}$
-complements also exist for
${\mathbb {Q}}$
-complements also exist for
![]() $(\widetilde {X},p_*^{-1}\Delta +\sum _{i=1}^r F_i)$
as long as
$(\widetilde {X},p_*^{-1}\Delta +\sum _{i=1}^r F_i)$
as long as
![]() $\varepsilon $
is sufficiently small. Since v is in the complex hull of
$\varepsilon $
is sufficiently small. Since v is in the complex hull of
![]() $\mathrm {ord}_{F_i}$
, this yields a
$\mathrm {ord}_{F_i}$
, this yields a
![]() ${\mathbb {Q}}$
-complement
${\mathbb {Q}}$
-complement
![]() $\Gamma $
of
$\Gamma $
of
![]() $(X,\Delta )$
that has v as an lc place.
$(X,\Delta )$
that has v as an lc place.
Lemma 5.6. There exists some constant
![]() $c>0$
such that
$c>0$
such that
![]() $S_g(v_0;G)>c$
for all effective
$S_g(v_0;G)>c$
for all effective
![]() ${\mathbb {Q}}$
-divisors
${\mathbb {Q}}$
-divisors
![]() $G\sim _{\mathbb {Q}} -(K_X+\Delta )$
on X. In particular, for any
$G\sim _{\mathbb {Q}} -(K_X+\Delta )$
on X. In particular, for any
![]() $m\gg 0$
and any g-weighted
$m\gg 0$
and any g-weighted
![]() $(m,v_0)$
-basis type divisor D that is compatible with G, we have
$(m,v_0)$
-basis type divisor D that is compatible with G, we have
![]() $D\ge cG$
.
$D\ge cG$
.
Proof. Let
![]() $T=T_{X,\Delta }(v_0)<\infty $
, and let
$T=T_{X,\Delta }(v_0)<\infty $
, and let
 $$\begin{align*}c_0=\frac{\inf_{x\in[0,T]} g(x)}{\sup_{x\in[0,T]} g(x)}>0. \end{align*}$$
$$\begin{align*}c_0=\frac{\inf_{x\in[0,T]} g(x)}{\sup_{x\in[0,T]} g(x)}>0. \end{align*}$$
Let
![]() $\boldsymbol {\nu }$
denote the compatible DH measure associated to
$\boldsymbol {\nu }$
denote the compatible DH measure associated to
![]() ${\mathcal {F}}_{v_0}$
and
${\mathcal {F}}_{v_0}$
and
![]() ${\mathcal {F}}_G$
as in Section 3.1.3. Then
${\mathcal {F}}_G$
as in Section 3.1.3. Then
![]() $\boldsymbol {\nu }$
is supported in
$\boldsymbol {\nu }$
is supported in
![]() $[0,T]\times \mathbb {R}$
and we have
$[0,T]\times \mathbb {R}$
and we have
 $$\begin{align*}S_g(v_0;G)=\frac{\int_{\mathbb{R}^2} yg(x)\mathrm{d} \boldsymbol{\nu}}{\int_{\mathbb{R}^2} g(x)\mathrm{d} \boldsymbol{\nu}}\ge c_0\cdot \frac{\int_{\mathbb{R}^2} y\mathrm{d} \boldsymbol{\nu}}{\int_{\mathbb{R}^2} \mathrm{d} \boldsymbol{\nu}} = c_0\cdot S_{X,\Delta}(G)=\frac{c_0}{n+1}, \end{align*}$$
$$\begin{align*}S_g(v_0;G)=\frac{\int_{\mathbb{R}^2} yg(x)\mathrm{d} \boldsymbol{\nu}}{\int_{\mathbb{R}^2} g(x)\mathrm{d} \boldsymbol{\nu}}\ge c_0\cdot \frac{\int_{\mathbb{R}^2} y\mathrm{d} \boldsymbol{\nu}}{\int_{\mathbb{R}^2} \mathrm{d} \boldsymbol{\nu}} = c_0\cdot S_{X,\Delta}(G)=\frac{c_0}{n+1}, \end{align*}$$
where the last equality is by [Reference Liu, Xu and ZhuangLXZ22, Lemma 2.20]. Thus, we may take, for example,
![]() $c=\frac {c_0}{3n}$
.
$c=\frac {c_0}{3n}$
.
We are now ready to prove Theorem 5.4.
Proof of Theorem 5.4.
The plan is to use Lemma 5.5 to show that v is a monomial lc place of a special complement (in the sense of [Reference Liu, Xu and ZhuangLXZ22, Definition 3.3]) and then apply [Reference Liu, Xu and ZhuangLXZ22, Theorem 4.2] to get the finite generation. To this end, let
![]() $\pi :(Y,E=\sum _{i=1}^r E_i)\to (X,\Delta )$
be a
$\pi :(Y,E=\sum _{i=1}^r E_i)\to (X,\Delta )$
be a
![]() $\mathbb {T}$
-equivariant log smooth model such that
$\mathbb {T}$
-equivariant log smooth model such that
![]() $\mathrm {QM}(Y,E)$
is a simplicial cone whose interior contains v,
$\mathrm {QM}(Y,E)$
is a simplicial cone whose interior contains v,
![]() $C_Y(v)=\cap _{i=1}^r E_i$
, and there is a
$C_Y(v)=\cap _{i=1}^r E_i$
, and there is a
![]() $\pi $
-exceptional and
$\pi $
-exceptional and
![]() $\pi $
-ample
$\pi $
-ample
![]() ${\mathbb {Q}}$
-divisor
${\mathbb {Q}}$
-divisor
![]() $-F$
on Y.
$-F$
on Y.
Let
![]() $G_Y$
be a
$G_Y$
be a
![]() $\mathbb {T}$
-invariant
$\mathbb {T}$
-invariant
![]() ${\mathbb {Q}}$
-divisor in the ample
${\mathbb {Q}}$
-divisor in the ample
![]() ${\mathbb {Q}}$
-linear system
${\mathbb {Q}}$
-linear system
![]() $|-\pi ^*(K_X+\Delta )-\varepsilon F|_{{\mathbb {Q}}}$
(
$|-\pi ^*(K_X+\Delta )-\varepsilon F|_{{\mathbb {Q}}}$
(
![]() $0<\varepsilon \ll 1$
) whose support does not contain
$0<\varepsilon \ll 1$
) whose support does not contain
![]() $C_Y(v_0)$
(such
$C_Y(v_0)$
(such
![]() $G_Y$
exists because there is some
$G_Y$
exists because there is some
![]() $\mathbb {T}$
-invariant element
$\mathbb {T}$
-invariant element
![]() $\Gamma $
in
$\Gamma $
in
![]() $H^0(Y,m(-\pi ^*(K_X+\Delta )-\varepsilon F))$
for sufficiently divisible m with
$H^0(Y,m(-\pi ^*(K_X+\Delta )-\varepsilon F))$
for sufficiently divisible m with
![]() $v_0(\Gamma )\neq 0$
). Let
$v_0(\Gamma )\neq 0$
). Let
![]() $G:=\pi _*G_Y$
. For any
$G:=\pi _*G_Y$
. For any
![]() $m\in \mathbb {N}$
, let
$m\in \mathbb {N}$
, let
![]() $D_m\in |-K_X-\Delta |_{\mathbb {R}}$
be a
$D_m\in |-K_X-\Delta |_{\mathbb {R}}$
be a
![]() $\mathbb {T}$
-invariant g-weighted
$\mathbb {T}$
-invariant g-weighted
![]() $(m,v_0)$
-basis type divisor that is also compatible with both v and G. Such divisors exist because:
$(m,v_0)$
-basis type divisor that is also compatible with both v and G. Such divisors exist because:
-
• Both v and G are
 $\mathbb {T}$
-invariant (so we can choose compatible basis in each individual piece in the weight decomposition), and
$\mathbb {T}$
-invariant (so we can choose compatible basis in each individual piece in the weight decomposition), and -
• By our assumption, any
 $\mathbb {T}$
-invariant basis that is compatible with both v and G is automatically compatible with
$\mathbb {T}$
-invariant basis that is compatible with both v and G is automatically compatible with
 $v_0$
.
$v_0$
.
By Lemma 5.6, there exists some
![]() $c\in {\mathbb {Q}}_+$
such that
$c\in {\mathbb {Q}}_+$
such that
![]() $D_m\ge cG$
for all
$D_m\ge cG$
for all
![]() $m\gg 0$
. Let
$m\gg 0$
. Let
![]() $\delta _m=\min \{\delta _{g,\mathbb {T},m}(X,\Delta ,v_0),1\}$
. Then
$\delta _m=\min \{\delta _{g,\mathbb {T},m}(X,\Delta ,v_0),1\}$
. Then
![]() $(X,\Delta +\delta _m D_m)$
is lc and
$(X,\Delta +\delta _m D_m)$
is lc and
![]() $\lim _{m\to \infty } \delta _m = \delta _{g,\mathbb {T}}(X,\Delta ,v_0)$
by Lemma 4.5 and the assumption that
$\lim _{m\to \infty } \delta _m = \delta _{g,\mathbb {T}}(X,\Delta ,v_0)$
by Lemma 4.5 and the assumption that
![]() $\delta _{g,\mathbb {T}}(X,\Delta ,v_0)\le 1$
.
$\delta _{g,\mathbb {T}}(X,\Delta ,v_0)\le 1$
.
Since v computes
![]() $\delta _{g,\mathbb {T}}(X,\Delta ,v_0)$
, we also have
$\delta _{g,\mathbb {T}}(X,\Delta ,v_0)$
, we also have
Note that by construction
![]() $D_m=\sum \lambda _i D_m^{(i)}$
for some
$D_m=\sum \lambda _i D_m^{(i)}$
for some
![]() $\lambda \in \mathbb {R}_+$
and some effective
$\lambda \in \mathbb {R}_+$
and some effective
![]() ${\mathbb {Q}}$
-divisors
${\mathbb {Q}}$
-divisors
![]() $D_m^{(i)}\sim _{\mathbb {Q}} -(K_X+\Delta )$
. Thus, by perturbing the coefficients
$D_m^{(i)}\sim _{\mathbb {Q}} -(K_X+\Delta )$
. Thus, by perturbing the coefficients
![]() $\lambda _i$
, for each
$\lambda _i$
, for each
![]() $m\gg 0$
we get a
$m\gg 0$
we get a
![]() ${\mathbb {Q}}$
-divisor
${\mathbb {Q}}$
-divisor
![]() $D^{\prime }_m=\sum \lambda ^{\prime }_i D_m^{(i)}$
such that
$D^{\prime }_m=\sum \lambda ^{\prime }_i D_m^{(i)}$
such that
![]() $\delta _m D_m> D^{\prime }_m\ge \frac {1}{2}cG$
and
$\delta _m D_m> D^{\prime }_m\ge \frac {1}{2}cG$
and
![]() $\lim _{m\to \infty } v(D^{\prime }_m)=A_{X,\Delta }(v)$
. It follows that
$\lim _{m\to \infty } v(D^{\prime }_m)=A_{X,\Delta }(v)$
. It follows that
![]() $(X,\Delta +cG+\widetilde {D}_m)$
is lc and
$(X,\Delta +cG+\widetilde {D}_m)$
is lc and
![]() $-(K_X+\Delta +cG+\widetilde {D}_m)$
is ample where
$-(K_X+\Delta +cG+\widetilde {D}_m)$
is ample where
![]() $\widetilde {D}_m=D^{\prime }_m-\frac {1}{2}cG$
. By Lemma 5.5, we see that v is an lc place of
$\widetilde {D}_m=D^{\prime }_m-\frac {1}{2}cG$
. By Lemma 5.5, we see that v is an lc place of
![]() $(X,\Delta +\frac {1}{2}cG+\Gamma )$
for some
$(X,\Delta +\frac {1}{2}cG+\Gamma )$
for some
![]() ${\mathbb {Q}}$
-complement
${\mathbb {Q}}$
-complement
![]() $\Gamma $
of
$\Gamma $
of
![]() $(X,\Delta +\frac {1}{2}cG)$
. Recall the
$(X,\Delta +\frac {1}{2}cG)$
. Recall the
![]() $\pi _*^{-1}G$
is ample and does not contain
$\pi _*^{-1}G$
is ample and does not contain
![]() $C_Y(v)$
. By [Reference Liu, Xu and ZhuangLXZ22, Theorem 4.2], this implies that
$C_Y(v)$
. By [Reference Liu, Xu and ZhuangLXZ22, Theorem 4.2], this implies that
![]() $\mathrm {gr}_v R$
is finitely generated.
$\mathrm {gr}_v R$
is finitely generated.
Corollary 5.7. Assume that
![]() $(X,\Delta )$
is not K-semistable. Let
$(X,\Delta )$
is not K-semistable. Let
![]() $v_0\in \mathrm {Val}_X^{\circ }$
be the unique valuation computing
$v_0\in \mathrm {Val}_X^{\circ }$
be the unique valuation computing
![]() $h(X,\Delta )$
. Then
$h(X,\Delta )$
. Then
![]() $\mathrm {gr}_{v_0} R$
is finitely generated.
$\mathrm {gr}_{v_0} R$
is finitely generated.
Proof. By [Reference Han and LiHL20b, Theorem 1.5],
![]() $v_0$
is quasi-monomial. So the result follows immediately from Corollary 5.2 and Theorem 5.4 (with
$v_0$
is quasi-monomial. So the result follows immediately from Corollary 5.2 and Theorem 5.4 (with
![]() $g(x)=e^{-x}$
and
$g(x)=e^{-x}$
and
![]() $\mathbb {T}=\{1\}$
).
$\mathbb {T}=\{1\}$
).
Proof of Theorem 1.2.
By Corollary 5.7, we know that v yields a special
![]() $\mathbb {R}$
-test configuration in the sense of [Reference Han and LiHL20b, Definition 2.8]. Thus, by [Reference Han and LiHL20b, Theorem 1.6], we know that
$\mathbb {R}$
-test configuration in the sense of [Reference Han and LiHL20b, Definition 2.8]. Thus, by [Reference Han and LiHL20b, Theorem 1.6], we know that
![]() $(X_0,\Delta _0,\xi _v)$
is a K-semistable triple.
$(X_0,\Delta _0,\xi _v)$
is a K-semistable triple.
Corollary 5.8. Any quasi-monomial valuation
![]() $v\in \mathrm {Val}_{X}^{\mathbb {T},\circ }$
computing
$v\in \mathrm {Val}_{X}^{\mathbb {T},\circ }$
computing
![]() $\delta _g(X,\Delta ,\xi )$
, where
$\delta _g(X,\Delta ,\xi )$
, where
![]() $\xi \neq 0$
, has a finitely generated associated graded ring.
$\xi \neq 0$
, has a finitely generated associated graded ring.
Proof. In view of Theorem 5.4, it suffices to show that
![]() $\delta _g(X,\Delta ,\xi )\le 1$
. Indeed, we will prove a stronger statement:
$\delta _g(X,\Delta ,\xi )\le 1$
. Indeed, we will prove a stronger statement:
for all
![]() $v_0\in \mathrm {Val}_X^{\mathbb {T},\circ }$
,
$v_0\in \mathrm {Val}_X^{\mathbb {T},\circ }$
,
![]() $m\in \mathbb {N}$
and all positive functions
$m\in \mathbb {N}$
and all positive functions
![]() $g\in C^0(\mathbb {R})$
, as long as
$g\in C^0(\mathbb {R})$
, as long as
![]() $\mathbb {T}\neq \{1\}$
. To see this, let D be a
$\mathbb {T}\neq \{1\}$
. To see this, let D be a
![]() $\mathbb {T}$
-invariant g-weighted
$\mathbb {T}$
-invariant g-weighted
![]() $(m,v_0)$
-basis type divisor. If
$(m,v_0)$
-basis type divisor. If
![]() $(X,\Delta +D)$
is klt, then after perturbing the coefficients of D as in the proof of Theorem 5.4, we get a
$(X,\Delta +D)$
is klt, then after perturbing the coefficients of D as in the proof of Theorem 5.4, we get a
![]() $\mathbb {T}$
-invariant
$\mathbb {T}$
-invariant
![]() ${\mathbb {Q}}$
-divisor
${\mathbb {Q}}$
-divisor
![]() $\widetilde {D}>D$
proportional to
$\widetilde {D}>D$
proportional to
![]() $-(K_X+\Delta )$
such that
$-(K_X+\Delta )$
such that
![]() $(X,\Delta +\widetilde {D})$
is still klt and
$(X,\Delta +\widetilde {D})$
is still klt and
![]() $K_X+\Delta +\widetilde {D}$
is ample. So such pairs have finite automorphism groups and this is a contradiction as
$K_X+\Delta +\widetilde {D}$
is ample. So such pairs have finite automorphism groups and this is a contradiction as
![]() $\mathbb {T}<\operatorname {Aut}(X,\Delta +\widetilde {D})$
by construction. Thus,
$\mathbb {T}<\operatorname {Aut}(X,\Delta +\widetilde {D})$
by construction. Thus,
![]() $(X,\Delta +D)$
is not klt and
$(X,\Delta +D)$
is not klt and
![]() $\mathrm {lct}(X,\Delta ;D)\le 1$
. This proves equation (5.3).
$\mathrm {lct}(X,\Delta ;D)\le 1$
. This proves equation (5.3).
Corollary 5.9. Any g-Ding polystable triple
![]() $(X,\Delta ,\xi )$
is also reduced uniformly g-Ding stable. In particular, it admits a Kähler–Ricci g-soliton when
$(X,\Delta ,\xi )$
is also reduced uniformly g-Ding stable. In particular, it admits a Kähler–Ricci g-soliton when
![]() .
.
Proof. The proof is very similar to that of [Reference Liu, Xu and ZhuangLXZ22, Theorem 5.2]. Let
![]() $\mathbb {T}<\operatorname {Aut}(X,\Delta ,\xi )$
be a maximal torus such that
$\mathbb {T}<\operatorname {Aut}(X,\Delta ,\xi )$
be a maximal torus such that
![]() $\xi \in N_{\mathbb {R}}$
. Assume to the contrary that
$\xi \in N_{\mathbb {R}}$
. Assume to the contrary that
![]() $(X,\Delta ,\xi )$
is g-Ding polystable but not reduced uniformly g-Ding stable. Then by Proposition 4.14, we know that
$(X,\Delta ,\xi )$
is g-Ding polystable but not reduced uniformly g-Ding stable. Then by Proposition 4.14, we know that
![]() $\delta _g(X,\Delta ,\xi )=1$
is computed by some quasi-monomial valuation
$\delta _g(X,\Delta ,\xi )=1$
is computed by some quasi-monomial valuation
![]() $v\in \mathrm {Val}_X^{\mathbb {T},\circ }$
that is not of the form
$v\in \mathrm {Val}_X^{\mathbb {T},\circ }$
that is not of the form
![]() $\mathrm {wt}_{\eta }$
. By Corollary 5.8, the associated graded ring
$\mathrm {wt}_{\eta }$
. By Corollary 5.8, the associated graded ring
![]() $\mathrm {gr}_v R$
is finitely generated. Let
$\mathrm {gr}_v R$
is finitely generated. Let
![]() $\pi \colon (Y,E)\to (X,\Delta )$
be a
$\pi \colon (Y,E)\to (X,\Delta )$
be a
![]() $\mathbb {T}$
-equivariant log smooth model such that
$\mathbb {T}$
-equivariant log smooth model such that
![]() $\mathrm {QM}(Y,E)$
is a simplicial cone containing v and that its dimension is the same as the rational rank of v. As in [Reference XuXu21, Claim 3.10], this implies that in a neighbourhood of v in
$\mathrm {QM}(Y,E)$
is a simplicial cone containing v and that its dimension is the same as the rational rank of v. As in [Reference XuXu21, Claim 3.10], this implies that in a neighbourhood of v in
![]() $\mathrm {QM}(Y,E)$
, the function
$\mathrm {QM}(Y,E)$
, the function
![]() $w\mapsto S_g(v_0;w)$
is linear, and we have
$w\mapsto S_g(v_0;w)$
is linear, and we have
![]() $\mathrm {gr}_wR\cong \mathrm {gr}_vR$
.
$\mathrm {gr}_wR\cong \mathrm {gr}_vR$
.
Thus,
![]() $\delta _g(X,\Delta ,\xi )$
is also computed by some
$\delta _g(X,\Delta ,\xi )$
is also computed by some
![]() $\mathbb {T}$
-invariant divisorial valuation
$\mathbb {T}$
-invariant divisorial valuation
![]() $w\in \mathrm {QM}(Y,E)$
that is sufficiently close to v. In particular,
$w\in \mathrm {QM}(Y,E)$
that is sufficiently close to v. In particular,
![]() $\mathbf {D}^{\mathrm {NA}}_g({\mathcal {F}}_w)\le A_{X,\Delta }(w)-S_g(v_0;w)=0$
(the first inequality is by Corollary 3.11) and
$\mathbf {D}^{\mathrm {NA}}_g({\mathcal {F}}_w)\le A_{X,\Delta }(w)-S_g(v_0;w)=0$
(the first inequality is by Corollary 3.11) and
![]() $w\neq \mathrm {wt}_{\eta }$
for any
$w\neq \mathrm {wt}_{\eta }$
for any
![]() $\eta \in N_{\mathbb {R}}$
. It induces a nonproduct type
$\eta \in N_{\mathbb {R}}$
. It induces a nonproduct type
![]() $\mathbb {T}$
-equivariant test configuration
$\mathbb {T}$
-equivariant test configuration
![]() $({\mathcal {X}},\Delta _{{\mathcal {X}}},{\mathcal {L}})$
such that
$({\mathcal {X}},\Delta _{{\mathcal {X}}},{\mathcal {L}})$
such that
![]() $\mathbf {D}^{\mathrm {NA}}_g({\mathcal {X}},\Delta _{{\mathcal {X}}},{\mathcal {L}})\le 0$
. This contradicts the g-Ding polystability of
$\mathbf {D}^{\mathrm {NA}}_g({\mathcal {X}},\Delta _{{\mathcal {X}}},{\mathcal {L}})\le 0$
. This contradicts the g-Ding polystability of
![]() $(X,\Delta ,\xi )$
and proves the first part of the corollary. The remaining part follows from Theorem 4.9.
$(X,\Delta ,\xi )$
and proves the first part of the corollary. The remaining part follows from Theorem 4.9.
Proof of Theorem 1.3.
By [Reference Berman and NyströmBWN14, Theorem 1.5],
![]() $(X,\Delta ,\xi )$
is K-polystable if it admits a Kähler–Ricci soliton. Thus, the result follows immediately from Theorem 4.9 and Corollary 5.9 by setting
$(X,\Delta ,\xi )$
is K-polystable if it admits a Kähler–Ricci soliton. Thus, the result follows immediately from Theorem 4.9 and Corollary 5.9 by setting
![]() $g(x)=e^{-x}$
.
$g(x)=e^{-x}$
.
Remark 5.10. The above proof that reduced uniform Ding stability implies K-polystability uses Kähler–Ricci solitons, but it can be proved algebraically. Though, there is some subtlety, since the data of a triple
![]() $(X,\Delta ,\xi )$
includes a torus
$(X,\Delta ,\xi )$
includes a torus
![]() $\mathbb {T}$
so that
$\mathbb {T}$
so that
![]() $\xi \in N_{R} : = \mathrm { Hom}(\mathbb {G}_m,\mathbb {T})\otimes _{\mathbb {Z}}\mathbb {R}$
and
$\xi \in N_{R} : = \mathrm { Hom}(\mathbb {G}_m,\mathbb {T})\otimes _{\mathbb {Z}}\mathbb {R}$
and
![]() $\mathbb {T}$
is not necessarily maximal. While the K-polystability of
$\mathbb {T}$
is not necessarily maximal. While the K-polystability of
![]() $(X,\Delta ,\xi )$
is with respect to
$(X,\Delta ,\xi )$
is with respect to
![]() $\mathbb {T}$
, reduced uniform Ding stability is defined using a maximal torus
$\mathbb {T}$
, reduced uniform Ding stability is defined using a maximal torus
![]() $\mathbb {T} < \mathbb {T}^{\max } < \operatorname {Aut}(X,\Delta )$
.
$\mathbb {T} < \mathbb {T}^{\max } < \operatorname {Aut}(X,\Delta )$
.
To prove the equivalence, observe that if
![]() $(X,\Delta ,\xi )$
is reduced uniformly Ding stable, then it is K-polystable with respect to
$(X,\Delta ,\xi )$
is reduced uniformly Ding stable, then it is K-polystable with respect to
![]() $\mathbb {T}^{\max }$
by [Reference Han and LiHL20, Proposition 5.16]. To show it is K-polystable with respect to
$\mathbb {T}^{\max }$
by [Reference Han and LiHL20, Proposition 5.16]. To show it is K-polystable with respect to
![]() $\mathbb {T}$
, first by [Reference Han and LiHL20b, (168) or (189)], it follows that
$\mathbb {T}$
, first by [Reference Han and LiHL20b, (168) or (189)], it follows that
![]() $(X,\Delta ,\xi )$
is K-semistable with respect to
$(X,\Delta ,\xi )$
is K-semistable with respect to
![]() $\mathbb {T}$
. Then by verbatim applying the proof of [Reference Li, Wang and XuLWX21, Theorem 3.7] (see also [Reference Han and LiHL20b, Section 8]), we know the K-polystablity of
$\mathbb {T}$
. Then by verbatim applying the proof of [Reference Li, Wang and XuLWX21, Theorem 3.7] (see also [Reference Han and LiHL20b, Section 8]), we know the K-polystablity of
![]() $(X,\Delta ,\xi )$
with respect to
$(X,\Delta ,\xi )$
with respect to
![]() $\mathbb {T}^{\max }$
implies the K-polystability of
$\mathbb {T}^{\max }$
implies the K-polystability of
![]() $(X,\Delta ,\xi )$
with respect to
$(X,\Delta ,\xi )$
with respect to
![]() $\mathbb {T}$
.
$\mathbb {T}$
.
Proof of Theorem 1.1.
It is a combination of Theorem 1.2, [Reference Han and LiHL20b, Theorem 1.3] and Theorem 1.3.
As an application, we show the following theorem, which generalizes [Reference Wang and ZhuWZ04] from the smooth case to general toric log Fano pairs. See also [Reference Han and LiHL20, Section 8].
Theorem 5.11. For any toric log Fano pair
![]() $(X,\Delta )$
over
$(X,\Delta )$
over
![]() $\mathbb {C}$
, there exists a vector
$\mathbb {C}$
, there exists a vector
![]() $\xi \in N_{\mathbb R}:=\mathrm {Hom}(\mathbb {G}_m, \mathbb {T})\otimes _{\mathbb {Z}}\mathbb {R}$
where
$\xi \in N_{\mathbb R}:=\mathrm {Hom}(\mathbb {G}_m, \mathbb {T})\otimes _{\mathbb {Z}}\mathbb {R}$
where
![]() $\mathbb {T}$
is the maximal torus acting on
$\mathbb {T}$
is the maximal torus acting on
![]() $(X,\Delta )$
, such that
$(X,\Delta )$
, such that
![]() $(X,\Delta ,\xi )$
admits a Kähler–Ricci soliton.
$(X,\Delta ,\xi )$
admits a Kähler–Ricci soliton.
Proof. By Corollary 3.17, there is a unique valuation
![]() $v\in \mathrm {Val}_X$
which computes
$v\in \mathrm {Val}_X$
which computes
![]() $h(X,\Delta )$
. By the uniqueness, v is
$h(X,\Delta )$
. By the uniqueness, v is
![]() $\mathbb {T}$
-invariant, that is,
$\mathbb {T}$
-invariant, that is,
![]() $v=\mathrm {wt}_{\xi }$
for some
$v=\mathrm {wt}_{\xi }$
for some
![]() $\xi \in N_{\mathbb {R}}$
. Therefore, the K-semistable triple produced in Theorem 1.2 is
$\xi \in N_{\mathbb {R}}$
. Therefore, the K-semistable triple produced in Theorem 1.2 is
![]() $(X,\Delta , \xi )$
.
$(X,\Delta , \xi )$
.
Since
![]() $(X,\Delta ,\xi )$
is K-semistable and toric, it is reduced uniformly Ding stable by Theorem 4.12. Indeed, condition (3) of the theorem holds trivially, since any
$(X,\Delta ,\xi )$
is K-semistable and toric, it is reduced uniformly Ding stable by Theorem 4.12. Indeed, condition (3) of the theorem holds trivially, since any
![]() $w\in \mathrm { Val}_{X}^{\mathbb {T},\circ }$
is of the form
$w\in \mathrm { Val}_{X}^{\mathbb {T},\circ }$
is of the form
![]() $w=\mathrm {wt}_{\eta }$
for some
$w=\mathrm {wt}_{\eta }$
for some
![]() $\eta \in N_{\mathbb {R}}$
and, hence, satisfies
$\eta \in N_{\mathbb {R}}$
and, hence, satisfies
![]() $\mathbf {J}^{\mathrm {NA}}_{g,\mathbb {T}}(w) = 0$
where
$\mathbf {J}^{\mathrm {NA}}_{g,\mathbb {T}}(w) = 0$
where
![]() $g=e^{-x}$
. Therefore,
$g=e^{-x}$
. Therefore,
![]() $(X,\Delta ,\xi )$
admits a Kähler–Ricci soliton by [Reference Han and LiHL20].
$(X,\Delta ,\xi )$
admits a Kähler–Ricci soliton by [Reference Han and LiHL20].
6 Moduli stack
In this section, we will prove Theorem 1.5. It suffices to verify the boundedness and openness; see Theorem 6.3 and Theorem 6.4.
Theorem 6.1. For a fixed dimension n, volume V, a positive integer N and a negative constant
![]() $h_0<0$
, families of n-dimensional log Fano pairs
$h_0<0$
, families of n-dimensional log Fano pairs
![]() $(X,\Delta )$
with
$(X,\Delta )$
with
![]() $(-K_X-\Delta )^n=V$
,
$(-K_X-\Delta )^n=V$
,
![]() $N\Delta $
integral and
$N\Delta $
integral and
![]() $h(X,\Delta )\ge h_0$
are parameterized by an Artin stack
$h(X,\Delta )\ge h_0$
are parameterized by an Artin stack
![]() $\mathcal {M}^{\mathrm {Fano}}_{n,V,N,h^+_0}$
of finite type.
$\mathcal {M}^{\mathrm {Fano}}_{n,V,N,h^+_0}$
of finite type.
The following result gives the boundedness.
Proposition 6.2. Let
![]() $(X,\Delta )$
be a log Fano pair, and let
$(X,\Delta )$
be a log Fano pair, and let
![]() $c\in \mathbb {R}$
. Assume that
$c\in \mathbb {R}$
. Assume that
![]() $\tilde {\beta }_{X,\Delta }(v)\ge c$
for all divisorial valuations v on X. Then
$\tilde {\beta }_{X,\Delta }(v)\ge c$
for all divisorial valuations v on X. Then
![]() $\alpha (X,\Delta )\ge \alpha $
for some constant
$\alpha (X,\Delta )\ge \alpha $
for some constant
![]() $\alpha>0$
that only depends on c and
$\alpha>0$
that only depends on c and
![]() $\dim (X)$
.
$\dim (X)$
.
Here,
![]() $\alpha (X,\Delta )$
denotes Tian’s
$\alpha (X,\Delta )$
denotes Tian’s
![]() $\alpha $
-invariant. In the proof, we use that
$\alpha $
-invariant. In the proof, we use that
![]() $\alpha (X,\Delta )$
equals
$\alpha (X,\Delta )$
equals
![]() $\inf _{v}\frac {A_{X,\Delta }(v)}{T(v)}$
, where the infimum runs through all divisorial valuations on X; see, for example, [Reference Blum and JonssonBJ20].
$\inf _{v}\frac {A_{X,\Delta }(v)}{T(v)}$
, where the infimum runs through all divisorial valuations on X; see, for example, [Reference Blum and JonssonBJ20].
Proof. It suffices to find some constant
![]() $M=M(c,n)>0$
that only depends on c and
$M=M(c,n)>0$
that only depends on c and
![]() $n=\dim (X)$
such that
$n=\dim (X)$
such that
![]() $T(v)\le M$
for all divisorial valuations v with
$T(v)\le M$
for all divisorial valuations v with
![]() $A_{X,\Delta }(v)=1$
. For now, fix any such v and let
$A_{X,\Delta }(v)=1$
. For now, fix any such v and let
![]() ${\mathcal {F}}={\mathcal {F}}_v$
,
${\mathcal {F}}={\mathcal {F}}_v$
,
![]() $T=T_{X,\Delta }(v)$
,
$T=T_{X,\Delta }(v)$
,
![]() $\widetilde {S}=\widetilde {S}(v)$
. We will apply a modified argument from [Reference Blum and JonssonBJ20, Lemma 2.6]. Let
$\widetilde {S}=\widetilde {S}(v)$
. We will apply a modified argument from [Reference Blum and JonssonBJ20, Lemma 2.6]. Let
![]() $f(\lambda )=\frac { \mathrm {vol}( V_{\bullet }^{ (\lambda )}) }{L^n}$
. Note that
$f(\lambda )=\frac { \mathrm {vol}( V_{\bullet }^{ (\lambda )}) }{L^n}$
. Note that
![]() $f(0)=1$
,
$f(0)=1$
,
![]() $f(T)=0$
and
$f(T)=0$
and
![]() $\mathrm {DH}_{{\mathcal {F}}} = -f'(\lambda ) \mathrm {d} \lambda $
. By [Reference LazarsfeldLaz04, Theorem 11.4.9], the function
$\mathrm {DH}_{{\mathcal {F}}} = -f'(\lambda ) \mathrm {d} \lambda $
. By [Reference LazarsfeldLaz04, Theorem 11.4.9], the function
![]() $\lambda \mapsto f(\lambda )^{\frac {1}{n}}$
is concave on
$\lambda \mapsto f(\lambda )^{\frac {1}{n}}$
is concave on
![]() $(0,T)$
, thus
$(0,T)$
, thus
 $$\begin{align*}f(\lambda)\ge \left(1-\frac{\lambda}{T}\right)^n. \end{align*}$$
$$\begin{align*}f(\lambda)\ge \left(1-\frac{\lambda}{T}\right)^n. \end{align*}$$
On the other hand, integration by parts yields
 $$\begin{align*}e^{-\widetilde{S}} = \int_0^T e^{-\lambda} \mathrm{DH}_{{\mathcal{F}}}(\mathrm{d} \lambda) = 1 - \int_0^T e^{-\lambda} f(\lambda) \mathrm{d} \lambda, \end{align*}$$
$$\begin{align*}e^{-\widetilde{S}} = \int_0^T e^{-\lambda} \mathrm{DH}_{{\mathcal{F}}}(\mathrm{d} \lambda) = 1 - \int_0^T e^{-\lambda} f(\lambda) \mathrm{d} \lambda, \end{align*}$$
hence
![]() $e^{-\widetilde {S}}\le 1 - \int _0^T e^{-\lambda } \left (1-\frac {\lambda }{T}\right )^n \mathrm {d} \lambda $
. We may further rewrite the right-hand side as
$e^{-\widetilde {S}}\le 1 - \int _0^T e^{-\lambda } \left (1-\frac {\lambda }{T}\right )^n \mathrm {d} \lambda $
. We may further rewrite the right-hand side as
 $$ \begin{align*} \int_0^{\infty} e^{-\lambda} \mathrm{d} \lambda - \int_0^T e^{-\lambda} \left(1-\frac{\lambda}{T}\right)^n \mathrm{d} \lambda & = \int_0^T e^{-\lambda} \left[ 1-\left(1-\frac{\lambda}{T}\right)^n \right] \mathrm{d} \lambda + \int_T^{\infty} e^{-\lambda} \mathrm{d} \lambda \\ & \le \int_0^T \frac{n\lambda}{T} e^{-\lambda} \mathrm{d} \lambda + \int_T^{\infty} e^{-\lambda} \mathrm{d} \lambda \\ & \le \frac{n}{T}+e^{-T}. \end{align*} $$
$$ \begin{align*} \int_0^{\infty} e^{-\lambda} \mathrm{d} \lambda - \int_0^T e^{-\lambda} \left(1-\frac{\lambda}{T}\right)^n \mathrm{d} \lambda & = \int_0^T e^{-\lambda} \left[ 1-\left(1-\frac{\lambda}{T}\right)^n \right] \mathrm{d} \lambda + \int_T^{\infty} e^{-\lambda} \mathrm{d} \lambda \\ & \le \int_0^T \frac{n\lambda}{T} e^{-\lambda} \mathrm{d} \lambda + \int_T^{\infty} e^{-\lambda} \mathrm{d} \lambda \\ & \le \frac{n}{T}+e^{-T}. \end{align*} $$
By assumption,
![]() $1-\widetilde {S} = \tilde {\beta }(v)\ge c$
, hence
$1-\widetilde {S} = \tilde {\beta }(v)\ge c$
, hence
![]() $e^{-\widetilde {S}}\ge e^{c-1}$
. It follows that
$e^{-\widetilde {S}}\ge e^{c-1}$
. It follows that
From this, we deduce that T is bounded from above by some constant that only depends on c and n. The proof is now complete.
Theorem 6.3. Fixed positive integers n, N, a positive number
![]() $V_0$
and a constant
$V_0$
and a constant
![]() $h_0 $
. Denote by
$h_0 $
. Denote by
![]() $\mathcal {P}$
the set of n-dimensional log Fano pairs
$\mathcal {P}$
the set of n-dimensional log Fano pairs
![]() $(X,\Delta )$
with
$(X,\Delta )$
with
![]() $N\cdot \Delta $
integral which satisfy
$N\cdot \Delta $
integral which satisfy
![]() $(-K_X-\Delta )^n\ge V_0$
and
$(-K_X-\Delta )^n\ge V_0$
and
![]() $h(X,\Delta )\ge h_0$
. Then
$h(X,\Delta )\ge h_0$
. Then
![]() $\mathcal {P}$
is bounded.
$\mathcal {P}$
is bounded.
Proof. For fixed
![]() $\alpha _0>0$
, the set of log Fano pairs
$\alpha _0>0$
, the set of log Fano pairs
![]() $(X,\Delta )$
with
$(X,\Delta )$
with
![]() $n=\dim (X)$
,
$n=\dim (X)$
,
![]() $N\cdot \Delta $
integral and
$N\cdot \Delta $
integral and
![]() $(-K_X-\Delta )^n \geq V_0$
, and
$(-K_X-\Delta )^n \geq V_0$
, and
![]() $\alpha (X,\Delta )>\alpha _0$
are bounded by [Reference ChenChe20] [Reference JiangJia20] [Reference Xu and ZhuangXZ21]. Applying Proposition 6.2 then completes the proof.
$\alpha (X,\Delta )>\alpha _0$
are bounded by [Reference ChenChe20] [Reference JiangJia20] [Reference Xu and ZhuangXZ21]. Applying Proposition 6.2 then completes the proof.
Next, we will prove the openness. It suffices to show the following theorem.
Theorem 6.4. Let
![]() $(X,\Delta )\to B$
be a locally stable family of log Fano pairs over a scheme B of finite type. Then
$(X,\Delta )\to B$
be a locally stable family of log Fano pairs over a scheme B of finite type. Then
is a constructible and lower semicontinuous.
Proof. By passing to a resolution of
![]() $B_{\mathrm {red}}$
, we may assume B is smooth. By the proof of Theorem 5.4, we know that the minimizer of
$B_{\mathrm {red}}$
, we may assume B is smooth. By the proof of Theorem 5.4, we know that the minimizer of
![]() $\tilde {\beta }_{X,\Delta }$
is an lc place of a
$\tilde {\beta }_{X,\Delta }$
is an lc place of a
![]() $\mathbb {Q}$
-complement. Then as showed in [Reference Blum, Liu and XuBLX22, Theorem 3.5],
$\mathbb {Q}$
-complement. Then as showed in [Reference Blum, Liu and XuBLX22, Theorem 3.5],
for some constant N which only depends on
![]() $\dim X$
and coefficients of
$\dim X$
and coefficients of
![]() $\Delta $
. Then the rest of the proof is similar to the one in [Reference Blum and LiuBL22, Reference Blum, Liu and XuBLX22]. For the sake of completeness, we give a sketch here.
$\Delta $
. Then the rest of the proof is similar to the one in [Reference Blum and LiuBL22, Reference Blum, Liu and XuBLX22]. For the sake of completeness, we give a sketch here.
We know that there is a finite type variety
![]() $\phi \colon S\to B$
with a relative Cartier divisor
$\phi \colon S\to B$
with a relative Cartier divisor
![]() $D\subset X\times _BS$
over S such that
$D\subset X\times _BS$
over S such that
-
1. For any
 $s\in S$
, the fiber
$s\in S$
, the fiber
 $D_s$
is an N-complement of
$D_s$
is an N-complement of
 $(X_t, \Delta _t)$
, where
$(X_t, \Delta _t)$
, where
 $t=\phi (s)$
, and
$t=\phi (s)$
, and
 $(X_t, D_s+\Delta _t)$
is log canonical but not klt, and
$(X_t, D_s+\Delta _t)$
is log canonical but not klt, and -
2. For any N-complement
 $\Gamma _t$
of
$\Gamma _t$
of
 $(X_t,\Delta _t)$
, there is a point
$(X_t,\Delta _t)$
, there is a point
 $s\in S$
, such that
$s\in S$
, such that
 $D_s\cong \Gamma _t$
.
$D_s\cong \Gamma _t$
.
After resolving and stratifying S, as well as passing to a finite base change, we can assume S is a union of its smooth connected component
![]() $S_i$
such that
$S_i$
such that
![]() $(X\times _BS_i, \Delta \times _BS_i+D\times _SS_i)$
admits a fiberwise log resolution.
$(X\times _BS_i, \Delta \times _BS_i+D\times _SS_i)$
admits a fiberwise log resolution.
For a fixed i, we can identify the dual complex
![]() $\mathcal {CW}_i:={\mathcal {DMR}}(X_t, \Delta _t+D_t)$
for any
$\mathcal {CW}_i:={\mathcal {DMR}}(X_t, \Delta _t+D_t)$
for any
![]() $t\in S_i$
. We claim
$t\in S_i$
. We claim
![]() $\tilde {\beta }_{X_t,\Delta _t}(v_t)$
does not depend on t, for different valuations
$\tilde {\beta }_{X_t,\Delta _t}(v_t)$
does not depend on t, for different valuations
![]() $v_t$
correspond to the same point of
$v_t$
correspond to the same point of
![]() $\mathcal {CW}_i$
. This is obvious for
$\mathcal {CW}_i$
. This is obvious for
![]() $A_{X_t,\Delta _t}(v_t)$
. It also proved in [Reference Blum, Liu and XuBLX22], using the invariance of plurigenera ([Reference Hacon, McKernan and XuHMX13]), for
$A_{X_t,\Delta _t}(v_t)$
. It also proved in [Reference Blum, Liu and XuBLX22], using the invariance of plurigenera ([Reference Hacon, McKernan and XuHMX13]), for
![]() $v_t$
corresponding to the same point of
$v_t$
corresponding to the same point of
![]() $\mathcal {CW}$
over any
$\mathcal {CW}$
over any
![]() $t\in S_i$
, the induced DH-measure
$t\in S_i$
, the induced DH-measure
![]() $\mathrm {DH}_{{\mathcal {F}}_{v_t}}$
on
$\mathrm {DH}_{{\mathcal {F}}_{v_t}}$
on
![]() $\mathbb R$
is the same. Therefore,
$\mathbb R$
is the same. Therefore,
does not depend on t.
Hence, for each i, we can define
![]() $a_i=\min \{ \tilde {\beta }(v_t)\ |\ v_t\in \mathcal {CW}_i\}$
, and we know that
$a_i=\min \{ \tilde {\beta }(v_t)\ |\ v_t\in \mathcal {CW}_i\}$
, and we know that
![]() $h(X_t,\Delta _t)=\min \{a_i | \ t\in \phi (S_i)\},$
which implies that
$h(X_t,\Delta _t)=\min \{a_i | \ t\in \phi (S_i)\},$
which implies that
![]() $h(X_t,\Delta _t)$
is constructible.
$h(X_t,\Delta _t)$
is constructible.
In light of the above constructibility result, to prove the lower semicontinuity of h it suffices to consider the case when B is the spectrum of a DVR R essentially of finite type over
![]() . Let K denote the fraction field of R and
. Let K denote the fraction field of R and
![]() $\kappa $
the residue field. By the properness of the flag variety, we know that any filtration
$\kappa $
the residue field. By the properness of the flag variety, we know that any filtration
![]() ${\mathcal {F}}_K$
on
${\mathcal {F}}_K$
on
![]() $\bigoplus _mH^0(-mr(K_{X_K}+\Delta _{X_K}))$
extends to a filtration
$\bigoplus _mH^0(-mr(K_{X_K}+\Delta _{X_K}))$
extends to a filtration
![]() ${\mathcal {F}}_{\kappa } $
on
${\mathcal {F}}_{\kappa } $
on
![]() $\bigoplus _mH^0(-mr(K_{X_{\kappa }}+\Delta _{X_{\kappa }}))$
(see [Reference Blum and LiuBL22]). By Lemma 3.8 and the lower semicontinuity of the log canonical threshold,
$\bigoplus _mH^0(-mr(K_{X_{\kappa }}+\Delta _{X_{\kappa }}))$
(see [Reference Blum and LiuBL22]). By Lemma 3.8 and the lower semicontinuity of the log canonical threshold,
Since
![]() $\mathrm {DH}_{{\mathcal {F}}_K}(d \lambda )= \mathrm {DH}_{{\mathcal {F}}_{\kappa } }(d \lambda )$
, we also have
$\mathrm {DH}_{{\mathcal {F}}_K}(d \lambda )= \mathrm {DH}_{{\mathcal {F}}_{\kappa } }(d \lambda )$
, we also have
![]() $\widetilde {S}({\mathcal {F}}_K)= \widetilde {S}({\mathcal {F}}_{\kappa })$
. Therefore, h is lower semicontinuous.
$\widetilde {S}({\mathcal {F}}_K)= \widetilde {S}({\mathcal {F}}_{\kappa })$
. Therefore, h is lower semicontinuous.
Acknowledgements
We would like to thank Mattias Jonsson, Valentino Tosatti and Xiaowei Wang for helpful conversations. We are also grateful to the anonymous referee for valuable comments.
Conflicts of Interest
The authors have no conflict of interest to declare.
Financial support
HB is partially supported by NSF DMS-1803102 and DMS-2200690. YL is partially supported by NSF DMS-2148266 (formerly DMS-2001317) and an Alfred P. Sloan research fellowship. CX is partially supported by NSF DMS-2153115 (formerly DMS-1901849), DMS-2139613 (formerly), DMS-2201349 and a Simons Investigator. ZZ is partially supported by NSF DMS-2240926 (formerly DMS-2055531) and a Clay research fellowship.