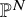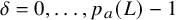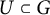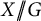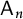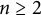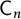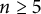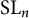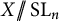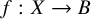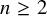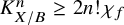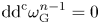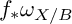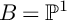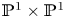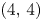Refine search
Actions for selected content:
50 results
On the non-properness set of a local homeomorphism
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 30 September 2025, pp. 1-15
-
- Article
- Export citation
Minimal Kinematics on
 $\mathcal{M}_{0,n}$
$\mathcal{M}_{0,n}$
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DEGENERATIONS OF ORBIFOLD CURVES AS NONCOMMUTATIVE VARIETIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 261 / 2026
- Published online by Cambridge University Press:
- 15 July 2025, e4
- Print publication:
- 2026
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Upper bounds on the genus of hyperelliptic Albanese fibrations
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 02 May 2025, e84
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EIGENPERIODS AND THE MODULI OF POINTS IN THE LINE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 259 / September 2025
- Published online by Cambridge University Press:
- 24 February 2025, pp. 524-547
- Print publication:
- September 2025
-
- Article
- Export citation
Semistable degenerations of Calabi–Yau manifolds and mirror P=W conjectures
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 07 November 2024, e94
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Classification of subpencils for hyperplane sections on certain K3 surfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 23 October 2023, pp. 1022-1043
-
- Article
- Export citation
On Bloch’s map for torsion cycles over non-closed fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 22 June 2023, e53
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nonemptiness of severi varieties on enriques surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 19 June 2023, e52
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Slope equality of non-hyperelliptic Eisenbud–Harris special fibrations of genus 4
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 20 January 2023, pp. 284-287
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Small G-varieties
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 04 January 2023, pp. 173-215
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Relative Severi inequality for fibrations of maximal Albanese dimension over curves
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 16 June 2022, e45
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Singular Gauduchon metrics
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 17 August 2022, pp. 1314-1328
- Print publication:
- June 2022
-
- Article
- Export citation
FUJITA DECOMPOSITION AND MASSEY PRODUCT FOR FIBERED VARIETIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 247 / September 2022
- Published online by Cambridge University Press:
- 29 November 2021, pp. 624-652
- Print publication:
- September 2022
-
- Article
- Export citation
ON THE CHOW THEORY OF PROJECTIVIZATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 11 November 2021, pp. 1465-1508
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
P = W for Lagrangian fibrations and degenerations of hyper-Kähler manifolds
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 25 June 2021, e50
-
- Article
-
- You have access
- Open access
- Export citation
A specialization inequality for tropical complexes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 1051-1078
- Print publication:
- May 2021
-
- Article
- Export citation
Perverse Leray filtration and specialisation with applications to the Hitchin morphism
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 20 April 2021, pp. 443-487
- Print publication:
- March 2022
-
- Article
- Export citation
KSBA compactification of the moduli space of K3 surfaces with a purely non-symplectic automorphism of order four
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 12 April 2021, pp. 99-127
-
- Article
- Export citation
Extending tamely ramified strict 1-motives into két log 1-motives
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 09 March 2021, e20
-
- Article
-
- You have access
- Open access
- Export citation