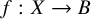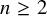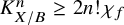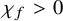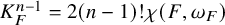1 Introduction
The Severi inequality states that
for an n-dimensional minimal variety X of general type and maximal Albanese dimension. It was originally stated for surfaces by Severi [Reference Severi21] and was proved by Pardini [Reference Pardini20]. Later, it was generalised to arbitrary dimension by Barja [Reference Barja2] as well as the second author [Reference Zhang25]. From now on, we refer to this inequality as the absolute Severi inequality in order to distinguish from the result in the current paper.
The goal of this paper is to establish a relative version of the absolute Severi inequality. More precisely, we prove that
for a relatively minimal fibration
![]() $f: X \to B$
of maximal Albanese dimension from an n-dimensional variety X to a curve B. This inequality was conjecturally formulated by Barja in [Reference Barja2, §1]. The
$f: X \to B$
of maximal Albanese dimension from an n-dimensional variety X to a curve B. This inequality was conjecturally formulated by Barja in [Reference Barja2, §1]. The
![]() $g(B) = 0$
case of this relative inequality can be applied to give a new proof of the above absolute Severi inequality. Moreover, the above relative inequality is sharp, and if
$g(B) = 0$
case of this relative inequality can be applied to give a new proof of the above absolute Severi inequality. Moreover, the above relative inequality is sharp, and if
![]() $K_{X/B}^n = 2n! \chi _f> 0$
, we prove that the general fibre F of f has to satisfy the absolute Severi equality that
$K_{X/B}^n = 2n! \chi _f> 0$
, we prove that the general fibre F of f has to satisfy the absolute Severi equality that
We also use our method to deduce some sharper relative results of the same type under extra assumptions. As an upshot, the corresponding
![]() $g(B) = 0$
case implies the recent geographical results of absolute Severi type obtained by Barja, Pardini and Stoppino [Reference Barja, Pardini and Stoppino6].
$g(B) = 0$
case implies the recent geographical results of absolute Severi type obtained by Barja, Pardini and Stoppino [Reference Barja, Pardini and Stoppino6].
Throughout this paper, we work over an arbitrary algebraically closed field k of characteristic zero. All varieties are assumed to be projective.
1.1 Albanese dimension of fibrations and
 $\chi _f$
$\chi _f$
We start with some notation. In the study of irregular varieties, a major tool is to consider the Albanese map. For an irregular variety X, the so-called Albanese dimension
![]() ${\mathrm {albdim}}(X)$
of X is one of the most important invariants of X. In the following, we consider its relative version.
${\mathrm {albdim}}(X)$
of X is one of the most important invariants of X. In the following, we consider its relative version.
Let
![]() $f: X \to Y$
be a fibration between two normal varieties X and Y with a general fibre F. Let
$f: X \to Y$
be a fibration between two normal varieties X and Y with a general fibre F. Let
![]() $a: X \to {\mathrm {Alb}}(X)$
be the Albanese map of X.
$a: X \to {\mathrm {Alb}}(X)$
be the Albanese map of X.
Definition 1.1. The Albanese dimension of f, denoted by
![]() ${\mathrm {albdim}}(f)$
, is defined to be
${\mathrm {albdim}}(f)$
, is defined to be
![]() $\dim a(F)$
, namely the dimension of the image of F under the Albanese map of X. We say that f is of maximal Albanese dimension, if
$\dim a(F)$
, namely the dimension of the image of F under the Albanese map of X. We say that f is of maximal Albanese dimension, if
![]() ${\mathrm {albdim}}(f) = \dim F$
.
${\mathrm {albdim}}(f) = \dim F$
.
It is easy to check that the following properties hold:
-
(1) When f is the structural morphism (i.e.,
 $Y = {\mathrm {Spec}} (k)$
), then Thus the Albanese dimension for fibrations is indeed a generalisation of that for varieties.
$Y = {\mathrm {Spec}} (k)$
), then Thus the Albanese dimension for fibrations is indeed a generalisation of that for varieties. $$ \begin{align*} {\mathrm{albdim}}(f) = {\mathrm{albdim}}(X). \end{align*} $$
$$ \begin{align*} {\mathrm{albdim}}(f) = {\mathrm{albdim}}(X). \end{align*} $$
-
(2) In general, we have
In particular, if f is the Stein factorisation of the Albanese map of X, then $$ \begin{align*} {\mathrm{albdim}}(f) \le {\mathrm{albdim}}(X) - {\mathrm{albdim}}(Y). \end{align*} $$
$$ \begin{align*} {\mathrm{albdim}}(f) \le {\mathrm{albdim}}(X) - {\mathrm{albdim}}(Y). \end{align*} $$
 ${\mathrm {albdim}}(f) = 0$
.
${\mathrm {albdim}}(f) = 0$
.
-
(3) If both Y and f are of maximal Albanese dimension, so is X.
Another important invariant associated to f is the relative Euler characteristic
Regarding this invariant, the first interesting case is when
![]() $f: X \to Y$
is a surface fibration: that is, X is a smooth surface and Y is a curve. In this case, it is well known that
$f: X \to Y$
is a surface fibration: that is, X is a smooth surface and Y is a curve. In this case, it is well known that
In particular, by [Reference Fujita11, Main Theorem], we know that
![]() $\chi _f \ge 0$
. There are a number of important results related to
$\chi _f \ge 0$
. There are a number of important results related to
![]() $\chi _f$
, such as the Arakelov inequality [Reference Arakelov1] (see [Reference Viehweg22] for a survey together with generalisations), the slope inequality of Cornalba-Harris [Reference Cornalba and Harris9] and Xiao [Reference Xiao23], and the geography of irregular surfaces (see [Reference Mendes Lopes and Pardini17] for a detailed survey). The study of these results as well as their refinements and generalisations has been active throughout recent decades.
$\chi _f$
, such as the Arakelov inequality [Reference Arakelov1] (see [Reference Viehweg22] for a survey together with generalisations), the slope inequality of Cornalba-Harris [Reference Cornalba and Harris9] and Xiao [Reference Xiao23], and the geography of irregular surfaces (see [Reference Mendes Lopes and Pardini17] for a detailed survey). The study of these results as well as their refinements and generalisations has been active throughout recent decades.
Another interesting case, which is more related to this paper, is when f is a fibration of maximal Albanese dimension and Y is a curve. In this case, by the work of Hacon and Pardini [Reference Hacon and Pardini12, Theorem 2.4] (see Proposition 4.1 for a slightly generalised version adapting to the setting of this paper), we know that
where
![]() ${\mathcal {P}}$
is a general torsion element in
${\mathcal {P}}$
is a general torsion element in
![]() ${\mathrm {Pic}}^0(X)$
. Moreover, Hacon and Pardini showed that
${\mathrm {Pic}}^0(X)$
. Moreover, Hacon and Pardini showed that
![]() $\chi _f \ge 0$
still holds in this case.
$\chi _f \ge 0$
still holds in this case.
1.2 Main results
Now we state the first main theorem of this paper.
Theorem 1.2 Relative Severi inequality
Let
![]() $f: X \to B$
be a relatively minimal fibration from a variety X of dimension
$f: X \to B$
be a relatively minimal fibration from a variety X of dimension
![]() $n \ge 2$
to a smooth curve B. Suppose that f is of maximal Albanese dimension. Then we have the following sharp inequality:
$n \ge 2$
to a smooth curve B. Suppose that f is of maximal Albanese dimension. Then we have the following sharp inequality:
We call the inequality in equation (1.1) a relative Severi inequality because it literally replaces the absolute invariants
![]() $K_X^n$
and
$K_X^n$
and
![]() $\chi (X, \omega _X)$
in the absolute Severi inequality by the relative invariants
$\chi (X, \omega _X)$
in the absolute Severi inequality by the relative invariants
![]() $K_{X/B}^n$
and
$K_{X/B}^n$
and
![]() $\chi _f$
.
$\chi _f$
.
Let us put Theorem 1.2 into perspective. When
![]() $n=2$
, it is already known by Xiao [Reference Xiao23, Corollary 1]. More precisely, Xiao proved that for a relatively minimal surface fibration
$n=2$
, it is already known by Xiao [Reference Xiao23, Corollary 1]. More precisely, Xiao proved that for a relatively minimal surface fibration
![]() $f: X \to B$
with a general fibre of genus
$f: X \to B$
with a general fibre of genus
![]() $g \ge 2$
, the inequality in equation (1.1) holds, provided that
$g \ge 2$
, the inequality in equation (1.1) holds, provided that
![]() $h^1(X, {\mathcal {O}}_X)> g(B)$
. Note that this assumption is equivalent to f being of maximal Albanese dimension, as the fibre in this case is just a curve.
$h^1(X, {\mathcal {O}}_X)> g(B)$
. Note that this assumption is equivalent to f being of maximal Albanese dimension, as the fibre in this case is just a curve.
For general
![]() $n> 2$
, the problem with finding such inequalities has already been addressed by Mendes Lopes and Pardini [Reference Mendes Lopes and Pardini17, §5.3], whose purpose was to generalise, using Pardini’s original approach in [Reference Pardini20], the Severi inequality for surfaces to higher dimensions. To our knowledge, the precise version of equation (1.1) was first formulated conjecturally by Barja in [Reference Barja2, §1, Page 545]. Barja also observed that equation (1.1) is in fact a consequence of the f-positivity conjecture [Reference Barja and Stoppino4, Conjecture 1] of himself and Stoppino.Footnote 1 Another interesting observation, which probably motivates the formulation in equation (1.1), is that when X is of maximal Albanese dimension, one can indeed deduce the absolute Severi inequality by combining Pardini’s approach and equation (1.1) for
$n> 2$
, the problem with finding such inequalities has already been addressed by Mendes Lopes and Pardini [Reference Mendes Lopes and Pardini17, §5.3], whose purpose was to generalise, using Pardini’s original approach in [Reference Pardini20], the Severi inequality for surfaces to higher dimensions. To our knowledge, the precise version of equation (1.1) was first formulated conjecturally by Barja in [Reference Barja2, §1, Page 545]. Barja also observed that equation (1.1) is in fact a consequence of the f-positivity conjecture [Reference Barja and Stoppino4, Conjecture 1] of himself and Stoppino.Footnote 1 Another interesting observation, which probably motivates the formulation in equation (1.1), is that when X is of maximal Albanese dimension, one can indeed deduce the absolute Severi inequality by combining Pardini’s approach and equation (1.1) for
![]() $g(B) = 0$
(see [Reference Barja and Stoppino4, Proposition 4.4] for details).
$g(B) = 0$
(see [Reference Barja and Stoppino4, Proposition 4.4] for details).
When
![]() $g(B) = 1$
, it is easy to see that equation (1.1) coincides with the absolute Severi inequality. In addition to this and prior to our result, Barja proved equation (1.1) for
$g(B) = 1$
, it is easy to see that equation (1.1) coincides with the absolute Severi inequality. In addition to this and prior to our result, Barja proved equation (1.1) for
![]() $g(B) = 0$
under the extra assumptions that X is of maximal Albanese dimension and
$g(B) = 0$
under the extra assumptions that X is of maximal Albanese dimension and
![]() $K_X$
is nef. Barja also obtained a weaker version of equation (1.1) when
$K_X$
is nef. Barja also obtained a weaker version of equation (1.1) when
![]() $g(B) \ge 2$
. See [Reference Barja2, Corollary C] as well as its proof for details.
$g(B) \ge 2$
. See [Reference Barja2, Corollary C] as well as its proof for details.
Our Theorem 1.2 verifies completely the conjectural formulation of Barja for the base curve B of arbitrary genus. Moreover, if
![]() $g(B) = 0$
, our assumption that f is of maximal Albanese dimension is strictly weaker than X itself being of maximal Albanese dimension. As mentioned before, Theorem 1.2 for
$g(B) = 0$
, our assumption that f is of maximal Albanese dimension is strictly weaker than X itself being of maximal Albanese dimension. As mentioned before, Theorem 1.2 for
![]() $g(B) = 0$
can be applied to give an alternative proof of the absolute Severi inequality that is different from that in [Reference Barja2] or [Reference Zhang25].Footnote 2
$g(B) = 0$
can be applied to give an alternative proof of the absolute Severi inequality that is different from that in [Reference Barja2] or [Reference Zhang25].Footnote 2
Since equation (1.1) is sharp, a new question naturally arises: can one characterise the equality case? In this paper, we also consider this problem. We prove the following result.
Theorem 1.3. In Theorem 1.2, if the equality in equation (1.1) holds and
![]() $\chi _f> 0$
, then
$\chi _f> 0$
, then
-
(1) the Albanese map of X maps a general fibre of f onto an abelian variety of dimension
 $n-1$
. In particular,
$n-1$
. In particular,  $$ \begin{align*} h^1(X, {\mathcal{O}}_X) - g(B) = n-1; \end{align*} $$
$$ \begin{align*} h^1(X, {\mathcal{O}}_X) - g(B) = n-1; \end{align*} $$
-
(2) the general fibre F of f satisfies the absolute Severi equality: that is,
 $$ \begin{align*} K_F^{n-1}=2(n-1)!\chi(F, \omega_F). \end{align*} $$
$$ \begin{align*} K_F^{n-1}=2(n-1)!\chi(F, \omega_F). \end{align*} $$
Previously, (1) was known only when
![]() $n=2$
due to Xiao [Reference Xiao23, Theorem 3]. This paper mainly concerns the higher-dimensional case, and our result shows that (1) holds for any
$n=2$
due to Xiao [Reference Xiao23, Theorem 3]. This paper mainly concerns the higher-dimensional case, and our result shows that (1) holds for any
![]() $n \ge 2$
. The much more interesting and stronger part comes from (2): unlike (1) or the absolute Severi inequality, (2) is trivial when
$n \ge 2$
. The much more interesting and stronger part comes from (2): unlike (1) or the absolute Severi inequality, (2) is trivial when
![]() $n=2$
– that is, when the fibre is a curve – which says that
$n=2$
– that is, when the fibre is a curve – which says that
![]() $\deg K_F = 2\chi (F, \omega _F)$
. It holds true for any surface fibration, not necessarily of maximal Albanese dimension. However, for
$\deg K_F = 2\chi (F, \omega _F)$
. It holds true for any surface fibration, not necessarily of maximal Albanese dimension. However, for
![]() $n> 2$
, (2) was completely unknown before, and it reveals a new connection between the geometry of a family of higher-dimensional varieties and the geometry of a general member in this family.
$n> 2$
, (2) was completely unknown before, and it reveals a new connection between the geometry of a family of higher-dimensional varieties and the geometry of a general member in this family.
Recall that for a surface fibration
![]() $f: X \to B$
, the relative irregularity is defined as
$f: X \to B$
, the relative irregularity is defined as
![]() $q_f := h^1(X, {\mathcal {O}}_X) - g(B)$
. Recently, Pardini proposed a problem [Reference Ciliberto, Dedieu, Flamini, Pardini, Galati and Rollenske8, Problem 2] to study various notions of relative irregularity for families of higher-dimensional varieties. The result (1) also sheds some light on this problem, suggesting that the number
$q_f := h^1(X, {\mathcal {O}}_X) - g(B)$
. Recently, Pardini proposed a problem [Reference Ciliberto, Dedieu, Flamini, Pardini, Galati and Rollenske8, Problem 2] to study various notions of relative irregularity for families of higher-dimensional varieties. The result (1) also sheds some light on this problem, suggesting that the number
![]() $h^1(X, {\mathcal {O}}_X) - g(B)$
may also serve as the relative irregularity for higher-dimensional fibrations over curves.
$h^1(X, {\mathcal {O}}_X) - g(B)$
may also serve as the relative irregularity for higher-dimensional fibrations over curves.
When
![]() $\dim F \ge 2$
, by a very recent result of Barja, Pardini and Stoppino [Reference Barja, Pardini and Stoppino3, Theorem 1.2] characterising the variety satisfying the absolute Severi equality (see also [Reference Barja, Pardini and Stoppino5, Reference Lu and Zuo16] when
$\dim F \ge 2$
, by a very recent result of Barja, Pardini and Stoppino [Reference Barja, Pardini and Stoppino3, Theorem 1.2] characterising the variety satisfying the absolute Severi equality (see also [Reference Barja, Pardini and Stoppino5, Reference Lu and Zuo16] when
![]() $\dim F = 2$
), we know that (2) actually implies (1). However, our proof of (1) is independent of (2).
$\dim F = 2$
), we know that (2) actually implies (1). However, our proof of (1) is independent of (2).
1.3 Related results
If more assumptions are imposed on the Albanese map of X, we obtain sharper results. For example, we prove the following theorem.
Theorem 1.4. Let
![]() $f: X \to B$
be a relatively minimal fibration from a variety X of dimension
$f: X \to B$
be a relatively minimal fibration from a variety X of dimension
![]() $n \ge 3$
to a smooth curve B. Denote by F a general fibre of f. Suppose that f is of maximal Albanese dimension and
$n \ge 3$
to a smooth curve B. Denote by F a general fibre of f. Suppose that f is of maximal Albanese dimension and
![]() $a: X \to {\mathrm {Alb}}(X)$
is the Albanese map of X.
$a: X \to {\mathrm {Alb}}(X)$
is the Albanese map of X.
-
(1) If
 $a|_F$
is birational, then
$a|_F$
is birational, then  $$ \begin{align*} K_{X/B}^n \ge \frac{5n!}{2} \chi_f. \end{align*} $$
$$ \begin{align*} K_{X/B}^n \ge \frac{5n!}{2} \chi_f. \end{align*} $$
-
(2) If
 $a|_F$
is not composed with an involution, then
$a|_F$
is not composed with an involution, then  $$ \begin{align*} K_{X/B}^n \ge \frac{9n!}{4} \chi_f. \end{align*} $$
$$ \begin{align*} K_{X/B}^n \ge \frac{9n!}{4} \chi_f. \end{align*} $$
Combining Theorem 1.4 in the
![]() $g(B) = 0$
case with the method in [Reference Barja and Stoppino4, Proposition 14], it is easy to get the following conclusion, which was recently obtained by Barja, Pardini and Stoppino in [Reference Barja, Pardini and Stoppino6, §1].
$g(B) = 0$
case with the method in [Reference Barja and Stoppino4, Proposition 14], it is easy to get the following conclusion, which was recently obtained by Barja, Pardini and Stoppino in [Reference Barja, Pardini and Stoppino6, §1].
Corollary 1.5. Let X be a minimal variety of general type of dimension
![]() $n \ge 3$
. Suppose that X is of maximal Albanese dimension.
$n \ge 3$
. Suppose that X is of maximal Albanese dimension.
-
(1) If the Albanese map of X is birational onto its image, then
 $$ \begin{align*} K_X^n \ge \frac{5n!}{2} \chi(X, \omega_X). \end{align*} $$
$$ \begin{align*} K_X^n \ge \frac{5n!}{2} \chi(X, \omega_X). \end{align*} $$
-
(2) If the Albanese map of X is not composed with an involution, then
 $$ \begin{align*} K_X^n \ge \frac{9n!}{4} \chi(X, \omega_X). \end{align*} $$
$$ \begin{align*} K_X^n \ge \frac{9n!}{4} \chi(X, \omega_X). \end{align*} $$
In the same spirit as before, we may view Theorem 1.4 as a relative version of Corollary 1.5.
In [Reference Barja, Pardini and Stoppino6], Barja, Pardini and Stoppino consider a more general map
![]() $a: X \to A$
such that
$a: X \to A$
such that
![]() $a^*: {\mathrm {Pic}}^0(A) \to {\mathrm {Pic}}^0(X)$
is injective (which they call strongly generating) and prove Corollary 1.5 when a is birational or when a is not composed with an involution. In fact, by the universal property of the Albanese map, we see that if a is birational or is not composed with an involution, so is the Albanese map of X.
$a^*: {\mathrm {Pic}}^0(A) \to {\mathrm {Pic}}^0(X)$
is injective (which they call strongly generating) and prove Corollary 1.5 when a is birational or when a is not composed with an involution. In fact, by the universal property of the Albanese map, we see that if a is birational or is not composed with an involution, so is the Albanese map of X.
Furthermore, we would like to mention that the proof of the absolute Severi type inequalities by Barja, Pardini and Stoppino in [Reference Barja, Pardini and Stoppino6] relies on their study of the continuous rank function. More precisely, they deduce these absolute results by integrating the derivative of the so-called continuous rank function. From the viewpoint of our paper, those absolute inequalities are consequences of their corresponding relative counterparts. To summarise, we have seen again, as in the work of Pardini [Reference Pardini20], that the study of the relative geography, namely the relation among relative birational invariants (such as the relative canonical volume, the relative Euler characteristic, etc.) plays a crucial role in understanding the geography of algebraic varieties in the classical sense.
Notation and conventions
In this paper, a fibration always means a surjective morphism with connected fibres.
Let
![]() $f: X \to B$
be a fibration over a curve B. We say that f is relatively minimal if X is normal with at worst terminal singularities and
$f: X \to B$
be a fibration over a curve B. We say that f is relatively minimal if X is normal with at worst terminal singularities and
![]() $K_X$
is f-nef. The assumption implies that a general fibre F of f is also normal with at worst terminal singularities by the adjunction. Moreover, if a general fibre of f is of maximal Albanese dimension (which is exactly under the setting of Theorem 1.2), then the relative minimality also ensures that
$K_X$
is f-nef. The assumption implies that a general fibre F of f is also normal with at worst terminal singularities by the adjunction. Moreover, if a general fibre of f is of maximal Albanese dimension (which is exactly under the setting of Theorem 1.2), then the relative minimality also ensures that
![]() $K_{X/B}$
is nef.Footnote 3
$K_{X/B}$
is nef.Footnote 3
For divisors, we always use
![]() $\sim $
to denote the linear equivalence and
$\sim $
to denote the linear equivalence and
![]() $\equiv $
to denote the numerical equivalence. Let
$\equiv $
to denote the numerical equivalence. Let
![]() $D_1$
and
$D_1$
and
![]() $D_2$
be two
$D_2$
be two
![]() ${\mathbb {Q}}$
-divisors on a variety V. The notation
${\mathbb {Q}}$
-divisors on a variety V. The notation
![]() $D_1 \ge D_2$
means
$D_1 \ge D_2$
means
![]() $D_1-D_2$
is effective. Let D be a
$D_1-D_2$
is effective. Let D be a
![]() ${\mathbb {Q}}$
-divisor on V. We use
${\mathbb {Q}}$
-divisor on V. We use
![]() ${\lfloor D \rfloor }$
to denote its integral part. The volume of D is defined as
${\lfloor D \rfloor }$
to denote its integral part. The volume of D is defined as
 $$ \begin{align*}{\mathrm{Vol}}(D):=\limsup_{m \to \infty} \frac{h^0(V, {\lfloor mD \rfloor})}{m^{\dim V} / (\dim V)!}. \end{align*} $$
$$ \begin{align*}{\mathrm{Vol}}(D):=\limsup_{m \to \infty} \frac{h^0(V, {\lfloor mD \rfloor})}{m^{\dim V} / (\dim V)!}. \end{align*} $$
2 A Clifford type inequality
In this section, we recall a Clifford type result in [Reference Yuan and Zhang24] that will be used later. All results in this section hold also in positive characteristics.
2.1
 $\varepsilon $
for divisors
$\varepsilon $
for divisors
Let V be a smooth variety of dimension
![]() $n> 0$
, and let L be a
$n> 0$
, and let L be a
![]() ${\mathbb {Q}}$
-divisor on V. For any big divisor M on V with
${\mathbb {Q}}$
-divisor on V. For any big divisor M on V with
![]() $|M|$
base point free, take the smallest integer
$|M|$
base point free, take the smallest integer
![]() $\lambda _M> 0$
so that the divisor
$\lambda _M> 0$
so that the divisor
![]() $\lambda _M M - L$
is pseudo-effective. When
$\lambda _M M - L$
is pseudo-effective. When
![]() $n \ge 2$
, we define
$n \ge 2$
, we define
When
![]() $n=1$
, we simply set
$n=1$
, we simply set
For any
![]() $n> 0$
, define
$n> 0$
, define
where the infimum is taken over all divisors M on V chosen as above. In particular, when
![]() $n=1$
, we have
$n=1$
, we have
It is straightforward to check that
Proposition 2.1. The above
![]() $\varepsilon $
satisfies the following properties:
$\varepsilon $
satisfies the following properties:
-
(1) If
 $L' \ge L$
, then
$L' \ge L$
, then
 $\varepsilon (V, L', M) \ge \varepsilon (V, L, M)$
for any M chosen as above. In particular,
$\varepsilon (V, L', M) \ge \varepsilon (V, L, M)$
for any M chosen as above. In particular,
 $\varepsilon (V, L') \ge \varepsilon (V, L)$
.
$\varepsilon (V, L') \ge \varepsilon (V, L)$
. -
(2) Let
 $\sigma : V' \to V$
be a birational morphism. Then
$\sigma : V' \to V$
be a birational morphism. Then
 $\varepsilon (V', \sigma ^*L) \le \varepsilon (V, L)$
.
$\varepsilon (V', \sigma ^*L) \le \varepsilon (V, L)$
.
2.2 A Clifford type inequality
The main result in this section is the following one, which will be used later in the proof of Theorem 1.2.
Theorem 2.2. Let V be a smooth variety of dimension
![]() $n> 0$
. Suppose that L is a
$n> 0$
. Suppose that L is a
![]() ${\mathbb {Q}}$
-divisor on V such that
${\mathbb {Q}}$
-divisor on V such that
![]() $K_V-L$
is pseudo-effective. Then
$K_V-L$
is pseudo-effective. Then
Proof. By [Reference Yuan and Zhang24, Theorem 1.2], which was stated only for integral divisors, we have
Note that
![]() ${\mathrm {Vol}}({\lfloor L \rfloor }) \le {\mathrm {Vol}}(L)$
, and by Proposition 2.1,
${\mathrm {Vol}}({\lfloor L \rfloor }) \le {\mathrm {Vol}}(L)$
, and by Proposition 2.1,
![]() $\varepsilon (V, {\lfloor L \rfloor }) \le \varepsilon (V, L)$
. Thus the result follows easily.
$\varepsilon (V, {\lfloor L \rfloor }) \le \varepsilon (V, L)$
. Thus the result follows easily.
Remark 2.3. As is explained in [Reference Yuan and Zhang24], Theorem 2.2 is a natural generalisation of the classical Clifford inequality.
3 Sharper estimate under extra assumptions
To prove Theorem 1.3, we need some estimates on the dimension of
![]() $H^0(V, L)$
similar to Theorem 2.2 but stronger. All the sharper bounds in this section are inspired by the work of Barja, Pardini, and Stoppino in [Reference Barja, Pardini and Stoppino6], where they proved the so-called ‘continuous’ estimates. However, under our setting, we need explicit results instead, and the method we will employ is based on [Reference Yuan and Zhang24, Reference Zhang25, Reference Zhang26].
$H^0(V, L)$
similar to Theorem 2.2 but stronger. All the sharper bounds in this section are inspired by the work of Barja, Pardini, and Stoppino in [Reference Barja, Pardini and Stoppino6], where they proved the so-called ‘continuous’ estimates. However, under our setting, we need explicit results instead, and the method we will employ is based on [Reference Yuan and Zhang24, Reference Zhang25, Reference Zhang26].
3.1 A filtration for nef divisors
Let
![]() $f: V \to B$
be a fibration from a smooth variety V of dimension n to a smooth curve B with a general fibre F. Let L be a nef divisor on V. We first recall the following theorem.
$f: V \to B$
be a fibration from a smooth variety V of dimension n to a smooth curve B with a general fibre F. Let L be a nef divisor on V. We first recall the following theorem.
Theorem 3.1 [Reference Zhang26, Theorem 4.1]
Let
![]() $f: V \to B$
, F and L be as above. Then there is a birational morphism
$f: V \to B$
, F and L be as above. Then there is a birational morphism
![]() $\sigma : V_L \to V$
and a sequence of triples
$\sigma : V_L \to V$
and a sequence of triples
on
![]() $V_L$
with the following properties:
$V_L$
with the following properties:
-
○
 $(L_0, Z_0, a_0)=(\sigma ^*L, 0, {\mathrm {int}}_{f_L}(L_0))$
, where
$(L_0, Z_0, a_0)=(\sigma ^*L, 0, {\mathrm {int}}_{f_L}(L_0))$
, where
 $f_L: V_L \stackrel {\sigma }{\to } V \stackrel {f}{\to } B$
is the induced fibration.
$f_L: V_L \stackrel {\sigma }{\to } V \stackrel {f}{\to } B$
is the induced fibration. -
○ For any
 $i=0, \cdots , N-1$
, there is a decomposition such that
$i=0, \cdots , N-1$
, there is a decomposition such that $$ \begin{align*} |L_i-a_iF_L|= |L_{i+1}| + Z_{i+1} \end{align*} $$
$$ \begin{align*} |L_i-a_iF_L|= |L_{i+1}| + Z_{i+1} \end{align*} $$
 $Z_{i+1} \ge 0$
is the fixed part of
$Z_{i+1} \ge 0$
is the fixed part of
 $|L_i-a_iF_L|$
and the movable part
$|L_i-a_iF_L|$
and the movable part
 $|L_{i+1}|$
of
$|L_{i+1}|$
of
 $|L_i-a_iF_L|$
is base point free. Here
$|L_i-a_iF_L|$
is base point free. Here
 $F_L = \sigma ^*F$
denotes a general fibre of
$F_L = \sigma ^*F$
denotes a general fibre of
 $f_L$
, and
$f_L$
, and
 $a_{i} = {\mathrm {int}}_{f_L}(L_{i})$
.
$a_{i} = {\mathrm {int}}_{f_L}(L_{i})$
.
-
○ We have
 $h^0(V_L, L_N-a_NF_L)=0$
.
$h^0(V_L, L_N-a_NF_L)=0$
.
In the above theorem, for any
![]() $0 \le i \le N$
, the number
$0 \le i \le N$
, the number
![]() ${\mathrm {int}}_{f_L}(L_i)$
is defined by
${\mathrm {int}}_{f_L}(L_i)$
is defined by
Thus via Theorem 3.1, we obtain a filtration
of nef divisors on a birational model
![]() $V_L$
of V. For simplicity, we denote by F a general fibre of
$V_L$
of V. For simplicity, we denote by F a general fibre of
![]() $f_L: V_L \to B$
in the rest of this section.
$f_L: V_L \to B$
in the rest of this section.
Proposition 3.2 [Reference Yuan and Zhang24, Proposition 2.2]
We have the following two inequalities:
 $$ \begin{align*} h^0(V, L) & \le \sum_{i=0}^{N} a_i h^0(F, L_i|_F); \\ L^n & \ge n \sum_{i=0}^{N} a_i (L_i|_F)^{n-1} - n(L_0|_F)^{n-1}. \end{align*} $$
$$ \begin{align*} h^0(V, L) & \le \sum_{i=0}^{N} a_i h^0(F, L_i|_F); \\ L^n & \ge n \sum_{i=0}^{N} a_i (L_i|_F)^{n-1} - n(L_0|_F)^{n-1}. \end{align*} $$
Proposition 3.3 [Reference Yuan and Zhang24, Lemma 2.3]
We have
 $$ \begin{align*} L_0^n \ge \left(\sum_{i=0}^{N} a_i - 1 \right) (L_0|_F)^{n-1}. \end{align*} $$
$$ \begin{align*} L_0^n \ge \left(\sum_{i=0}^{N} a_i - 1 \right) (L_0|_F)^{n-1}. \end{align*} $$
3.2 Sharper bound involving subcanonicity
Let V be a smooth variety of dimension
![]() $n> 0$
with the Kodaira dimension
$n> 0$
with the Kodaira dimension
![]() $\kappa (V) \ge 0$
, and let L be a
$\kappa (V) \ge 0$
, and let L be a
![]() ${\mathbb {Q}}$
-divisor on V. Let M be a big divisor on V such that
${\mathbb {Q}}$
-divisor on V. Let M be a big divisor on V such that
![]() $|M|$
is base point free. We recall that the numerical subcanonicity of L with respect to M is defined in [Reference Barja, Pardini and Stoppino6, Definition 5.1] as follows:
$|M|$
is base point free. We recall that the numerical subcanonicity of L with respect to M is defined in [Reference Barja, Pardini and Stoppino6, Definition 5.1] as follows:
 $$ \begin{align*}r(L, M):= \frac{LM^{n-1}}{K_VM^{n-1}}. \end{align*} $$
$$ \begin{align*}r(L, M):= \frac{LM^{n-1}}{K_VM^{n-1}}. \end{align*} $$
When
![]() $n=1$
, set
$n=1$
, set
![]() $r(L, M) = \frac {\deg L}{\deg K_V}$
. When
$r(L, M) = \frac {\deg L}{\deg K_V}$
. When
![]() $K_VM^{n-1} = 0$
, we have
$K_VM^{n-1} = 0$
, we have
![]() $\kappa (V) = 0$
. In this case, we set
$\kappa (V) = 0$
. In this case, we set
![]() $r(L, M) = + \infty $
. Define a function
$r(L, M) = + \infty $
. Define a function
![]() $\delta $
as follows:
$\delta $
as follows:
 $$ \begin{align*}\delta(x) = \left\{ \begin{array} {ll} 2, & x \le 1; \\ \frac{2x}{2x-1}, & x> 1. \end{array} \right. \end{align*} $$
$$ \begin{align*}\delta(x) = \left\{ \begin{array} {ll} 2, & x \le 1; \\ \frac{2x}{2x-1}, & x> 1. \end{array} \right. \end{align*} $$
Theorem 3.4. Let L and M be as above, and write
![]() $r = r(L, M)$
. Then
$r = r(L, M)$
. Then
Proof. The proof is by induction, and we present it in several steps.
Notice that the required inequality holds trivially if
![]() $h^0(V,{\lfloor L \rfloor })=0$
. We may make assumption
$h^0(V,{\lfloor L \rfloor })=0$
. We may make assumption
![]() $h^0(V, {\lfloor L \rfloor })>0$
from now on.
$h^0(V, {\lfloor L \rfloor })>0$
from now on.
Step 1: Reduce to the case when L is nef.
In fact, by replacing V by an appropriate blowing up, we may assume that
where
![]() $L'$
is the movable part of
$L'$
is the movable part of
![]() $|{\lfloor L \rfloor }|$
and Z is its fixed part. It is clear that
$|{\lfloor L \rfloor }|$
and Z is its fixed part. It is clear that
Thus it suffices to prove Theorem 3.4 for
![]() $L'$
.
$L'$
.
From now on, we assume that L is a nef divisor.
Step 2: The
![]() $n=1$
case.
$n=1$
case.
When
![]() $n=1$
, Theorem 3.4 is straightforward. If
$n=1$
, Theorem 3.4 is straightforward. If
![]() $h^1(V, L) \ne 0$
, the classical Clifford inequality implies Theorem 3.4. Otherwise, by the Riemann-Roch theorem,
$h^1(V, L) \ne 0$
, the classical Clifford inequality implies Theorem 3.4. Otherwise, by the Riemann-Roch theorem,
 $$ \begin{align*} h^0(V, L) = \deg L - \frac{1}{2} \deg K_V = \left(1 - \frac{1}{2r}\right) \deg L. \end{align*} $$
$$ \begin{align*} h^0(V, L) = \deg L - \frac{1}{2} \deg K_V = \left(1 - \frac{1}{2r}\right) \deg L. \end{align*} $$
Thus the proof is completed.
Step 3: The proof when
![]() $L^n> 0$
.
$L^n> 0$
.
Now we assume that Theorem 3.4 holds for dimension
![]() $k < n$
. Choose a general pencil in
$k < n$
. Choose a general pencil in
![]() $|M|$
, and blow up the indeterminacies of this pencil, denoted by
$|M|$
, and blow up the indeterminacies of this pencil, denoted by
![]() $\pi : V_0 \to V$
. We get a fibration
$\pi : V_0 \to V$
. We get a fibration
such that the general fibre F of f is isomorphic to a general member of the chosen pencil. By the adjunction,
![]() $\kappa (F) \ge 0$
. Write
$\kappa (F) \ge 0$
. Write
![]() $M_0 = \pi ^*M$
and
$M_0 = \pi ^*M$
and
![]() $L_0 = \pi ^*L$
. It follows that
$L_0 = \pi ^*L$
. It follows that
 $$ \begin{align*} r(L, M) = \frac{L_0M_0^{n-2}F}{(\pi^*K_V)M_0^{n-2}F} \ge r(L_0|_F, M_0|_F), \end{align*} $$
$$ \begin{align*} r(L, M) = \frac{L_0M_0^{n-2}F}{(\pi^*K_V)M_0^{n-2}F} \ge r(L_0|_F, M_0|_F), \end{align*} $$
where the last inequality follows from the adjunction.
Apply Theorem 3.1 to f and
![]() $L_0$
. Replacing
$L_0$
. Replacing
![]() $V_0$
by a further blowing up if necessary, we get triples
$V_0$
by a further blowing up if necessary, we get triples
on
![]() $V_0$
, and
$V_0$
, and
![]() $L_i$
and
$L_i$
and
![]() $a_i$
satisfy the inequalities in Proposition 3.2 and 3.3. Note that by the definition of
$a_i$
satisfy the inequalities in Proposition 3.2 and 3.3. Note that by the definition of
![]() $r(L, M)$
, we see that
$r(L, M)$
, we see that
By induction and using the fact that the function
![]() $\delta $
is nonincreasing, we have
$\delta $
is nonincreasing, we have
Combine this with Proposition 3.2. It follows that
 $$ \begin{align*} h^0(V_0, L_0) - \frac{1}{\delta(r)n!} L_0^n \le (n-1) \sum_{i=0}^{N} a_i\varepsilon(F, L_i|_F, M_0|_F) + \frac{1}{(n-1)!}(L_0|_F)^{n-1}. \end{align*} $$
$$ \begin{align*} h^0(V_0, L_0) - \frac{1}{\delta(r)n!} L_0^n \le (n-1) \sum_{i=0}^{N} a_i\varepsilon(F, L_i|_F, M_0|_F) + \frac{1}{(n-1)!}(L_0|_F)^{n-1}. \end{align*} $$
To estimate the right-hand side of the above inequality, let
![]() $\lambda $
be the smallest integer such that
$\lambda $
be the smallest integer such that
![]() $\lambda M-L$
is pseudo-effective. Note that
$\lambda M-L$
is pseudo-effective. Note that
![]() $L^n> 0$
.
$L^n> 0$
.
-
(1) It implies that
 $L^n \le \lambda L^{n-1}M = \lambda (L_0|_F)^{n-1}$
. In particular,
$L^n \le \lambda L^{n-1}M = \lambda (L_0|_F)^{n-1}$
. In particular,
 $(L_0|_F)^{n-1}> 0$
. Thus, by Proposition 3.3,
$(L_0|_F)^{n-1}> 0$
. Thus, by Proposition 3.3,  $$ \begin{align*} \sum_{i=0}^{N} a_i \le \frac{L_0^n}{(L_0|_F)^n} + 1 \le \lambda + 1. \end{align*} $$
$$ \begin{align*} \sum_{i=0}^{N} a_i \le \frac{L_0^n}{(L_0|_F)^n} + 1 \le \lambda + 1. \end{align*} $$
-
(2) By Proposition 2.1 (1),
Moreover, since $$ \begin{align*} \varepsilon(F, L_i|_F, M_0|_F) \le \varepsilon(F, L_0|_F, M_0|_F). \end{align*} $$
$$ \begin{align*} \varepsilon(F, L_i|_F, M_0|_F) \le \varepsilon(F, L_0|_F, M_0|_F). \end{align*} $$
 $\lambda M_0|_F - L_0|_F$
is also pseudo-effective, we have
$\lambda M_0|_F - L_0|_F$
is also pseudo-effective, we have  $$ \begin{align*} \varepsilon(F, L_0|_F, M_0|_F) \le (\lambda+1)^{n-2}(M_0|_F)^{n-1} = (\lambda+1)^{n-2}M^n. \end{align*} $$
$$ \begin{align*} \varepsilon(F, L_0|_F, M_0|_F) \le (\lambda+1)^{n-2}(M_0|_F)^{n-1} = (\lambda+1)^{n-2}M^n. \end{align*} $$
-
(3) We have
 $$ \begin{align*} (L_0|_F)^{n-1} = L^{n-1}M \le \lambda L^{n-2}M^2 \le \cdots \le \lambda^{n-1}M^n. \end{align*} $$
$$ \begin{align*} (L_0|_F)^{n-1} = L^{n-1}M \le \lambda L^{n-2}M^2 \le \cdots \le \lambda^{n-1}M^n. \end{align*} $$
Combining all of the above inequalities, it follows that
 $$ \begin{align*} h^0(V_0, L_0) - \frac{1}{\delta(r)n!} L_0^n & \le (n-1)(\lambda+1)^{n-1}M^n + \frac{1}{(n-1)!} \lambda^{n-1}M^n \\ & \le n \varepsilon(V, L, M). \end{align*} $$
$$ \begin{align*} h^0(V_0, L_0) - \frac{1}{\delta(r)n!} L_0^n & \le (n-1)(\lambda+1)^{n-1}M^n + \frac{1}{(n-1)!} \lambda^{n-1}M^n \\ & \le n \varepsilon(V, L, M). \end{align*} $$
Thus the proof in this case is completed.
Step 4. The proof when
![]() $L^n = 0$
.
$L^n = 0$
.
In this case, the proof is easier. Since L is not big, we know that
Take W to be a general member in
![]() $|M|$
, and we have
$|M|$
, and we have
Therefore, by induction, we deduce that
Let
![]() $\lambda $
be the smallest integer such that
$\lambda $
be the smallest integer such that
![]() $\lambda M - L$
is pseudo-effective. Similar to Step 3, we have
$\lambda M - L$
is pseudo-effective. Similar to Step 3, we have
-
(1)
 $(L|_W)^{n-1} = L^{n-1}M \le \lambda ^{n-1}M^n$
;
$(L|_W)^{n-1} = L^{n-1}M \le \lambda ^{n-1}M^n$
; -
(2)
 $\varepsilon (W, L|_W, M|_W) \le (\lambda +1)^{n-2}M^n$
.
$\varepsilon (W, L|_W, M|_W) \le (\lambda +1)^{n-2}M^n$
.
Combining the above inequalities, it follows that
Thus the whole proof is completed.
3.3 Sharper bound involving the mapping degree
Let V be a smooth variety of dimension
![]() $n \ge 2$
, and let L be a
$n \ge 2$
, and let L be a
![]() ${\mathbb {Q}}$
-divisor on V such that
${\mathbb {Q}}$
-divisor on V such that
![]() $K_V-L$
is pseudo-effective. Instead of the subcanonicity, we suppose that
$K_V-L$
is pseudo-effective. Instead of the subcanonicity, we suppose that
is a generically finite morphism onto a (possibly singular) variety
![]() $\Sigma $
. Let H be a sufficiently ample divisor on
$\Sigma $
. Let H be a sufficiently ample divisor on
![]() $\Sigma $
, and write
$\Sigma $
, and write
![]() $M = a^*H$
. The assumption will be used until the end of this section.
$M = a^*H$
. The assumption will be used until the end of this section.
3.3.1 Preparation
We first assume that V is a surface and
![]() $|L|$
is base point free. Although this assumption looks simple, all the results we need can be reduced to this setting.
$|L|$
is base point free. Although this assumption looks simple, all the results we need can be reduced to this setting.
Lemma 3.5. If
![]() $h^0(V, L-M) = 0$
, then
$h^0(V, L-M) = 0$
, then
Proof. Choose a general curve
![]() $C \in a^*|H|$
. By Bertini’s theorem, we may assume that C is smooth. The assumption
$C \in a^*|H|$
. By Bertini’s theorem, we may assume that C is smooth. The assumption
![]() $h^0(V, L-M) = 0$
just tells us that
$h^0(V, L-M) = 0$
just tells us that
![]() $h^0(V, L) \le h^0(C, L|_C)$
. Thus the first inequality is just a combination of the Clifford inequality and the Riemann-Roch theorem again.
$h^0(V, L) \le h^0(C, L|_C)$
. Thus the first inequality is just a combination of the Clifford inequality and the Riemann-Roch theorem again.
The second inequality is directly from the definition of
![]() $\varepsilon $
. Let
$\varepsilon $
. Let
![]() $\lambda $
be the smallest integer such that
$\lambda $
be the smallest integer such that
![]() $\lambda M - L$
is pseudo-effective. Then
$\lambda M - L$
is pseudo-effective. Then
The proof is completed.
Now suppose that
![]() $h^0(V, L-M)> 0$
. Let
$h^0(V, L-M)> 0$
. Let
Obviously,
![]() $\gamma \ge 1$
.
$\gamma \ge 1$
.
Lemma 3.6. If
![]() $h^0(V, L-M)> 0$
, then
$h^0(V, L-M)> 0$
, then
Proof. Take a general member
![]() $D \in |L|$
. By assumption, D is big. Thus we may assume that D is smooth and irreducible. Consider the following exact sequence:
$D \in |L|$
. By assumption, D is big. Thus we may assume that D is smooth and irreducible. Consider the following exact sequence:
Since
![]() $K_V - L$
is pseudo-effective, we know that
$K_V - L$
is pseudo-effective, we know that
![]() $\deg (2L|_D) \le \deg (K_V|_D + L|_D) = \deg K_D$
: that is,
$\deg (2L|_D) \le \deg (K_V|_D + L|_D) = \deg K_D$
: that is,
![]() $K_D - 2L|_D$
is pseudo-effective. Apply the Clifford inequality (when
$K_D - 2L|_D$
is pseudo-effective. Apply the Clifford inequality (when
![]() $h^1(D, 2L|_D)> 0$
) or the Riemann-Roch theorem (when
$h^1(D, 2L|_D)> 0$
) or the Riemann-Roch theorem (when
![]() $h^1(D, 2L|_D) = 0$
) for
$h^1(D, 2L|_D) = 0$
) for
![]() $2L|_D$
, and it follows that
$2L|_D$
, and it follows that
The proof is completed.
Let
![]() $C \in a^*|H|$
be a general member, hence smooth. Consider the two restriction maps
$C \in a^*|H|$
be a general member, hence smooth. Consider the two restriction maps
and
The kernels of the above two maps are
![]() $H^0(V, L-(i+1)M)$
and
$H^0(V, L-(i+1)M)$
and
![]() $H^0(V, 2L-(j+1)M)$
, respectively.
$H^0(V, 2L-(j+1)M)$
, respectively.
Let
![]() $V_{1, i}$
(respectively,
$V_{1, i}$
(respectively,
![]() $V_{2, j}$
) denote the image of
$V_{2, j}$
) denote the image of
![]() $H^0(V, L-iM)$
(respectively,
$H^0(V, L-iM)$
(respectively,
![]() $H^0(V, 2L-jM)$
) under
$H^0(V, 2L-jM)$
) under
![]() $\mathrm {res}_{1, i}$
(respectively,
$\mathrm {res}_{1, i}$
(respectively,
![]() $\mathrm {res}_{2, j}$
).
$\mathrm {res}_{2, j}$
).
Lemma 3.7. We have
 $$ \begin{align*} h^0(V, L) & = \sum_{i=0}^{\gamma-1} \dim V_{1, i} + h^0(V, L-\gamma M) \\ h^0(V, 2L) & = \sum_{j=0}^{2\gamma-1} \dim V_{2, j} + h^0(V, 2L-2\gamma M) \ge 2\sum_{i=0}^{\gamma-1} \dim V_{2, 2i} - \dim V_{2, 0}. \end{align*} $$
$$ \begin{align*} h^0(V, L) & = \sum_{i=0}^{\gamma-1} \dim V_{1, i} + h^0(V, L-\gamma M) \\ h^0(V, 2L) & = \sum_{j=0}^{2\gamma-1} \dim V_{2, j} + h^0(V, 2L-2\gamma M) \ge 2\sum_{i=0}^{\gamma-1} \dim V_{2, 2i} - \dim V_{2, 0}. \end{align*} $$
Proof. The two equalities are obvious. The last inequality in the second formula holds simply because
![]() $h^0(V, 2L-2\gamma M)> 0$
and
$h^0(V, 2L-2\gamma M)> 0$
and
![]() $\dim V_{2, 2i-1} \ge \dim V_{2, 2i}$
for any
$\dim V_{2, 2i-1} \ge \dim V_{2, 2i}$
for any
![]() $1 \le i \le \gamma -1$
.
$1 \le i \le \gamma -1$
.
Let
![]() $|N_i|$
denote the movable part of
$|N_i|$
denote the movable part of
![]() $|L-iM|$
. Note that the base locus of
$|L-iM|$
. Note that the base locus of
![]() $|N_i|$
is either empty or of dimension zero. We deduce that
$|N_i|$
is either empty or of dimension zero. We deduce that
![]() $N_i$
is nef. Also, we have
$N_i$
is nef. Also, we have
Lemma 3.8. For
![]() $0 \le i \le \gamma $
, we have
$0 \le i \le \gamma $
, we have
If, moreover, the linear system
![]() $|N_i||_C$
induces a birational map on C, then
$|N_i||_C$
induces a birational map on C, then
Proof. This is just [Reference Barja, Pardini and Stoppino6, Lemma 5.3] for
![]() $k=2$
.
$k=2$
.
In the following, we will apply the above results to deduce more inequalities subject to the degree of the map a. The notation here will be used frequently.
3.3.2
 $\deg a = 1$
$\deg a = 1$
We first consider the case when a is birational.
Theorem 3.9. Suppose that
![]() $\deg a = 1$
, and
$\deg a = 1$
, and
![]() $K_V - L$
is pseudo-effective. Then we have
$K_V - L$
is pseudo-effective. Then we have
Similar to the proof of Theorem 3.4, we may assume that L is nef. We may even assume that
![]() $|L|$
is base point free. Moreover, we only need to prove Theorem 3.9 when
$|L|$
is base point free. Moreover, we only need to prove Theorem 3.9 when
![]() $n = 2$
(i.e., Lemma 3.10), and the general result follows by an inductive argument almost identical to Step 3 and Step 4 in the proof of Theorem 3.4.
$n = 2$
(i.e., Lemma 3.10), and the general result follows by an inductive argument almost identical to Step 3 and Step 4 in the proof of Theorem 3.4.
One little difference is that, instead of choosing a general pencil in
![]() $|M|$
as in Step 3 of the proof of Theorem 3.4, here we choose a general pencil in the sublinear system
$|M|$
as in Step 3 of the proof of Theorem 3.4, here we choose a general pencil in the sublinear system
![]() $a^*|H| \subseteq |M|$
. Since
$a^*|H| \subseteq |M|$
. Since
![]() $a^*|H|$
is also base point free, the smoothness of a general member in it is guaranteed by Bertini’s theorem. This adjustment will be used until the end of this section. Note that the restriction of a on a general member of
$a^*|H|$
is also base point free, the smoothness of a general member in it is guaranteed by Bertini’s theorem. This adjustment will be used until the end of this section. Note that the restriction of a on a general member of
![]() $a^*|H|$
has degree one. This is the key point for us to use the induction.
$a^*|H|$
has degree one. This is the key point for us to use the induction.
With this adjustment and by Lemma 3.5, we eventually reduce Theorem 3.9 to the following lemma.
Lemma 3.10. Theorem 3.9 holds when
![]() $n=2$
,
$n=2$
,
![]() $|L|$
is base point free and
$|L|$
is base point free and
![]() $h^0(V, L-M)> 0$
.
$h^0(V, L-M)> 0$
.
Proof. We claim that
Suppose the claim holds. Together with Lemma 3.6, we deduce that
and the proof will be completed by noting that
just as in the proof of Lemma 3.5.
To prove the claim, let C,
![]() $\gamma $
,
$\gamma $
,
![]() $V_{1, i}$
,
$V_{1, i}$
,
![]() $V_{2, j}$
be the same as in Section 3.3.1. For
$V_{2, j}$
be the same as in Section 3.3.1. For
![]() $0 \le i \le \gamma -1$
,
$0 \le i \le \gamma -1$
,
![]() $|M|$
is a sublinear system of
$|M|$
is a sublinear system of
![]() $|L-iM|$
, which means
$|L-iM|$
, which means
![]() $|M||_C$
is a sublinear system of
$|M||_C$
is a sublinear system of
![]() $V_{1, i}$
. Note that
$V_{1, i}$
. Note that
![]() $|M||_C$
induces a birational map from C. We deduce that the map induced by
$|M||_C$
induces a birational map from C. We deduce that the map induced by
![]() $V_{1, i} \ (0 \le i \le \gamma -1)$
is birational. Thus it follows from Lemma 3.7 and the second inequality in Lemma 3.8 that
$V_{1, i} \ (0 \le i \le \gamma -1)$
is birational. Thus it follows from Lemma 3.7 and the second inequality in Lemma 3.8 that
Let us estimate the right-hand side of the above inequality.
-
(1) Since
 $h^0(V, L-(\gamma +1)M) = 0$
, by Lemma 3.5, we have In particular,
$h^0(V, L-(\gamma +1)M) = 0$
, by Lemma 3.5, we have In particular, $$ \begin{align*} h^0(V, L-\gamma M) \le \frac{1}{2}(LM - \gamma M^2) + 1 \le LM - \gamma M^2 + 1. \end{align*} $$
$$ \begin{align*} h^0(V, L-\gamma M) \le \frac{1}{2}(LM - \gamma M^2) + 1 \le LM - \gamma M^2 + 1. \end{align*} $$
 $$ \begin{align*} h^0(V, L-\gamma M) + \gamma \le LM + 1. \end{align*} $$
$$ \begin{align*} h^0(V, L-\gamma M) + \gamma \le LM + 1. \end{align*} $$
-
(2) Note that
 $\dim V_{2, 0} \le h^0(C, 2L|_C)$
. By the Clifford inequality and the Riemann-Roch theorem, similar to before, we simply deduce that
$\dim V_{2, 0} \le h^0(C, 2L|_C)$
. By the Clifford inequality and the Riemann-Roch theorem, similar to before, we simply deduce that  $$ \begin{align*} \dim V_{2, 0} \le h^0(C, 2L|_C) \le \deg(2L|_C) + 1 = 2LM + 1. \end{align*} $$
$$ \begin{align*} \dim V_{2, 0} \le h^0(C, 2L|_C) \le \deg(2L|_C) + 1 = 2LM + 1. \end{align*} $$
Combining the above two inequalities, we prove the claim.
3.3.3
 $a$
is not composed with an involution
$a$
is not composed with an involution
Second, we consider the case when a is not composed with an involution. That is, there is no generically finite map
![]() $V \dashrightarrow V'$
of degree two through which a factors birationally.
$V \dashrightarrow V'$
of degree two through which a factors birationally.
Theorem 3.11. Suppose that a is not composed with an involution and
![]() $K_V - L$
is pseudo-effective. Then we have
$K_V - L$
is pseudo-effective. Then we have
Similar to what we did for Theorem 3.9, we may assume that
![]() $n=2$
,
$n=2$
,
![]() $|L|$
is base point free and
$|L|$
is base point free and
![]() $h^0(V, L-M)> 0$
. For general n, we use the induction. Note that by our assumption, the restriction of a on a general member of
$h^0(V, L-M)> 0$
. For general n, we use the induction. Note that by our assumption, the restriction of a on a general member of
![]() $a^*|H|$
is not composed with an involution either. See [Reference Barja, Pardini and Stoppino6, Proposition 2.8], for example. This guarantees that the inductive argument also works in this situation. Therefore, Theorem 3.11 boils down to the following lemma.
$a^*|H|$
is not composed with an involution either. See [Reference Barja, Pardini and Stoppino6, Proposition 2.8], for example. This guarantees that the inductive argument also works in this situation. Therefore, Theorem 3.11 boils down to the following lemma.
Lemma 3.12. Theorem 3.11 holds when
![]() $n=2$
,
$n=2$
,
![]() $|L|$
is base point free and
$|L|$
is base point free and
![]() $h^0(V, L-M)> 0$
.
$h^0(V, L-M)> 0$
.
Proof. We sketch the proof here since it is similar to that of Lemma 3.10.
Let C,
![]() $\gamma $
,
$\gamma $
,
![]() $V_{1, i}$
,
$V_{1, i}$
,
![]() $V_{2, j}$
,
$V_{2, j}$
,
![]() $N_i$
be identical to those in Section 3.3.1. Let
$N_i$
be identical to those in Section 3.3.1. Let
With this notation, using the same strategy as for proving equation (3.1), we deduce that
 $$ \begin{align*} h^0(V, 2L) - 6h^0(V, L) \ge - 8LM - 7 - 2\sum_{i=i_0}^{\gamma-1} \dim V_{1, i}. \end{align*} $$
$$ \begin{align*} h^0(V, 2L) - 6h^0(V, L) \ge - 8LM - 7 - 2\sum_{i=i_0}^{\gamma-1} \dim V_{1, i}. \end{align*} $$
Comparing to the proof of equation (3.1), the only modification we make here is that, for
![]() $i \ge i_0$
, we have to use the first inequality in Lemma 3.8 to compare
$i \ge i_0$
, we have to use the first inequality in Lemma 3.8 to compare
![]() $\dim V_{2, 2i}$
with
$\dim V_{2, 2i}$
with
![]() $\dim V_{1, i}$
, which is the reason for having an extra term
$\dim V_{1, i}$
, which is the reason for having an extra term
![]() $-2\sum _{i=i_0}^{\gamma -1} \dim V_{1, i}$
on the right-hand side.
$-2\sum _{i=i_0}^{\gamma -1} \dim V_{1, i}$
on the right-hand side.
Combining this inequality with Lemma 3.6, it follows that
 $$ \begin{align} L^2 \ge 5h^0(V, L) - 2\sum_{i=i_0}^{\gamma-1} \dim V_{1, i} - 8 (LM +1). \end{align} $$
$$ \begin{align} L^2 \ge 5h^0(V, L) - 2\sum_{i=i_0}^{\gamma-1} \dim V_{1, i} - 8 (LM +1). \end{align} $$
On the other hand, recall that for any
![]() $0 \le i \le \gamma -1$
,
$0 \le i \le \gamma -1$
,
![]() $N_i$
is nef and
$N_i$
is nef and
Note that in the current setting,
![]() $N_0 = L$
and
$N_0 = L$
and
![]() $|N_{i+1}|$
is also the movable part of
$|N_{i+1}|$
is also the movable part of
![]() $|N_i-M|$
.
$|N_i-M|$
.
For any
![]() $i> 0$
, we have
$i> 0$
, we have
where the last inequality follows from the fact that
![]() $K_C - (L|_C - iM|_C)$
is pseudo-effective. When
$K_C - (L|_C - iM|_C)$
is pseudo-effective. When
![]() $i \ge i_0$
,
$i \ge i_0$
,
![]() $V_{1, i}$
induces a map on C of degree at least three. Otherwise, the map
$V_{1, i}$
induces a map on C of degree at least three. Otherwise, the map
![]() $\phi _{|L-iM|}$
induced by the linear system
$\phi _{|L-iM|}$
induced by the linear system
![]() $|L-iM|$
would factor through a degree two map from V, and a would factor through
$|L-iM|$
would factor through a degree two map from V, and a would factor through
![]() $\phi _{|L-iM|}$
, which is a contradiction. Let
$\phi _{|L-iM|}$
, which is a contradiction. Let
be the morphism induced by the movable part of
![]() $V_{1, i}$
. Then
$V_{1, i}$
. Then
![]() $\deg \phi _i \ge 3$
. Since
$\deg \phi _i \ge 3$
. Since
![]() $\phi _i$
factor through the normalisation of
$\phi _i$
factor through the normalisation of
![]() $C^{\prime }_i$
, we may assume that the curve
$C^{\prime }_i$
, we may assume that the curve
![]() $C^{\prime }_i$
is normal, hence smooth. Then
$C^{\prime }_i$
is normal, hence smooth. Then
where
![]() $L^{\prime }_i$
and
$L^{\prime }_i$
and
![]() $Z^{\prime }_i$
are effective divisors on
$Z^{\prime }_i$
are effective divisors on
![]() $C'$
. Since
$C'$
. Since
similar to equation (3.3), we deduce that for
![]() $i \ge \max \{1, i_0\}$
,
$i \ge \max \{1, i_0\}$
,
Note that we also have
 $$ \begin{align*} \dim V_{1, 0} \le \left\{ \begin{array} {ll} \frac{1}{2}LM + 1, & i_0> 0; \\ & \\ \frac{1}{3}LM + 1, & i_0 = 0. \end{array} \right. \end{align*} $$
$$ \begin{align*} \dim V_{1, 0} \le \left\{ \begin{array} {ll} \frac{1}{2}LM + 1, & i_0> 0; \\ & \\ \frac{1}{3}LM + 1, & i_0 = 0. \end{array} \right. \end{align*} $$
Together with equations (3.3) and (3.4) for all
![]() $i> 0$
, we deduce that
$i> 0$
, we deduce that
 $$ \begin{align} L^2 & = \sum_{i=1}^{\gamma-1} (N_{i-1}^2 - N_i^2) + N_{\gamma-1}^2 \nonumber \\ & \ge 4 \sum_{i=0}^{i_0-1} \dim V_{1, i} + 6 \sum_{i=i_0}^{\gamma-1} \dim V_{1, i} - 2LM - 6\gamma + N_{\gamma-1}^2 \nonumber\\ & \ge 4h^0(V, L) + 2 \sum_{i=i_0}^{\gamma-1} \dim V_{1, i} - 4h^0(V, L-\gamma M) - 2LM - 6\gamma \nonumber \\ & \ge 4h^0(V, L) + 2 \sum_{i=i_0}^{\gamma-1} \dim V_{1, i} - 4LM - 6 \gamma - 4. \end{align} $$
$$ \begin{align} L^2 & = \sum_{i=1}^{\gamma-1} (N_{i-1}^2 - N_i^2) + N_{\gamma-1}^2 \nonumber \\ & \ge 4 \sum_{i=0}^{i_0-1} \dim V_{1, i} + 6 \sum_{i=i_0}^{\gamma-1} \dim V_{1, i} - 2LM - 6\gamma + N_{\gamma-1}^2 \nonumber\\ & \ge 4h^0(V, L) + 2 \sum_{i=i_0}^{\gamma-1} \dim V_{1, i} - 4h^0(V, L-\gamma M) - 2LM - 6\gamma \nonumber \\ & \ge 4h^0(V, L) + 2 \sum_{i=i_0}^{\gamma-1} \dim V_{1, i} - 4LM - 6 \gamma - 4. \end{align} $$
The third inequality here is due to Lemma 3.7. For the last inequality, by Lemma 3.5 and the definition of
![]() $\gamma $
, we have
$\gamma $
, we have
Then it is easy to deduce that
Thus equation (3.5) is verified.
Now, adding equations (3.2) and (3.5), it follows that
that is,
Finally, let
![]() $\lambda $
be the smallest integer such that
$\lambda $
be the smallest integer such that
![]() $\lambda M-L$
is pseudo-effective. Noting that
$\lambda M-L$
is pseudo-effective. Noting that
![]() $\gamma \le \lambda $
, we deduce that
$\gamma \le \lambda $
, we deduce that
Thus the whole proof of this lemma is completed.
3.3.4
 $a$
is composed with an involution and
$a$
is composed with an involution and
 $\kappa (\Sigma )> 0$
$\kappa (\Sigma )> 0$
Finally, we consider the case when a is composed with an involution and
![]() $\Sigma $
is birational to a smooth projective variety of positive Kodaira dimension. Let
$\Sigma $
is birational to a smooth projective variety of positive Kodaira dimension. Let
![]() $\pi : \Sigma ' \to \Sigma $
be a resolution of singularities of
$\pi : \Sigma ' \to \Sigma $
be a resolution of singularities of
![]() $\Sigma $
. Then
$\Sigma $
. Then
![]() $\kappa (\Sigma ')> 0$
. Set
$\kappa (\Sigma ')> 0$
. Set
 $$ \begin{align*}r'(L, M, \Sigma') := \frac{LM^{n-1}}{2K_{\Sigma'}(\pi^*H)^{n-1}.} \end{align*} $$
$$ \begin{align*}r'(L, M, \Sigma') := \frac{LM^{n-1}}{2K_{\Sigma'}(\pi^*H)^{n-1}.} \end{align*} $$
By the assumption,
![]() $K_{\Sigma '}(\pi ^*H)^{n-1}> 0$
. Thus
$K_{\Sigma '}(\pi ^*H)^{n-1}> 0$
. Thus
![]() $r'(L, M, \Sigma ') < \infty $
.
$r'(L, M, \Sigma ') < \infty $
.
Theorem 3.13. Let the notation be as above. Write
![]() $r' = r'(L, M, \Sigma ')$
. Suppose that
$r' = r'(L, M, \Sigma ')$
. Suppose that
![]() $K_V-L$
is pseudo-effective. Then we have
$K_V-L$
is pseudo-effective. Then we have
Moreover, for any
![]() ${\mathbb {Q}}$
-divisor
${\mathbb {Q}}$
-divisor
![]() $L_1 \le L$
, we have
$L_1 \le L$
, we have
Here the function
![]() $\delta (x)$
is the same as that in Theorem 3.4. Note that under this setting,
$\delta (x)$
is the same as that in Theorem 3.4. Note that under this setting,
![]() $\delta (r')> 1$
. Moreover, since
$\delta (r')> 1$
. Moreover, since
![]() $r^{\prime }_1:=r'(L_1, M, \Sigma ') \le r'$
, we have
$r^{\prime }_1:=r'(L_1, M, \Sigma ') \le r'$
, we have
![]() $\delta (r^{\prime }_1) \ge \delta (r')$
and
$\delta (r^{\prime }_1) \ge \delta (r')$
and
![]() $\frac {2 \delta (r^{\prime }_1) - 1}{5 \delta (r^{\prime }_1) - 3} \le \frac {2 \delta (r') - 1}{5 \delta (r') - 3}$
. Therefore, the second inequality in Theorem 3.13 can be deduced from the first one for
$\frac {2 \delta (r^{\prime }_1) - 1}{5 \delta (r^{\prime }_1) - 3} \le \frac {2 \delta (r') - 1}{5 \delta (r') - 3}$
. Therefore, the second inequality in Theorem 3.13 can be deduced from the first one for
![]() $L_1$
.
$L_1$
.
Note that the restriction of a on a general member of
![]() $a^*|H|$
is composed with an involution. Furthermore, by the adjunction, a smooth model of a general member of
$a^*|H|$
is composed with an involution. Furthermore, by the adjunction, a smooth model of a general member of
![]() $|H|$
has positive Kodaira dimension. Thus the induction method works here, and Theorem 3.13 is finally reduced to the following result.
$|H|$
has positive Kodaira dimension. Thus the induction method works here, and Theorem 3.13 is finally reduced to the following result.
Lemma 3.14. Theorem 3.13 holds when
![]() $n=2$
,
$n=2$
,
![]() $|L|$
is base point free and
$|L|$
is base point free and
![]() $h^0(V, L-M)> 0$
.
$h^0(V, L-M)> 0$
.
Proof. The proof is just a modification of the proof of Lemma 3.12. We sketch it and leave the details to the interested reader.
Let C,
![]() $\gamma $
,
$\gamma $
,
![]() $V_{1, i}$
,
$V_{1, i}$
,
![]() $V_{2, j}$
,
$V_{2, j}$
,
![]() $N_i$
and
$N_i$
and
![]() $i_0$
be identical to those in the proof of Lemma 3.12. Then it is easy to see that equation (3.2) still holds here: that is,
$i_0$
be identical to those in the proof of Lemma 3.12. Then it is easy to see that equation (3.2) still holds here: that is,
 $$ \begin{align} L^2 \ge 5h^0(V, L) - 2\sum_{i=i_0}^{\gamma-1} \dim V_{1, i} - 8 (LM +1). \end{align} $$
$$ \begin{align} L^2 \ge 5h^0(V, L) - 2\sum_{i=i_0}^{\gamma-1} \dim V_{1, i} - 8 (LM +1). \end{align} $$
For any
![]() $1 \le i \le \gamma -1$
, equation (3.3) also holds here: that is,
$1 \le i \le \gamma -1$
, equation (3.3) also holds here: that is,
The major modification is a replacement of equation (3.4). For
![]() $i_0 \le i \le \gamma - 1$
,
$i_0 \le i \le \gamma - 1$
,
![]() $V_{1, i}$
induces a map on C of degree at least two. Let
$V_{1, i}$
induces a map on C of degree at least two. Let
![]() $\phi _i: C \to C^{\prime }_i$
,
$\phi _i: C \to C^{\prime }_i$
,
![]() $L^{\prime }_i$
and
$L^{\prime }_i$
and
![]() $Z^{\prime }_i$
be as in the proof of Lemma 3.12. We may further assume that the curve
$Z^{\prime }_i$
be as in the proof of Lemma 3.12. We may further assume that the curve
![]() $C^{\prime }_i$
is normal. By Theorem 3.4 and the fact that
$C^{\prime }_i$
is normal. By Theorem 3.4 and the fact that
![]() $\deg \phi _i \ge 2$
, we deduce that
$\deg \phi _i \ge 2$
, we deduce that
 $$ \begin{align*} \dim V_{1, i} \, \le \, h^0(C^{\prime}_i, L^{\prime}_i) \le \frac{1}{\delta(r^{\prime}_i)} \deg L^{\prime}_i + 1 \le \frac{1}{2\delta(r^{\prime}_i)} N_iM + 1, \end{align*} $$
$$ \begin{align*} \dim V_{1, i} \, \le \, h^0(C^{\prime}_i, L^{\prime}_i) \le \frac{1}{\delta(r^{\prime}_i)} \deg L^{\prime}_i + 1 \le \frac{1}{2\delta(r^{\prime}_i)} N_iM + 1, \end{align*} $$
where
![]() $r^{\prime }_i = \frac {\deg L^{\prime }_i}{\deg K_{C^{\prime }_i}}$
. Now we claim that
$r^{\prime }_i = \frac {\deg L^{\prime }_i}{\deg K_{C^{\prime }_i}}$
. Now we claim that
for any
![]() $i \ge i_0$
as above. With this claim, we deduce that for
$i \ge i_0$
as above. With this claim, we deduce that for
![]() $i \ge \max \{1, i_0\}$
,
$i \ge \max \{1, i_0\}$
,
To prove the claim, we only need to prove that
![]() $r^{\prime }_i \le r'$
. Since we already have
$r^{\prime }_i \le r'$
. Since we already have
![]() $\deg L^{\prime }_i \le \frac {1}{2} LM$
as above, it suffices to prove that
$\deg L^{\prime }_i \le \frac {1}{2} LM$
as above, it suffices to prove that
![]() $\deg K_{C^{\prime }_i} \ge K_{\Sigma '}(\pi ^*H)$
. This is rather obvious. The key is to note that
$\deg K_{C^{\prime }_i} \ge K_{\Sigma '}(\pi ^*H)$
. This is rather obvious. The key is to note that
![]() $a|_C$
factors through
$a|_C$
factors through
![]() $\phi _i$
. Via this factorisation,
$\phi _i$
. Via this factorisation,
![]() $C^{\prime }_i$
maps to a general curve in
$C^{\prime }_i$
maps to a general curve in
![]() $|H|$
on
$|H|$
on
![]() $\Sigma $
. Since
$\Sigma $
. Since
![]() $\pi ^*|H|$
is base point free, by Bertini’s theorem, a general member of
$\pi ^*|H|$
is base point free, by Bertini’s theorem, a general member of
![]() $\pi ^*|H|$
is smooth. Moreover, the aforementioned map on
$\pi ^*|H|$
is smooth. Moreover, the aforementioned map on
![]() $C^{\prime }_i$
lifts to a map from
$C^{\prime }_i$
lifts to a map from
![]() $C^{\prime }_i$
to a general member
$C^{\prime }_i$
to a general member
![]() $C''\in \pi ^*|H|$
. Therefore, by the Hurwitz formula and the adjunction formula,
$C''\in \pi ^*|H|$
. Therefore, by the Hurwitz formula and the adjunction formula,
Thus the claim is verified, and equation (3.8) is established.
Having the above modification, we can proceed the proof as before. Sum up equations (3.7) and (3.8) over all the above
![]() $i> 0$
. Note that
$i> 0$
. Note that
 $$ \begin{align*} \dim V_{1, 0} \le \left\{ \begin{array} {ll} \frac{1}{2}LM + 1, & i_0> 0; \\ & \\ \frac{1}{2 \delta(r')}LM + 1, & i_0 = 0. \end{array} \right. \end{align*} $$
$$ \begin{align*} \dim V_{1, 0} \le \left\{ \begin{array} {ll} \frac{1}{2}LM + 1, & i_0> 0; \\ & \\ \frac{1}{2 \delta(r')}LM + 1, & i_0 = 0. \end{array} \right. \end{align*} $$
It follows that
 $$ \begin{align*} L^2 & \ge 4 \sum_{i=0}^{i_0-1} \dim V_{1, i} + 4\delta(r') \sum_{i=i_0}^{\gamma-1} \dim V_{1, i} - 2LM - 4 \delta(r')\gamma + N_{\gamma-1}^2 \\ & \ge 4h^0(V, L) + 4(\delta(r') - 1) \sum_{i=i_0}^{\gamma-1} \dim V_{1, i} - 4h^0(V, L-\gamma M) \\ & \quad - 2LM - 4 \delta(r') \gamma. \end{align*} $$
$$ \begin{align*} L^2 & \ge 4 \sum_{i=0}^{i_0-1} \dim V_{1, i} + 4\delta(r') \sum_{i=i_0}^{\gamma-1} \dim V_{1, i} - 2LM - 4 \delta(r')\gamma + N_{\gamma-1}^2 \\ & \ge 4h^0(V, L) + 4(\delta(r') - 1) \sum_{i=i_0}^{\gamma-1} \dim V_{1, i} - 4h^0(V, L-\gamma M) \\ & \quad - 2LM - 4 \delta(r') \gamma. \end{align*} $$
Using the argument for proving equation (3.5), we can similarly deduce that
The above two inequalities imply that
 $$ \begin{align} L^2 \ge 4h^0(V, L) + 4(\delta(r') - 1) \sum_{i=i_0}^{\gamma-1} \dim V_{1, i} - 4LM - 4 \delta(r') \gamma - 4. \end{align} $$
$$ \begin{align} L^2 \ge 4h^0(V, L) + 4(\delta(r') - 1) \sum_{i=i_0}^{\gamma-1} \dim V_{1, i} - 4LM - 4 \delta(r') \gamma - 4. \end{align} $$
For simplicity, we write
![]() $\delta = \delta (r')$
. As before, we use equations (3.6) and (3.9) to eliminate
$\delta = \delta (r')$
. As before, we use equations (3.6) and (3.9) to eliminate
![]() $\sum _{i=i_0}^{\gamma -1} \dim V_{1, i}$
. It follows that
$\sum _{i=i_0}^{\gamma -1} \dim V_{1, i}$
. It follows that
that is,
Since
![]() $1 < \delta \le 2$
, it is straightforward to check that the above inequality implies that
$1 < \delta \le 2$
, it is straightforward to check that the above inequality implies that
Once again, let
![]() $\lambda $
be the smallest integer such that
$\lambda $
be the smallest integer such that
![]() $\lambda M - L$
is pseudo-effective. Since
$\lambda M - L$
is pseudo-effective. Since
![]() $M^2 = (\deg a)H^2 \ge 2$
and
$M^2 = (\deg a)H^2 \ge 2$
and
![]() $\gamma \le \lambda $
, we deduce that
$\gamma \le \lambda $
, we deduce that
Thus the whole proof is completed.
4 Some results about
 $\chi _f$
$\chi _f$
Let
![]() $f: X \to B$
be a fibration from a smooth variety X to a smooth curve B of genus g, with a general fibre F. Recall that
$f: X \to B$
be a fibration from a smooth variety X to a smooth curve B of genus g, with a general fibre F. Recall that
The goal of this section is to list some results about this relative invariant. We always assume that f is of maximal Albanese dimension. Denote by
the Albanese map of X. Let
![]() $q = \dim A = h^1(X, {\mathcal {O}}_X)$
. The above notation will be used throughout this section.
$q = \dim A = h^1(X, {\mathcal {O}}_X)$
. The above notation will be used throughout this section.
4.1
 $\chi _f$
equals the degree of a twisted Hodge bundle
$\chi _f$
equals the degree of a twisted Hodge bundle
The following result relates
![]() $\chi _f$
to the degree of a twisted Hodge bundle.
$\chi _f$
to the degree of a twisted Hodge bundle.
Proposition 4.1. With the above notation, we have
where
![]() ${\mathcal {P}}$
is a general torsion element in
${\mathcal {P}}$
is a general torsion element in
![]() ${\mathrm {Pic}}^0(X)$
.Footnote 4
${\mathrm {Pic}}^0(X)$
.Footnote 4
Proof. This result has been proved by Hacon and Pardini [Reference Hacon and Pardini12, Theorem 2.4] assuming
![]() $g(B) \ge 2$
. In fact, this assumption can be removed. Here we give a slightly different proof that works for any curve B.
$g(B) \ge 2$
. In fact, this assumption can be removed. Here we give a slightly different proof that works for any curve B.
By the assumption,
![]() $a|_F: F \to A$
is generically finite onto its image. Let
$a|_F: F \to A$
is generically finite onto its image. Let
![]() ${\mathcal {P}} \in {\mathrm {Pic}}^0(X)$
be a general torsion element. Applying exactly the proof of [Reference Hacon and Pardini12, Corollary 2.3], we conclude that
${\mathcal {P}} \in {\mathrm {Pic}}^0(X)$
be a general torsion element. Applying exactly the proof of [Reference Hacon and Pardini12, Corollary 2.3], we conclude that
![]() $f_* (\omega _{X/B} \otimes {\mathcal {P}})$
is torsion free, hence a locally free sheaf on B of rank
$f_* (\omega _{X/B} \otimes {\mathcal {P}})$
is torsion free, hence a locally free sheaf on B of rank
![]() $r = \chi (F, \omega _F)$
. Still, by [Reference Hacon and Pardini12, Corollary 2.3], for any
$r = \chi (F, \omega _F)$
. Still, by [Reference Hacon and Pardini12, Corollary 2.3], for any
![]() $i> 0$
,
$i> 0$
,
Together with the Leray spectral sequence, we know that for any
![]() $i \ge 0$
,
$i \ge 0$
,
In particular,
Combine all of the above, and apply the Riemann-Roch theorem for
![]() $f_* (\omega _X \otimes {\mathcal {P}})$
. It follows that
$f_* (\omega _X \otimes {\mathcal {P}})$
. It follows that
 $$ \begin{align*} \deg f_*(\omega_{X/B} \otimes {\mathcal{P}}) & = \deg f_*(\omega_X \otimes {\mathcal{P}}) - 2 \chi(F, \omega_F) \chi(B, \omega_B) \\ & = \chi (B, f_* (\omega_X \otimes {\mathcal{P}}) ) - \chi(F, \omega_F) \chi(B, \omega_B) \\\phantom{\deg f_*(\omega_{X/B} \otimes {\mathcal{P}})} & = \chi(X, \omega_X) - \chi(F, \omega_F) \chi(B, \omega_B) \\ & = \chi_f. \end{align*} $$
$$ \begin{align*} \deg f_*(\omega_{X/B} \otimes {\mathcal{P}}) & = \deg f_*(\omega_X \otimes {\mathcal{P}}) - 2 \chi(F, \omega_F) \chi(B, \omega_B) \\ & = \chi (B, f_* (\omega_X \otimes {\mathcal{P}}) ) - \chi(F, \omega_F) \chi(B, \omega_B) \\\phantom{\deg f_*(\omega_{X/B} \otimes {\mathcal{P}})} & = \chi(X, \omega_X) - \chi(F, \omega_F) \chi(B, \omega_B) \\ & = \chi_f. \end{align*} $$
Thus the proof is completed.
4.2 The degree of the Hodge bundle under étale covers
In this subsection, we assume that
![]() $g> 0$
. Thus X itself is of maximal Albanese dimension.
$g> 0$
. Thus X itself is of maximal Albanese dimension.
Let
![]() $\mu _m: A \to A$
be the multiplication-by-m map of A. Let
$\mu _m: A \to A$
be the multiplication-by-m map of A. Let
![]() $X_m = X \times _{\mu _m} A$
. Since a is the Albanese map,
$X_m = X \times _{\mu _m} A$
. Since a is the Albanese map,
![]() $X_m$
is irreducible. Let
$X_m$
is irreducible. Let
![]() $J(B)$
be the Jacobian variety of B. By the abuse of notation, let
$J(B)$
be the Jacobian variety of B. By the abuse of notation, let
![]() $\mu _m: J(B) \to J(B)$
also denote the multiplication-by-m map of
$\mu _m: J(B) \to J(B)$
also denote the multiplication-by-m map of
![]() $J(B)$
, and let
$J(B)$
, and let
![]() $B_m=B \times _{\mu _m} J(B)$
. Thus we have the following commutative diagram:
$B_m=B \times _{\mu _m} J(B)$
. Thus we have the following commutative diagram:

Now we claim that if m is a sufficiently large prime number, the morphism
is always a fibration: that is, it has connected fibres. To see this, let
![]() $A_F = \ker h$
, which is also an abelian variety. We may assume that up to a translation by a point in
$A_F = \ker h$
, which is also an abelian variety. We may assume that up to a translation by a point in
![]() $J(B)$
,
$J(B)$
,
![]() $a(F)$
generates
$a(F)$
generates
![]() $A_F$
. Thus the kernel of the map
$A_F$
. Thus the kernel of the map
![]() $(a|_F)^*: {\mathrm {Pic}}^0(A_F) \to {\mathrm {Pic}}^0(F)$
is finite. Thus for any integer m coprime to the cardinality of this kernel, the general fibre of
$(a|_F)^*: {\mathrm {Pic}}^0(A_F) \to {\mathrm {Pic}}^0(F)$
is finite. Thus for any integer m coprime to the cardinality of this kernel, the general fibre of
![]() $f_m$
is irreducible.
$f_m$
is irreducible.
Proposition 4.2. With the above notation, we have
Proof. From the above construction, we know that for any
![]() $m> 0$
, the morphism
$m> 0$
, the morphism
![]() $\sigma _m: B_m \to B$
is étale. By the projection formula,
$\sigma _m: B_m \to B$
is étale. By the projection formula,
where
![]() $T_m(B) \subset {\mathrm {Pic}}^0(B)$
is the subgroup of all m-torsion line bundles on B. There is a natural injective group homomorphism
$T_m(B) \subset {\mathrm {Pic}}^0(B)$
is the subgroup of all m-torsion line bundles on B. There is a natural injective group homomorphism
given by the pull-back of f, where
![]() $T_m(X) \subset {\mathrm {Pic}}^0(X)$
is the subgroup of all m-torsion line bundles on X. Let m be a sufficiently large prime number, and let
$T_m(X) \subset {\mathrm {Pic}}^0(X)$
is the subgroup of all m-torsion line bundles on X. Let m be a sufficiently large prime number, and let
![]() $X^{\prime }_m = X \times _B B_m$
. Then we have the following commutative diagram:
$X^{\prime }_m = X \times _B B_m$
. Then we have the following commutative diagram:

It is clear that
![]() $\nu ^{\prime }_m: X_m \to X^{\prime }_m$
is a Galois cover with
$\nu ^{\prime }_m: X_m \to X^{\prime }_m$
is a Galois cover with
![]() ${\mathrm {Gal}}(\nu ^{\prime }_m) \simeq \frac {T_m(X)}{f^*T_m(B)}$
. Thus, by the projection formula,
${\mathrm {Gal}}(\nu ^{\prime }_m) \simeq \frac {T_m(X)}{f^*T_m(B)}$
. Thus, by the projection formula,
 $$ \begin{align*}{\nu^{\prime}_m}_* \omega_{X_m/B_m} = \bigoplus_{{\mathcal{Q}} + f^*T_m(B)} \omega_{X^{\prime}_m/B_m} \otimes (\sigma^{\prime}_m)^*{\mathcal{Q}}. \end{align*} $$
$$ \begin{align*}{\nu^{\prime}_m}_* \omega_{X_m/B_m} = \bigoplus_{{\mathcal{Q}} + f^*T_m(B)} \omega_{X^{\prime}_m/B_m} \otimes (\sigma^{\prime}_m)^*{\mathcal{Q}}. \end{align*} $$
Here the summation runs over all cosets of
![]() $f^*T_m(B)$
in
$f^*T_m(B)$
in
![]() $T_m(X)$
(whose cardinality equals
$T_m(X)$
(whose cardinality equals
![]() $m^{2q-2g}$
), and
$m^{2q-2g}$
), and
![]() ${\mathcal {Q}}$
is any representative in each corresponding coset. Thus we have the following splitting:
${\mathcal {Q}}$
is any representative in each corresponding coset. Thus we have the following splitting:
 $$ \begin{align*} {f_m}_* \omega_{X_m/B_m} = {f^{\prime}_m}_* \left( {\nu^{\prime}_m}_* \omega_{X_m/B_m} \right) = \bigoplus_{{\mathcal{Q}} + f^*T_m(B)} \sigma_m^*(f_* (\omega_{X/B} \otimes {\mathcal{Q}})). \end{align*} $$
$$ \begin{align*} {f_m}_* \omega_{X_m/B_m} = {f^{\prime}_m}_* \left( {\nu^{\prime}_m}_* \omega_{X_m/B_m} \right) = \bigoplus_{{\mathcal{Q}} + f^*T_m(B)} \sigma_m^*(f_* (\omega_{X/B} \otimes {\mathcal{Q}})). \end{align*} $$
All the above imply particularly that
 $$ \begin{align*} \deg {f_m}_* \omega_{X_m/B_m} & = \deg {\sigma_m}_* \left({f_m}_* \omega_{X_m/B_m} \right) \\ & = \deg \left({\sigma_m}_* \left( {f_m}_* \omega_{X_m} \right) \otimes \omega_B^{-1} \right) \\ & = \deg \left( f_* \left({\nu_m}_* \omega_{X_m} \right) \otimes \omega_B^{-1} \right). \end{align*} $$
$$ \begin{align*} \deg {f_m}_* \omega_{X_m/B_m} & = \deg {\sigma_m}_* \left({f_m}_* \omega_{X_m/B_m} \right) \\ & = \deg \left({\sigma_m}_* \left( {f_m}_* \omega_{X_m} \right) \otimes \omega_B^{-1} \right) \\ & = \deg \left( f_* \left({\nu_m}_* \omega_{X_m} \right) \otimes \omega_B^{-1} \right). \end{align*} $$
On the other hand, by the projection formula,
Thus it follows that
Let
![]() $S_m(X) = \{{\mathcal {P}} \in T_m(X) | \deg f_*(\omega _{X/B} \otimes {\mathcal {P}}) = \chi _f \}$
be the subset of
$S_m(X) = \{{\mathcal {P}} \in T_m(X) | \deg f_*(\omega _{X/B} \otimes {\mathcal {P}}) = \chi _f \}$
be the subset of
![]() $T_m(X)$
. By Proposition 4.1, we know that the set
$T_m(X)$
. By Proposition 4.1, we know that the set
is contained in a proper subvariety of
![]() ${\mathrm {Pic}}^0(X)$
. In particular,
${\mathrm {Pic}}^0(X)$
. In particular,
Note that
![]() $\deg f_*(\omega _{X/B} \otimes {\mathcal {P}})$
is always nonnegative (e.g., see [Reference Hacon and Pardini12]) and bounded from above independent of m. We deduce that
$\deg f_*(\omega _{X/B} \otimes {\mathcal {P}})$
is always nonnegative (e.g., see [Reference Hacon and Pardini12]) and bounded from above independent of m. We deduce that
Thus the proof is completed.
5 Slope inequalities for fibrations over curves
In this section, we prove a slope inequality for fibrations over curves whose general fibre is a smooth variety of general type. Throughout this section, we always assume that
is a fibration from a smooth variety X of dimension
![]() $n \ge 2$
to a smooth curve B. Denote by F a general fibre of f.
$n \ge 2$
to a smooth curve B. Denote by F a general fibre of f.
5.1 Xiao’s method
Here we review Xiao’s method and list some inequalities deduced from it. Most of the following facts can be found in [Reference Xiao23] when
![]() $n=2$
and in [Reference Ohno19, Reference Konno15, Reference Barja and Stoppino4] for general
$n=2$
and in [Reference Ohno19, Reference Konno15, Reference Barja and Stoppino4] for general
![]() $n \ge 2$
.
$n \ge 2$
.
Let L be a nef
![]() ${\mathbb {Q}}$
-divisor on X. Let
${\mathbb {Q}}$
-divisor on X. Let
be the Harder-Narasimhan filtration of
![]() $f_* {\mathcal {O}}_X({\lfloor L \rfloor })$
. For any
$f_* {\mathcal {O}}_X({\lfloor L \rfloor })$
. For any
![]() $0 \le i \le m$
, set
$0 \le i \le m$
, set
Then we have
as well as
 $$ \begin{align} \deg {\mathcal{E}}_k = \sum_{i=1}^{k-1} r_i (\mu_i - \mu_{i+1}) +r_k \mu_{k} \end{align} $$
$$ \begin{align} \deg {\mathcal{E}}_k = \sum_{i=1}^{k-1} r_i (\mu_i - \mu_{i+1}) +r_k \mu_{k} \end{align} $$
for each
![]() $1\le k\le m$
.
$1\le k\le m$
.
For each
![]() $1 \le i \le m$
, consider the rational map
$1 \le i \le m$
, consider the rational map
![]() $\phi _i: X \dashrightarrow \mathbb {P}_B(\mathcal {E}_i)$
associated to the evaluation morphism
$\phi _i: X \dashrightarrow \mathbb {P}_B(\mathcal {E}_i)$
associated to the evaluation morphism
![]() $f^*{\mathcal {E}}_i \to {\mathcal {O}}_X({\lfloor L \rfloor })$
. We may choose a common blowing up
$f^*{\mathcal {E}}_i \to {\mathcal {O}}_X({\lfloor L \rfloor })$
. We may choose a common blowing up
![]() $\sigma : Y \to X$
, which resolves all indeterminacies of
$\sigma : Y \to X$
, which resolves all indeterminacies of
![]() $\phi _i$
. Denote by
$\phi _i$
. Denote by
![]() $F_1$
a general fibre of
$F_1$
a general fibre of
![]() $f \circ \sigma : Y \to B$
. Applying Xiao’s method, we obtain a sequence of nef
$f \circ \sigma : Y \to B$
. Applying Xiao’s method, we obtain a sequence of nef
![]() $\mathbb {Q}$
-Cartier divisors
$\mathbb {Q}$
-Cartier divisors
on Y. Here
![]() $N_i = (\phi _i \circ \sigma )^*H_{{\mathcal {E}}_i} - \mu _iF_1$
, where
$N_i = (\phi _i \circ \sigma )^*H_{{\mathcal {E}}_i} - \mu _iF_1$
, where
![]() $H_{{\mathcal {E}}_i}$
is a hyperplane section of
$H_{{\mathcal {E}}_i}$
is a hyperplane section of
![]() ${\mathbb {P}}_{B}({\mathcal {E}}_i)$
. For each
${\mathbb {P}}_{B}({\mathcal {E}}_i)$
. For each
![]() $1 \le i \le m$
,
$1 \le i \le m$
,
![]() $N_i|_{F_1}$
is Cartier,
$N_i|_{F_1}$
is Cartier,
![]() $h^0(F_1, N_i|_{F_1})=r_i$
,
$h^0(F_1, N_i|_{F_1})=r_i$
,
and
In particular,
![]() $\sigma ^*L - \mu _1 F_1$
is pseudo-effective, and for
$\sigma ^*L - \mu _1 F_1$
is pseudo-effective, and for
![]() $1\le i\le m-1$
, we have
$1\le i\le m-1$
, we have
Thus the following lemma follows easily by induction.
Lemma 5.1. Keep the same notation as above. Suppose that for some
![]() $1\le i\le m$
, we have
$1\le i\le m$
, we have
![]() $\mu _i\ge 0$
. Let
$\mu _i\ge 0$
. Let
![]() $k:=\max \{i|\ 1\le i\le m \ \text {and}\ \mu _i \ge 0 \}$
. Then we have
$k:=\max \{i|\ 1\le i\le m \ \text {and}\ \mu _i \ge 0 \}$
. Then we have
 $$ \begin{align*} L^n\ge n\sum_{i=1}^{k-1}(\mu_i-\mu_{i+1})(N_i|_{F_1})^{n-1}+n\mu_k(N_k|_{F_1})^{n-1}. \end{align*} $$
$$ \begin{align*} L^n\ge n\sum_{i=1}^{k-1}(\mu_i-\mu_{i+1})(N_i|_{F_1})^{n-1}+n\mu_k(N_k|_{F_1})^{n-1}. \end{align*} $$
Proof. Inductively using the above estimate, we have
 $$ \begin{align*} N_k^n \ge N_1^n + n\sum_{i=1}^{k-1}(\mu_i-\mu_{i+1})(N_i|_{F_1})^{n-1}\ge n\sum_{i=1}^{k-1}(\mu_i-\mu_{i+1})(N_i|_{F_1})^{n-1}. \end{align*} $$
$$ \begin{align*} N_k^n \ge N_1^n + n\sum_{i=1}^{k-1}(\mu_i-\mu_{i+1})(N_i|_{F_1})^{n-1}\ge n\sum_{i=1}^{k-1}(\mu_i-\mu_{i+1})(N_i|_{F_1})^{n-1}. \end{align*} $$
The last inequality holds since
![]() $N_1$
is nef. Notice that
$N_1$
is nef. Notice that
![]() $\sigma ^*L\ge N_k+\mu _k F_1$
and
$\sigma ^*L\ge N_k+\mu _k F_1$
and
![]() $\mu _k\ge 0$
. We have
$\mu _k\ge 0$
. We have
Thus the proof is completed by combining the above estimates.
5.2 A basic slope inequality
We have the following result.
Proposition 5.2. Let
![]() $f: X \to B$
and F be as before. Suppose that L is a nef
$f: X \to B$
and F be as before. Suppose that L is a nef
![]() ${\mathbb {Q}}$
-divisor on X such that
${\mathbb {Q}}$
-divisor on X such that
![]() $L|_F$
is big and
$L|_F$
is big and
![]() $K_F - L|_F$
is pseudo-effective. Then we have
$K_F - L|_F$
is pseudo-effective. Then we have
 $$ \begin{align*} \left(1 + \frac{2n!(n-1) \varepsilon(F, L|_F)}{(L|_F)^{n-1}}\right) L^n \ge 2n! \deg f_* {\mathcal{O}}_X({\lfloor L \rfloor}). \end{align*} $$
$$ \begin{align*} \left(1 + \frac{2n!(n-1) \varepsilon(F, L|_F)}{(L|_F)^{n-1}}\right) L^n \ge 2n! \deg f_* {\mathcal{O}}_X({\lfloor L \rfloor}). \end{align*} $$
Proof. The inequality holds trivially when
![]() $\deg f_*{\mathcal {O}}_X({\lfloor L \rfloor })\le 0$
. Thus we may assume that
$\deg f_*{\mathcal {O}}_X({\lfloor L \rfloor })\le 0$
. Thus we may assume that
![]() $\deg f_*{\mathcal {O}}_X({\lfloor L \rfloor })>0$
.
$\deg f_*{\mathcal {O}}_X({\lfloor L \rfloor })>0$
.
Let
be the Harder-Narasimhan filtration of
![]() $f_* {\mathcal {O}}_X({\lfloor L \rfloor })$
. Keep the same notation as in Section 5.1. Since
$f_* {\mathcal {O}}_X({\lfloor L \rfloor })$
. Keep the same notation as in Section 5.1. Since
![]() $\deg f_*{\mathcal {O}}_X({\lfloor L \rfloor })>0$
, we have
$\deg f_*{\mathcal {O}}_X({\lfloor L \rfloor })>0$
, we have
![]() $\mu _i>0$
for some
$\mu _i>0$
for some
![]() $1\le i\le m$
. Let
$1\le i\le m$
. Let
![]() $k:=\max \{i|\ 1 \le i \le m \ \text {and}\ \mu _i\ge 0 \}$
. We have
$k:=\max \{i|\ 1 \le i \le m \ \text {and}\ \mu _i\ge 0 \}$
. We have
By equation (5.1) and Lemma 5.1, we have the following two inequalities:
 $$ \begin{align*} L^n & \ge n \sum_{i=1}^{k-1} (\mu_i-\mu_{i+1})(N_i|_{F_1})^{n-1}+n\mu_k(N_k|_{F_1})^{n-1}, \\ \deg {\mathcal{E}}_k & = \sum_{i=1}^{k-1} r_i (\mu_i - \mu_{i+1})+r_k\mu_k. \end{align*} $$
$$ \begin{align*} L^n & \ge n \sum_{i=1}^{k-1} (\mu_i-\mu_{i+1})(N_i|_{F_1})^{n-1}+n\mu_k(N_k|_{F_1})^{n-1}, \\ \deg {\mathcal{E}}_k & = \sum_{i=1}^{k-1} r_i (\mu_i - \mu_{i+1})+r_k\mu_k. \end{align*} $$
On the other hand, note that
![]() $N_i|_{F_1} \le \sigma ^*L|_{F_1}$
for any
$N_i|_{F_1} \le \sigma ^*L|_{F_1}$
for any
![]() $1 \le i \le m$
and
$1 \le i \le m$
and
![]() $K_{F_1} -\sigma ^*L|_{F_1} \ge \sigma ^*(K_F - L|_F)$
is pseudo-effective. By Theorem 2.2 and Proposition 2.1, we have
$K_{F_1} -\sigma ^*L|_{F_1} \ge \sigma ^*(K_F - L|_F)$
is pseudo-effective. By Theorem 2.2 and Proposition 2.1, we have
Combine the above three (in)equalities. We deduce that
 $$ \begin{align*} L^n & \ge 2n! \deg {\mathcal{E}}_k - 2n!(n-1) \varepsilon(F, L|_F) (\sum_{i=1}^{k-1} (\mu_i - \mu_{i+1})+\mu_{k}) \\ & = 2n! \deg {\mathcal{E}}_k - 2n!(n-1) \varepsilon(F, L|_F) \mu_1\\ &\ge 2n!\deg f_*{\mathcal{O}}_X({\lfloor L \rfloor})-2n!(n-1) \varepsilon(F, L|_F) \mu_1, \end{align*} $$
$$ \begin{align*} L^n & \ge 2n! \deg {\mathcal{E}}_k - 2n!(n-1) \varepsilon(F, L|_F) (\sum_{i=1}^{k-1} (\mu_i - \mu_{i+1})+\mu_{k}) \\ & = 2n! \deg {\mathcal{E}}_k - 2n!(n-1) \varepsilon(F, L|_F) \mu_1\\ &\ge 2n!\deg f_*{\mathcal{O}}_X({\lfloor L \rfloor})-2n!(n-1) \varepsilon(F, L|_F) \mu_1, \end{align*} $$
where the last inequality follows by equation (5.2).
What is left to us is to estimate
![]() $\mu _1$
. Note that
$\mu _1$
. Note that
![]() $\sigma ^*L - \mu _1 F_1$
is pseudo-effective. Thus
$\sigma ^*L - \mu _1 F_1$
is pseudo-effective. Thus
As a result, we deduce that
 $$ \begin{align*} \left(1 + \frac{2n!(n-1) \varepsilon(F, L|_F)}{(L|_F)^{n-1}}\right) L^n \ge 2n! \deg f_* {\mathcal{O}}_X({\lfloor L \rfloor}). \end{align*} $$
$$ \begin{align*} \left(1 + \frac{2n!(n-1) \varepsilon(F, L|_F)}{(L|_F)^{n-1}}\right) L^n \ge 2n! \deg f_* {\mathcal{O}}_X({\lfloor L \rfloor}). \end{align*} $$
Thus the proof is completed.
Before going further, we would like to remark that the inequality in Proposition 5.2 is by no means sharp. For example, when
![]() $n=2$
, f is a relatively minimal fibration by curves of genus
$n=2$
, f is a relatively minimal fibration by curves of genus
![]() $g \ge 2$
, and
$g \ge 2$
, and
![]() $L = K_{X/B}$
(in this case
$L = K_{X/B}$
(in this case
![]() $\varepsilon (F, L|_F) = 1$
), Proposition 5.2 yields
$\varepsilon (F, L|_F) = 1$
), Proposition 5.2 yields
 $$ \begin{align*}K_{X/B}^2 \ge \left(\frac{4g-4}{g+1}\right) \deg f_* \omega_{X/B}, \end{align*} $$
$$ \begin{align*}K_{X/B}^2 \ge \left(\frac{4g-4}{g+1}\right) \deg f_* \omega_{X/B}, \end{align*} $$
which is weaker than the optimal slope inequality with the slope
![]() $\frac {4g-4}{g}$
. This is because our estimate is not as delicate as Xiao’s original version in [Reference Xiao23], which also considers the intersection number contributed by the horizontal part
$\frac {4g-4}{g}$
. This is because our estimate is not as delicate as Xiao’s original version in [Reference Xiao23], which also considers the intersection number contributed by the horizontal part
![]() $N_i|_{F_1}-N_{i+1}|_{F_1}$
. See the proof of [Reference Xiao23, Lemma 2] for details. In other words, we have not employed Xiao’s method in its full strength. However, Proposition 5.2 is already enough to deduce Theorem 1.2. Moreover, instead of using Theorem 1.2, Proposition 5.2 is sufficient for us to run the argument as in [Reference Barja and Stoppino4, Proposition 4.4] to deduce the absolute Severi inequality.
$N_i|_{F_1}-N_{i+1}|_{F_1}$
. See the proof of [Reference Xiao23, Lemma 2] for details. In other words, we have not employed Xiao’s method in its full strength. However, Proposition 5.2 is already enough to deduce Theorem 1.2. Moreover, instead of using Theorem 1.2, Proposition 5.2 is sufficient for us to run the argument as in [Reference Barja and Stoppino4, Proposition 4.4] to deduce the absolute Severi inequality.
5.3 Sharper slope inequalities
In the following, we assume that
is a generically finite map onto a projective variety
![]() $\Sigma $
. Let H be a sufficiently ample divisor on
$\Sigma $
. Let H be a sufficiently ample divisor on
![]() $\Sigma $
. Let
$\Sigma $
. Let
![]() $M = a^*H$
.
$M = a^*H$
.
Proposition 5.3. Let
![]() $f: X \to B$
and F be as before. Suppose that L is a nef
$f: X \to B$
and F be as before. Suppose that L is a nef
![]() ${\mathbb {Q}}$
-divisor on X such that
${\mathbb {Q}}$
-divisor on X such that
![]() $L|_F$
is big and
$L|_F$
is big and
![]() $K_F - L|_F$
is pseudo-effective.
$K_F - L|_F$
is pseudo-effective.
-
(1) If a is birational, then
 $$ \begin{align*} \left(1 + \frac{5n!(n-1) \varepsilon(F, L|_F, M)}{2(L|_F)^{n-1}}\right) L^n \ge \frac{5n!}{2} \deg f_* {\mathcal{O}}_X({\lfloor L \rfloor}). \end{align*} $$
$$ \begin{align*} \left(1 + \frac{5n!(n-1) \varepsilon(F, L|_F, M)}{2(L|_F)^{n-1}}\right) L^n \ge \frac{5n!}{2} \deg f_* {\mathcal{O}}_X({\lfloor L \rfloor}). \end{align*} $$
-
(2) If a is not composed with an involution, then
 $$ \begin{align*} \left(1 + \frac{9n!(n-1) \varepsilon(F, L|_F, M)}{4(L|_F)^{n-1}}\right) L^n \ge \frac{9n!}{4} \deg f_* {\mathcal{O}}_X({\lfloor L \rfloor}). \end{align*} $$
$$ \begin{align*} \left(1 + \frac{9n!(n-1) \varepsilon(F, L|_F, M)}{4(L|_F)^{n-1}}\right) L^n \ge \frac{9n!}{4} \deg f_* {\mathcal{O}}_X({\lfloor L \rfloor}). \end{align*} $$
-
(3) If a is composed with an involution and
 $\Sigma $
has a smooth model of positive Kodaira dimension, then Here
$\Sigma $
has a smooth model of positive Kodaira dimension, then Here $$ \begin{align*} \left(1 + \frac{(5\delta(r') - 3) n!(n-1) \varepsilon(F, L|_F, M)}{(2 \delta(r') - 1)(L|_F)^{n-1}}\right) L^n \ge \frac{(5\delta(r') - 3) n!}{2 \delta(r') - 1} \deg f_* {\mathcal{O}}_X({\lfloor L \rfloor}). \end{align*} $$
$$ \begin{align*} \left(1 + \frac{(5\delta(r') - 3) n!(n-1) \varepsilon(F, L|_F, M)}{(2 \delta(r') - 1)(L|_F)^{n-1}}\right) L^n \ge \frac{(5\delta(r') - 3) n!}{2 \delta(r') - 1} \deg f_* {\mathcal{O}}_X({\lfloor L \rfloor}). \end{align*} $$
 $r'$
and
$r'$
and
 $\delta $
are the same as in Theorem 3.13.
$\delta $
are the same as in Theorem 3.13.
6 Proof of the main theorems
In the final section, we prove the main theorems of this paper. We always assume that
![]() $f: X \to B$
is a relatively minimal fibration from a variety X of dimension
$f: X \to B$
is a relatively minimal fibration from a variety X of dimension
![]() $n \ge 2$
to a smooth curve B with a general fibre F and f is of maximal Albanese dimension. Let
$n \ge 2$
to a smooth curve B with a general fibre F and f is of maximal Albanese dimension. Let
be the Albanese map of X. Write
![]() $q = h^1(X, {\mathcal {O}}_X) = \dim A$
.
$q = h^1(X, {\mathcal {O}}_X) = \dim A$
.
6.1 Preparation when
 $g(B)>0$
$g(B)>0$
Before proving the results, we list some notations that will be used throughout the section. We first assume that
![]() $g(B)>0$
. Note that in this case, X itself is of maximal Albanese dimension.
$g(B)>0$
. Note that in this case, X itself is of maximal Albanese dimension.
Let
![]() $\pi : Y \to X$
be a resolution of singularities of X. Thus Y is also of maximal Albanese dimension. Let
$\pi : Y \to X$
be a resolution of singularities of X. Thus Y is also of maximal Albanese dimension. Let
be the induced fibration with a general fibre
![]() $F'$
, and let
$F'$
, and let
be the Albanese map of Y.
Let m be a sufficiently large prime number. Similar to Section 4.2 but adding Y to it, we have the following commutative diagram:

Here
![]() $\mu _m$
still denotes the multiplication-by-m map of A or
$\mu _m$
still denotes the multiplication-by-m map of A or
![]() $J(B)$
, the Jacobian variety of B,
$J(B)$
, the Jacobian variety of B,
![]() $X_m$
and
$X_m$
and
![]() $f_m$
are identical to those in Section 4.2,
$f_m$
are identical to those in Section 4.2,
![]() $Y_m = Y \times _{\mu _m} A$
and
$Y_m = Y \times _{\mu _m} A$
and
is the Stein factorisation of the morphism
![]() $Y_m \to Y \to B$
. Clearly,
$Y_m \to Y \to B$
. Clearly,
![]() $X_m$
has at worst terminal singularities, and
$X_m$
has at worst terminal singularities, and
![]() $\pi _m: Y_m \to X_m$
is also a resolution of singularities of
$\pi _m: Y_m \to X_m$
is also a resolution of singularities of
![]() $X_m$
. Denote by
$X_m$
. Denote by
![]() $F^{\prime }_m$
a general fibre of
$F^{\prime }_m$
a general fibre of
![]() $f^{\prime }_m$
. Moreover, we will fix a sufficiently ample divisor H on A. By [Reference Birkenhake and Lange7, Proposition 2.3.5],
$f^{\prime }_m$
. Moreover, we will fix a sufficiently ample divisor H on A. By [Reference Birkenhake and Lange7, Proposition 2.3.5],
6.2 Proof of Theorem 1.2
We divide the proof into two cases.
6.2.1 Case I:
 $g(B)> 0$
$g(B)> 0$
We first prove Theorem 1.2 when
![]() $g:=g(B)> 0$
.
$g:=g(B)> 0$
.
If F is not of general type, neither is
![]() $F'$
. In this case, for a general torsion element
$F'$
. In this case, for a general torsion element
![]() ${\mathcal {P}} \in {\mathrm {Pic}}^0(Y)$
,
${\mathcal {P}} \in {\mathrm {Pic}}^0(Y)$
,
![]() $f_* (\omega _{Y/B} \otimes {\mathcal {P}})$
is of rank
$f_* (\omega _{Y/B} \otimes {\mathcal {P}})$
is of rank
![]() $\chi (F', \omega _{F'}) = 0$
. We deduce that
$\chi (F', \omega _{F'}) = 0$
. We deduce that
![]() $f_* (\omega _{Y/B} \otimes {\mathcal {P}}) = 0$
. By Proposition 4.1,
$f_* (\omega _{Y/B} \otimes {\mathcal {P}}) = 0$
. By Proposition 4.1,
![]() $\chi _f = \chi _{f'} = 0$
. Thus equation (1.1) holds trivially.
$\chi _f = \chi _{f'} = 0$
. Thus equation (1.1) holds trivially.
From now on, we will always assume that F is of general type. Set
Clearly,
![]() $L_m$
is nef, and
$L_m$
is nef, and
![]() $L_m|_{F^{\prime }_m}$
is big. Since X has at worst terminal singularities,
$L_m|_{F^{\prime }_m}$
is big. Since X has at worst terminal singularities,
![]() $K_Y - \pi ^*K_X$
is effective. Thus
$K_Y - \pi ^*K_X$
is effective. Thus
![]() $K_{F^{\prime }_m} - L_m|_{F^{\prime }_m}$
is pseudo-effective. Moreover, since
$K_{F^{\prime }_m} - L_m|_{F^{\prime }_m}$
is pseudo-effective. Moreover, since
by [Reference Fujita11, Main Theorem], we deduce that
![]() ${f^{\prime }_m}_* {\mathcal {O}}_{Y_m}({\lfloor L_m \rfloor })$
is semi-positive.
${f^{\prime }_m}_* {\mathcal {O}}_{Y_m}({\lfloor L_m \rfloor })$
is semi-positive.
Since
![]() $\deg \nu _m = m^{2q}$
, we have
$\deg \nu _m = m^{2q}$
, we have
There is a natural restriction morphism
It is an étale morphism and
![]() $\deg \nu _m|_{F^{\prime }_m} = m^{2q-2g}$
. Therefore, we deduce that
$\deg \nu _m|_{F^{\prime }_m} = m^{2q-2g}$
. Therefore, we deduce that
Moreover, we claim that
In fact, we may assume that
![]() $b^*H-L$
is pseudo-effective. By equation (6.1),
$b^*H-L$
is pseudo-effective. By equation (6.1),
![]() $m^2(b_m^* H)-L_m$
is also pseudo-effective. Thus
$m^2(b_m^* H)-L_m$
is also pseudo-effective. Thus
 $$ \begin{align*} \varepsilon(F^{\prime}_m, L_m|_{F^{\prime}_m}, (b^*_m H)|_{F^{\prime}_m}) & \le (m^2+1)^{n-2}\left((b_m^*H)|_{F^{\prime}_m}\right)^{n-1} \\ & \le \frac{2^{n-2}}{m^2} \left((b_m^*(\mu_m^*H))|_{F^{\prime}_m}\right)^{n-1} \\ & = \frac{2^{n-2}}{m^2} \left((\nu_m^*(b^*H)))|_{F^{\prime}_m}\right)^{n-1} \\ & = 2^{n-2} m^{2q-2g-2} \left((b^*H)|_{F'}\right)^{n-1}. \end{align*} $$
$$ \begin{align*} \varepsilon(F^{\prime}_m, L_m|_{F^{\prime}_m}, (b^*_m H)|_{F^{\prime}_m}) & \le (m^2+1)^{n-2}\left((b_m^*H)|_{F^{\prime}_m}\right)^{n-1} \\ & \le \frac{2^{n-2}}{m^2} \left((b_m^*(\mu_m^*H))|_{F^{\prime}_m}\right)^{n-1} \\ & = \frac{2^{n-2}}{m^2} \left((\nu_m^*(b^*H)))|_{F^{\prime}_m}\right)^{n-1} \\ & = 2^{n-2} m^{2q-2g-2} \left((b^*H)|_{F'}\right)^{n-1}. \end{align*} $$
Thus the claim is verified.
Now, applying Proposition 5.2 to
![]() $f^{\prime }_m$
and
$f^{\prime }_m$
and
![]() $L_m$
, we deduce that
$L_m$
, we deduce that
 $$ \begin{align} \left(1 + \frac{2n!(n-1) \varepsilon(F^{\prime}_m, L_m|_{F^{\prime}_m})} {(L_m|_{F^{\prime}_m})^{n-1}} \right) L_m^n \ge 2n! \deg {f^{\prime}_m}_* {\mathcal{O}}_{Y_m}({\lfloor L_m \rfloor}). \end{align} $$
$$ \begin{align} \left(1 + \frac{2n!(n-1) \varepsilon(F^{\prime}_m, L_m|_{F^{\prime}_m})} {(L_m|_{F^{\prime}_m})^{n-1}} \right) L_m^n \ge 2n! \deg {f^{\prime}_m}_* {\mathcal{O}}_{Y_m}({\lfloor L_m \rfloor}). \end{align} $$
Recall that
Together with equations (6.2), (6.3) and (6.4), the above inequality in equation (6.5) implies that
 $$ \begin{align} \left(1 + O(m^{-2}) \right) K_{X/B}^n \ge 2n! \left(\frac{\deg {f^{\prime}_m}_* \omega_{Y_m/B_m}}{m^{2q}} \right). \end{align} $$
$$ \begin{align} \left(1 + O(m^{-2}) \right) K_{X/B}^n \ge 2n! \left(\frac{\deg {f^{\prime}_m}_* \omega_{Y_m/B_m}}{m^{2q}} \right). \end{align} $$
Let
![]() $m \to \infty $
. The left-hand side of equation (6.6) clearly tends to
$m \to \infty $
. The left-hand side of equation (6.6) clearly tends to
![]() $K_{X/B}^n$
. By Proposition 4.2, the right-hand side tends to
$K_{X/B}^n$
. By Proposition 4.2, the right-hand side tends to
![]() $\chi _{f'} = \chi (Y, \omega _Y) - \chi (F', \omega _{F'}) \chi (B, \omega _B)$
, which is nothing but
$\chi _{f'} = \chi (Y, \omega _Y) - \chi (F', \omega _{F'}) \chi (B, \omega _B)$
, which is nothing but
![]() $\chi _f$
. Thus the proof for
$\chi _f$
. Thus the proof for
![]() $g>0$
is completed.
$g>0$
is completed.
6.2.2 Case II:
 $g(B) = 0$
$g(B) = 0$
Now we prove Theorem 1.2 when
![]() $g(B) = 0$
. It is easy to see that the argument for
$g(B) = 0$
. It is easy to see that the argument for
![]() $g(B)> 0$
does not directly apply here. However, we can reduce this case to the previous one via a base change.
$g(B)> 0$
does not directly apply here. However, we can reduce this case to the previous one via a base change.
Choose four general distinct closed points
![]() $P_1$
, …,
$P_1$
, …,
![]() $P_4$
on B. Let
$P_4$
on B. Let
![]() $\sigma : C \to B$
be a double cover branched along
$\sigma : C \to B$
be a double cover branched along
![]() $P_1$
, …,
$P_1$
, …,
![]() $P_4$
. By the Hurwitz formula,
$P_4$
. By the Hurwitz formula,
![]() $g(C) = 1$
. Let
$g(C) = 1$
. Let
![]() $Y=X \times _B C$
and
$Y=X \times _B C$
and
be the induced fibration. Thus we have the following commutative diagram:

Since f is relatively of maximal Albanese dimension, so is
![]() $f'$
. As
$f'$
. As
![]() $g(C) = 1$
, Y itself is of maximal Albanese dimension. Since
$g(C) = 1$
, Y itself is of maximal Albanese dimension. Since
![]() $P_1$
, …,
$P_1$
, …,
![]() $P_4$
are general, we deduce that Y is normal. Moreover, we claim that Y has at worst terminal singularities. In fact, let
$P_4$
are general, we deduce that Y is normal. Moreover, we claim that Y has at worst terminal singularities. In fact, let
![]() $\mu : X' \to X$
be a resolution of singularities of X. Then
$\mu : X' \to X$
be a resolution of singularities of X. Then
![]() $X' \times _B C \to Y$
is just a resolution of singularities of Y, and the claim is an easy consequence of the adjunction.
$X' \times _B C \to Y$
is just a resolution of singularities of Y, and the claim is an easy consequence of the adjunction.
Since
![]() $K_{Y/C} = \pi ^*K_{X/B}$
,
$K_{Y/C} = \pi ^*K_{X/B}$
,
![]() $f'$
is also relatively minimal, and we have
$f'$
is also relatively minimal, and we have
We also have
from the above double cover. Thus, from the adjunction formula, we deduce that
 $$ \begin{align} \chi_{f'} & = \chi(Y, \omega_Y) - \chi(C, \omega_C) \chi(F, \omega_F) \nonumber \\ & = \chi(X, \omega_X) + \chi(X, \omega_X \otimes {\mathcal{O}}_X(2F)) \\ & = 2 \chi(X, \omega_X) + 2 \chi(F, \omega_F) \nonumber \\ & = 2 \chi_f. \nonumber \end{align} $$
$$ \begin{align} \chi_{f'} & = \chi(Y, \omega_Y) - \chi(C, \omega_C) \chi(F, \omega_F) \nonumber \\ & = \chi(X, \omega_X) + \chi(X, \omega_X \otimes {\mathcal{O}}_X(2F)) \\ & = 2 \chi(X, \omega_X) + 2 \chi(F, \omega_F) \nonumber \\ & = 2 \chi_f. \nonumber \end{align} $$
Now that
![]() $g(C) = 1> 0$
, we have
$g(C) = 1> 0$
, we have
as in Section 6.2.1. Together with equations (6.7) and (6.8), it implies that
Thus the whole proof of Theorem 1.2 is completed.
Remark 6.1. With this framework, it is easy to see that in order to get inequalities of the same type as equation (1.1) with various slopes, we only need to (up to a base change to the
![]() $g(B)> 0$
case) replace equation (6.5) by a corresponding explicit estimate with the same slope, and the same argument will give rise to the desired results. This is a crucial observation to us.
$g(B)> 0$
case) replace equation (6.5) by a corresponding explicit estimate with the same slope, and the same argument will give rise to the desired results. This is a crucial observation to us.
6.3 Sharper inequalities
As an example of the above remark, we can easily obtain the following result.
Theorem 6.2 Theorem 1.4
Let
![]() $f: X \to B$
be a relatively minimal fibration from a variety X of dimension
$f: X \to B$
be a relatively minimal fibration from a variety X of dimension
![]() $n \ge 3$
to a smooth curve B. Denote by F a general fibre of f. Suppose that f is of maximal Albanese dimension and
$n \ge 3$
to a smooth curve B. Denote by F a general fibre of f. Suppose that f is of maximal Albanese dimension and
![]() $a: X \to {\mathrm {Alb}}(X)$
is the Albanese map of X.
$a: X \to {\mathrm {Alb}}(X)$
is the Albanese map of X.
-
(1) If
 $a|_F$
is birational, then
$a|_F$
is birational, then  $$ \begin{align*} K_{X/B}^n \ge \frac{5n!}{2} \chi_f. \end{align*} $$
$$ \begin{align*} K_{X/B}^n \ge \frac{5n!}{2} \chi_f. \end{align*} $$
-
(2) If
 $a|_F$
is not composed with an involution, then
$a|_F$
is not composed with an involution, then  $$ \begin{align*} K_{X/B}^n \ge \frac{9n!}{4} \chi_f. \end{align*} $$
$$ \begin{align*} K_{X/B}^n \ge \frac{9n!}{4} \chi_f. \end{align*} $$
Proof. Remark 6.1 allows us to assume that
![]() $g> 0$
. In the following, we adopt the notation in Section 6.1.
$g> 0$
. In the following, we adopt the notation in Section 6.1.
To prove (1), note that now
![]() $B \to J(B)$
is an embedding. It implies that a separates any two distinct fibres of f. In particular, a is birational. Thus for every sufficiently large prime number
$B \to J(B)$
is an embedding. It implies that a separates any two distinct fibres of f. In particular, a is birational. Thus for every sufficiently large prime number
![]() $m> 0$
,
$m> 0$
,
![]() $b_m$
is birational. So is
$b_m$
is birational. So is
![]() $b_m|_{F^{\prime }_m}$
. Then we simply replace the estimate equation (6.5) in the proof of Theorem 1.2 by the inequality in Proposition 5.3 (1) for
$b_m|_{F^{\prime }_m}$
. Then we simply replace the estimate equation (6.5) in the proof of Theorem 1.2 by the inequality in Proposition 5.3 (1) for
![]() $f^{\prime }_m$
and
$f^{\prime }_m$
and
![]() $L_m$
, and the conclusion will follow by letting
$L_m$
, and the conclusion will follow by letting
![]() $m \to \infty $
.
$m \to \infty $
.
The proof of (2) is similar. In this case, we know that
![]() $b|_{F'}$
is not composed with an involution. Let
$b|_{F'}$
is not composed with an involution. Let
![]() $d = \deg a|_F = \deg b|_{F'}$
. By the following Lemma 6.3,
$d = \deg a|_F = \deg b|_{F'}$
. By the following Lemma 6.3,
![]() $b_m|_{F^{\prime }_m}$
is not composed with an involution as long as
$b_m|_{F^{\prime }_m}$
is not composed with an involution as long as
![]() $m> d$
. Thus the conclusion will follow similarly by letting
$m> d$
. Thus the conclusion will follow similarly by letting
![]() $m \to \infty $
.
$m \to \infty $
.
Lemma 6.3. Let
![]() $\alpha : V \to W$
be a generically finite morphism between two varieties of degree
$\alpha : V \to W$
be a generically finite morphism between two varieties of degree
![]() $d> 0$
such that
$d> 0$
such that
![]() $\alpha $
is not composed with an involution. Let
$\alpha $
is not composed with an involution. Let
![]() $p> d$
be any prime number. Let
$p> d$
be any prime number. Let
![]() $W_p \to W$
be a Galois cover with
$W_p \to W$
be a Galois cover with
![]() $G = \mathrm {Gal}(W_p/W)$
a p-group. Let
$G = \mathrm {Gal}(W_p/W)$
a p-group. Let
![]() $V_p: = V \times _W W_p$
, and let
$V_p: = V \times _W W_p$
, and let
![]() $\alpha _p: V_p \to W_p$
be the induced morphism. Then
$\alpha _p: V_p \to W_p$
be the induced morphism. Then
![]() $\alpha _p$
is not composed with an involution.
$\alpha _p$
is not composed with an involution.
Proof. By our assumption,
![]() $K(V) \simeq \frac {K(W)(t)}{(f(t))}$
, where
$K(V) \simeq \frac {K(W)(t)}{(f(t))}$
, where
![]() $f(t)$
is an irreducible polynomial of degree d with coefficients in
$f(t)$
is an irreducible polynomial of degree d with coefficients in
![]() $K(W)$
. Using Galois theory, we can find a variety U and a generically finite map
$K(W)$
. Using Galois theory, we can find a variety U and a generically finite map
![]() $\beta : U \to V$
such that
$\beta : U \to V$
such that
![]() $K(U)$
is the splitting field of
$K(U)$
is the splitting field of
![]() $f(t)$
. Thus
$f(t)$
. Thus
![]() $K(U)/K(W)$
is a Galois extension. Write
$K(U)/K(W)$
is a Galois extension. Write
Then H is a subgroup of
![]() $S_d$
. In particular,
$S_d$
. In particular,
![]() $|H|$
divides
$|H|$
divides
![]() $d!$
. Since
$d!$
. Since
![]() $p> d$
and G is a p-group, we have
$p> d$
and G is a p-group, we have
![]() $(|G|, |H|) = 1$
.
$(|G|, |H|) = 1$
.
Let
![]() $U_p = U \times _V V_p$
. We claim that
$U_p = U \times _V V_p$
. We claim that
![]() $U_p$
is irreducible. Otherwise, let
$U_p$
is irreducible. Otherwise, let
![]() $U^{\prime }_p$
be an irreducible component of
$U^{\prime }_p$
be an irreducible component of
![]() $U_p$
. Now the morphism
$U_p$
. Now the morphism
![]() $U^{\prime }_p \to W$
has two factorisations
$U^{\prime }_p \to W$
has two factorisations
![]() $U^{\prime }_p \to U \to W$
and
$U^{\prime }_p \to U \to W$
and
![]() $U^{\prime }_p \to W_p \to W$
. Thus both
$U^{\prime }_p \to W_p \to W$
. Thus both
![]() $|H|$
and
$|H|$
and
![]() $|G|$
divide
$|G|$
divide
![]() $[K(U^{\prime }_p) : K(W)]$
. Since
$[K(U^{\prime }_p) : K(W)]$
. Since
![]() $(|G|, |H|) = 1$
, we have
$(|G|, |H|) = 1$
, we have
On the other hand, since the degree of the map
![]() $U^{\prime }_p \to V_p$
is strictly less than
$U^{\prime }_p \to V_p$
is strictly less than
![]() $\deg \beta $
, we have
$\deg \beta $
, we have
This is a contradiction. As a result,
![]() $U_p$
is irreducible. In particular, the natural morphism
$U_p$
is irreducible. In particular, the natural morphism
![]() $U_p \to U$
is also a Galois cover and
$U_p \to U$
is also a Galois cover and
We claim that the extension
![]() $K(U_p)/K(W)$
is also Galois. Write
$K(U_p)/K(W)$
is also Galois. Write
It is clear that
On the other hand, since
![]() $H = {\mathrm {Gal}}(K(U_p)/K(W_p))$
, we may view both G and H as subgroups of
$H = {\mathrm {Gal}}(K(U_p)/K(W_p))$
, we may view both G and H as subgroups of
![]() $G_p$
. Since
$G_p$
. Since
![]() $(|G|, |H|) = 1$
, we deduce that
$(|G|, |H|) = 1$
, we deduce that
Therefore,
![]() $|G_p| = |G| |H|$
, and the claim is verified. As a consequence of this claim, G is a normal subgroup in
$|G_p| = |G| |H|$
, and the claim is verified. As a consequence of this claim, G is a normal subgroup in
![]() $G_p$
.
$G_p$
.
Now suppose that
![]() $\alpha _p$
is composed with an involution. This means there exists a variety
$\alpha _p$
is composed with an involution. This means there exists a variety
![]() $V^{\prime }_p$
such that
$V^{\prime }_p$
such that
![]() $K(V_p) \supset K(V^{\prime }_p) \supseteq K(W_p)$
and
$K(V_p) \supset K(V^{\prime }_p) \supseteq K(W_p)$
and
Write
![]() $H_1={\mathrm {Aut}}(K(U_p)/K(V_p))$
and
$H_1={\mathrm {Aut}}(K(U_p)/K(V_p))$
and
![]() $H^{\prime }_1={\mathrm {Aut}}(K(U_p)/K(V^{\prime }_p))$
. Then the fundamental theorem of Galois theory tells us that
$H^{\prime }_1={\mathrm {Aut}}(K(U_p)/K(V^{\prime }_p))$
. Then the fundamental theorem of Galois theory tells us that
![]() $H_1 \subset H^{\prime }_1$
are both subgroups of
$H_1 \subset H^{\prime }_1$
are both subgroups of
![]() $G_p$
and
$G_p$
and
Since G is normal, we consider another two subgroups
![]() $H_1G \subset H^{\prime }_1G$
of
$H_1G \subset H^{\prime }_1G$
of
![]() $G_p$
. Then we still have
$G_p$
. Then we still have
Note that
![]() $K(U_p)^{H_1G} = K(V)$
. Again by the fundamental theorem of Galois theory,
$K(U_p)^{H_1G} = K(V)$
. Again by the fundamental theorem of Galois theory,
![]() $K(U_p)^{H^{\prime }_1G}$
is a subfield of
$K(U_p)^{H^{\prime }_1G}$
is a subfield of
![]() $K(V)$
and
$K(V)$
and
This implies that
![]() $\alpha $
is composed with an involution. However, this is absurd. Thus the proof is completed.
$\alpha $
is composed with an involution. However, this is absurd. Thus the proof is completed.
Remark 6.4. After we finished the first version of the paper, Barja informed us of the result [Reference Barja, Pardini and Stoppino6, Lemma 2.9], which states that if one further assumes that V is of general type, then
![]() ${\mathrm {Gal}}(\alpha _p) = {\mathrm {Gal}}(\alpha )$
for any prime number p larger than a certain nonexplicit constant, depending on the volume and the dimension of V.
${\mathrm {Gal}}(\alpha _p) = {\mathrm {Gal}}(\alpha )$
for any prime number p larger than a certain nonexplicit constant, depending on the volume and the dimension of V.
6.4 An example
We provide an example showing that equation (1.1) is sharp.
Let
![]() $Y:=B \times A$
be a product of a smooth curve B of genus g and an abelian variety A of dimension
$Y:=B \times A$
be a product of a smooth curve B of genus g and an abelian variety A of dimension
![]() $n-1$
, with two natural projections
$n-1$
, with two natural projections
![]() $p_1: Y \to B$
and
$p_1: Y \to B$
and
![]() $p_2: Y \to A$
. Take two sufficiently ample divisors
$p_2: Y \to A$
. Take two sufficiently ample divisors
![]() $L_1$
on B and
$L_1$
on B and
![]() $L_2$
on A, respectively. Denote
$L_2$
on A, respectively. Denote
![]() $L = p_1^*L_1 + p_2^*L_2$
. Choose a smooth divisor
$L = p_1^*L_1 + p_2^*L_2$
. Choose a smooth divisor
![]() $D \in |2L|$
on Y. Let
$D \in |2L|$
on Y. Let
![]() $\pi : X \to Y$
be a double cover branched along D. It is easy to see that
$\pi : X \to Y$
be a double cover branched along D. It is easy to see that
is a relatively minimal fibration whose general fibre F is a double cover of A branched along
![]() $L_2$
and thus is of general type. Moreover, f is relatively minimal of maximal Albanese dimension.
$L_2$
and thus is of general type. Moreover, f is relatively minimal of maximal Albanese dimension.
Since
![]() $K_{X/B} \sim \pi ^*L$
, we have
$K_{X/B} \sim \pi ^*L$
, we have
On the other hand, since
and
by the Künneth formula, we have
 $$ \begin{align*} \chi(X, \omega_X) & = \chi(Y, {\mathcal{O}}_Y(p_1^*K_B)) + \chi(Y, {\mathcal{O}}_Y(L + p_1^*K_B)) \\ & = \chi(B, \omega_B) \chi(A, {\mathcal{O}}_A) + \chi(B, {\mathcal{O}}_B(L_1+K_B)) \chi(A, {\mathcal{O}}_A(L_2)) \\ & = \chi(B, {\mathcal{O}}_B(L_1+K_B)) \chi(A, {\mathcal{O}}_A(L_2)), \end{align*} $$
$$ \begin{align*} \chi(X, \omega_X) & = \chi(Y, {\mathcal{O}}_Y(p_1^*K_B)) + \chi(Y, {\mathcal{O}}_Y(L + p_1^*K_B)) \\ & = \chi(B, \omega_B) \chi(A, {\mathcal{O}}_A) + \chi(B, {\mathcal{O}}_B(L_1+K_B)) \chi(A, {\mathcal{O}}_A(L_2)) \\ & = \chi(B, {\mathcal{O}}_B(L_1+K_B)) \chi(A, {\mathcal{O}}_A(L_2)), \end{align*} $$
and
It follows that
 $$ \begin{align*}\chi_f = \chi(A, {\mathcal{O}}_A(L_2)) \left( \chi(B, {\mathcal{O}}_B(L_1+K_B)) - \chi(B, \omega_B) \right) = \frac{L_2^{n-1}}{(n-1)!} \deg L_1. \end{align*} $$
$$ \begin{align*}\chi_f = \chi(A, {\mathcal{O}}_A(L_2)) \left( \chi(B, {\mathcal{O}}_B(L_1+K_B)) - \chi(B, \omega_B) \right) = \frac{L_2^{n-1}}{(n-1)!} \deg L_1. \end{align*} $$
Thus for this fibration f, we have
![]() $K_{X/B}^n = 2n! \chi _f> 0$
.
$K_{X/B}^n = 2n! \chi _f> 0$
.
6.5 Proof of Theorem 1.3
Since the result is either known or trivial when
![]() $n = 2$
, in the following, we assume that
$n = 2$
, in the following, we assume that
![]() $n \ge 3$
and
$n \ge 3$
and
We first prove Theorem 1.3 (1). Via a base change argument as in Section 6.2.2, we may assume that
![]() $g(B)> 0$
. Thus we are under the setting of Section 6.1. Moreover, by Theorem 1.4, we know that
$g(B)> 0$
. Thus we are under the setting of Section 6.1. Moreover, by Theorem 1.4, we know that
![]() $a|_F$
is composed with an involution.
$a|_F$
is composed with an involution.
Resume all notation in Section 6.1. Write
![]() $\Sigma = a(F)$
. Then
$\Sigma = a(F)$
. Then
![]() $\Sigma $
is a subvariety of an abelian variety
$\Sigma $
is a subvariety of an abelian variety
![]() $A_F$
, a general fibre of
$A_F$
, a general fibre of
![]() $A \to J(B)$
of dimension
$A \to J(B)$
of dimension
![]() $q - g(B)$
, and
$q - g(B)$
, and
![]() $\Sigma $
generates
$\Sigma $
generates
![]() $A_F$
. To show that
$A_F$
. To show that
![]() $\Sigma = A_F$
, we only need to show that the smooth model of
$\Sigma = A_F$
, we only need to show that the smooth model of
![]() $\Sigma $
has Kodaira dimension zero.
$\Sigma $
has Kodaira dimension zero.
Let
![]() $\sigma : \Sigma ' \to \Sigma $
be a resolution of singularities of
$\sigma : \Sigma ' \to \Sigma $
be a resolution of singularities of
![]() $\Sigma $
. Let
$\Sigma $
. Let
![]() $\Sigma _m = a_m(F_m)$
and
$\Sigma _m = a_m(F_m)$
and
![]() $\Sigma ^{\prime }_m = \Sigma _m \times _{\sigma } \Sigma '$
. Then
$\Sigma ^{\prime }_m = \Sigma _m \times _{\sigma } \Sigma '$
. Then
![]() $\sigma _m: \Sigma ^{\prime }_m \to \Sigma _m$
is also a resolution of singularities of
$\sigma _m: \Sigma ^{\prime }_m \to \Sigma _m$
is also a resolution of singularities of
![]() $\Sigma _m$
. Let
$\Sigma _m$
. Let
![]() $\nu _m: \Sigma ^{\prime }_m \to \Sigma '$
be the induced étale map. Thus we have the following diagram:
$\nu _m: \Sigma ^{\prime }_m \to \Sigma '$
be the induced étale map. Thus we have the following diagram:

Denote
With this notation, by equation (6.1), we have
 $$ \begin{align*}r':= \frac{(L|_{F'}) \left((b^*H)|_{F'} \right)^{n-2}}{K_{\Sigma'} \left( \sigma^*(H|_\Sigma) \right)^{n-2}} = \frac{(L_m|_{F^{\prime}_m}) \left((b_m^*H)|_{F^{\prime}_m} \right)^{n-2}}{K_{\Sigma^{\prime}_m} \left(\sigma_m^*(H|_{\Sigma_m})\right)^{n-2}} =: r^{\prime}_m. \end{align*} $$
$$ \begin{align*}r':= \frac{(L|_{F'}) \left((b^*H)|_{F'} \right)^{n-2}}{K_{\Sigma'} \left( \sigma^*(H|_\Sigma) \right)^{n-2}} = \frac{(L_m|_{F^{\prime}_m}) \left((b_m^*H)|_{F^{\prime}_m} \right)^{n-2}}{K_{\Sigma^{\prime}_m} \left(\sigma_m^*(H|_{\Sigma_m})\right)^{n-2}} =: r^{\prime}_m. \end{align*} $$
It simply implies that
Now we use the framework of the proof of Theorem 1.2 again and replace equation (6.5) by the one in Proposition 5.3 (3). Together with the above equality, we deduce that
However, if
![]() $\kappa (\Sigma ')> 0$
, we would have
$\kappa (\Sigma ')> 0$
, we would have
![]() $\delta (r')> 1$
and thus
$\delta (r')> 1$
and thus
![]() $\frac {5\delta (r') - 3}{2 \delta (r') - 1}> 2$
. This is a contradiction. As a result,
$\frac {5\delta (r') - 3}{2 \delta (r') - 1}> 2$
. This is a contradiction. As a result,
![]() $\kappa (\Sigma ') = 0$
and
$\kappa (\Sigma ') = 0$
and
![]() $\Sigma = A_F$
.
$\Sigma = A_F$
.
Now we prove Theorem 1.3 (2). Note that
![]() $K_{X/B}^n> 0$
implies that
$K_{X/B}^n> 0$
implies that
![]() $K_{X/B}$
is also big. In particular, a general fibre F of f is a minimal variety of general type. By [Reference Kawamata, Matsuda and Matsuki14, Theorem 1-2-5], we have
$K_{X/B}$
is also big. In particular, a general fibre F of f is a minimal variety of general type. By [Reference Kawamata, Matsuda and Matsuki14, Theorem 1-2-5], we have
for any
![]() $i>0$
and
$i>0$
and
![]() $l \ge 2$
. Thus for any
$l \ge 2$
. Thus for any
![]() $l \ge 2$
, we have
$l \ge 2$
, we have
Let
![]() $P_l(F)$
denote the
$P_l(F)$
denote the
![]() $l^{\mathrm {th}}$
plurigenus of F. Then we have
$l^{\mathrm {th}}$
plurigenus of F. Then we have
 $$ \begin{align*} \deg f_*\omega_{X/B}^{[l]} & = \chi(B, f_*\omega_{X/B}^{[l]}) - P_l(F) \chi(B, {\mathcal{O}}_B) \\ & = \chi(X, \omega_{X/B}^{[l]}) - P_l(F) \chi(B, {\mathcal{O}}_B) \\ & = \frac{l^n K_{X/B}^n}{n!} + o(l^n). \end{align*} $$
$$ \begin{align*} \deg f_*\omega_{X/B}^{[l]} & = \chi(B, f_*\omega_{X/B}^{[l]}) - P_l(F) \chi(B, {\mathcal{O}}_B) \\ & = \chi(X, \omega_{X/B}^{[l]}) - P_l(F) \chi(B, {\mathcal{O}}_B) \\ & = \frac{l^n K_{X/B}^n}{n!} + o(l^n). \end{align*} $$
In particular, for
![]() $l \gg 0$
,
$l \gg 0$
,
![]() $\det f_*\omega _{X/B}^{[l]}$
is an ample line bundle on B. By [Reference Viehweg22, Proposition 4.6], we know that for
$\det f_*\omega _{X/B}^{[l]}$
is an ample line bundle on B. By [Reference Viehweg22, Proposition 4.6], we know that for
![]() $l \gg 0$
, the vector bundle
$l \gg 0$
, the vector bundle
![]() $f_*\omega _{X/B}^{[l]}$
is ample. Thus, by [Reference Ohno19, Theorem 1.4],
$f_*\omega _{X/B}^{[l]}$
is ample. Thus, by [Reference Ohno19, Theorem 1.4],
![]() $mK_{X/B} - F$
is nef for a sufficiently large
$mK_{X/B} - F$
is nef for a sufficiently large
![]() $m \in {\mathbb {Z}}$
. Replacing B by one of its cyclic covers of degree m, which is either étale (if
$m \in {\mathbb {Z}}$
. Replacing B by one of its cyclic covers of degree m, which is either étale (if
![]() $g(B)> 0$
) or ramified at general points (if
$g(B)> 0$
) or ramified at general points (if
![]() $g(B) = 0$
), and replacing
$g(B) = 0$
), and replacing
![]() $f: X \to B$
by the fibration induced by this base change, we may assume that
$f: X \to B$
by the fibration induced by this base change, we may assume that
![]() $K_{X/B} - F$
is nef. Similar to Section 6.2.2, we know that this induced fibration is also relatively minimal and of maximal Albanese dimension. Moreover, we still have
$K_{X/B} - F$
is nef. Similar to Section 6.2.2, we know that this induced fibration is also relatively minimal and of maximal Albanese dimension. Moreover, we still have
for this new fibration f.
Using the same strategy as in the proof of Theorem 1.2, but replacing
![]() $K_{X/B}$
by
$K_{X/B}$
by
![]() $K_{X/B}-F$
, we deduce that
$K_{X/B}-F$
, we deduce that
where
![]() ${\mathcal {P}}\in {\mathrm {Pic}}^0(X)$
is a general torsion element. That is,
${\mathcal {P}}\in {\mathrm {Pic}}^0(X)$
is a general torsion element. That is,
By the assumption that
![]() $K_{X/B}^n = 2n! \chi _f$
, we have
$K_{X/B}^n = 2n! \chi _f$
, we have
Since F is minimal of maximal Albanese dimension, together with the absolute Severi inequality for F, we deduce that
Thus the proof is completed.
Acknowledgements
Y.H. would like to thank Professors JongHae Keum and Jun-Muk Hwang for their generous support during his stay at KIAS. T.Z. would like to thank Professor Miguel Á. Barja for the comment on his conjectural inequality in equation (1.1) in an email in 2017 and many more valuable comments on the first version of this paper, as well as Professor Kang Zuo for many enlightening comments about Viehweg’s result in [Reference Viehweg22], which is crucial for proving Theorem 1.3. T.Z. also would like to thank Professors Zhi Jiang and Lidia Stoppino for their interest in this paper. Both authors would like to sincerely thank the anonymous referee for their comments and suggestions.
Conflicts of Interest
None.
Funding statement
Y. H. was supported by National Researcher Program of National Research Foundation of Korea (Grant No. 2010-0020413) and the Shanghai Pujiang Program Grant No. 21PJ1405200. T.Z. was supported by the National Natural Science Foundation of China (NSFC) General Grant No. 12071139 and the Science and Technology Commission of Shanghai Municipality (Grant No. 18dz2271000).