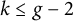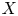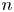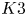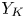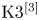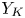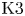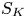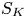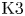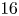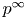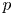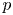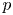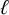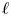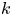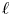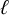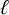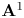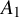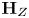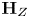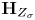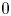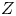Refine search
Actions for selected content:
76 results
On the rationality problem for low degree hypersurfaces
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 22 December 2025, e25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Abelian varieties with no power isogenous to a Jacobian
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 6 / June 2025
- Published online by Cambridge University Press:
- 30 October 2025, pp. 1404-1457
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Non-torsion algebraic cycles on the Jacobians of Fermat quotients
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 22 November 2024, pp. 60-72
- Print publication:
- March 2025
-
- Article
- Export citation
Rational Hodge isometries of hyper-Kähler varieties of
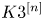 $K3^{[n]}$ type are algebraic
$K3^{[n]}$ type are algebraic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 07 May 2024, pp. 1261-1303
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sixfolds of generalized Kummer type and K3 surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 05 January 2024, pp. 388-410
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Boundedness of the p-primary torsion of the Brauer group of an abelian variety
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 05 January 2024, pp. 463-480
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On Bloch’s map for torsion cycles over non-closed fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 22 June 2023, e53
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Refined unramified cohomology of schemes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 7 / July 2023
- Published online by Cambridge University Press:
- 15 June 2023, pp. 1466-1530
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Integral Fourier transforms and the integral Hodge conjecture for one-cycles on abelian varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 15 May 2023, pp. 1188-1213
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Noninjectivity of the cycle class map in continuous
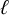 $\ell $-adic cohomology
$\ell $-adic cohomology
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 01 February 2023, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Reciprocity sheaves and logarithmic motives
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 13 February 2023, pp. 355-379
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the cohomology of reciprocity sheaves
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 30 August 2022, e72
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Deligne-Beilinson cohomology of the universal K3 surface
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 15 August 2022, e64
-
- Article
- Export citation
The complexity of higher Chow groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 29 July 2022, pp. 903-911
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Torsion codimension
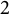 $2$ cycles on supersingular abelian varieties
$2$ cycles on supersingular abelian varieties
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 23 June 2022, pp. 458-466
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Absolute Hodge and ℓ-adic monodromy
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 13 May 2022, pp. 568-584
- Print publication:
- March 2022
-
- Article
- Export citation
ZERO-CYCLES ON NORMAL PROJECTIVE VARIETIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 11 February 2022, pp. 2241-2295
- Print publication:
- September 2023
-
- Article
- Export citation
Torsion properties of modified diagonal classes on triple products of modular curves
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 31 January 2022, pp. 68-86
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE CHOW THEORY OF PROJECTIVIZATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 11 November 2021, pp. 1465-1508
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebraic cycles and Lehn–Lehn–Sorger–van Straten eightfolds
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 04 October 2021, pp. 884-907
-
- Article
- Export citation