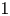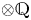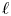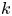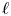1. Introduction
Unramified cohomology of a smooth variety may be defined as the subgroup of the cohomology of the generic point given by all classes that have trivial residues at all codimension-one points, see [Reference Bloch and OgusBO74] and [Reference Colliot-ThélèneCol95, 4.1.1(a)]. Bloch and Ogus [Reference Bloch and OgusBO74] showed that unramified cohomology in degree three is related to the Griffiths group of codimension-two cycles. Colliot-Thélène and Voisin [Reference Colliot-Thélène and VoisinCV12] computed the failure of the integral Hodge conjecture for codimension-two cycles on smooth complex projective varieties in terms of unramified cohomology in degree three; a similar statement holds for the integral Tate conjecture by Kahn [Reference KahnKah12]. A relation between torsion codimension-three cycles with unramified cohomology in degree four is due to Voisin [Reference VoisinVoi12] and Ma [Reference MaMa17].
The results in [Reference Colliot-Thélène and VoisinCV12, Reference KahnKah12, Reference VoisinVoi12, Reference MaMa17] use two main ingredients: the Gersten conjecture proven by Bloch and Ogus [Reference Bloch and OgusBO74], which identifies unramified cohomology of smooth varieties with the global sections of a certain Zariski sheaf, and the Bloch–Kato conjecture, proven in [Reference Merkurjev and SuslinMS83, Reference VoevodskyVoe11].
This paper arose from the observation that the aforementioned results from [Reference Colliot-Thélène and VoisinCV12, Reference KahnKah12] have more elementary proofs, not relying on the Gersten conjecture, nor on the Bloch–Kato conjecture, see § 3 for more details. This leads us to the notion of refined unramified cohomology, which generalizes unramified cohomology. Our arguments work for cycles of arbitrary codimensions, over arbitrary fields, and even on singular schemes, see Theorems 1.6 and 1.8.
Our main results on algebraic torsion cycles that we explain next combine the machinery of refined unramified cohomology with the Bloch–Kato conjecture [Reference VoevodskyVoe11].
1.1 Torsion cycles and Abel–Jacobi invariants
A cycle ![]() $z\in \operatorname {CH}^i(X\!)$ on a complex variety
$z\in \operatorname {CH}^i(X\!)$ on a complex variety ![]() $X$ has coniveau
$X$ has coniveau ![]() $j$, i.e.
$j$, i.e. ![]() $z\in N^j\operatorname {CH}^i(X\!)$, if
$z\in N^j\operatorname {CH}^i(X\!)$, if ![]() $z$ is homologically trivial on a closed subset of codimension
$z$ is homologically trivial on a closed subset of codimension ![]() $j$. That is,
$j$. That is, ![]() $z\in N^j$ if
$z\in N^j$ if ![]() $z=\partial \gamma$ is the boundary of a locally finite singular chain
$z=\partial \gamma$ is the boundary of a locally finite singular chain ![]() $\gamma$ whose support is contained in a closed algebraic subset of codimension
$\gamma$ whose support is contained in a closed algebraic subset of codimension ![]() $j$ in
$j$ in ![]() $X$. This yields a finite descending filtration with
$X$. This yields a finite descending filtration with ![]() $N^0=\operatorname {CH}^i(X\!)_{\hom }$ and
$N^0=\operatorname {CH}^i(X\!)_{\hom }$ and ![]() $N^{i-1}=\operatorname {CH}^i(X\!)_{\operatorname {alg}}$, the subgroups of homologically and algebraically trivial cycles, respectively, cf. [Reference BlochBlo85] and [Reference TotaroTot97, p. 491, Remark 2].
$N^{i-1}=\operatorname {CH}^i(X\!)_{\operatorname {alg}}$, the subgroups of homologically and algebraically trivial cycles, respectively, cf. [Reference BlochBlo85] and [Reference TotaroTot97, p. 491, Remark 2].
Jannsen showed that on smooth complex projective varieties, ![]() $N_j\operatorname {CH}^i(X\!):=N^{i-j}\operatorname {CH}^i(X\!)$ is a filtration by adequate equivalence relations, see [Reference JannsenJan00, Theorem 5.6] (stated
$N_j\operatorname {CH}^i(X\!):=N^{i-j}\operatorname {CH}^i(X\!)$ is a filtration by adequate equivalence relations, see [Reference JannsenJan00, Theorem 5.6] (stated ![]() $\otimes \mathbb {Q}$, but the same arguments work integrally). In particular,
$\otimes \mathbb {Q}$, but the same arguments work integrally). In particular, ![]() $N^\ast$ interpolates naturally between algebraic and homological equivalence, respectively, and it is multiplicative in a strong sense:
$N^\ast$ interpolates naturally between algebraic and homological equivalence, respectively, and it is multiplicative in a strong sense: ![]() $N^j\operatorname {CH}^i(X\!)\cdot \operatorname {CH}^h(X\!)\subset N^{j+h}\operatorname {CH}^{i+h}(X\!)$.
$N^j\operatorname {CH}^i(X\!)\cdot \operatorname {CH}^h(X\!)\subset N^{j+h}\operatorname {CH}^{i+h}(X\!)$.
Theorem 1.1 Let ![]() $X$ be a smooth projective variety over
$X$ be a smooth projective variety over ![]() $\mathbb {C}$ and let
$\mathbb {C}$ and let ![]() $i\geqslant 2$. A homologically trivial torsion cycle
$i\geqslant 2$. A homologically trivial torsion cycle ![]() $z\in \operatorname {CH}^i(X\!)_{\operatorname {tors}}$ has coniveau 1 if and only if Griffiths’ Abel–Jacobi invariant
$z\in \operatorname {CH}^i(X\!)_{\operatorname {tors}}$ has coniveau 1 if and only if Griffiths’ Abel–Jacobi invariant ![]() $\lambda (z)\in H^{2i-1}(X,\mathbb {Q}/\mathbb {Z})$ admits a lift to
$\lambda (z)\in H^{2i-1}(X,\mathbb {Q}/\mathbb {Z})$ admits a lift to ![]() $N^1H^{2i-1}(X,\mathbb {Q})$.
$N^1H^{2i-1}(X,\mathbb {Q})$.
This theorem uses the fact that the torsion subgroup of Griffiths’ intermediate Jacobian ![]() $J^{2i-1}(X\!)$ identifies canonically to the image of
$J^{2i-1}(X\!)$ identifies canonically to the image of ![]() $H^{2i-1}(X,\mathbb {Q})$ in
$H^{2i-1}(X,\mathbb {Q})$ in ![]() $H^{2i-1}(X,\mathbb {Q}/\mathbb {Z})$, cf. [Reference BlochBlo79, p. 116]. The subgroup
$H^{2i-1}(X,\mathbb {Q}/\mathbb {Z})$, cf. [Reference BlochBlo79, p. 116]. The subgroup ![]() $N^1H^{2i-1}(X,\mathbb {Q})\subset H^{2i-1}(X,\mathbb {Q})$ consists of those classes that vanish away from a divisor.
$N^1H^{2i-1}(X,\mathbb {Q})\subset H^{2i-1}(X,\mathbb {Q})$ consists of those classes that vanish away from a divisor.
The case ![]() $i=2$ may be deduced from [Reference Merkurjev and SuslinMS83, § 18]; the case
$i=2$ may be deduced from [Reference Merkurjev and SuslinMS83, § 18]; the case ![]() $i\geqslant 3$ is new. Torsion cycles to which the theorem applies are constructed, e.g., in [Reference TotaroTot97, Reference Soulé and VoisinSV05, Reference SchreiederSch20].
$i\geqslant 3$ is new. Torsion cycles to which the theorem applies are constructed, e.g., in [Reference TotaroTot97, Reference Soulé and VoisinSV05, Reference SchreiederSch20].
Corollary 1.2 Let ![]() $X$ be a smooth projective variety over
$X$ be a smooth projective variety over ![]() $\mathbb {C}$. Then for any positive integer
$\mathbb {C}$. Then for any positive integer ![]() $n$, the
$n$, the ![]() $n$-torsion subgroup of
$n$-torsion subgroup of ![]() $\operatorname {CH}^i(X\!)_{\operatorname {tors}}/N^1\operatorname {CH}^i(X\!)_{\operatorname {tors}}$ is finite.
$\operatorname {CH}^i(X\!)_{\operatorname {tors}}/N^1\operatorname {CH}^i(X\!)_{\operatorname {tors}}$ is finite.
We illustrate the above corollary in the case of cycles of codimension three. In this case the coniveau filtration is of the form ![]() $N^2\subset N^1\subset N^0\subset \operatorname {CH}^3(X\!)$. The above corollary shows that the
$N^2\subset N^1\subset N^0\subset \operatorname {CH}^3(X\!)$. The above corollary shows that the ![]() $n$-torsion in
$n$-torsion in ![]() $\operatorname {CH}^3(X\!)$ is finite modulo
$\operatorname {CH}^3(X\!)$ is finite modulo ![]() $N^1$. In contrast, it is shown in [Reference SchoenSch00, Reference Rosenschon and SrinivasRS10, Reference TotaroTot16] that the
$N^1$. In contrast, it is shown in [Reference SchoenSch00, Reference Rosenschon and SrinivasRS10, Reference TotaroTot16] that the ![]() $n$-torsion in
$n$-torsion in ![]() $N^2\operatorname {CH}^3(X\!)$ can be infinite (the torsion classes constructed there are all algebraically trivial, hence contained in
$N^2\operatorname {CH}^3(X\!)$ can be infinite (the torsion classes constructed there are all algebraically trivial, hence contained in ![]() $N^2$). Similarly, using the theory developed in this paper, we show in [Reference SchreiederSch20] that at least for
$N^2$). Similarly, using the theory developed in this paper, we show in [Reference SchreiederSch20] that at least for ![]() $n$ even, the
$n$ even, the ![]() $n$-torsion in
$n$-torsion in ![]() $\operatorname {CH}^3(X\!)_{\operatorname {tors}}/N^2$ is in general infinite. It follows that
$\operatorname {CH}^3(X\!)_{\operatorname {tors}}/N^2$ is in general infinite. It follows that ![]() $\operatorname {CH}^3(X\!)_{\operatorname {tors}}/N^0$ and
$\operatorname {CH}^3(X\!)_{\operatorname {tors}}/N^0$ and ![]() $N^0\operatorname {CH}^3(X\!)_{\operatorname {tors}}/N^1$ are the only graded pieces of
$N^0\operatorname {CH}^3(X\!)_{\operatorname {tors}}/N^1$ are the only graded pieces of ![]() $\operatorname {CH}^3(X\!)_{\operatorname {tors}}$ whose torsion is always finite. In this sense, Corollary 1.2 is optimal for
$\operatorname {CH}^3(X\!)_{\operatorname {tors}}$ whose torsion is always finite. In this sense, Corollary 1.2 is optimal for ![]() $i=3$. We also note that
$i=3$. We also note that ![]() $\operatorname {CH}^i(X\!)/N^1\operatorname {CH}^i(X\!)$ is for
$\operatorname {CH}^i(X\!)/N^1\operatorname {CH}^i(X\!)$ is for ![]() $i=2$ in general not a finitely generated group, see [Reference ClemensCle83, Reference VoisinVoi00] (it is conceivable that the same holds all
$i=2$ in general not a finitely generated group, see [Reference ClemensCle83, Reference VoisinVoi00] (it is conceivable that the same holds all ![]() $i\geqslant 2$).
$i\geqslant 2$).
Another immediate consequence of Theorem 1.1 is as follows.
Corollary 1.3 Let ![]() $X$ be a smooth projective variety over
$X$ be a smooth projective variety over ![]() $\mathbb {C}$. A homologically trivial torsion cycle
$\mathbb {C}$. A homologically trivial torsion cycle ![]() $z\in \operatorname {CH}^i(X\!)_{\operatorname {tors}}$ with trivial Abel–Jacobi invariant has coniveau 1.
$z\in \operatorname {CH}^i(X\!)_{\operatorname {tors}}$ with trivial Abel–Jacobi invariant has coniveau 1.
Corollary 1.3 proves a torsion analogue of a conjecture of Jannsen (going back to a question of Esnault) who writes in [Reference JannsenJan00, p. 227, (5)] that ‘cycles in the kernel of the Abel–Jacobi map should be homologous to zero on a divisor, at least modulo torsion’. Jannsen showed that his conjecture follows from deep motivic conjectures: the existence of a Bloch–Beilinson filtration ![]() $F^\ast$ (see, e.g., [Reference JannsenJan00, § 2.1]) together with the standard conjecture B imply
$F^\ast$ (see, e.g., [Reference JannsenJan00, § 2.1]) together with the standard conjecture B imply ![]() $F^{j}\subset N^{j-1}$ at least rationally, see [Reference JannsenJan00, p. 226, (4)]. Jannsen's conjecture generalizes a conjecture of Nori [Reference NoriNor93], which predicts that the transcendental Abel–Jacobi map on codimension-two cycles modulo algebraic equivalence is injective, see [Reference TotaroTot97, p. 468].
$F^{j}\subset N^{j-1}$ at least rationally, see [Reference JannsenJan00, p. 226, (4)]. Jannsen's conjecture generalizes a conjecture of Nori [Reference NoriNor93], which predicts that the transcendental Abel–Jacobi map on codimension-two cycles modulo algebraic equivalence is injective, see [Reference TotaroTot97, p. 468].
Nowadays, essentially all deep conjectures in the theory of algebraic cycles on smooth complex projective varieties are formulated rationally. For instance, Hodge originally formulated his famous conjecture integrally, but when Atiyah and Hirzebruch showed that it fails for torsion cycles [Reference Atiyah and HirzebruchAH62], it became clear that one should phrase it rationally. Nonetheless, investigating instances where the Hodge conjecture may hold integrally remained an active field of research, see, e.g., [Reference VoisinVoi06, Reference Colliot-Thélène and VoisinCV12, Reference Benoist and WittenbergBW20, Reference PerryPer22]. Similarly, it is natural to investigate to which extent other cycle conjectures may hold integrally, or on torsion cycles, see, e.g., [Reference TotaroTot97, § 8]. In view of the many torsion counterexamples to the integral Hodge conjecture (see, e.g., [Reference Atiyah and HirzebruchAH62, Reference TotaroTot97, Reference Soulé and VoisinSV05, Reference Benoist and OttemBO20]), it may be surprising that the integral Jannsen conjecture holds by Corollary 1.3 unconditionally on torsion cycles.
The proof of Theorem 1.1 uses a homological interpretation of the transcendental Abel–Jacobi invariant on torsion cycles that does not require the smoothness assumption on ![]() $X$. The main point of this observation is that it allows for
$X$. The main point of this observation is that it allows for ![]() $0\leqslant j\leqslant i-2$ to define higher Abel–Jacobi invariants,
$0\leqslant j\leqslant i-2$ to define higher Abel–Jacobi invariants,
by applying suitable Abel–Jacobi mappings on closed subschemes of ![]() $X$. Here,
$X$. Here,
where ![]() $d:=\dim X$,
$d:=\dim X$, ![]() $Z\subset X$ runs through all closed subschemes with
$Z\subset X$ runs through all closed subschemes with ![]() $j=\dim X-\dim Z$ and
$j=\dim X-\dim Z$ and ![]() $N^\ast$ denotes Grothendieck's coniveau filtration on the respective Borel–Moore homology group.
$N^\ast$ denotes Grothendieck's coniveau filtration on the respective Borel–Moore homology group.
Theorem 1.4 Let ![]() $X$ be a separated scheme of finite type over
$X$ be a separated scheme of finite type over ![]() $\mathbb {C}$. Then for all
$\mathbb {C}$. Then for all ![]() $0\leqslant j \leqslant i-2$, we have
$0\leqslant j \leqslant i-2$, we have
As ![]() $N^{i-1}\operatorname {CH}^i(X\!)=\operatorname {CH}^i(X\!)_{\operatorname {alg}}$ is divisible, this theorem implies that the torsion subgroup of
$N^{i-1}\operatorname {CH}^i(X\!)=\operatorname {CH}^i(X\!)_{\operatorname {alg}}$ is divisible, this theorem implies that the torsion subgroup of ![]() $A^i(X\!):=\operatorname {CH}^i(X\!)/\sim _{\operatorname {alg}}$ admits a finite filtration (by coniveau) such that the graded pieces are determined by higher Abel–Jacobi invariants. This should be compared to Green's conjecture [Reference GreenGre98, Reference VoisinVoi99], which predicts that rational Chow groups of smooth complex projective varieties carry a finite filtration (expected to be the Bloch–Beilinson filtration) such that the graded quotients are determined by higher Abel–Jacobi invariants.
$A^i(X\!):=\operatorname {CH}^i(X\!)/\sim _{\operatorname {alg}}$ admits a finite filtration (by coniveau) such that the graded pieces are determined by higher Abel–Jacobi invariants. This should be compared to Green's conjecture [Reference GreenGre98, Reference VoisinVoi99], which predicts that rational Chow groups of smooth complex projective varieties carry a finite filtration (expected to be the Bloch–Beilinson filtration) such that the graded quotients are determined by higher Abel–Jacobi invariants.
Theorem 1.4 admits the following ![]() $\ell$-adic analogue, concerning the
$\ell$-adic analogue, concerning the ![]() $\ell$-power torsion subgroup
$\ell$-power torsion subgroup ![]() $\operatorname {CH}^i(X\!)[\ell ^\infty ]$ of
$\operatorname {CH}^i(X\!)[\ell ^\infty ]$ of ![]() $\operatorname {CH}^i(X\!):=\operatorname {CH}_{\dim X-i}(X\!)$.
$\operatorname {CH}^i(X\!):=\operatorname {CH}_{\dim X-i}(X\!)$.
Theorem 1.5 Let ![]() $X$ be a separated scheme of finite type over a field
$X$ be a separated scheme of finite type over a field ![]() $k$ and let
$k$ and let ![]() $\ell$ be a prime invertible in
$\ell$ be a prime invertible in ![]() $k$. Assume that
$k$. Assume that ![]() $k$ contains all
$k$ contains all ![]() $\ell$-power roots of unity. Then for all
$\ell$-power roots of unity. Then for all ![]() $0\leqslant j\leqslant i-2$, we have
$0\leqslant j\leqslant i-2$, we have
The coniveau filtration on ![]() $\operatorname {CH}^i(X\!)[\ell ^\infty ]$ as well as the (higher) Abel–Jacobi invariants are defined analogues to the case of complex schemes above, where we replace ordinary Borel–Moore homology by its
$\operatorname {CH}^i(X\!)[\ell ^\infty ]$ as well as the (higher) Abel–Jacobi invariants are defined analogues to the case of complex schemes above, where we replace ordinary Borel–Moore homology by its ![]() $\ell$-adic pro-étale analogue [Reference Bhatt and ScholzeBS15], see Proposition 6.6 and Definition 7.29.
$\ell$-adic pro-étale analogue [Reference Bhatt and ScholzeBS15], see Proposition 6.6 and Definition 7.29.
Theorem 1.5 proves analogues of Theorems 1.1 and 1.4 over any field ![]() $k$ that contains all
$k$ that contains all ![]() $\ell$-power roots of unity. This includes in particular an
$\ell$-power roots of unity. This includes in particular an ![]() $\ell ^{\infty }$-torsion version of Jannsen's conjecture over any field that contains all
$\ell ^{\infty }$-torsion version of Jannsen's conjecture over any field that contains all ![]() $\ell$-power roots of unity, such as (function fields over) algebraically closed fields.
$\ell$-power roots of unity, such as (function fields over) algebraically closed fields.
1.2 Refined unramified cohomology and algebraic cycles
Let ![]() $X$ be a separated scheme of finite type over a field
$X$ be a separated scheme of finite type over a field ![]() $k$. We consider the increasing filtration
$k$. We consider the increasing filtration
and ![]() $\operatorname {codim}(x):=\dim X-\dim (\overline {\{x\}})$. Each
$\operatorname {codim}(x):=\dim X-\dim (\overline {\{x\}})$. Each ![]() $F_jX$ may be seen as a pro-object in the category of schemes. For a given (co-)homology functor
$F_jX$ may be seen as a pro-object in the category of schemes. For a given (co-)homology functor ![]() $H^i(-,A(n))$ that admits pullbacks along open immersions of schemes of the same dimension, the (co-)homology of
$H^i(-,A(n))$ that admits pullbacks along open immersions of schemes of the same dimension, the (co-)homology of ![]() $F_jX$ is defined as direct limit over all open subsets
$F_jX$ is defined as direct limit over all open subsets ![]() $U\subset X$ with
$U\subset X$ with ![]() $F_jX\subset U$. We then define the associated
$F_jX\subset U$. We then define the associated ![]() $j$th refined unramified cohomology by
$j$th refined unramified cohomology by
The Gysin sequence (see (1.4)) shows that the case ![]() $j=0$ corresponds to classical unramified cohomology.
$j=0$ corresponds to classical unramified cohomology.
1.2.1 Complex schemes
Now let ![]() $k=\mathbb {C}$. For an abelian group
$k=\mathbb {C}$. For an abelian group ![]() $A$, let
$A$, let
where ![]() $H^{\rm BM}_\ast$ denotes Borel–Moore homology of the underlying analytic space
$H^{\rm BM}_\ast$ denotes Borel–Moore homology of the underlying analytic space ![]() $X_{\operatorname {an}}$ and
$X_{\operatorname {an}}$ and ![]() $A(m)=A\otimes _\mathbb {Z} (2 \pi i)^{m}\mathbb {Z}$ denotes the
$A(m)=A\otimes _\mathbb {Z} (2 \pi i)^{m}\mathbb {Z}$ denotes the ![]() $m$th Tate twist. Restriction maps as required previously exist in this setting and so we get refined unramified cohomology groups
$m$th Tate twist. Restriction maps as required previously exist in this setting and so we get refined unramified cohomology groups ![]() $H^i_{j,{\rm nr}}(X,A(n))$.
$H^i_{j,{\rm nr}}(X,A(n))$.
By [Reference FultonFul98, § 19.1], there is a cycle class map
where ![]() $\operatorname {CH}^i(X\!):=\operatorname {CH}_{d_X-i}(X\!)$. We let
$\operatorname {CH}^i(X\!):=\operatorname {CH}_{d_X-i}(X\!)$. We let ![]() $\operatorname {Griff}^i(X\!):=\ker (\operatorname {cl}_X^i\!)/\sim _{\operatorname {alg}}$.
$\operatorname {Griff}^i(X\!):=\ker (\operatorname {cl}_X^i\!)/\sim _{\operatorname {alg}}$.
If ![]() $X$ is smooth and equi-dimensional, then
$X$ is smooth and equi-dimensional, then ![]() $H^{\rm BM}_{2d_X-i}(X_{\operatorname {an}},A)\simeq H^{i}_{\rm sing}(X_{\operatorname {an}}, A)$ and the above map agrees with the usual cycle class map in singular cohomology.
$H^{\rm BM}_{2d_X-i}(X_{\operatorname {an}},A)\simeq H^{i}_{\rm sing}(X_{\operatorname {an}}, A)$ and the above map agrees with the usual cycle class map in singular cohomology.
Theorem 1.6 Let ![]() $X$ be a separated scheme of finite type over
$X$ be a separated scheme of finite type over ![]() $\mathbb {C}$ and define refined unramified cohomology as in (1.1) with cohomology theory in (1.2).
$\mathbb {C}$ and define refined unramified cohomology as in (1.1) with cohomology theory in (1.2).
(i) There are canonical isomorphisms
 \[ \operatorname{coker}(\operatorname{cl}_X^i\!) _{\operatorname{tors}}\simeq \frac{H^{2i-1}_{i-2,{\rm nr}}(X,\mathbb{Q}/\mathbb{Z}(i))}{H^{2i-1}_{i-2,{\rm nr}}( X,\mathbb{Q}(i) )},\quad \operatorname{Griff} ^i(X\!)\simeq \frac{H^{2i-1}_{i-2,{\rm nr}}(X,\mathbb{Z}(i)) }{H^{2i-1} (X,\mathbb{Z}(i)) } . \]
\[ \operatorname{coker}(\operatorname{cl}_X^i\!) _{\operatorname{tors}}\simeq \frac{H^{2i-1}_{i-2,{\rm nr}}(X,\mathbb{Q}/\mathbb{Z}(i))}{H^{2i-1}_{i-2,{\rm nr}}( X,\mathbb{Q}(i) )},\quad \operatorname{Griff} ^i(X\!)\simeq \frac{H^{2i-1}_{i-2,{\rm nr}}(X,\mathbb{Z}(i)) }{H^{2i-1} (X,\mathbb{Z}(i)) } . \]
(ii) There is a transcendental Abel–Jacobi map
If \[ \lambda_{{\rm tr}}^i: \operatorname{Griff}^i(X\!)_{\operatorname{tors}} \longrightarrow \frac{H^{2i-1}(X,\mathbb{Q}/\mathbb{Z}(i))}{N^{i-1}H^{2i-1}(X,\mathbb{Q}(i) )}. \]
\[ \lambda_{{\rm tr}}^i: \operatorname{Griff}^i(X\!)_{\operatorname{tors}} \longrightarrow \frac{H^{2i-1}(X,\mathbb{Q}/\mathbb{Z}(i))}{N^{i-1}H^{2i-1}(X,\mathbb{Q}(i) )}. \]
 $X$ is a smooth projective variety, this agrees with Griffiths’ transcendental Abel–Jacobi map [Reference GriffithsGri69] restricted to torsion cycles. Its kernel is isomorphic to
and its image is given by
$X$ is a smooth projective variety, this agrees with Griffiths’ transcendental Abel–Jacobi map [Reference GriffithsGri69] restricted to torsion cycles. Its kernel is isomorphic to
and its image is given by \[ \ker(\lambda_{{\rm tr}}^i)\simeq H^{2i-2}_{i-3,{\rm nr}} (X,\mathbb{Q}/\mathbb{Z}(i)) /G^{i}H^{2i-2}_{i-3,{\rm nr}} (X,\mathbb{Q}/\mathbb{Z}(i) ) \]
\[ \ker(\lambda_{{\rm tr}}^i)\simeq H^{2i-2}_{i-3,{\rm nr}} (X,\mathbb{Q}/\mathbb{Z}(i)) /G^{i}H^{2i-2}_{i-3,{\rm nr}} (X,\mathbb{Q}/\mathbb{Z}(i) ) \]
 $\operatorname {im}(\lambda _{{\rm tr}}^i)=N^{i-1}H^{2i-1}(X,\mathbb {Q} /\mathbb {Z} (i))_{\operatorname {div}}/N^{i-1}H^{2i-1}(X,\mathbb {Q} (i) )$.
$\operatorname {im}(\lambda _{{\rm tr}}^i)=N^{i-1}H^{2i-1}(X,\mathbb {Q} /\mathbb {Z} (i))_{\operatorname {div}}/N^{i-1}H^{2i-1}(X,\mathbb {Q} (i) )$.
In this theorem, ![]() $N^\ast$ denotes Grothendieck's coniveau filtration and
$N^\ast$ denotes Grothendieck's coniveau filtration and ![]() $H^\ast (X,\mathbb {Q}/\mathbb {Z}(i))_{\operatorname {div}}\subset H^\ast (X,\mathbb {Q}/\mathbb {Z}(i))$ denotes the divisible subgroup. Moreover,
$H^\ast (X,\mathbb {Q}/\mathbb {Z}(i))_{\operatorname {div}}\subset H^\ast (X,\mathbb {Q}/\mathbb {Z}(i))$ denotes the divisible subgroup. Moreover, ![]() $G^{i}H^{2i-2}_{i-3,{\rm nr}} (X,\mathbb {Q} /\mathbb {Z}(i) )$ denotes the subspace of
$G^{i}H^{2i-2}_{i-3,{\rm nr}} (X,\mathbb {Q} /\mathbb {Z}(i) )$ denotes the subspace of ![]() $H^{2i-2}_{i-3,{\rm nr}} (X,\mathbb {Q} /\mathbb {Z}(i))$ generated by classes that admit a lift
$H^{2i-2}_{i-3,{\rm nr}} (X,\mathbb {Q} /\mathbb {Z}(i))$ generated by classes that admit a lift ![]() $\alpha \in H^{2i-2}(F_{i-2}X,\mathbb {Q} /\mathbb {Z}(i) )$ whose image
$\alpha \in H^{2i-2}(F_{i-2}X,\mathbb {Q} /\mathbb {Z}(i) )$ whose image ![]() $\delta (\alpha )\in H^{2i-1}(F_{i-2}X, \mathbb {Z}(i) )$ via the Bockstein map lifts to
$\delta (\alpha )\in H^{2i-1}(F_{i-2}X, \mathbb {Z}(i) )$ via the Bockstein map lifts to ![]() $H^{2i-1}(X, \mathbb {Z}(i) )$, cf. Definition 5.4 and Lemma 7.18.
$H^{2i-1}(X, \mathbb {Z}(i) )$, cf. Definition 5.4 and Lemma 7.18.
The theorem contains the aforementioned results from [Reference Bloch and OgusBO74, Reference Colliot-Thélène and VoisinCV12, Reference VoisinVoi12, Reference MaMa17] as the special case where ![]() $i=2$ in item (i) and
$i=2$ in item (i) and ![]() $i=3$ in item (ii), and where
$i=3$ in item (ii), and where ![]() $X$ is a smooth projective variety. Item (i) uses Hilbert theorem 90, but not the Bloch–Kato conjecture. Item (ii) uses the Bloch–Kato conjecture in degree two, proven by Merkurjev and Suslin, but not in higher degrees.
$X$ is a smooth projective variety. Item (i) uses Hilbert theorem 90, but not the Bloch–Kato conjecture. Item (ii) uses the Bloch–Kato conjecture in degree two, proven by Merkurjev and Suslin, but not in higher degrees.
Item (i) in Theorem 1.6 leads to new results on the integral Hodge conjecture for uniruled varieties. Indeed, Voisin [Reference VoisinVoi06] proved that the integral Hodge conjecture holds for smooth complex projective threefolds ![]() $X$ that are uniruled (i.e.
$X$ that are uniruled (i.e. ![]() $Z^\ast (X\!)_{\operatorname {tors}}=0$) and conjectured that it should fail for codimension-two cycles on rationally connected varieties of dimension at least four. This has later been proven in [Reference Colliot-Thélène and VoisinCV12] (
$Z^\ast (X\!)_{\operatorname {tors}}=0$) and conjectured that it should fail for codimension-two cycles on rationally connected varieties of dimension at least four. This has later been proven in [Reference Colliot-Thélène and VoisinCV12] (![]() $\dim X\geqslant 6$) and in full generality in [Reference SchreiederSch19]. Taking products
$\dim X\geqslant 6$) and in full generality in [Reference SchreiederSch19]. Taking products ![]() $X\times \mathbb {P}^n$ with
$X\times \mathbb {P}^n$ with ![]() $\mathbb {P}^n$, the examples in [Reference Colliot-Thélène and VoisinCV12, Reference SchreiederSch19] also yield counterexamples to the integral Hodge conjecture on unirational varieties for cycles of codimension greater than two. However, in some sense these non-algebraic Hodge classes should still be regarded as degree-four classes, because they are Gysin pushforwards of non-algebraic degree-four Hodge classes on a subvariety of
$\mathbb {P}^n$, the examples in [Reference Colliot-Thélène and VoisinCV12, Reference SchreiederSch19] also yield counterexamples to the integral Hodge conjecture on unirational varieties for cycles of codimension greater than two. However, in some sense these non-algebraic Hodge classes should still be regarded as degree-four classes, because they are Gysin pushforwards of non-algebraic degree-four Hodge classes on a subvariety of ![]() $X\times \mathbb {P}^n$ (namely
$X\times \mathbb {P}^n$ (namely ![]() $X\times \{pt.\}$).
$X\times \{pt.\}$).
The tools of this paper allow us to go further by studying the integral Hodge conjecture for Hodge classes (of arbitrary degree) in the following strong sense.
Corollary 1.7 For any integer ![]() $i\geqslant 2$, there is a smooth uniruled complex projective variety
$i\geqslant 2$, there is a smooth uniruled complex projective variety ![]() $X$ such that the integral Hodge conjecture fails for codimension-
$X$ such that the integral Hodge conjecture fails for codimension-![]() $i$ cycles on
$i$ cycles on ![]() $X$ in a way that cannot be explained by the failure on proper subvarieties of
$X$ in a way that cannot be explained by the failure on proper subvarieties of ![]() $X$ in the following sense: there is a class
$X$ in the following sense: there is a class ![]() $\alpha \in \operatorname {coker}(\operatorname {cl}_X^i\!) _{\operatorname {tors}}$ such that for any closed subscheme
$\alpha \in \operatorname {coker}(\operatorname {cl}_X^i\!) _{\operatorname {tors}}$ such that for any closed subscheme ![]() $Z\subset X$ of codimension
$Z\subset X$ of codimension ![]() $j\geqslant 1$, the class
$j\geqslant 1$, the class ![]() $\alpha$ is not in the image of the natural map
$\alpha$ is not in the image of the natural map ![]() $\operatorname {coker}(\operatorname {cl}_Z^{i-j}) _{\operatorname {tors}} \to \operatorname {coker}(\operatorname {cl}_X^i\!) _{\operatorname {tors}}$.
$\operatorname {coker}(\operatorname {cl}_Z^{i-j}) _{\operatorname {tors}} \to \operatorname {coker}(\operatorname {cl}_X^i\!) _{\operatorname {tors}}$.
In this corollary we may take ![]() $X=Y\times E$, where
$X=Y\times E$, where ![]() $Y$ is a certain unirational variety of dimension
$Y$ is a certain unirational variety of dimension ![]() $3i$ and
$3i$ and ![]() $E$ is an elliptic curve, see Theorem 10.6. The problem of finding a unirational variety
$E$ is an elliptic curve, see Theorem 10.6. The problem of finding a unirational variety ![]() $X$ with the property stated in the corollary remains open for
$X$ with the property stated in the corollary remains open for ![]() $i\geqslant 3$.
$i\geqslant 3$.
1.2.2 Arbitrary ground fields
Theorem 1.6 admits an ![]() $\ell$-adic analogue over any field
$\ell$-adic analogue over any field ![]() $k$ in which
$k$ in which ![]() $\ell$ is invertible. The corresponding (co-)homology functor will be the
$\ell$ is invertible. The corresponding (co-)homology functor will be the ![]() $\ell$-adic pro-étale Borel–Moore cohomology, see [Reference Bhatt and ScholzeBS15] and Proposition 6.6. For instance,
$\ell$-adic pro-étale Borel–Moore cohomology, see [Reference Bhatt and ScholzeBS15] and Proposition 6.6. For instance,
where ![]() $\pi _X:X\to \operatorname {Spec} k$ is the structure map and
$\pi _X:X\to \operatorname {Spec} k$ is the structure map and ![]() $d_X=\dim X$. We construct in § 7.2 cycle class maps
$d_X=\dim X$. We construct in § 7.2 cycle class maps
which for ![]() $X$ smooth and equi-dimensional coincide with Jannsen's cycle class in continuous étale cohomology, see Lemma 9.1. Let
$X$ smooth and equi-dimensional coincide with Jannsen's cycle class in continuous étale cohomology, see Lemma 9.1. Let ![]() $N^\ast$ be the associated coniveau filtration on
$N^\ast$ be the associated coniveau filtration on ![]() $\operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }$ and put
$\operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }$ and put
This is the ![]() $\ell$-adic Griffiths group of homologically trivial
$\ell$-adic Griffiths group of homologically trivial ![]() $\ell$-adic cycles modulo algebraic equivalence if
$\ell$-adic cycles modulo algebraic equivalence if ![]() $k$ is algebraically closed, and it is the group of homologically trivial
$k$ is algebraically closed, and it is the group of homologically trivial ![]() $\ell$-adic cycles modulo rational equivalence if
$\ell$-adic cycles modulo rational equivalence if ![]() $k$ is finitely generated, see [Reference JannsenJan00, Lemmas 5.7 and 5.8] and Lemma 7.5. We denote the torsion subgroup of
$k$ is finitely generated, see [Reference JannsenJan00, Lemmas 5.7 and 5.8] and Lemma 7.5. We denote the torsion subgroup of ![]() $A_0^i(X\!)_{\mathbb {Z}_\ell }$ by
$A_0^i(X\!)_{\mathbb {Z}_\ell }$ by ![]() $A_0^i(X\!)[\ell ^\infty ]$.
$A_0^i(X\!)[\ell ^\infty ]$.
Theorem 1.8 Let ![]() $k$ be a field and let
$k$ be a field and let ![]() $\ell$ be a prime invertible in
$\ell$ be a prime invertible in ![]() $k$. Let
$k$. Let ![]() $X$ be a separated scheme of finite type over
$X$ be a separated scheme of finite type over ![]() $k$ and define refined unramified cohomology as in (1.1) with cohomology theory in (1.3).
$k$ and define refined unramified cohomology as in (1.1) with cohomology theory in (1.3).
(i) There are canonical isomorphisms
 \[ \operatorname{coker}(\operatorname{cl}_X^i\!) [\ell^\infty] \simeq \frac{H^{2i-1}_{i-2,{\rm nr}}(X,\mathbb{Q}_\ell /\mathbb{Z}_\ell (i))}{H^{2i-1}_{i-2,{\rm nr}}( X,\mathbb{Q}_\ell(i) ) } \quad \text{and}\quad A^i_0(X\!)_{\mathbb{Z}_\ell}\simeq \frac{H^{2i-1}_{i-2,{\rm nr}}(X,\mathbb{Z}_\ell(i))}{H^{2i-1}(X,\mathbb{Z}_\ell(i))}. \]
\[ \operatorname{coker}(\operatorname{cl}_X^i\!) [\ell^\infty] \simeq \frac{H^{2i-1}_{i-2,{\rm nr}}(X,\mathbb{Q}_\ell /\mathbb{Z}_\ell (i))}{H^{2i-1}_{i-2,{\rm nr}}( X,\mathbb{Q}_\ell(i) ) } \quad \text{and}\quad A^i_0(X\!)_{\mathbb{Z}_\ell}\simeq \frac{H^{2i-1}_{i-2,{\rm nr}}(X,\mathbb{Z}_\ell(i))}{H^{2i-1}(X,\mathbb{Z}_\ell(i))}. \]
(ii) There is a transcendental Abel–Jacobi map
If \[ \lambda_{{\rm tr}}^i: A^i_0(X\!)[\ell^\infty] \longrightarrow H^{2i-1}(X,\mathbb{Q}_\ell/\mathbb{Z}_\ell(i))/ N^{i-1}H^{2i-1}(X,\mathbb{Q}_\ell(i) ) . \]
\[ \lambda_{{\rm tr}}^i: A^i_0(X\!)[\ell^\infty] \longrightarrow H^{2i-1}(X,\mathbb{Q}_\ell/\mathbb{Z}_\ell(i))/ N^{i-1}H^{2i-1}(X,\mathbb{Q}_\ell(i) ) . \]
 $X$ is a smooth projective variety and
$X$ is a smooth projective variety and  $k$ is algebraically closed, then this map is induced by Bloch's Abel–Jacobi map on torsion cycles [Reference BlochBlo79]. Its kernel is isomorphic to
and its image is given by
$k$ is algebraically closed, then this map is induced by Bloch's Abel–Jacobi map on torsion cycles [Reference BlochBlo79]. Its kernel is isomorphic to
and its image is given by \[ \ker(\lambda_{{\rm tr}}^i)\simeq H^{2i-2}_{i-3,{\rm nr}} (X,\mathbb{Q}_\ell /\mathbb{Z}_\ell (i)) /G^{i}H^{2i-2}_{i-3,{\rm nr}} (X,\mathbb{Q}_\ell/\mathbb{Z}_\ell(i) ) \]
\[ \ker(\lambda_{{\rm tr}}^i)\simeq H^{2i-2}_{i-3,{\rm nr}} (X,\mathbb{Q}_\ell /\mathbb{Z}_\ell (i)) /G^{i}H^{2i-2}_{i-3,{\rm nr}} (X,\mathbb{Q}_\ell/\mathbb{Z}_\ell(i) ) \]
 $\operatorname {im}(\lambda _{{\rm tr}}^i)=N^{i-1}H^{2i-1}(X,\mathbb {Q}_\ell /\mathbb {Z}_\ell (i))_{\operatorname {div} }/N^{i-1}H^{2i-1}(X,\mathbb {Q}_\ell (i) )$.
$\operatorname {im}(\lambda _{{\rm tr}}^i)=N^{i-1}H^{2i-1}(X,\mathbb {Q}_\ell /\mathbb {Z}_\ell (i))_{\operatorname {div} }/N^{i-1}H^{2i-1}(X,\mathbb {Q}_\ell (i) )$.
The filtration ![]() $N^\ast$ is the coniveau filtration and
$N^\ast$ is the coniveau filtration and ![]() $G^\ast$ is defined similarly as in Theorem 1.6, see Definition 5.4 and Lemma 7.18. Moreover,
$G^\ast$ is defined similarly as in Theorem 1.6, see Definition 5.4 and Lemma 7.18. Moreover, ![]() $H^{2i-1}(X,\mathbb {Q}_\ell /\mathbb {Z}_\ell (i))_{\operatorname {div} } \subset H^{2i-1}(X,\mathbb {Q}_\ell /\mathbb {Z}_\ell (i))$ denotes the image of
$H^{2i-1}(X,\mathbb {Q}_\ell /\mathbb {Z}_\ell (i))_{\operatorname {div} } \subset H^{2i-1}(X,\mathbb {Q}_\ell /\mathbb {Z}_\ell (i))$ denotes the image of ![]() $H^{2i-1}(X,\mathbb {Q}_\ell (i))\to H^{2i-1}(X,\mathbb {Q}_\ell /\mathbb {Z}_\ell (i))$.
$H^{2i-1}(X,\mathbb {Q}_\ell (i))\to H^{2i-1}(X,\mathbb {Q}_\ell /\mathbb {Z}_\ell (i))$.
The computation of ![]() $\ker (\lambda _{{\rm tr}}^i)$ uses as before Merkurjev and Suslin's theorem. The Bloch–Kato conjecture is not used otherwise (in particular, not in item (i)).
$\ker (\lambda _{{\rm tr}}^i)$ uses as before Merkurjev and Suslin's theorem. The Bloch–Kato conjecture is not used otherwise (in particular, not in item (i)).
The first isomorphism in item (i) generalizes a result of Kahn [Reference KahnKah12] who proved it for ![]() $i=2$ and
$i=2$ and ![]() $X$ smooth projective.
$X$ smooth projective.
1.3 Comparison with Bloch–Ogus theory and Kato homology
Let ![]() $X$ be an algebraic scheme over a field
$X$ be an algebraic scheme over a field ![]() $k$ and let
$k$ and let ![]() $H^i(-,A(n))$ be one of the (co)-homology theories considered previously. For a point
$H^i(-,A(n))$ be one of the (co)-homology theories considered previously. For a point ![]() $x\in X$ with closure
$x\in X$ with closure ![]() $Z_x:=\overline {\{x\}}\subset X$, we let
$Z_x:=\overline {\{x\}}\subset X$, we let ![]() $H^i(x,A(n))=H^i(F_0Z_x,A(n))$. The Gysin sequence (i.e. long exact sequence of pairs), yields in the colimit a long exact sequence
$H^i(x,A(n))=H^i(F_0Z_x,A(n))$. The Gysin sequence (i.e. long exact sequence of pairs), yields in the colimit a long exact sequence
see Lemma 5.8. Note that the image of ![]() $f$ agrees, by definition, with the refined unramified cohomology group
$f$ agrees, by definition, with the refined unramified cohomology group ![]() $H^{p-1+q}_{p-1,{\rm nr}}(X,A(n))$, which thus coincides with the kernel of the residue map
$H^{p-1+q}_{p-1,{\rm nr}}(X,A(n))$, which thus coincides with the kernel of the residue map ![]() $\partial$ above. This shows, in particular, that
$\partial$ above. This shows, in particular, that ![]() $H^q_{0,{\rm nr}}(X,A(n))$ corresponds to traditional unramified cohomology.
$H^q_{0,{\rm nr}}(X,A(n))$ corresponds to traditional unramified cohomology.
The above sequence gives rise to an exact couple ![]() $D_1\stackrel {f}{\to } D_1\stackrel {\partial }{\to } E_1\stackrel {\iota _\ast }{\to } D_1$, where
$D_1\stackrel {f}{\to } D_1\stackrel {\partial }{\to } E_1\stackrel {\iota _\ast }{\to } D_1$, where
and ![]() $f$,
$f$, ![]() $\partial$, and
$\partial$, and ![]() $\iota _\ast$ have bi-degrees
$\iota _\ast$ have bi-degrees ![]() $(-1,1)$,
$(-1,1)$, ![]() $(0,0)$, and
$(0,0)$, and ![]() $(1,0)$, respectively. The associated spectral sequence
$(1,0)$, respectively. The associated spectral sequence ![]() $E_1^{p,q}\Longrightarrow H^{p+q}(X,A(n))$ is convergent. The derived couple has the form
$E_1^{p,q}\Longrightarrow H^{p+q}(X,A(n))$ is convergent. The derived couple has the form ![]() $D_2 \to D_2\to E_2\to D_2$, where
$D_2 \to D_2\to E_2\to D_2$, where
is the direct sum of all refined unramified cohomology groups of ![]() $X$.
$X$.
It follows from Lemma 5.12 that ![]() $d_1:E_1\to E_1$ agrees with the differential of the coniveau spectral sequence from [Reference Bloch and OgusBO74, § 3], but see also Remark 1.9. Hence,
$d_1:E_1\to E_1$ agrees with the differential of the coniveau spectral sequence from [Reference Bloch and OgusBO74, § 3], but see also Remark 1.9. Hence, ![]() $E_2$ agrees with the second page of the coniveau spectral sequence and the derived couple
$E_2$ agrees with the second page of the coniveau spectral sequence and the derived couple ![]() $D_2 \to D_2\to E_2\to D_2$ shows that
$D_2 \to D_2\to E_2\to D_2$ shows that ![]() $E_2$ is up to extensions determined by
$E_2$ is up to extensions determined by ![]() $D_2$, hence by refined unramified cohomology, see Proposition 7.35. In the special case where
$D_2$, hence by refined unramified cohomology, see Proposition 7.35. In the special case where ![]() $X$ is smooth and equi-dimensional, the Gersten conjecture proven in [Reference Bloch and OgusBO74] (see also [Reference Colliot-Thélène, Hoobler and KahnCHK97]) thus implies that the cohomologies
$X$ is smooth and equi-dimensional, the Gersten conjecture proven in [Reference Bloch and OgusBO74] (see also [Reference Colliot-Thélène, Hoobler and KahnCHK97]) thus implies that the cohomologies ![]() $H^p(X_{\rm Zar},\mathcal {H}^q )$ of the Zariski sheaf associated to
$H^p(X_{\rm Zar},\mathcal {H}^q )$ of the Zariski sheaf associated to ![]() are up to extensions determined by refined unramified cohomology.
are up to extensions determined by refined unramified cohomology.
Without any smoothness assumption on ![]() $X$, but under the condition that the ground field
$X$, but under the condition that the ground field ![]() $k$ has finite cohomological dimension
$k$ has finite cohomological dimension ![]() $c$, the derived couple
$c$, the derived couple ![]() $D_2\to D_2\to E_2\to D_2$ yields for
$D_2\to D_2\to E_2\to D_2$ yields for ![]() $A=\mathbb {Z}/\ell ^r$ canonical isomorphisms
$A=\mathbb {Z}/\ell ^r$ canonical isomorphisms
see Corollary 7.36. By definition, ![]() $E_2^{p,d+c}$ agrees with the Kato homology of
$E_2^{p,d+c}$ agrees with the Kato homology of ![]() $X$ (see, e.g., [Reference KatoKat86, Reference Kerz and SaitoKS12, Reference TianTia20]), and so we find that the latter is, in fact, a special instance of refined unramified cohomology, cf. Remark 7.37. We remark that for
$X$ (see, e.g., [Reference KatoKat86, Reference Kerz and SaitoKS12, Reference TianTia20]), and so we find that the latter is, in fact, a special instance of refined unramified cohomology, cf. Remark 7.37. We remark that for ![]() $X$ smooth projective, Kato homology as well as traditional unramified cohomology are stable birational invariants of
$X$ smooth projective, Kato homology as well as traditional unramified cohomology are stable birational invariants of ![]() $X$, see, e.g., [Reference Colliot-Thélène and OjangurenCO89, Reference Colliot-Thélène and VoisinCV12, Reference TianTia20].
$X$, see, e.g., [Reference Colliot-Thélène and OjangurenCO89, Reference Colliot-Thélène and VoisinCV12, Reference TianTia20].
Remark 1.9 One of the key differences of this paper compared with previous work is the observation that for our purposes, the couple ![]() $D_1\to D_1\to E_1\to D_1$ is better suited than the couple
$D_1\to D_1\to E_1\to D_1$ is better suited than the couple ![]() $D_1'\stackrel {f'}{\to } D_1'\to E_1\to D_1'$, used in [Reference Bloch and OgusBO74, § 3] to define the coniveau spectral sequence. (Both couples stem from the long exact sequence of triples, but applied to different geometric situations.) Moreover, we will not pass to the coniveau spectral sequence (as done, e.g., in [Reference BlochBlo79, Reference Colliot-Thélène and VoisinCV12, Reference KahnKah12, Reference VoisinVoi12, Reference MaMa17]), but work directly with the above couple, which contains more information.
$D_1'\stackrel {f'}{\to } D_1'\to E_1\to D_1'$, used in [Reference Bloch and OgusBO74, § 3] to define the coniveau spectral sequence. (Both couples stem from the long exact sequence of triples, but applied to different geometric situations.) Moreover, we will not pass to the coniveau spectral sequence (as done, e.g., in [Reference BlochBlo79, Reference Colliot-Thélène and VoisinCV12, Reference KahnKah12, Reference VoisinVoi12, Reference MaMa17]), but work directly with the above couple, which contains more information.
Remark 1.10 Assume that ![]() $X$ is smooth and equi-dimensional. The main result of [Reference Bloch and OgusBO74] (see also [Reference Colliot-Thélène, Hoobler and KahnCHK97]) is that the map
$X$ is smooth and equi-dimensional. The main result of [Reference Bloch and OgusBO74] (see also [Reference Colliot-Thélène, Hoobler and KahnCHK97]) is that the map ![]() $f':D_1'\to D_1'$ is zero locally on
$f':D_1'\to D_1'$ is zero locally on ![]() $X$ with the exception of only some trivial bi-degrees; as a consequence,
$X$ with the exception of only some trivial bi-degrees; as a consequence, ![]() $E_2^{p,q}=0$ locally on
$E_2^{p,q}=0$ locally on ![]() $X$ for all
$X$ for all ![]() $p\neq 0$. In contrast, the image of
$p\neq 0$. In contrast, the image of ![]() $f:D_1\to D_1$ is refined unramified cohomology and this invariant in general does not vanish locally on
$f:D_1\to D_1$ is refined unramified cohomology and this invariant in general does not vanish locally on ![]() $X$. In fact, the local vanishing of
$X$. In fact, the local vanishing of ![]() $E_2^{p,q}$ for
$E_2^{p,q}$ for ![]() $p\neq 0$ implies that
$p\neq 0$ implies that ![]() $f:D^{p+1,q-1}_2\to D^{p,q}_2$ is an isomorphism locally on
$f:D^{p+1,q-1}_2\to D^{p,q}_2$ is an isomorphism locally on ![]() $X$ for all
$X$ for all ![]() $p\geqslant 1$. It follows that the Zariski sheaf
$p\geqslant 1$. It follows that the Zariski sheaf ![]() $\mathcal {H}^i_{j,{\rm nr}}$ associated to
$\mathcal {H}^i_{j,{\rm nr}}$ associated to ![]() does not depend on
does not depend on ![]() $j\geqslant 0$, hence agrees with
$j\geqslant 0$, hence agrees with ![]() $\mathcal {H}^i$ for all
$\mathcal {H}^i$ for all ![]() $j\geqslant 0$, which is in general non-zero. (This shows in particular that at least in the smooth case, refined unramified cohomology contains no interesting local information.)
$j\geqslant 0$, which is in general non-zero. (This shows in particular that at least in the smooth case, refined unramified cohomology contains no interesting local information.)
1.4 Homology or cohomology?
The results described previously relied on a twisted Borel–Moore homology theory ![]() $H^{\rm BM}_\ast (-,A(n))$ with corresponding Borel–Moore cohomology theory
$H^{\rm BM}_\ast (-,A(n))$ with corresponding Borel–Moore cohomology theory ![]() $H^i(X,A(n)):=H^{\rm BM}_{2d_X-i}(X,A(d_X-n))$, see (1.2) and (1.3). We collect the properties of this functor that are crucial for us in § 4. In sheaf theoretic terms, Borel–Moore cohomology will in practice be the (hyper-)cohomology of some complex of sheaves. If
$H^i(X,A(n)):=H^{\rm BM}_{2d_X-i}(X,A(d_X-n))$, see (1.2) and (1.3). We collect the properties of this functor that are crucial for us in § 4. In sheaf theoretic terms, Borel–Moore cohomology will in practice be the (hyper-)cohomology of some complex of sheaves. If ![]() $X$ is smooth and equi-dimensional, Poincaré duality identifies this complex to a locally constant sheaf. (For instance,
$X$ is smooth and equi-dimensional, Poincaré duality identifies this complex to a locally constant sheaf. (For instance, ![]() $\ell$-adic Borel–Moore pro-étale cohomology is given by
$\ell$-adic Borel–Moore pro-étale cohomology is given by ![]() $H^i(X,\mathbb {Z}_\ell (n))=\operatorname {R} ^i\Gamma (X_{\text{pro}{\unicode{x00E9}} {\rm t}},\pi _X^! \widehat {\mathbb {Z}}_\ell (n-d_X)[-2d_X])$, where
$H^i(X,\mathbb {Z}_\ell (n))=\operatorname {R} ^i\Gamma (X_{\text{pro}{\unicode{x00E9}} {\rm t}},\pi _X^! \widehat {\mathbb {Z}}_\ell (n-d_X)[-2d_X])$, where ![]() $\pi _X:X\to \operatorname {Spec} k$ and
$\pi _X:X\to \operatorname {Spec} k$ and ![]() $\pi _X^!\simeq \pi _X^\ast (d_X)[2d_X]$ if
$\pi _X^!\simeq \pi _X^\ast (d_X)[2d_X]$ if ![]() $X$ is smooth and equi-dimensional of dimension
$X$ is smooth and equi-dimensional of dimension ![]() $d_X$, see § 6.1.) The resulting theory thus coincides on smooth equi-dimensional algebraic schemes with ordinary cohomology, but it differs in general. In particular, as long as one is interested only in smooth equi-dimensional schemes,
$d_X$, see § 6.1.) The resulting theory thus coincides on smooth equi-dimensional algebraic schemes with ordinary cohomology, but it differs in general. In particular, as long as one is interested only in smooth equi-dimensional schemes, ![]() $H^i(X,A(n))$ can be identified with ordinary cohomology in all our applications. (Working with singular schemes is, however, important for the proof of several of the main results such as Theorems 1.1, 1.4, and 1.5 even if the total space is smooth projective.)
$H^i(X,A(n))$ can be identified with ordinary cohomology in all our applications. (Working with singular schemes is, however, important for the proof of several of the main results such as Theorems 1.1, 1.4, and 1.5 even if the total space is smooth projective.)
The functoriality properties of Borel–Moore cohomology differ from those of ordinary cohomology: the latter has arbitrary pullbacks but no pushforwards, whereas the former admits only pullbacks along étale maps, but has proper pushforwards (which shift the degree), see § 4. The situation is similar to the distinction between ordinary singular homology and Borel–Moore homology (i.e. finite versus locally finite singular chains) in topology, which have also different functoriality properties; they agree for compact analytic spaces but differ in general.
Instead of exploiting the notion of Borel–Moore cohomology, we could of course use the formula ![]() $H^i(X,A(n))=H^{\rm BM}_{2d_X-i}(X,A(d_X-n))$ to write everything in terms of Borel–Moore homology, which may be preferred by some readers. The reason we use Borel–Moore cohomology and wrote this paper cohomologically is that in the important special case where
$H^i(X,A(n))=H^{\rm BM}_{2d_X-i}(X,A(d_X-n))$ to write everything in terms of Borel–Moore homology, which may be preferred by some readers. The reason we use Borel–Moore cohomology and wrote this paper cohomologically is that in the important special case where ![]() $X$ is smooth and equi-dimensional,
$X$ is smooth and equi-dimensional, ![]() $H^i(X,A(n))$ will coincide with ordinary cohomology in all our applications. This has, in particular, the advantage that the formulas that we prove for singular varieties and in arbitrary codimension reduce in the special case of smooth projective varieties to those in [Reference Colliot-Thélène and VoisinCV12, Reference KahnKah12, Reference VoisinVoi12, Reference MaMa17], which motivate this paper. Moreover, the applications of the theory in [Reference SchreiederSch20, Reference SchreiederSch22] concern smooth projective varieties and use the identification of Borel–Moore cohomology with ordinary cohomology. This allows one to make use of cup products, which are crucial (and which require a cohomological formulation). Writing this paper homologically would thus make it significantly harder to read those applications.
$H^i(X,A(n))$ will coincide with ordinary cohomology in all our applications. This has, in particular, the advantage that the formulas that we prove for singular varieties and in arbitrary codimension reduce in the special case of smooth projective varieties to those in [Reference Colliot-Thélène and VoisinCV12, Reference KahnKah12, Reference VoisinVoi12, Reference MaMa17], which motivate this paper. Moreover, the applications of the theory in [Reference SchreiederSch20, Reference SchreiederSch22] concern smooth projective varieties and use the identification of Borel–Moore cohomology with ordinary cohomology. This allows one to make use of cup products, which are crucial (and which require a cohomological formulation). Writing this paper homologically would thus make it significantly harder to read those applications.
After all, it is a matter of formal manipulations to rewrite this paper homologically, but note that it will not be enough to just use ![]() $H^i(X,A(n))=H^{\rm BM}_{2d_X-i}(X,A(d_X-n))$, one should also change the indices in the filtration
$H^i(X,A(n))=H^{\rm BM}_{2d_X-i}(X,A(d_X-n))$, one should also change the indices in the filtration ![]() $F_\ast X$ to make the indices in the resulting formulas in Theorems 1.6 and 1.8 appealing. Unfortunately, the translation between the homological and the cohomological notation is tedious, so that we restrict ourselves to only one version here.
$F_\ast X$ to make the indices in the resulting formulas in Theorems 1.6 and 1.8 appealing. Unfortunately, the translation between the homological and the cohomological notation is tedious, so that we restrict ourselves to only one version here.
Although only a matter of notation, we do believe that the notion of Borel–Moore cohomology may also be useful in the future.
2. Notation
A field is said to be finitely generated, if it is finitely generated over its prime field. An algebraic scheme is a separated scheme of finite type over a field. A variety is an integral algebraic scheme. An open subset of a scheme will always refer to a Zariski open subset, unless specified otherwise. The dimension of an algebraic scheme is the maximum of the dimensions of its irreducible components.
For an algebraic scheme ![]() $X$, we write
$X$, we write ![]() $X_{(i)}$ for the set of all points
$X_{(i)}$ for the set of all points ![]() $x\in X$ with
$x\in X$ with ![]() $\dim (\overline {\{x\}})=i$. We then define
$\dim (\overline {\{x\}})=i$. We then define ![]() $X^{(i)}:=X_{(d_X-i)}$, where
$X^{(i)}:=X_{(d_X-i)}$, where ![]() $d_X=\dim X$. That is,
$d_X=\dim X$. That is, ![]() $x\in X$ lies in
$x\in X$ lies in ![]() $X^{(i)}$ if and only if
$X^{(i)}$ if and only if ![]() $\dim X-\dim (\overline {\{x\}})=i$. Note that this is slightly non-standard, as it does not imply that the codimension of
$\dim X-\dim (\overline {\{x\}})=i$. Note that this is slightly non-standard, as it does not imply that the codimension of ![]() $x$ defined locally in
$x$ defined locally in ![]() $X$ is
$X$ is ![]() $i$, but it has the advantage that the Chow group
$i$, but it has the advantage that the Chow group ![]() $\operatorname {CH}^i(X\!):=\operatorname {CH}_{d_X-i}(X\!)$ (see [Reference FultonFul98]) is the quotient of
$\operatorname {CH}^i(X\!):=\operatorname {CH}_{d_X-i}(X\!)$ (see [Reference FultonFul98]) is the quotient of ![]() $\bigoplus _{x\in X^{(i)}}[x]\mathbb {Z}$ by rational equivalence, where
$\bigoplus _{x\in X^{(i)}}[x]\mathbb {Z}$ by rational equivalence, where ![]() $[x]\mathbb {Z}$ denotes the free
$[x]\mathbb {Z}$ denotes the free ![]() $\mathbb {Z}$-module with generator
$\mathbb {Z}$-module with generator ![]() $[x]$. We refer to [Reference FultonFul98, § 10.3] for the definition of algebraic equivalence of cycles on algebraic schemes.
$[x]$. We refer to [Reference FultonFul98, § 10.3] for the definition of algebraic equivalence of cycles on algebraic schemes.
Whenever ![]() $G$ and
$G$ and ![]() $H$ are abelian groups (or
$H$ are abelian groups (or ![]() $R$-modules for some ring
$R$-modules for some ring ![]() $R$) so that there is a canonical map
$R$) so that there is a canonical map ![]() $H\to G$ (and there is no reason to confuse this map with a different map), we write
$H\to G$ (and there is no reason to confuse this map with a different map), we write ![]() $G/H$ as a short hand for
$G/H$ as a short hand for ![]() $\operatorname {coker}(H\to G)$. For an abelian group
$\operatorname {coker}(H\to G)$. For an abelian group ![]() $G$, we denote by
$G$, we denote by ![]() $G[\ell ^r]$ the subgroup of
$G[\ell ^r]$ the subgroup of ![]() $\ell ^r$-torsion elements, and by
$\ell ^r$-torsion elements, and by ![]() $G[\ell ^\infty ]:=\bigcup _{r}G[\ell ^r]$ the subgroup of elements that are
$G[\ell ^\infty ]:=\bigcup _{r}G[\ell ^r]$ the subgroup of elements that are ![]() $\ell ^r$-torsion for some
$\ell ^r$-torsion for some ![]() $r\geqslant 1$. We further write
$r\geqslant 1$. We further write ![]() $\operatorname {Tors}(G)$ or
$\operatorname {Tors}(G)$ or ![]() $G_{\operatorname {tors}}$ for the torsion subgroup of
$G_{\operatorname {tors}}$ for the torsion subgroup of ![]() $G$.
$G$.
Let ![]() $I$ be a directed index set and let
$I$ be a directed index set and let ![]() $(G_i)_{i\in I}$ be a direct system of abelian groups. We then denote by
$(G_i)_{i\in I}$ be a direct system of abelian groups. We then denote by
the direct limit of this system. Synonymously, we sometimes also call this the (filtered) colimit of ![]() $(G_i)_{i\in I}$ and denote it by
$(G_i)_{i\in I}$ and denote it by ![]() $\operatorname {colim} G_i$.
$\operatorname {colim} G_i$.
3. Warm-up: a simple proof of the Colliot-Thélène–Voisin theorem
Let ![]() $X$ be a smooth complex variety. In this section, we present as a warm-up a proof of the formula
$X$ be a smooth complex variety. In this section, we present as a warm-up a proof of the formula
which is due to Colliot-Thélène and Voisin [Reference Colliot-Thélène and VoisinCV12]. Their original proof relied on Voevodsky's proof of the Bloch–Kato conjecture; Kahn [Reference KahnKah12] later showed that Bloch–Kato in degree two, i.e. the Merkurjev–Suslin theorem, suffices to prove the result. Both approaches use the Gersten conjecture proven by Bloch and Ogus, which identifies unramified cohomology with the global sections of a certain Zariski sheaf, see [Reference Bloch and OgusBO74]. In this section, we explain a simpler argument that does not need Bloch–Kato in any degree and which does not make use of the Gersten conjecture. The proof presented here generalizes easily to give the result for arbitrary codimension and, in fact, on possibly singular schemes, see Theorem 7.7. This is the starting point of the more general theory presented in the body of the paper.
To fix notation in this section, we denote by ![]() $H^i(X,A)$ singular cohomology of the underlying analytic space
$H^i(X,A)$ singular cohomology of the underlying analytic space ![]() $X_{\operatorname {an}}$ with coefficients in an abelian group
$X_{\operatorname {an}}$ with coefficients in an abelian group ![]() $A$. This coincides with Borel–Moore cohomology as considered in the rest of this paper, because
$A$. This coincides with Borel–Moore cohomology as considered in the rest of this paper, because ![]() $X$ is smooth and irreducible (hence, equi-dimensional).
$X$ is smooth and irreducible (hence, equi-dimensional).
As before, we define ![]() $H^i(F_jX,A)$ as the direct limit over
$H^i(F_jX,A)$ as the direct limit over ![]() $H^i(U,A)$ where
$H^i(U,A)$ where ![]() $U\subset X$ runs through all (Zariski) open subsets whose complement has codimension at least
$U\subset X$ runs through all (Zariski) open subsets whose complement has codimension at least ![]() $j+1$. The unramified cohomology of
$j+1$. The unramified cohomology of ![]() $X$ is defined by
$X$ is defined by ![]() $H^i_{nr}(X,A)=\operatorname {im}(H^i(F_1X,A)\to H^i(F_0X,A))$. The Gysin sequence implies that this agrees with the definition given in [Reference Colliot-ThélèneCol95, Theorem 4.1.1(a)] (cf. Lemma 5.8). In other words, an element
$H^i_{nr}(X,A)=\operatorname {im}(H^i(F_1X,A)\to H^i(F_0X,A))$. The Gysin sequence implies that this agrees with the definition given in [Reference Colliot-ThélèneCol95, Theorem 4.1.1(a)] (cf. Lemma 5.8). In other words, an element ![]() $[\alpha ]\in H^i_{nr}(X,A)$ is represented by a class
$[\alpha ]\in H^i_{nr}(X,A)$ is represented by a class ![]() $\alpha \in H^i(U,A)$ for some open subset
$\alpha \in H^i(U,A)$ for some open subset ![]() $U\subset X$ whose complement has codimension at least two (such open subsets are called ‘big’) and two such representatives yield the same element in
$U\subset X$ whose complement has codimension at least two (such open subsets are called ‘big’) and two such representatives yield the same element in ![]() $H^i_{nr}(X,A)$ if they coincide on some dense open subset of
$H^i_{nr}(X,A)$ if they coincide on some dense open subset of ![]() $X$.
$X$.
Our proof of (3.1) relies on the following lemma.
Lemma 3.1 The natural restriction map is an isomorphism
Proof. As ![]() $f$ is clearly surjective, it suffices to prove that it is injective.
$f$ is clearly surjective, it suffices to prove that it is injective.
Note that ![]() $H^{3} ( F_1X,\mathbb {Q} )\to H^{3}_{nr}( X,\mathbb {Q} )$ is surjective by definition. Hence, in order to prove the injectivity of
$H^{3} ( F_1X,\mathbb {Q} )\to H^{3}_{nr}( X,\mathbb {Q} )$ is surjective by definition. Hence, in order to prove the injectivity of ![]() $f$ it suffices to show the following: Let
$f$ it suffices to show the following: Let ![]() $U\subset X$ be a big open subset and let
$U\subset X$ be a big open subset and let ![]() $\alpha \in H^3(U,\mathbb {Q}/\mathbb {Z})$ such that
$\alpha \in H^3(U,\mathbb {Q}/\mathbb {Z})$ such that
for some dense open subset ![]() $V\subset U$. Then we need to show that up to removing a codimension-two subset from
$V\subset U$. Then we need to show that up to removing a codimension-two subset from ![]() $U$, the class
$U$, the class ![]() $\alpha$ lifts to
$\alpha$ lifts to ![]() $H^3(U,\mathbb {Q})$. Equivalently, we need to show that the image
$H^3(U,\mathbb {Q})$. Equivalently, we need to show that the image ![]() $\delta (\alpha )\in H^4(U,\mathbb {Z})_{\operatorname {tors}}$ via the Bockstein map (associated to
$\delta (\alpha )\in H^4(U,\mathbb {Z})_{\operatorname {tors}}$ via the Bockstein map (associated to ![]() $0\to \mathbb {Z}\to \mathbb {Q}\to \mathbb {Q}/\mathbb {Z}\to 0$) vanishes after removing a codimension-two subset from
$0\to \mathbb {Z}\to \mathbb {Q}\to \mathbb {Q}/\mathbb {Z}\to 0$) vanishes after removing a codimension-two subset from ![]() $U$.
$U$.
Up to removing a codimension-two subset from ![]() $U$, we may assume that
$U$, we may assume that ![]() $D:=U\setminus V$ is smooth of pure codimension one in
$D:=U\setminus V$ is smooth of pure codimension one in ![]() $U$. As
$U$. As ![]() $\alpha |_V=0$, the Gysin sequence shows that there is a class
$\alpha |_V=0$, the Gysin sequence shows that there is a class ![]() $\xi \in H^1(D,\mathbb {Q}/\mathbb {Z})$ with
$\xi \in H^1(D,\mathbb {Q}/\mathbb {Z})$ with ![]() $\alpha =\iota _\ast \xi$, where
$\alpha =\iota _\ast \xi$, where ![]() $\iota _\ast :H^1(D,\mathbb {Q}/\mathbb {Z})\to H^3(U,\mathbb {Q}/\mathbb {Z})$ denotes the Gysin pushforward. Identifying the respective cohomology groups via Poincaré duality with Borel–Moore homology, it follows directly from the definitions that the Bockstein map is compatible with
$\iota _\ast :H^1(D,\mathbb {Q}/\mathbb {Z})\to H^3(U,\mathbb {Q}/\mathbb {Z})$ denotes the Gysin pushforward. Identifying the respective cohomology groups via Poincaré duality with Borel–Moore homology, it follows directly from the definitions that the Bockstein map is compatible with ![]() $\iota _\ast$. It thus suffices to show that
$\iota _\ast$. It thus suffices to show that
vanishes after removing a codimension-one subset of ![]() $D$. This, in turn, is a well-known consequence of Hilbert theorem 90, see [Reference BlochBlo10, end of Lecture 5], which concludes the proof of the lemma.
$D$. This, in turn, is a well-known consequence of Hilbert theorem 90, see [Reference BlochBlo10, end of Lecture 5], which concludes the proof of the lemma.
By the above lemma, it suffices to construct an isomorphism
Here we note that both sides in (3.2) remain unchanged if we remove from ![]() $X$ a closed codimension-three subset (this is obvious for the right-hand side and it follows from the Gysin sequence and purity for the left-hand side). We allow ourselves to perform such shrinkings in what follows (this could be avoided if we were using Borel–Moore cohomology so that we can work with singular schemes). Let
$X$ a closed codimension-three subset (this is obvious for the right-hand side and it follows from the Gysin sequence and purity for the left-hand side). We allow ourselves to perform such shrinkings in what follows (this could be avoided if we were using Borel–Moore cohomology so that we can work with singular schemes). Let ![]() $\alpha \in H^4(X,\mathbb {Z})$ such that some multiple
$\alpha \in H^4(X,\mathbb {Z})$ such that some multiple ![]() $n\alpha =\operatorname {cl}_X^2(z)$ is algebraic. Let
$n\alpha =\operatorname {cl}_X^2(z)$ is algebraic. Let ![]() $Z:=\operatorname {supp} z$. Up to removing
$Z:=\operatorname {supp} z$. Up to removing ![]() $Z^{\operatorname {sing}}$ from
$Z^{\operatorname {sing}}$ from ![]() $X$, we may assume that
$X$, we may assume that ![]() $Z$ is smooth. The Gysin sequence then yields
$Z$ is smooth. The Gysin sequence then yields
where ![]() $\partial$ denotes the residue map and the pushforward
$\partial$ denotes the residue map and the pushforward ![]() $\iota _\ast$ corresponds to the cycle class map. As
$\iota _\ast$ corresponds to the cycle class map. As ![]() $n\alpha =\operatorname {cl}^2_X(z)\in \operatorname {im}(\iota _\ast )$, we find that
$n\alpha =\operatorname {cl}^2_X(z)\in \operatorname {im}(\iota _\ast )$, we find that ![]() $\alpha |_U\in H^4(U,\mathbb {Z})_{\operatorname {tors}}$ is torsion. The Bockstein map
$\alpha |_U\in H^4(U,\mathbb {Z})_{\operatorname {tors}}$ is torsion. The Bockstein map ![]() $\delta :H^3(U,\mathbb {Q}/\mathbb {Z})\to H^4(U,\mathbb {Z})$ induces an isomorphism
$\delta :H^3(U,\mathbb {Q}/\mathbb {Z})\to H^4(U,\mathbb {Z})$ induces an isomorphism
The right-hand side in the isomorphism maps naturally to the right-hand side in (3.2) (in fact, the latter is just the direct limit of the former where one runs through all big open subsets ![]() $U\subset X$). The map
$U\subset X$). The map ![]() $g$ above is then defined by
$g$ above is then defined by
The Gysin sequence implies that this definition is well-defined, i.e. ![]() $g(\alpha )$ does not change if we add to
$g(\alpha )$ does not change if we add to ![]() $\alpha$ some algebraic class.
$\alpha$ some algebraic class.
We aim to construct an inverse of ![]() $g$. To this end, let
$g$. To this end, let ![]() $\beta \in H^3(U,\mathbb {Q}/\mathbb {Z})$ for some big open subset
$\beta \in H^3(U,\mathbb {Q}/\mathbb {Z})$ for some big open subset ![]() $U\subset X$. The class
$U\subset X$. The class ![]() $\alpha ':=\delta (\beta )\in H^4(U,\mathbb {Z})$ is a torsion class. Let
$\alpha ':=\delta (\beta )\in H^4(U,\mathbb {Z})$ is a torsion class. Let ![]() $Z=X\setminus U$. Up to shrinking
$Z=X\setminus U$. Up to shrinking ![]() $X$, we may assume that
$X$, we may assume that ![]() $Z$ is smooth of pure codimension two in
$Z$ is smooth of pure codimension two in ![]() $X$. Then we have an exact sequence as in (3.3) and the (trivial) fact that
$X$. Then we have an exact sequence as in (3.3) and the (trivial) fact that ![]() $H^1(Z,\mathbb {Z})$ is torsion-free implies that the torsion class
$H^1(Z,\mathbb {Z})$ is torsion-free implies that the torsion class ![]() $\alpha '\in H^4(U,\mathbb {Z})$ lifts to a class
$\alpha '\in H^4(U,\mathbb {Z})$ lifts to a class ![]() $\alpha \in H^4(X,\mathbb {Z})$. The fact that
$\alpha \in H^4(X,\mathbb {Z})$. The fact that ![]() $\alpha '$ is torsion implies that some multiple of
$\alpha '$ is torsion implies that some multiple of ![]() $\alpha$ is algebraic and, hence,
$\alpha$ is algebraic and, hence, ![]() $[\alpha ]\in \operatorname {coker}(\operatorname {cl}^2_X\!)_{\operatorname {tors}}$. If
$[\alpha ]\in \operatorname {coker}(\operatorname {cl}^2_X\!)_{\operatorname {tors}}$. If ![]() $\beta$ lifts to a class in
$\beta$ lifts to a class in ![]() $H^3(U,\mathbb {Q})$, then
$H^3(U,\mathbb {Q})$, then ![]() $\alpha '=0$ and so the above construction yields a map
$\alpha '=0$ and so the above construction yields a map
It follows from the construction that ![]() $g$ and
$g$ and ![]() $g'$ are inverse to each other. Hence,
$g'$ are inverse to each other. Hence, ![]() $g$ is an isomorphism and the formula in (3.1) is proved.
$g$ is an isomorphism and the formula in (3.1) is proved.
4. Borel–Moore cohomology
We list here properties of a functor, that we call Borel–Moore cohomology, which allows us to run the arguments from § 3 (and more). Technically speaking, Borel–Moore cohomology will in all our applications agree up to shifts with Borel–Moore homology, see also § 1.4 above. In practice and in terms of sheaf theory, this means that Borel–Moore cohomology will be the hypercohomology of some complex of sheaves on some site; the complex in question has by Poincaré duality the property that it simplifies on smooth equi-dimensional schemes to a locally constant sheaf. In other words, on smooth equi-dimensional varieties, Borel–Moore cohomology will agree with ordinary cohomology. However, on singular spaces, Borel–Moore cohomology and ordinary cohomology differ: for Borel–Moore cohomology we require pullbacks only along open immersions of equi-dimensional schemes (and not along arbitrary morphisms), whereas we require pushforwards along proper morphisms of possibly singular schemes (and not only for smooth equi-dimensional schemes).
Definition 4.1 Let ![]() $\mathcal {V}$ be a category of Noetherian schemes such that the morphisms are given by open immersions
$\mathcal {V}$ be a category of Noetherian schemes such that the morphisms are given by open immersions ![]() $U\hookrightarrow X$ of schemes with
$U\hookrightarrow X$ of schemes with ![]() $\dim (U)=\dim (X\!)$. We call
$\dim (U)=\dim (X\!)$. We call ![]() $\mathcal {V}$ constructible, if for any
$\mathcal {V}$ constructible, if for any ![]() $X\in \mathcal {V}$, the following hold:
$X\in \mathcal {V}$, the following hold:
– if
 $Y\hookrightarrow X$ is an open or closed immersion, then
$Y\hookrightarrow X$ is an open or closed immersion, then  $Y\in \mathcal {V}$;
$Y\in \mathcal {V}$;– if
 $X\in \mathcal {V}$ is reduced, then the normalization of
$X\in \mathcal {V}$ is reduced, then the normalization of  $X$ is also in
$X$ is also in  $\mathcal {V}$.
$\mathcal {V}$.
Definition 4.2 Let ![]() $\mathcal {V}$ be a constructible category of Noetherian schemes as in Definition
$\mathcal {V}$ be a constructible category of Noetherian schemes as in Definition
. Let ![]() $R$ be a ring and let
$R$ be a ring and let ![]() $\mathcal {A}\subset \operatorname {Mod}_R$ be a full subcategory of
$\mathcal {A}\subset \operatorname {Mod}_R$ be a full subcategory of ![]() $R$-modules with
$R$-modules with ![]() $R\in \mathcal {A}$. A twisted Borel–Moore cohomology theory on
$R\in \mathcal {A}$. A twisted Borel–Moore cohomology theory on ![]() $\mathcal {V}$ with coefficients in
$\mathcal {V}$ with coefficients in ![]() $\mathcal {A}$ is a family of contravariant functors
$\mathcal {A}$ is a family of contravariant functors
that are covariant in ![]() $A$ and such that the following holds, where we write for simplicity
$A$ and such that the following holds, where we write for simplicity
(P1) For
 $X,Y\in \mathcal {V}$ and any proper morphism
$X,Y\in \mathcal {V}$ and any proper morphism  $f:X\to Y$ of schemes of relative codimension
$f:X\to Y$ of schemes of relative codimension  $c=\dim Y-\dim X$, there are functorial pushforward maps
compatible with pullbacks along morphisms in
$c=\dim Y-\dim X$, there are functorial pushforward maps
compatible with pullbacks along morphisms in \[ f_\ast : H^{i-2c}(X,A(n-c))\longrightarrow H^{i }(Y,A(n )), \]
\[ f_\ast : H^{i-2c}(X,A(n-c))\longrightarrow H^{i }(Y,A(n )), \]
 $\mathcal {V}$.
$\mathcal {V}$.(P2) For any pair
 $(X,Z)$ of schemes in
$(X,Z)$ of schemes in  $\mathcal {V}$ with a closed immersion
$\mathcal {V}$ with a closed immersion  $Z\hookrightarrow X$ of codimension
$Z\hookrightarrow X$ of codimension  $c=\dim (X\!)-\dim (Z)$ and with complement
$c=\dim (X\!)-\dim (Z)$ and with complement  $U$ with
$U$ with  $\dim (X\!)=\dim (U)$, there is a Gysin exact sequence
where
$\dim (X\!)=\dim (U)$, there is a Gysin exact sequence
where \[ \cdots\longrightarrow H^i(X,A(n))\stackrel{r}{\longrightarrow} H^i(U,A(n))\stackrel{{\partial}}{\longrightarrow} H^{i+1-2c}(Z,A(n-c))\stackrel{{\iota_\ast}}{\longrightarrow} H^{i+1}(X,A(n)) \longrightarrow \cdots \]
\[ \cdots\longrightarrow H^i(X,A(n))\stackrel{r}{\longrightarrow} H^i(U,A(n))\stackrel{{\partial}}{\longrightarrow} H^{i+1-2c}(Z,A(n-c))\stackrel{{\iota_\ast}}{\longrightarrow} H^{i+1}(X,A(n)) \longrightarrow \cdots \]
 $r$ is induced by functoriality,
$r$ is induced by functoriality,  $\partial$ is called residue map and
$\partial$ is called residue map and  $\iota _\ast$ is induced by proper pushforward from (P1). The Gysin sequence is functorial with respect to pullbacks along open immersions
$\iota _\ast$ is induced by proper pushforward from (P1). The Gysin sequence is functorial with respect to pullbacks along open immersions  $f:V\hookrightarrow X$ with
$f:V\hookrightarrow X$ with  $\dim V= \dim X$,
$\dim V= \dim X$,  $\dim (V\cap Z)=\dim Z$, and
$\dim (V\cap Z)=\dim Z$, and  $\dim (V\setminus (V\cap Z))=\dim V$, giving rise to the following commutative diagram for all
$\dim (V\setminus (V\cap Z))=\dim V$, giving rise to the following commutative diagram for all  $i$.
Similarly, if
$i$.
Similarly, if
 $f:X'\to X$ is proper with
$f:X'\to X$ is proper with  $Z'=f^{-1}(Z)$ and
$Z'=f^{-1}(Z)$ and  $\dim X'=\dim (X'\setminus Z')$, then the proper pushforward along
$\dim X'=\dim (X'\setminus Z')$, then the proper pushforward along  $f$ induces for all
$f$ induces for all  $i$ the following commutative diagram.
$i$ the following commutative diagram.

(P3) For any
 $X\in \mathcal {V}$ and
$X\in \mathcal {V}$ and  $x\in X$, the groups
(4.2)where
$x\in X$, the groups
(4.2)where \begin{equation} H^i(x,A(n)):=\lim_{\substack{\longrightarrow\\\emptyset \neq V_x\subset \overline{\{x\}}}} H^i(V_x,A(n)) , \end{equation}
\begin{equation} H^i(x,A(n)):=\lim_{\substack{\longrightarrow\\\emptyset \neq V_x\subset \overline{\{x\}}}} H^i(V_x,A(n)) , \end{equation} $V_x$ runs through all (Zariski) open dense subsets of
$V_x$ runs through all (Zariski) open dense subsets of  $\overline {\{x\}}\subset X$ (with the reduced subscheme structure), satisfy
$\overline {\{x\}}\subset X$ (with the reduced subscheme structure), satisfy  $H^{i}(x,A(n))=0$ for
$H^{i}(x,A(n))=0$ for  $i<0$. Moreover, there are isomorphisms
$i<0$. Moreover, there are isomorphisms  $H^0(x,A(0))\simeq A$ that are functorial in
$H^0(x,A(0))\simeq A$ that are functorial in  $A$, and for
$A$, and for  $A=R$ there is a distinguished class
$A=R$ there is a distinguished class  $[x]\in H^0(x,R(0))$ (called the fundamental class) such that
$[x]\in H^0(x,R(0))$ (called the fundamental class) such that  $H^0(x,R(0))=[x] R$ is freely generated by
$H^0(x,R(0))=[x] R$ is freely generated by  $[x]$.
$[x]$.
Remark 4.3 We warn the reader that even if ![]() $\operatorname {Spec} \kappa (x)\in \mathcal {V}$, the cohomology of a point
$\operatorname {Spec} \kappa (x)\in \mathcal {V}$, the cohomology of a point ![]() $x\in X$ in (4.2) may not agree with
$x\in X$ in (4.2) may not agree with ![]() $H^i(\operatorname {Spec} \kappa (x) ,A(n))$. This phenomenon is not new but already present in [Reference Bloch and OgusBO74] and in any other work where the Bloch–Ogus resolution for non-torsion coefficients is used.
$H^i(\operatorname {Spec} \kappa (x) ,A(n))$. This phenomenon is not new but already present in [Reference Bloch and OgusBO74] and in any other work where the Bloch–Ogus resolution for non-torsion coefficients is used.
In what follows, we usually write ![]() $\mu _{\ell ^r}^{\otimes n}:=\mathbb {Z}/\ell ^r(n)$.
$\mu _{\ell ^r}^{\otimes n}:=\mathbb {Z}/\ell ^r(n)$.
Definition 4.4 Let ![]() $\mathcal {V}$ be a constructible category of Noetherian schemes as in Definition 4.1. Let
$\mathcal {V}$ be a constructible category of Noetherian schemes as in Definition 4.1. Let ![]() $\ell$ be a prime and let
$\ell$ be a prime and let ![]() $R=\mathbb {Z}_\ell$. A twisted Borel–Moore cohomology theory on
$R=\mathbb {Z}_\ell$. A twisted Borel–Moore cohomology theory on ![]() $\mathcal {V}$ with coefficients in
$\mathcal {V}$ with coefficients in ![]() $\mathcal {A}\subset \operatorname {Mod}_{\mathbb {Z}_\ell }$ (see Definition 4.2) is called
$\mathcal {A}\subset \operatorname {Mod}_{\mathbb {Z}_\ell }$ (see Definition 4.2) is called ![]() $\ell$-adic, if
$\ell$-adic, if ![]() $\mathbb {Z}_\ell$,
$\mathbb {Z}_\ell$, ![]() $\mathbb {Q}_\ell$,
$\mathbb {Q}_\ell$, ![]() $\mathbb {Q}_\ell /\mathbb {Z}_\ell$, and
$\mathbb {Q}_\ell /\mathbb {Z}_\ell$, and ![]() $\mathbb {Z}/\ell ^r$ for all
$\mathbb {Z}/\ell ^r$ for all ![]() $r\geqslant 1$ are contained in
$r\geqslant 1$ are contained in ![]() $\mathcal {A}$, such that the following hold.
$\mathcal {A}$, such that the following hold.
(P4) Functoriality in the coefficients induces isomorphisms of functors
 \[ \lim_{\substack{\longrightarrow\\r}} H^i(-,\mu_{\ell^r}^{\otimes n})\stackrel{{\sim}}{\longrightarrow} H^i(-,\mathbb{Q}_\ell/\mathbb{Z}_{\ell}(n)) \quad \text{and}\quad H^i(-,\mathbb{Z}_{\ell}(n))\otimes_{\mathbb{Z}_\ell}\mathbb{Q}_{\ell}\stackrel{{\sim}}{\longrightarrow} H^i(-,\mathbb{Q}_{\ell}(n)) . \]
\[ \lim_{\substack{\longrightarrow\\r}} H^i(-,\mu_{\ell^r}^{\otimes n})\stackrel{{\sim}}{\longrightarrow} H^i(-,\mathbb{Q}_\ell/\mathbb{Z}_{\ell}(n)) \quad \text{and}\quad H^i(-,\mathbb{Z}_{\ell}(n))\otimes_{\mathbb{Z}_\ell}\mathbb{Q}_{\ell}\stackrel{{\sim}}{\longrightarrow} H^i(-,\mathbb{Q}_{\ell}(n)) . \]
(P5) For any
 $X\in \mathcal {V}$, there is a long exact Bockstein sequence
where
$X\in \mathcal {V}$, there is a long exact Bockstein sequence
where \[ \cdots \longrightarrow H^i(X,\mathbb{Z}_\ell(n))\stackrel{{\times \ell^r}}{\longrightarrow} H^i(X,\mathbb{Z}_\ell(n)) \longrightarrow H^i(X,\mu_{\ell^r}^{\otimes n}) \stackrel{{\partial}}{\longrightarrow} H^{i+1}(X,\mathbb{Z}_\ell(n)) \stackrel{{\times \ell^r}}{\longrightarrow} \cdots, \]
\[ \cdots \longrightarrow H^i(X,\mathbb{Z}_\ell(n))\stackrel{{\times \ell^r}}{\longrightarrow} H^i(X,\mathbb{Z}_\ell(n)) \longrightarrow H^i(X,\mu_{\ell^r}^{\otimes n}) \stackrel{{\partial}}{\longrightarrow} H^{i+1}(X,\mathbb{Z}_\ell(n)) \stackrel{{\times \ell^r}}{\longrightarrow} \cdots, \]
 $H^i(X,\mathbb {Z}_\ell (n)) \to H^i(X,\mu _{\ell ^r}^{\otimes n})$ is given by functoriality in the coefficients and where
$H^i(X,\mathbb {Z}_\ell (n)) \to H^i(X,\mu _{\ell ^r}^{\otimes n})$ is given by functoriality in the coefficients and where  $\delta$ is called the Bockstein map. This sequence is functorial with respect to proper pushforwards and pullbacks along morphisms in
$\delta$ is called the Bockstein map. This sequence is functorial with respect to proper pushforwards and pullbacks along morphisms in  $\mathcal {V}$.
$\mathcal {V}$.(P6) For any
 $X\in \mathcal {V}$ and
$X\in \mathcal {V}$ and  $x\in X$, there is a map
$x\in X$, there is a map  $\epsilon : \kappa (x)^\ast \to H^1( x,\mathbb {Z}_\ell (1))$ such that Hilbert theorem 90 holds in the sense that the map
$\epsilon : \kappa (x)^\ast \to H^1( x,\mathbb {Z}_\ell (1))$ such that Hilbert theorem 90 holds in the sense that the map  $\overline {\epsilon }:\kappa (x)^\ast \to H^1( x,\mu _{\ell ^r}^{\otimes 1})$ induced by reduction modulo
$\overline {\epsilon }:\kappa (x)^\ast \to H^1( x,\mu _{\ell ^r}^{\otimes 1})$ induced by reduction modulo  $\ell ^r$ is surjective. Moreover, for
$\ell ^r$ is surjective. Moreover, for  $X\in \mathcal {V}$ integral with generic point
$X\in \mathcal {V}$ integral with generic point  $\eta$, there is a unit
$\eta$, there is a unit  $u\in \mathbb {Z}_\ell$ such that for any regular point
$u\in \mathbb {Z}_\ell$ such that for any regular point  $x\in X^{(1)}$, the natural composition
where
$x\in X^{(1)}$, the natural composition
where \[ \kappa(\eta)^\ast \stackrel{{\epsilon}}{\longrightarrow} H^1(\eta,\mathbb{Z}_{\ell}(1))\stackrel{{\partial}}{\longrightarrow} H^0( x ,\mathbb{Z}_{\ell}(0))=[x] \mathbb{Z}_{\ell}, \]
\[ \kappa(\eta)^\ast \stackrel{{\epsilon}}{\longrightarrow} H^1(\eta,\mathbb{Z}_{\ell}(1))\stackrel{{\partial}}{\longrightarrow} H^0( x ,\mathbb{Z}_{\ell}(0))=[x] \mathbb{Z}_{\ell}, \]
 $\partial$ is induced by (P2) and the last equality comes from (P3), sends
$\partial$ is induced by (P2) and the last equality comes from (P3), sends  $f$ to
$f$ to  $[x](u\cdot \nu _x(f))$. Here,
$[x](u\cdot \nu _x(f))$. Here,  $\nu _x$ denotes the valuation on
$\nu _x$ denotes the valuation on  $\kappa (\eta )$ induced by
$\kappa (\eta )$ induced by  $x$.
$x$.
Let ![]() $X\in \mathcal {V}$ be integral and let
$X\in \mathcal {V}$ be integral and let ![]() $U\subset X$ be a big open subset, i.e.
$U\subset X$ be a big open subset, i.e. ![]() $\dim (X\setminus U)<\dim X-1$. Then
$\dim (X\setminus U)<\dim X-1$. Then ![]() $H^2(U,\mathbb {Z}_\ell (1))\simeq H^2(X,\mathbb {Z}_\ell (1))$ by (P2) and (P3) (see Corollary 5.10 below). Taking the direct limit over all
$H^2(U,\mathbb {Z}_\ell (1))\simeq H^2(X,\mathbb {Z}_\ell (1))$ by (P2) and (P3) (see Corollary 5.10 below). Taking the direct limit over all ![]() $U$ and using
$U$ and using ![]() $H^0(x,\mathbb {Z}_\ell (0))=[x]\mathbb {Z}_\ell$ from (P3), we find that the proper pushforwards from (P1) induce a cycle class map
$H^0(x,\mathbb {Z}_\ell (0))=[x]\mathbb {Z}_\ell$ from (P3), we find that the proper pushforwards from (P1) induce a cycle class map
The following two options are of particular interest.
(P7.1) If
 $X$ is integral and regular, the kernel of (4.3) is given by
$X$ is integral and regular, the kernel of (4.3) is given by  $\mathbb {Z}_\ell$-linear combinations of algebraically trivial divisors.
$\mathbb {Z}_\ell$-linear combinations of algebraically trivial divisors.(P7.2) If
 $X$ is integral and regular, the kernel of (4.3) is given by
$X$ is integral and regular, the kernel of (4.3) is given by  $\mathbb {Z}_\ell$-linear combinations of principal divisors.
$\mathbb {Z}_\ell$-linear combinations of principal divisors.
Definition 4.5 Let ![]() $\mathcal {V}$ be a constructible category of Noetherian schemes, see Definition 4.1. An
$\mathcal {V}$ be a constructible category of Noetherian schemes, see Definition 4.1. An ![]() $\ell$-adic twisted Borel–Moore cohomology theory
$\ell$-adic twisted Borel–Moore cohomology theory ![]() $H^\ast (-,A(n))$ on
$H^\ast (-,A(n))$ on ![]() $\mathcal {V}$ as in Definition 4.4 is adapted to algebraic equivalence, if (P7.1) holds, and it is adapted to rational equivalence, if (P7.2) holds.
$\mathcal {V}$ as in Definition 4.4 is adapted to algebraic equivalence, if (P7.1) holds, and it is adapted to rational equivalence, if (P7.2) holds.
In addition to ![]() $\ell$-adic theories, we also need the following integral variant. To this end, we perform in each of the statements (P4)–(P6), (P7.1), and (P7.2) the formal replacement of symbols:
$\ell$-adic theories, we also need the following integral variant. To this end, we perform in each of the statements (P4)–(P6), (P7.1), and (P7.2) the formal replacement of symbols:
and denote the corresponding statements by (P4![]() $'$)–(P6
$'$)–(P6![]() $'$), (P7.1
$'$), (P7.1![]() $'$), and (P7.2
$'$), and (P7.2![]() $'$), respectively.
$'$), respectively.
Definition 4.6 Let ![]() $\mathcal {V}$ be a constructible category of Noetherian schemes (see Definition 4.1) and let
$\mathcal {V}$ be a constructible category of Noetherian schemes (see Definition 4.1) and let ![]() $R=\mathbb {Z}$. A twisted Borel–Moore cohomology theory on
$R=\mathbb {Z}$. A twisted Borel–Moore cohomology theory on ![]() $\mathcal {V}$ with coefficients in
$\mathcal {V}$ with coefficients in ![]() $\mathcal {A}\subset \operatorname {Mod}_{\mathbb {Z}}$ as in Definition 4.2 is called integral, if
$\mathcal {A}\subset \operatorname {Mod}_{\mathbb {Z}}$ as in Definition 4.2 is called integral, if ![]() $\mathbb {Z}$,
$\mathbb {Z}$, ![]() $\mathbb {Q}$,
$\mathbb {Q}$, ![]() $\mathbb {Q}/\mathbb {Z}$, and
$\mathbb {Q}/\mathbb {Z}$, and ![]() $\mathbb {Z}/r$ for all
$\mathbb {Z}/r$ for all ![]() $r\geqslant 1$ are contained in
$r\geqslant 1$ are contained in ![]() $\mathcal {A}$, such that items (P4
$\mathcal {A}$, such that items (P4![]() $'$)–(P6
$'$)–(P6![]() $'$) hold. The theory is adapted to algebraic (respectively, rational) equivalence, if item (P7.1
$'$) hold. The theory is adapted to algebraic (respectively, rational) equivalence, if item (P7.1![]() $'$) (respectively, (P7.2
$'$) (respectively, (P7.2![]() $'$)) holds true.
$'$)) holds true.
Remark 4.7 It seems natural to add in (P1) the requirement that pushforwards are compatible with the functoriality in the coefficients. We did not do so because in this paper we only need this compatibility for the natural maps ![]() $\mathbb {Z}_\ell \stackrel {\times \ell }{\to } \mathbb {Z}_\ell$,
$\mathbb {Z}_\ell \stackrel {\times \ell }{\to } \mathbb {Z}_\ell$, ![]() $\mathbb {Z}_\ell \to \mathbb {Z}/\ell ^r$,
$\mathbb {Z}_\ell \to \mathbb {Z}/\ell ^r$, ![]() $\mathbb {Z}_\ell \to \mathbb {Q}_\ell$, and
$\mathbb {Z}_\ell \to \mathbb {Q}_\ell$, and ![]() $\mathbb {Q}_\ell \to \mathbb {Q}_\ell /\mathbb {Z}_\ell$, where it follows from (P4) together with the compatibility of the Bockstein sequence with proper pushforwards formulated in (P5).
$\mathbb {Q}_\ell \to \mathbb {Q}_\ell /\mathbb {Z}_\ell$, where it follows from (P4) together with the compatibility of the Bockstein sequence with proper pushforwards formulated in (P5).
5. Definition of refined unramified cohomology and simple consequences
In this section, we fix a constructible category ![]() $\mathcal {V}$ of Noetherian schemes, see Definition 4.1. We further fix a ring
$\mathcal {V}$ of Noetherian schemes, see Definition 4.1. We further fix a ring ![]() $R$ and a twisted Borel–Moore cohomology theory
$R$ and a twisted Borel–Moore cohomology theory ![]() $H^\ast (-,A(n))$ on
$H^\ast (-,A(n))$ on ![]() $\mathcal {V}$ with coefficients in a full subcategory
$\mathcal {V}$ with coefficients in a full subcategory ![]() $\mathcal {A}\subset \operatorname {Mod}_R$, see Definition 4.2. In particular, (P1)–(P3) hold true.
$\mathcal {A}\subset \operatorname {Mod}_R$, see Definition 4.2. In particular, (P1)–(P3) hold true.
For ![]() $X\in \mathcal {V}$ we write
$X\in \mathcal {V}$ we write ![]() $F_jX:=\{x\in X\mid \operatorname {codim}(x)\leqslant j \}$, where
$F_jX:=\{x\in X\mid \operatorname {codim}(x)\leqslant j \}$, where ![]() $\operatorname {codim}(x):=\dim (X\!)- \dim (\overline {\{x\}})$. We then define
$\operatorname {codim}(x):=\dim (X\!)- \dim (\overline {\{x\}})$. We then define
where the direct limit runs through all open subschemes ![]() $U\subset X$ with
$U\subset X$ with ![]() $F_jX\subset U$. As the direct limit functor (i.e. filtered colimits) is exact, many of the properties of
$F_jX\subset U$. As the direct limit functor (i.e. filtered colimits) is exact, many of the properties of ![]() $H^\ast (X,A(n))$ remain true for
$H^\ast (X,A(n))$ remain true for ![]() $F_jX$ in place of
$F_jX$ in place of ![]() $X$. Moreover, for
$X$. Moreover, for ![]() $m\geqslant j$, there are canonical restriction maps
$m\geqslant j$, there are canonical restriction maps ![]() $H^i(F_mX,A(n)) \to H^i(F_jX,A(n))$.
$H^i(F_mX,A(n)) \to H^i(F_jX,A(n))$.
Definition 5.1 The ![]() $j$th refined unramified cohomology of
$j$th refined unramified cohomology of ![]() $X\in \mathcal {V}$ with respect to a twisted Borel–Moore cohomology theory
$X\in \mathcal {V}$ with respect to a twisted Borel–Moore cohomology theory ![]() $H^\ast (-,A(n))$ on
$H^\ast (-,A(n))$ on ![]() $\mathcal {V}$ with coefficients in a full subcategory
$\mathcal {V}$ with coefficients in a full subcategory ![]() $\mathcal {A}\subset \operatorname {Mod}_R$, is given by
$\mathcal {A}\subset \operatorname {Mod}_R$, is given by
5.1 Three filtrations
Following Grothendieck, the coniveau filtration on ![]() $H^i(X,A(n))$ is defined by
$H^i(X,A(n))$ is defined by
There is a similar coniveau filtration on refined unramified cohomology, defined as follows.
Definition 5.2 Let ![]() $X\in \mathcal {V}$. The coniveau filtration
$X\in \mathcal {V}$. The coniveau filtration ![]() $N^\ast$ is for
$N^\ast$ is for ![]() $h\leqslant j+1$ given by
$h\leqslant j+1$ given by
and
Somewhat dually to the coniveau filtration, we have the following filtration, which is also decreasing.
Definition 5.3 Let ![]() $X\in \mathcal {V}$. The decreasing filtration
$X\in \mathcal {V}$. The decreasing filtration ![]() $F^\ast$ is for
$F^\ast$ is for ![]() $m\geqslant j$ given by
$m\geqslant j$ given by
and
Note that for ![]() $m\geqslant j+1$,
$m\geqslant j+1$, ![]() $F^m H^i(F_jX,A(n))=F^mH^i_{j,{\rm nr}}(X,A(n))$.
$F^m H^i(F_jX,A(n))=F^mH^i_{j,{\rm nr}}(X,A(n))$.
Related to ![]() $F^\ast$ there is another filtration that will be important for us, and which exists only for
$F^\ast$ there is another filtration that will be important for us, and which exists only for ![]() $A=\mathbb {Z}/\ell ^r$ or
$A=\mathbb {Z}/\ell ^r$ or ![]() $A=\mathbb {Q}_\ell /\mathbb {Z}_\ell$. To define it, note that exactness of the direct limit functor ensures that the Bockstein sequence in (P5) holds for
$A=\mathbb {Q}_\ell /\mathbb {Z}_\ell$. To define it, note that exactness of the direct limit functor ensures that the Bockstein sequence in (P5) holds for ![]() $F_jX$ in place of
$F_jX$ in place of ![]() $X$. In particular, there is a Bockstein map
$X$. In particular, there is a Bockstein map
Definition 5.4 Let ![]() $X\in \mathcal {V}$. The decreasing filtration
$X\in \mathcal {V}$. The decreasing filtration ![]() $G^\ast$ is for
$G^\ast$ is for ![]() $m\geqslant j$ given by
$m\geqslant j$ given by
We then define
Using the isomorphism in (P4), we finally let
Remark 5.5 By definition, ![]() $F^\ast$ and
$F^\ast$ and ![]() $N^\ast$ on
$N^\ast$ on ![]() $H^i_{j,{\rm nr}}(X,A(n))$ are induced by the corresponding filtration on
$H^i_{j,{\rm nr}}(X,A(n))$ are induced by the corresponding filtration on ![]() $H^i(F_jX,A(n))$. We warn the reader that the corresponding assertion does not hold true for
$H^i(F_jX,A(n))$. We warn the reader that the corresponding assertion does not hold true for ![]() $G^\ast$.
$G^\ast$.
5.2 Consequence of the Gysin sequence
Lemma 5.6 Let ![]() $X\sqcup Y\in \mathcal {V}$ with
$X\sqcup Y\in \mathcal {V}$ with ![]() $\dim X=\dim Y$ and let
$\dim X=\dim Y$ and let ![]() $A\in \mathcal {A}$. Then the canonical map given by pullback is an isomorphism:
$A\in \mathcal {A}$. Then the canonical map given by pullback is an isomorphism:
Proof. Let ![]() $i_X$ (respectively,
$i_X$ (respectively, ![]() $i_Y$) denote the inclusions of
$i_Y$) denote the inclusions of ![]() $X$ (respectively,
$X$ (respectively, ![]() $Y$) into
$Y$) into ![]() $X\sqcup Y$. By the Gysin sequence (P2), we have an exact sequence
$X\sqcup Y$. By the Gysin sequence (P2), we have an exact sequence
Functoriality of this sequence with respect to proper pushforward and pullbacks along morphisms in ![]() $\mathcal {V}$ shows that
$\mathcal {V}$ shows that ![]() $i_{X\ast }$ and
$i_{X\ast }$ and ![]() $i_Y^\ast$ admit splittings. Hence, the above sequence is part of a short exact sequence that splits, which proves the lemma.
$i_Y^\ast$ admit splittings. Hence, the above sequence is part of a short exact sequence that splits, which proves the lemma.
Lemma 5.7 Let ![]() $X\in \mathcal {V}$ and
$X\in \mathcal {V}$ and ![]() $A\in \mathcal {A}$. Then for any
$A\in \mathcal {A}$. Then for any ![]() $n\in \mathbb {Z}$ and
$n\in \mathbb {Z}$ and ![]() $m,j\geqslant 0$, the Gysin sequence in (P2) induces a long exact sequence:
$m,j\geqslant 0$, the Gysin sequence in (P2) induces a long exact sequence:
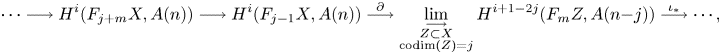 \[ \cdots \longrightarrow H^i( F_{j+m}X,A(n)) \longrightarrow H^i(F_{j-1}X,A(n)) \stackrel{{\partial}}{\longrightarrow} \lim_{\substack{\longrightarrow \\ Z\subset X\\ \operatorname{codim}(Z)=j}} H^{i+1-2j}( F_mZ,A(n-j)) \stackrel{{\iota_\ast}}{\longrightarrow} \cdots , \]
\[ \cdots \longrightarrow H^i( F_{j+m}X,A(n)) \longrightarrow H^i(F_{j-1}X,A(n)) \stackrel{{\partial}}{\longrightarrow} \lim_{\substack{\longrightarrow \\ Z\subset X\\ \operatorname{codim}(Z)=j}} H^{i+1-2j}( F_mZ,A(n-j)) \stackrel{{\iota_\ast}}{\longrightarrow} \cdots , \]
where the direct limit runs through all closed reduced subschemes ![]() $Z\subset X$ of codimension
$Z\subset X$ of codimension ![]() $\operatorname {codim}(Z)=\dim X-\dim Z=j$.
$\operatorname {codim}(Z)=\dim X-\dim Z=j$.
Proof. This follows immediately from (P2) by taking direct limits. We explain the details for convenience of the reader. Let ![]() $Z\subset X$ be closed with
$Z\subset X$ be closed with ![]() $\dim Z=\dim X-j$. Further, let
$\dim Z=\dim X-j$. Further, let ![]() $W\subset Z$ be closed of dimension
$W\subset Z$ be closed of dimension ![]() $\dim W=\dim Z-m-1=\dim X-j-m-1$. By (P2), we get an exact sequence
$\dim W=\dim Z-m-1=\dim X-j-m-1$. By (P2), we get an exact sequence
We can now consider the index set ![]() $I$ that consists of pairs
$I$ that consists of pairs ![]() $(Z,W)$ of closed subsets
$(Z,W)$ of closed subsets ![]() $W\subset Z\subset X$ with
$W\subset Z\subset X$ with ![]() $\dim W=\dim Z-m-1=\dim X-j-m-1$. This is a directed set with respect to the preorder given by declaring
$\dim W=\dim Z-m-1=\dim X-j-m-1$. This is a directed set with respect to the preorder given by declaring ![]() $(Z,W)\leqslant (Z',W')$ if and only if
$(Z,W)\leqslant (Z',W')$ if and only if ![]() $Z\subset Z'$ and
$Z\subset Z'$ and ![]() $W\subset W'$. Taking the direct limit over this index set, the above long exact sequence yields the sequence
$W\subset W'$. Taking the direct limit over this index set, the above long exact sequence yields the sequence
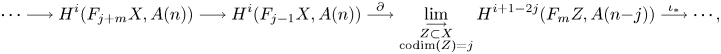 \[ \cdots \longrightarrow H^i( F_{j+m}X,A(n)) \longrightarrow H^i(F_{j-1}X,A(n)) \stackrel{{\partial}}{\longrightarrow} \lim_{\substack{\longrightarrow \\ Z\subset X\\ \operatorname{codim}(Z)=j}} H^{i+1-2j}( F_mZ,A(n-j)) \stackrel{{\iota_\ast}}{\longrightarrow} \cdots , \]
\[ \cdots \longrightarrow H^i( F_{j+m}X,A(n)) \longrightarrow H^i(F_{j-1}X,A(n)) \stackrel{{\partial}}{\longrightarrow} \lim_{\substack{\longrightarrow \\ Z\subset X\\ \operatorname{codim}(Z)=j}} H^{i+1-2j}( F_mZ,A(n-j)) \stackrel{{\iota_\ast}}{\longrightarrow} \cdots , \]
which is exact because the direct limit functor is exact. This proves the lemma.
Lemma 5.8 Let ![]() $X\in \mathcal {V}$ and
$X\in \mathcal {V}$ and ![]() $A\in \mathcal {A}$. Then for any
$A\in \mathcal {A}$. Then for any ![]() $j,n\in \mathbb {Z}$, (P2) induces a long exact sequence
$j,n\in \mathbb {Z}$, (P2) induces a long exact sequence
where ![]() $\iota _\ast$ (respectively,
$\iota _\ast$ (respectively, ![]() $\partial$) is induced by the pushforward (respectively, residue) map from the Gysin exact sequence (P2).
$\partial$) is induced by the pushforward (respectively, residue) map from the Gysin exact sequence (P2).
Corollary 5.9 Let ![]() $X\in \mathcal {V}$. Then for any
$X\in \mathcal {V}$. Then for any ![]() $n\in \mathbb {Z}$ and
$n\in \mathbb {Z}$ and ![]() $j,m\geqslant 0$, the following sequence is exact:
$j,m\geqslant 0$, the following sequence is exact:
 \[ \lim_{\substack{\longrightarrow \\ Z\subset X\\ \operatorname{codim}(Z)=j}} H^{i-2j}_{m,{\rm nr}}(Z,A(n-j)) \stackrel{{\iota_\ast}}{\longrightarrow} H^i_{j+m,{\rm nr}}( X,A(n)) \longrightarrow H^i_{j-1,{\rm nr}}(X,A(n)) , \]
\[ \lim_{\substack{\longrightarrow \\ Z\subset X\\ \operatorname{codim}(Z)=j}} H^{i-2j}_{m,{\rm nr}}(Z,A(n-j)) \stackrel{{\iota_\ast}}{\longrightarrow} H^i_{j+m,{\rm nr}}( X,A(n)) \longrightarrow H^i_{j-1,{\rm nr}}(X,A(n)) , \]
where the direct limit runs through all closed reduced subschemes ![]() $Z\subset X$ of codimension
$Z\subset X$ of codimension ![]() $\operatorname {codim}(Z)=\dim X-\dim Z=j$.
$\operatorname {codim}(Z)=\dim X-\dim Z=j$.
Proof. The composition of the two arrows in the corollary is zero by Lemma 5.7. Conversely, assume that ![]() $\alpha \in H^i_{j+m,{\rm nr}}( X,A(n))$ maps to zero in
$\alpha \in H^i_{j+m,{\rm nr}}( X,A(n))$ maps to zero in ![]() $H^i_{j-1,{\rm nr}}(X,A(n))$. By Lemma 5.7,
$H^i_{j-1,{\rm nr}}(X,A(n))$. By Lemma 5.7, ![]() $\alpha =\iota _\ast \xi$ for some
$\alpha =\iota _\ast \xi$ for some ![]() $\xi \in H^{i-2j} (F_mZ,A(n-j))$ and some
$\xi \in H^{i-2j} (F_mZ,A(n-j))$ and some ![]() $Z\subset X$ of codimension
$Z\subset X$ of codimension ![]() $j$. As
$j$. As ![]() $\alpha$ is unramified, Lemma 5.8 shows that
$\alpha$ is unramified, Lemma 5.8 shows that
where the first equality uses that the Gysin sequence is functorial with respect to proper pushforwards (see (P2)), so that ![]() $\iota _\ast$ and
$\iota _\ast$ and ![]() $\partial$ commute. However, this implies that the class
$\partial$ commute. However, this implies that the class
vanishes, as the above right-hand side is a subgroup of the right-hand side of (5.2), and ![]() $\iota _\ast$ identifies to the inclusion. Hence, Lemma 5.8 implies
$\iota _\ast$ identifies to the inclusion. Hence, Lemma 5.8 implies ![]() $\xi \in H^{i-2j}_{m,{\rm nr}} (Z,A(n-j))$, as we want. This concludes the proof of the corollary.
$\xi \in H^{i-2j}_{m,{\rm nr}} (Z,A(n-j))$, as we want. This concludes the proof of the corollary.
Corollary 5.10 Let ![]() $X\in \mathcal {V}$ and
$X\in \mathcal {V}$ and ![]() $A\in \mathcal {A}$. Then
$A\in \mathcal {A}$. Then ![]() $H^i(F_jX,A(n))\simeq H^i(X,A(n))$ for all
$H^i(F_jX,A(n))\simeq H^i(X,A(n))$ for all ![]() $j\geqslant \lceil i/2\rceil$.
$j\geqslant \lceil i/2\rceil$.
Proof. As ![]() $H^i(x,A(n))$ vanishes for
$H^i(x,A(n))$ vanishes for ![]() $i<0$ by (P3), Lemma 5.8 implies
$i<0$ by (P3), Lemma 5.8 implies
for all ![]() $j$ with
$j$ with ![]() $j>\lceil i/2\rceil$. This proves the corollary by induction on
$j>\lceil i/2\rceil$. This proves the corollary by induction on ![]() $j$, because
$j$, because ![]() $H^i(F_jX,A(n))=H^i(X,A(n))$ for
$H^i(F_jX,A(n))=H^i(X,A(n))$ for ![]() $j\geqslant \dim (X\!)$.
$j\geqslant \dim (X\!)$.
Corollary 5.11 Let ![]() $X\in \mathcal {V}$ and
$X\in \mathcal {V}$ and ![]() $A\in \mathcal {A}$. Assume that there is a non-negative integer
$A\in \mathcal {A}$. Assume that there is a non-negative integer ![]() $c$, such that for any
$c$, such that for any ![]() $X\in \mathcal {V}$ and
$X\in \mathcal {V}$ and ![]() $x\in X_{(j)}$,
$x\in X_{(j)}$, ![]() $H^i(x,A(n))=0$ for
$H^i(x,A(n))=0$ for ![]() $i>j+c$ and all
$i>j+c$ and all ![]() $n$. Then
$n$. Then ![]() $H^i(F_jX,A(n))=0$ for all
$H^i(F_jX,A(n))=0$ for all ![]() $i>\dim X+j+c$ and all
$i>\dim X+j+c$ and all ![]() $n$.
$n$.
Proof. Our assumption implies by Lemma 5.8 that ![]() $H^i(F_jX,A(n))\simeq H^i(F_{j-1}X,A(n))$ for all
$H^i(F_jX,A(n))\simeq H^i(F_{j-1}X,A(n))$ for all ![]() $j$ with
$j$ with ![]() $i>j+\dim X+c$. Hence,
$i>j+\dim X+c$. Hence, ![]() $H^i(F_jX,A(n))\simeq H^i(F_{0}X,A(n))$ for all
$H^i(F_jX,A(n))\simeq H^i(F_{0}X,A(n))$ for all ![]() $j$ with
$j$ with ![]() $i>j+\dim X+c$. But
$i>j+\dim X+c$. But ![]() $H^i(F_{0}X,A(n))=0$ for all
$H^i(F_{0}X,A(n))=0$ for all ![]() $i>\dim X+c$ by Lemma 5.6 and our assumption, because
$i>\dim X+c$ by Lemma 5.6 and our assumption, because ![]() $F_0X$ is the union of the generic points of the maximal-dimensional components of
$F_0X$ is the union of the generic points of the maximal-dimensional components of ![]() $X$. This proves the corollary.
$X$. This proves the corollary.
The following lemma identifies the differential ![]() $d_1$ on the
$d_1$ on the ![]() $E_1$-page of the coniveau spectral sequence of Bloch and Ogus [Reference Bloch and OgusBO74, § 3] with the composition
$E_1$-page of the coniveau spectral sequence of Bloch and Ogus [Reference Bloch and OgusBO74, § 3] with the composition ![]() $\partial \circ \iota _\ast$.
$\partial \circ \iota _\ast$.
Lemma 5.12 Let ![]() $X\in \mathcal {V}$ and
$X\in \mathcal {V}$ and ![]() $A \in \mathcal {A}$. Let
$A \in \mathcal {A}$. Let ![]() $w\in X^{(p-1)}$ with closure
$w\in X^{(p-1)}$ with closure ![]() $W\subset X$ and let
$W\subset X$ and let ![]() $\tau :\tilde {W}\to W$ be the normalization with generic point
$\tau :\tilde {W}\to W$ be the normalization with generic point ![]() $\eta _{\tilde {W}}\in \tilde {W}$. Then the following diagram commutes for all integers
$\eta _{\tilde {W}}\in \tilde {W}$. Then the following diagram commutes for all integers ![]() $i$ and
$i$ and ![]() $n$:
$n$:
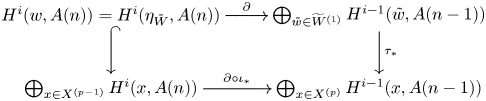
where the vertical arrow on the left is the natural inclusion, the vertical arrow on the right is induced by the proper pushforward maps from (P1), the upper horizontal arrow is induced by the residue map in (P2), and the lower horizontal arrow is given by
where ![]() $\iota _\ast$ (respectively,
$\iota _\ast$ (respectively, ![]() $\partial$) is the pushforward (respectively, residue map) induced by (P2).
$\partial$) is the pushforward (respectively, residue map) induced by (P2).
Proof. Note that ![]() $W\in \mathcal {V}$ and, hence,
$W\in \mathcal {V}$ and, hence, ![]() $\widetilde W\in \mathcal {V}$, cf. Definition 4.1. The lemma is thus a direct consequence of the functoriality of the Gysin sequence (P2) with respect to proper pushforwards (P1), as required in (P2).
$\widetilde W\in \mathcal {V}$, cf. Definition 4.1. The lemma is thus a direct consequence of the functoriality of the Gysin sequence (P2) with respect to proper pushforwards (P1), as required in (P2).
5.3 Torsion-freeness of the cohomology of points
In this section, we fix a prime ![]() $\ell$ and assume that the twisted Borel–Moore cohomology theory
$\ell$ and assume that the twisted Borel–Moore cohomology theory ![]() $H^\ast (-,A(n))$ on
$H^\ast (-,A(n))$ on ![]() $\mathcal {V}$ is
$\mathcal {V}$ is ![]() $\ell$-adic, see Definition 4.4. It is an observation of Bloch (see [Reference BlochBlo10, end of Lecture 5]) that properties (P5) and (P6) have the following important consequence.
$\ell$-adic, see Definition 4.4. It is an observation of Bloch (see [Reference BlochBlo10, end of Lecture 5]) that properties (P5) and (P6) have the following important consequence.
Lemma 5.13 Let ![]() $\mathcal {V}$ be a constructible category of Noetherian schemes as in Definition 4.1. Fix a prime
$\mathcal {V}$ be a constructible category of Noetherian schemes as in Definition 4.1. Fix a prime ![]() $\ell$ and assume that
$\ell$ and assume that ![]() $H^\ast (-,A(n))$ is an
$H^\ast (-,A(n))$ is an ![]() $\ell$-adic twisted Borel–Moore cohomology theory on
$\ell$-adic twisted Borel–Moore cohomology theory on ![]() $\mathcal {V}$ as in Definition 4.4. Then for any
$\mathcal {V}$ as in Definition 4.4. Then for any ![]() $X\in \mathcal {V}$ and
$X\in \mathcal {V}$ and ![]() $x\in X$,
$x\in X$, ![]() $H^i(x,\mathbb {Z}_\ell (i-1))$ is torsion-free for
$H^i(x,\mathbb {Z}_\ell (i-1))$ is torsion-free for ![]() $1\leqslant i\leqslant 2$.
$1\leqslant i\leqslant 2$.
Proof. Taking direct limits of abelian groups is exact, so that property (P5) implies that
This vanishes for ![]() $i=1$, as in this case we have by (P5) an exact sequence
$i=1$, as in this case we have by (P5) an exact sequence
which by (P3) identifies to ![]() $\mathbb {Z}_\ell \stackrel {\times \ell ^r}{\to } \mathbb {Z}_\ell \to \mathbb {Z}/\ell$ and so the last arrow is surjective.
$\mathbb {Z}_\ell \stackrel {\times \ell ^r}{\to } \mathbb {Z}_\ell \to \mathbb {Z}/\ell$ and so the last arrow is surjective.
By (P6), there is a surjection ![]() which factors through
which factors through ![]() $H^{1}(x,\mathbb {Z}_\ell (1))$ and so the above cokernel also vanishes for
$H^{1}(x,\mathbb {Z}_\ell (1))$ and so the above cokernel also vanishes for ![]() $i=2$. This concludes the proof.
$i=2$. This concludes the proof.
Remark 5.14 The above proof shows more generally that ![]() $H^{i+1}(x,\mathbb {Z}_\ell (i))$ is torsion-free if there are surjections
$H^{i+1}(x,\mathbb {Z}_\ell (i))$ is torsion-free if there are surjections ![]() that factor through
that factor through ![]() $H^{i}(x,\mathbb {Z}_{\ell }(i))$. In particular,
$H^{i}(x,\mathbb {Z}_{\ell }(i))$. In particular, ![]() $H^{i+1}(x,\mathbb {Z}_\ell (i))$ is torsion-free if a version of the Bloch–Kato conjecture holds in degree
$H^{i+1}(x,\mathbb {Z}_\ell (i))$ is torsion-free if a version of the Bloch–Kato conjecture holds in degree ![]() $i$ in the sense that there is a map
$i$ in the sense that there is a map ![]() $K^M_i(\kappa (x))\to H^i(x,\mathbb {Z}_\ell (i))$ which induces isomorphisms
$K^M_i(\kappa (x))\to H^i(x,\mathbb {Z}_\ell (i))$ which induces isomorphisms ![]() $K^M_i(\kappa (x))/\ell ^r\simeq H^i(x,\mu _{\ell ^r}^{\otimes i})$. It follows from Voevodsky's proof of the Bloch–Kato conjecture [Reference VoevodskyVoe11] that the theories that we discuss in Propositions 6.6 and 6.9 have this property.
$K^M_i(\kappa (x))/\ell ^r\simeq H^i(x,\mu _{\ell ^r}^{\otimes i})$. It follows from Voevodsky's proof of the Bloch–Kato conjecture [Reference VoevodskyVoe11] that the theories that we discuss in Propositions 6.6 and 6.9 have this property.
6. Examples of Borel–Moore cohomologies
In this section, we discuss some examples of functors that satisfy the properties from § 4. The results are certainly well-known to experts and we only include them for convenience of the reader.
6.1  $\ell$-adic Borel–Moore pro-étale cohomology
$\ell$-adic Borel–Moore pro-étale cohomology
6.1.1 Continuous étale cohomology of Jannsen
Let ![]() $X$ be a scheme over a field
$X$ be a scheme over a field ![]() $k$ and let
$k$ and let ![]() $\operatorname {Ab}(X_{\unicode{x00E9}{\rm t}})^{\mathbb {N}}$ be the abelian category of inverse systems of abelian étale sheaves on the small étale site
$\operatorname {Ab}(X_{\unicode{x00E9}{\rm t}})^{\mathbb {N}}$ be the abelian category of inverse systems of abelian étale sheaves on the small étale site ![]() $X_{\unicode{x00E9}{\rm t}}$ of
$X_{\unicode{x00E9}{\rm t}}$ of ![]() $X$. This category has enough injectives (see [Reference JannsenJan88]) and we may consider the left exact functor
$X$. This category has enough injectives (see [Reference JannsenJan88]) and we may consider the left exact functor
Jannsen then defines the continuous étale cohomology groups
These groups are closely related to the corresponding étale cohomology groups via the following canonical short exact sequence (see [Reference JannsenJan88, § 1.6]):
where ![]() $\varprojlim$ denotes the inverse limit functor over
$\varprojlim$ denotes the inverse limit functor over ![]() $r$.
$r$.
By [Reference JannsenJan88, (3.27)], we have the following Kummer exact sequence in ![]() $\operatorname {Ab}(X_{\unicode{x00E9}{\rm t}})^{\mathbb {N}}$:
$\operatorname {Ab}(X_{\unicode{x00E9}{\rm t}})^{\mathbb {N}}$:
where ![]() $\ell$ is a prime invertible in
$\ell$ is a prime invertible in ![]() $k$. Taking cohomology, the boundary map of the corresponding long exact sequence yields maps
$k$. Taking cohomology, the boundary map of the corresponding long exact sequence yields maps
where ![]() $H^i_{\rm cont}(X,\mathbb {Z}_\ell (n)):=H^i_{\rm cont}(X,(\mu _{\ell ^r}^{\otimes n})_r)$.
$H^i_{\rm cont}(X,\mathbb {Z}_\ell (n)):=H^i_{\rm cont}(X,(\mu _{\ell ^r}^{\otimes n})_r)$.
6.1.2 Pro-étale cohomology of Bhatt and Scholze
For a scheme ![]() $X$ we denote by
$X$ we denote by ![]() $X_{\text{pro}{\unicode{x00E9}} {\rm t}}$ the pro-étale site of
$X_{\text{pro}{\unicode{x00E9}} {\rm t}}$ the pro-étale site of ![]() $X$ formed by weakly étale maps of schemes
$X$ formed by weakly étale maps of schemes ![]() $U\to X$ (with
$U\to X$ (with ![]() $U$ of not too big cardinality), see [Reference Bhatt and ScholzeBS15, Definition 4.1.1 and Remark 4.1.2]. As every étale map is weakly étale, there is a natural map of associated topoi:
$U$ of not too big cardinality), see [Reference Bhatt and ScholzeBS15, Definition 4.1.1 and Remark 4.1.2]. As every étale map is weakly étale, there is a natural map of associated topoi:
The pullback ![]() $\nu ^\ast :D^+(X_{\unicode{x00E9}{\rm t}})\to D^+(X_{\text{pro}{\unicode{x00E9}} {\rm t}})$ on bounded below derived categories is fully faithful and the adjunction
$\nu ^\ast :D^+(X_{\unicode{x00E9}{\rm t}})\to D^+(X_{\text{pro}{\unicode{x00E9}} {\rm t}})$ on bounded below derived categories is fully faithful and the adjunction ![]() $\operatorname {id}\to \operatorname {R} \nu _\ast \nu ^\ast$ is an isomorphism, see [Reference Bhatt and ScholzeBS15, Proposition 5.2.6]. For a sheaf
$\operatorname {id}\to \operatorname {R} \nu _\ast \nu ^\ast$ is an isomorphism, see [Reference Bhatt and ScholzeBS15, Proposition 5.2.6]. For a sheaf ![]() $F\in \operatorname {Ab}(X_{\text{pro}{\unicode{x00E9}} {\rm t}})$ of abelian groups on
$F\in \operatorname {Ab}(X_{\text{pro}{\unicode{x00E9}} {\rm t}})$ of abelian groups on ![]() $X_{\text{pro}{\unicode{x00E9}} {\rm t}}$, one defines
$X_{\text{pro}{\unicode{x00E9}} {\rm t}}$, one defines
where ![]() $\operatorname {R}^i \Gamma$ denotes the
$\operatorname {R}^i \Gamma$ denotes the ![]() $i$th right derived functor of the global section functor
$i$th right derived functor of the global section functor ![]() .
.
If the transition maps in the inverse system ![]() $(F_r)\in \operatorname {Ab}(X_{\unicode{x00E9}{\rm t}})^{\mathbb {N}}$ are surjective, then there is a canonical isomorphism
$(F_r)\in \operatorname {Ab}(X_{\unicode{x00E9}{\rm t}})^{\mathbb {N}}$ are surjective, then there is a canonical isomorphism
see [Reference Bhatt and ScholzeBS15, § 5.6].
6.1.3 Constructible complexes in the pro-étale topology
We present in this section some parts of the six functor formalism on constructible complexes of Bhatt and Scholze in the special case of algebraic schemes, i.e. separated schemes of finite type over a field, which suffices for our purposes. In Remark 6.3 we add some comments on the more general setting from [Reference Bhatt and ScholzeBS15].
Let ![]() $X$ be an algebraic scheme over a field
$X$ be an algebraic scheme over a field ![]() $k$ and recall
$k$ and recall ![]() $\nu$ from (6.4). For a prime
$\nu$ from (6.4). For a prime ![]() $\ell$ invertible in
$\ell$ invertible in ![]() $k$, let
$k$, let
and write ![]() $\widehat {\mathbb {Z}}_\ell :=\widehat {\mathbb {Z}}_\ell (0)$. Note that
$\widehat {\mathbb {Z}}_\ell :=\widehat {\mathbb {Z}}_\ell (0)$. Note that ![]() $\widehat {\mathbb {Z}}_\ell$ is a sheaf of rings on
$\widehat {\mathbb {Z}}_\ell$ is a sheaf of rings on ![]() $X_{\text{pro}{\unicode{x00E9}} {\rm t}}$ and
$X_{\text{pro}{\unicode{x00E9}} {\rm t}}$ and ![]() $\widehat {\mathbb {Z}}_\ell (n)$ are
$\widehat {\mathbb {Z}}_\ell (n)$ are ![]() $\widehat {\mathbb {Z}}_\ell$-modules, which are, in fact, locally free (e.g. they are free on the pro-étale covering
$\widehat {\mathbb {Z}}_\ell$-modules, which are, in fact, locally free (e.g. they are free on the pro-étale covering ![]() $X_{\overline {k}}\to X$). We may then consider the derived category
$X_{\overline {k}}\to X$). We may then consider the derived category ![]() $D(X_{\text{pro}{\unicode{x00E9}} {\rm t}},\widehat {\mathbb {Z}}_\ell )$ of the abelian category
$D(X_{\text{pro}{\unicode{x00E9}} {\rm t}},\widehat {\mathbb {Z}}_\ell )$ of the abelian category ![]() $\operatorname {Mod}(X_{\text{pro}{\unicode{x00E9}} {\rm t}},\widehat {\mathbb {Z}}_\ell )$ of sheaves of
$\operatorname {Mod}(X_{\text{pro}{\unicode{x00E9}} {\rm t}},\widehat {\mathbb {Z}}_\ell )$ of sheaves of ![]() $\widehat {\mathbb {Z}}_\ell$-modules on
$\widehat {\mathbb {Z}}_\ell$-modules on ![]() $X_{\text{pro}{\unicode{x00E9}} {\rm t}}$. A complex
$X_{\text{pro}{\unicode{x00E9}} {\rm t}}$. A complex ![]() $K\in D(X_{\text{pro}{\unicode{x00E9}} {\rm t}},\widehat {\mathbb {Z}}_\ell )$ is constructible, if it is complete, i.e.
$K\in D(X_{\text{pro}{\unicode{x00E9}} {\rm t}},\widehat {\mathbb {Z}}_\ell )$ is constructible, if it is complete, i.e. ![]() $K\stackrel {\simeq }{\to } \operatorname {R} \lim (K\otimes ^{\mathbb {L}}_{\widehat {\mathbb {Z}}_\ell } \mathbb {Z}/\ell ^r)$, and
$K\stackrel {\simeq }{\to } \operatorname {R} \lim (K\otimes ^{\mathbb {L}}_{\widehat {\mathbb {Z}}_\ell } \mathbb {Z}/\ell ^r)$, and ![]() $K\otimes ^{\mathbb {L}}_{\widehat {\mathbb {Z}}_\ell } \mathbb {Z}/\ell ^r\simeq \nu ^\ast K_r$ for a constructible complex
$K\otimes ^{\mathbb {L}}_{\widehat {\mathbb {Z}}_\ell } \mathbb {Z}/\ell ^r\simeq \nu ^\ast K_r$ for a constructible complex ![]() $K_r\in D(X_{\unicode{x00E9}{\rm t}},\mathbb {Z}/\ell ^r)$, see [Reference Bhatt and ScholzeBS15, Definition 6.5.1]. The full subcategory spanned by constructible complexes is denoted by
$K_r\in D(X_{\unicode{x00E9}{\rm t}},\mathbb {Z}/\ell ^r)$, see [Reference Bhatt and ScholzeBS15, Definition 6.5.1]. The full subcategory spanned by constructible complexes is denoted by ![]() $D_{\rm cons}(X_{\text{pro}{\unicode{x00E9}} {\rm t}},\widehat {\mathbb {Z}}_\ell )\subset D(X_{\text{pro}{\unicode{x00E9}} {\rm t}},\widehat {\mathbb {Z}}_\ell )$. Constructible complexes are bounded, see [Reference Bhatt and ScholzeBS15, Lemma 6.5.3].
$D_{\rm cons}(X_{\text{pro}{\unicode{x00E9}} {\rm t}},\widehat {\mathbb {Z}}_\ell )\subset D(X_{\text{pro}{\unicode{x00E9}} {\rm t}},\widehat {\mathbb {Z}}_\ell )$. Constructible complexes are bounded, see [Reference Bhatt and ScholzeBS15, Lemma 6.5.3].
For a morphism ![]() $f:X\to Y$ of algebraic schemes,
$f:X\to Y$ of algebraic schemes, ![]() $\operatorname {R} f_\ast$ respects constructibility and is right adjoint to
$\operatorname {R} f_\ast$ respects constructibility and is right adjoint to ![]() $f^\ast _{\rm comp}:D_{\rm cons}(Y_{\text{pro}{\unicode{x00E9}} {\rm t}},\widehat {\mathbb {Z}}_\ell )\to D_{\rm cons}(X_{\text{pro}{\unicode{x00E9}} {\rm t}},\widehat {\mathbb {Z}}_\ell )$, which is given by pullback followed by (derived) completion, see [Reference Bhatt and ScholzeBS15, Lemma 6.7.2]. There is also a functor
$f^\ast _{\rm comp}:D_{\rm cons}(Y_{\text{pro}{\unicode{x00E9}} {\rm t}},\widehat {\mathbb {Z}}_\ell )\to D_{\rm cons}(X_{\text{pro}{\unicode{x00E9}} {\rm t}},\widehat {\mathbb {Z}}_\ell )$, which is given by pullback followed by (derived) completion, see [Reference Bhatt and ScholzeBS15, Lemma 6.7.2]. There is also a functor ![]() $\operatorname {R} f_!:D_{\rm cons}(X_{\text{pro}{\unicode{x00E9}} {\rm t}},\widehat {\mathbb {Z}}_\ell )\to D_{\rm cons}(Y_{\text{pro}{\unicode{x00E9}} {\rm t}},\widehat {\mathbb {Z}}_\ell )$ (see [Reference Bhatt and ScholzeBS15, Definition 6.7.6]) with a right adjoint
$\operatorname {R} f_!:D_{\rm cons}(X_{\text{pro}{\unicode{x00E9}} {\rm t}},\widehat {\mathbb {Z}}_\ell )\to D_{\rm cons}(Y_{\text{pro}{\unicode{x00E9}} {\rm t}},\widehat {\mathbb {Z}}_\ell )$ (see [Reference Bhatt and ScholzeBS15, Definition 6.7.6]) with a right adjoint ![]() $f^!: D_{\rm cons}(Y_{\text{pro}{\unicode{x00E9}} {\rm t}},\widehat {\mathbb {Z}}_\ell )\to D_{\rm cons}( X_{\text{pro}{\unicode{x00E9}} {\rm t}},\widehat {\mathbb {Z}}_\ell )$, see [Reference Bhatt and ScholzeBS15, Lemma 6.7.19]. If
$f^!: D_{\rm cons}(Y_{\text{pro}{\unicode{x00E9}} {\rm t}},\widehat {\mathbb {Z}}_\ell )\to D_{\rm cons}( X_{\text{pro}{\unicode{x00E9}} {\rm t}},\widehat {\mathbb {Z}}_\ell )$, see [Reference Bhatt and ScholzeBS15, Lemma 6.7.19]. If ![]() $f$ is proper,
$f$ is proper, ![]() $\operatorname {R} f_!=\operatorname {R} f_\ast$ (by definition).
$\operatorname {R} f_!=\operatorname {R} f_\ast$ (by definition).
To explain the construction of ![]() $f^!$ in [Reference Bhatt and ScholzeBS15], note that the pullback
$f^!$ in [Reference Bhatt and ScholzeBS15], note that the pullback
is an equivalence (see the paragraph after [Reference Bhatt and ScholzeBS15, Definition 6.5.1]). Using this, we freely identify complexes on the two sides with each other. For instance, we freely identify ![]() $\mu _{\ell ^r}^{\otimes n}$ on
$\mu _{\ell ^r}^{\otimes n}$ on ![]() $Y_{\unicode{x00E9}{\rm t}}$ with its pullback
$Y_{\unicode{x00E9}{\rm t}}$ with its pullback ![]() $\nu ^\ast \mu _{\ell ^r}^{\otimes n}$ to
$\nu ^\ast \mu _{\ell ^r}^{\otimes n}$ to ![]() $Y_{\text{pro}{\unicode{x00E9}} {\rm t}}$. Now let
$Y_{\text{pro}{\unicode{x00E9}} {\rm t}}$. Now let ![]() $K\in D_{\rm cons}( Y_{\text{pro}{\unicode{x00E9}} {\rm t}},\widehat {\mathbb {Z}}_\ell )$ with truncation
$K\in D_{\rm cons}( Y_{\text{pro}{\unicode{x00E9}} {\rm t}},\widehat {\mathbb {Z}}_\ell )$ with truncation ![]() $K_r=K\otimes ^{\mathbb {L}}_{ \mathbb {Z}_\ell }\mathbb {Z}/\ell ^r$ and let
$K_r=K\otimes ^{\mathbb {L}}_{ \mathbb {Z}_\ell }\mathbb {Z}/\ell ^r$ and let ![]() $f_r^!:D_{\rm cons}(Y_{\unicode{x00E9}{\rm t}}, \mathbb {Z}/\ell ^r )\to D_{\rm cons}( X_{\unicode{x00E9}{\rm t}}, \mathbb {Z}/\ell ^r)$ be the exceptional pullback on the étale site, induced by
$f_r^!:D_{\rm cons}(Y_{\unicode{x00E9}{\rm t}}, \mathbb {Z}/\ell ^r )\to D_{\rm cons}( X_{\unicode{x00E9}{\rm t}}, \mathbb {Z}/\ell ^r)$ be the exceptional pullback on the étale site, induced by ![]() $f$, cf. [Reference Artin, Grothendieck and VerdierSGA4.3, Exposé XVIII]. As any constructible complex of sheaves of
$f$, cf. [Reference Artin, Grothendieck and VerdierSGA4.3, Exposé XVIII]. As any constructible complex of sheaves of ![]() $\mathbb {Z}/\ell ^r$-modules on
$\mathbb {Z}/\ell ^r$-modules on ![]() $X_{\text{pro}{\unicode{x00E9}} {\rm t}}$ is also a constructible complex of
$X_{\text{pro}{\unicode{x00E9}} {\rm t}}$ is also a constructible complex of ![]() $\widehat {\mathbb {Z}}_\ell$-modules on
$\widehat {\mathbb {Z}}_\ell$-modules on ![]() $X_{\text{pro}{\unicode{x00E9}} {\rm t}}$, we may by (6.7) identify
$X_{\text{pro}{\unicode{x00E9}} {\rm t}}$, we may by (6.7) identify ![]() $f_r^!K_r$ with an object in
$f_r^!K_r$ with an object in ![]() $D_{\rm cons}( X_{\text{pro}{\unicode{x00E9}} {\rm t}},\widehat {\mathbb {Z}}_\ell )$. By [Reference Bhatt and ScholzeBS15, Lemma 6.7.18], the natural reduction maps
$D_{\rm cons}( X_{\text{pro}{\unicode{x00E9}} {\rm t}},\widehat {\mathbb {Z}}_\ell )$. By [Reference Bhatt and ScholzeBS15, Lemma 6.7.18], the natural reduction maps ![]() $K_r\to K_m$ for
$K_r\to K_m$ for ![]() $m\leqslant r$ make
$m\leqslant r$ make ![]() $(f_r^!K_r)$ into a projective system and so, following Bhatt and Scholze (see [Reference Bhatt and ScholzeBS15, Lemma 6.7.19]), one may define
$(f_r^!K_r)$ into a projective system and so, following Bhatt and Scholze (see [Reference Bhatt and ScholzeBS15, Lemma 6.7.19]), one may define
This construction implies that many properties known from the étale site carry over to the pro-étale site.
Lemma 6.1 Let ![]() $f:X\to Y$ be a morphism between algebraic schemes over a field
$f:X\to Y$ be a morphism between algebraic schemes over a field ![]() $k$ and let
$k$ and let ![]() $\ell$ be a prime invertible in
$\ell$ be a prime invertible in ![]() $k$. Then the following hold in
$k$. Then the following hold in ![]() $D_{\rm cons}(X_{\text{pro}{\unicode{x00E9}} {\rm t}},\widehat {\mathbb {Z}}_\ell )$.
$D_{\rm cons}(X_{\text{pro}{\unicode{x00E9}} {\rm t}},\widehat {\mathbb {Z}}_\ell )$.
(i) If
 $f$ is weakly étale or a closed immersion, then
$f$ is weakly étale or a closed immersion, then  $f_{\rm comp}^\ast \simeq f^\ast$.
$f_{\rm comp}^\ast \simeq f^\ast$.(ii) If
 $f$ is étale, then
$f$ is étale, then  $f^!\simeq f^\ast \simeq f^\ast _{\rm comp}$.
$f^!\simeq f^\ast \simeq f^\ast _{\rm comp}$.(iii) If
 $g:Y\to Z$ is another morphism, then there is a natural isomorphism of functors
$g:Y\to Z$ is another morphism, then there is a natural isomorphism of functors  $f^!g^!\stackrel {\simeq }{\longrightarrow } (g\circ f)^!$.
$f^!g^!\stackrel {\simeq }{\longrightarrow } (g\circ f)^!$.(iv) If
 $f$ is smooth of pure relative dimension
$f$ is smooth of pure relative dimension  $d$, then there is a canonical isomorphism of functors
$d$, then there is a canonical isomorphism of functors  $f_{\rm comp}^\ast (d)[2d]\stackrel {\simeq }{\longrightarrow } f^!$, where
$f_{\rm comp}^\ast (d)[2d]\stackrel {\simeq }{\longrightarrow } f^!$, where  $f_{\rm comp}^\ast (n):=f_{\rm comp}^\ast (-\otimes _{\widehat {\mathbb {Z}}_\ell } \widehat {\mathbb {Z}}_{\ell }(n))$.
$f_{\rm comp}^\ast (n):=f_{\rm comp}^\ast (-\otimes _{\widehat {\mathbb {Z}}_\ell } \widehat {\mathbb {Z}}_{\ell }(n))$.(v) Let
 $f$ be smooth of pure relative dimension
$f$ be smooth of pure relative dimension  $d$. Then for any étale map
$d$. Then for any étale map  $j:U\to X$, the diagram
commutes, where the horizontal maps are induced by the canonical isomorphisms from item (iv) and the vertical arrows are induced by the canonical maps given by functoriality of
$j:U\to X$, the diagram
commutes, where the horizontal maps are induced by the canonical isomorphisms from item (iv) and the vertical arrows are induced by the canonical maps given by functoriality of
 $f^\ast _{\rm comp}$ and
$f^\ast _{\rm comp}$ and  $f^!$.
$f^!$.
Proof. Item (i) follows from [Reference Bhatt and ScholzeBS15, Remark 6.5.10]. Item (ii) follows from this together with the fact that for any ![]() $K\in D_{\rm cons}(Y_{\text{pro}{\unicode{x00E9}} {\rm t}},\widehat {\mathbb {Z}}_\ell )$,
$K\in D_{\rm cons}(Y_{\text{pro}{\unicode{x00E9}} {\rm t}},\widehat {\mathbb {Z}}_\ell )$,
because ![]() $f_r^!=f_r^\ast$ since
$f_r^!=f_r^\ast$ since ![]() $f$ is étale; see [Reference Artin, Grothendieck and VerdierSGA4.3, XVIII, Proposition 3.1.8(iii)].
$f$ is étale; see [Reference Artin, Grothendieck and VerdierSGA4.3, XVIII, Proposition 3.1.8(iii)].
Let ![]() $K\in D_{\rm cons}(Z_{\text{pro}{\unicode{x00E9}} {\rm t}},\widehat {\mathbb {Z}}_\ell )$ with truncations
$K\in D_{\rm cons}(Z_{\text{pro}{\unicode{x00E9}} {\rm t}},\widehat {\mathbb {Z}}_\ell )$ with truncations ![]() $K_r=K\otimes _{\widehat {\mathbb {Z}}_\ell }^{\mathbb {L}} \mathbb {Z}/\ell ^r \in D_{\rm cons}(Y_{\unicode{x00E9}{\rm t}},\mathbb {Z}/\ell ^r)$. By (6.7) and the construction of
$K_r=K\otimes _{\widehat {\mathbb {Z}}_\ell }^{\mathbb {L}} \mathbb {Z}/\ell ^r \in D_{\rm cons}(Y_{\unicode{x00E9}{\rm t}},\mathbb {Z}/\ell ^r)$. By (6.7) and the construction of ![]() $f^!$ from (6.8), there is a natural map
$f^!$ from (6.8), there is a natural map
induced by the natural isomorphism ![]() $f_r^!\circ g_r^!\stackrel {\sim }{\to } (g_r\circ f_r)^!$, given by adjunction and
$f_r^!\circ g_r^!\stackrel {\sim }{\to } (g_r\circ f_r)^!$, given by adjunction and ![]() $\operatorname {R} (g_r)_!\operatorname {R} (f_r)_!\stackrel {\simeq }{\to } \operatorname {R} (g_r\circ f_r)_!$. This proves item (iii).
$\operatorname {R} (g_r)_!\operatorname {R} (f_r)_!\stackrel {\simeq }{\to } \operatorname {R} (g_r\circ f_r)_!$. This proves item (iii).
Let ![]() $K\in D_{\rm cons}(Y_{\text{pro}{\unicode{x00E9}} {\rm t}} ,\widehat {\mathbb {Z}}_\ell )$ with truncations
$K\in D_{\rm cons}(Y_{\text{pro}{\unicode{x00E9}} {\rm t}} ,\widehat {\mathbb {Z}}_\ell )$ with truncations ![]() $K_r=K\otimes _{\widehat {\mathbb {Z}}_\ell }^{\mathbb {L}} \mathbb {Z}/\ell ^r \in D_{\rm cons}(Y_{\unicode{x00E9}{\rm t}},\mathbb {Z}/\ell ^r)$. Assume that
$K_r=K\otimes _{\widehat {\mathbb {Z}}_\ell }^{\mathbb {L}} \mathbb {Z}/\ell ^r \in D_{\rm cons}(Y_{\unicode{x00E9}{\rm t}},\mathbb {Z}/\ell ^r)$. Assume that ![]() $f$ is smooth of pure relative dimension
$f$ is smooth of pure relative dimension ![]() $d$. By Poincaré duality on the étale site, there are canonical identifications
$d$. By Poincaré duality on the étale site, there are canonical identifications ![]() $f_r^!= f_r^\ast (d)[2d]$, see [Reference Artin, Grothendieck and VerdierSGA4.3, XVIII, Théorème 3.2.5] (cf. [Reference VerdierVer67, § 4.4]). We thus obtain a canonical isomorphism:
$f_r^!= f_r^\ast (d)[2d]$, see [Reference Artin, Grothendieck and VerdierSGA4.3, XVIII, Théorème 3.2.5] (cf. [Reference VerdierVer67, § 4.4]). We thus obtain a canonical isomorphism:
This holds functorially in ![]() $K$ and so we get an isomorphism
$K$ and so we get an isomorphism ![]() $f_{\rm comp}^\ast (d)[2d]\stackrel {\simeq }{\to } f^!$, which proves item (iv).
$f_{\rm comp}^\ast (d)[2d]\stackrel {\simeq }{\to } f^!$, which proves item (iv).
By item (ii), ![]() $j_{\rm comp}^\ast \simeq j^!$ and so the commutativity of the diagram in item (v) follows from the fact that the isomorphism in item (iv) is compatible with respect to compositions of smooth maps. The latter follows by construction of
$j_{\rm comp}^\ast \simeq j^!$ and so the commutativity of the diagram in item (v) follows from the fact that the isomorphism in item (iv) is compatible with respect to compositions of smooth maps. The latter follows by construction of ![]() $f^!$ from the analogous result for constructible complexes on the étale site and, hence, from [Reference Artin, Grothendieck and VerdierSGA4.3, XVIII, diagram above Théorème 3.2.5]. This concludes the proof of the lemma.
$f^!$ from the analogous result for constructible complexes on the étale site and, hence, from [Reference Artin, Grothendieck and VerdierSGA4.3, XVIII, diagram above Théorème 3.2.5]. This concludes the proof of the lemma.
Let ![]() $f:X\to Y$ be a morphism between algebraic
$f:X\to Y$ be a morphism between algebraic ![]() $k$-schemes. By adjunction, there are natural transformations
$k$-schemes. By adjunction, there are natural transformations
between functors on ![]() $D_{\rm cons}(Y_{\text{pro}{\unicode{x00E9}} {\rm t}},\widehat {\mathbb {Z}}_\ell )$. For
$D_{\rm cons}(Y_{\text{pro}{\unicode{x00E9}} {\rm t}},\widehat {\mathbb {Z}}_\ell )$. For ![]() $K\in D_{\rm cons}(Y_{\text{pro}{\unicode{x00E9}} {\rm t}},\widehat {\mathbb {Z}}_\ell )$, the maps are defined by asking (see [Reference Bhatt and ScholzeBS15, Lemmas 6.7.2 and 6.7.19]) that the following diagrams commute:
$K\in D_{\rm cons}(Y_{\text{pro}{\unicode{x00E9}} {\rm t}},\widehat {\mathbb {Z}}_\ell )$, the maps are defined by asking (see [Reference Bhatt and ScholzeBS15, Lemmas 6.7.2 and 6.7.19]) that the following diagrams commute:
where ![]() $K_r=K\otimes ^{\mathbb {L}}_{\widehat {\mathbb {Z}}_\ell }\mathbb {Z}/\ell ^r\in D_{\rm cons}(Y_{\unicode{x00E9}{\rm t}}, \mathbb {Z}/\ell ^r)$,
$K_r=K\otimes ^{\mathbb {L}}_{\widehat {\mathbb {Z}}_\ell }\mathbb {Z}/\ell ^r\in D_{\rm cons}(Y_{\unicode{x00E9}{\rm t}}, \mathbb {Z}/\ell ^r)$, ![]() $f_r^\bullet$,
$f_r^\bullet$, ![]() $f_{r\bullet }$ denote the corresponding functors on
$f_{r\bullet }$ denote the corresponding functors on ![]() $D_{\rm cons}(Y_{\unicode{x00E9}{\rm t}}, \mathbb {Z}/\ell ^r)$ (respectively,
$D_{\rm cons}(Y_{\unicode{x00E9}{\rm t}}, \mathbb {Z}/\ell ^r)$ (respectively, ![]() $D_{\rm cons}(X_{\unicode{x00E9}{\rm t}}, \mathbb {Z}/\ell ^r)$) induced by
$D_{\rm cons}(X_{\unicode{x00E9}{\rm t}}, \mathbb {Z}/\ell ^r)$) induced by ![]() $f$, and where as before we identify
$f$, and where as before we identify ![]() $K_r$ with
$K_r$ with ![]() $\nu ^\ast K_r$, using the equivalence (6.7).
$\nu ^\ast K_r$, using the equivalence (6.7).
For ![]() $K\in D_{\rm cons}(Y_{\text{pro}{\unicode{x00E9}} {\rm t}},\widehat {\mathbb {Z}}_\ell )$,
$K\in D_{\rm cons}(Y_{\text{pro}{\unicode{x00E9}} {\rm t}},\widehat {\mathbb {Z}}_\ell )$, ![]() $\theta _f$ induces pullback maps:
$\theta _f$ induces pullback maps:
If ![]() $f$ is proper, then
$f$ is proper, then ![]() $\operatorname {R} f_!=\operatorname {R} f_\ast$ and so
$\operatorname {R} f_!=\operatorname {R} f_\ast$ and so ![]() $\operatorname {Tr}_f$ induces a pushforward map:
$\operatorname {Tr}_f$ induces a pushforward map:
Lemma 6.2 Let ![]() $K\in D_{\rm cons}(Y_{\text{pro}{\unicode{x00E9}} {\rm t}},\widehat {\mathbb {Z}}_\ell )$ with truncations
$K\in D_{\rm cons}(Y_{\text{pro}{\unicode{x00E9}} {\rm t}},\widehat {\mathbb {Z}}_\ell )$ with truncations ![]() $K_r=K\otimes ^{\mathbb {L}}_{\widehat {\mathbb {Z}}_\ell }\mathbb {Z}/\ell ^r\in D_{\rm cons}( Y_{\unicode{x00E9}{\rm t}}, \mathbb {Z}/\ell ^r )$. Then for any morphism
$K_r=K\otimes ^{\mathbb {L}}_{\widehat {\mathbb {Z}}_\ell }\mathbb {Z}/\ell ^r\in D_{\rm cons}( Y_{\unicode{x00E9}{\rm t}}, \mathbb {Z}/\ell ^r )$. Then for any morphism ![]() $f:X\to Y$ between algebraic
$f:X\to Y$ between algebraic ![]() $k$-schemes, the following diagram commutes with exact rows.
$k$-schemes, the following diagram commutes with exact rows.
If ![]() $f$ is proper, then the following commutes with exact rows as well.
$f$ is proper, then the following commutes with exact rows as well.
Proof. The horizontal lines are parts of short exact sequences given by the composed functor spectral sequence of ![]() $\operatorname {R} \lim \circ \operatorname {R} \Gamma$, where we note that
$\operatorname {R} \lim \circ \operatorname {R} \Gamma$, where we note that ![]() $\operatorname {R} \lim$ has cohomological dimension
$\operatorname {R} \lim$ has cohomological dimension ![]() $\leqslant 1$ on abelian groups. The lemma thus follows immediately from the commutative diagrams in (6.10).
$\leqslant 1$ on abelian groups. The lemma thus follows immediately from the commutative diagrams in (6.10).
Remark 6.3 Bhatt and Scholze's six functor formalism on constructible complexes of ![]() $\widehat {\mathbb {Z}}_\ell$-sheaves on the pro-étale site works more generally for quasi-excellent quasi-compact quasi-separated schemes over
$\widehat {\mathbb {Z}}_\ell$-sheaves on the pro-étale site works more generally for quasi-excellent quasi-compact quasi-separated schemes over ![]() $\mathbb {Z}[1/\ell ]$ and separated finitely presented maps between them, see [Reference Bhatt and ScholzeBS15, § 6.7]. Lemmas 6.1 and 6.2 remain true in this set-up (with the same proofs).
$\mathbb {Z}[1/\ell ]$ and separated finitely presented maps between them, see [Reference Bhatt and ScholzeBS15, § 6.7]. Lemmas 6.1 and 6.2 remain true in this set-up (with the same proofs).
Remark 6.4 Related to Bhatt and Scholze's pro-étale theory [Reference Bhatt and ScholzeBS15], there is Ekedahl's ![]() $\ell$-adic formalism [Reference EkhedalEkh90], which leads to a six functor formalism (see [Reference EkhedalEkh90, Theorem 6.3]) that is closer in spirit to Jannsen's continuous étale cohomology groups. We prefer to use Bhatt and Scholze's theory, as it allows us to work with actual sheaves on a site, whereas Ekedahl's formalism as well as Jannsen's theory involve inverse systems of sheaves. The resulting triangulated categories agree under suitable finiteness assumptions, see [Reference Bhatt and ScholzeBS15, § 5.5].
$\ell$-adic formalism [Reference EkhedalEkh90], which leads to a six functor formalism (see [Reference EkhedalEkh90, Theorem 6.3]) that is closer in spirit to Jannsen's continuous étale cohomology groups. We prefer to use Bhatt and Scholze's theory, as it allows us to work with actual sheaves on a site, whereas Ekedahl's formalism as well as Jannsen's theory involve inverse systems of sheaves. The resulting triangulated categories agree under suitable finiteness assumptions, see [Reference Bhatt and ScholzeBS15, § 5.5].
6.1.4 Properties (P1)–(P6), (P7.1), and (P7.2)
Let ![]() $k$ be a field and let
$k$ be a field and let ![]() $\ell$ be a prime that is invertible in
$\ell$ be a prime that is invertible in ![]() $k$. Let
$k$. Let ![]() $\mathcal {V}$ be the category whose objects are separated schemes of finite type over
$\mathcal {V}$ be the category whose objects are separated schemes of finite type over ![]() $k$ and where the morphisms are open immersions of schemes of the same dimension. For
$k$ and where the morphisms are open immersions of schemes of the same dimension. For ![]() $X\in \mathcal {V}$ of dimension
$X\in \mathcal {V}$ of dimension ![]() $d$ with structure morphism
$d$ with structure morphism ![]() $\pi _X:X\to \operatorname {Spec} k$, we define
$\pi _X:X\to \operatorname {Spec} k$, we define
where ![]() $\widehat {\mathbb {Z}}_\ell (n)$ denotes the sheaf on
$\widehat {\mathbb {Z}}_\ell (n)$ denotes the sheaf on ![]() $X_{\text{pro}{\unicode{x00E9}} {\rm t}}$ defined in (6.6). By item (ii) in Lemma 6.1 and (6.11), the cohomology groups in (6.13)–(6.15) are contravariantly functorial with respect to morphisms in
$X_{\text{pro}{\unicode{x00E9}} {\rm t}}$ defined in (6.6). By item (ii) in Lemma 6.1 and (6.11), the cohomology groups in (6.13)–(6.15) are contravariantly functorial with respect to morphisms in ![]() $\mathcal {V}$ (in fact, with respect to arbitrary étale maps
$\mathcal {V}$ (in fact, with respect to arbitrary étale maps ![]() $U\rightarrow X$ with
$U\rightarrow X$ with ![]() $\dim U=\dim X$).
$\dim U=\dim X$).
Lemma 6.5 Assume that ![]() $X\in \mathcal {V}$ is equi-dimensional and smooth over
$X\in \mathcal {V}$ is equi-dimensional and smooth over ![]() $k$. Then there are canonical isomorphisms
$k$. Then there are canonical isomorphisms
and
which are compatible with respect to pullbacks along open immersions.
Proof. As ![]() $\pi :X\to \operatorname {Spec} k$ is smooth of pure dimension
$\pi :X\to \operatorname {Spec} k$ is smooth of pure dimension ![]() $d$, there is a canonical isomorphism
$d$, there is a canonical isomorphism ![]() $(\pi _X)_{\rm comp}^\ast (d)[2d]\stackrel {\simeq }{\to } \pi _X^!$, see item (iv) in Lemma 6.1. This isomorphism is compatible with respect to pullbacks along open immersions by item (v) in Lemma 6.1. This yields the first isomorphism in each row of the lemma. The comparison to continuous étale cohomology follows from (6.5) and that to étale cohomology for finite coefficients from (6.1), because
$(\pi _X)_{\rm comp}^\ast (d)[2d]\stackrel {\simeq }{\to } \pi _X^!$, see item (iv) in Lemma 6.1. This isomorphism is compatible with respect to pullbacks along open immersions by item (v) in Lemma 6.1. This yields the first isomorphism in each row of the lemma. The comparison to continuous étale cohomology follows from (6.5) and that to étale cohomology for finite coefficients from (6.1), because ![]() $\operatorname {R} \lim ^1$ vanishes on constant inductive systems. This concludes the proof of the lemma.
$\operatorname {R} \lim ^1$ vanishes on constant inductive systems. This concludes the proof of the lemma.
The main result of this section is the following.
Proposition 6.6 Let ![]() $k$ be a field and let
$k$ be a field and let ![]() $\ell$ be a prime that is invertible in
$\ell$ be a prime that is invertible in ![]() $k$. Let
$k$. Let ![]() $\mathcal {A}\subset \operatorname {Mod}_{\mathbb {Z}_\ell }$ be the full subcategory of
$\mathcal {A}\subset \operatorname {Mod}_{\mathbb {Z}_\ell }$ be the full subcategory of ![]() $\mathbb {Z}_\ell$-modules containing
$\mathbb {Z}_\ell$-modules containing ![]() $\mathbb {Z}_\ell$,
$\mathbb {Z}_\ell$, ![]() $\mathbb {Q}_\ell$,
$\mathbb {Q}_\ell$, ![]() $\mathbb {Q}_\ell /\mathbb {Z}_\ell$, and
$\mathbb {Q}_\ell /\mathbb {Z}_\ell$, and ![]() $\mathbb {Z}/\ell ^r$ for all
$\mathbb {Z}/\ell ^r$ for all ![]() $r\geqslant 1$. Let
$r\geqslant 1$. Let ![]() $\mathcal {V}$ be the category of separated schemes of finite type over
$\mathcal {V}$ be the category of separated schemes of finite type over ![]() $k$ with morphisms given by open immersions
$k$ with morphisms given by open immersions ![]() $U\hookrightarrow X$ with
$U\hookrightarrow X$ with ![]() $\dim U=\dim X$. Let the cohomology functor (4.1) be given by (6.13)–(6.15). Then (P1)–(P5) from Definitions 4.2 and 4.4 hold true. If
$\dim U=\dim X$. Let the cohomology functor (4.1) be given by (6.13)–(6.15). Then (P1)–(P5) from Definitions 4.2 and 4.4 hold true. If ![]() $k$ is perfect, then (P6) holds true as well. Moreover:
$k$ is perfect, then (P6) holds true as well. Moreover:
– property (P7.1) holds if
 $k$ is algebraically closed;
$k$ is algebraically closed;– property (P7.2) holds if
 $k$ is the perfect closure of a finitely generated field.
$k$ is the perfect closure of a finitely generated field.
In the terminology of Definitions 4.2, 4.4, and 4.5, the proposition states that ![]() $H^\ast (-,A(n))$ is a twisted Borel–Moore cohomology theory on
$H^\ast (-,A(n))$ is a twisted Borel–Moore cohomology theory on ![]() $\mathcal {V}$ that is
$\mathcal {V}$ that is ![]() $\ell$-adic if
$\ell$-adic if ![]() $k$ is perfect and it is adapted to algebraic equivalence if
$k$ is perfect and it is adapted to algebraic equivalence if ![]() $k$ is algebraically closed, whereas it is adapted to rational equivalence if
$k$ is algebraically closed, whereas it is adapted to rational equivalence if ![]() $k$ is the perfect closure of a finitely generated field.
$k$ is the perfect closure of a finitely generated field.
Proof of Proposition 6.6 Item (P4) is clear (by definition). As the direct limit functor as well as ![]() $\otimes _{\mathbb {Z}_\ell }\mathbb {Q}_\ell$ is exact, it suffices to prove the remaining properties for
$\otimes _{\mathbb {Z}_\ell }\mathbb {Q}_\ell$ is exact, it suffices to prove the remaining properties for ![]() $A=\mathbb {Z}/\ell ^r$ and
$A=\mathbb {Z}/\ell ^r$ and ![]() $A=\mathbb {Z}_\ell$.
$A=\mathbb {Z}_\ell$.
Step 1: item (P1). Let ![]() $X,Y\in \mathcal {V}$ and let
$X,Y\in \mathcal {V}$ and let ![]() $f:X\to Y$ be a proper morphism of schemes with
$f:X\to Y$ be a proper morphism of schemes with ![]() $c=\dim Y-\dim X$. The existence of the pushforward
$c=\dim Y-\dim X$. The existence of the pushforward ![]() $f_\ast :H^{i-2c}(X,A(n-c))\to H^i(Y,A(n))$ follows from (6.12) and item (iii) in Lemma 6.1. Functoriality in
$f_\ast :H^{i-2c}(X,A(n-c))\to H^i(Y,A(n))$ follows from (6.12) and item (iii) in Lemma 6.1. Functoriality in ![]() $f$ (i.e.
$f$ (i.e. ![]() $(f\circ g)_\ast =f_\ast g_\ast$) follows from the functoriality of the trace map (which by (6.9) may either be deduced from the corresponding statement on the étale site, or directly from item (iii) in Lemma 6.1). Compatibility of
$(f\circ g)_\ast =f_\ast g_\ast$) follows from the functoriality of the trace map (which by (6.9) may either be deduced from the corresponding statement on the étale site, or directly from item (iii) in Lemma 6.1). Compatibility of ![]() $f_\ast$ with pullbacks along open immersions may by Lemma 6.2 be checked in the case where
$f_\ast$ with pullbacks along open immersions may by Lemma 6.2 be checked in the case where ![]() $A=\mathbb {Z}/\ell ^r$ on the étale site of
$A=\mathbb {Z}/\ell ^r$ on the étale site of ![]() $X$, which is well-known (and holds, in fact, for arbitrary étale maps in place of open immersions), see [Reference Bloch and OgusBO74, (1.2.2) and § 2.1]. This proves (P1).
$X$, which is well-known (and holds, in fact, for arbitrary étale maps in place of open immersions), see [Reference Bloch and OgusBO74, (1.2.2) and § 2.1]. This proves (P1).
Step 2: item (P2). Let ![]() $X\in \mathcal {V}$ and let
$X\in \mathcal {V}$ and let ![]() $i:Z\hookrightarrow X$ be a closed immersion with complement
$i:Z\hookrightarrow X$ be a closed immersion with complement ![]() $j:U\hookrightarrow X$. Let
$j:U\hookrightarrow X$. Let ![]() $c=\dim X-\dim Z$. By [Reference Bhatt and ScholzeBS15, Lemma 6.1.16], there is an exact triangle
$c=\dim X-\dim Z$. By [Reference Bhatt and ScholzeBS15, Lemma 6.1.16], there is an exact triangle
where we used ![]() $j^\ast \simeq j_{\rm comp}^\ast$ (see Lemma 6.1). By Lemma 6.1,
$j^\ast \simeq j_{\rm comp}^\ast$ (see Lemma 6.1). By Lemma 6.1, ![]() $j_{\rm comp}^\ast \simeq j^!$,
$j_{\rm comp}^\ast \simeq j^!$, ![]() $\pi _Z^!\stackrel {\simeq }{\to } i^! \pi _X^!$, and
$\pi _Z^!\stackrel {\simeq }{\to } i^! \pi _X^!$, and ![]() $\pi _{U}^!\stackrel {\simeq }{\to } j_{\rm comp}^\ast \pi _X^!$. Hence, the above triangle identifies to an exact triangle
$\pi _{U}^!\stackrel {\simeq }{\to } j_{\rm comp}^\ast \pi _X^!$. Hence, the above triangle identifies to an exact triangle
Applying ![]() $\operatorname {R} \Gamma (X_{\text{pro}{\unicode{x00E9}} {\rm t}},-)$, the corresponding long exact sequence yields the Gysin sequence claimed in (P2). The map
$\operatorname {R} \Gamma (X_{\text{pro}{\unicode{x00E9}} {\rm t}},-)$, the corresponding long exact sequence yields the Gysin sequence claimed in (P2). The map ![]() $\iota _\ast$ in the Gysin sequence from item (P2) coincides, by construction, with the proper pushforward with respect to the inclusion
$\iota _\ast$ in the Gysin sequence from item (P2) coincides, by construction, with the proper pushforward with respect to the inclusion ![]() $Z\hookrightarrow X$. Functoriality with respect to open immersions follows by Lemma 6.2 from the case
$Z\hookrightarrow X$. Functoriality with respect to open immersions follows by Lemma 6.2 from the case ![]() $A=\mathbb {Z}/\ell ^r$ on the étale site which is well-known (and holds, in fact, for arbitrary étale maps), see, e.g., [Reference Bloch and OgusBO74, (1.1.2), Lemma 1.4, and (2.1)]. Similarly, functoriality with respect to proper pushforwards follows by Lemma 6.2 from the case of finite coefficients
$A=\mathbb {Z}/\ell ^r$ on the étale site which is well-known (and holds, in fact, for arbitrary étale maps), see, e.g., [Reference Bloch and OgusBO74, (1.1.2), Lemma 1.4, and (2.1)]. Similarly, functoriality with respect to proper pushforwards follows by Lemma 6.2 from the case of finite coefficients ![]() $A=\mathbb {Z}/\ell ^r$ on the étale site, which is well-known, see, e.g., [Reference Bloch and OgusBO74, (1.2.4) and (2.1)]. This proves (P2).
$A=\mathbb {Z}/\ell ^r$ on the étale site, which is well-known, see, e.g., [Reference Bloch and OgusBO74, (1.2.4) and (2.1)]. This proves (P2).
Step 3: item (P3). By the topological invariance of the pro-étale topos (see [Reference Bhatt and ScholzeBS15, Lemma 5.4.2]), we may replace ![]() $X$ be the base change to the perfect closure
$X$ be the base change to the perfect closure ![]() $k^{per}$ of
$k^{per}$ of ![]() $k$, and
$k$, and ![]() $x$ by the unique point in
$x$ by the unique point in ![]() $X_{k^{per}}$ that lies over it via the natural map
$X_{k^{per}}$ that lies over it via the natural map ![]() $X_{k^{per}}\to X$ (where we use that the latter is a universal homeomorphism). After this reduction step, we may assume that
$X_{k^{per}}\to X$ (where we use that the latter is a universal homeomorphism). After this reduction step, we may assume that ![]() $k$ is perfect.
$k$ is perfect.
Note that ![]() $H^i(x,A(n))$ in (4.2) is defined as a direct limit where it suffices to run only through the cohomology of regular (hence, smooth, because
$H^i(x,A(n))$ in (4.2) is defined as a direct limit where it suffices to run only through the cohomology of regular (hence, smooth, because ![]() $k$ is perfect) schemes, so that the vanishing
$k$ is perfect) schemes, so that the vanishing ![]() $H^i(x,A(n))=0$ for
$H^i(x,A(n))=0$ for ![]() $i<0$ as well as the canonical isomorphism
$i<0$ as well as the canonical isomorphism ![]() $H^0(x,A(0))\simeq A$ which is functorial in
$H^0(x,A(0))\simeq A$ which is functorial in ![]() $A$ follows from Lemma 6.5. The fundamental class
$A$ follows from Lemma 6.5. The fundamental class ![]() $[x]\in H^0(x,\mathbb {Z}_\ell (0))$ corresponds via the canonical isomorphism
$[x]\in H^0(x,\mathbb {Z}_\ell (0))$ corresponds via the canonical isomorphism ![]() $H^0(x,\mathbb {Z}_\ell (0))\simeq \mathbb {Z}_\ell$ to
$H^0(x,\mathbb {Z}_\ell (0))\simeq \mathbb {Z}_\ell$ to ![]() $1\in \mathbb {Z}_\ell$. More precisely, let
$1\in \mathbb {Z}_\ell$. More precisely, let ![]() $U\subset \overline {\{x\}}$ be dense and smooth over
$U\subset \overline {\{x\}}$ be dense and smooth over ![]() $k$. By Lemma 6.5, the canonical isomorphism in item (iv) of Lemma 6.1 induces a canonical isomorphism
$k$. By Lemma 6.5, the canonical isomorphism in item (iv) of Lemma 6.1 induces a canonical isomorphism
which is compatible with respect to restrictions to open subsets. The class of ![]() $H^0(U,\mathbb {Z}_\ell (0))$ induced by the unit section of the pro-étale sheaf
$H^0(U,\mathbb {Z}_\ell (0))$ induced by the unit section of the pro-étale sheaf ![]() $\widehat {\mathbb {Z}}_\ell (0)$ yields a canonical fundamental class
$\widehat {\mathbb {Z}}_\ell (0)$ yields a canonical fundamental class ![]() $[U]\in H^0(U,\mathbb {Z}_\ell (0))$ with
$[U]\in H^0(U,\mathbb {Z}_\ell (0))$ with ![]() $H^0(U,\mathbb {Z}_\ell (0))=[U]\mathbb {Z}_\ell$. This class is compatible with respect to restrictions to open subsets (see item (v) in Lemma 6.1), hence induces a canonical class
$H^0(U,\mathbb {Z}_\ell (0))=[U]\mathbb {Z}_\ell$. This class is compatible with respect to restrictions to open subsets (see item (v) in Lemma 6.1), hence induces a canonical class ![]() $[x]\in H^0(x,\mathbb {Z}_\ell (0))$ in the limit. This proves (P3).
$[x]\in H^0(x,\mathbb {Z}_\ell (0))$ in the limit. This proves (P3).
Step 4: item (P5). There is a canonical short exact sequence
of sheaves on ![]() $(\operatorname {Spec} k)_{\text{pro}{\unicode{x00E9}} {\rm t}}$. Applying
$(\operatorname {Spec} k)_{\text{pro}{\unicode{x00E9}} {\rm t}}$. Applying ![]() $\pi _X^!$, we arrive at the exact triangle
$\pi _X^!$, we arrive at the exact triangle
The Bockstein sequence in (P5) is (up to some shifts) the long exact sequence associated to this triangle after applying ![]() $\operatorname {R} \Gamma (X_{\text{pro}{\unicode{x00E9}} {\rm t}},-)$. Functoriality of the exceptional pullback
$\operatorname {R} \Gamma (X_{\text{pro}{\unicode{x00E9}} {\rm t}},-)$. Functoriality of the exceptional pullback ![]() $\pi _X^!$ shows that the Bockstein sequence is functorial with respect to pullbacks along morphisms in
$\pi _X^!$ shows that the Bockstein sequence is functorial with respect to pullbacks along morphisms in ![]() $\mathcal {V}$ and with respect to proper pushforwards from (P1). This proves (P5).
$\mathcal {V}$ and with respect to proper pushforwards from (P1). This proves (P5).
Step 5: item (P6) for ![]() $k$ perfect. Let
$k$ perfect. Let ![]() $X\in \mathcal {V}$ and let
$X\in \mathcal {V}$ and let ![]() $x\in X^{(1)}$. In the direct limit (4.2) that defines
$x\in X^{(1)}$. In the direct limit (4.2) that defines ![]() $H^i(x,A(n))$, we may restrict ourselves to regular (hence, smooth, as
$H^i(x,A(n))$, we may restrict ourselves to regular (hence, smooth, as ![]() $k$ is perfect) dense open subsets
$k$ is perfect) dense open subsets ![]() $V_x\subset \overline {\{x\}}$, so that Lemma 6.5 identifies
$V_x\subset \overline {\{x\}}$, so that Lemma 6.5 identifies ![]() $H^i(V_x,A(n))$ canonically with continuous étale cohomology. The map
$H^i(V_x,A(n))$ canonically with continuous étale cohomology. The map ![]() $\epsilon :\kappa (x)^\ast \to H^1(x,\mathbb {Z}_\ell (1))$ is then induced by the Kummer sequence in continuous étale cohomology, see (6.3). Surjectivity of the reduction
$\epsilon :\kappa (x)^\ast \to H^1(x,\mathbb {Z}_\ell (1))$ is then induced by the Kummer sequence in continuous étale cohomology, see (6.3). Surjectivity of the reduction ![]() $\overline {\epsilon }:\kappa (x)^\ast \to H^1(x,\mu _{\ell ^r}\!)$ follows from the Kummer sequence in étale cohomology and Grothendieck's Hilbert theorem 90, which implies that
$\overline {\epsilon }:\kappa (x)^\ast \to H^1(x,\mu _{\ell ^r}\!)$ follows from the Kummer sequence in étale cohomology and Grothendieck's Hilbert theorem 90, which implies that
Let ![]() $X\in \mathcal {V}$ be integral of dimension
$X\in \mathcal {V}$ be integral of dimension ![]() $d$ with generic point
$d$ with generic point ![]() $\eta$ and let
$\eta$ and let ![]() $x\in X^{(1)}$ be a regular point with closure
$x\in X^{(1)}$ be a regular point with closure ![]() $i:D\hookrightarrow X$. We claim that the composition
$i:D\hookrightarrow X$. We claim that the composition ![]() ${\partial \circ \epsilon : \kappa (\eta )^\ast \to H^0(x ,\mathbb {Z}_{\ell }(0))=[x] \mathbb {Z}_{\ell }}$ satisfies
${\partial \circ \epsilon : \kappa (\eta )^\ast \to H^0(x ,\mathbb {Z}_{\ell }(0))=[x] \mathbb {Z}_{\ell }}$ satisfies
where ![]() $\nu _x$ denotes the valuation on
$\nu _x$ denotes the valuation on ![]() $\kappa (\eta )$ induced by
$\kappa (\eta )$ induced by ![]() $x$. It suffices to check this after reduction modulo
$x$. It suffices to check this after reduction modulo ![]() $\ell ^r$ for
$\ell ^r$ for ![]() $r\geqslant 1$. It follows from [Reference DeligneSGA4, p. 147, (cycle), Lemme 2.3.6] that the fundamental class
$r\geqslant 1$. It follows from [Reference DeligneSGA4, p. 147, (cycle), Lemme 2.3.6] that the fundamental class ![]() $[x]\in H^0(x,\mu _{\ell ^r}^{\otimes 0})$ that we defined above via Poincaré duality (i.e. via item (iv) in Lemma 6.1) is induced by the cycle class
$[x]\in H^0(x,\mu _{\ell ^r}^{\otimes 0})$ that we defined above via Poincaré duality (i.e. via item (iv) in Lemma 6.1) is induced by the cycle class
from [Reference DeligneSGA4, p. 138, (cycle), Définition 2.1.2]. The claim in question follows therefore from the anticommutativity of the diagram in [Reference DeligneSGA4, p. 138, (cycle), (2.1.3)]. This concludes the proof of (P6).
By Lemma 5.8 and Corollary 5.10 (which apply because we have proven (P1)–(P6) already), the proper pushforward map from (P1) together with ![]() $H^0(x,\mathbb {Z}_\ell (0))=[x]\mathbb {Z}_\ell$ from (P3) yields for any
$H^0(x,\mathbb {Z}_\ell (0))=[x]\mathbb {Z}_\ell$ from (P3) yields for any ![]() $X\in \mathcal {V}$ a canonical map
$X\in \mathcal {V}$ a canonical map
as claimed in (4.3). If ![]() $X$ is a smooth variety, then there is a canonical isomorphism
$X$ is a smooth variety, then there is a canonical isomorphism ![]() $H^2(X,\mathbb {Z}_\ell (1)) \simeq H^2_{\rm cont}(X,\mathbb {Z}_\ell (1))$ (see Lemma 6.5) and so we may compare
$H^2(X,\mathbb {Z}_\ell (1)) \simeq H^2_{\rm cont}(X,\mathbb {Z}_\ell (1))$ (see Lemma 6.5) and so we may compare ![]() $\iota _\ast$ to the first Chern class map
$\iota _\ast$ to the first Chern class map ![]() $c_1$ from (6.3), as follows.
$c_1$ from (6.3), as follows.
Lemma 6.7 Let ![]() $k$ be a field and let
$k$ be a field and let ![]() $X$ be a smooth
$X$ be a smooth ![]() $k$-variety. For any Weil divisor
$k$-variety. For any Weil divisor ![]() $D\in \bigoplus _{x\in X^{(1)}} [x]\mathbb {Z}$, we have:
$D\in \bigoplus _{x\in X^{(1)}} [x]\mathbb {Z}$, we have:
(i)
 $\iota _\ast D=c_1(\mathcal {O}_X(D))$, where
$\iota _\ast D=c_1(\mathcal {O}_X(D))$, where  $\iota _\ast$ is the cycle class map from (4.3) and
$\iota _\ast$ is the cycle class map from (4.3) and  $c_1$ is from (6.3);
$c_1$ is from (6.3);(ii)
 $c_1(\mathcal {O}_X(D)) =0$ if and only if
$c_1(\mathcal {O}_X(D)) =0$ if and only if  $\mathcal {O}_X(D)\in \operatorname {Pic}(X\!)$ is contained in the subgroup of
$\mathcal {O}_X(D)\in \operatorname {Pic}(X\!)$ is contained in the subgroup of  $\ell$-divisible elements of
$\ell$-divisible elements of  $\operatorname {Pic}(X\!)$.
$\operatorname {Pic}(X\!)$.
Proof. The first assertion is [Reference JannsenJan88, Lemma 3.26]. For the second assertion, note that the Kummer sequence (6.2) yields an exact sequence
Functoriality of the extension in (6.1) shows that the image of the first map is given by subgroup of ![]() $\ell$-divisible elements of
$\ell$-divisible elements of ![]() $\operatorname {Pic}(X\!)$ (cf. [Reference JannsenJan88, Remark 6.15]), which concludes the proof of the lemma.
$\operatorname {Pic}(X\!)$ (cf. [Reference JannsenJan88, Remark 6.15]), which concludes the proof of the lemma.
Step 6: item (P7.1) for ![]() $k$ algebraically closed. Let us now assume that
$k$ algebraically closed. Let us now assume that ![]() $k$ is algebraically closed and let
$k$ is algebraically closed and let ![]() $X$ be a regular (hence, smooth, as
$X$ be a regular (hence, smooth, as ![]() $k=\overline {k}$) variety over
$k=\overline {k}$) variety over ![]() $k$. Note that (P7.1) is well-known in the case where
$k$. Note that (P7.1) is well-known in the case where ![]() $X$ is smooth projective, and we deduce the general case from this statement in what follows. We denote by
$X$ is smooth projective, and we deduce the general case from this statement in what follows. We denote by ![]() $\operatorname {NS}(X\!)=\operatorname {Pic}(X\!)/\sim _{\operatorname {alg}}$ the group of divisors modulo algebraic equivalence on
$\operatorname {NS}(X\!)=\operatorname {Pic}(X\!)/\sim _{\operatorname {alg}}$ the group of divisors modulo algebraic equivalence on ![]() $X$. As
$X$. As ![]() $k$ is algebraically closed, the subgroup of algebraically trivial divisors in
$k$ is algebraically closed, the subgroup of algebraically trivial divisors in ![]() $\operatorname {Pic}(X\!)$ is
$\operatorname {Pic}(X\!)$ is ![]() $\ell$-divisible. By Lemma 6.7, the first Chern class map from (6.3) descends to a map
$\ell$-divisible. By Lemma 6.7, the first Chern class map from (6.3) descends to a map ![]() $c_1:\operatorname {NS}(X\!)\otimes \mathbb {Z}_\ell \to H^2(X,\mathbb {Z}_\ell (1))$ and, again by Lemma 6.7, it suffices to show that this is injective. Let
$c_1:\operatorname {NS}(X\!)\otimes \mathbb {Z}_\ell \to H^2(X,\mathbb {Z}_\ell (1))$ and, again by Lemma 6.7, it suffices to show that this is injective. Let ![]() $\overline {X}$ be a projective normal compactification of
$\overline {X}$ be a projective normal compactification of ![]() $X$ and let
$X$ and let ![]() $\tau :\overline {X}'\to \overline {X}$ be an alteration (i.e. a projective generically finite morphism with regular source) of degree prime to
$\tau :\overline {X}'\to \overline {X}$ be an alteration (i.e. a projective generically finite morphism with regular source) of degree prime to ![]() $\ell$, which exists by [Reference Illusie, Laszlo and OrgogozoILO14, Exposé X, Théorème 2.1]. Since
$\ell$, which exists by [Reference Illusie, Laszlo and OrgogozoILO14, Exposé X, Théorème 2.1]. Since ![]() $k$ is algebraically closed,
$k$ is algebraically closed, ![]() $\overline {X}'$ is smooth. Putting
$\overline {X}'$ is smooth. Putting ![]() $X':=\tau ^{-1}(X\!)$, we get the following commutative diagram.
$X':=\tau ^{-1}(X\!)$, we get the following commutative diagram.
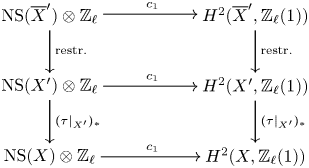
We claim that it suffices to show that the horizontal arrow in the middle is injective. To see this, let ![]() $\alpha \in \operatorname {NS}( X)\otimes \mathbb {Z}_\ell$. Then
$\alpha \in \operatorname {NS}( X)\otimes \mathbb {Z}_\ell$. Then ![]() $c_1(\tau ^\ast \alpha )=\tau ^\ast c_1(\alpha )$ and so injectivity of the horizontal arrow in the middle implies
$c_1(\tau ^\ast \alpha )=\tau ^\ast c_1(\alpha )$ and so injectivity of the horizontal arrow in the middle implies ![]() $c_1(\alpha )\neq 0$ unless
$c_1(\alpha )\neq 0$ unless ![]() $\tau ^\ast \alpha =0$, which, in turn, implies
$\tau ^\ast \alpha =0$, which, in turn, implies ![]() $\tau _\ast \tau ^\ast \alpha =\deg \tau \cdot \alpha =0$ and so
$\tau _\ast \tau ^\ast \alpha =\deg \tau \cdot \alpha =0$ and so ![]() $\alpha =0$ because
$\alpha =0$ because ![]() $\deg \tau$ is coprime to
$\deg \tau$ is coprime to ![]() $\ell$.
$\ell$.
By the localization sequence, the kernel of ![]() $\operatorname {NS}(\overline {X}') \otimes \mathbb {Z}_\ell \to \operatorname {NS}(X')\otimes \mathbb {Z}_\ell$ is generated by classes of divisors supported on
$\operatorname {NS}(\overline {X}') \otimes \mathbb {Z}_\ell \to \operatorname {NS}(X')\otimes \mathbb {Z}_\ell$ is generated by classes of divisors supported on ![]() $\overline {X}'\setminus X$. Similarly, the Gysin sequence (see (P2)) shows that the kernel of the restriction map
$\overline {X}'\setminus X$. Similarly, the Gysin sequence (see (P2)) shows that the kernel of the restriction map ![]() $H^2(\overline {X}',\mathbb {Z}_\ell (1)) \to H^2(X',\mathbb {Z}_\ell (1))$ is generated by the cycle classes of these divisors. As the first horizontal map in the above diagram is injective by [Reference MilneMil80, p. 216, V.3.28], whereas the restriction map
$H^2(\overline {X}',\mathbb {Z}_\ell (1)) \to H^2(X',\mathbb {Z}_\ell (1))$ is generated by the cycle classes of these divisors. As the first horizontal map in the above diagram is injective by [Reference MilneMil80, p. 216, V.3.28], whereas the restriction map ![]() $\operatorname {NS}(\overline {X}')\to \operatorname {NS}( X')$ is surjective (see [Reference FultonFul98, Proposition 1.8]), this shows that the horizontal arrow in the middle of the above diagram is injective, as desired. This proves (P7.1).
$\operatorname {NS}(\overline {X}')\to \operatorname {NS}( X')$ is surjective (see [Reference FultonFul98, Proposition 1.8]), this shows that the horizontal arrow in the middle of the above diagram is injective, as desired. This proves (P7.1).
Step 7: item (P7.2) for ![]() $k$ the perfect closure of a finitely generated field. We use the following well-known lemma.
$k$ the perfect closure of a finitely generated field. We use the following well-known lemma.
Lemma 6.8 Let ![]() $X$ be a separated scheme of finite type over a field
$X$ be a separated scheme of finite type over a field ![]() $k$ of characteristic
$k$ of characteristic ![]() $p>0$ and let
$p>0$ and let ![]() $E/k$ be a purely inseparable extension. Then the flat pullback map
$E/k$ be a purely inseparable extension. Then the flat pullback map ![]() $\operatorname {CH}^i(X\!)[1/p]\to \operatorname {CH}^i(X_E)[1/p]$ is an isomorphism.
$\operatorname {CH}^i(X\!)[1/p]\to \operatorname {CH}^i(X_E)[1/p]$ is an isomorphism.
Proof. The argument is well-known; we recall it for convenience. By a standard limit argument, it suffices to treat the case where ![]() $E/k$ is a finite extension of degree
$E/k$ is a finite extension of degree ![]() $p^s$ for some
$p^s$ for some ![]() $s$. Let
$s$. Let ![]() $f:X_E\to X$ be the canonical map. Then
$f:X_E\to X$ be the canonical map. Then ![]() $f_\ast \circ f^\ast =p^s\cdot \operatorname {id}$ and so
$f_\ast \circ f^\ast =p^s\cdot \operatorname {id}$ and so ![]() $f^\ast$ is injective after inverting
$f^\ast$ is injective after inverting ![]() $p$. As
$p$. As ![]() $f$ is a universal homeomorphism, we have that for any subvariety
$f$ is a universal homeomorphism, we have that for any subvariety ![]() $Z\subset X_E$:
$Z\subset X_E$: ![]() $f^\ast f_\ast [Z]=m[Z]$ for some
$f^\ast f_\ast [Z]=m[Z]$ for some ![]() $m\geqslant 1$ and
$m\geqslant 1$ and ![]() $f_\ast \circ f^\ast =p^s\cdot \operatorname {id}$ implies that
$f_\ast \circ f^\ast =p^s\cdot \operatorname {id}$ implies that ![]() $m$ must be a
$m$ must be a ![]() $p$-power. Hence,
$p$-power. Hence, ![]() $f^\ast$ is surjective after inverting
$f^\ast$ is surjective after inverting ![]() $p$, as desired.
$p$, as desired.
Now let ![]() $k$ be the perfect closure of a finitely generated field
$k$ be the perfect closure of a finitely generated field ![]() $k_0\subset k$, and let
$k_0\subset k$, and let ![]() $X$ be a regular (hence smooth) variety over
$X$ be a regular (hence smooth) variety over ![]() $k$. By Lemma 6.7, it suffices to show that the map
$k$. By Lemma 6.7, it suffices to show that the map
induced by ![]() $c_1$ from (6.3) is injective, where we note that the right-hand side identifies to continuous étale cohomology by Lemma 6.5. Using the existence of prime to
$c_1$ from (6.3) is injective, where we note that the right-hand side identifies to continuous étale cohomology by Lemma 6.5. Using the existence of prime to ![]() $\ell$ alterations, the same argument as in step 6 reduces us to the case where
$\ell$ alterations, the same argument as in step 6 reduces us to the case where ![]() $X$ is smooth projective over
$X$ is smooth projective over ![]() $k$. At this point the argument is similar to [Reference JannsenJan88, Remark 6.15].
$k$. At this point the argument is similar to [Reference JannsenJan88, Remark 6.15].
As ![]() $X$ is defined over some finitely generated field, we may assume (up to enlarging
$X$ is defined over some finitely generated field, we may assume (up to enlarging ![]() $k_0$) that
$k_0$) that ![]() $X=X_0\times _{k_0}k$ for some smooth
$X=X_0\times _{k_0}k$ for some smooth ![]() $k_0$-variety
$k_0$-variety ![]() $X_0$.
$X_0$.
Assume for the moment that ![]() $X_0$ is geometrically integral. By Grothendieck's theorem, the Picard functor on
$X_0$ is geometrically integral. By Grothendieck's theorem, the Picard functor on ![]() $X_0$ is then represented by the Picard scheme
$X_0$ is then represented by the Picard scheme ![]() $\operatorname {\textbf {Pic}}_{X_0/k}$, see e.g. [Reference KleimanKle05, Theorem 9.4.8]. In particular,
$\operatorname {\textbf {Pic}}_{X_0/k}$, see e.g. [Reference KleimanKle05, Theorem 9.4.8]. In particular, ![]() $\operatorname {Pic}(X_0)$ is given by the group of
$\operatorname {Pic}(X_0)$ is given by the group of ![]() $k_0$-rational points of
$k_0$-rational points of ![]() $\operatorname {\textbf {Pic}}_{X_0/k}$. The quotient of
$\operatorname {\textbf {Pic}}_{X_0/k}$. The quotient of ![]() $\operatorname {\textbf {Pic}}_{X_0/k}$ by the identity component is always a finitely generated group scheme (the Néron–Severi group). Moreover, the identity component is an abelian variety over
$\operatorname {\textbf {Pic}}_{X_0/k}$ by the identity component is always a finitely generated group scheme (the Néron–Severi group). Moreover, the identity component is an abelian variety over ![]() $k_0$ and because
$k_0$ and because ![]() $k_0$ is finitely generated, its group of
$k_0$ is finitely generated, its group of ![]() $k_0$-rational points is finitely generated by Néron's Mordell–Weil theorem [Reference NéronNér52]. It follows that
$k_0$-rational points is finitely generated by Néron's Mordell–Weil theorem [Reference NéronNér52]. It follows that ![]() $\operatorname {Pic} (X_0)$ is a finitely generated abelian group.
$\operatorname {Pic} (X_0)$ is a finitely generated abelian group.
In general, ![]() $X_0$ will split into a finite union of geometrically integral smooth projective varieties after a finite extension of the base field. The above argument together with a pull and push argument then shows that, in general,
$X_0$ will split into a finite union of geometrically integral smooth projective varieties after a finite extension of the base field. The above argument together with a pull and push argument then shows that, in general, ![]() $\operatorname {Pic}(X_0)$ contains an
$\operatorname {Pic}(X_0)$ contains an ![]() $n$-torsion subgroup
$n$-torsion subgroup ![]() $T$ for some
$T$ for some ![]() $n\geqslant 1$ such that
$n\geqslant 1$ such that ![]() $Q:=\operatorname {Pic}(X_0)/T$ is a finitely generated abelian group. We consider the short exact sequence
$Q:=\operatorname {Pic}(X_0)/T$ is a finitely generated abelian group. We consider the short exact sequence ![]() $0\to T\to \operatorname {Pic}(X_0)\to Q\to 0$. As
$0\to T\to \operatorname {Pic}(X_0)\to Q\to 0$. As ![]() $Q$ is finitely generated and
$Q$ is finitely generated and ![]() $T$ is
$T$ is ![]() $n$-torsion, this sequence remains exact if we apply either the
$n$-torsion, this sequence remains exact if we apply either the ![]() $\ell$-adic completion functor or
$\ell$-adic completion functor or ![]() $\otimes _\mathbb {Z} \mathbb {Z}_\ell$. Comparing the two resulting short exact sequences, we find that
$\otimes _\mathbb {Z} \mathbb {Z}_\ell$. Comparing the two resulting short exact sequences, we find that
The usual Kummer sequence on the étale site yields compatible injections ![]() $\operatorname {Pic}(X_0)/\ell ^r\hookrightarrow H^2(X_0,\mu _{\ell ^r}^{\otimes 1})$, i.e. an injection of projective systems. Applying the inverse limit functor, this yields by (6.18) an injection
$\operatorname {Pic}(X_0)/\ell ^r\hookrightarrow H^2(X_0,\mu _{\ell ^r}^{\otimes 1})$, i.e. an injection of projective systems. Applying the inverse limit functor, this yields by (6.18) an injection ![]() $\operatorname {Pic}(X_0)\otimes _\mathbb {Z}\mathbb {Z}_\ell \hookrightarrow \lim H^2(X_0,\mu _{\ell ^r}^{\otimes 1})$. By (6.1) and the construction of
$\operatorname {Pic}(X_0)\otimes _\mathbb {Z}\mathbb {Z}_\ell \hookrightarrow \lim H^2(X_0,\mu _{\ell ^r}^{\otimes 1})$. By (6.1) and the construction of ![]() $c_1$ in (6.3), this injection factors through
$c_1$ in (6.3), this injection factors through
and so the latter must be injective as well. It follows that (6.17) is injective, because ![]() $c_1$ is functorial with respect to pullbacks, and the canonical pullback maps yield isomorphisms
$c_1$ is functorial with respect to pullbacks, and the canonical pullback maps yield isomorphisms ![]() $\operatorname {Pic}(X_0)\otimes _\mathbb {Z} \mathbb {Z}_\ell \simeq \operatorname {Pic}(X\!)\otimes _\mathbb {Z} \mathbb {Z}_\ell$ (see Lemma 6.8) and
$\operatorname {Pic}(X_0)\otimes _\mathbb {Z} \mathbb {Z}_\ell \simeq \operatorname {Pic}(X\!)\otimes _\mathbb {Z} \mathbb {Z}_\ell$ (see Lemma 6.8) and ![]() $H^2(X_0,\mathbb {Z}_\ell (1))\simeq H^2(X,\mathbb {Z}_\ell (1))$ (see [Reference Bhatt and ScholzeBS15, Lemma 5.4.2]), because
$H^2(X_0,\mathbb {Z}_\ell (1))\simeq H^2(X,\mathbb {Z}_\ell (1))$ (see [Reference Bhatt and ScholzeBS15, Lemma 5.4.2]), because ![]() $k/k_0$ is purely inseparable by assumption. This concludes the proof of (P7.2) and, hence, finishes the proof of the proposition.
$k/k_0$ is purely inseparable by assumption. This concludes the proof of (P7.2) and, hence, finishes the proof of the proposition.
6.2 Borel–Moore cohomology of complex analytic spaces
If ![]() $X$ is a complex algebraic scheme with underlying analytic space
$X$ is a complex algebraic scheme with underlying analytic space ![]() $X_{\operatorname {an}}$ and
$X_{\operatorname {an}}$ and ![]() $A$ is an abelian group, then one may (and we do) define its Borel–Moore homology
$A$ is an abelian group, then one may (and we do) define its Borel–Moore homology ![]() $H^{\rm BM}_i(X_{\operatorname {an}},A)$ analogous to singular homology with values in
$H^{\rm BM}_i(X_{\operatorname {an}},A)$ analogous to singular homology with values in ![]() $A$, but with locally finite chains instead of finite chains, see [Reference BredonBre97, Theorem V.12.14 and Corollary V.12.21]. An alternative sheaf theoretic definition of the same group can be found in [Reference Borel and MooreBM60] and [Reference BredonBre97, Chapter V]; a definition in terms of relative singular cohomology is given in [Reference FultonFul98, Example 19.1.1] and the references therein. If
$A$, but with locally finite chains instead of finite chains, see [Reference BredonBre97, Theorem V.12.14 and Corollary V.12.21]. An alternative sheaf theoretic definition of the same group can be found in [Reference Borel and MooreBM60] and [Reference BredonBre97, Chapter V]; a definition in terms of relative singular cohomology is given in [Reference FultonFul98, Example 19.1.1] and the references therein. If ![]() $X$ is smooth and equi-dimensional of dimension
$X$ is smooth and equi-dimensional of dimension ![]() $d_X$, then
$d_X$, then ![]() $H^{\rm BM}_i(X_{\operatorname {an}},A)\simeq H^{2d_X-i}_{\rm sing}(X_{\operatorname {an}},A)$ by Poincaré duality, see [Reference BredonBre97, Chapter V, § 9].
$H^{\rm BM}_i(X_{\operatorname {an}},A)\simeq H^{2d_X-i}_{\rm sing}(X_{\operatorname {an}},A)$ by Poincaré duality, see [Reference BredonBre97, Chapter V, § 9].
Proposition 6.9 Let ![]() $\mathcal {V}$ be the category whose objects are separated schemes of finite type over
$\mathcal {V}$ be the category whose objects are separated schemes of finite type over ![]() $\mathbb {C}$ and whose morphisms are given by open immersions of schemes of the same dimension. Further let
$\mathbb {C}$ and whose morphisms are given by open immersions of schemes of the same dimension. Further let ![]() $\mathcal {A}=\operatorname {Mod}_{\mathbb {Z}}$ and put
$\mathcal {A}=\operatorname {Mod}_{\mathbb {Z}}$ and put ![]() $A(n):=A\otimes _{\mathbb {Z}}(2\pi i)^n\mathbb {Z}$ for all
$A(n):=A\otimes _{\mathbb {Z}}(2\pi i)^n\mathbb {Z}$ for all ![]() $A\in \mathcal {A}$ and
$A\in \mathcal {A}$ and ![]() $n\in \mathbb {Z}$. Then let
$n\in \mathbb {Z}$. Then let
where the right-hand side denotes Borel–Moore homology of the underlying analytic space, and where ![]() $d_X=\dim X$. Then
$d_X=\dim X$. Then ![]() $H^\ast (-,A(n))$ defines an integral twisted Borel–Moore cohomology theory that is adapted to algebraic equivalence, see Definition 4.6.
$H^\ast (-,A(n))$ defines an integral twisted Borel–Moore cohomology theory that is adapted to algebraic equivalence, see Definition 4.6.
Proof. Property (P1![]() $'$) follows from covariant functoriality of Borel–Moore homology with respect to proper maps, and item (P2
$'$) follows from covariant functoriality of Borel–Moore homology with respect to proper maps, and item (P2![]() $'$) is a consequence of the long exact sequence of pairs in Borel–Moore homology, see, e.g., [Reference FultonFul98, § 19.1] and the references therein. If
$'$) is a consequence of the long exact sequence of pairs in Borel–Moore homology, see, e.g., [Reference FultonFul98, § 19.1] and the references therein. If ![]() $X$ is smooth and integral, then
$X$ is smooth and integral, then ![]() $H^i(X,A(n))\simeq H^i_{\rm sing}(X_{\operatorname {an}},A(n))$. In particular,
$H^i(X,A(n))\simeq H^i_{\rm sing}(X_{\operatorname {an}},A(n))$. In particular, ![]() $H^0(X,A(0))\simeq A$ and there is a canonical class
$H^0(X,A(0))\simeq A$ and there is a canonical class
which corresponds to ![]() $1\in \mathbb {Z}$. This proves (P3
$1\in \mathbb {Z}$. This proves (P3![]() $'$), as in the direct limit (4.2), it suffices to run through smooth integral varieties
$'$), as in the direct limit (4.2), it suffices to run through smooth integral varieties ![]() $V_{x}\subset \overline {\{x\}}$.
$V_{x}\subset \overline {\{x\}}$.
It remains to prove that (P4![]() $'$)–(P6
$'$)–(P6![]() $'$) and (P7.1
$'$) and (P7.1![]() $'$) hold, where we recall that these properties are formally deduced from (P4)–(P6) and (P7.1) by the replacement of symbols
$'$) hold, where we recall that these properties are formally deduced from (P4)–(P6) and (P7.1) by the replacement of symbols ![]() $\mathbb {Z}_\ell \rightsquigarrow \mathbb {Z}$,
$\mathbb {Z}_\ell \rightsquigarrow \mathbb {Z}$, ![]() $\mathbb {Q}_\ell \rightsquigarrow \mathbb {Q}$, and
$\mathbb {Q}_\ell \rightsquigarrow \mathbb {Q}$, and ![]() $\ell ^r \rightsquigarrow r$.
$\ell ^r \rightsquigarrow r$.
Item (P4![]() $'$) is clear and item (P5
$'$) is clear and item (P5![]() $'$) follows from the long exact sequence associated to the coefficient sequence
$'$) follows from the long exact sequence associated to the coefficient sequence ![]() $0\to \mathbb {Z}(1)\stackrel {\times r}{\to } \mathbb {Z}(1)\to \mathbb {Z}/r(1)\to 0$; functoriality of the Bockstein sequence with respect to pullbacks and pushforwards in Borel–Moore (co-)homology are well-known and left to the reader.
$0\to \mathbb {Z}(1)\stackrel {\times r}{\to } \mathbb {Z}(1)\to \mathbb {Z}/r(1)\to 0$; functoriality of the Bockstein sequence with respect to pullbacks and pushforwards in Borel–Moore (co-)homology are well-known and left to the reader.
For property (P6![]() $'$), note that in the direct limit (4.2) it suffices to run through regular (Zariski) open subsets
$'$), note that in the direct limit (4.2) it suffices to run through regular (Zariski) open subsets ![]() $V:=V_x$ of the closure of
$V:=V_x$ of the closure of ![]() $x$ in
$x$ in ![]() $X$. In this case,
$X$. In this case, ![]() $H^i(V ,A(n))$ identifies to singular cohomology and so the exponential sequence yields a map
$H^i(V ,A(n))$ identifies to singular cohomology and so the exponential sequence yields a map ![]() $H^0(V_{\operatorname {an}} ,\mathcal {O}_{V_{\operatorname {an}}}^\ast )\to H^1(V ,\mathbb {Z}(1))$. Taking direct limits, and using that algebraic functions are holomorphic, we get a map
$H^0(V_{\operatorname {an}} ,\mathcal {O}_{V_{\operatorname {an}}}^\ast )\to H^1(V ,\mathbb {Z}(1))$. Taking direct limits, and using that algebraic functions are holomorphic, we get a map ![]() $\epsilon : \kappa (x)^\ast \to H^1(x,\mathbb {Z}(1)).$ For any positive integer
$\epsilon : \kappa (x)^\ast \to H^1(x,\mathbb {Z}(1)).$ For any positive integer ![]() $r$, this induces by reduction modulo
$r$, this induces by reduction modulo ![]() $r$ a map
$r$ a map
and we need to prove that this is surjective.
Consider the following commutative diagram of sheaves on ![]() $V_{\operatorname {an}}$ (cf. [Reference Colliot-Thélène and VoisinCV12, § 3.1]).
$V_{\operatorname {an}}$ (cf. [Reference Colliot-Thélène and VoisinCV12, § 3.1]).
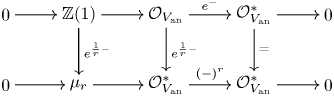
The rows in this diagram are exact and we get a boundary map ![]() $\beta :H^0(V_{\operatorname {an}}, \mathcal {O}^\ast _{V_{\operatorname {an}}})\to H^1(V,\mu _r)$. Taking the direct limit over all (Zariski) open dense
$\beta :H^0(V_{\operatorname {an}}, \mathcal {O}^\ast _{V_{\operatorname {an}}})\to H^1(V,\mu _r)$. Taking the direct limit over all (Zariski) open dense ![]() $V\subset \overline {\{x\}}$ and restricting
$V\subset \overline {\{x\}}$ and restricting ![]() $\beta$ to algebraic functions, we get a map
$\beta$ to algebraic functions, we get a map ![]() $\overline {\beta }: \kappa (x)^\ast \to H^1(x,\mu _r)$. Commutativity of the above diagram shows that
$\overline {\beta }: \kappa (x)^\ast \to H^1(x,\mu _r)$. Commutativity of the above diagram shows that ![]() $\overline {\beta }$ identifies to
$\overline {\beta }$ identifies to ![]() $\overline {\epsilon }$ under the isomorphism
$\overline {\epsilon }$ under the isomorphism ![]() $\mathbb {Z}/r(1)\to \mu _r$,
$\mathbb {Z}/r(1)\to \mu _r$, ![]() . It thus suffices to show that
. It thus suffices to show that ![]() $\overline {\beta }$ is surjective. This follows by comparing the sequence above with the Kummer sequence
$\overline {\beta }$ is surjective. This follows by comparing the sequence above with the Kummer sequence ![]() $0\to \mu _r\to \mathbb {G}_m\to \mathbb {G}_m\to 0$ on the étale site
$0\to \mu _r\to \mathbb {G}_m\to \mathbb {G}_m\to 0$ on the étale site ![]() $V_{\unicode{x00E9}{\rm t}}$ and using that
$V_{\unicode{x00E9}{\rm t}}$ and using that ![]() $H^1(V_{\operatorname {an}},\mu _r)\simeq H^1(V_{\unicode{x00E9}{\rm t}},\mu _r)$ (see, e.g., [Reference MilneMil80, p. 117, III.3.12]) and
$H^1(V_{\operatorname {an}},\mu _r)\simeq H^1(V_{\unicode{x00E9}{\rm t}},\mu _r)$ (see, e.g., [Reference MilneMil80, p. 117, III.3.12]) and
because ![]() $H^1(V_{\unicode{x00E9}{\rm t}},\mathbb {G}_m)\simeq \operatorname {Pic}(V)$ by Grothendieck's Hilbert theorem 90. We have thus shown that
$H^1(V_{\unicode{x00E9}{\rm t}},\mathbb {G}_m)\simeq \operatorname {Pic}(V)$ by Grothendieck's Hilbert theorem 90. We have thus shown that ![]() $\overline {\epsilon }$ is surjective. Finally, let
$\overline {\epsilon }$ is surjective. Finally, let ![]() $X\in \mathcal {V}$ integral with generic point
$X\in \mathcal {V}$ integral with generic point ![]() $\eta$ and a regular point
$\eta$ and a regular point ![]() $x\in X^{(1)}$. We claim that the natural composition
$x\in X^{(1)}$. We claim that the natural composition
where ![]() $\partial$ is induced by (P2
$\partial$ is induced by (P2![]() $'$), maps
$'$), maps ![]() $f$ to
$f$ to ![]() $[x](-\nu _x(f))$, where
$[x](-\nu _x(f))$, where ![]() $\nu _x$ denotes the valuation on
$\nu _x$ denotes the valuation on ![]() $\kappa (\eta )$ induced by
$\kappa (\eta )$ induced by ![]() $x$. It suffices to check this modulo an arbitrary prime power, which, thanks to the comparison between étale cohomology and singular cohomology with finite coefficients (see [Reference MilneMil80, p. 117, III.3.12]), follows from step 5 in the proof of Proposition 6.6. This concludes the proof of (P6
$x$. It suffices to check this modulo an arbitrary prime power, which, thanks to the comparison between étale cohomology and singular cohomology with finite coefficients (see [Reference MilneMil80, p. 117, III.3.12]), follows from step 5 in the proof of Proposition 6.6. This concludes the proof of (P6![]() $'$).
$'$).
Finally, property (P7.1![]() $'$) is well-known in the case where
$'$) is well-known in the case where ![]() $X$ is smooth projective and follows for arbitrary smooth
$X$ is smooth projective and follows for arbitrary smooth ![]() $X$ by choosing a smooth compactification (using resolution of singularities) by a similar argument as in step 6 of the proof of Proposition 6.6. This concludes the proof of the proposition.
$X$ by choosing a smooth compactification (using resolution of singularities) by a similar argument as in step 6 of the proof of Proposition 6.6. This concludes the proof of the proposition.
7. Comparison theorems to algebraic cycles
In this section, we fix a prime ![]() $\ell$ and an
$\ell$ and an ![]() $\ell$-adic twisted Borel–Moore cohomology theory
$\ell$-adic twisted Borel–Moore cohomology theory ![]() $H^\ast (-,A(n))$ on a constructible category of Noetherian schemes
$H^\ast (-,A(n))$ on a constructible category of Noetherian schemes ![]() $\mathcal {V}$ with coefficients in a full subcategory
$\mathcal {V}$ with coefficients in a full subcategory ![]() $\mathcal {A}\subset \operatorname {Mod}_{\mathbb {Z}_\ell }$, see Definition 4.4. In particular, (P1)–(P6) hold true. The main result is that this set-up allows us to compute several cycle groups efficiently.
$\mathcal {A}\subset \operatorname {Mod}_{\mathbb {Z}_\ell }$, see Definition 4.4. In particular, (P1)–(P6) hold true. The main result is that this set-up allows us to compute several cycle groups efficiently.
7.1  $\ell$-adic Chow groups
$\ell$-adic Chow groups
We use the notation ![]() $\operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }:=\operatorname {CH}^i(X\!)\otimes _\mathbb {Z} \mathbb {Z}_\ell$.
$\operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }:=\operatorname {CH}^i(X\!)\otimes _\mathbb {Z} \mathbb {Z}_\ell$.
Lemma 7.1 For any ![]() $X\in \mathcal {V}$, there is a canonical isomorphism
$X\in \mathcal {V}$, there is a canonical isomorphism
 \[ \operatorname{CH}^i(X\!)_{\mathbb{Z}_\ell}\simeq \frac{\bigoplus_{x\in X^{(i)}} [x]\mathbb{Z}_\ell }{\operatorname{im} \big(\!\bigoplus_{x\in X^{(i-1)}} \kappa(x)^\ast \otimes_{\mathbb{Z}} \mathbb{Z}_\ell \stackrel{{\epsilon}}{\longrightarrow} \bigoplus_{x\in X^{(i-1)}} H^1(x,\mathbb{Z}_\ell(1)) \stackrel{{\partial\circ\iota_\ast}}{\longrightarrow} \bigoplus_{x\in X^{(i)}} [x]\mathbb{Z}_\ell \big) } , \]
\[ \operatorname{CH}^i(X\!)_{\mathbb{Z}_\ell}\simeq \frac{\bigoplus_{x\in X^{(i)}} [x]\mathbb{Z}_\ell }{\operatorname{im} \big(\!\bigoplus_{x\in X^{(i-1)}} \kappa(x)^\ast \otimes_{\mathbb{Z}} \mathbb{Z}_\ell \stackrel{{\epsilon}}{\longrightarrow} \bigoplus_{x\in X^{(i-1)}} H^1(x,\mathbb{Z}_\ell(1)) \stackrel{{\partial\circ\iota_\ast}}{\longrightarrow} \bigoplus_{x\in X^{(i)}} [x]\mathbb{Z}_\ell \big) } , \]
where ![]() $\epsilon$ is induced by the map from (P6), and where
$\epsilon$ is induced by the map from (P6), and where ![]() $\partial \circ \iota _\ast$ denotes the composition
$\partial \circ \iota _\ast$ denotes the composition
where ![]() $\iota _\ast$ and
$\iota _\ast$ and ![]() $\partial$ are induced by (P2) and the last equality uses (P3).
$\partial$ are induced by (P2) and the last equality uses (P3).
Proof. We recall our convention that for a Noetherian scheme ![]() $X$,
$X$, ![]() $X^{(j)}$ denotes the set of points
$X^{(j)}$ denotes the set of points ![]() $x\in X$ of dimension
$x\in X$ of dimension ![]() $\dim (\overline {\{x\}})=\dim (X\!)-j$. In particular,
$\dim (\overline {\{x\}})=\dim (X\!)-j$. In particular, ![]() $\operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }$ is the quotient of
$\operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }$ is the quotient of ![]() $\bigoplus _{x\in X^{(i)}} [x]\mathbb {Z}_\ell$ by the
$\bigoplus _{x\in X^{(i)}} [x]\mathbb {Z}_\ell$ by the ![]() $\mathbb {Z}_\ell$-submodule generated by cycles that are given by the pushforward of a principal divisor on the normalization of some subvariety
$\mathbb {Z}_\ell$-submodule generated by cycles that are given by the pushforward of a principal divisor on the normalization of some subvariety ![]() $W\subset X$ with
$W\subset X$ with ![]() $\dim W=\dim X-i+1$. The lemma therefore follows directly from Lemma 5.12 and the second part of (P6). This concludes the proof.
$\dim W=\dim X-i+1$. The lemma therefore follows directly from Lemma 5.12 and the second part of (P6). This concludes the proof.
In view of Lemma 7.1, it is natural to make the following definition.
Definition 7.2 For ![]() $X\in \mathcal {V}$, we define
$X\in \mathcal {V}$, we define
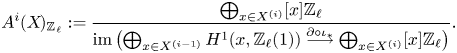 \[ A^i(X\!)_{\mathbb{Z}_\ell}:=\frac{\bigoplus_{x\in X^{(i)}} [x]\mathbb{Z}_\ell }{\operatorname{im} \big(\!\bigoplus_{x\in X^{(i-1)}} H^1(x,\mathbb{Z}_\ell(1)) \stackrel{{\partial\circ \iota_\ast}}{\longrightarrow} \bigoplus_{x\in X^{(i)}} [x]\mathbb{Z}_\ell \big) }. \]
\[ A^i(X\!)_{\mathbb{Z}_\ell}:=\frac{\bigoplus_{x\in X^{(i)}} [x]\mathbb{Z}_\ell }{\operatorname{im} \big(\!\bigoplus_{x\in X^{(i-1)}} H^1(x,\mathbb{Z}_\ell(1)) \stackrel{{\partial\circ \iota_\ast}}{\longrightarrow} \bigoplus_{x\in X^{(i)}} [x]\mathbb{Z}_\ell \big) }. \]
By Lemma 7.1, there is a canonical surjection
We compute the kernel of this surjection in Lemma 7.4.
7.2 Cycle class maps and coniveau filtration
By Corollary 5.10, ![]() $H^{2i}(X,\mathbb {Z}_\ell (i))\simeq H^{2i}(F_iX,\mathbb {Z}_\ell (i))$. The Gysin sequence from Lemma 5.8 therefore yields a map
$H^{2i}(X,\mathbb {Z}_\ell (i))\simeq H^{2i}(F_iX,\mathbb {Z}_\ell (i))$. The Gysin sequence from Lemma 5.8 therefore yields a map
which is zero on the image of ![]() $\partial : \bigoplus _{x\in X^{(i-1)}} H^1(x,\mathbb {Z}_\ell (1))\to \bigoplus _{x\in X^{(i)}}[x]\mathbb {Z}_\ell$. It thus follows from Lemma 7.1 and Definition 7.2 that there is a well-defined cycle class map
$\partial : \bigoplus _{x\in X^{(i-1)}} H^1(x,\mathbb {Z}_\ell (1))\to \bigoplus _{x\in X^{(i)}}[x]\mathbb {Z}_\ell$. It thus follows from Lemma 7.1 and Definition 7.2 that there is a well-defined cycle class map
which factors through the canonical surjection ![]() . We then define
. We then define
As the category ![]() $\mathcal {V}$ is constructible,
$\mathcal {V}$ is constructible, ![]() $Z\in \mathcal {V}$ for any closed subscheme
$Z\in \mathcal {V}$ for any closed subscheme ![]() $Z\subset X$. Using this, we can define the coniveau filtration
$Z\subset X$. Using this, we can define the coniveau filtration ![]() $N^\ast$ on
$N^\ast$ on ![]() $\operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }$ as follows.
$\operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }$ as follows.
Definition 7.3 A class ![]() $z\in \operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }$ has coniveau
$z\in \operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }$ has coniveau ![]() $j$, i.e.
$j$, i.e. ![]() $z\in N^j\operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }$, if and only if it is homologically trivial on a closed subscheme of codimension
$z\in N^j\operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }$, if and only if it is homologically trivial on a closed subscheme of codimension ![]() $j$. More precisely,
$j$. More precisely, ![]() $z\in N^j\operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }$ if and only if there is a closed subscheme
$z\in N^j\operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }$ if and only if there is a closed subscheme ![]() $\iota : Z\hookrightarrow X$ with
$\iota : Z\hookrightarrow X$ with ![]() $j=\dim X-\dim Z$ and a cycle
$j=\dim X-\dim Z$ and a cycle ![]() $z'\in \operatorname {CH}^{i-j}_0(Z)_{\mathbb {Z}_\ell }$ with
$z'\in \operatorname {CH}^{i-j}_0(Z)_{\mathbb {Z}_\ell }$ with ![]() $z=\iota _\ast z'\in \operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }$.
$z=\iota _\ast z'\in \operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }$.
For the case when ![]() $X$ is not equi-dimensional, we recall from § 2 that
$X$ is not equi-dimensional, we recall from § 2 that ![]() $X^{(i)}:=X_{(d-i)}$ and so
$X^{(i)}:=X_{(d-i)}$ and so ![]() $\operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }$ is the group of
$\operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }$ is the group of ![]() $\ell$-adic cycles of dimension
$\ell$-adic cycles of dimension ![]() $d-i$, where
$d-i$, where ![]() $d=\dim X$.
$d=\dim X$.
The coniveau filtration ![]() $N^\ast$ on
$N^\ast$ on ![]() $\operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }$ is of the following form
$\operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }$ is of the following form
This definition is related to the groups ![]() $A^i(X\!)_{\mathbb {Z}_\ell }$ from Definition 7.2, as follows.
$A^i(X\!)_{\mathbb {Z}_\ell }$ from Definition 7.2, as follows.
Lemma 7.4 Let ![]() $X\in \mathcal {V}$. Then
$X\in \mathcal {V}$. Then ![]() $A^i(X\!)_{\mathbb {Z}_\ell }=\operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }/N^{i-1}\operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }$.
$A^i(X\!)_{\mathbb {Z}_\ell }=\operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }/N^{i-1}\operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }$.
Proof. We need to show that a codimension-![]() $i$ cycle on
$i$ cycle on ![]() $X$ has coniveau
$X$ has coniveau ![]() $i-1$ if and only if it is represented by a cycle in
$i-1$ if and only if it is represented by a cycle in
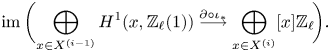 \begin{equation} \operatorname{im} \bigg(\!\bigoplus_{x\in X^{(i-1)}} H^1(x,\mathbb{Z}_\ell(1))
\stackrel{{\partial\circ
\iota_\ast}}{\longrightarrow} \bigoplus_{x\in X^{(i)}} [x]\mathbb{Z}_\ell\!\bigg).
\end{equation}
\begin{equation} \operatorname{im} \bigg(\!\bigoplus_{x\in X^{(i-1)}} H^1(x,\mathbb{Z}_\ell(1))
\stackrel{{\partial\circ
\iota_\ast}}{\longrightarrow} \bigoplus_{x\in X^{(i)}} [x]\mathbb{Z}_\ell\!\bigg).
\end{equation}
For ![]() $Z\in \mathcal {V}$ the Gysin sequence (P2) yields a residue map
$Z\in \mathcal {V}$ the Gysin sequence (P2) yields a residue map
The compatibility of the Gysin sequence with proper pushforwards yields the following commutative diagram.
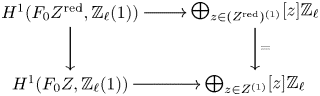
Here ![]() $Z^{\operatorname {red}}$ denotes the reduced scheme that underlies
$Z^{\operatorname {red}}$ denotes the reduced scheme that underlies ![]() $Z$. If
$Z$. If ![]() $Z\subset X$ is closed so that
$Z\subset X$ is closed so that ![]() $U=X\setminus Z$ satisfies
$U=X\setminus Z$ satisfies ![]() $\dim U=\dim X$, then the comparison of the Gysin sequences for the pairs
$\dim U=\dim X$, then the comparison of the Gysin sequences for the pairs ![]() $(X,Z)$ and
$(X,Z)$ and ![]() $(X,Z^{\operatorname {red}})$ shows by the five lemma that the pushforward map
$(X,Z^{\operatorname {red}})$ shows by the five lemma that the pushforward map ![]() $H^i(Z^{\operatorname {red}},A(n))\to H^i(Z,A(n))$ is an isomorphism. This argument remains valid if we replace
$H^i(Z^{\operatorname {red}},A(n))\to H^i(Z,A(n))$ is an isomorphism. This argument remains valid if we replace ![]() $Z$ by some dense open subset
$Z$ by some dense open subset ![]() $Z^\circ \subset Z$ and
$Z^\circ \subset Z$ and ![]() $X$ by
$X$ by ![]() $X\setminus (Z\setminus Z^\circ )$. It follows that in the above diagram the vertical arrow on the left is an isomorphism for all
$X\setminus (Z\setminus Z^\circ )$. It follows that in the above diagram the vertical arrow on the left is an isomorphism for all ![]() $Z\subset X$ closed with
$Z\subset X$ closed with ![]() $\dim (X\setminus Z)=\dim X$. The image in (7.2) therefore agrees with
$\dim (X\setminus Z)=\dim X$. The image in (7.2) therefore agrees with
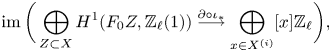 \[ \operatorname{im} \bigg( \bigoplus_{Z\subset X} H^1(F_0Z,\mathbb{Z}_\ell(1)) \stackrel{{\partial\circ\iota_\ast}}{\longrightarrow} \bigoplus_{x\in X^{(i)}} [x]\mathbb{Z}_\ell \bigg) , \]
\[ \operatorname{im} \bigg( \bigoplus_{Z\subset X} H^1(F_0Z,\mathbb{Z}_\ell(1)) \stackrel{{\partial\circ\iota_\ast}}{\longrightarrow} \bigoplus_{x\in X^{(i)}} [x]\mathbb{Z}_\ell \bigg) , \]
where ![]() $Z\subset X$ runs through all closed subschemes
$Z\subset X$ runs through all closed subschemes ![]() $Z\subset X$ with
$Z\subset X$ with ![]() $i-1=\dim X-\dim Z$ and
$i-1=\dim X-\dim Z$ and ![]() $\iota :Z\hookrightarrow X$ denotes the inclusion.
$\iota :Z\hookrightarrow X$ denotes the inclusion.
Let us now fix a subscheme ![]() $Z\subset X$ with
$Z\subset X$ with ![]() $i-1=\dim X-\dim Z$. As the Gysin sequence (P2) is functorial with respect to proper pushforwards, we get from Lemma 5.8 the following commutative diagram with exact rows.
$i-1=\dim X-\dim Z$. As the Gysin sequence (P2) is functorial with respect to proper pushforwards, we get from Lemma 5.8 the following commutative diagram with exact rows.
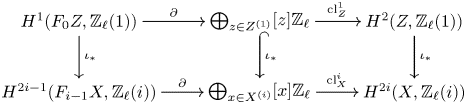
Exactness of the first row shows that the ![]() $\ell$-adic cycles that are homologically trivial on
$\ell$-adic cycles that are homologically trivial on ![]() $Z$ are exactly those in the image of
$Z$ are exactly those in the image of ![]() $\partial$ in the left upper corner. This description together with the commutativity of the square on the left implies the lemma.
$\partial$ in the left upper corner. This description together with the commutativity of the square on the left implies the lemma.
By the above lemma, ![]() $A^i(X\!)_{\mathbb {Z}_\ell }=\operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }/N^{i-1}\operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }$. The following lemma computes this quotient (and, hence,
$A^i(X\!)_{\mathbb {Z}_\ell }=\operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }/N^{i-1}\operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }$. The following lemma computes this quotient (and, hence, ![]() $N^{i-1}\operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }$) in the cases where (P7.1) and (P7.2) hold, respectively; the result is essentially due to Jannsen, see [Reference JannsenJan00, Lemmas 5.7 and 5.8] where it is proven
$N^{i-1}\operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }$) in the cases where (P7.1) and (P7.2) hold, respectively; the result is essentially due to Jannsen, see [Reference JannsenJan00, Lemmas 5.7 and 5.8] where it is proven ![]() $\otimes \mathbb {Q}_\ell$.
$\otimes \mathbb {Q}_\ell$.
Before we state the next result, we refer the reader to [Reference FultonFul98, § 10.3] for the definition of algebraic equivalence of algebraic cycles.
Lemma 7.5 For ![]() $X\in \mathcal {V}$, the following holds:
$X\in \mathcal {V}$, the following holds:
(i) If (P7.1) holds, then
 \[ N^{i-1}\operatorname{CH}^i(X\!)_{\mathbb{Z}_\ell}=\operatorname{CH}^i(X\!)_{\operatorname{alg}}\otimes_\mathbb{Z} \mathbb{Z}_\ell \quad \text{and}\quad A^i(X\!)_{\mathbb{Z}_\ell}=(\operatorname{CH}^i(X\!)/\sim_{\operatorname{alg}})\otimes_\mathbb{Z} \mathbb{Z}_\ell . \]
\[ N^{i-1}\operatorname{CH}^i(X\!)_{\mathbb{Z}_\ell}=\operatorname{CH}^i(X\!)_{\operatorname{alg}}\otimes_\mathbb{Z} \mathbb{Z}_\ell \quad \text{and}\quad A^i(X\!)_{\mathbb{Z}_\ell}=(\operatorname{CH}^i(X\!)/\sim_{\operatorname{alg}})\otimes_\mathbb{Z} \mathbb{Z}_\ell . \]
(ii) If (P7.2) holds, then
 $N^{i-1}\operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }=0$ and
$N^{i-1}\operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }=0$ and  $A^i(X\!)_{\mathbb {Z}_\ell }=\operatorname {CH}^i(X\!)\otimes _\mathbb {Z} \mathbb {Z}_\ell$.
$A^i(X\!)_{\mathbb {Z}_\ell }=\operatorname {CH}^i(X\!)\otimes _\mathbb {Z} \mathbb {Z}_\ell$.
Proof. We aim to describe the image of
By Lemma 5.12, the image is generated by the images of the maps
where ![]() $W\subset X$ runs through all closed subvarieties of codimension
$W\subset X$ runs through all closed subvarieties of codimension ![]() $\dim X-\dim W=i-1$ and
$\dim X-\dim W=i-1$ and ![]() $\tau :W'\to W$ denotes the normalization. By Lemma 5.8, the image of
$\tau :W'\to W$ denotes the normalization. By Lemma 5.8, the image of ![]() $\partial$ above is given by the kernel of
$\partial$ above is given by the kernel of
where the last isomorphism is due to Corollary 5.10. Since ![]() $W'$ is normal, it is regular in codimension one and so we may in (7.3) up to shrinking
$W'$ is normal, it is regular in codimension one and so we may in (7.3) up to shrinking ![]() $W'$ assume that
$W'$ assume that ![]() $W'$ is regular. The kernel of (7.3) then coincides with the
$W'$ is regular. The kernel of (7.3) then coincides with the ![]() $\mathbb {Z}_\ell$-module spanned by algebraically trivial divisors on
$\mathbb {Z}_\ell$-module spanned by algebraically trivial divisors on ![]() $W'$ if (P7.1) holds, and it coincides with the
$W'$ if (P7.1) holds, and it coincides with the ![]() $\mathbb {Z}_\ell$-module spanned by principal divisors if (P7.2) holds. This description proves the lemma.
$\mathbb {Z}_\ell$-module spanned by principal divisors if (P7.2) holds. This description proves the lemma.
7.3 The cokernel of the cycle class map
Definition 7.6 For ![]() $X\in \mathcal {V}$, we define
$X\in \mathcal {V}$, we define
and ![]() $Z^i(X\!)[\ell ^r]:=Z^i(X\!)_{\mathbb {Z}_\ell } [\ell ^r]$, where the cycle class map
$Z^i(X\!)[\ell ^r]:=Z^i(X\!)_{\mathbb {Z}_\ell } [\ell ^r]$, where the cycle class map ![]() $\operatorname {cl}_X^i$ is from (7.1).
$\operatorname {cl}_X^i$ is from (7.1).
The following result generalizes Colliot-Thélène and Voisin's computation of the failure of the integral Hodge conjecture for codimension-two cycles on smooth complex projective varieties from [Reference Colliot-Thélène and VoisinCV12]. The argument follows the same lines as in § 3 above.
Theorem 7.7 For any ![]() $X\in \mathcal {V}$, there are canonical isomorphisms:
$X\in \mathcal {V}$, there are canonical isomorphisms:
The image of ![]() $H^{2i}(X,\mathbb {Z}_\ell (i))[\ell ^r]\to Z^i(X\!) [\ell ^r]$ corresponds via the isomorphism in (7.4) to the subspace generated by the image of
$H^{2i}(X,\mathbb {Z}_\ell (i))[\ell ^r]\to Z^i(X\!) [\ell ^r]$ corresponds via the isomorphism in (7.4) to the subspace generated by the image of ![]() $H^{2i-1} (X,\mu _{\ell ^r}^{\otimes i})\to H^{2i-1}_{i-2,{\rm nr}}(X,\mu _{\ell ^r}^{\otimes i})$. Similarly, the image of
$H^{2i-1} (X,\mu _{\ell ^r}^{\otimes i})\to H^{2i-1}_{i-2,{\rm nr}}(X,\mu _{\ell ^r}^{\otimes i})$. Similarly, the image of ![]() $H^{2i}(X,\mathbb {Z}_\ell (i))[\ell ^\infty ]\to Z^i(X\!) [\ell ^\infty ]$ corresponds via the isomorphism in (7.5) to the subspace generated by the image of
$H^{2i}(X,\mathbb {Z}_\ell (i))[\ell ^\infty ]\to Z^i(X\!) [\ell ^\infty ]$ corresponds via the isomorphism in (7.5) to the subspace generated by the image of
Before we turn to the proof of the above theorem we need the following.
Lemma 7.8 Let ![]() $X\in \mathcal {V}$. Then the natural map
$X\in \mathcal {V}$. Then the natural map
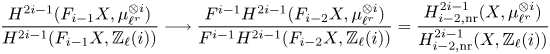 \[ \frac{ H^{2i-1} (F_{i-1}X,\mu_{\ell^r}^{\otimes i})}{ H^{2i-1} (F_{i-1}X,\mathbb{Z}_\ell(i))}\longrightarrow \frac{F^{i-1} H^{2i-1} (F_{i-2}X,\mu_{\ell^r}^{\otimes i})}{ F^{i-1} H^{2i-1} (F_{i-2}X,\mathbb{Z}_\ell(i))}=\frac{ H^{2i-1}_{i-2,{\rm nr}}(X,\mu_{\ell^r}^{\otimes i})}{ H^{2i-1}_{i-2,{\rm nr}}( X,\mathbb{Z}_{\ell}( i))} \]
\[ \frac{ H^{2i-1} (F_{i-1}X,\mu_{\ell^r}^{\otimes i})}{ H^{2i-1} (F_{i-1}X,\mathbb{Z}_\ell(i))}\longrightarrow \frac{F^{i-1} H^{2i-1} (F_{i-2}X,\mu_{\ell^r}^{\otimes i})}{ F^{i-1} H^{2i-1} (F_{i-2}X,\mathbb{Z}_\ell(i))}=\frac{ H^{2i-1}_{i-2,{\rm nr}}(X,\mu_{\ell^r}^{\otimes i})}{ H^{2i-1}_{i-2,{\rm nr}}( X,\mathbb{Z}_{\ell}( i))} \]
is an isomorphism.
Proof. As the above map is clearly surjective, it suffices to show that it is injective. As
it thus suffices to show that any element
satisfies
which by (P5) implies that ![]() $\alpha$ lifts to an integral class. By Lemma 5.8,
$\alpha$ lifts to an integral class. By Lemma 5.8, ![]() $\alpha =\iota _\ast \xi$ for some
$\alpha =\iota _\ast \xi$ for some
As ![]() $\delta$ commutes with
$\delta$ commutes with ![]() $\iota _\ast$ by functoriality of the Bockstein sequence in (P5), we find
$\iota _\ast$ by functoriality of the Bockstein sequence in (P5), we find ![]() $\delta (\alpha )=\iota _\ast (\delta (\xi ))$. On the other hand,
$\delta (\alpha )=\iota _\ast (\delta (\xi ))$. On the other hand,
is ![]() $\ell ^r$-torsion by property (P5), whereas the above direct sum is torsion-free by Lemma 5.13. Hence,
$\ell ^r$-torsion by property (P5), whereas the above direct sum is torsion-free by Lemma 5.13. Hence, ![]() $\delta (\alpha )=0$, which concludes the proof of the lemma.
$\delta (\alpha )=0$, which concludes the proof of the lemma.
Proof of Theorem 7.7 By Lemma 5.8, we have an exact sequence
By Lemma 5.13, the last term in this sequence is torsion-free and so
By property (P5), the Bockstein map thus induces an isomorphism
By Lemma 7.8, we then get a canonical isomorphism
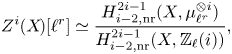 \[ Z^i(X\!) [\ell ^r]\simeq\frac{ H^{2i-1}_{i-2,{\rm nr}}(X,\mu_{\ell^r}^{\otimes i})}{ H^{2i-1}_{i-2,{\rm nr}}( X,\mathbb{Z}_{\ell}( i))} , \]
\[ Z^i(X\!) [\ell ^r]\simeq\frac{ H^{2i-1}_{i-2,{\rm nr}}(X,\mu_{\ell^r}^{\otimes i})}{ H^{2i-1}_{i-2,{\rm nr}}( X,\mathbb{Z}_{\ell}( i))} , \]
which proves (7.4).
Now let ![]() $\alpha \in H^{2i-1} (F_{i-1}X,\mu _{\ell ^r}^{\otimes i})$ with image
$\alpha \in H^{2i-1} (F_{i-1}X,\mu _{\ell ^r}^{\otimes i})$ with image
By Corollary 5.10, ![]() $H^{2i-1}(F_{i}X,\mu _{\ell ^r}^{\otimes i}) \simeq H^{2i-1}(X,\mu _{\ell ^r}^{\otimes i})$ and so
$H^{2i-1}(F_{i}X,\mu _{\ell ^r}^{\otimes i}) \simeq H^{2i-1}(X,\mu _{\ell ^r}^{\otimes i})$ and so ![]() $[\alpha ]$ lifts to
$[\alpha ]$ lifts to ![]() $F^{i} H^{2i-1}(F_{i-1}X,\mu _{\ell ^r}^{\otimes i})$ if and only if
$F^{i} H^{2i-1}(F_{i-1}X,\mu _{\ell ^r}^{\otimes i})$ if and only if ![]() $\delta (\alpha )\in H^{2i} (F_{i-1}X,\mathbb {Z}_\ell (i))[\ell ^r]$ lifts to an
$\delta (\alpha )\in H^{2i} (F_{i-1}X,\mathbb {Z}_\ell (i))[\ell ^r]$ lifts to an ![]() $\ell ^r$-torsion class in
$\ell ^r$-torsion class in ![]() $H^{2i} (X,\mathbb {Z}_\ell (i))$. Hence, the image of the
$H^{2i} (X,\mathbb {Z}_\ell (i))$. Hence, the image of the ![]() $\ell ^r$-torsion classes
$\ell ^r$-torsion classes ![]() $H^{2i}(X,\mathbb {Z}_\ell (i))[\ell ^r]$ inside
$H^{2i}(X,\mathbb {Z}_\ell (i))[\ell ^r]$ inside ![]() $Z^i(X\!) [\ell ^r]$ correspond via (7.6) to the subspace
$Z^i(X\!) [\ell ^r]$ correspond via (7.6) to the subspace
where we recall that ![]() $F^i H^{2i-1} (F_{i-1}X,\mu _{\ell ^r}^{\otimes i})\subset H^{2i-1} (F_{i-1}X,\mu _{\ell ^r}^{\otimes i})$ is the image of
$F^i H^{2i-1} (F_{i-1}X,\mu _{\ell ^r}^{\otimes i})\subset H^{2i-1} (F_{i-1}X,\mu _{\ell ^r}^{\otimes i})$ is the image of ![]() $H^{2i-1} (X,\mu _{\ell ^r}^{\otimes i})$, see Corollary 5.10. Combining this with the isomorphism in Lemma 7.8, we find that the image of
$H^{2i-1} (X,\mu _{\ell ^r}^{\otimes i})$, see Corollary 5.10. Combining this with the isomorphism in Lemma 7.8, we find that the image of ![]() $H^{2i}(X,\mathbb {Z}_\ell (i))[\ell ^r]\to Z^i(X\!) [\ell ^r]$ corresponds via the isomorphism in (7.4) to the subspace generated by the image of
$H^{2i}(X,\mathbb {Z}_\ell (i))[\ell ^r]\to Z^i(X\!) [\ell ^r]$ corresponds via the isomorphism in (7.4) to the subspace generated by the image of ![]() $H^{2i-1} (X,\mu _{\ell ^r}^{\otimes i})\to H^{2i-1}_{i-2,{\rm nr}}(X,\mu _{\ell ^r}^{\otimes i})$, as claimed.
$H^{2i-1} (X,\mu _{\ell ^r}^{\otimes i})\to H^{2i-1}_{i-2,{\rm nr}}(X,\mu _{\ell ^r}^{\otimes i})$, as claimed.
By (P4), the identity (7.5) as well as the assertion on the image of ![]() $H^{2i}(X,\mathbb {Z}_\ell (i))[\ell ^\infty ]\to Z^i(X\!) [\ell ^\infty ]$ follow from what we have proven above by taking direct limits over
$H^{2i}(X,\mathbb {Z}_\ell (i))[\ell ^\infty ]\to Z^i(X\!) [\ell ^\infty ]$ follow from what we have proven above by taking direct limits over ![]() $r$. This concludes the proof of the theorem.
$r$. This concludes the proof of the theorem.
The proof has the following consequence, that we want to record here.
Corollary 7.9 Let ![]() $X\in \mathcal {V}$ and
$X\in \mathcal {V}$ and ![]() $\alpha \in H^{2i-1}(F_{i-1}X,\mu _{\ell ^r}^{\otimes i})$. Then
$\alpha \in H^{2i-1}(F_{i-1}X,\mu _{\ell ^r}^{\otimes i})$. Then
Proof. By Lemma 5.8, we have an exact sequence
For any ![]() $\alpha \in H^{2i-1}(F_{i-1}X,\mu _{\ell ^r}^{\otimes i})$, the class
$\alpha \in H^{2i-1}(F_{i-1}X,\mu _{\ell ^r}^{\otimes i})$, the class ![]() $\delta (\alpha )\in H^{2i}(F_{i-1}X,\mathbb {Z}_\ell (i))$ is torsion and so Lemma 5.13 implies that it maps to zero in
$\delta (\alpha )\in H^{2i}(F_{i-1}X,\mathbb {Z}_\ell (i))$ is torsion and so Lemma 5.13 implies that it maps to zero in ![]() $\bigoplus _{x\in X^{(i)}} H^1(x,\mathbb {Z}_\ell (0))$.
$\bigoplus _{x\in X^{(i)}} H^1(x,\mathbb {Z}_\ell (0))$.
7.4 The  $\ell$-adic Griffiths group
$\ell$-adic Griffiths group
Recall from (7.1) that the cycle class map ![]() $\operatorname {cl}_X^i:\operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }\to H^{2i}(X,\mathbb {Z}_\ell (i))$ factorizes through
$\operatorname {cl}_X^i:\operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }\to H^{2i}(X,\mathbb {Z}_\ell (i))$ factorizes through ![]() $A^i(X\!)_{\mathbb {Z}_\ell }$ from Definition 7.2. We denote the induced cycle class map on
$A^i(X\!)_{\mathbb {Z}_\ell }$ from Definition 7.2. We denote the induced cycle class map on ![]() $A^i(X\!)_{\mathbb {Z}_\ell }$ by
$A^i(X\!)_{\mathbb {Z}_\ell }$ by ![]() $\widetilde {\operatorname {cl}}_X^i$.
$\widetilde {\operatorname {cl}}_X^i$.
Definition 7.10 For ![]() $X\in \mathcal {V}$, we define
$X\in \mathcal {V}$, we define
By Lemma 7.5, ![]() $A_0 ^i(X\!)_{\mathbb {Z}_\ell }$ coincides with the
$A_0 ^i(X\!)_{\mathbb {Z}_\ell }$ coincides with the ![]() $\ell$-adic Griffiths group of homologically trivial
$\ell$-adic Griffiths group of homologically trivial ![]() $\mathbb {Z}_\ell$-cycles modulo algebraic equivalence if (P7.1) holds, whereas it is given by the kernel of the cycle class map
$\mathbb {Z}_\ell$-cycles modulo algebraic equivalence if (P7.1) holds, whereas it is given by the kernel of the cycle class map ![]() $\operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }\to H^{2i}(X,\mathbb {Z}_\ell (i))$ if (P7.2) holds.
$\operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }\to H^{2i}(X,\mathbb {Z}_\ell (i))$ if (P7.2) holds.
Using the definition of ![]() $A^i(X\!)_{\mathbb {Z}_\ell }$ from § 7.1, we get
$A^i(X\!)_{\mathbb {Z}_\ell }$ from § 7.1, we get
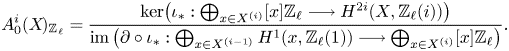 \begin{equation} A_0 ^i(X\!)_{\mathbb{Z}_\ell}=\frac{\ker\bigl( \iota_\ast:\bigoplus_{x\in X^{(i)}}[x]\mathbb{Z}_\ell\longrightarrow H^{2i}(X,\mathbb{Z}_\ell(i))\big) }{\operatorname{im} \big( \partial\circ \iota_\ast: \bigoplus_{x\in X^{(i-1)}} H^1(x,\mathbb{Z}_\ell(1)) \longrightarrow \bigoplus_{x\in X^{(i)}} [x]\mathbb{Z}_\ell \big) } . \end{equation}
\begin{equation} A_0 ^i(X\!)_{\mathbb{Z}_\ell}=\frac{\ker\bigl( \iota_\ast:\bigoplus_{x\in X^{(i)}}[x]\mathbb{Z}_\ell\longrightarrow H^{2i}(X,\mathbb{Z}_\ell(i))\big) }{\operatorname{im} \big( \partial\circ \iota_\ast: \bigoplus_{x\in X^{(i-1)}} H^1(x,\mathbb{Z}_\ell(1)) \longrightarrow \bigoplus_{x\in X^{(i)}} [x]\mathbb{Z}_\ell \big) } . \end{equation}The following result is motivated by Bloch and Ogus’ computation of the second Griffiths group of a smooth complex projective variety in [Reference Bloch and OgusBO74, (7.5)].
Proposition 7.11 For ![]() $X\in \mathcal {V}$, there is a canonical isomorphism
$X\in \mathcal {V}$, there is a canonical isomorphism
Proof. By Lemma 5.8 and Corollary 5.10, we have exact sequences
and
This shows by (7.7) that ![]() $A_0 ^i(X\!)_{\mathbb {Z}_\ell }$ is isomorphic to
$A_0 ^i(X\!)_{\mathbb {Z}_\ell }$ is isomorphic to
which proves the proposition by definition of ![]() $H^{2i-1}_{i-2,{\rm nr}}( X,\mathbb {Z}_\ell (i))$.
$H^{2i-1}_{i-2,{\rm nr}}( X,\mathbb {Z}_\ell (i))$.
Combining Theorem 7.7 and Proposition 7.11, we obtain the following.
Corollary 7.12 Let ![]() $X\in \mathcal {V}$. Then there is a canonical short exact sequence
$X\in \mathcal {V}$. Then there is a canonical short exact sequence
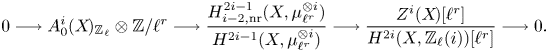 \[ 0\longrightarrow A_0 ^i(X\!)_{\mathbb{Z}_\ell}\otimes \mathbb{Z}/\ell^r\longrightarrow \frac{ H^{2i-1}_{i-2,{\rm nr}}( X,\mu_{\ell^r}^{\otimes i} )}{H^{2i-1}(X,\mu_{\ell^r}^{\otimes i}) }\longrightarrow \frac{Z^{i}(X\!)[\ell^r]}{H^{2i}(X,\mathbb{Z}_\ell(i))[\ell^r]}\longrightarrow 0 . \]
\[ 0\longrightarrow A_0 ^i(X\!)_{\mathbb{Z}_\ell}\otimes \mathbb{Z}/\ell^r\longrightarrow \frac{ H^{2i-1}_{i-2,{\rm nr}}( X,\mu_{\ell^r}^{\otimes i} )}{H^{2i-1}(X,\mu_{\ell^r}^{\otimes i}) }\longrightarrow \frac{Z^{i}(X\!)[\ell^r]}{H^{2i}(X,\mathbb{Z}_\ell(i))[\ell^r]}\longrightarrow 0 . \]
Proof. By Proposition 7.11, there is an exact sequence
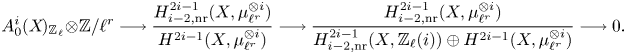 \[ A_0 ^i(X\!)_{\mathbb{Z}_\ell}\otimes \mathbb{Z}/\ell^r\longrightarrow \frac{H^{2i-1}_{i-2,{\rm nr}}( X,\mu_{\ell^r}^{\otimes i} )}{H^{2i-1}(X,\mu_{\ell^r}^{\otimes i}) }\longrightarrow \frac{H^{2i-1}_{i-2,{\rm nr}}( X,\mu_{\ell^r}^{\otimes i} )}{H^{2i-1}_{i-2,{\rm nr}}( X,\mathbb{Z}_{\ell}(i) )\oplus H^{2i-1}(X,\mu_{\ell^r}^{\otimes i}) }\longrightarrow 0 . \]
\[ A_0 ^i(X\!)_{\mathbb{Z}_\ell}\otimes \mathbb{Z}/\ell^r\longrightarrow \frac{H^{2i-1}_{i-2,{\rm nr}}( X,\mu_{\ell^r}^{\otimes i} )}{H^{2i-1}(X,\mu_{\ell^r}^{\otimes i}) }\longrightarrow \frac{H^{2i-1}_{i-2,{\rm nr}}( X,\mu_{\ell^r}^{\otimes i} )}{H^{2i-1}_{i-2,{\rm nr}}( X,\mathbb{Z}_{\ell}(i) )\oplus H^{2i-1}(X,\mu_{\ell^r}^{\otimes i}) }\longrightarrow 0 . \]
By Theorem 7.7, ![]() $Z^{i}(X\!)[\ell ^r]\simeq H^{2i-1}_{i-2,{\rm nr}}( X,\mu _{\ell ^r}^{\otimes i} )/ H^{2i-1}_{i-2,{\rm nr}}( X,\mathbb {Z}_{\ell }(i))$. One checks that the natural map
$Z^{i}(X\!)[\ell ^r]\simeq H^{2i-1}_{i-2,{\rm nr}}( X,\mu _{\ell ^r}^{\otimes i} )/ H^{2i-1}_{i-2,{\rm nr}}( X,\mathbb {Z}_{\ell }(i))$. One checks that the natural map ![]() $H^{2i-1}(X,\mu _{\ell ^r}^{\otimes i})\to Z^{i}(X\!)[\ell ^r]$ is induced by the Bockstein morphism and so its image coincides with the image of the natural map
$H^{2i-1}(X,\mu _{\ell ^r}^{\otimes i})\to Z^{i}(X\!)[\ell ^r]$ is induced by the Bockstein morphism and so its image coincides with the image of the natural map ![]() $H^{2i}(X,\mathbb {Z}_\ell (i))[\ell ^r]\to Z^{i}(X\!)[\ell ^r]$. We thus obtain an exact sequence
$H^{2i}(X,\mathbb {Z}_\ell (i))[\ell ^r]\to Z^{i}(X\!)[\ell ^r]$. We thus obtain an exact sequence
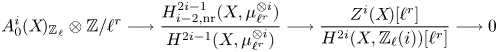 \begin{equation} A_0 ^i(X\!)_{\mathbb{Z}_\ell}\otimes \mathbb{Z}/\ell^r\longrightarrow \frac{H^{2i-1}_{i-2,{\rm nr}}( X,\mu_{\ell^r}^{\otimes i} )}{H^{2i-1}(X,\mu_{\ell^r}^{\otimes i}) }\longrightarrow \frac{Z^{i}(X\!)[\ell^r]}{H^{2i}(X,\mathbb{Z}_\ell(i))[\ell^r]}\longrightarrow 0 \end{equation}
\begin{equation} A_0 ^i(X\!)_{\mathbb{Z}_\ell}\otimes \mathbb{Z}/\ell^r\longrightarrow \frac{H^{2i-1}_{i-2,{\rm nr}}( X,\mu_{\ell^r}^{\otimes i} )}{H^{2i-1}(X,\mu_{\ell^r}^{\otimes i}) }\longrightarrow \frac{Z^{i}(X\!)[\ell^r]}{H^{2i}(X,\mathbb{Z}_\ell(i))[\ell^r]}\longrightarrow 0 \end{equation}
and it remains to show that the first arrow is injective. For this, let ![]() $z\in \bigoplus _{x\in X^{(i)}}[x]\mathbb {Z}_\ell$ with
$z\in \bigoplus _{x\in X^{(i)}}[x]\mathbb {Z}_\ell$ with ![]() $\iota _\ast z=0$ and let
$\iota _\ast z=0$ and let ![]() $[z]\in A_0 ^i(X\!)_{\mathbb {Z}_\ell }$. By Lemma 5.8, there is a class
$[z]\in A_0 ^i(X\!)_{\mathbb {Z}_\ell }$. By Lemma 5.8, there is a class ![]() $\alpha \in H^{2i-1}(F_{i-1}X,\mathbb {Z}_\ell (i))$ with
$\alpha \in H^{2i-1}(F_{i-1}X,\mathbb {Z}_\ell (i))$ with ![]() $\partial \alpha =z$. The map in question sends
$\partial \alpha =z$. The map in question sends ![]() $[z]$ to the image of
$[z]$ to the image of ![]() $\alpha$ in
$\alpha$ in
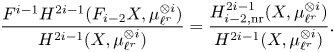 \[ \frac{F^{i-1} H^{2i-1}(F_{i-2}X,\mu_{\ell^r}^{\otimes i} )}{H^{2i-1}(X,\mu_{\ell^r}^{\otimes i}) }= \frac{H^{2i-1}_{i-2,{\rm nr}}( X,\mu_{\ell^r}^{\otimes i} )}{H^{2i-1}(X,\mu_{\ell^r}^{\otimes i}) } . \]
\[ \frac{F^{i-1} H^{2i-1}(F_{i-2}X,\mu_{\ell^r}^{\otimes i} )}{H^{2i-1}(X,\mu_{\ell^r}^{\otimes i}) }= \frac{H^{2i-1}_{i-2,{\rm nr}}( X,\mu_{\ell^r}^{\otimes i} )}{H^{2i-1}(X,\mu_{\ell^r}^{\otimes i}) } . \]
If this vanishes, then there is a class ![]() $\xi \in \bigoplus _{x\in X^{(i-1)}}H^1(x,\mu _{\ell ^r}^{\otimes 1})$ such that
$\xi \in \bigoplus _{x\in X^{(i-1)}}H^1(x,\mu _{\ell ^r}^{\otimes 1})$ such that
where ![]() $\overline {\alpha }$ denotes the image of
$\overline {\alpha }$ denotes the image of ![]() $\alpha$ in
$\alpha$ in ![]() $H^{2i-1}(F_{i-1}X,\mu _{\ell ^r}^{\otimes i})$. By property (P6), we can pick a lift
$H^{2i-1}(F_{i-1}X,\mu _{\ell ^r}^{\otimes i})$. By property (P6), we can pick a lift ![]() $\xi '\in \bigoplus _{x\in X^{(i-1)}}H^1(x,\mathbb {Z}_{\ell }(1))$ of
$\xi '\in \bigoplus _{x\in X^{(i-1)}}H^1(x,\mathbb {Z}_{\ell }(1))$ of ![]() $\xi$ and find that
$\xi$ and find that
is zero modulo ![]() $\ell ^r$. The above cycle and
$\ell ^r$. The above cycle and ![]() $z=\partial \alpha$ have the same class in
$z=\partial \alpha$ have the same class in ![]() $A^i(X\!)_{\mathbb {Z}_\ell }$ and so
$A^i(X\!)_{\mathbb {Z}_\ell }$ and so ![]() $z$ has trivial image in
$z$ has trivial image in ![]() $A_0 ^i(X\!)_{\mathbb {Z}_\ell } / \ell ^r$. This shows that the first map in (7.8) is injective and so the exact sequence from the corollary follows. This concludes the proof.
$A_0 ^i(X\!)_{\mathbb {Z}_\ell } / \ell ^r$. This shows that the first map in (7.8) is injective and so the exact sequence from the corollary follows. This concludes the proof.
The following result gives a geometric interpretation of the extension
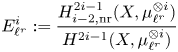 \[ E_{\ell^r}^i:= \frac{ H^{2i-1}_{i-2,{\rm nr}}( X,\mu_{\ell^r}^{\otimes i} )}{H^{2i-1}(X,\mu_{\ell^r}^{\otimes i}) } \]
\[ E_{\ell^r}^i:= \frac{ H^{2i-1}_{i-2,{\rm nr}}( X,\mu_{\ell^r}^{\otimes i} )}{H^{2i-1}(X,\mu_{\ell^r}^{\otimes i}) } \]
from Corollary 7.12.
Lemma 7.13 For ![]() $X\in \mathcal {V}$, there is a canonical isomorphism
$X\in \mathcal {V}$, there is a canonical isomorphism
where ![]() $\bar {\operatorname {cl}}^i_X$ denotes by reduction modulo
$\bar {\operatorname {cl}}^i_X$ denotes by reduction modulo ![]() $\ell ^r$ of the cycle class map
$\ell ^r$ of the cycle class map ![]() $\widetilde {\operatorname {cl}}_X^i:A^i(X\!)_{\mathbb {Z}_\ell }\to H^{2i}(X,\mathbb {Z}_\ell (i))$.
$\widetilde {\operatorname {cl}}_X^i:A^i(X\!)_{\mathbb {Z}_\ell }\to H^{2i}(X,\mathbb {Z}_\ell (i))$.
Proof. By Lemma 5.8, we have exact sequences
and
Combining these two sequences, we find that ![]() $E_{\ell ^r}^i(X\!)$ is isomorphic to
$E_{\ell ^r}^i(X\!)$ is isomorphic to
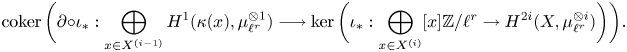 \[ \operatorname{coker}\, \biggl( \partial\circ \iota_\ast:\bigoplus_{x\in X^{(i-1)}}H^1(\kappa(x),\mu_{\ell^r}^{\otimes 1}) \longrightarrow \ker\, \biggl(\iota_\ast: \bigoplus_{x\in X^{(i)}}[x]\mathbb{Z}/\ell^r \to H^{2i}(X,\mu_{\ell^r}^{\otimes i})\biggr) \biggr) . \]
\[ \operatorname{coker}\, \biggl( \partial\circ \iota_\ast:\bigoplus_{x\in X^{(i-1)}}H^1(\kappa(x),\mu_{\ell^r}^{\otimes 1}) \longrightarrow \ker\, \biggl(\iota_\ast: \bigoplus_{x\in X^{(i)}}[x]\mathbb{Z}/\ell^r \to H^{2i}(X,\mu_{\ell^r}^{\otimes i})\biggr) \biggr) . \]
By (P5) and (P6), ![]() $H^1(\kappa (x),\mathbb {Z}_\ell (1))/\ell ^r\simeq H^1(\kappa (x),\mu _{\ell ^r}^{\otimes 1})$ and so the above cokernel injects into
$H^1(\kappa (x),\mathbb {Z}_\ell (1))/\ell ^r\simeq H^1(\kappa (x),\mu _{\ell ^r}^{\otimes 1})$ and so the above cokernel injects into
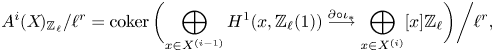 \[ A^i(X\!)_{\mathbb{Z}_\ell}/\ell ^r= \operatorname{coker}\,\biggl( \bigoplus_{x\in X^{(i-1)}} H^1(x,\mathbb{Z}_\ell(1)) \stackrel{{\partial\circ\iota_\ast}}{\longrightarrow} \bigoplus_{x\in X^{(i)}} [x]\mathbb{Z}_\ell \biggr)\bigg/\ell^r , \]
\[ A^i(X\!)_{\mathbb{Z}_\ell}/\ell ^r= \operatorname{coker}\,\biggl( \bigoplus_{x\in X^{(i-1)}} H^1(x,\mathbb{Z}_\ell(1)) \stackrel{{\partial\circ\iota_\ast}}{\longrightarrow} \bigoplus_{x\in X^{(i)}} [x]\mathbb{Z}_\ell \biggr)\bigg/\ell^r , \]
cf. Definition 7.2. Moreover, a class ![]() $z\in A^i(X\!)_{\mathbb {Z}_\ell }$ with reduction
$z\in A^i(X\!)_{\mathbb {Z}_\ell }$ with reduction ![]() $[z]\in A^i(X\!)_{\mathbb {Z}_\ell }/\ell ^r$ satisfies
$[z]\in A^i(X\!)_{\mathbb {Z}_\ell }/\ell ^r$ satisfies ![]() $[z]\in E_{\ell ^r}^i$ if and only if
$[z]\in E_{\ell ^r}^i$ if and only if
where we use that ![]() $H^{2i}(X,\mathbb {Z}_\ell (i))/\ell ^r \hookrightarrow H^{2i}(X,\mu _{\ell ^r}^{\otimes i})$ by (P5). This concludes the proof of the lemma, because
$H^{2i}(X,\mathbb {Z}_\ell (i))/\ell ^r \hookrightarrow H^{2i}(X,\mu _{\ell ^r}^{\otimes i})$ by (P5). This concludes the proof of the lemma, because
is injective by (P5).
7.5 A transcendental Abel–Jacobi map on torsion cycles
We write for simplicity ![]() $A_0 ^i(X\!)[\ell ^r]:=A_0 ^i(X\!)_{\mathbb {Z}_\ell }[\ell ^r]$, where
$A_0 ^i(X\!)[\ell ^r]:=A_0 ^i(X\!)_{\mathbb {Z}_\ell }[\ell ^r]$, where ![]() $A_0 ^i(X\!)_{\mathbb {Z}_\ell }$ denotes the kernel of the cycle class map
$A_0 ^i(X\!)_{\mathbb {Z}_\ell }$ denotes the kernel of the cycle class map ![]() $\widetilde{{\rm cl}}_X^i:A^i(X\!)_{\mathbb {Z}_\ell }\to H^{2i}(X,\mathbb {Z}_\ell (i))$, see Definition 7.10.
$\widetilde{{\rm cl}}_X^i:A^i(X\!)_{\mathbb {Z}_\ell }\to H^{2i}(X,\mathbb {Z}_\ell (i))$, see Definition 7.10.
In this section, we show that there is a canonical map
where we recall that ![]() $N^jH^i(X,A(n))=\ker (H^i(X,A(n))\to H^i(F_{j-1}X,A(n)))$. Our result is motivated by Bloch's Abel–Jacobi map on
$N^jH^i(X,A(n))=\ker (H^i(X,A(n))\to H^i(F_{j-1}X,A(n)))$. Our result is motivated by Bloch's Abel–Jacobi map on ![]() $\operatorname {CH}^i(X\!)[\ell ^\infty ]$ constructed in [Reference BlochBlo79] in the case where
$\operatorname {CH}^i(X\!)[\ell ^\infty ]$ constructed in [Reference BlochBlo79] in the case where ![]() $X$ is smooth projective over an algebraically closed field. We compare the two constructions in § 8. We show that for
$X$ is smooth projective over an algebraically closed field. We compare the two constructions in § 8. We show that for ![]() $k=\bar {k}$ and when
$k=\bar {k}$ and when ![]() $H^\ast$ denotes Borel–Moore pro-étal cohomology (see Proposition 6.6), then the above map is the transcendental Abel–Jacobi map on torsion cycles, i.e. the smallest quotient of Bloch's map that descends to a map on
$H^\ast$ denotes Borel–Moore pro-étal cohomology (see Proposition 6.6), then the above map is the transcendental Abel–Jacobi map on torsion cycles, i.e. the smallest quotient of Bloch's map that descends to a map on
(The adjective transcendental stems from the fact that ![]() $N^{i-1}\operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }=\operatorname {CH}^i(X\!)_{\operatorname {alg}}\otimes _{\mathbb {Z}}\mathbb {Z}_\ell$ is the space of algebraically trivial
$N^{i-1}\operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }=\operatorname {CH}^i(X\!)_{\operatorname {alg}}\otimes _{\mathbb {Z}}\mathbb {Z}_\ell$ is the space of algebraically trivial ![]() $\ell$-adic cycles in this case.) We call the above map the transcendental Abel–Jacobi map, regardless of the ground field and the Borel–Moore cohomology theory chosen.
$\ell$-adic cycles in this case.) We call the above map the transcendental Abel–Jacobi map, regardless of the ground field and the Borel–Moore cohomology theory chosen.
Lemma 5.8 and Corollary 5.10, we have an exact sequence
Now let ![]() $[z]\in A_0 ^i(X\!)[\ell ^r]$ for some
$[z]\in A_0 ^i(X\!)[\ell ^r]$ for some ![]() $r$ and some
$r$ and some ![]() $z\in \bigoplus _{x\in X^{(i)}}[x]\mathbb {Z}_\ell$. Then
$z\in \bigoplus _{x\in X^{(i)}}[x]\mathbb {Z}_\ell$. Then ![]() $\iota _\ast z=\widetilde {\operatorname {cl}}_X^i(z)=0$ by the definition of
$\iota _\ast z=\widetilde {\operatorname {cl}}_X^i(z)=0$ by the definition of ![]() $\widetilde {\operatorname {cl}}_X^i$ and so we may choose a lift
$\widetilde {\operatorname {cl}}_X^i$ and so we may choose a lift ![]() $\alpha \in H^{2i-1}(F_{i-1}X,\mathbb {Z}_\ell (i))$ via (7.10). This is well-defined up to classes that come from
$\alpha \in H^{2i-1}(F_{i-1}X,\mathbb {Z}_\ell (i))$ via (7.10). This is well-defined up to classes that come from ![]() $H^{2i-1}(X,\mathbb {Z}_\ell (i))$. As
$H^{2i-1}(X,\mathbb {Z}_\ell (i))$. As ![]() $[z]$ is
$[z]$ is ![]() $\ell ^r$-torsion, (7.7) implies that
$\ell ^r$-torsion, (7.7) implies that ![]() $\partial (\ell ^r\alpha -\iota _\ast \xi )=0$ for some
$\partial (\ell ^r\alpha -\iota _\ast \xi )=0$ for some ![]() $\xi \in \bigoplus _{x\in X^{(i-1)}}H^1(x,\mathbb {Z}_\ell (1))$. Hence, there is a class
$\xi \in \bigoplus _{x\in X^{(i-1)}}H^1(x,\mathbb {Z}_\ell (1))$. Hence, there is a class ![]() $\beta \in H^{2i-1}(X,\mathbb {Z}_\ell (i))$ with
$\beta \in H^{2i-1}(X,\mathbb {Z}_\ell (i))$ with
By (P4), ![]() $\beta /\ell ^r\in H^{2i-1}(X,\mathbb {Q}_\ell (i))$. Using functoriality of
$\beta /\ell ^r\in H^{2i-1}(X,\mathbb {Q}_\ell (i))$. Using functoriality of ![]() $H^\ast (-,A(n))$ in the coefficients, we may consider the image of that class in
$H^\ast (-,A(n))$ in the coefficients, we may consider the image of that class in ![]() $H^{2i-1}(X,\mathbb {Q}_\ell /\mathbb {Z}_\ell (i))$ and define (7.9) via
$H^{2i-1}(X,\mathbb {Q}_\ell /\mathbb {Z}_\ell (i))$ and define (7.9) via
Lemma 7.14 The map ![]() $\lambda ^i_{{\rm tr}}$ given by (7.12) is well-defined.
$\lambda ^i_{{\rm tr}}$ given by (7.12) is well-defined.
Proof. Let us first fix a representative ![]() $z$ of
$z$ of ![]() $[z]$. Then
$[z]$. Then ![]() $\lambda ^i_{{\rm tr}}([z])$ does not depend on the choice of
$\lambda ^i_{{\rm tr}}([z])$ does not depend on the choice of ![]() $\alpha$, as this would change
$\alpha$, as this would change ![]() $\beta$ by a class in
$\beta$ by a class in ![]() $\ell ^r\cdot H^{2i-1}(X,\mathbb {Z}_\ell (i) )$. In addition, the class
$\ell ^r\cdot H^{2i-1}(X,\mathbb {Z}_\ell (i) )$. In addition, the class ![]() $\xi$ is well-defined up to classes
$\xi$ is well-defined up to classes ![]() $\zeta \in \bigoplus _{x\in X^{(i-1)}}H^1(x,\mathbb {Z}_\ell (1))$ with
$\zeta \in \bigoplus _{x\in X^{(i-1)}}H^1(x,\mathbb {Z}_\ell (1))$ with ![]() $\partial (\iota _\ast \zeta )=0$. This changes
$\partial (\iota _\ast \zeta )=0$. This changes ![]() $\beta$ by
$\beta$ by
and, hence, by a class in ![]() $N^{i-1}H^{2i-1}(X,\mathbb {Z}_\ell (i) )$. In particular,
$N^{i-1}H^{2i-1}(X,\mathbb {Z}_\ell (i) )$. In particular,
remains unchanged.
Finally, if we replace ![]() $z$ by a cycle
$z$ by a cycle ![]() $z'$ that represents the same class in
$z'$ that represents the same class in ![]() $A_0 ^i(X\!)_{\mathbb {Z}_\ell }$, then, by (7.7),
$A_0 ^i(X\!)_{\mathbb {Z}_\ell }$, then, by (7.7), ![]() $z-z'=\partial \iota _\ast \zeta$ for some
$z-z'=\partial \iota _\ast \zeta$ for some ![]() $\zeta \in \bigoplus _{x\in X^{(i-1)}}H^1(x,\mathbb {Z}_\ell (1))$. However, then we can replace
$\zeta \in \bigoplus _{x\in X^{(i-1)}}H^1(x,\mathbb {Z}_\ell (1))$. However, then we can replace ![]() $\alpha$ by
$\alpha$ by ![]() $\alpha -\iota _\ast \zeta$ and
$\alpha -\iota _\ast \zeta$ and ![]() $\xi$ by
$\xi$ by ![]() $\xi -\ell ^r\cdot \zeta$, so that the class
$\xi -\ell ^r\cdot \zeta$, so that the class ![]() $\beta$ does not change at all via this process. This proves the lemma.
$\beta$ does not change at all via this process. This proves the lemma.
The following alternative description of ![]() $\lambda _{{\rm tr}}^i$ is useful.
$\lambda _{{\rm tr}}^i$ is useful.
Lemma 7.15 Let ![]() $X\in \mathcal {V}$ and let
$X\in \mathcal {V}$ and let ![]() $[z]\in A_0 ^i(X\!)_{\mathbb {Z}_\ell }$ be an
$[z]\in A_0 ^i(X\!)_{\mathbb {Z}_\ell }$ be an ![]() $\ell ^r$-torsion class. By Proposition 7.11,
$\ell ^r$-torsion class. By Proposition 7.11, ![]() $[z]$ is represented by a class
$[z]$ is represented by a class ![]() $\alpha \in H^{2i-1}_{i-2,{\rm nr}}(X,\mathbb {Z}_\ell (i))$ such that
$\alpha \in H^{2i-1}_{i-2,{\rm nr}}(X,\mathbb {Z}_\ell (i))$ such that ![]() $\ell ^r\cdot \alpha$ lifts to a class
$\ell ^r\cdot \alpha$ lifts to a class ![]() $\beta \in H^{2i-1}(X,\mathbb {Z}_\ell (i))$. Then
$\beta \in H^{2i-1}(X,\mathbb {Z}_\ell (i))$. Then
Proof. By the proof of Proposition 7.11, ![]() $\alpha$ lifts to a class
$\alpha$ lifts to a class ![]() $\alpha '\in H^{2i-1} (F_{i-1}X,\mathbb {Z}_\ell (i))$ such that
$\alpha '\in H^{2i-1} (F_{i-1}X,\mathbb {Z}_\ell (i))$ such that ![]() $\partial \alpha '=z\in \bigoplus _{x\in X^{(i)}}[x]\mathbb {Z}_\ell$ is a representative of
$\partial \alpha '=z\in \bigoplus _{x\in X^{(i)}}[x]\mathbb {Z}_\ell$ is a representative of ![]() $[z]\in A_0 ^i(X\!)_{\mathbb {Z}_\ell }$. As
$[z]\in A_0 ^i(X\!)_{\mathbb {Z}_\ell }$. As ![]() $[z]$ is
$[z]$ is ![]() $\ell ^r$-torsion, the construction of
$\ell ^r$-torsion, the construction of ![]() $\lambda _{{\rm tr}}^{i}$ shows that there is a class
$\lambda _{{\rm tr}}^{i}$ shows that there is a class ![]() $\beta '\in H^{2i-1}(X,\mathbb {Z}_\ell (i))$ and
$\beta '\in H^{2i-1}(X,\mathbb {Z}_\ell (i))$ and ![]() $\xi \in \bigoplus _{x\in X^{(i-1)}}H^1(x,\mathbb {Z}_\ell (1))$ such that
$\xi \in \bigoplus _{x\in X^{(i-1)}}H^1(x,\mathbb {Z}_\ell (1))$ such that
and
As ![]() $\beta$ and
$\beta$ and ![]() $\beta '$ both restrict to the same class on
$\beta '$ both restrict to the same class on ![]() $F_{i-2}X$, we find that
$F_{i-2}X$, we find that
Hence, ![]() $\lambda _{{\rm tr}}^{i}([z])=[\beta /\ell ^r]$, which concludes the proof of the lemma.
$\lambda _{{\rm tr}}^{i}([z])=[\beta /\ell ^r]$, which concludes the proof of the lemma.
7.6 The image of the transcendental Abel–Jacobi map on torsion cycles
For ![]() $X\in \mathcal {V}$ we write
$X\in \mathcal {V}$ we write
which is a divisible subgroup of ![]() $H^i(X,\mathbb {Q}_\ell /\mathbb {Z}_\ell (n))$; if the torsion subgroup of
$H^i(X,\mathbb {Q}_\ell /\mathbb {Z}_\ell (n))$; if the torsion subgroup of ![]() $H^{i+1}(X,\mathbb {Z}_\ell (n))$ is finitely generated, then
$H^{i+1}(X,\mathbb {Z}_\ell (n))$ is finitely generated, then ![]() $H^i(X,\mathbb {Q}_\ell /\mathbb {Z}_\ell (n))_{\rm div}$ is, in fact, the maximal divisible subgroup of
$H^i(X,\mathbb {Q}_\ell /\mathbb {Z}_\ell (n))_{\rm div}$ is, in fact, the maximal divisible subgroup of ![]() $H^i(X,\mathbb {Q}_\ell /\mathbb {Z}_\ell (n))$. For
$H^i(X,\mathbb {Q}_\ell /\mathbb {Z}_\ell (n))$. For ![]() $j\geqslant 0$, we consider the coniveau filtration
$j\geqslant 0$, we consider the coniveau filtration
The following result computes the image of ![]() $\lambda _{{\rm tr}}^i$. It is motivated by the description of the image of the Abel–Jacobi map on
$\lambda _{{\rm tr}}^i$. It is motivated by the description of the image of the Abel–Jacobi map on ![]() $\operatorname {CH}^2(X\!)_{\operatorname {tors}}$ for smooth projective varieties over algebraically closed fields, due to Bloch and Merkurjev and Suslin, see [Reference Merkurjev and SuslinMS83, § 18.4].
$\operatorname {CH}^2(X\!)_{\operatorname {tors}}$ for smooth projective varieties over algebraically closed fields, due to Bloch and Merkurjev and Suslin, see [Reference Merkurjev and SuslinMS83, § 18.4].
Proposition 7.16 For ![]() $X\in \mathcal {V}$, the transcendental Abel–Jacobi map
$X\in \mathcal {V}$, the transcendental Abel–Jacobi map ![]() $\lambda ^i_{{\rm tr}}$ from Lemma 7.14 satisfies
$\lambda ^i_{{\rm tr}}$ from Lemma 7.14 satisfies
Proof. Let ![]() $[z]\in A_0 ^i(X\!)[\ell ^\infty ]$ and let
$[z]\in A_0 ^i(X\!)[\ell ^\infty ]$ and let ![]() $\alpha \in H^{2i-1}(F_{i-1}X,\mathbb {Z}_\ell (i))$ with
$\alpha \in H^{2i-1}(F_{i-1}X,\mathbb {Z}_\ell (i))$ with ![]() $\partial \alpha =z$. Assume that
$\partial \alpha =z$. Assume that ![]() $\ell ^r\cdot [z]=0$. Then, as we have shown, there are classes
$\ell ^r\cdot [z]=0$. Then, as we have shown, there are classes ![]() $\xi \in \bigoplus _{x\in X^{(i-1)}}H^1(x,\mathbb {Z}_\ell (1))$ and
$\xi \in \bigoplus _{x\in X^{(i-1)}}H^1(x,\mathbb {Z}_\ell (1))$ and ![]() $\beta \in H^{2i-1}(X,\mathbb {Z}_\ell (i))$ such that (7.11) holds true. By definition,
$\beta \in H^{2i-1}(X,\mathbb {Z}_\ell (i))$ such that (7.11) holds true. By definition, ![]() $\lambda ^i_{{\rm tr}}([z])= [\beta /\ell ^r]$ is the class represented by the image of
$\lambda ^i_{{\rm tr}}([z])= [\beta /\ell ^r]$ is the class represented by the image of ![]() $\beta /\ell ^r\in H^{2i-1}(X,\mathbb {Q}_\ell (i))$. This shows, in particular,
$\beta /\ell ^r\in H^{2i-1}(X,\mathbb {Q}_\ell (i))$. This shows, in particular,
Next, note that ![]() $\iota _\ast \xi$ vanishes on
$\iota _\ast \xi$ vanishes on ![]() $F_{i-2}X$ and so (7.11) implies that
$F_{i-2}X$ and so (7.11) implies that
because ![]() $\alpha$ is an integral class. Hence,
$\alpha$ is an integral class. Hence,
as desired.
Conversely, let
By Lemma 5.8,
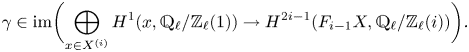 \[ \gamma \in \operatorname{im}\biggl( \bigoplus_{x\in X^{(i)}}H^1(x,\mathbb{Q}_\ell/\mathbb{Z}_\ell(1))\to H^{2i-1}(F_{i-1}X,\mathbb{Q}_\ell/\mathbb{Z}_\ell(i)) \biggr). \]
\[ \gamma \in \operatorname{im}\biggl( \bigoplus_{x\in X^{(i)}}H^1(x,\mathbb{Q}_\ell/\mathbb{Z}_\ell(1))\to H^{2i-1}(F_{i-1}X,\mathbb{Q}_\ell/\mathbb{Z}_\ell(i)) \biggr). \]
As ![]() $H^1(x, \mathbb {Q}_\ell (1))\to H^1(x,\mathbb {Q}_\ell /\mathbb {Z}_\ell (1))$ is surjective by (P4) and (P6), we conclude (using again (P4)) that there is a class
$H^1(x, \mathbb {Q}_\ell (1))\to H^1(x,\mathbb {Q}_\ell /\mathbb {Z}_\ell (1))$ is surjective by (P4) and (P6), we conclude (using again (P4)) that there is a class ![]() $\xi \in \bigoplus _{x\in X^{(i)}}H^1(x, \mathbb {Z}_\ell (1))$ and a positive integer
$\xi \in \bigoplus _{x\in X^{(i)}}H^1(x, \mathbb {Z}_\ell (1))$ and a positive integer ![]() $r$ such that
$r$ such that ![]() $\gamma$ lifts to the class
$\gamma$ lifts to the class
As ![]() $\gamma$ lifts to a rational class by assumption, (P4) implies there is a class
$\gamma$ lifts to a rational class by assumption, (P4) implies there is a class ![]() $\beta \in H^{2i-1}(X,\mathbb {Z}_\ell (i))$ and a positive integer
$\beta \in H^{2i-1}(X,\mathbb {Z}_\ell (i))$ and a positive integer ![]() $r'$ such that
$r'$ such that ![]() $\gamma$ lifts to
$\gamma$ lifts to ![]() $\beta /\ell ^{r'}\in H^{2i-1}( X,\mathbb {Q}_\ell (i))$. Up to replacing
$\beta /\ell ^{r'}\in H^{2i-1}( X,\mathbb {Q}_\ell (i))$. Up to replacing ![]() $r$ and
$r$ and ![]() $r'$ by their maximum (and
$r'$ by their maximum (and ![]() $\xi$, respectively
$\xi$, respectively ![]() $\beta$, by a suitable multiple), we may assume that
$\beta$, by a suitable multiple), we may assume that ![]() $r=r'$. Then let
$r=r'$. Then let
Note that the image of ![]() $\alpha '$ in
$\alpha '$ in ![]() $H^{2i-1}(F_{i-1}X,\mathbb {Q}_\ell /\mathbb {Z}_\ell (i))$ vanishes. By (P4) and (P5), it follows that
$H^{2i-1}(F_{i-1}X,\mathbb {Q}_\ell /\mathbb {Z}_\ell (i))$ vanishes. By (P4) and (P5), it follows that ![]() $\alpha '$ lifts to a class
$\alpha '$ lifts to a class ![]() $\alpha \in H^{2i-1}(F_{i-1}X,\mathbb {Z}_\ell (i))$. We then find that there is a torsion class
$\alpha \in H^{2i-1}(F_{i-1}X,\mathbb {Z}_\ell (i))$. We then find that there is a torsion class ![]() $\tau \in H^{2i-1}(F_{i-1}X,\mathbb {Z}_\ell (i))$ such that
$\tau \in H^{2i-1}(F_{i-1}X,\mathbb {Z}_\ell (i))$ such that
As ![]() $\tau$ is torsion, there is a positive integer
$\tau$ is torsion, there is a positive integer ![]() $s$ such that
$s$ such that ![]() $\ell ^s\cdot \tau =0$ and we get
$\ell ^s\cdot \tau =0$ and we get
Let ![]() $z:=\partial \alpha$ with associated class
$z:=\partial \alpha$ with associated class ![]() $[z]\in A_0 ^i(X\!)$. Then the above identity shows that
$[z]\in A_0 ^i(X\!)$. Then the above identity shows that ![]() $[z]$ is
$[z]$ is ![]() $\ell ^{r+s}$-torsion with associated transcendental Abel–Jacobi invariant
$\ell ^{r+s}$-torsion with associated transcendental Abel–Jacobi invariant
Hence, ![]() $[\gamma ]\in \operatorname {im}(\lambda _{{\rm tr}}^i)$, which concludes the proof of the proposition.
$[\gamma ]\in \operatorname {im}(\lambda _{{\rm tr}}^i)$, which concludes the proof of the proposition.
7.7 The kernel of the transcendental Abel–Jacobi map on torsion cycles
Definition 7.17 For ![]() $X\in \mathcal {V}$, we define
$X\in \mathcal {V}$, we define
where ![]() $\lambda ^i_{{\rm tr}}$ is the transcendental Abel–Jacobi map defined in § 7.5. We further let
$\lambda ^i_{{\rm tr}}$ is the transcendental Abel–Jacobi map defined in § 7.5. We further let ![]() $\mathcal {T}^i(X\!)[\ell ^r]\subset \mathcal {T}^i(X\!)[\ell ^\infty ]$ denote the subgroup of
$\mathcal {T}^i(X\!)[\ell ^r]\subset \mathcal {T}^i(X\!)[\ell ^\infty ]$ denote the subgroup of ![]() $\ell ^r$-torsion elements.
$\ell ^r$-torsion elements.
Recall the filtrations ![]() $F^\ast$ and
$F^\ast$ and ![]() $G^\ast$ from Definitions 5.3 and 5.4.
$G^\ast$ from Definitions 5.3 and 5.4.
Lemma 7.18 Let ![]() $X\in \mathcal {V}$. Then
$X\in \mathcal {V}$. Then
is the subspace of classes ![]() $\alpha \in H^{2i-2}_{i-3,{\rm nr}}( X,\mu _{\ell ^r}^{\otimes i})$ that admit a lift
$\alpha \in H^{2i-2}_{i-3,{\rm nr}}( X,\mu _{\ell ^r}^{\otimes i})$ that admit a lift ![]() $\alpha '\in H^{2i-2} (F_{i-2} X,\mu _{\ell ^r}^{\otimes i})$ such that
$\alpha '\in H^{2i-2} (F_{i-2} X,\mu _{\ell ^r}^{\otimes i})$ such that ![]() $\delta (\alpha ')\in H^{2i-1} (F_{i-2} X,\mathbb {Z}_{\ell }(i))$ lifts to
$\delta (\alpha ')\in H^{2i-1} (F_{i-2} X,\mathbb {Z}_{\ell }(i))$ lifts to ![]() $H^{2i-1} ( X,\mathbb {Z}_{\ell }(i))$.
$H^{2i-1} ( X,\mathbb {Z}_{\ell }(i))$.
Proof. This is an immediate consequence of the definition and the fact that
because ![]() $H^{2i-1} (F_{i} X,\mathbb {Z}_{\ell }(i))\simeq H^{2i-1} ( X,\mathbb {Z}_{\ell }(i))$ by Corollary 5.10.
$H^{2i-1} (F_{i} X,\mathbb {Z}_{\ell }(i))\simeq H^{2i-1} ( X,\mathbb {Z}_{\ell }(i))$ by Corollary 5.10.
The following result is motivated by [Reference VoisinVoi12, Reference MaMa17], where ![]() $\mathcal {T}^3(X\!)[\ell ^\infty ]$ is computed for smooth projective varieties over
$\mathcal {T}^3(X\!)[\ell ^\infty ]$ is computed for smooth projective varieties over ![]() $k=\mathbb {C}$.
$k=\mathbb {C}$.
Theorem 7.19 Let ![]() $X\in \mathcal {V}$ and assume that for any
$X\in \mathcal {V}$ and assume that for any ![]() $x\in X$,
$x\in X$, ![]() $H^3(x,\mathbb {Z}_{\ell }(2))$ is torsion-free. Then there are canonical isomorphisms
$H^3(x,\mathbb {Z}_{\ell }(2))$ is torsion-free. Then there are canonical isomorphisms
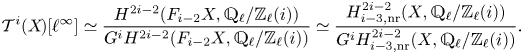 \[ \mathcal{T}^i(X\!)[\ell^\infty] \simeq \frac{ H^{2i-2}(F_{i-2}X,\mathbb{Q}_\ell/\mathbb{Z}_\ell(i)) }{G^{i} H^{2i-2}(F_{i-2}X,\mathbb{Q}_\ell/\mathbb{Z}_\ell(i)) } \simeq \frac{ H^{2i-2}_{i-3,{\rm nr}}( X,\mathbb{Q}_\ell/\mathbb{Z}_\ell(i)) }{G^{i} H^{2i-2}_{i-3,{\rm nr}}( X,\mathbb{Q}_\ell/\mathbb{Z}_\ell(i)) }. \]
\[ \mathcal{T}^i(X\!)[\ell^\infty] \simeq \frac{ H^{2i-2}(F_{i-2}X,\mathbb{Q}_\ell/\mathbb{Z}_\ell(i)) }{G^{i} H^{2i-2}(F_{i-2}X,\mathbb{Q}_\ell/\mathbb{Z}_\ell(i)) } \simeq \frac{ H^{2i-2}_{i-3,{\rm nr}}( X,\mathbb{Q}_\ell/\mathbb{Z}_\ell(i)) }{G^{i} H^{2i-2}_{i-3,{\rm nr}}( X,\mathbb{Q}_\ell/\mathbb{Z}_\ell(i)) }. \]
This theorem is deduced from the following two propositions.
Proposition 7.20 For any ![]() $X\in \mathcal {V}$, there is a canonical isomorphism
$X\in \mathcal {V}$, there is a canonical isomorphism
Proof. Let ![]() $[z]\in A_0 ^i(X\!)[\ell ^r]$ for some
$[z]\in A_0 ^i(X\!)[\ell ^r]$ for some ![]() $r$. By construction and Lemma 7.14,
$r$. By construction and Lemma 7.14, ![]() $\lambda ^i_{{\rm tr}}([z])=0$ if and only if for some classes
$\lambda ^i_{{\rm tr}}([z])=0$ if and only if for some classes ![]() $\alpha \in H^{2i-1}(F_{i-1}X,\mathbb {Z}_\ell (i))$,
$\alpha \in H^{2i-1}(F_{i-1}X,\mathbb {Z}_\ell (i))$, ![]() $\xi \in \bigoplus _{x\in X^{(i-1)}}H^1(x,\mathbb {Z}_\ell (1))$, and
$\xi \in \bigoplus _{x\in X^{(i-1)}}H^1(x,\mathbb {Z}_\ell (1))$, and ![]() $\beta \in H^{2i-1}( X,\mathbb {Z}_\ell (i))$ with
$\beta \in H^{2i-1}( X,\mathbb {Z}_\ell (i))$ with ![]() $z=\partial \alpha$ and
$z=\partial \alpha$ and
we have that ![]() $\beta /\ell ^r\in H^{2i-1}(X,\mathbb {Q}_\ell /\mathbb {Z}_\ell (i))$ admits a lift
$\beta /\ell ^r\in H^{2i-1}(X,\mathbb {Q}_\ell /\mathbb {Z}_\ell (i))$ admits a lift
This means that
for some ![]() $\epsilon \in H^{2i-1}(X,\mathbb {Z}_\ell (i) )$. Replacing
$\epsilon \in H^{2i-1}(X,\mathbb {Z}_\ell (i) )$. Replacing ![]() $\alpha$ by
$\alpha$ by ![]() $\alpha -\epsilon$, we may assume that
$\alpha -\epsilon$, we may assume that ![]() $\epsilon =0$ and so
$\epsilon =0$ and so ![]() $\beta /\ell ^r\in N^{i-1}H^{2i-1}(X,\mathbb {Q}_\ell (i) )$.
$\beta /\ell ^r\in N^{i-1}H^{2i-1}(X,\mathbb {Q}_\ell (i) )$.
By Lemma 5.8, there is an exact sequence
where ![]() $f$ denotes the canonical restriction map. As
$f$ denotes the canonical restriction map. As ![]() $\beta /\ell ^r\in N^{i-1}H^{2i-1}(X,\mathbb {Q}_\ell (i) )$, we find that
$\beta /\ell ^r\in N^{i-1}H^{2i-1}(X,\mathbb {Q}_\ell (i) )$, we find that ![]() $\lambda ^i_{{\rm tr}}([z])=0$ implies that the image
$\lambda ^i_{{\rm tr}}([z])=0$ implies that the image ![]() $f(\alpha )\in H^{2i-1}(F_{i-2}X,\mathbb {Z}_\ell (i))$ of
$f(\alpha )\in H^{2i-1}(F_{i-2}X,\mathbb {Z}_\ell (i))$ of ![]() $\alpha$ is torsion. We claim that the map
$\alpha$ is torsion. We claim that the map
is well-defined. Here we emphasize that the class ![]() $\alpha \in H^{2i-1}(F_{i-1}X,\mathbb {Z}_\ell (i))$ used in the definition of
$\alpha \in H^{2i-1}(F_{i-1}X,\mathbb {Z}_\ell (i))$ used in the definition of ![]() $\varphi ([z])$ is not an arbitrary representative that satisfies
$\varphi ([z])$ is not an arbitrary representative that satisfies ![]() $\partial \alpha =z$, but it is chosen in such a way that
$\partial \alpha =z$, but it is chosen in such a way that ![]() $\beta$ from (7.13) satisfies
$\beta$ from (7.13) satisfies ![]() $\beta /\ell ^r\in N^{i-1}H^{2i-1}(X,\mathbb {Q}_\ell (i))$.
$\beta /\ell ^r\in N^{i-1}H^{2i-1}(X,\mathbb {Q}_\ell (i))$.
To prove that ![]() $\varphi$ is well-defined, let us first fix
$\varphi$ is well-defined, let us first fix ![]() $z$. Then the condition
$z$. Then the condition ![]() $\partial \alpha =z$ shows that
$\partial \alpha =z$ shows that ![]() $\alpha$ is unique up to classes in
$\alpha$ is unique up to classes in ![]() $H^{2i-1}(X,\mathbb {Z}_\ell (i) )$ and so
$H^{2i-1}(X,\mathbb {Z}_\ell (i) )$ and so ![]() $[f(\alpha )]$ is independent of the choice of
$[f(\alpha )]$ is independent of the choice of ![]() $\alpha$ for fixed
$\alpha$ for fixed ![]() $z$ as we quotient out
$z$ as we quotient out ![]() $F^iH^{2i-1}(F_{i-2}X,\mathbb {Z}_\ell (i))[\ell ^\infty ]$ in the above formula. If
$F^iH^{2i-1}(F_{i-2}X,\mathbb {Z}_\ell (i))[\ell ^\infty ]$ in the above formula. If ![]() $z'$ and
$z'$ and ![]() $z$ have the same class in
$z$ have the same class in ![]() $A^i(X\!)_{\mathbb {Z}_\ell }$, then, by (7.7),
$A^i(X\!)_{\mathbb {Z}_\ell }$, then, by (7.7), ![]() $z-z'=\partial \iota _\ast \zeta$ for some
$z-z'=\partial \iota _\ast \zeta$ for some ![]() $\zeta \in \bigoplus _{x\in X^{(i-1)}}H^1(x,\mathbb {Z}_\ell (1))$. The class
$\zeta \in \bigoplus _{x\in X^{(i-1)}}H^1(x,\mathbb {Z}_\ell (1))$. The class ![]() $\alpha ':=\alpha -\iota _\ast \zeta$ then satisfies
$\alpha ':=\alpha -\iota _\ast \zeta$ then satisfies ![]() $\partial (\alpha -\iota _\ast \zeta )=z'$ and, by (7.13),
$\partial (\alpha -\iota _\ast \zeta )=z'$ and, by (7.13),
As ![]() $\beta /\ell ^r\in N^{i-1}H^{2i-1}(X,\mathbb {Q}_\ell (i) )$, we find that
$\beta /\ell ^r\in N^{i-1}H^{2i-1}(X,\mathbb {Q}_\ell (i) )$, we find that ![]() $\alpha '$ may be used to compute
$\alpha '$ may be used to compute ![]() $\varphi ([z'])$, that is,
$\varphi ([z'])$, that is, ![]() $\varphi ([z'])=f(\alpha ')$. By exactness of the above sequence,
$\varphi ([z'])=f(\alpha ')$. By exactness of the above sequence, ![]() $f(\alpha ')=f(\alpha )$ and so
$f(\alpha ')=f(\alpha )$ and so ![]() $\varphi ([z'])=\varphi ([z])$. This proves that
$\varphi ([z'])=\varphi ([z])$. This proves that ![]() $\varphi$ is well-defined, as claimed. It remains to see that
$\varphi$ is well-defined, as claimed. It remains to see that ![]() $\varphi$ is an isomorphism.
$\varphi$ is an isomorphism.
To see that ![]() $\varphi$ is injective, assume that in the above construction,
$\varphi$ is injective, assume that in the above construction, ![]() $f(\alpha )$ lifts to a class in
$f(\alpha )$ lifts to a class in ![]() $H^{2i-1}(X,\mathbb {Z}_\ell (i))$. Then, by Lemma 5.8, there is a class
$H^{2i-1}(X,\mathbb {Z}_\ell (i))$. Then, by Lemma 5.8, there is a class ![]() $\epsilon \in \bigoplus _{x\in X^{(i-1)}}H^1(x,\mathbb {Z}_\ell (1))$ such that
$\epsilon \in \bigoplus _{x\in X^{(i-1)}}H^1(x,\mathbb {Z}_\ell (1))$ such that
lifts to ![]() $H^{2i-1}(X,\mathbb {Z}_\ell (i))$. As
$H^{2i-1}(X,\mathbb {Z}_\ell (i))$. As ![]() $\partial \alpha$ and
$\partial \alpha$ and ![]() $\partial (\alpha -\iota _\ast \epsilon )=0$ have the same image in
$\partial (\alpha -\iota _\ast \epsilon )=0$ have the same image in ![]() $A_0 ^i(X\!)_{\mathbb {Z}_\ell }$, it follows that
$A_0 ^i(X\!)_{\mathbb {Z}_\ell }$, it follows that
as desired.
Next, we claim that ![]() $\varphi$ is surjective. For this, let
$\varphi$ is surjective. For this, let ![]() $\gamma \in H^{2i-1}(F_{i-2}X,\mathbb {Z}_\ell (i))[\ell ^r]$. Then
$\gamma \in H^{2i-1}(F_{i-2}X,\mathbb {Z}_\ell (i))[\ell ^r]$. Then
is torsion and so it must vanish by Lemma 5.13. Hence, ![]() $\gamma =f(\alpha )$ for some
$\gamma =f(\alpha )$ for some ![]() $\alpha \in H^{2i-1}(F_{i-1}X,\mathbb {Z}_\ell (i))$. The cycle
$\alpha \in H^{2i-1}(F_{i-1}X,\mathbb {Z}_\ell (i))$. The cycle ![]() $z=\partial \alpha$ is then homologically trivial (i.e. lies in the kernel of
$z=\partial \alpha$ is then homologically trivial (i.e. lies in the kernel of ![]() $\operatorname {cl}^i_X\!$) by exactness of (7.10). The class
$\operatorname {cl}^i_X\!$) by exactness of (7.10). The class ![]() $[z] \in A_0 ^i(X\!)_{\mathbb {Z}_\ell }$ of
$[z] \in A_0 ^i(X\!)_{\mathbb {Z}_\ell }$ of ![]() $z$ is
$z$ is ![]() $\ell ^r$-torsion, because
$\ell ^r$-torsion, because ![]() $f(\ell ^r \alpha )=0$ and so
$f(\ell ^r \alpha )=0$ and so ![]() $\ell ^r\alpha =\iota _\ast \xi$ (and, hence,
$\ell ^r\alpha =\iota _\ast \xi$ (and, hence, ![]() $\ell ^r z=\partial \iota _\ast \xi$) for some
$\ell ^r z=\partial \iota _\ast \xi$) for some ![]() $\xi \in \bigoplus _{x\in X^{(i-1)}}H^1(x,\mathbb {Z}_\ell (1))$. In particular,
$\xi \in \bigoplus _{x\in X^{(i-1)}}H^1(x,\mathbb {Z}_\ell (1))$. In particular, ![]() $0=\ell ^r\alpha -\iota _\ast \xi$ and so
$0=\ell ^r\alpha -\iota _\ast \xi$ and so ![]() $\lambda _{{\rm tr}}^i([z])=0$ by construction in § 7.5. Hence,
$\lambda _{{\rm tr}}^i([z])=0$ by construction in § 7.5. Hence, ![]() $[z]\in \mathcal {T}^i(X\!)[\ell ^r]$. By the previous definition of
$[z]\in \mathcal {T}^i(X\!)[\ell ^r]$. By the previous definition of ![]() $\varphi$, we have
$\varphi$, we have ![]() $\varphi ([z])=f(\alpha )=\gamma$. This concludes the proof of the proposition.
$\varphi ([z])=f(\alpha )=\gamma$. This concludes the proof of the proposition.
Proposition 7.21 Let ![]() $X\in \mathcal {V}$ and assume that for any
$X\in \mathcal {V}$ and assume that for any ![]() $x\in X$,
$x\in X$, ![]() $H^3(x,\mathbb {Z}_{\ell }(2))$ is torsion-free. Then the natural map
$H^3(x,\mathbb {Z}_{\ell }(2))$ is torsion-free. Then the natural map
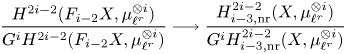 \[ \frac{ H^{2i-2}(F_{i-2}X,\mu_{\ell^r}^{\otimes i}) }{G^{i} H^{2i-2}(F_{i-2}X,\mu_{\ell^r}^{\otimes i}) }\longrightarrow \frac{ H^{2i-2}_{i-3,{\rm nr}}( X,\mu_{\ell^r}^{\otimes i}) }{G^{i} H^{2i-2}_{i-3,{\rm nr}}( X,\mu_{\ell^r}^{\otimes i}) } \]
\[ \frac{ H^{2i-2}(F_{i-2}X,\mu_{\ell^r}^{\otimes i}) }{G^{i} H^{2i-2}(F_{i-2}X,\mu_{\ell^r}^{\otimes i}) }\longrightarrow \frac{ H^{2i-2}_{i-3,{\rm nr}}( X,\mu_{\ell^r}^{\otimes i}) }{G^{i} H^{2i-2}_{i-3,{\rm nr}}( X,\mu_{\ell^r}^{\otimes i}) } \]
is an isomorphism.
Proof. The map in question is surjective by definition.
Now let ![]() $\alpha \in H^{2i-2}(F_{i-2}X,\mu _{\ell ^r}^{\otimes i})$ so that the image
$\alpha \in H^{2i-2}(F_{i-2}X,\mu _{\ell ^r}^{\otimes i})$ so that the image ![]() $\alpha '\in H^{2i-2}(F_{i-3}X,\mu _{\ell ^r}^{\otimes i})$ of
$\alpha '\in H^{2i-2}(F_{i-3}X,\mu _{\ell ^r}^{\otimes i})$ of ![]() $\alpha$ is contained in
$\alpha$ is contained in ![]() $G^{i} H^{2i-2}_{i-3,{\rm nr}}(X,\mu _{\ell ^r}^{\otimes i})$. By Lemma 7.18, this means that there is a lift
$G^{i} H^{2i-2}_{i-3,{\rm nr}}(X,\mu _{\ell ^r}^{\otimes i})$. By Lemma 7.18, this means that there is a lift ![]() $\alpha ''\in H^{2i-2}(F_{i-2}X,\mu _{\ell ^r}^{\otimes i})$ of
$\alpha ''\in H^{2i-2}(F_{i-2}X,\mu _{\ell ^r}^{\otimes i})$ of ![]() $\alpha '$ such that
$\alpha '$ such that
lifts to a class ![]() $\beta \in H^{2i-1}(X,\mathbb {Z}_{\ell }(i))$. Then
$\beta \in H^{2i-1}(X,\mathbb {Z}_{\ell }(i))$. Then ![]() $\alpha -\alpha ''$ lies in the kernel of
$\alpha -\alpha ''$ lies in the kernel of
Lemma 5.8 thus implies that
for some ![]() $\xi \in \bigoplus _{x\in X^{(i-2)}}H^2(x,\mu _{\ell ^r}^{\otimes 2})$. The class
$\xi \in \bigoplus _{x\in X^{(i-2)}}H^2(x,\mu _{\ell ^r}^{\otimes 2})$. The class
is torsion by property (P5) and so it vanishes, because ![]() $H^3(x,\mathbb {Z}_{\ell }(2))$ is torsion-free by assumption. This shows that
$H^3(x,\mathbb {Z}_{\ell }(2))$ is torsion-free by assumption. This shows that ![]() $\delta (\alpha )=\delta (\alpha '')$. As
$\delta (\alpha )=\delta (\alpha '')$. As ![]() $\delta (\alpha '')$ extends to the class
$\delta (\alpha '')$ extends to the class ![]() $\beta \in H^{2i-1}(X,\mathbb {Z}_{\ell }(i))$, the same holds for
$\beta \in H^{2i-1}(X,\mathbb {Z}_{\ell }(i))$, the same holds for ![]() $\delta (\alpha )$ and so
$\delta (\alpha )$ and so
This proves that the map in question is injective, as desired.
Remark 7.22 The torsion-freeness assumption in the proposition (respectively, in Theorem 7.19) will in all applications be satisfied by Merkurjev and Suslin's theorem [Reference Merkurjev and SuslinMS83], i.e. by the Bloch–Kato conjecture in degree two, see Remark 5.14.
Proof of Theorem 7.19 We claim that the Bockstein map
from property (P5) induces an isomorphism
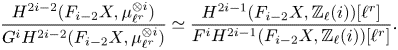 \begin{equation} \frac{ H^{2i-2}(F_{i-2}X,\mu_{\ell^r}^{\otimes i}) }{G^{i} H^{2i-2}(F_{i-2}X,\mu_{\ell^r}^{\otimes i}) }\simeq \frac{ H^{2i-1}(F_{i-2}X,\mathbb{Z}_\ell(i))[\ell^r] }{ F^i H^{2i-1}(F_{i-2}X,\mathbb{Z}_\ell(i))[\ell^r]} . \end{equation}
\begin{equation} \frac{ H^{2i-2}(F_{i-2}X,\mu_{\ell^r}^{\otimes i}) }{G^{i} H^{2i-2}(F_{i-2}X,\mu_{\ell^r}^{\otimes i}) }\simeq \frac{ H^{2i-1}(F_{i-2}X,\mathbb{Z}_\ell(i))[\ell^r] }{ F^i H^{2i-1}(F_{i-2}X,\mathbb{Z}_\ell(i))[\ell^r]} . \end{equation}
By (P5), the image of ![]() $\delta$ is
$\delta$ is ![]() $H^{2i-1}(F_{i-2}X,\mathbb {Z}_\ell (i))[\ell ^r]$ and so it suffices to show that
$H^{2i-1}(F_{i-2}X,\mathbb {Z}_\ell (i))[\ell ^r]$ and so it suffices to show that
which is exactly the definition of ![]() $G^i$ (see Definition 5.4). This proves the claim. Taking direct limits and using (P4), we get an isomorphism
$G^i$ (see Definition 5.4). This proves the claim. Taking direct limits and using (P4), we get an isomorphism
The first isomorphism in Theorem 7.19 follows therefore from Proposition 7.20. The second isomorphism follows from Proposition 7.21 by taking direct limits. This concludes the proof of the theorem.
Corollary 7.23 For any ![]() $X\in \mathcal {V}$ there are subgroups
$X\in \mathcal {V}$ there are subgroups ![]() $\mathcal {T}_0^i(X\!)[\ell ^r] \subset \mathcal {T}^i(X\!)[\ell ^r]$ with
$\mathcal {T}_0^i(X\!)[\ell ^r] \subset \mathcal {T}^i(X\!)[\ell ^r]$ with ![]() $\mathcal {T}^i(X\!)[\ell ^\infty ]=\bigcup _r \mathcal {T}^i_0(X\!)[\ell ^r]$ and a canonical isomorphism
$\mathcal {T}^i(X\!)[\ell ^\infty ]=\bigcup _r \mathcal {T}^i_0(X\!)[\ell ^r]$ and a canonical isomorphism
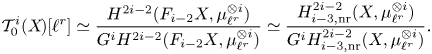 \[ \mathcal{T}_0^i(X\!)[\ell^r] \simeq \frac{ H^{2i-2}(F_{i-2}X,\mu_{\ell^r}^{\otimes i}) }{ G^{i} H^{2i-2}(F_{i-2} X,\mu_{\ell^r}^{\otimes i})} \simeq \frac{ H^{2i-2}_{i-3,{\rm nr}}( X,\mu_{\ell^r}^{\otimes i}) }{ G^{i} H^{2i-2}_{i-3,{\rm nr}}(X,\mu_{\ell^r}^{\otimes i})} . \]
\[ \mathcal{T}_0^i(X\!)[\ell^r] \simeq \frac{ H^{2i-2}(F_{i-2}X,\mu_{\ell^r}^{\otimes i}) }{ G^{i} H^{2i-2}(F_{i-2} X,\mu_{\ell^r}^{\otimes i})} \simeq \frac{ H^{2i-2}_{i-3,{\rm nr}}( X,\mu_{\ell^r}^{\otimes i}) }{ G^{i} H^{2i-2}_{i-3,{\rm nr}}(X,\mu_{\ell^r}^{\otimes i})} . \]
Proof. By Proposition 7.20, there is a canonical isomorphism
Using this isomorphism, we define
Hence, ![]() $\mathcal {T}_0^i(X\!)[\ell ^r]\subset \mathcal {T}^i(X\!)[\ell ^\infty ]$ is a subgroup of
$\mathcal {T}_0^i(X\!)[\ell ^r]\subset \mathcal {T}^i(X\!)[\ell ^\infty ]$ is a subgroup of ![]() $\ell ^r$-torsion elements and so
$\ell ^r$-torsion elements and so ![]() $\mathcal {T}_0^i(X\!)[\ell ^r] \subset \mathcal {T}^i(X\!)[\ell ^r]$. Note also that
$\mathcal {T}_0^i(X\!)[\ell ^r] \subset \mathcal {T}^i(X\!)[\ell ^r]$. Note also that ![]() $\mathcal {T}^i(X\!)[\ell ^\infty ]=\bigcup _r \mathcal {T}^i_0(X\!)[\ell ^r]$. The corollary thus follows from (7.14) and Proposition 7.21.
$\mathcal {T}^i(X\!)[\ell ^\infty ]=\bigcup _r \mathcal {T}^i_0(X\!)[\ell ^r]$. The corollary thus follows from (7.14) and Proposition 7.21.
For the final result of this subsection, we need the following definition, where for ![]() $X\in \mathcal {V}$ we let
$X\in \mathcal {V}$ we let
be the composition of the Bockstein map ![]() $\delta$ from (P5) with the reduction modulo
$\delta$ from (P5) with the reduction modulo ![]() $\ell ^r$ map
$\ell ^r$ map
given by functoriality in the coefficients.
Definition 7.24 For any ![]() $X\in \mathcal {V}$, we define a decreasing filtration
$X\in \mathcal {V}$, we define a decreasing filtration ![]() $\widetilde {G}^\ast$ on
$\widetilde {G}^\ast$ on ![]() $H^i(F_jX,\mu _{\ell ^r}^{\otimes n})$ by
$H^i(F_jX,\mu _{\ell ^r}^{\otimes n})$ by
Moreover,
It follows directly from the definition that ![]() $G^m H^i(F_jX,\mu _{\ell ^r}^{\otimes n}) \subset \widetilde {G}^m H^i(F_j X,\mu _{\ell ^r}^{\otimes n})$.
$G^m H^i(F_jX,\mu _{\ell ^r}^{\otimes n}) \subset \widetilde {G}^m H^i(F_j X,\mu _{\ell ^r}^{\otimes n})$.
Proposition 7.25 For any ![]() $X\in \mathcal {V}$, the kernel of the canonical surjection
$X\in \mathcal {V}$, the kernel of the canonical surjection
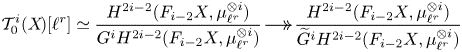
is given by all classes in ![]() $\mathcal {T}_0^i(X\!)[\ell ^r]$ that are
$\mathcal {T}_0^i(X\!)[\ell ^r]$ that are ![]() $\ell ^r$-divisible in
$\ell ^r$-divisible in ![]() $A^i(X\!)_{\mathbb {Z}_\ell }$.
$A^i(X\!)_{\mathbb {Z}_\ell }$.
Proof. By Proposition 7.11, there is a canonical isomorphism
The natural inclusion
corresponds via the isomorphism in Corollary 7.23 to the map
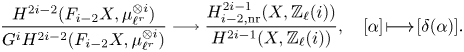
Here, the fact that ![]() $\delta (\alpha )\in H^{2i-1}(F_{i-2}X,\mathbb {Z}_\ell (i))$ lies in
$\delta (\alpha )\in H^{2i-1}(F_{i-2}X,\mathbb {Z}_\ell (i))$ lies in ![]() $F^{i-1} H^{2i-1}(F_{i-2}X,\mathbb {Z}_\ell (i))$ follows from Lemma 5.8, because
$F^{i-1} H^{2i-1}(F_{i-2}X,\mathbb {Z}_\ell (i))$ follows from Lemma 5.8, because ![]() $\delta (\alpha )$ is torsion whereas
$\delta (\alpha )$ is torsion whereas ![]() $\bigoplus _{x\in X^{(i-1)}}H^2( x,\mathbb {Z}_\ell (i))$ is torsion-free by Lemma 5.13.
$\bigoplus _{x\in X^{(i-1)}}H^2( x,\mathbb {Z}_\ell (i))$ is torsion-free by Lemma 5.13.
Now let ![]() $[\alpha ]\in \mathcal {T}_0^i(X\!)[\ell ^r]$ with
$[\alpha ]\in \mathcal {T}_0^i(X\!)[\ell ^r]$ with ![]() $\alpha \in H^{2i-2}(F_{i-2}X,\mu _{\ell ^r}^{\otimes i})$. As we have shown, the class
$\alpha \in H^{2i-2}(F_{i-2}X,\mu _{\ell ^r}^{\otimes i})$. As we have shown, the class
admits a lift
By Lemma 5.8, the lift is unique up to classes coming from ![]() $\bigoplus _{x\in X^{(i-1)}}H^1(\kappa (x),\mathbb {Z}_\ell (1))$. Moreover, there is an exact sequence
$\bigoplus _{x\in X^{(i-1)}}H^1(\kappa (x),\mathbb {Z}_\ell (1))$. Moreover, there is an exact sequence
The class
is unique up to an element of the image of
The cokernel of this map is isomorphic to ![]() $A^i(X\!)_{\mathbb {Z}_\ell }$, see Definition 7.2. As
$A^i(X\!)_{\mathbb {Z}_\ell }$, see Definition 7.2. As ![]() $\partial$ is trivial on classes that lift to
$\partial$ is trivial on classes that lift to ![]() $H^{2i-1}(X,\mathbb {Z}_\ell (i))$, we get a well-defined map
$H^{2i-1}(X,\mathbb {Z}_\ell (i))$, we get a well-defined map
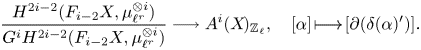
This map identifies via the isomorphism in Corollary 7.23 to the inclusion ![]() $\mathcal {T}_0^i(X\!)[\ell ^r]\hookrightarrow A^i(X\!)_{\mathbb {Z}_\ell }$.
$\mathcal {T}_0^i(X\!)[\ell ^r]\hookrightarrow A^i(X\!)_{\mathbb {Z}_\ell }$.
Let us first assume that
is divisible by ![]() $\ell ^r$. Then up to a suitable choice of the lift
$\ell ^r$. Then up to a suitable choice of the lift ![]() $\delta (\alpha )'$, we may assume that
$\delta (\alpha )'$, we may assume that ![]() $\partial (\delta (\alpha )')$ is zero modulo
$\partial (\delta (\alpha )')$ is zero modulo ![]() $\ell ^r$. By Lemma 5.8, there is an exact sequence
$\ell ^r$. By Lemma 5.8, there is an exact sequence
We thus conclude that the reduction ![]() $\tilde {\delta }(\alpha )'$ modulo
$\tilde {\delta }(\alpha )'$ modulo ![]() $\ell ^r$ of
$\ell ^r$ of ![]() $\delta (\alpha )'$ lifts to a class in
$\delta (\alpha )'$ lifts to a class in ![]() $H^{2i-1}(X,\mu _{\ell ^r}^{\otimes i})$. As
$H^{2i-1}(X,\mu _{\ell ^r}^{\otimes i})$. As ![]() $\tilde {\delta }(\alpha )'$ is a lift of
$\tilde {\delta }(\alpha )'$ is a lift of ![]() $\tilde {\delta } (\alpha )$, this implies
$\tilde {\delta } (\alpha )$, this implies ![]() $\alpha \in \widetilde {G}^i H^{2i-1}(F_{i-2}X,\mu _{\ell ^r}^{\otimes i})$.
$\alpha \in \widetilde {G}^i H^{2i-1}(F_{i-2}X,\mu _{\ell ^r}^{\otimes i})$.
Conversely, assume that ![]() $\alpha \in H^{2i-2}(F_{i-2}X,\mu _{\ell ^r}^{\otimes i})$ lies in
$\alpha \in H^{2i-2}(F_{i-2}X,\mu _{\ell ^r}^{\otimes i})$ lies in ![]() $\widetilde {G}^i H^{2i-2}(F_{i-2} X,\mu _{\ell ^r}^{\otimes i})$. That is,
$\widetilde {G}^i H^{2i-2}(F_{i-2} X,\mu _{\ell ^r}^{\otimes i})$. That is,
lifts to a class in ![]() $H^{2i-1}(X,\mu _{\ell ^r}^{\otimes i})$. Consider the lift
$H^{2i-1}(X,\mu _{\ell ^r}^{\otimes i})$. Consider the lift ![]() $\delta (\alpha )'\in H^{2i-1}(F_{i-1} X,\mathbb {Z}_\ell (i))$ of
$\delta (\alpha )'\in H^{2i-1}(F_{i-1} X,\mathbb {Z}_\ell (i))$ of ![]() $\delta (\alpha )$ from above. The reduction
$\delta (\alpha )$ from above. The reduction ![]() $\overline {\delta (\alpha )'}\in H^{2i-1}(F_{i-1} X,\mu _{\ell ^r}^{\otimes i})$ modulo
$\overline {\delta (\alpha )'}\in H^{2i-1}(F_{i-1} X,\mu _{\ell ^r}^{\otimes i})$ modulo ![]() $\ell ^r$ of the lift
$\ell ^r$ of the lift ![]() $\delta (\alpha )'$ is a lift of
$\delta (\alpha )'$ is a lift of ![]() $\tilde {\delta }(\alpha )$. As
$\tilde {\delta }(\alpha )$. As ![]() $\tilde {\delta }(\alpha )$ lifts to
$\tilde {\delta }(\alpha )$ lifts to ![]() $H^{2i-1}(X,\mu _{\ell ^r}^{\otimes i})$, Lemma 5.8 implies that there is a class
$H^{2i-1}(X,\mu _{\ell ^r}^{\otimes i})$, Lemma 5.8 implies that there is a class
such that
As ![]() $\xi$ lifts by (P6) to a class in
$\xi$ lifts by (P6) to a class in ![]() $\bigoplus _{x\in X^{(i-1)}}H^1(\kappa (x),\mathbb {Z}_{\ell }(1))$, and because
$\bigoplus _{x\in X^{(i-1)}}H^1(\kappa (x),\mathbb {Z}_{\ell }(1))$, and because ![]() $\partial \big ( \overline {\delta (\alpha )' } \big )$ is the reduction modulo
$\partial \big ( \overline {\delta (\alpha )' } \big )$ is the reduction modulo ![]() $\ell ^r$ of
$\ell ^r$ of ![]() $\partial (\delta (\alpha )')$, we conclude that
$\partial (\delta (\alpha )')$, we conclude that
is zero modulo ![]() $\ell ^r$. Hence, the class
$\ell ^r$. Hence, the class ![]() $[\alpha ]\in \mathcal {T}_0^i(X\!)[\ell ^r]$ is divisible by
$[\alpha ]\in \mathcal {T}_0^i(X\!)[\ell ^r]$ is divisible by ![]() $\ell ^r$ in
$\ell ^r$ in ![]() $A^i(X\!)_{\mathbb {Z}_\ell }$, as we want. This concludes the proof of the proposition.
$A^i(X\!)_{\mathbb {Z}_\ell }$, as we want. This concludes the proof of the proposition.
7.8 More on the coniveau filtration on Chow groups
Recall the coniveau filtration ![]() $N^\ast$ on
$N^\ast$ on ![]() $\operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }$ from Definition 7.3. By Lemma 7.4,
$\operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }$ from Definition 7.3. By Lemma 7.4,
It follows that ![]() $N^\ast$ induces a filtration on
$N^\ast$ induces a filtration on ![]() $A^i_0(X\!)_{\mathbb {Z}_\ell }$, given by
$A^i_0(X\!)_{\mathbb {Z}_\ell }$, given by
for ![]() $0\leqslant j\leqslant i-1$. Note that
$0\leqslant j\leqslant i-1$. Note that ![]() $N^{i-1}A_0 ^i(X\!)_{\mathbb {Z}_\ell }=0$. We thus have a finite decreasing filtration of the form
$N^{i-1}A_0 ^i(X\!)_{\mathbb {Z}_\ell }=0$. We thus have a finite decreasing filtration of the form
Let ![]() $f:X\to Y$ be a proper morphism of schemes
$f:X\to Y$ be a proper morphism of schemes ![]() $X,Y\in \mathcal {V}$ and let
$X,Y\in \mathcal {V}$ and let ![]() $c=\dim Y-\dim X$. The definition of
$c=\dim Y-\dim X$. The definition of ![]() $A^i(X\!)_{\mathbb {Z}_\ell }$ and
$A^i(X\!)_{\mathbb {Z}_\ell }$ and ![]() $A^i_0(X\!)_{\mathbb {Z}_\ell }$ (see Definitions 7.2 and 7.10) together with the functoriality of the Gysin sequence (P2) with respect to the pushforward maps from (P1) implies that there are natural pushforward maps
$A^i_0(X\!)_{\mathbb {Z}_\ell }$ (see Definitions 7.2 and 7.10) together with the functoriality of the Gysin sequence (P2) with respect to the pushforward maps from (P1) implies that there are natural pushforward maps
Using these maps, we get the following description of the above filtration on ![]() $A^i_0(X\!)_{\mathbb {Z}_\ell }$.
$A^i_0(X\!)_{\mathbb {Z}_\ell }$.
Lemma 7.26 Let ![]() $X\in \mathcal {V}$. The coniveau filtration
$X\in \mathcal {V}$. The coniveau filtration ![]() $N^\ast$ on
$N^\ast$ on ![]() $A_0 ^i(X\!)_{\mathbb {Z}_\ell }$ is given by
$A_0 ^i(X\!)_{\mathbb {Z}_\ell }$ is given by
where ![]() $Z\subset X$ runs through all closed subschemes with
$Z\subset X$ runs through all closed subschemes with ![]() $\dim Z=\dim X-j$.
$\dim Z=\dim X-j$.
The following lemma shows that the coniveau filtration on algebraic cycles is surprisingly well-behaved.
Lemma 7.27 For ![]() $X\in \mathcal {V}$, the canonical pushforward maps
$X\in \mathcal {V}$, the canonical pushforward maps
are isomorphisms, where ![]() $Z\subset X$ runs through all closed subschemes with
$Z\subset X$ runs through all closed subschemes with ![]() $\dim Z=\dim X-j$.
$\dim Z=\dim X-j$.
Proof. Both pushforward maps in question are surjective by definition, cf. Lemma 7.26. Moreover, injectivity is trivial unless ![]() $0\leqslant j\leqslant i-1$, which we assume from now on.
$0\leqslant j\leqslant i-1$, which we assume from now on.
We first prove injectivity of the first map. Let ![]() $z\in \operatorname {CH}^{i-j}(Z)_{\mathbb {Z}_\ell }$ be a cycle that is rationally equivalent to zero on
$z\in \operatorname {CH}^{i-j}(Z)_{\mathbb {Z}_\ell }$ be a cycle that is rationally equivalent to zero on ![]() $X$. Then there is a closed subscheme
$X$. Then there is a closed subscheme ![]() $W\subset X$ with
$W\subset X$ with ![]() $i-1=\dim X-\dim W$ such that
$i-1=\dim X-\dim W$ such that ![]() $z$ is rationally equivalent to zero on
$z$ is rationally equivalent to zero on ![]() $Z\cup W$. Since
$Z\cup W$. Since ![]() $j\leqslant i-1$, we find that the subscheme
$j\leqslant i-1$, we find that the subscheme ![]() $Z\cup W$ appears in the direct limit in question, which settles the injectivity of the first map in the lemma.
$Z\cup W$ appears in the direct limit in question, which settles the injectivity of the first map in the lemma.
Injectivity of the second map is similar.
For the following proposition, recall the definition of the coniveau filtration ![]() $N^\ast$ on refined unramified cohomology from Definition 5.2.
$N^\ast$ on refined unramified cohomology from Definition 5.2.
Proposition 7.28 For ![]() $X\in \mathcal {V}$, the isomorphism from Proposition 7.11 induces an isomorphism
$X\in \mathcal {V}$, the isomorphism from Proposition 7.11 induces an isomorphism
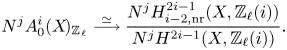 \[ N^jA_0 ^i(X\!)_{\mathbb{Z}_\ell} \stackrel{{\simeq}}{\longrightarrow} \frac{N^jH^{2i-1}_{i-2,{\rm nr}}(X,\mathbb{Z}_\ell(i))}{N^jH^{2i-1}(X,\mathbb{Z}_\ell(i))} . \]
\[ N^jA_0 ^i(X\!)_{\mathbb{Z}_\ell} \stackrel{{\simeq}}{\longrightarrow} \frac{N^jH^{2i-1}_{i-2,{\rm nr}}(X,\mathbb{Z}_\ell(i))}{N^jH^{2i-1}(X,\mathbb{Z}_\ell(i))} . \]
Proof. By Proposition 7.11, there is a canonical isomorphism
By Corollary 5.9, for any ![]() $0\leqslant j\leqslant i-1$, there is a canonical exact sequence
$0\leqslant j\leqslant i-1$, there is a canonical exact sequence
where the direct limit runs through all closed reduced subschemes ![]() $Z\subset X$ of dimension
$Z\subset X$ of dimension ![]() $\dim Z=\dim X-j$. Here the first map is induced by the pushforward map with respect to
$\dim Z=\dim X-j$. Here the first map is induced by the pushforward map with respect to ![]() $Z\hookrightarrow X$ and the second map is the canonical restriction map.
$Z\hookrightarrow X$ and the second map is the canonical restriction map.
The above sequence induces a sequence
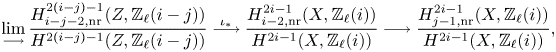 \[ \lim_{\longrightarrow}\frac{H^{2(i-j)-1}_{i-j-2,{\rm nr}}(Z,\mathbb{Z}_\ell(i-j))}{H^{2(i-j)-1} (Z,\mathbb{Z}_\ell(i-j))} \stackrel{{\iota_\ast}}{\longrightarrow} \frac{H^{2i-1}_{i-2,{\rm nr}}(X,\mathbb{Z}_\ell(i))}{ H^{2i-1}(X,\mathbb{Z}_\ell(i))}\longrightarrow \frac{ H^{2i-1}_{j-1,{\rm nr}}(X,\mathbb{Z}_\ell(i))}{ H^{2i-1} (X,\mathbb{Z}_\ell(i))} , \]
\[ \lim_{\longrightarrow}\frac{H^{2(i-j)-1}_{i-j-2,{\rm nr}}(Z,\mathbb{Z}_\ell(i-j))}{H^{2(i-j)-1} (Z,\mathbb{Z}_\ell(i-j))} \stackrel{{\iota_\ast}}{\longrightarrow} \frac{H^{2i-1}_{i-2,{\rm nr}}(X,\mathbb{Z}_\ell(i))}{ H^{2i-1}(X,\mathbb{Z}_\ell(i))}\longrightarrow \frac{ H^{2i-1}_{j-1,{\rm nr}}(X,\mathbb{Z}_\ell(i))}{ H^{2i-1} (X,\mathbb{Z}_\ell(i))} , \]
and one directly checks that this sequence remains exact. By Proposition 7.11, the first arrow in this sequence identifies to the natural map
It follows from the functoriality of the Gysin sequence with respect to proper pushforwards (see (P2)) that this map agrees with the pushforward of cycles induced by ![]() $Z\hookrightarrow X$. Hence, the image of the above map is given by
$Z\hookrightarrow X$. Hence, the image of the above map is given by ![]() $N^jA_0 ^i(X\!)_{\mathbb {Z}_\ell }$. The above exact sequence thus yields a canonical isomorphism
$N^jA_0 ^i(X\!)_{\mathbb {Z}_\ell }$. The above exact sequence thus yields a canonical isomorphism
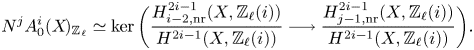 \[ N^jA_0 ^i(X\!)_{\mathbb{Z}_\ell}\simeq \ker\,\biggl( \frac{H^{2i-1}_{i-2,{\rm nr}}(X,\mathbb{Z}_\ell(i))}{
H^{2i-1}(X,\mathbb{Z}_\ell(i))}\longrightarrow
\frac{H^{2i-1}_{j-1,{\rm nr}}(X,\mathbb{Z}_\ell(i))}{
H^{2i-1} (X,\mathbb{Z}_\ell(i))} \biggr) .
\]
\[ N^jA_0 ^i(X\!)_{\mathbb{Z}_\ell}\simeq \ker\,\biggl( \frac{H^{2i-1}_{i-2,{\rm nr}}(X,\mathbb{Z}_\ell(i))}{
H^{2i-1}(X,\mathbb{Z}_\ell(i))}\longrightarrow
\frac{H^{2i-1}_{j-1,{\rm nr}}(X,\mathbb{Z}_\ell(i))}{
H^{2i-1} (X,\mathbb{Z}_\ell(i))} \biggr) .
\]
By the definition of the coniveau filtration (see Definition 5.2), we thus obtain
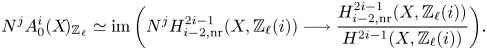 \[ N^jA_0 ^i(X\!)_{\mathbb{Z}_\ell}\simeq \operatorname{im}\,\biggl(N^jH^{2i-1}_{i-2,{\rm nr}}(X,\mathbb{Z}_\ell(i)) \longrightarrow \frac{H^{2i-1}_{i-2,{\rm nr}}(X,\mathbb{Z}_\ell(i))}{ H^{2i-1}(X,\mathbb{Z}_\ell(i))} \biggr) . \]
\[ N^jA_0 ^i(X\!)_{\mathbb{Z}_\ell}\simeq \operatorname{im}\,\biggl(N^jH^{2i-1}_{i-2,{\rm nr}}(X,\mathbb{Z}_\ell(i)) \longrightarrow \frac{H^{2i-1}_{i-2,{\rm nr}}(X,\mathbb{Z}_\ell(i))}{ H^{2i-1}(X,\mathbb{Z}_\ell(i))} \biggr) . \]
The kernel of the above map is given by the image of ![]() $N^jH^{2i-1}(X,\mathbb {Z}_\ell (i))$ and so
$N^jH^{2i-1}(X,\mathbb {Z}_\ell (i))$ and so
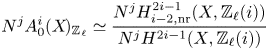 \[ N^jA_0 ^i(X\!)_{\mathbb{Z}_\ell}\simeq \frac{N^jH^{2i-1}_{i-2,{\rm nr}}(X,\mathbb{Z}_\ell(i))}{N^jH^{2i-1}(X,\mathbb{Z}_\ell(i))} \]
\[ N^jA_0 ^i(X\!)_{\mathbb{Z}_\ell}\simeq \frac{N^jH^{2i-1}_{i-2,{\rm nr}}(X,\mathbb{Z}_\ell(i))}{N^jH^{2i-1}(X,\mathbb{Z}_\ell(i))} \]
as desired. This concludes the proof of the proposition.
7.9 Higher transcendental Abel–Jacobi mappings
The coniveau filtration ![]() $N^\ast$ on
$N^\ast$ on ![]() $\operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }$ induces a filtration
$\operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }$ induces a filtration ![]() $N^\ast$ on
$N^\ast$ on
and, hence, on the torsion subgroup ![]() $A^i_0(X\!)[\ell ^\infty ]\subset A^i_0(X\!)_{\mathbb {Z}_\ell }$. The goal of this section is to show that the graded pieces of this filtration are detected by higher Abel–Jacobi invariants. To this end it will be convenient to consider
$A^i_0(X\!)[\ell ^\infty ]\subset A^i_0(X\!)_{\mathbb {Z}_\ell }$. The goal of this section is to show that the graded pieces of this filtration are detected by higher Abel–Jacobi invariants. To this end it will be convenient to consider
Here we use a bar in our notation to emphasize that we are quotienting out ![]() $N^1H^{2i-1}(X,\mathbb {Q}_\ell (i))$ and not
$N^1H^{2i-1}(X,\mathbb {Q}_\ell (i))$ and not ![]() $N^{i-1}H^{2i-1}(X,\mathbb {Q}_\ell (i))$, as in the construction of
$N^{i-1}H^{2i-1}(X,\mathbb {Q}_\ell (i))$, as in the construction of ![]() $\lambda _{{\rm tr}}^i$ in § 7.5. For
$\lambda _{{\rm tr}}^i$ in § 7.5. For ![]() $i\geqslant 2$, we have
$i\geqslant 2$, we have ![]() $N^{i-1}H^{2i-1}(X,\mathbb {Q}_\ell (i))\subset N^1H^{2i-1}(X,\mathbb {Q}_\ell (i))$ and so
$N^{i-1}H^{2i-1}(X,\mathbb {Q}_\ell (i))\subset N^1H^{2i-1}(X,\mathbb {Q}_\ell (i))$ and so ![]() $\lambda _{{\rm tr}}^i$ induces a canonical map
$\lambda _{{\rm tr}}^i$ induces a canonical map
where we note that ![]() $A^i_0(X\!)_{\mathbb {Z}_\ell }=0$ for
$A^i_0(X\!)_{\mathbb {Z}_\ell }=0$ for ![]() $i\leqslant 1$ by Lemma 7.4.
$i\leqslant 1$ by Lemma 7.4.
Definition 7.29 For ![]() $0\leqslant j\leqslant i$, we define the
$0\leqslant j\leqslant i$, we define the ![]() $j$th higher transcendental
$j$th higher transcendental ![]() $\ell ^\infty$-torsion intermediate Jacobian of
$\ell ^\infty$-torsion intermediate Jacobian of ![]() $X$ by
$X$ by
where ![]() $Z\subset X$ runs through all subschemes with
$Z\subset X$ runs through all subschemes with ![]() $\dim Z=\dim X-j$.
$\dim Z=\dim X-j$.
It follows from Lemma 7.27 that the map ![]() $\bar {\lambda }_{{\rm tr}}^{i-j}$ from (7.16), applied to the subschemes
$\bar {\lambda }_{{\rm tr}}^{i-j}$ from (7.16), applied to the subschemes ![]() $Z\subset X$ with
$Z\subset X$ with ![]() $\dim Z=\dim X-j$, yields in the limit a canonical higher Abel–Jacobi map
$\dim Z=\dim X-j$, yields in the limit a canonical higher Abel–Jacobi map
Note that ![]() $\overline {J}^i_{0,tr}(X\!)[\ell ^{\infty }]=\overline {J}^i_{{\rm tr}}(X\!)[\ell ^{\infty }]$ and
$\overline {J}^i_{0,tr}(X\!)[\ell ^{\infty }]=\overline {J}^i_{{\rm tr}}(X\!)[\ell ^{\infty }]$ and ![]() $\bar {\lambda }_{0,tr}^i=\bar {\lambda }_{{\rm tr}}^i$. The following theorem computes the kernel of
$\bar {\lambda }_{0,tr}^i=\bar {\lambda }_{{\rm tr}}^i$. The following theorem computes the kernel of ![]() $\bar {\lambda }_{j,{\rm tr}}^i$
$\bar {\lambda }_{j,{\rm tr}}^i$
Theorem 7.30 Let ![]() $X\in \mathcal {V}$ and assume that the twisted
$X\in \mathcal {V}$ and assume that the twisted ![]() $\ell$-adic Borel–Moore cohomology theory
$\ell$-adic Borel–Moore cohomology theory ![]() $H^\ast$ on
$H^\ast$ on ![]() $\mathcal {V}$ has the property that for all
$\mathcal {V}$ has the property that for all ![]() $Z\subset X$ with
$Z\subset X$ with ![]() $\dim Z=\dim X-j$, the group
$\dim Z=\dim X-j$, the group ![]() $H^{2(i-j)-1}(F_0Z,\mathbb {Z}_\ell (i-j))$ is torsion-free. Then for any
$H^{2(i-j)-1}(F_0Z,\mathbb {Z}_\ell (i-j))$ is torsion-free. Then for any ![]() $j\geqslant 0$, we have
$j\geqslant 0$, we have ![]() $\ker \bigl ( \bar {\lambda }_{j,{\rm tr}}^i\big )=N^{j+1}A_0 ^i(X\!)[\ell ^{\infty }] .$
$\ker \bigl ( \bar {\lambda }_{j,{\rm tr}}^i\big )=N^{j+1}A_0 ^i(X\!)[\ell ^{\infty }] .$
Proof. By Lemma 7.27 and the construction of ![]() $\bar {\lambda }_{j,{\rm tr}}^i$ via direct limits, it suffices by induction to show that
$\bar {\lambda }_{j,{\rm tr}}^i$ via direct limits, it suffices by induction to show that
To this end, let ![]() $[z]\in A_0 ^i(X\!)[\ell ^{\infty }]$ and let
$[z]\in A_0 ^i(X\!)[\ell ^{\infty }]$ and let ![]() $\alpha \in H^{2i-1}_{i-2,{\rm nr}}(X,\mathbb {Z}_\ell (i))$ be a representative of
$\alpha \in H^{2i-1}_{i-2,{\rm nr}}(X,\mathbb {Z}_\ell (i))$ be a representative of ![]() $[z]$ via the isomorphism in Proposition 7.11. Let
$[z]$ via the isomorphism in Proposition 7.11. Let ![]() $r\geqslant 1$ such that
$r\geqslant 1$ such that ![]() $\ell ^r[z]=0\in A_0 ^i(X\!)[\ell ^{\infty }]$. Then
$\ell ^r[z]=0\in A_0 ^i(X\!)[\ell ^{\infty }]$. Then ![]() $\ell ^r\cdot \alpha$ lifts to a class
$\ell ^r\cdot \alpha$ lifts to a class ![]() $\beta \in H^{2i-1}(X,\mathbb {Z}_\ell (i))$. By Lemma 7.15,
$\beta \in H^{2i-1}(X,\mathbb {Z}_\ell (i))$. By Lemma 7.15,
Assume now that ![]() $\bar {\lambda }_{{\rm tr}}^i([z])=0$. As
$\bar {\lambda }_{{\rm tr}}^i([z])=0$. As ![]() $H^{2i-1}(F_0X,\mathbb {Z}_\ell (i))$ is torsion-free by assumption, the preimage of
$H^{2i-1}(F_0X,\mathbb {Z}_\ell (i))$ is torsion-free by assumption, the preimage of ![]() $N^1H^{2i-1}(X,\mathbb {Q}_\ell (i))$ via the natural map
$N^1H^{2i-1}(X,\mathbb {Q}_\ell (i))$ via the natural map ![]() $H^{2i-1}(X,\mathbb {Z}_\ell (i))\to H^{2i-1}(X,\mathbb {Q}_\ell (i))$ is given by
$H^{2i-1}(X,\mathbb {Z}_\ell (i))\to H^{2i-1}(X,\mathbb {Q}_\ell (i))$ is given by ![]() $N^1H^{2i-1}(X,\mathbb {Z}_\ell (i))$. Hence, (P4) and the assumption
$N^1H^{2i-1}(X,\mathbb {Z}_\ell (i))$. Hence, (P4) and the assumption ![]() $[\beta /\ell ^r]=0$ implies that there is a class
$[\beta /\ell ^r]=0$ implies that there is a class ![]() $\beta '\in N^1H^{2i-1}(X,\mathbb {Z}_\ell (i))$ and a positive integer
$\beta '\in N^1H^{2i-1}(X,\mathbb {Z}_\ell (i))$ and a positive integer ![]() $r'$ such that
$r'$ such that
Up to replacing ![]() $r$ and
$r$ and ![]() $r'$ by their maximum and
$r'$ by their maximum and ![]() $\beta$, respectively,
$\beta$, respectively, ![]() $\beta '$ by a suitable multiple, we may assume that
$\beta '$ by a suitable multiple, we may assume that ![]() $r=r'$. We then consider the class
$r=r'$. We then consider the class
As ![]() $r=r'$,
$r=r'$, ![]() $\gamma /\ell ^r=0\in H^{2i-1}(X,\mathbb {Q}_\ell /\mathbb {Z}_\ell (i))$. Hence, there is a class
$\gamma /\ell ^r=0\in H^{2i-1}(X,\mathbb {Q}_\ell /\mathbb {Z}_\ell (i))$. Hence, there is a class ![]() $\delta \in H^{2i-1}(X,\mathbb {Z}_\ell (i))$ and a torsion class
$\delta \in H^{2i-1}(X,\mathbb {Z}_\ell (i))$ and a torsion class ![]() $\tau \in H^{2i-1}(X,\mathbb {Z}_\ell (i))$ with
$\tau \in H^{2i-1}(X,\mathbb {Z}_\ell (i))$ with
As ![]() $\tau$ is torsion, there is a positive integer
$\tau$ is torsion, there is a positive integer ![]() $s$ such that
$s$ such that ![]() $\ell ^s\tau =0$. Hence,
$\ell ^s\tau =0$. Hence,
is a lift of ![]() $\ell ^{r+s}\alpha \in H^{2i-1}_{i-2,{\rm nr}}(X,\mathbb {Z}_\ell (i))$. As
$\ell ^{r+s}\alpha \in H^{2i-1}_{i-2,{\rm nr}}(X,\mathbb {Z}_\ell (i))$. As ![]() $\beta '\in N^1$, we deduce that the image of
$\beta '\in N^1$, we deduce that the image of ![]() $\ell ^{r+s}\alpha$ in
$\ell ^{r+s}\alpha$ in ![]() $H^{2i-1}(F_0X,\mathbb {Z}_\ell (i))$ agrees with the image of
$H^{2i-1}(F_0X,\mathbb {Z}_\ell (i))$ agrees with the image of ![]() $\ell ^{r+s}\delta$. Replacing
$\ell ^{r+s}\delta$. Replacing ![]() $\alpha$ by
$\alpha$ by ![]() $\alpha -\delta$ (which does not change the class
$\alpha -\delta$ (which does not change the class ![]() $[z]$ that
$[z]$ that ![]() $\alpha$ represents, because
$\alpha$ represents, because ![]() $\partial \delta =0$), we may assume that
$\partial \delta =0$), we may assume that ![]() $\delta =0$ and we find that the image of
$\delta =0$ and we find that the image of ![]() $\ell ^{r+s}\alpha$ in
$\ell ^{r+s}\alpha$ in ![]() $H^{2i-1}(F_0X,\mathbb {Z}_\ell (i))$ vanishes. The latter is torsion-free by assumption and so we conclude that the image of
$H^{2i-1}(F_0X,\mathbb {Z}_\ell (i))$ vanishes. The latter is torsion-free by assumption and so we conclude that the image of ![]() $\alpha$ in
$\alpha$ in ![]() $H^{2i-1}(F_0X,\mathbb {Z}_\ell (i))$ vanishes. By Proposition 7.28, this implies
$H^{2i-1}(F_0X,\mathbb {Z}_\ell (i))$ vanishes. By Proposition 7.28, this implies ![]() $[z]\in N^{1}A_0 ^i(X\!)[\ell ^{\infty }]$, as we want. This concludes the proof of the theorem.
$[z]\in N^{1}A_0 ^i(X\!)[\ell ^{\infty }]$, as we want. This concludes the proof of the theorem.
Remark 7.31 The torsion-freeness condition in the theorem will in our applications be satisfied by the Bloch–Kato conjecture, proven by Voevodsky, see Remark 5.14.
7.10 The second piece of the coniveau filtration
In [Reference VoisinVoi12, Reference MaMa17], Voisin and Ma showed that ![]() $\mathcal {T}^3(X\!)[\ell ^\infty ]$ is related to unramified cohomology up to an error term given by the torsion subgroup of
$\mathcal {T}^3(X\!)[\ell ^\infty ]$ is related to unramified cohomology up to an error term given by the torsion subgroup of ![]() $H^{5}(X,\mathbb {Z}_\ell (3))/N^2H^{5}(X,\mathbb {Z}_\ell (3))$. The next result shows that this error term is exactly what is captured by the
$H^{5}(X,\mathbb {Z}_\ell (3))/N^2H^{5}(X,\mathbb {Z}_\ell (3))$. The next result shows that this error term is exactly what is captured by the ![]() $G^\ast$-filtration on traditional unramified
$G^\ast$-filtration on traditional unramified ![]() $\mathbb {Q}_\ell /\mathbb {Z}_\ell$-cohomology from Definition 5.4. In particular, the statement in Theorem 7.19 specializes in the case of codimension-three cycles on smooth complex projective varieties to the result in [Reference VoisinVoi12, Reference MaMa17].
$\mathbb {Q}_\ell /\mathbb {Z}_\ell$-cohomology from Definition 5.4. In particular, the statement in Theorem 7.19 specializes in the case of codimension-three cycles on smooth complex projective varieties to the result in [Reference VoisinVoi12, Reference MaMa17].
Proposition 7.32 For ![]() $X\in \mathcal {V}$, there is a canonical surjection
$X\in \mathcal {V}$, there is a canonical surjection
which maps the image of ![]() $H^{i}(X,\mathbb {Z}_\ell (n))_{\operatorname {tors}}$ on the left onto the image of
$H^{i}(X,\mathbb {Z}_\ell (n))_{\operatorname {tors}}$ on the left onto the image of ![]() $H^{i-1}(X,\mathbb {Q}_\ell /\mathbb {Z}_\ell (n))$ on the right. If
$H^{i-1}(X,\mathbb {Q}_\ell /\mathbb {Z}_\ell (n))$ on the right. If ![]() $H^{i-2}(x,\mathbb {Z}_\ell (n))$ is torsion-free for all
$H^{i-2}(x,\mathbb {Z}_\ell (n))$ is torsion-free for all ![]() $x\in X^{(1)}$, then
$x\in X^{(1)}$, then ![]() $\varphi$ is an isomorphism.
$\varphi$ is an isomorphism.
Remark 7.33 By Remark 5.14, Voevodsky's proof of the Bloch–Kato conjecture implies that ![]() $H^{i-2}(x,\mathbb {Z}_\ell (i-3))$ is torsion-free for the cohomology theories in Propositions 6.6 and 6.9, so that the surjection in the above proposition will be an isomorphism for
$H^{i-2}(x,\mathbb {Z}_\ell (i-3))$ is torsion-free for the cohomology theories in Propositions 6.6 and 6.9, so that the surjection in the above proposition will be an isomorphism for ![]() $n=i-3$ in those cases, but we do not use this result in the remainder of this paper.
$n=i-3$ in those cases, but we do not use this result in the remainder of this paper.
Proof of Proposition 7.32 Recall that ![]() $N^2H^{i}(X,\mathbb {Z}_\ell (n))=\ker (H^{i}(X,\mathbb {Z}_\ell (n))\to H^{i}(F_{1}X,\mathbb {Z}_\ell (n)))$. Hence,
$N^2H^{i}(X,\mathbb {Z}_\ell (n))=\ker (H^{i}(X,\mathbb {Z}_\ell (n))\to H^{i}(F_{1}X,\mathbb {Z}_\ell (n)))$. Hence,
because ![]() $H^{i}(F_{\lceil i/2\rceil }X,\mathbb {Z}_\ell (n)))\simeq H^{i}( X,\mathbb {Z}_\ell (n)))$ by Corollary 5.10.
$H^{i}(F_{\lceil i/2\rceil }X,\mathbb {Z}_\ell (n)))\simeq H^{i}( X,\mathbb {Z}_\ell (n)))$ by Corollary 5.10.
By (P4) and exactness of the direct limit functor, the integral Bockstein sequence (P5) yields in the limit ![]() $r\to \infty$ a Bockstein sequence
$r\to \infty$ a Bockstein sequence
where by slight abuse of notation we still denote the boundary map by ![]() $\delta$. By the description of
$\delta$. By the description of ![]() $\mathbb {Q}_\ell$-cohomology in (P4), the image of
$\mathbb {Q}_\ell$-cohomology in (P4), the image of ![]() $\delta$ agrees with the torsion subgroup of
$\delta$ agrees with the torsion subgroup of ![]() $H^{i+1}(X,\mathbb {Z}_\ell (n))$. Using exactness of the direct limit functor once again, we find that the above sequence remains exact for
$H^{i+1}(X,\mathbb {Z}_\ell (n))$. Using exactness of the direct limit functor once again, we find that the above sequence remains exact for ![]() $F_jX$ in place of
$F_jX$ in place of ![]() $X$. By the definition of
$X$. By the definition of ![]() $G^\ast$ in Definition 5.4,
$G^\ast$ in Definition 5.4, ![]() $\delta$ therefore induces an exact sequence
$\delta$ therefore induces an exact sequence
From this we conclude a canonical isomorphism
induced by ![]() $\delta$. Combining this with (7.18), we get the surjection
$\delta$. Combining this with (7.18), we get the surjection ![]() $\varphi$ as claimed in the proposition.
$\varphi$ as claimed in the proposition.
It remains to analyze the kernel of the canonical map
To this end, let ![]() $\alpha \in G^{\lceil i/2\rceil }H^{i-1} (F_1X,\mathbb {Q}_\ell /\mathbb {Z}_\ell (n))$ be a class that vanishes on
$\alpha \in G^{\lceil i/2\rceil }H^{i-1} (F_1X,\mathbb {Q}_\ell /\mathbb {Z}_\ell (n))$ be a class that vanishes on ![]() $F_0X$. By Lemma 5.8,
$F_0X$. By Lemma 5.8,
If ![]() $H^{i-2}(x,\mathbb {Z}_\ell (n))$ is torsion-free for all
$H^{i-2}(x,\mathbb {Z}_\ell (n))$ is torsion-free for all ![]() $x\in X^{(1)}$, then
$x\in X^{(1)}$, then ![]() $\delta (\xi )=0$ and so
$\delta (\xi )=0$ and so ![]() $\delta (\alpha )=0$ by functoriality of the Bockstein sequence (see (P5)). Hence,
$\delta (\alpha )=0$ by functoriality of the Bockstein sequence (see (P5)). Hence, ![]() $\alpha$ lifts to a class in
$\alpha$ lifts to a class in ![]() $H^{i-1}(F_1X,\mathbb {Q}_\ell (n))$ and so it vanishes in the above quotient. This concludes the proof of the proposition.
$H^{i-1}(F_1X,\mathbb {Q}_\ell (n))$ and so it vanishes in the above quotient. This concludes the proof of the proposition.
Remark 7.34 A version of Proposition 7.32 has been proven independently by Ma [Reference MaMa22].
7.11 Comparison with Bloch–Ogus theory and to Kato homology
In this section, we define
where ![]() $H^\ast (x)$ is short hand for
$H^\ast (x)$ is short hand for ![]() $H^\ast (x,A(n-c))$, where
$H^\ast (x,A(n-c))$, where ![]() $c=\operatorname {codim}(x)=\dim X-\dim (\overline {\{x\}})$. If
$c=\operatorname {codim}(x)=\dim X-\dim (\overline {\{x\}})$. If ![]() $X$ is smooth and equi-dimensional over a field
$X$ is smooth and equi-dimensional over a field ![]() $k$ and
$k$ and ![]() $H^\ast$ satisfies the properties of Bloch–Ogus in [Reference Bloch and OgusBO74, § 1] (see, e.g., [Reference Bloch and OgusBO74, § 2]), then
$H^\ast$ satisfies the properties of Bloch–Ogus in [Reference Bloch and OgusBO74, § 1] (see, e.g., [Reference Bloch and OgusBO74, § 2]), then ![]() $E_2^{j,i+j}(X,A(n))\simeq H^j(X,\mathcal {H}^{i+j}_X(A(n)))$ identifies by [Reference Bloch and OgusBO74] to the
$E_2^{j,i+j}(X,A(n))\simeq H^j(X,\mathcal {H}^{i+j}_X(A(n)))$ identifies by [Reference Bloch and OgusBO74] to the ![]() $j$th cohomology of the Zariski sheaf associated to
$j$th cohomology of the Zariski sheaf associated to ![]() .
.
Proposition 7.35 For any ![]() $X\in \mathcal {V}$, there is a canonical long exact sequence
$X\in \mathcal {V}$, there is a canonical long exact sequence
Proof. The result follows, as explained in § 1.3, from the derived couple associated to the couple from Lemma 5.8. With the aim of making the involved maps explicit, we spell out the argument in some detail in what follows.
Let ![]() $[\xi ]\in E_2^{j,i+j}(X,A(n))$ with
$[\xi ]\in E_2^{j,i+j}(X,A(n))$ with ![]() $\xi \in \bigoplus _{x\in X^{(j)}} H^{i}(x)$ and
$\xi \in \bigoplus _{x\in X^{(j)}} H^{i}(x)$ and ![]() $\partial \circ \iota _\ast (\xi )=0$. By Lemma 5.8, the condition
$\partial \circ \iota _\ast (\xi )=0$. By Lemma 5.8, the condition ![]() $\partial \circ \iota _\ast (\xi )=0$ is equivalent to
$\partial \circ \iota _\ast (\xi )=0$ is equivalent to
If ![]() $\xi =\partial \circ \iota _\ast (\zeta )$ for some
$\xi =\partial \circ \iota _\ast (\zeta )$ for some ![]() $\zeta \in \bigoplus _{x\in X^{(j-1)}} H^{i+1}(x)$, then
$\zeta \in \bigoplus _{x\in X^{(j-1)}} H^{i+1}(x)$, then
by the exactness of the Gysin sequence. It follows that there is a well-defined map
Any class in the image of this map lies in the kernel of
because ![]() $\iota _\ast \xi$ vanishes when restricted to
$\iota _\ast \xi$ vanishes when restricted to ![]() $F_{j-1}X$ by Lemma 5.8. Conversely, any class
$F_{j-1}X$ by Lemma 5.8. Conversely, any class ![]() $\alpha \in H^{i+2j}_{j,{\rm nr}}(X,A(n))$ in the kernel of the above restriction map is, by Lemma 5.8, of the form
$\alpha \in H^{i+2j}_{j,{\rm nr}}(X,A(n))$ in the kernel of the above restriction map is, by Lemma 5.8, of the form ![]() $\alpha =\iota _\ast \xi$ for some
$\alpha =\iota _\ast \xi$ for some ![]() $\xi \in \bigoplus _{x\in X^{(j)}} H^{i}(x)$. The fact that
$\xi \in \bigoplus _{x\in X^{(j)}} H^{i}(x)$. The fact that ![]() $\alpha \in H^{i+2j}_{j,{\rm nr}}(X,A(n)) \subset H^{i+2j} (F_jX,A(n))$ is unramified implies
$\alpha \in H^{i+2j}_{j,{\rm nr}}(X,A(n)) \subset H^{i+2j} (F_jX,A(n))$ is unramified implies ![]() $\partial \circ \iota _\ast (\xi )=0$, and so
$\partial \circ \iota _\ast (\xi )=0$, and so ![]() $\alpha$ lies in the image of (
$\alpha$ lies in the image of (
). Hence, the composition of (
7.20) and (7.21) is exact.
Now let ![]() $[\xi ]\in E_2^{j,i+j}(X,A(n))$ with
$[\xi ]\in E_2^{j,i+j}(X,A(n))$ with ![]() $\xi \in \bigoplus _{x\in X^{(j)}} H^{i}(x)$ and
$\xi \in \bigoplus _{x\in X^{(j)}} H^{i}(x)$ and ![]() $\partial \circ \iota _\ast (\xi )=0$ be a class in the kernel of (7.20). By the exactness of the Gysin sequence, this means that
$\partial \circ \iota _\ast (\xi )=0$ be a class in the kernel of (7.20). By the exactness of the Gysin sequence, this means that ![]() $\xi =\partial \alpha$ for some
$\xi =\partial \alpha$ for some ![]() $\alpha \in H^{i+2j-1}(F_{j-1}X,A(n))$. Hence, the natural sequence
$\alpha \in H^{i+2j-1}(F_{j-1}X,A(n))$. Hence, the natural sequence
is exact. The image of
lies in the kernel of the first map in (7.22) by the definition in (7.19). By the Gysin sequence, it follows that (7.22) descends to an exact sequence
Let ![]() $[\alpha ]\in H^{i+2j-1}_{j-2,{\rm nr}}(X,A(n))$ with
$[\alpha ]\in H^{i+2j-1}_{j-2,{\rm nr}}(X,A(n))$ with ![]() $\alpha \in H^{i+2j-1}(F_{j-1}X,A(n))$ and assume that
$\alpha \in H^{i+2j-1}(F_{j-1}X,A(n))$ and assume that
This means that there is a class ![]() $\zeta \in \bigoplus _{x\in X^{(j-1)}} H^{i+1}(x)$ with
$\zeta \in \bigoplus _{x\in X^{(j-1)}} H^{i+1}(x)$ with ![]() $\partial (\alpha -\iota _\ast \zeta )=0$. Hence, up to replacing
$\partial (\alpha -\iota _\ast \zeta )=0$. Hence, up to replacing ![]() $\alpha$ by
$\alpha$ by ![]() $\alpha -\iota _\ast \zeta$, we may assume
$\alpha -\iota _\ast \zeta$, we may assume ![]() $\partial \alpha =0$ and so
$\partial \alpha =0$ and so
Conversely, any class in ![]() $F^{j}H^{i+2j-1}(F_{j-2}X,A(n))$ clearly maps to zero in
$F^{j}H^{i+2j-1}(F_{j-2}X,A(n))$ clearly maps to zero in ![]() $H^j(X,\mathcal {H}^{i+j}_X(A(n)))$. Hence, the kernel of the first map in (7.23) agrees with the image of the canonical restriction map
$H^j(X,\mathcal {H}^{i+j}_X(A(n)))$. Hence, the kernel of the first map in (7.23) agrees with the image of the canonical restriction map
This concludes the proof of the proposition.
Corollary 7.36 Let ![]() $c\geqslant 0$ be a non-negative integer. Let
$c\geqslant 0$ be a non-negative integer. Let ![]() $X\in \mathcal {V}$ with
$X\in \mathcal {V}$ with ![]() $d:=\dim X$ and assume that for any
$d:=\dim X$ and assume that for any ![]() $x\in X_{(j)}$,
$x\in X_{(j)}$, ![]() $H^i(x,\mu _{\ell ^r}^{\otimes n})=0$ for
$H^i(x,\mu _{\ell ^r}^{\otimes n})=0$ for ![]() $i>j+c$. Then there is a canonical isomorphism
$i>j+c$. Then there is a canonical isomorphism
Proof. Our assumption implies by Corollary 5.11:
The result in question is then an immediate consequence of Proposition 7.35.
Remark 7.37 The condition in Corollary 7.36 is satisfied for ![]() $c=0$ if
$c=0$ if ![]() $k=\mathbb {C}$ and the underlying cohomology theory is singular/étale cohomology. It is also satisfied if
$k=\mathbb {C}$ and the underlying cohomology theory is singular/étale cohomology. It is also satisfied if ![]() $k$ has finite cohomological dimension
$k$ has finite cohomological dimension ![]() $c$ and the cohomology theory is twisted
$c$ and the cohomology theory is twisted ![]() $\ell$-adic pro-étale cohomology, which for finite coefficients agrees with étale cohomology and so
$\ell$-adic pro-étale cohomology, which for finite coefficients agrees with étale cohomology and so ![]() $H^i(x,\mu _{\ell ^r}^{\otimes n})$ identifies by [Reference MilneMil80, p. 88, III.1.16] to the Galois cohomology of the residue field
$H^i(x,\mu _{\ell ^r}^{\otimes n})$ identifies by [Reference MilneMil80, p. 88, III.1.16] to the Galois cohomology of the residue field ![]() $\kappa (x)$. In both cases,
$\kappa (x)$. In both cases, ![]() $E_2^{j,d+c}(X,\mu _{\ell ^r}^{\otimes n})$ coincides, by definition, with Kato homology of
$E_2^{j,d+c}(X,\mu _{\ell ^r}^{\otimes n})$ coincides, by definition, with Kato homology of ![]() $X$, see [Reference KatoKat86, Reference Kerz and SaitoKS12, Reference TianTia20]. Corollary 7.36 thus shows that Kato homology is a special case of refined unramified cohomology.
$X$, see [Reference KatoKat86, Reference Kerz and SaitoKS12, Reference TianTia20]. Corollary 7.36 thus shows that Kato homology is a special case of refined unramified cohomology.
8. Comparison with Bloch's map
In [Reference BlochBlo79], Bloch constructed an Abel–Jacobi map on torsion cycles in the Chow group of smooth projective varieties over algebraically closed ground fields. Bloch's map induces a transcendental Abel–Jacobi map on torsion cycles in the Griffiths group of such varieties and we aim to show in this section that Bloch's map agrees with the map that we constructed in § 7.5 (applied to the cohomology theory from Proposition 6.6 in the case where ![]() $k=\bar {k}$ is algebraically closed and
$k=\bar {k}$ is algebraically closed and ![]() $X$ is smooth projective).
$X$ is smooth projective).
In contrast to Bloch's map, the transcendental Abel–Jacobi map that we defined in § 7.5 works for arbitrary algebraic schemes over a field. This is crucial for the construction of the higher Abel–Jacobi maps in § 7.9.
8.1  $\ell ^r$-torsion in Chow groups
$\ell ^r$-torsion in Chow groups
Fix a prime ![]() $\ell$ and an
$\ell$ and an ![]() $\ell$-adic twisted Borel–Moore cohomology theory
$\ell$-adic twisted Borel–Moore cohomology theory ![]() $H^\ast (-,A(n))$ on a constructible category of Noetherian schemes
$H^\ast (-,A(n))$ on a constructible category of Noetherian schemes ![]() $\mathcal {V}$ with coefficients in a full subcategory
$\mathcal {V}$ with coefficients in a full subcategory ![]() $\mathcal {A}\subset \operatorname {Mod}_{\mathbb {Z}_\ell }$, as in Definitions 4.2 and 4.4. For
$\mathcal {A}\subset \operatorname {Mod}_{\mathbb {Z}_\ell }$, as in Definitions 4.2 and 4.4. For ![]() $X\in \mathcal {V}$,
$X\in \mathcal {V}$, ![]() $x\in X$ there are isomorphisms
$x\in X$ there are isomorphisms ![]() $H^0(x,A(0))\simeq A$ that are functorial in
$H^0(x,A(0))\simeq A$ that are functorial in ![]() $A$. Moreover, there is a distinguished class
$A$. Moreover, there is a distinguished class ![]() $[x]\in H^0(x,\mathbb {Z}_\ell (0))$ and we denote the image of that class in
$[x]\in H^0(x,\mathbb {Z}_\ell (0))$ and we denote the image of that class in ![]() $H^0(x,\mu _{\ell ^r}^{\otimes 0})$ by the same symbol, so that
$H^0(x,\mu _{\ell ^r}^{\otimes 0})$ by the same symbol, so that ![]() $H^0(x,\mu _{\ell ^r}^{\otimes 0})=[x]\mathbb {Z}/\ell ^r$. For any
$H^0(x,\mu _{\ell ^r}^{\otimes 0})=[x]\mathbb {Z}/\ell ^r$. For any ![]() $X\in \mathcal {V}$, properties (P1)–(P3), (P5), and (P6) thus imply the existence of the following commutative diagram with exact rows (cf. [Reference BlochBlo79, (2.1)]).
$X\in \mathcal {V}$, properties (P1)–(P3), (P5), and (P6) thus imply the existence of the following commutative diagram with exact rows (cf. [Reference BlochBlo79, (2.1)]).
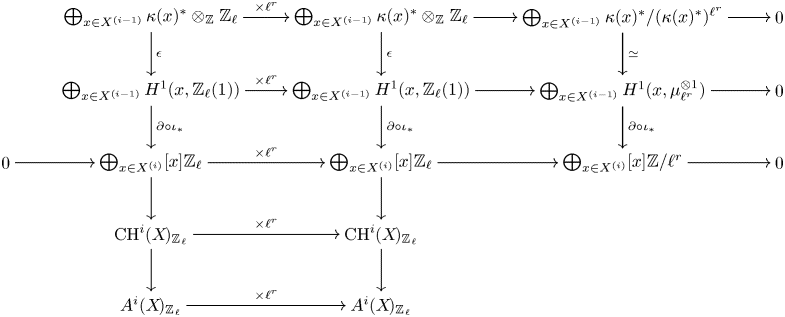
The following result is motivated by [Reference BlochBlo79, § 2].
Lemma 8.1 For any ![]() $X\in \mathcal {V}$, there are canonical isomorphisms
$X\in \mathcal {V}$, there are canonical isomorphisms
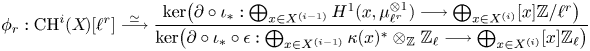 \[ \phi_r: \operatorname{CH}^i(X\!)[\ell^r] \stackrel{{\simeq}}{\longrightarrow} \frac{\ker\bigl(\partial\circ \iota_\ast:\bigoplus_{x\in X^{(i-1)}} H^1( x,\mu_{\ell^r}^{\otimes 1}) \longrightarrow \bigoplus_{x\in X^{(i)}} [x] \mathbb{Z}/\ell^r \big) }{ \ker\bigl(\partial\circ \iota_\ast\circ \epsilon:\bigoplus_{x\in X^{(i-1)}} \kappa(x)^\ast\otimes_\mathbb{Z} \mathbb{Z}_\ell \longrightarrow \bigoplus_{x\in X^{(i)}}[x]\mathbb{Z}_\ell \big) } \]
\[ \phi_r: \operatorname{CH}^i(X\!)[\ell^r] \stackrel{{\simeq}}{\longrightarrow} \frac{\ker\bigl(\partial\circ \iota_\ast:\bigoplus_{x\in X^{(i-1)}} H^1( x,\mu_{\ell^r}^{\otimes 1}) \longrightarrow \bigoplus_{x\in X^{(i)}} [x] \mathbb{Z}/\ell^r \big) }{ \ker\bigl(\partial\circ \iota_\ast\circ \epsilon:\bigoplus_{x\in X^{(i-1)}} \kappa(x)^\ast\otimes_\mathbb{Z} \mathbb{Z}_\ell \longrightarrow \bigoplus_{x\in X^{(i)}}[x]\mathbb{Z}_\ell \big) } \]
and
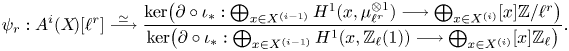 \[ \psi_r: A^i(X\!)[\ell^r] \stackrel{{\simeq}}{\longrightarrow} \frac{\ker\bigl(\partial\circ \iota_\ast:\bigoplus_{x\in X^{(i-1)}} H^1(x,\mu_{\ell^r}^{\otimes 1}) \longrightarrow \bigoplus_{x\in X^{(i)}} [x]\mathbb{Z}/\ell^r \big) }{\ker\bigl(\partial\circ \iota_\ast:\bigoplus_{x\in X^{(i-1)}}H^1( x,\mathbb{Z}_{\ell}(1)) \longrightarrow \bigoplus_{x\in X^{(i)}}[x]\mathbb{Z}_\ell \big)} . \]
\[ \psi_r: A^i(X\!)[\ell^r] \stackrel{{\simeq}}{\longrightarrow} \frac{\ker\bigl(\partial\circ \iota_\ast:\bigoplus_{x\in X^{(i-1)}} H^1(x,\mu_{\ell^r}^{\otimes 1}) \longrightarrow \bigoplus_{x\in X^{(i)}} [x]\mathbb{Z}/\ell^r \big) }{\ker\bigl(\partial\circ \iota_\ast:\bigoplus_{x\in X^{(i-1)}}H^1( x,\mathbb{Z}_{\ell}(1)) \longrightarrow \bigoplus_{x\in X^{(i)}}[x]\mathbb{Z}_\ell \big)} . \]
Proof. Note that the first arrow in the third row of the above diagram is injective, whereas the last arrows in the first two rows are surjective by property (P6). The result is therefore an immediate consequence of the snake lemma and the presentation of ![]() $\operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }$ in Lemma 7.1 and the definition of
$\operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }$ in Lemma 7.1 and the definition of ![]() $A^i(X\!)_{\mathbb {Z}_\ell }$ in Definition 7.2, respectively.
$A^i(X\!)_{\mathbb {Z}_\ell }$ in Definition 7.2, respectively.
8.2 The case of smooth projective varieties over algebraically closed fields
In this section, we assume that ![]() $k$ is an algebraically closed field,
$k$ is an algebraically closed field, ![]() $\ell$ is a prime that is invertible in
$\ell$ is a prime that is invertible in ![]() $k$ and
$k$ and ![]() $\mathcal {V}$ denotes the category of separated schemes of finite type over
$\mathcal {V}$ denotes the category of separated schemes of finite type over ![]() $k$. Let
$k$. Let ![]() $\mathcal {A}\subset \operatorname {Mod}_{\mathbb {Z}_\ell }$ be the full subcategory spanned by
$\mathcal {A}\subset \operatorname {Mod}_{\mathbb {Z}_\ell }$ be the full subcategory spanned by ![]() $\mathbb {Z}_\ell,\mathbb {Q}_\ell,\mathbb {Q}_\ell /\mathbb {Z}_\ell$ and
$\mathbb {Z}_\ell,\mathbb {Q}_\ell,\mathbb {Q}_\ell /\mathbb {Z}_\ell$ and ![]() $\mathbb {Z}/\ell ^r$ for all
$\mathbb {Z}/\ell ^r$ for all ![]() $r\geqslant 1$. We further fix the
$r\geqslant 1$. We further fix the ![]() $\ell$-adic twisted Borel–Moore cohomology theory on
$\ell$-adic twisted Borel–Moore cohomology theory on ![]() $\mathcal {V}$ with coefficients in
$\mathcal {V}$ with coefficients in ![]() $\mathcal {A}$ given by Proposition 6.6, cf. Definitions 4.2 and 4.4. We also note that (P7.1) holds true by Proposition 6.6, as
$\mathcal {A}$ given by Proposition 6.6, cf. Definitions 4.2 and 4.4. We also note that (P7.1) holds true by Proposition 6.6, as ![]() $k$ is algebraically closed.
$k$ is algebraically closed.
If ![]() $X\in \mathcal {V}$ is regular and equi-dimensional, then
$X\in \mathcal {V}$ is regular and equi-dimensional, then
where the first isomorphism comes from Lemma 6.5 and the second isomorphism uses that ![]() $k$ is algebraically closed, so that continuous étale cohomology of algebraic schemes over
$k$ is algebraically closed, so that continuous étale cohomology of algebraic schemes over ![]() $k$ coincides with usual étale cohomology, as the
$k$ coincides with usual étale cohomology, as the ![]() $\operatorname {R}^1 \lim$ term in (6.1) vanishes in this case by finiteness of the corresponding étale cohomology groups, cf. [Reference JannsenJan88]. (As usual, étale cohomology with
$\operatorname {R}^1 \lim$ term in (6.1) vanishes in this case by finiteness of the corresponding étale cohomology groups, cf. [Reference JannsenJan88]. (As usual, étale cohomology with ![]() $\mathbb {Z}_\ell$-coefficients has to be understood in the above formula as the inverse limit
$\mathbb {Z}_\ell$-coefficients has to be understood in the above formula as the inverse limit ![]() $\lim H^i(X_{\unicode{x00E9}{\rm t}},\mu _{\ell ^r}^{\otimes n})$ and cohomology with
$\lim H^i(X_{\unicode{x00E9}{\rm t}},\mu _{\ell ^r}^{\otimes n})$ and cohomology with ![]() $\mathbb {Q}_\ell$ or
$\mathbb {Q}_\ell$ or ![]() $\mathbb {Q}_\ell /\mathbb {Z}_\ell$ coefficients is as usual defined by asking that (P4) holds.)
$\mathbb {Q}_\ell /\mathbb {Z}_\ell$ coefficients is as usual defined by asking that (P4) holds.)
Bloch [Reference BlochBlo79] used Bloch–Ogus theory [Reference Bloch and OgusBO74] and the Weil conjectures, proven by Deligne [Reference DeligneDel74], to construct a map
which agrees with the Abel–Jacobi map on homologically trivial cycles in the case where ![]() $k=\mathbb {C}$, see [Reference BlochBlo79, Proposition 3.7]. To give a description of Bloch's map in the present context, we need the following.
$k=\mathbb {C}$, see [Reference BlochBlo79, Proposition 3.7]. To give a description of Bloch's map in the present context, we need the following.
Lemma 8.2 Let ![]() $k$ be an algebraically closed field and let
$k$ be an algebraically closed field and let ![]() $\ell$ be a prime that is invertible in
$\ell$ be a prime that is invertible in ![]() $k$. Let
$k$. Let ![]() $X$ be a smooth projective variety over
$X$ be a smooth projective variety over ![]() $k$. Then the image of
$k$. Then the image of
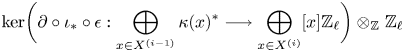 \[ \ker\biggl(\partial\circ \iota_\ast\circ \epsilon:\bigoplus_{x\in X^{(i-1)}} \kappa(x)^\ast \longrightarrow \bigoplus_{x\in X^{(i)}}[x]\mathbb{Z}_\ell \biggr)\otimes_\mathbb{Z} \mathbb{Z}_\ell \]
\[ \ker\biggl(\partial\circ \iota_\ast\circ \epsilon:\bigoplus_{x\in X^{(i-1)}} \kappa(x)^\ast \longrightarrow \bigoplus_{x\in X^{(i)}}[x]\mathbb{Z}_\ell \biggr)\otimes_\mathbb{Z} \mathbb{Z}_\ell \]
via the composition
is torsion.
Proof. Our proof is similar to [Reference BlochBlo79, Lemma 2.4] but we avoid Bloch–Ogus theory.
Let ![]() $\xi \in \bigoplus _{x\in X^{(i-1)}} \kappa (x)^\ast \otimes _\mathbb {Z} \mathbb {Z}_\ell$ with
$\xi \in \bigoplus _{x\in X^{(i-1)}} \kappa (x)^\ast \otimes _\mathbb {Z} \mathbb {Z}_\ell$ with ![]() $\partial (\iota _\ast (\epsilon (\xi )))=0$. By Lemma 5.8, we get
$\partial (\iota _\ast (\epsilon (\xi )))=0$. By Lemma 5.8, we get
If ![]() $k$ is the algebraic closure of a finite field, then
$k$ is the algebraic closure of a finite field, then ![]() $X$ and
$X$ and ![]() $\xi$ are both defined over
$\xi$ are both defined over ![]() $\mathbb {F}_q$ for some finite field
$\mathbb {F}_q$ for some finite field ![]() $\mathbb {F}_q\subset k$. In particular,
$\mathbb {F}_q\subset k$. In particular, ![]() $X=X_0\times _{\mathbb {F}_q} k$ and the Frobenius
$X=X_0\times _{\mathbb {F}_q} k$ and the Frobenius ![]() $F$ (given by
$F$ (given by ![]() on
on ![]() $X_0$ and by
$X_0$ and by ![]() $\operatorname {id}$ on
$\operatorname {id}$ on ![]() $k$) satisfies
$k$) satisfies
As ![]() $X$ is smooth projective, the Weil conjectures [Reference DeligneDel74] imply that
$X$ is smooth projective, the Weil conjectures [Reference DeligneDel74] imply that ![]() $q$ cannot appear as an eigenvalue of the action of
$q$ cannot appear as an eigenvalue of the action of ![]() $F$ on
$F$ on ![]() $H^{2i-1}(X,\mathbb {Q}_\ell (i))$ and so
$H^{2i-1}(X,\mathbb {Q}_\ell (i))$ and so ![]() $\iota _\ast ( \epsilon (\xi ))$ must be torsion, as claimed.
$\iota _\ast ( \epsilon (\xi ))$ must be torsion, as claimed.
If ![]() $k$ is not the algebraic closure of a finite field, then the result in question follows from spreading out the problem over a finitely generated field, which allows us to specialize to a finite field and so the smooth proper base change theorem yields the result. This proves the lemma.
$k$ is not the algebraic closure of a finite field, then the result in question follows from spreading out the problem over a finitely generated field, which allows us to specialize to a finite field and so the smooth proper base change theorem yields the result. This proves the lemma.
Taking the direct limit of the isomorphisms from Lemma 8.1, we obtain an isomorphism
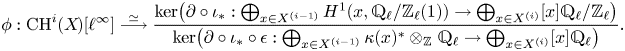 \[ \phi : \operatorname{CH}^i(X\!)[\ell^\infty] \stackrel{{\simeq}}{\longrightarrow} \frac{\ker\bigl(\partial\circ \iota_\ast:\bigoplus_{x\in X^{(i-1)}} H^1( x,\mathbb{Q}_\ell/\mathbb{Z}_\ell(1)) \to \bigoplus_{x\in X^{(i)}} [x] \mathbb{Q}_\ell/\mathbb{Z}_\ell \big) }{ \ker\bigl(\partial\circ \iota_\ast\circ \epsilon:\bigoplus_{x\in X^{(i-1)}} \kappa(x)^\ast\otimes_\mathbb{Z} \mathbb{Q}_\ell \to \bigoplus_{x\in X^{(i)}}[x]\mathbb{Q}_\ell \big) } . \]
\[ \phi : \operatorname{CH}^i(X\!)[\ell^\infty] \stackrel{{\simeq}}{\longrightarrow} \frac{\ker\bigl(\partial\circ \iota_\ast:\bigoplus_{x\in X^{(i-1)}} H^1( x,\mathbb{Q}_\ell/\mathbb{Z}_\ell(1)) \to \bigoplus_{x\in X^{(i)}} [x] \mathbb{Q}_\ell/\mathbb{Z}_\ell \big) }{ \ker\bigl(\partial\circ \iota_\ast\circ \epsilon:\bigoplus_{x\in X^{(i-1)}} \kappa(x)^\ast\otimes_\mathbb{Z} \mathbb{Q}_\ell \to \bigoplus_{x\in X^{(i)}}[x]\mathbb{Q}_\ell \big) } . \]
Proposition 8.3 There is a well-defined map
given by
Proof. The natural map
is zero. Lemma 8.2 thus implies that for any ![]() $\xi \in \bigoplus _{x\in X^{(i-1)}} \kappa (x)^\ast \otimes _\mathbb {Z} \mathbb {Q}_\ell$ with
$\xi \in \bigoplus _{x\in X^{(i-1)}} \kappa (x)^\ast \otimes _\mathbb {Z} \mathbb {Q}_\ell$ with ![]() $\partial (\iota _\ast (\epsilon (\xi )))=0$,
$\partial (\iota _\ast (\epsilon (\xi )))=0$,
vanishes. This concludes the proof.
The minus sign in Proposition 8.3 is necessary to make our definition compatible with ![]() $\lambda ^i_{{\rm tr}}$ defined in § 7.5; a similar sign issue was noted by Bloch, see [Reference BlochBlo79, p. 112].
$\lambda ^i_{{\rm tr}}$ defined in § 7.5; a similar sign issue was noted by Bloch, see [Reference BlochBlo79, p. 112].
Lemma 8.4 The map ![]() $\lambda '$ constructed above coincides with the map (8.1) constructed by Bloch:
$\lambda '$ constructed above coincides with the map (8.1) constructed by Bloch: ![]() $\lambda =\lambda '$.
$\lambda =\lambda '$.
Proof. This follows directly from Lemma 5.12 by comparing our construction with Bloch's construction via diagram (2.2) in [Reference BlochBlo79], where we recall that Bloch included the minus sign in [Reference BlochBlo79, p. 112].
As mentioned previously, because ![]() $k$ is algebraically closed, (P7.1) holds true. Lemma 7.5 thus implies
$k$ is algebraically closed, (P7.1) holds true. Lemma 7.5 thus implies
is the group of homologically trivial codimension-![]() $i$ cycles with coefficients in
$i$ cycles with coefficients in ![]() $\mathbb {Z}_\ell$ modulo algebraic equivalence. In particular,
$\mathbb {Z}_\ell$ modulo algebraic equivalence. In particular, ![]() $A_0 ^i(X\!)[\ell ^\infty ]=\operatorname {Griff}^i(X\!)[\ell ^\infty ]$ is the group of classes in
$A_0 ^i(X\!)[\ell ^\infty ]=\operatorname {Griff}^i(X\!)[\ell ^\infty ]$ is the group of classes in ![]() $\operatorname {Griff}^i(X\!)$ that are annihilated by some power of
$\operatorname {Griff}^i(X\!)$ that are annihilated by some power of ![]() $\ell$.
$\ell$.
Proposition 8.5 Let ![]() $k$ be an algebraically closed field and let
$k$ be an algebraically closed field and let ![]() $X$ be a smooth projective variety over
$X$ be a smooth projective variety over ![]() $k$. The map
$k$. The map
constructed in § 7.5 is induced by Bloch's map in (8.1) and, hence, agrees with the transcendental Abel–Jacobi map if ![]() $k=\mathbb {C}$.
$k=\mathbb {C}$.
Proof. If ![]() $k=\mathbb {C}$, then Bloch's map agrees with the Abel–Jacobi map on torsion cycles, see [Reference BlochBlo79, Proposition 3.7]. It thus suffices to show that
$k=\mathbb {C}$, then Bloch's map agrees with the Abel–Jacobi map on torsion cycles, see [Reference BlochBlo79, Proposition 3.7]. It thus suffices to show that ![]() $\lambda _{{\rm tr}}^i$ from § 7.5 is induced by Bloch's map in (8.1). For this, let
$\lambda _{{\rm tr}}^i$ from § 7.5 is induced by Bloch's map in (8.1). For this, let ![]() $z\in \bigoplus _{x\in X^{(i)}}[x]\mathbb {Z}_\ell$ be a homologically trivial cycle. Then
$z\in \bigoplus _{x\in X^{(i)}}[x]\mathbb {Z}_\ell$ be a homologically trivial cycle. Then ![]() $\partial \alpha =z$ for some
$\partial \alpha =z$ for some ![]() $\alpha \in H^{2i-1}(F_{i-1}X,\mathbb {Z}_\ell (i))$. Assume that
$\alpha \in H^{2i-1}(F_{i-1}X,\mathbb {Z}_\ell (i))$. Assume that ![]() $z$ is
$z$ is ![]() $\ell ^r$-torsion modulo algebraic equivalence. As in § 7.5, we find classes
$\ell ^r$-torsion modulo algebraic equivalence. As in § 7.5, we find classes ![]() $\beta \in H^{2i-1}(X,\mathbb {Z}_\ell (i))$ and
$\beta \in H^{2i-1}(X,\mathbb {Z}_\ell (i))$ and ![]() $\xi \in \bigoplus _{x\in X^{(i-1)}}H^1(x,\mathbb {Z}_\ell (i))$ with
$\xi \in \bigoplus _{x\in X^{(i-1)}}H^1(x,\mathbb {Z}_\ell (i))$ with
In particular, ![]() $\partial \circ \iota _\ast (\xi ) /\ell ^r=z$ and so
$\partial \circ \iota _\ast (\xi ) /\ell ^r=z$ and so ![]() $\psi _r([z])=[\xi /\ell ^r]$, where
$\psi _r([z])=[\xi /\ell ^r]$, where ![]() $\psi _r$ is the isomorphism from Lemma 8.1. By our construction of Bloch's map, we thus find
$\psi _r$ is the isomorphism from Lemma 8.1. By our construction of Bloch's map, we thus find
On the other hand,
by our construction of ![]() $\lambda ^i_{{\rm tr}}$ in § 7.5. The result thus follows from the fact that
$\lambda ^i_{{\rm tr}}$ in § 7.5. The result thus follows from the fact that
because ![]() $\alpha$ is an integral class. This proves the proposition.
$\alpha$ is an integral class. This proves the proposition.
9. Proof of the main results ( $\ell$-adic)
$\ell$-adic)
9.1  $\ell$-adic twisted Borel–Moore cohomology
$\ell$-adic twisted Borel–Moore cohomology
Fix a field ![]() $k$ and a prime
$k$ and a prime ![]() $\ell$ that is invertible in
$\ell$ that is invertible in ![]() $k$. Let
$k$. Let ![]() $\mathcal {V}$ be the category whose objects are separated schemes of finite type over
$\mathcal {V}$ be the category whose objects are separated schemes of finite type over ![]() $k$ and such that the morphisms are given by open immersions of schemes of the same dimension. This is a constructible category of Noetherian schemes as in Definition 4.1. Let
$k$ and such that the morphisms are given by open immersions of schemes of the same dimension. This is a constructible category of Noetherian schemes as in Definition 4.1. Let ![]() $\mathcal {A}\subset \operatorname {Mod}_{\mathbb {Z}_\ell }$ be the full subcategory with objects
$\mathcal {A}\subset \operatorname {Mod}_{\mathbb {Z}_\ell }$ be the full subcategory with objects ![]() $\mathbb {Z}_\ell,\mathbb {Q}_\ell,\mathbb {Q}_\ell /\mathbb {Z}_\ell$ and
$\mathbb {Z}_\ell,\mathbb {Q}_\ell,\mathbb {Q}_\ell /\mathbb {Z}_\ell$ and ![]() $\mathbb {Z}/\ell ^r$ for all
$\mathbb {Z}/\ell ^r$ for all ![]() $r\geqslant 1$. By Proposition 6.6,
$r\geqslant 1$. By Proposition 6.6, ![]() $\ell$-adic pro-étale Borel–Moore cohomology
$\ell$-adic pro-étale Borel–Moore cohomology ![]() $H^\ast (-,A(n))$ as defined in (6.13)–(6.15) is a twisted Borel–Moore cohomology theory on
$H^\ast (-,A(n))$ as defined in (6.13)–(6.15) is a twisted Borel–Moore cohomology theory on ![]() $\mathcal {V}$ with coefficients in
$\mathcal {V}$ with coefficients in ![]() $\mathcal {A}$ which is
$\mathcal {A}$ which is ![]() $\ell$-adic if
$\ell$-adic if ![]() $k$ is perfect, see Definitions 4.2 and 4.4. In particular, all results from § 5 and 7 hold true in this set-up. Here we recall that for
$k$ is perfect, see Definitions 4.2 and 4.4. In particular, all results from § 5 and 7 hold true in this set-up. Here we recall that for ![]() $i\geqslant 1$:
$i\geqslant 1$:
for ![]() $0\leqslant j\leqslant i-1$, see Lemma 7.4. Moreover, Lemma 7.5 implies that
$0\leqslant j\leqslant i-1$, see Lemma 7.4. Moreover, Lemma 7.5 implies that ![]() $A_0 ^i(X\!)_{\mathbb {Z}_\ell } = \operatorname {Griff} ^i(X\!)_{\mathbb {Z}_\ell }$ if
$A_0 ^i(X\!)_{\mathbb {Z}_\ell } = \operatorname {Griff} ^i(X\!)_{\mathbb {Z}_\ell }$ if ![]() $k$ is algebraically closed and
$k$ is algebraically closed and ![]() $A_0 ^i(X\!)_{\mathbb {Z}_\ell } = \ker (\operatorname {cl}_X^i\!)\subset \operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }$ if
$A_0 ^i(X\!)_{\mathbb {Z}_\ell } = \ker (\operatorname {cl}_X^i\!)\subset \operatorname {CH}^i(X\!)_{\mathbb {Z}_\ell }$ if ![]() $k$ is the perfect closure of a finitely generated field.
$k$ is the perfect closure of a finitely generated field.
Lemma 9.1 In the above notation, assume in addition that ![]() $X$ is smooth and equi-dimensional. Then the cycle class map
$X$ is smooth and equi-dimensional. Then the cycle class map
constructed in (7.1) coincides with Jannsen's cycle class map in continuous étale cohomology from [Reference JannsenJan88].
Proof. By Lemma 6.8 and the topological invariance of the pro-étale topos (see [Reference Bhatt and ScholzeBS15, Lemma 5.4.2]), we may replace ![]() $k$ by its perfect closure and assume that
$k$ by its perfect closure and assume that ![]() $k$ is perfect. Let
$k$ is perfect. Let ![]() $X$ be a smooth variety over
$X$ be a smooth variety over ![]() $k$. By Lemma 6.5,
$k$. By Lemma 6.5, ![]() $H^\ast (X,A(n))$ agrees with the corresponding continuous étale cohomology group. The cycle class map in (7.1) is defined via the Gysin pushforward, where one uses excision to reduce to the case of a cycle whose support is smooth. Our claim thus follows from [Reference JannsenJan88, Remark 3.24].
$H^\ast (X,A(n))$ agrees with the corresponding continuous étale cohomology group. The cycle class map in (7.1) is defined via the Gysin pushforward, where one uses excision to reduce to the case of a cycle whose support is smooth. Our claim thus follows from [Reference JannsenJan88, Remark 3.24].
9.2 Proof of Theorem 1.8
Proof of Theorem 1.8 We use the notation from § 9.1 and claim that it suffices to prove Theorem 1.8 after replacing ![]() $k$ by its perfect closure
$k$ by its perfect closure ![]() $k^{per}$. Indeed, this does not change
$k^{per}$. Indeed, this does not change ![]() $\ell$-adic Chow groups by Lemma 6.8 and it does not change the (pro-)étale topos (see [Reference Bhatt and ScholzeBS15, Lemma 5.4.2]), so that
$\ell$-adic Chow groups by Lemma 6.8 and it does not change the (pro-)étale topos (see [Reference Bhatt and ScholzeBS15, Lemma 5.4.2]), so that ![]() $H^\ast (-,A(n))$ remains unchanged by passing from
$H^\ast (-,A(n))$ remains unchanged by passing from ![]() $k$ to
$k$ to ![]() $k^{per}$.
$k^{per}$.
We may and will from now on assume that ![]() $k$ is perfect, so that
$k$ is perfect, so that ![]() $H^\ast (-,A(n))$ is an
$H^\ast (-,A(n))$ is an ![]() $\ell$-adic twisted Borel–Moore cohomology theory on
$\ell$-adic twisted Borel–Moore cohomology theory on ![]() $\mathcal {V}$ by Proposition 6.6. For any
$\mathcal {V}$ by Proposition 6.6. For any ![]() $X\in \mathcal {V}$, we thus get a cycle class map
$X\in \mathcal {V}$, we thus get a cycle class map
constructed in § 7.2. If ![]() $X$ is smooth and equi-dimensional, then, by Lemma 6.5,
$X$ is smooth and equi-dimensional, then, by Lemma 6.5, ![]() $H^i(X,\mathbb {Z}_\ell (n))\simeq H^i_{\rm cont}(X_{\unicode{x00E9}{\rm t}},\mathbb {Z}_\ell (n))$ agrees with Jannsen's
$H^i(X,\mathbb {Z}_\ell (n))\simeq H^i_{\rm cont}(X_{\unicode{x00E9}{\rm t}},\mathbb {Z}_\ell (n))$ agrees with Jannsen's ![]() $\ell$-adic continuous étale cohomology groups, see § 6.1.1. It follows from the construction of
$\ell$-adic continuous étale cohomology groups, see § 6.1.1. It follows from the construction of ![]() $\operatorname {cl}^i_X$ via the Gysin sequence (see (P2)) that if
$\operatorname {cl}^i_X$ via the Gysin sequence (see (P2)) that if ![]() $X$ is a smooth variety, then
$X$ is a smooth variety, then ![]() $\operatorname {cl}^i_X$ agrees with Jannsen's cycle class map (see Lemma 9.1).
$\operatorname {cl}^i_X$ agrees with Jannsen's cycle class map (see Lemma 9.1).
Recall from Definitions 7.2 and 7.10 the groups ![]() $A^i(X\!)_{\mathbb {Z}_\ell }$ and
$A^i(X\!)_{\mathbb {Z}_\ell }$ and ![]() $A_0^i(X\!)_{\mathbb {Z}_\ell }$ and recall the description from (9.1) (that we used as a definition in the introduction).
$A_0^i(X\!)_{\mathbb {Z}_\ell }$ and recall the description from (9.1) (that we used as a definition in the introduction).
Item (i) in Theorem 1.8 is then a consequence of Theorem 7.7 and Proposition 7.11.
By § 7.5, there is a map
where ![]() $N^jH^i(X,A(n)):=\ker (H^i(X,A(n))\to H^i(F_{j-1}X,A(n)))$. If
$N^jH^i(X,A(n)):=\ker (H^i(X,A(n))\to H^i(F_{j-1}X,A(n)))$. If ![]() $k$ is algebraically closed and
$k$ is algebraically closed and ![]() $X$ is smooth projective, then this map agrees by Proposition 8.5 with Bloch's transcendental Abel–Jacobi mapping on torsion cycles from [Reference BlochBlo79] (cf. § 8). Item (ii) thus follows from Theorem 7.19 and Proposition 7.16. This concludes the proof of Theorem 1.8.
$X$ is smooth projective, then this map agrees by Proposition 8.5 with Bloch's transcendental Abel–Jacobi mapping on torsion cycles from [Reference BlochBlo79] (cf. § 8). Item (ii) thus follows from Theorem 7.19 and Proposition 7.16. This concludes the proof of Theorem 1.8.
9.3 Proof of Theorem 1.5
The following lemma shows that in our set-up, the result of Theorem 7.30 holds true whenever ![]() $k$ contains all
$k$ contains all ![]() $\ell$-roots of unity.
$\ell$-roots of unity.
Lemma 9.2 In the notation of § 9.1, the following holds. Then for any ![]() $X\in \mathcal {V}$ and any
$X\in \mathcal {V}$ and any ![]() $i$ and
$i$ and ![]() $n$,
$n$, ![]() $H^i(F_0X,\mathbb {Z}_\ell (n))$ is torsion-free if one of the following conditions holds:
$H^i(F_0X,\mathbb {Z}_\ell (n))$ is torsion-free if one of the following conditions holds:
(i)
 $n=i-1$;
$n=i-1$;(ii)
 $k$ contains all
$k$ contains all  $\ell$-power roots of unity.
$\ell$-power roots of unity.
Proof. By additivity of the cohomology functor (see Lemma 5.6), we may assume that ![]() $X$ is irreducible with generic point
$X$ is irreducible with generic point ![]() $\eta _X\in X$. If
$\eta _X\in X$. If ![]() $k$ contains all
$k$ contains all ![]() $\ell$-power roots of unity,
$\ell$-power roots of unity, ![]() $H^i(F_0X,\mathbb {Z}_\ell (n))\simeq H^i(F_0X,\mathbb {Z}_\ell (i-1))$ for all
$H^i(F_0X,\mathbb {Z}_\ell (n))\simeq H^i(F_0X,\mathbb {Z}_\ell (i-1))$ for all ![]() $i$ and
$i$ and ![]() $n$. It thus suffices to prove the lemma under assumption (9.2). As
$n$. It thus suffices to prove the lemma under assumption (9.2). As ![]() $X$ is irreducible,
$X$ is irreducible, ![]() $H^i(F_0X,\mathbb {Z}_\ell (i-1))= H^i(\eta _X,\mathbb {Z}_\ell (i-1))$ and so the claim follows from Remark 5.14 and Voevodsky's proof of the Bloch–Kato conjecture [Reference VoevodskyVoe11].
$H^i(F_0X,\mathbb {Z}_\ell (i-1))= H^i(\eta _X,\mathbb {Z}_\ell (i-1))$ and so the claim follows from Remark 5.14 and Voevodsky's proof of the Bloch–Kato conjecture [Reference VoevodskyVoe11].
By (7.17) there is a higher Abel–Jacobi mapping
where ![]() $N^\ast$ denotes the coniveau filtration on
$N^\ast$ denotes the coniveau filtration on ![]() $A_0 ^i(X\!)[\ell ^{\infty }]$ from § 7.8.
$A_0 ^i(X\!)[\ell ^{\infty }]$ from § 7.8.
Theorem 9.3 Let ![]() $X$ be a separated scheme of finite type over
$X$ be a separated scheme of finite type over ![]() $k$. Let
$k$. Let ![]() $i\geqslant 2$ and assume that one of the following holds:
$i\geqslant 2$ and assume that one of the following holds:
(i)
 $k$ contains all
$k$ contains all  $\ell$-power roots of unity; or
$\ell$-power roots of unity; or(ii)
 $i=2$.
$i=2$.
Then for all ![]() $0\leqslant j\leqslant i-2$, we have
$0\leqslant j\leqslant i-2$, we have
Proof. We aim to apply Theorem 7.30. To this end we need to ensure that for any closed subscheme ![]() $Z\subset X$,
$Z\subset X$, ![]() $H^{2(i-j)-1}(F_0Z,\mathbb {Z}_\ell (i-j))$ is torsion-free. By Lemma 9.2, this condition is satisfied if
$H^{2(i-j)-1}(F_0Z,\mathbb {Z}_\ell (i-j))$ is torsion-free. By Lemma 9.2, this condition is satisfied if ![]() $k$ contains all
$k$ contains all ![]() $\ell$-power roots of unity, or if
$\ell$-power roots of unity, or if ![]() $i=2$ and
$i=2$ and ![]() $j=0$. This concludes the proof.
$j=0$. This concludes the proof.
We are now in a position to prove Theorem 1.5, which follows from the following slightly stronger result.
Theorem 9.4 Let ![]() $X$ be a separated scheme of finite type over a field
$X$ be a separated scheme of finite type over a field ![]() $k$ and let
$k$ and let ![]() $\ell$ be a prime invertible in
$\ell$ be a prime invertible in ![]() $k$. Let
$k$. Let ![]() $i\geqslant 2$ and assume that one of the following holds:
$i\geqslant 2$ and assume that one of the following holds:
(i)
 $k$ contains all
$k$ contains all  $\ell$-power roots of unity; or
$\ell$-power roots of unity; or(ii)
 $i=2$.
$i=2$.
Then for all ![]() $0\leqslant j\leqslant i-2$, we have
$0\leqslant j\leqslant i-2$, we have
Proof. By (9.1),
The higher transcendental Abel–Jacobi mapping from (7.17) thus yields for ![]() $0\leqslant j\leqslant i-2$ mappings
$0\leqslant j\leqslant i-2$ mappings
where ![]() $Z\subset X$ runs through all closed subschemes with
$Z\subset X$ runs through all closed subschemes with ![]() $j=\dim X-\dim Z$. Theorem 9.3 then implies that for
$j=\dim X-\dim Z$. Theorem 9.3 then implies that for ![]() $0\leqslant j\leqslant i-2$, the kernel of the above map is given by
$0\leqslant j\leqslant i-2$, the kernel of the above map is given by ![]() $N^{j+1}\operatorname {CH}^i(X\!)[\ell ^\infty ]$, as desired.
$N^{j+1}\operatorname {CH}^i(X\!)[\ell ^\infty ]$, as desired.
9.4 Applications of Theorems 1.5 and 9.4
The simplest (non-trivial) consequence of Theorem 9.4 is as follows.
Corollary 9.5 Let ![]() $X$ be a smooth equi-dimensional algebraic scheme over a finitely generated field
$X$ be a smooth equi-dimensional algebraic scheme over a finitely generated field ![]() $k$. Let
$k$. Let ![]() $\ell$ be a prime invertible in
$\ell$ be a prime invertible in ![]() $k$ and let
$k$ and let ![]() $\operatorname {CH}^i_{0}(X\!)[\ell ^\infty ]$ denote the group of
$\operatorname {CH}^i_{0}(X\!)[\ell ^\infty ]$ denote the group of ![]() $\ell$-power torsion cycles with trivial cycle class in Jannsen's continuous
$\ell$-power torsion cycles with trivial cycle class in Jannsen's continuous ![]() $\ell$-adic étale cohomology. Then there is a canonical injection
$\ell$-adic étale cohomology. Then there is a canonical injection
Corollary 9.5 should be compared with a result of Merkurjev and Suslin [Reference Merkurjev and SuslinMS83, § 18], who showed that Bloch's Abel–Jacobi mapping on ![]() $\ell$-power torsion cycles on smooth projective varieties over algebraically closed fields [Reference BlochBlo79] is injective on codimension-two cycles. Corollary 9.5 has previously been proven in the particular case where
$\ell$-power torsion cycles on smooth projective varieties over algebraically closed fields [Reference BlochBlo79] is injective on codimension-two cycles. Corollary 9.5 has previously been proven in the particular case where ![]() $k=\mathbb {F}_q$ is a finite field and
$k=\mathbb {F}_q$ is a finite field and ![]() $X$ is smooth projective in [Reference Colliot-Thélène, Sansuc and SouléCSS83, Théorème 4] (in fact, [Reference Colliot-Thélène, Sansuc and SouléCSS83, Théorème 4] proves that
$X$ is smooth projective in [Reference Colliot-Thélène, Sansuc and SouléCSS83, Théorème 4] (in fact, [Reference Colliot-Thélène, Sansuc and SouléCSS83, Théorème 4] proves that ![]() $\operatorname {CH}^2_{0}(X\!)[\ell ^\infty ]=0$ in this case; this also follows from our set-up, see Proposition 7.16 and note that
$\operatorname {CH}^2_{0}(X\!)[\ell ^\infty ]=0$ in this case; this also follows from our set-up, see Proposition 7.16 and note that ![]() $H^3_{\rm cont}(X_{\unicode{x00E9}{\rm t}},\mathbb {Q}_\ell (2))=H^3 (X_{\unicode{x00E9}{\rm t}},\mathbb {Q}_\ell (2))=0$ for weight reasons, cf. [Reference Colliot-Thélène, Sansuc and SouléCSS83, pp. 780–781]).
$H^3_{\rm cont}(X_{\unicode{x00E9}{\rm t}},\mathbb {Q}_\ell (2))=H^3 (X_{\unicode{x00E9}{\rm t}},\mathbb {Q}_\ell (2))=0$ for weight reasons, cf. [Reference Colliot-Thélène, Sansuc and SouléCSS83, pp. 780–781]).
Proof of Corollary 9.5 By the same argument as in the proof of Theorem 1.8, we may replace ![]() $k$ by its perfect closure and hence assume that
$k$ by its perfect closure and hence assume that ![]() $k$ is the perfect closure of a finitely generated field. The result then follows from Theorem 1.5 (or Theorem 7.19) together with the fact that
$k$ is the perfect closure of a finitely generated field. The result then follows from Theorem 1.5 (or Theorem 7.19) together with the fact that ![]() $A^2_0(X\!)_{\mathbb {Z}_\ell }=\operatorname {CH}_0^2(X\!)_{\mathbb {Z}_\ell }$ if the ground field
$A^2_0(X\!)_{\mathbb {Z}_\ell }=\operatorname {CH}_0^2(X\!)_{\mathbb {Z}_\ell }$ if the ground field ![]() $k$ is (the perfect closure of a) finitely generated, see Proposition 6.6 and Lemma 7.5.
$k$ is (the perfect closure of a) finitely generated, see Proposition 6.6 and Lemma 7.5.
Let ![]() $X$ and
$X$ and ![]() $Y$ be smooth projective equi-dimensional
$Y$ be smooth projective equi-dimensional ![]() $k$-schemes. A cycle
$k$-schemes. A cycle ![]() $\Gamma \in \operatorname {CH}^{\dim X}(X\times Y)$ yields actions on Chow groups that are compatible with the cycle class maps in continuous étale cohomology. Hence, we get an action
$\Gamma \in \operatorname {CH}^{\dim X}(X\times Y)$ yields actions on Chow groups that are compatible with the cycle class maps in continuous étale cohomology. Hence, we get an action ![]() $\Gamma _\ast : N^0\operatorname {CH}^i(X\!)[\ell ^\infty ] \to N^0\operatorname {CH}^i(Y)[\ell ^\infty ]$. Similarly, there are actions
$\Gamma _\ast : N^0\operatorname {CH}^i(X\!)[\ell ^\infty ] \to N^0\operatorname {CH}^i(Y)[\ell ^\infty ]$. Similarly, there are actions ![]() $\Gamma _\ast : H^i_{\rm cont}(X_{\unicode{x00E9}{\rm t}},A(n))\to H^i_{\rm cont}(Y_{\unicode{x00E9}{\rm t}},A(n))$ for
$\Gamma _\ast : H^i_{\rm cont}(X_{\unicode{x00E9}{\rm t}},A(n))\to H^i_{\rm cont}(Y_{\unicode{x00E9}{\rm t}},A(n))$ for ![]() $A\in \{ \mathbb {Q}_\ell /\mathbb {Z}_\ell,\mathbb {Q}_\ell \}$. The latter respect Grothendieck's coniveau filtration
$A\in \{ \mathbb {Q}_\ell /\mathbb {Z}_\ell,\mathbb {Q}_\ell \}$. The latter respect Grothendieck's coniveau filtration ![]() $N^\ast$, as can be checked with the help of a moving lemma (see, e.g., [Reference LevineLev05, Theorem 2.13]). We conclude that correspondences act on source and target of the map
$N^\ast$, as can be checked with the help of a moving lemma (see, e.g., [Reference LevineLev05, Theorem 2.13]). We conclude that correspondences act on source and target of the map
induced from the map in § 7.5 (cf. Lemma 7.4). We will show in [Reference SchreiederSch22] that these actions are compatible with the map ![]() $\lambda _{{\rm tr}}^i$. The case
$\lambda _{{\rm tr}}^i$. The case ![]() $i=2$ is simpler, and we give a direct proof in the following lemma.
$i=2$ is simpler, and we give a direct proof in the following lemma.
Lemma 9.6 Let ![]() $X,Y$ be smooth projective equi-dimensional
$X,Y$ be smooth projective equi-dimensional ![]() $k$-schemes and let
$k$-schemes and let ![]() $\Gamma \in \operatorname {CH}^{\dim X}(X\times Y)$. Then the following diagram commutes.
$\Gamma \in \operatorname {CH}^{\dim X}(X\times Y)$. Then the following diagram commutes.
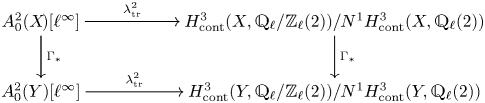
Proof. By the description of ![]() $\lambda _{{\rm tr}}^i$ from Lemma 7.15, it suffices to show that the isomorphism
$\lambda _{{\rm tr}}^i$ from Lemma 7.15, it suffices to show that the isomorphism
from Proposition 7.11 is compatible with the action of correspondences. As ![]() $X$ is smooth and equi-dimensional, the Gersten conjecture [Reference Bloch and OgusBO74, Reference Colliot-Thélène, Hoobler and KahnCHK97] identifies
$X$ is smooth and equi-dimensional, the Gersten conjecture [Reference Bloch and OgusBO74, Reference Colliot-Thélène, Hoobler and KahnCHK97] identifies ![]() $H^3_{nr}(X,\mathbb {Z}_\ell (2))$ with the global sections of the corresponding Bloch–Ogus sheaf, associated to
$H^3_{nr}(X,\mathbb {Z}_\ell (2))$ with the global sections of the corresponding Bloch–Ogus sheaf, associated to ![]() . This description makes it easy to define an action on unramified cohomology, cf. [Reference Colliot-Thélène and VoisinCV12, § 9, Appendice] (an action in a more general setting has been constructed by Rost [Reference RostRos96]). Using this description, one can readily check that the above isomorphism is compatible with the action of cycles, which concludes the lemma.
. This description makes it easy to define an action on unramified cohomology, cf. [Reference Colliot-Thélène and VoisinCV12, § 9, Appendice] (an action in a more general setting has been constructed by Rost [Reference RostRos96]). Using this description, one can readily check that the above isomorphism is compatible with the action of cycles, which concludes the lemma.
Corollary 9.5 implies for instance the Rost nilpotence conjecture for surfaces up to inverting the exponential characteristic, originally due to Gille [Reference GilleGil10, Reference GilleGil14] and with an alternative proof due to Rosenschon and Sawant [Reference Rosenschon and SawantRS18].
Corollary 9.7 Let ![]() $X$ be a smooth projective equi-dimensional scheme over a field
$X$ be a smooth projective equi-dimensional scheme over a field ![]() $k$ with base change
$k$ with base change ![]() $\bar {X}=X\times _k\bar {k}$, where
$\bar {X}=X\times _k\bar {k}$, where ![]() $\bar {k}$ denotes an algebraic closure. Let
$\bar {k}$ denotes an algebraic closure. Let ![]() $\Gamma \in \operatorname {CH}^{\dim X}(X\times X)$ and assume that the base change
$\Gamma \in \operatorname {CH}^{\dim X}(X\times X)$ and assume that the base change ![]() $\bar {\Gamma }=\Gamma \times _k\bar {k}$ acts trivially on
$\bar {\Gamma }=\Gamma \times _k\bar {k}$ acts trivially on ![]() $H^i(\bar {X}_{\unicode{x00E9}{\rm t}},\mathbb {Q}_\ell /\mathbb {Z}_\ell (2))$ for
$H^i(\bar {X}_{\unicode{x00E9}{\rm t}},\mathbb {Q}_\ell /\mathbb {Z}_\ell (2))$ for ![]() $i\leqslant 3$. Then the action
$i\leqslant 3$. Then the action
is zero for ![]() $N\geqslant 10$.
$N\geqslant 10$.
Proof. A straightforward limit argument reduces us to the case where ![]() $k$ is finitely generated. (This uses that étale cohomology does not change under algebraically closed field extensions.) By Lemma 9.6 and Corollary 9.5, it thus suffices to show that
$k$ is finitely generated. (This uses that étale cohomology does not change under algebraically closed field extensions.) By Lemma 9.6 and Corollary 9.5, it thus suffices to show that ![]() $\Gamma ^{\circ 5}$ acts trivially on
$\Gamma ^{\circ 5}$ acts trivially on ![]() $H^4_{\rm cont}(X_{\unicode{x00E9}{\rm t}},\mathbb {Z}_\ell (2))[\ell ^\infty ]$ and on
$H^4_{\rm cont}(X_{\unicode{x00E9}{\rm t}},\mathbb {Z}_\ell (2))[\ell ^\infty ]$ and on ![]() $H^3_{\rm cont}(X_{\unicode{x00E9}{\rm t}},\mathbb {Q}_\ell /\mathbb {Z}_\ell (2))$. The Bockstein sequence yields a canonical surjection
$H^3_{\rm cont}(X_{\unicode{x00E9}{\rm t}},\mathbb {Q}_\ell /\mathbb {Z}_\ell (2))$. The Bockstein sequence yields a canonical surjection
that is compatible with the action of correspondences. It thus suffices to show that ![]() $\Gamma _\ast ^{\circ 5}$ acts trivially on
$\Gamma _\ast ^{\circ 5}$ acts trivially on ![]() $H^3_{\rm cont}(X_{\unicode{x00E9}{\rm t}},\mathbb {Q}_\ell /\mathbb {Z}_\ell (2))$. Note that
$H^3_{\rm cont}(X_{\unicode{x00E9}{\rm t}},\mathbb {Q}_\ell /\mathbb {Z}_\ell (2))$. Note that ![]() $H^3_{\rm cont}(X_{\unicode{x00E9}{\rm t}},\mathbb {Q}_\ell /\mathbb {Z}_\ell (2))=\operatorname {colim}_ r H^3_{\rm cont}(X_{\unicode{x00E9}{\rm t}},\mu _{\ell ^r}^{\otimes 2})$ and
$H^3_{\rm cont}(X_{\unicode{x00E9}{\rm t}},\mathbb {Q}_\ell /\mathbb {Z}_\ell (2))=\operatorname {colim}_ r H^3_{\rm cont}(X_{\unicode{x00E9}{\rm t}},\mu _{\ell ^r}^{\otimes 2})$ and ![]() $H^3_{\rm cont}(X_{\unicode{x00E9}{\rm t}},\mu _{\ell ^r}^{\otimes 2})=H^3 (X_{\unicode{x00E9}{\rm t}},\mu _{\ell ^r}^{\otimes 2})$, cf. [Reference JannsenJan88, (3.1)]. The assertion in question thus follows from the fact that the Hochschild–Serre spectral sequence for étale cohomology (see [Reference MilneMil80, p. 105, III.2.20]) is compatible with the action of correspondences. (In the last step, we are implicitly working with the separable closure of
$H^3_{\rm cont}(X_{\unicode{x00E9}{\rm t}},\mu _{\ell ^r}^{\otimes 2})=H^3 (X_{\unicode{x00E9}{\rm t}},\mu _{\ell ^r}^{\otimes 2})$, cf. [Reference JannsenJan88, (3.1)]. The assertion in question thus follows from the fact that the Hochschild–Serre spectral sequence for étale cohomology (see [Reference MilneMil80, p. 105, III.2.20]) is compatible with the action of correspondences. (In the last step, we are implicitly working with the separable closure of ![]() $k$ and not with the algebraic closure; this is possible because neither Chow groups nor étale cohomology change by purely inseparable field extensions, see Lemma 6.8.)
$k$ and not with the algebraic closure; this is possible because neither Chow groups nor étale cohomology change by purely inseparable field extensions, see Lemma 6.8.)
Recall that the exponential characteristic ![]() $e$ of a field
$e$ of a field ![]() $k$ is
$k$ is ![]() $1$ if
$1$ if ![]() $\operatorname {char} k=0$ and
$\operatorname {char} k=0$ and ![]() $p$ if
$p$ if ![]() $p=\operatorname {char} k>0$.
$p=\operatorname {char} k>0$.
Corollary 9.8 Let ![]() $S$ be a smooth projective scheme of pure dimension two over a field
$S$ be a smooth projective scheme of pure dimension two over a field ![]() $k$ of exponential characteristic
$k$ of exponential characteristic ![]() $e$. Let
$e$. Let ![]() $\Gamma \in \operatorname {CH}^2(S\times _k S)$ be a correspondence with base change
$\Gamma \in \operatorname {CH}^2(S\times _k S)$ be a correspondence with base change ![]() $\bar {\Gamma }\in \operatorname {CH}^2(S_{\bar {k}}\times _{\bar {k}} S_{\bar {k}})$ to the algebraic closure
$\bar {\Gamma }\in \operatorname {CH}^2(S_{\bar {k}}\times _{\bar {k}} S_{\bar {k}})$ to the algebraic closure ![]() $\bar {k}$ of
$\bar {k}$ of ![]() $k$. Assume that
$k$. Assume that ![]() $\bar {\Gamma }$ is torsion and homologically trivial in
$\bar {\Gamma }$ is torsion and homologically trivial in ![]() $\ell$-adic étale cohomology for any prime
$\ell$-adic étale cohomology for any prime ![]() $\ell$ invertible in
$\ell$ invertible in ![]() $\bar {k}$. Then up to inverting
$\bar {k}$. Then up to inverting ![]() $e$, the composition
$e$, the composition ![]() $\Gamma ^{\circ N}$ is zero for
$\Gamma ^{\circ N}$ is zero for ![]() $N\geqslant 11$.
$N\geqslant 11$.
Proof. A standard norm argument shows that ![]() $\Gamma$ is torsion. By the Chinese remainder theorem, we may assume that
$\Gamma$ is torsion. By the Chinese remainder theorem, we may assume that ![]() $\Gamma$ is
$\Gamma$ is ![]() $\ell ^r$-torsion for some integer
$\ell ^r$-torsion for some integer ![]() $r\geqslant 0$ and some prime
$r\geqslant 0$ and some prime ![]() $\ell$ invertible in
$\ell$ invertible in ![]() $k$. Let
$k$. Let ![]() $X:=S\times S$. The assumptions imply that there is a correspondence
$X:=S\times S$. The assumptions imply that there is a correspondence ![]() $\Omega \in \operatorname {CH}^4(X\times X)[\ell ^\infty ]$ which is homologically trivial over
$\Omega \in \operatorname {CH}^4(X\times X)[\ell ^\infty ]$ which is homologically trivial over ![]() $\bar {k}$ and such that
$\bar {k}$ and such that ![]() $\Omega _\ast ^{\circ N}(\Gamma )=\Gamma ^{\circ N+1}$. The assertion thus follows from Corollary 9.7.
$\Omega _\ast ^{\circ N}(\Gamma )=\Gamma ^{\circ N+1}$. The assertion thus follows from Corollary 9.7.
Remark 9.9 Up to inverting the exponential characteristic, Corollary 9.8 is slightly stronger than the original conjecture of Rost for surfaces, proven in [Reference GilleGil10, Reference GilleGil14, Reference Rosenschon and SawantRS18]. Indeed, we are only asking that ![]() $\bar {\Gamma }$ is torsion and homologically trivial, while the original formulation asks that
$\bar {\Gamma }$ is torsion and homologically trivial, while the original formulation asks that ![]() $\Gamma$ is rationally equivalent to
$\Gamma$ is rationally equivalent to ![]() $0$ over
$0$ over ![]() $\bar {k}$ (or equivalently over some field extension of
$\bar {k}$ (or equivalently over some field extension of ![]() $k$).
$k$).
10. Proof of main results over  $\mathbb {C}$
$\mathbb {C}$
10.1 Integral twisted Borel–Moore cohomology
Let ![]() $\mathcal {V}$ be the category whose objects are separated schemes of finite type over
$\mathcal {V}$ be the category whose objects are separated schemes of finite type over ![]() $\mathbb {C}$ and such that the morphisms are given by open immersions of schemes of the same dimension. This is a constructible category of Noetherian schemes as in Definition 4.1. Let
$\mathbb {C}$ and such that the morphisms are given by open immersions of schemes of the same dimension. This is a constructible category of Noetherian schemes as in Definition 4.1. Let ![]() $\mathcal {A}:=\operatorname {Mod}_\mathbb {Z}$ and define for
$\mathcal {A}:=\operatorname {Mod}_\mathbb {Z}$ and define for ![]() $X\in \mathcal {V}$ and
$X\in \mathcal {V}$ and ![]() $A\in \mathcal {A}$,
$A\in \mathcal {A}$,
where ![]() $d_X:=\dim X$ and
$d_X:=\dim X$ and ![]() $H^{\rm BM}_\ast$ denotes Borel–Moore homology and
$H^{\rm BM}_\ast$ denotes Borel–Moore homology and ![]() $X_{\operatorname {an}}$ denotes the analytic space that underlies
$X_{\operatorname {an}}$ denotes the analytic space that underlies ![]() $X$ and
$X$ and ![]() $A(n):=A\otimes _{\mathbb {Z}}(2\pi i)^n \mathbb {Z}$ denotes the
$A(n):=A\otimes _{\mathbb {Z}}(2\pi i)^n \mathbb {Z}$ denotes the ![]() $n$th Tate twist of
$n$th Tate twist of ![]() $A$. By Proposition 6.9,
$A$. By Proposition 6.9, ![]() $H^\ast$ defines an integral twisted Borel–Moore cohomology theory that is adapted to algebraic equivalence, cf. Definition 4.6. It follows that all results from §§ 5 and 7 hold true in the above set-up if we formally make the replacements
$H^\ast$ defines an integral twisted Borel–Moore cohomology theory that is adapted to algebraic equivalence, cf. Definition 4.6. It follows that all results from §§ 5 and 7 hold true in the above set-up if we formally make the replacements ![]() $\mathbb {Z}_\ell \rightsquigarrow \mathbb {Z}$,
$\mathbb {Z}_\ell \rightsquigarrow \mathbb {Z}$, ![]() $\mathbb {Q}_\ell \rightsquigarrow \mathbb {Q}$,
$\mathbb {Q}_\ell \rightsquigarrow \mathbb {Q}$, ![]() $\ell ^r \rightsquigarrow r$, and
$\ell ^r \rightsquigarrow r$, and ![]() $[\ell ^\infty ] \rightsquigarrow { }_{\operatorname {tors}}$.
$[\ell ^\infty ] \rightsquigarrow { }_{\operatorname {tors}}$.
10.2 Proof of Theorem 1.6
Proof of Theorem 1.6 We use the notation from § 10.1. Performing the aforementioned formal replacements ![]() $\mathbb {Z}_\ell \rightsquigarrow \mathbb {Z}$,
$\mathbb {Z}_\ell \rightsquigarrow \mathbb {Z}$, ![]() $\mathbb {Q}_\ell \rightsquigarrow \mathbb {Q}$,
$\mathbb {Q}_\ell \rightsquigarrow \mathbb {Q}$, ![]() $\ell ^r \rightsquigarrow r$, and
$\ell ^r \rightsquigarrow r$, and ![]() $[\ell ^\infty ] \rightsquigarrow { }_{\operatorname {tors}}$, Lemma 7.5 shows that
$[\ell ^\infty ] \rightsquigarrow { }_{\operatorname {tors}}$, Lemma 7.5 shows that ![]() $A_0 ^i(X\!)_{\mathbb {Z}}=\operatorname {Griff} ^i(X\!)$ is the group of homologically trivial cycles modulo algebraic equivalence. The arguments in § 7.5 yield a map
$A_0 ^i(X\!)_{\mathbb {Z}}=\operatorname {Griff} ^i(X\!)$ is the group of homologically trivial cycles modulo algebraic equivalence. The arguments in § 7.5 yield a map
where ![]() $N^jH^i(X,A(n)):=\ker (H^i(X,A(n))\to H^i(F_{j-1}X,A(n)))$. If
$N^jH^i(X,A(n)):=\ker (H^i(X,A(n))\to H^i(F_{j-1}X,A(n)))$. If ![]() $X$ is smooth projective, we claim that this map agrees with Griffiths transcendental Abel–Jacobi map restricted to torsion cycles. By the Chinese remainder theorem, it suffices to show this for classes that are
$X$ is smooth projective, we claim that this map agrees with Griffiths transcendental Abel–Jacobi map restricted to torsion cycles. By the Chinese remainder theorem, it suffices to show this for classes that are ![]() $\ell$-power torsion for some prime
$\ell$-power torsion for some prime ![]() $\ell$. In this case our map identifies by Proposition 8.5 with Bloch's map, which, in turn, identifies with Griffiths map by [Reference BlochBlo79, Proposition 3.7].
$\ell$. In this case our map identifies by Proposition 8.5 with Bloch's map, which, in turn, identifies with Griffiths map by [Reference BlochBlo79, Proposition 3.7].
Theorem 1.6 follows now as previously from Theorem 7.7, Proposition 7.11, Theorem 7.19, and Proposition 7.16 (after performing the formal replacements ![]() $\mathbb {Z}_\ell \rightsquigarrow \mathbb {Z}$,
$\mathbb {Z}_\ell \rightsquigarrow \mathbb {Z}$, ![]() $\mathbb {Q}_\ell \rightsquigarrow \mathbb {Q}$,
$\mathbb {Q}_\ell \rightsquigarrow \mathbb {Q}$, ![]() $\ell ^r \rightsquigarrow r$, and
$\ell ^r \rightsquigarrow r$, and ![]() $[\ell ^\infty ] \rightsquigarrow { }_{\operatorname {tors}}$). This concludes the proof of Theorem 1.6.
$[\ell ^\infty ] \rightsquigarrow { }_{\operatorname {tors}}$). This concludes the proof of Theorem 1.6.
10.3 Proof of Theorems 1.1 and 1.4, and Corollaries 1.2 and 1.3
Lemma 10.1 In the notation of § 10.1, for any ![]() $X\in \mathcal {V}$ and any
$X\in \mathcal {V}$ and any ![]() $i$ and
$i$ and ![]() $n$,
$n$, ![]() $H^i(F_0X,\mathbb {Z}(n))$ is torsion-free.
$H^i(F_0X,\mathbb {Z}(n))$ is torsion-free.
Proof. By additivity of the cohomology functor (see Lemma 5.6), we may assume that ![]() $X$ is irreducible with generic point
$X$ is irreducible with generic point ![]() $\eta _X\in X$. By definition,
$\eta _X\in X$. By definition, ![]() $H^i(F_0X,\mathbb {Z}(n))\simeq H^i(F_0X,\mathbb {Z}(i-1))$ for all
$H^i(F_0X,\mathbb {Z}(n))\simeq H^i(F_0X,\mathbb {Z}(i-1))$ for all ![]() $i$ and
$i$ and ![]() $n$. As
$n$. As ![]() $X$ is irreducible, the latter coincides with
$X$ is irreducible, the latter coincides with ![]() $H^i(\eta _X,\mathbb {Z}(i-1))$ and so the claim follows from Remark 5.14 and Voevodsky's proof of the Bloch–Kato conjecture [Reference VoevodskyVoe11].
$H^i(\eta _X,\mathbb {Z}(i-1))$ and so the claim follows from Remark 5.14 and Voevodsky's proof of the Bloch–Kato conjecture [Reference VoevodskyVoe11].
Proof of Theorem 1.4 Theorem 1.4 follows with help of Lemma 10.1 via the same arguments as in the proof of Theorem 1.5. This requires as in Theorem 1.6 the formal replacements ![]() $\mathbb {Z}_\ell \rightsquigarrow \mathbb {Z}$,
$\mathbb {Z}_\ell \rightsquigarrow \mathbb {Z}$, ![]() $\mathbb {Q}_\ell \rightsquigarrow \mathbb {Q}$,
$\mathbb {Q}_\ell \rightsquigarrow \mathbb {Q}$, ![]() $\ell ^r \rightsquigarrow r$, and
$\ell ^r \rightsquigarrow r$, and ![]() $[\ell ^\infty ] \rightsquigarrow { }_{\operatorname {tors}}$ in § 7.
$[\ell ^\infty ] \rightsquigarrow { }_{\operatorname {tors}}$ in § 7.
Proof of Theorem 1.1 This is a consequence of Theorem 1.4 together with the fact that ![]() $\lambda _{{\rm tr}}^i$ factorizes for smooth projective varieties through Bloch's Abel–Jacobi map for torsion cycles, which, in turn, agrees with the Abel–Jacobi invariants due to Griffiths in that case, see Proposition 8.5. The assumption
$\lambda _{{\rm tr}}^i$ factorizes for smooth projective varieties through Bloch's Abel–Jacobi map for torsion cycles, which, in turn, agrees with the Abel–Jacobi invariants due to Griffiths in that case, see Proposition 8.5. The assumption ![]() $i\geqslant 2$ is needed, because the assertion in Theorem 1.4 is empty for
$i\geqslant 2$ is needed, because the assertion in Theorem 1.4 is empty for ![]() $i=1$.
$i=1$.
Proof of Corollary 1.2 By Theorem 1.1, the ![]() $n$-torsion of
$n$-torsion of ![]() $N^0\operatorname {CH}^i(X\!)_{\operatorname {tors}}/N^1\operatorname {CH}^i(X\!)_{\operatorname {tors}}$ injects into the
$N^0\operatorname {CH}^i(X\!)_{\operatorname {tors}}/N^1\operatorname {CH}^i(X\!)_{\operatorname {tors}}$ injects into the ![]() $n$-torsion of a quotient of
$n$-torsion of a quotient of ![]() $H^{2i-1}(X,\mathbb {Q}/\mathbb {Z})$, hence is finite. Moreover, the cycle class map yields an injection of
$H^{2i-1}(X,\mathbb {Q}/\mathbb {Z})$, hence is finite. Moreover, the cycle class map yields an injection of ![]() $\operatorname {CH}^i(X\!)/N^0\operatorname {CH}^i(X\!)$ into
$\operatorname {CH}^i(X\!)/N^0\operatorname {CH}^i(X\!)$ into ![]() $H^{2i}(X,\mathbb {Z})$ and so the
$H^{2i}(X,\mathbb {Z})$ and so the ![]() $n$-torsion subgroup of
$n$-torsion subgroup of ![]() $\operatorname {CH}^i(X\!)_{\operatorname {tors}}/N^0\operatorname {CH}^i(X\!)_{\operatorname {tors}}$ must be finite as well. Altogether we conclude that the
$\operatorname {CH}^i(X\!)_{\operatorname {tors}}/N^0\operatorname {CH}^i(X\!)_{\operatorname {tors}}$ must be finite as well. Altogether we conclude that the ![]() $n$-torsion subgroup of
$n$-torsion subgroup of ![]() $\operatorname {CH}^i(X\!)_{\operatorname {tors}}/N^1\operatorname {CH}^i(X\!)_{\operatorname {tors}}$ is finite, as claimed.
$\operatorname {CH}^i(X\!)_{\operatorname {tors}}/N^1\operatorname {CH}^i(X\!)_{\operatorname {tors}}$ is finite, as claimed.
Proof of Corollary 1.3 This is an immediate consequence of Theorem 1.1.
10.4 Applications of Theorem 1.4
For a complex algebraic scheme ![]() $X$, we recall that the coniveau filtration
$X$, we recall that the coniveau filtration ![]() $N^j$ on
$N^j$ on ![]() $\operatorname {Griff}^i(X\!)$ is defined by saying that a cycle
$\operatorname {Griff}^i(X\!)$ is defined by saying that a cycle ![]() $z\in \operatorname {Griff}^i(X\!)$ lies in
$z\in \operatorname {Griff}^i(X\!)$ lies in ![]() $N^j$ if and only if there is a closed subset
$N^j$ if and only if there is a closed subset ![]() $Z\subset X$ with
$Z\subset X$ with ![]() $j=\dim X-\dim Z$ and a homologically trivial cycle
$j=\dim X-\dim Z$ and a homologically trivial cycle ![]() $z'$ on
$z'$ on ![]() $Z$ such that
$Z$ such that ![]() $z$ agrees with the pushforward of
$z$ agrees with the pushforward of ![]() $z'$, cf. Definition 7.3. This yields a finite decreasing filtration on
$z'$, cf. Definition 7.3. This yields a finite decreasing filtration on ![]() $\operatorname {Griff}^i(X\!)$ with
$\operatorname {Griff}^i(X\!)$ with ![]() $N^{i-1}=0$, cf. Lemmas 7.4 and 7.5.
$N^{i-1}=0$, cf. Lemmas 7.4 and 7.5.
Corollary 10.2 Let ![]() $X$ be a separated scheme of finite type over
$X$ be a separated scheme of finite type over ![]() $\mathbb {C}$. Then
$\mathbb {C}$. Then
Proof. We use the notation from § 10.1. Proposition 7.16 implies that for any separated scheme ![]() $X$ of finite type over
$X$ of finite type over ![]() $\mathbb {C}$, we have
$\mathbb {C}$, we have
where ![]() $H^{2i-1}(X,\mathbb {Q} /\mathbb {Z} (i))_{\rm div}=\operatorname {im}( H^{2i-1}(X,\mathbb {Q} (i))\to H^{2i-1}(X,\mathbb {Q} /\mathbb {Z} (i)))$. As affine varieties have no cohomology in degrees greater than their dimension, and because
$H^{2i-1}(X,\mathbb {Q} /\mathbb {Z} (i))_{\rm div}=\operatorname {im}( H^{2i-1}(X,\mathbb {Q} (i))\to H^{2i-1}(X,\mathbb {Q} /\mathbb {Z} (i)))$. As affine varieties have no cohomology in degrees greater than their dimension, and because ![]() $H^i(X,A(n))$ depends only on the underlying reduced scheme and agrees with singular cohomology if
$H^i(X,A(n))$ depends only on the underlying reduced scheme and agrees with singular cohomology if ![]() $X$ is smooth, we find that
$X$ is smooth, we find that ![]() $N^{1}H^{2i-1}(X,\mathbb {Q} (i) )= H^{2i-1}(X,\mathbb {Q} (i) )$ for
$N^{1}H^{2i-1}(X,\mathbb {Q} (i) )= H^{2i-1}(X,\mathbb {Q} (i) )$ for ![]() $2i-1>\dim X$ and so
$2i-1>\dim X$ and so ![]() $\operatorname {im}(\bar {\lambda }_{{\rm tr}}^i)=0$ for
$\operatorname {im}(\bar {\lambda }_{{\rm tr}}^i)=0$ for ![]() $2i-1>\dim X$. It follows that
$2i-1>\dim X$. It follows that ![]() $\operatorname {im}(\bar {\lambda }_{j,{\rm tr}}^i)=0$ for
$\operatorname {im}(\bar {\lambda }_{j,{\rm tr}}^i)=0$ for ![]() $2i-2j-1>\dim X-j$, i.e. for
$2i-2j-1>\dim X-j$, i.e. for ![]() $j<2i-1-\dim X$. Theorem 1.4 thus implies that
$j<2i-1-\dim X$. Theorem 1.4 thus implies that ![]() $N^{j+1}\operatorname {Griff}^i(X\!)_{\operatorname {tors}}=N^j\operatorname {Griff}^i(X\!)_{\operatorname {tors}}$ for
$N^{j+1}\operatorname {Griff}^i(X\!)_{\operatorname {tors}}=N^j\operatorname {Griff}^i(X\!)_{\operatorname {tors}}$ for ![]() $j<2i-1-\dim X$, which proves Corollary 10.2.
$j<2i-1-\dim X$, which proves Corollary 10.2.
10.5 Algebraic cycles and traditional unramified cohomology in arbitrary degree
For ![]() $j\geqslant m$, there is a canonical restriction map
$j\geqslant m$, there is a canonical restriction map
Recall from § 5 that we denote its image by ![]() $F^{j+1}H^i_{m,{\rm nr}}(X,A(n))$. We describe the effect of applying the restriction map (10.2) to Theorem 1.6 next.
$F^{j+1}H^i_{m,{\rm nr}}(X,A(n))$. We describe the effect of applying the restriction map (10.2) to Theorem 1.6 next.
Corollary 10.3 Let ![]() $X$ be a separated scheme of finite type over
$X$ be a separated scheme of finite type over ![]() $\mathbb {C}$. Then for any
$\mathbb {C}$. Then for any ![]() $0\leqslant j\leqslant i-2$, there are canonical exact sequences
$0\leqslant j\leqslant i-2$, there are canonical exact sequences
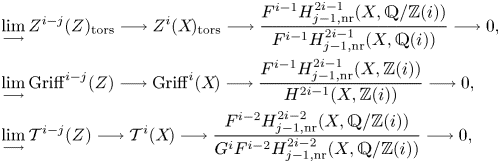 \begin{align*} &\lim_{\longrightarrow} Z^{i-j}(Z)_{\operatorname{tors}}\longrightarrow Z^{i}(X\!)_{\operatorname{tors}}\longrightarrow \frac{F^{i-1}H^{2i-1}_{j-1,{\rm nr}}(X,\mathbb{Q}/\mathbb{Z}(i) )}{F^{i-1}H^{2i-1}_{j-1,{\rm nr}}(X,\mathbb{Q}(i))}\longrightarrow 0 ,\\ &\lim_{\longrightarrow} \operatorname{Griff}^{i-j}(Z)\longrightarrow \operatorname{Griff}^i(X\!) \longrightarrow \frac{F^{i-1}H^{2i-1}_{j-1,{\rm nr}}(X,\mathbb{Z}(i))}{H^{2i-1}(X,\mathbb{Z}(i)) }\longrightarrow 0 ,\\ &\lim_{\longrightarrow} \mathcal{T}^{i-j}(Z)\longrightarrow \mathcal{T}^{i}(X\!) \longrightarrow \frac{F^{i-2}H^{2i-2}_{j-1,{\rm nr}}(X,\mathbb{Q} /\mathbb{Z}(i)) }{ G^{i} F^{i-2} H^{2i-2}_{j-1,{\rm nr}}(X,\mathbb{Q}/ \mathbb{Z} (i))}\longrightarrow 0, \end{align*}
\begin{align*} &\lim_{\longrightarrow} Z^{i-j}(Z)_{\operatorname{tors}}\longrightarrow Z^{i}(X\!)_{\operatorname{tors}}\longrightarrow \frac{F^{i-1}H^{2i-1}_{j-1,{\rm nr}}(X,\mathbb{Q}/\mathbb{Z}(i) )}{F^{i-1}H^{2i-1}_{j-1,{\rm nr}}(X,\mathbb{Q}(i))}\longrightarrow 0 ,\\ &\lim_{\longrightarrow} \operatorname{Griff}^{i-j}(Z)\longrightarrow \operatorname{Griff}^i(X\!) \longrightarrow \frac{F^{i-1}H^{2i-1}_{j-1,{\rm nr}}(X,\mathbb{Z}(i))}{H^{2i-1}(X,\mathbb{Z}(i)) }\longrightarrow 0 ,\\ &\lim_{\longrightarrow} \mathcal{T}^{i-j}(Z)\longrightarrow \mathcal{T}^{i}(X\!) \longrightarrow \frac{F^{i-2}H^{2i-2}_{j-1,{\rm nr}}(X,\mathbb{Q} /\mathbb{Z}(i)) }{ G^{i} F^{i-2} H^{2i-2}_{j-1,{\rm nr}}(X,\mathbb{Q}/ \mathbb{Z} (i))}\longrightarrow 0, \end{align*}
where in the direct limits, ![]() $Z\subset X$ runs through all reduced closed subschemes of
$Z\subset X$ runs through all reduced closed subschemes of ![]() $X$ with
$X$ with ![]() $\dim (X\!)-\dim (Z)=j$.
$\dim (X\!)-\dim (Z)=j$.
This corollary is particularly interesting for ![]() $j=1$. In this case, the refined unramified cohomology groups above agree with traditional unramified cohomology
$j=1$. In this case, the refined unramified cohomology groups above agree with traditional unramified cohomology ![]() $H^i_{nr}(X,A(n))=H^i_{0,{\rm nr}}(X,A(n))$. The corollary then identifies certain graded pieces of traditional unramified cohomology with certain birationally invariant quotients of the above cycle groups. In particular, non-trivial elements in certain pieces of the
$H^i_{nr}(X,A(n))=H^i_{0,{\rm nr}}(X,A(n))$. The corollary then identifies certain graded pieces of traditional unramified cohomology with certain birationally invariant quotients of the above cycle groups. In particular, non-trivial elements in certain pieces of the ![]() $F^\ast$ filtration on traditional unramified cohomology
$F^\ast$ filtration on traditional unramified cohomology ![]() $H^i_{nr}(X,A(n))=H^i_{0,{\rm nr}}(X,A(n))$ detect exactly those cycles on
$H^i_{nr}(X,A(n))=H^i_{0,{\rm nr}}(X,A(n))$ detect exactly those cycles on ![]() $X$ that are not supported in codimension one in the sense that they are not pushforwards of the respective cycle groups on some divisor on
$X$ that are not supported in codimension one in the sense that they are not pushforwards of the respective cycle groups on some divisor on ![]() $X$. This improves some results obtained independently by Ma in [Reference MaMa22].
$X$. This improves some results obtained independently by Ma in [Reference MaMa22].
Proof of Corollary 10.3 The corollary follows from Theorem 1.6 and Corollary 5.9. We give some details for ![]() $\operatorname {Griff}^i(X\!)$; the other cases are similar.
$\operatorname {Griff}^i(X\!)$; the other cases are similar.
We use the same notation as in the proof of Theorem 1.6 and fix the integral twisted Borel–Moore cohomology theory ![]() $H^\ast (-,A(n))$ on separated schemes of finite type over
$H^\ast (-,A(n))$ on separated schemes of finite type over ![]() $\mathbb {C}$ from Proposition 6.9. By Theorem 1.6, there is a canonical isomorphism
$\mathbb {C}$ from Proposition 6.9. By Theorem 1.6, there is a canonical isomorphism
By Corollary 5.9, for any ![]() $0\leqslant j\leqslant i-1$, there is a canonical exact sequence
$0\leqslant j\leqslant i-1$, there is a canonical exact sequence
where the direct limit runs through all closed reduced subschemes ![]() $Z\subset X$ of dimension
$Z\subset X$ of dimension ![]() $\dim Z=\dim X-j$. Here the first map is induced by the pushforward map with respect to
$\dim Z=\dim X-j$. Here the first map is induced by the pushforward map with respect to ![]() $Z\hookrightarrow X$ and the second map is the canonical restriction map. The latter is surjective by definition of the filtration
$Z\hookrightarrow X$ and the second map is the canonical restriction map. The latter is surjective by definition of the filtration ![]() $F^\ast$ (see Definition 5.3).
$F^\ast$ (see Definition 5.3).
The above sequence induces a sequence
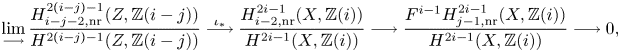 \[ \lim_{\longrightarrow}\frac{H^{2(i-j)-1}_{i-j-2,{\rm nr}}(Z,\mathbb{Z}(i-j))}{H^{2(i-j)-1} (Z,\mathbb{Z}(i-j))} \stackrel{{\iota_\ast}}{\longrightarrow} \frac{H^{2i-1}_{i-2,{\rm nr}}(X,\mathbb{Z}(i))}{ H^{2i-1}(X,\mathbb{Z}(i))}\longrightarrow \frac{F^{i-1} H^{2i-1}_{j-1,{\rm nr}}(X,\mathbb{Z}(i))}{ H^{2i-1} (X,\mathbb{Z}(i))} \longrightarrow 0, \]
\[ \lim_{\longrightarrow}\frac{H^{2(i-j)-1}_{i-j-2,{\rm nr}}(Z,\mathbb{Z}(i-j))}{H^{2(i-j)-1} (Z,\mathbb{Z}(i-j))} \stackrel{{\iota_\ast}}{\longrightarrow} \frac{H^{2i-1}_{i-2,{\rm nr}}(X,\mathbb{Z}(i))}{ H^{2i-1}(X,\mathbb{Z}(i))}\longrightarrow \frac{F^{i-1} H^{2i-1}_{j-1,{\rm nr}}(X,\mathbb{Z}(i))}{ H^{2i-1} (X,\mathbb{Z}(i))} \longrightarrow 0, \]
and one can check directly that this sequence remains exact. By Theorem 1.6, this sequence identifies to an exact sequence
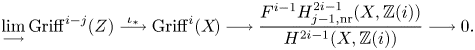 \[ \lim_{\longrightarrow}\operatorname{Griff}^{i-j}(Z)\stackrel{{\iota_\ast}}{\longrightarrow}\operatorname{Griff}^i(X\!) \longrightarrow \frac{F^{i-1} H^{2i-1}_{j-1,{\rm nr}}(X,\mathbb{Z}(i))}{ H^{2i-1} (X,\mathbb{Z}(i))} \longrightarrow 0. \]
\[ \lim_{\longrightarrow}\operatorname{Griff}^{i-j}(Z)\stackrel{{\iota_\ast}}{\longrightarrow}\operatorname{Griff}^i(X\!) \longrightarrow \frac{F^{i-1} H^{2i-1}_{j-1,{\rm nr}}(X,\mathbb{Z}(i))}{ H^{2i-1} (X,\mathbb{Z}(i))} \longrightarrow 0. \]
It follows from the functoriality of the Gysin sequence with respect to proper pushforwards (see (P2)) that the first map above agrees with the pushforward of cycles induced by ![]() $Z\hookrightarrow X$. This concludes the proof of the corollary.
$Z\hookrightarrow X$. This concludes the proof of the corollary.
10.6 Applications of Theorem 1.6
If ![]() $X$ is an integral scheme over
$X$ is an integral scheme over ![]() $\mathbb {C}$, we write in this section
$\mathbb {C}$, we write in this section
which is consistent with some of the notation used in the literature (see, e.g., [Reference Colliot-Thélène and VoisinCV12, Reference VoisinVoi12]). The above group is the cohomology of the generic point of ![]() $X$ as defined in (4.2). If
$X$ as defined in (4.2). If ![]() $A=\mathbb {Z}/\ell ^r$ or
$A=\mathbb {Z}/\ell ^r$ or ![]() $A=\mathbb {Q}/\mathbb {Z}$, this group coincides by [Reference MilneMil80, p. 88, III.1.16] with the corresponding Galois cohomology group of the field
$A=\mathbb {Q}/\mathbb {Z}$, this group coincides by [Reference MilneMil80, p. 88, III.1.16] with the corresponding Galois cohomology group of the field ![]() $\mathbb {C}(X\!)$.
$\mathbb {C}(X\!)$.
We need the following result that is proven with methods from [Reference SchreiederSch19].
Proposition 10.5 For any positive integer ![]() $n$, there is a smooth projective unirational variety
$n$, there is a smooth projective unirational variety ![]() $Y$ of dimension
$Y$ of dimension ![]() $3n$ over
$3n$ over ![]() $\mathbb {C}$ such that the composition
$\mathbb {C}$ such that the composition
is non-zero for all ![]() $i=1,\dots,n$.
$i=1,\dots,n$.
Proof. By the proof of [Reference SchreiederSch19, Theorem 1.5], there is a unirational smooth complex projective threefold ![]() $T$ together with a morphism
$T$ together with a morphism ![]() $f:T\to \mathbb {P}^2$ whose generic fiber is a conic, such that the following hold:
$f:T\to \mathbb {P}^2$ whose generic fiber is a conic, such that the following hold:
– the class
 $\alpha =(x_1/x_0,x_2/x_0)\in H^2(\mathbb {C}(\mathbb {P}^2),\mathbb {Z}/2)$ has the property that
$\alpha =(x_1/x_0,x_2/x_0)\in H^2(\mathbb {C}(\mathbb {P}^2),\mathbb {Z}/2)$ has the property that  $f^\ast \alpha \in H^2_{nr}(T,\mathbb {Z}/2)$ is unramified and non-trivial;
$f^\ast \alpha \in H^2_{nr}(T,\mathbb {Z}/2)$ is unramified and non-trivial;– there is a specialization
 $T_0$ of
$T_0$ of  $T$ such that the specialization
$T$ such that the specialization  $f_0:T_0\to \mathbb {P}^2$ of
$f_0:T_0\to \mathbb {P}^2$ of  $f$ has the property that its generic fiber has a
$f$ has the property that its generic fiber has a  $\mathbb {C}(\mathbb {P}^2)$-rational point in its smooth locus.
$\mathbb {C}(\mathbb {P}^2)$-rational point in its smooth locus.
Let us now consider ![]() $Y:=T^n$, which is a smooth complex projective variety of dimension
$Y:=T^n$, which is a smooth complex projective variety of dimension ![]() $3n$ that is unirational. Let
$3n$ that is unirational. Let ![]() $\operatorname {pr}_j:Y\to T$ denote the projection onto the
$\operatorname {pr}_j:Y\to T$ denote the projection onto the ![]() $j$th factor and consider the class
$j$th factor and consider the class
As ![]() $\alpha$ is of degree two, the unramified class
$\alpha$ is of degree two, the unramified class ![]() $f^\ast \alpha$ admits a lift to a class in
$f^\ast \alpha$ admits a lift to a class in ![]() $H^2(T,\mathbb {Z}/2)$, see Corollary 5.10. Hence,
$H^2(T,\mathbb {Z}/2)$, see Corollary 5.10. Hence, ![]() $\gamma _i$ admits a lift to a class in
$\gamma _i$ admits a lift to a class in ![]() $H^{2i}(Y,\mathbb {Z}/2)$ and so
$H^{2i}(Y,\mathbb {Z}/2)$ and so
It remains to show that the image ![]() $\gamma '_i$ of
$\gamma '_i$ of ![]() $\gamma _i$ in
$\gamma _i$ in ![]() $H^{2i}(\mathbb {C}(Y),\mathbb {Q}/\mathbb {Z})$ is non-zero for all
$H^{2i}(\mathbb {C}(Y),\mathbb {Q}/\mathbb {Z})$ is non-zero for all ![]() $i=1,\dots,n$. By construction of the class
$i=1,\dots,n$. By construction of the class ![]() $\gamma _i$, it suffices to prove that
$\gamma _i$, it suffices to prove that ![]() $\gamma '_n$ is non-zero and our argument is similar to the proofs of [Reference SchreiederSch19, Proposition 6.1] and [Reference SchreiederSch21, Theorem 5.3(3)].
$\gamma '_n$ is non-zero and our argument is similar to the proofs of [Reference SchreiederSch19, Proposition 6.1] and [Reference SchreiederSch21, Theorem 5.3(3)].
Assume for a contradiction that ![]() $\gamma ':=\gamma '_n$ is zero in
$\gamma ':=\gamma '_n$ is zero in ![]() $H^{2n}(\mathbb {C}(Y),\mathbb {Q}/\mathbb {Z})$. Then let us specialize
$H^{2n}(\mathbb {C}(Y),\mathbb {Q}/\mathbb {Z})$. Then let us specialize ![]() $T$ to
$T$ to ![]() $T_0$. Then
$T_0$. Then ![]() $Y$ specializes to a projective variety
$Y$ specializes to a projective variety ![]() $Y_0$ together with a morphism
$Y_0$ together with a morphism ![]() $Y_0\to (\mathbb {P}^2)^n$ whose generic fiber admits a rational point in its smooth locus. The specialization
$Y_0\to (\mathbb {P}^2)^n$ whose generic fiber admits a rational point in its smooth locus. The specialization ![]() $\gamma '_0$ of
$\gamma '_0$ of ![]() $\gamma '$ vanishes, because
$\gamma '$ vanishes, because ![]() $\gamma '$ vanishes by assumption. It follows that the restriction of
$\gamma '$ vanishes by assumption. It follows that the restriction of ![]() $\gamma _0'$ to the rational point in the smooth locus of the generic fiber of
$\gamma _0'$ to the rational point in the smooth locus of the generic fiber of ![]() $Y_0\to (\mathbb {P}^2)^n$ is zero. This restriction, in turn, is computed explicitly as the image of
$Y_0\to (\mathbb {P}^2)^n$ is zero. This restriction, in turn, is computed explicitly as the image of
in ![]() $H^{2n}(\mathbb {C}((\mathbb {P}^2)^n),\mathbb {Q}/\mathbb {Z})$. However, this class is non-zero, as one can check by computing successive residues. This is a contradiction, which concludes the proof.
$H^{2n}(\mathbb {C}((\mathbb {P}^2)^n),\mathbb {Q}/\mathbb {Z})$. However, this class is non-zero, as one can check by computing successive residues. This is a contradiction, which concludes the proof.
10.6.1 Integral Hodge conjecture for uniruled varieties
Recall that for any algebraic scheme ![]() $X$ of dimension
$X$ of dimension ![]() $d$ over
$d$ over ![]() $\mathbb {C}$, there is a cycle class map
$\mathbb {C}$, there is a cycle class map ![]() $\operatorname {cl}^i_X:\operatorname {CH}^i(X\!)\to H^{2i}(X,\mathbb {Z})$, where
$\operatorname {cl}^i_X:\operatorname {CH}^i(X\!)\to H^{2i}(X,\mathbb {Z})$, where ![]() $H^i(X,A):=H_{2d-i}^{\rm BM}(X_{\operatorname {an}},A)$. We denote its cokernel by
$H^i(X,A):=H_{2d-i}^{\rm BM}(X_{\operatorname {an}},A)$. We denote its cokernel by ![]() $Z^i(X\!):=\operatorname {coker}(\operatorname {cl}_X^i\!)$.
$Z^i(X\!):=\operatorname {coker}(\operatorname {cl}_X^i\!)$.
Theorem 10.6 For any ![]() $n\geqslant 1$, there is a smooth complex projective unirational variety
$n\geqslant 1$, there is a smooth complex projective unirational variety ![]() $Y$ of dimension
$Y$ of dimension ![]() $3n$ and an elliptic curve
$3n$ and an elliptic curve ![]() $E$ such that
$E$ such that ![]() $X:=E\times Y$ satisfies
$X:=E\times Y$ satisfies
where ![]() $D$ runs through all closed reduced subvarieties
$D$ runs through all closed reduced subvarieties ![]() $D\subset X$ of codimension one.
$D\subset X$ of codimension one.
Note that for any closed subscheme ![]() $Z\subsetneq X$ of codimension
$Z\subsetneq X$ of codimension ![]() $c\geqslant 1$, the pushforward
$c\geqslant 1$, the pushforward ![]() $Z^{i-c}(Z)\to Z^i(X\!)$ factors through
$Z^{i-c}(Z)\to Z^i(X\!)$ factors through ![]() $Z^{i-1}(D)$ for any divisor
$Z^{i-1}(D)$ for any divisor ![]() $D\subset X$ that contains
$D\subset X$ that contains ![]() $Z$, and so the non-trivial class in the cokernel of the above corollary is not hit by
$Z$, and so the non-trivial class in the cokernel of the above corollary is not hit by ![]() $Z^{i-c}(Z)_{\operatorname {tors}}$ and, hence, in particular not by the torsion in
$Z^{i-c}(Z)_{\operatorname {tors}}$ and, hence, in particular not by the torsion in ![]() $H^{2i-2c}(Z,\mathbb {Z})=H^{\rm BM}_{2d_X-2i}(Z,\mathbb {Z})$, where
$H^{2i-2c}(Z,\mathbb {Z})=H^{\rm BM}_{2d_X-2i}(Z,\mathbb {Z})$, where ![]() $d_X=\dim X$. In particular, the above theorem implies Corollary 1.7 stated in the introduction.
$d_X=\dim X$. In particular, the above theorem implies Corollary 1.7 stated in the introduction.
Proof of Theorem 10.6 By Proposition 10.5, there is a unirational smooth complex projective variety ![]() $Y$ of dimension
$Y$ of dimension ![]() $3n$ such that
$3n$ such that ![]() $H^{2i}(Y,\mathbb {Q}/\mathbb {Z})\longrightarrow H^{2i}(\mathbb {C}(Y),\mathbb {Q}/\mathbb {Z})$ is non-zero for all
$H^{2i}(Y,\mathbb {Q}/\mathbb {Z})\longrightarrow H^{2i}(\mathbb {C}(Y),\mathbb {Q}/\mathbb {Z})$ is non-zero for all ![]() $i=1,\dots,n$. It thus follows from a theorem of Colliot-Thélène [Reference Colliot-ThélèneCol19, Theorem 1.1] that there is an elliptic curve
$i=1,\dots,n$. It thus follows from a theorem of Colliot-Thélène [Reference Colliot-ThélèneCol19, Theorem 1.1] that there is an elliptic curve ![]() $E$ such that the product
$E$ such that the product ![]() $X=Y\times E$ has the property that
$X=Y\times E$ has the property that
is non-zero for all ![]() $i=1,\dots,n$. As the Chow group of zero cycles of
$i=1,\dots,n$. As the Chow group of zero cycles of ![]() $X$ is supported on a curve (i.e.
$X$ is supported on a curve (i.e. ![]() $\operatorname {CH}_0(\{pt.\}\times E)\to \operatorname {CH}_0(Y\times E)$ is surjective), the rational unramified cohomology groups of
$\operatorname {CH}_0(\{pt.\}\times E)\to \operatorname {CH}_0(Y\times E)$ is surjective), the rational unramified cohomology groups of ![]() $X$ above degree one vanish by a simple Bloch–Srinivas decomposition of the diagonal argument, see, e.g., [Reference Colliot-Thélène and VoisinCV12, Proposition 3.3.(i)].Footnote 1 The result thus follows from Corollary 10.3.
$X$ above degree one vanish by a simple Bloch–Srinivas decomposition of the diagonal argument, see, e.g., [Reference Colliot-Thélène and VoisinCV12, Proposition 3.3.(i)].Footnote 1 The result thus follows from Corollary 10.3.
10.6.2 Applications to the Artin–Mumford invariant
In [Reference Artin and MumfordAM72], Artin and Mumford showed that for any smooth complex projective variety ![]() $X$, the torsion subgroup of
$X$, the torsion subgroup of ![]() $H^3(X,\mathbb {Z})$ is a birational invariant and used this to construct unirational threefolds that are not rational. For
$H^3(X,\mathbb {Z})$ is a birational invariant and used this to construct unirational threefolds that are not rational. For ![]() $i>3$, the torsion subgroup of
$i>3$, the torsion subgroup of ![]() $H^{i}(X,\mathbb {Z})$ is not a birational invariant. However, Voisin observed (see [Reference VoisinVoi12, Remark 2.4]) that the Bloch–Kato conjecture proven by Voevodsky implies that the torsion subgroup of
$H^{i}(X,\mathbb {Z})$ is not a birational invariant. However, Voisin observed (see [Reference VoisinVoi12, Remark 2.4]) that the Bloch–Kato conjecture proven by Voevodsky implies that the torsion subgroup of ![]() $H^{5}(X,\mathbb {Z})/ N^2H^{5}(X,\mathbb {Z})$ is a birational invariant. By Proposition 7.32, there is a canonical surjection
$H^{5}(X,\mathbb {Z})/ N^2H^{5}(X,\mathbb {Z})$ is a birational invariant. By Proposition 7.32, there is a canonical surjection
(It follows from the Bloch–Kato conjecture, proven by Voevodsky, that this surjection is, in fact, an isomorphism, see Remark 7.33, but we do not use this.)
As an application, we prove that Voisin's generalization of the Artin–Mumford invariant is non-trivial in any odd degree.
Corollary 10.7 For any positive integer ![]() $i$, there is a unirational smooth complex projective variety
$i$, there is a unirational smooth complex projective variety ![]() $X$ with a torsion class in
$X$ with a torsion class in ![]() $H^{2i+1}(X,\mathbb {Z})$ that is non-zero in the quotient
$H^{2i+1}(X,\mathbb {Z})$ that is non-zero in the quotient
Proof. Rationally connected varieties have no rational unramified cohomology in positive degrees, see, e.g., [Reference Colliot-Thélène and VoisinCV12, Proposition 3.3(i)]. The claim in Corollary 10.7 follows therefore directly from Propositions 6.9, 7.32, and 10.5.
Acknowledgements
I am grateful for conversations with and comments from Giuseppe Ancona, Theodosis Alexandrou, Samet Balkan, Jean-Louis Colliot-Thélène, Matthias Paulsen, Anand Sawant, Domenico Valloni, Claire Voisin, and Lin Zhou. Thanks also go to Hélène Esnault and the referees for helpful comments on the presentation and to Bhargav Bhatt for checking (a previous version of) § 6.1.3. This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme under grant agreement No 948066 (ERC-StG RationAlgic).
Conflicts of Interest
None.