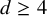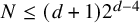1 Introduction
A variety X over a field k is retract rational if there is some integer
![]() $N\geq \dim X$
and rational maps
$N\geq \dim X$
and rational maps
![]() $f\colon X\dashrightarrow {\mathbb {P}}^N$
and
$f\colon X\dashrightarrow {\mathbb {P}}^N$
and
![]() $g\colon {\mathbb {P}}^N\dashrightarrow X$
such that the composition
$g\colon {\mathbb {P}}^N\dashrightarrow X$
such that the composition
![]() $g\circ f$
is defined and agrees with
$g\circ f$
is defined and agrees with
![]() $ \operatorname {id}_X$
. This notion is a direct analogue of retracts in topology; it was introduced into birational geometry by Saltman [Reference Saltman and Seligman41, Reference Saltman42] in the 1980s. Equivalently, X is retract rational if there is an integer
$ \operatorname {id}_X$
. This notion is a direct analogue of retracts in topology; it was introduced into birational geometry by Saltman [Reference Saltman and Seligman41, Reference Saltman42] in the 1980s. Equivalently, X is retract rational if there is an integer
![]() $N\geq \dim X$
, open dense subsets
$N\geq \dim X$
, open dense subsets
![]() $U\subset X$
and
$U\subset X$
and
![]() $V\subset {\mathbb {P}}^N$
, and a morphism
$V\subset {\mathbb {P}}^N$
, and a morphism
![]() $V\to U$
which is surjective on L-rational points for all field extensions
$V\to U$
which is surjective on L-rational points for all field extensions
![]() $L/k$
– this closely relates the notion to the classical question of parametrizing solutions of polynomial equations by rational functions. Rational or stably rational varieties are retract rational.
$L/k$
– this closely relates the notion to the classical question of parametrizing solutions of polynomial equations by rational functions. Rational or stably rational varieties are retract rational.
By the work of Asok–Morel [Reference Asok and Morel3, Theorem 2.3.6] and Kahn–Sujatha [Reference Kahn and Sujatha25, Theorem 8.5.1 and Proposition 8.6.2], a smooth proper retract rational variety X is
![]() $\mathbb {A}^1$
-connected in the sense of
$\mathbb {A}^1$
-connected in the sense of
![]() $\mathbb {A}^1$
-homotopy theory, that is,
$\mathbb {A}^1$
-homotopy theory, that is,
![]() $\pi _0^{\mathbb {A}^1}(X) = \{\ast \}$
. By [Reference Asok and Morel3, Remark 2.4.8],
$\pi _0^{\mathbb {A}^1}(X) = \{\ast \}$
. By [Reference Asok and Morel3, Remark 2.4.8],
![]() $\mathbb {A}^1$
-connectedness is equivalent to separable R-triviality, which means that
$\mathbb {A}^1$
-connectedness is equivalent to separable R-triviality, which means that
![]() $X(L)/R=\{\ast \}$
for any separable field extension
$X(L)/R=\{\ast \}$
for any separable field extension
![]() $L/k$
, where R denotes the equivalence relation on
$L/k$
, where R denotes the equivalence relation on
![]() $X(L)$
generated by
$X(L)$
generated by
![]() $x\sim y$
whenever
$x\sim y$
whenever
![]() $x,y\in X(L)$
lie on the same rational curve (defined over L). In other words,
$x,y\in X(L)$
lie on the same rational curve (defined over L). In other words,
![]() $\mathbb {A}^1$
-connectedness provides an arithmetic analogue of rational chain connectedness, which requires that any two L-rational points can be connected by a chain of rational curves for any algebraically closed field extension L of k. The following table illustrates the known implications for smooth proper varieties:
$\mathbb {A}^1$
-connectedness provides an arithmetic analogue of rational chain connectedness, which requires that any two L-rational points can be connected by a chain of rational curves for any algebraically closed field extension L of k. The following table illustrates the known implications for smooth proper varieties:

The rationality problem for a given rationally connected variety X asks ‘how rational it is’, that is, which of the properties in the above diagram are satisfied.
Not every unirational variety is
![]() $\mathbb A^1$
-connected [Reference Artin and Mumford2] and not every stably rational variety is rational [Reference Beauville, Colliot-Thélène, Sansuc and Swinnerton-Dyer4]. Moreover, there are retract rational varieties (over nonclosed fields) that are not stably rational, see, for example, [Reference Endô and Miyata15, Theorem 1.5 and Theorem 2.3]; it is an open problem to produce such examples over algebraically closed fields. Whether any
$\mathbb A^1$
-connected [Reference Artin and Mumford2] and not every stably rational variety is rational [Reference Beauville, Colliot-Thélène, Sansuc and Swinnerton-Dyer4]. Moreover, there are retract rational varieties (over nonclosed fields) that are not stably rational, see, for example, [Reference Endô and Miyata15, Theorem 1.5 and Theorem 2.3]; it is an open problem to produce such examples over algebraically closed fields. Whether any
![]() $\mathbb A^1$
-connected variety is retract rational is open over any field.
$\mathbb A^1$
-connected variety is retract rational is open over any field.
A smooth proper
![]() $\mathbb A^1$
-connected variety with a k-rational point has universally trivial Chow group of zero-cycles and hence admits a decomposition of the diagonal [Reference Bloch and Srinivas8], which is an interesting motivic and cycle-theoretic property in itself.
$\mathbb A^1$
-connected variety with a k-rational point has universally trivial Chow group of zero-cycles and hence admits a decomposition of the diagonal [Reference Bloch and Srinivas8], which is an interesting motivic and cycle-theoretic property in itself.
1.1 Hypersurfaces
A particularly interesting class of varieties for the rationality problem are smooth projective hypersurfaces
![]() $X\subset {\mathbb {P}}^{N+1}_k$
of degree d and dimension N over a field k. The interesting range for the problem is when
$X\subset {\mathbb {P}}^{N+1}_k$
of degree d and dimension N over a field k. The interesting range for the problem is when
![]() $d \leq N + 1$
, in which case X is Fano and thus rationally chain connected by [Reference Campana9, Reference Kollár, Miyaoka and Mori28].
$d \leq N + 1$
, in which case X is Fano and thus rationally chain connected by [Reference Campana9, Reference Kollár, Miyaoka and Mori28].
If
![]() $2^{d!}\leq N+1$
and
$2^{d!}\leq N+1$
and
![]() $k={\mathbb {C}}$
, then X is unirational, see [Reference Beheshti and Riedl5, Reference Harris, Mazur and Pandharipande18]. If
$k={\mathbb {C}}$
, then X is unirational, see [Reference Beheshti and Riedl5, Reference Harris, Mazur and Pandharipande18]. If
![]() $d=N+1$
and
$d=N+1$
and
![]() $k={\mathbb {C}}$
, then X is irrational (in fact birationally rigid) by a theorem of de Fernex [Reference de Fernex12, Reference de Fernex13], which extends earlier results by Iskovskikh–Manin [Reference Iskovskikh and Manin23] and Pukhlikov [Reference Pukhlikov37, Reference Pukhlikov38]. If
$k={\mathbb {C}}$
, then X is irrational (in fact birationally rigid) by a theorem of de Fernex [Reference de Fernex12, Reference de Fernex13], which extends earlier results by Iskovskikh–Manin [Reference Iskovskikh and Manin23] and Pukhlikov [Reference Pukhlikov37, Reference Pukhlikov38]. If
![]() $k={\mathbb {C}}$
and
$k={\mathbb {C}}$
and
![]() $X\subset {\mathbb {P}}^{N+1}_{\mathbb {C}}$
is very general of degree
$X\subset {\mathbb {P}}^{N+1}_{\mathbb {C}}$
is very general of degree
![]() $d\geq 2\lceil \frac {N+3}{3} \rceil $
, then it is not ruled and hence not rational by a theorem of Kollár [Reference Kollár26]. Under the slightly weaker bound
$d\geq 2\lceil \frac {N+3}{3} \rceil $
, then it is not ruled and hence not rational by a theorem of Kollár [Reference Kollár26]. Under the slightly weaker bound
![]() $d\geq 2\lceil \frac {N+2}{3}\rceil $
, Totaro [Reference Totaro48] showed that such hypersurfaces do not admit a decomposition of the diagonal, hence are neither stably nor retract rational, nor
$d\geq 2\lceil \frac {N+2}{3}\rceil $
, Totaro [Reference Totaro48] showed that such hypersurfaces do not admit a decomposition of the diagonal, hence are neither stably nor retract rational, nor
![]() $\mathbb A^1$
-connected. This used [Reference Voisin49, Reference Colliot-Thélène and Pirutka11]. Totaro’s result was improved in [Reference Schreieder44], where the same result under the logarithmic bound
$\mathbb A^1$
-connected. This used [Reference Voisin49, Reference Colliot-Thélène and Pirutka11]. Totaro’s result was improved in [Reference Schreieder44], where the same result under the logarithmic bound
![]() $d\geq \log _2N+2$
,
$d\geq \log _2N+2$
,
![]() $N\geq 3$
and over fields of characteristic
$N\geq 3$
and over fields of characteristic
![]() $\neq 2$
was proven; a similar bound holds in characteristic 2 by [Reference Schreieder45].
$\neq 2$
was proven; a similar bound holds in characteristic 2 by [Reference Schreieder45].
The logarithmic degree bound in [Reference Schreieder44] is equivalent to
![]() $N\leq 2^{d-2}$
. In the case of stable rationality over fields of characteristic zero, Moe [Reference Moe33] used the methods from [Reference Nicaise and Shinder35, Reference Kontsevich and Tschinkel29, Reference Nicaise and Ottem34] to improve this logarithmic bound by a factor
$N\leq 2^{d-2}$
. In the case of stable rationality over fields of characteristic zero, Moe [Reference Moe33] used the methods from [Reference Nicaise and Shinder35, Reference Kontsevich and Tschinkel29, Reference Nicaise and Ottem34] to improve this logarithmic bound by a factor
![]() $(d+1)/4$
to cover the cases
$(d+1)/4$
to cover the cases
![]() $N\leq (d+1)2^{d-4}$
. This paper generalizes Moe’s result as follows:
$N\leq (d+1)2^{d-4}$
. This paper generalizes Moe’s result as follows:
Theorem 1.1. Let k be a field of characteristic different from
![]() $2$
. Then a very general hypersurface
$2$
. Then a very general hypersurface
![]() $X\subset {\mathbb {P}}^{N+1}_k$
of degree
$X\subset {\mathbb {P}}^{N+1}_k$
of degree
![]() $d\geq 4$
and dimension
$d\geq 4$
and dimension
![]() $N\leq (d+1)2^{d-4}$
does not admit a decomposition of the diagonal, and hence is neither stably nor retract rational, nor
$N\leq (d+1)2^{d-4}$
does not admit a decomposition of the diagonal, and hence is neither stably nor retract rational, nor
![]() $\mathbb A^1$
-connected.
$\mathbb A^1$
-connected.
While stable irrationality in characteristic zero follows in the above degree range from [Reference Moe33, Theorem 5.2], the assertions on retract rationality and
![]() $\mathbb A^1$
-connectedness are new. In positive characteristic, for all
$\mathbb A^1$
-connectedness are new. In positive characteristic, for all
![]() $ N\leq (d+1)2^{d-4}$
not covered by [Reference Schreieder44], even rationality was previously open. For fixed degree d, a proportion of roughly
$ N\leq (d+1)2^{d-4}$
not covered by [Reference Schreieder44], even rationality was previously open. For fixed degree d, a proportion of roughly
![]() $\frac {d-3}{d+1}$
cases is new. The first new case concerns quintics of dimension
$\frac {d-3}{d+1}$
cases is new. The first new case concerns quintics of dimension
![]() $N=10$
.
$N=10$
.
By a very general hypersurface X over a field k we mean one where the coefficients of a defining equation are algebraically independent over the prime field. With this definition, very general hypersurfaces exist over any field (not necessarily uncountable) of sufficiently large transcendence degree over the prime field, cf. Lemma 2.5 below.
In characteristic 2, we obtain an analogous result under a slightly weaker bound:
Theorem 1.2. Let k be a field of characteristic
![]() $2$
. Then a very general hypersurface
$2$
. Then a very general hypersurface
![]() $X\subset {\mathbb {P}}^{N+1}_k$
of degree
$X\subset {\mathbb {P}}^{N+1}_k$
of degree
![]() $d\geq 5$
and dimension
$d\geq 5$
and dimension
![]() $N\leq \frac {d+1}{3}2^{d-4}$
does not admit a decomposition of the diagonal, hence is neither stably nor retract rational, nor
$N\leq \frac {d+1}{3}2^{d-4}$
does not admit a decomposition of the diagonal, hence is neither stably nor retract rational, nor
![]() $\mathbb {A}^1$
-connected.
$\mathbb {A}^1$
-connected.
In characteristic 2, the logarithmic bound in [Reference Schreieder45] is given by
![]() $N\leq 2^{d-3}$
. The above theorem improves this by a factor
$N\leq 2^{d-3}$
. The above theorem improves this by a factor
![]() $(d+1)/6$
; for fixed d, the proportion of new cases is given by
$(d+1)/6$
; for fixed d, the proportion of new cases is given by
![]() $(d-5)/(d+1)$
.
$(d-5)/(d+1)$
.
Slightly better numerical bounds than in Theorems 1.1 and 1.2 can be extracted from Theorem 7.1 (see also Theorem 1.3) below, which is our main result.
Our arguments allow us to bound the torsion order
![]() $\operatorname {Tor}(X)$
of the above hypersurfaces
$\operatorname {Tor}(X)$
of the above hypersurfaces
![]() $X\subset {\mathbb {P}}^{N+1}_k$
, that is, the smallest positive integer e such that
$X\subset {\mathbb {P}}^{N+1}_k$
, that is, the smallest positive integer e such that
![]() $e\cdot \Delta _X$
decomposes in the Chow group of
$e\cdot \Delta _X$
decomposes in the Chow group of
![]() $X\times X$
(or
$X\times X$
(or
![]() $e=\infty $
if no such integer exists). If
$e=\infty $
if no such integer exists). If
![]() $\operatorname {Tor}(X)>1$
, then X does not admit a decomposition of the diagonal, hence is not
$\operatorname {Tor}(X)>1$
, then X does not admit a decomposition of the diagonal, hence is not
![]() $\mathbb A^1$
-connected. Moreover, any dominant generically finite map
$\mathbb A^1$
-connected. Moreover, any dominant generically finite map
![]() $f\colon {\mathbb {P}}^{\dim X}\dashrightarrow X$
has degree
$f\colon {\mathbb {P}}^{\dim X}\dashrightarrow X$
has degree
![]() $\deg f $
divisible by
$\deg f $
divisible by
![]() $\operatorname {Tor}(X)$
and so the torsion order yields an interesting lower bound on the possible degrees of unirational parametrizations of X.
$\operatorname {Tor}(X)$
and so the torsion order yields an interesting lower bound on the possible degrees of unirational parametrizations of X.
If
![]() $X\subset {\mathbb {P}}^{N+1}_k$
is a smooth Fano hypersurface of degree d over some field k, then
$X\subset {\mathbb {P}}^{N+1}_k$
is a smooth Fano hypersurface of degree d over some field k, then
![]() $\operatorname {Tor}(X)$
always divides
$\operatorname {Tor}(X)$
always divides
![]() $d!$
, see [Reference Roitman40] and [Reference Chatzistamatiou and Levine10, Proposition 5.2]. This yields an upper bound for the possible torsion orders of Fano hypersurfaces. We then have the following result, which improves the previously known lower bounds from [Reference Chatzistamatiou and Levine10, Reference Schreieder45].
$d!$
, see [Reference Roitman40] and [Reference Chatzistamatiou and Levine10, Proposition 5.2]. This yields an upper bound for the possible torsion orders of Fano hypersurfaces. We then have the following result, which improves the previously known lower bounds from [Reference Chatzistamatiou and Levine10, Reference Schreieder45].
Theorem 1.3. Let k be a field and let
![]() $m \geq 2$
be an integer invertible in k. Let
$m \geq 2$
be an integer invertible in k. Let
![]() $n \geq 2$
,
$n \geq 2$
,
![]() $r \leq 2^n-2$
, and
$r \leq 2^n-2$
, and
![]() $s \leq \left (\left \lfloor \frac {n}{m}\right \rfloor - 1 \right ) (2^{n-1}-1)$
be non-negative integers and write
$s \leq \left (\left \lfloor \frac {n}{m}\right \rfloor - 1 \right ) (2^{n-1}-1)$
be non-negative integers and write ![]() . Then the torsion order of a very general Fano hypersurface
. Then the torsion order of a very general Fano hypersurface
![]() $X \subset {\mathbb {P}}^{N+1}_k$
of degree
$X \subset {\mathbb {P}}^{N+1}_k$
of degree
![]() $d \geq m + n$
is divisible by m.
$d \geq m + n$
is divisible by m.
In Theorem 7.1 below we prove the above result under the weaker upper bound on s given by
![]() $ s \leq \sum \limits _{l = 1}^n \binom {n}{l} \left \lfloor \frac {n-l}{m} \right \rfloor $
. Previously, the best known bound on the torsion orders of hypersurfaces was contained in [Reference Schreieder45] and corresponds to the case
$ s \leq \sum \limits _{l = 1}^n \binom {n}{l} \left \lfloor \frac {n-l}{m} \right \rfloor $
. Previously, the best known bound on the torsion orders of hypersurfaces was contained in [Reference Schreieder45] and corresponds to the case
![]() $s=0$
.
$s=0$
.
1.2 Outline of the argument
This paper provides a flexible cycle-theoretic analogue of the motivic obstruction from [Reference Nicaise and Shinder35, Reference Kontsevich and Tschinkel29], which applies to degenerations into unions of varieties such that the obstruction lies in some lower-dimensional strata, and not in the components, as in [Reference Voisin49, Reference Colliot-Thélène and Pirutka11, Reference Schreieder43].
Previously, a solution to this problem has been proposed by the second named author with Pavic in [Reference Pavic and Schreieder36], with an important recent generalization by the first named author in [Reference Lange30]. The main weakness of our previous approach is the fact that one has to compute an explicit strictly semi-stable model of the degeneration in question, control the combinatorics of the dual complex of the special fibre and control the Chow groups of 0- and 1-cycles of all components, which itself is a notoriously difficult task for almost any given smooth projective variety. These tasks have been solved in a computationally involved manner for quartic fivefolds [Reference Pavic and Schreieder36] and
![]() $(3,3)$
-complete intersections in
$(3,3)$
-complete intersections in
![]() ${\mathbb {P}}^7$
[Reference Lange and Skauli31]. However, we do not see how to apply our obstruction from [Reference Pavic and Schreieder36, Reference Lange30] systematically to examples of higher dimensions, such as to the higher-dimensional complete intersections or hypersurfaces treated via the aforementioned motivic method in [Reference Nicaise and Ottem34, Reference Moe33]; the total space of these degenerations is not strictly semi-stable (they have toric singularities) and the special fibre has a large number of components whose Chow groups seem inaccessible.
${\mathbb {P}}^7$
[Reference Lange and Skauli31]. However, we do not see how to apply our obstruction from [Reference Pavic and Schreieder36, Reference Lange30] systematically to examples of higher dimensions, such as to the higher-dimensional complete intersections or hypersurfaces treated via the aforementioned motivic method in [Reference Nicaise and Ottem34, Reference Moe33]; the total space of these degenerations is not strictly semi-stable (they have toric singularities) and the special fibre has a large number of components whose Chow groups seem inaccessible.
The main improvement proposed in this paper is an extension of our previous method from [Reference Pavic and Schreieder36, Reference Lange30] to the nonproper case and hence in effect to (very) singular degenerations that we could not handle before. On a technical level, the idea is to work with pairs of a variety X and a closed subset
![]() $W\subset X$
. To state our obstruction, we say that a variety X admits a decomposition of the diagonal with respect to a closed subset
$W\subset X$
. To state our obstruction, we say that a variety X admits a decomposition of the diagonal with respect to a closed subset
![]() $W\subset X$
, if the diagonal point
$W\subset X$
, if the diagonal point
![]() $\delta _X\in \operatorname {CH}_0(X_{k(X)})$
lies in the image of
$\delta _X\in \operatorname {CH}_0(X_{k(X)})$
lies in the image of
![]() $\operatorname {CH}_0(W_{k(X)})\to \operatorname {CH}_0(X_{k(X)})$
, see Section 3 below. With this terminology, an ordinary decomposition of the diagonal corresponds to one with respect to a zero-dimensional closed subset.
$\operatorname {CH}_0(W_{k(X)})\to \operatorname {CH}_0(X_{k(X)})$
, see Section 3 below. With this terminology, an ordinary decomposition of the diagonal corresponds to one with respect to a zero-dimensional closed subset.
The obstruction to rationality that we introduce and exploit reads as follows.
Theorem 1.4. Let R be a discrete valuation ring with algebraically closed residue field k and fraction field K. Let
![]() $\mathcal {X} \to \operatorname {Spec} R$
be a proper flat R-scheme with geometrically integral generic fibre
$\mathcal {X} \to \operatorname {Spec} R$
be a proper flat R-scheme with geometrically integral generic fibre
![]() $X=\mathcal X\times _RK$
and special fibre
$X=\mathcal X\times _RK$
and special fibre
![]() $Y=\mathcal X\times _Rk$
. Let
$Y=\mathcal X\times _Rk$
. Let
![]() $W_{\mathcal {X}} \subset \mathcal {X}$
be a closed subscheme and let
$W_{\mathcal {X}} \subset \mathcal {X}$
be a closed subscheme and let ![]() and
and ![]() be the intersections with the generic fibre and the special fibre, respectively. Assume that the following conditions are satisfied:
be the intersections with the generic fibre and the special fibre, respectively. Assume that the following conditions are satisfied:
-
(1)
 is strictly semi-stable over R (see Definition 2.2 below);
is strictly semi-stable over R (see Definition 2.2 below); -
(2)
 consists of two components
consists of two components
 $Y_0^\circ , Y_1^\circ $
, with intersection
$Y_0^\circ , Y_1^\circ $
, with intersection
 $Z^\circ =Y_0^\circ \cap Y_1^\circ $
.
$Z^\circ =Y_0^\circ \cap Y_1^\circ $
.
If the geometric generic fibre
![]() $\bar X=X\times \bar K$
admits a decomposition of the diagonal relative to the closed subset
$\bar X=X\times \bar K$
admits a decomposition of the diagonal relative to the closed subset ![]() , then, for any field extension
, then, for any field extension
![]() $L/k$
, the map
$L/k$
, the map
is surjective modulo any integer m that is invertible in k, where
![]() $\gamma _i|_{Z^\circ }$
denotes the pullback of
$\gamma _i|_{Z^\circ }$
denotes the pullback of
![]() $\gamma _i$
along the regular embedding
$\gamma _i$
along the regular embedding
![]() $Z^\circ \hookrightarrow Y_i^\circ $
, see [Reference Fulton17, Remark 2.3].
$Z^\circ \hookrightarrow Y_i^\circ $
, see [Reference Fulton17, Remark 2.3].
Theorem 1.4 admits a generalization to the case where
![]() $Y^\circ $
is an snc scheme without triple intersections, see Theorem 4.3 below. Our arguments do not generalize to degenerations where the obstruction lies in deeper strata, see Remark 4.14 below.
$Y^\circ $
is an snc scheme without triple intersections, see Theorem 4.3 below. Our arguments do not generalize to degenerations where the obstruction lies in deeper strata, see Remark 4.14 below.
The obstruction map
![]() $\Psi _{Y_L^\circ }$
from Theorem 1.4 is a refined version of the one in [Reference Pavic and Schreieder36, Reference Lange30]. The presence of
$\Psi _{Y_L^\circ }$
from Theorem 1.4 is a refined version of the one in [Reference Pavic and Schreieder36, Reference Lange30]. The presence of
![]() $W_{\mathcal X}$
in the above theorem yields the extra flexibility that was missing in [Reference Pavic and Schreieder36, Reference Lange30]. In applications we will declare the singular locus of
$W_{\mathcal X}$
in the above theorem yields the extra flexibility that was missing in [Reference Pavic and Schreieder36, Reference Lange30]. In applications we will declare the singular locus of
![]() $\mathcal X$
, the non-snc locus of Y, as well as all but two components of Y, to be contained in
$\mathcal X$
, the non-snc locus of Y, as well as all but two components of Y, to be contained in
![]() $W_{\mathcal X}$
. In particular, the family
$W_{\mathcal X}$
. In particular, the family
![]() $\mathcal X$
in the above theorem may be quite singular and the combinatorics of the special fibre Y can be complicated.
$\mathcal X$
in the above theorem may be quite singular and the combinatorics of the special fibre Y can be complicated.
To explain the mechanism of the above theorem, assume that
![]() $Z^\circ $
is integral and let
$Z^\circ $
is integral and let
![]() $Z\subset Y$
be the closure of
$Z\subset Y$
be the closure of
![]() $Z^\circ $
. Assume further that
$Z^\circ $
. Assume further that
![]() $\operatorname {CH}_1(Y_i^\circ \times _k L) = 0$
for
$\operatorname {CH}_1(Y_i^\circ \times _k L) = 0$
for
![]() $i=0,1$
and any field extension
$i=0,1$
and any field extension
![]() $L/k$
. (This will not hold on the nose in practice, but we will be able to achieve this after degeneration and show that this suffices for the argument.) In particular, the map
$L/k$
. (This will not hold on the nose in practice, but we will be able to achieve this after degeneration and show that this suffices for the argument.) In particular, the map
![]() $\Psi _{Y_L^\circ }$
in the above theorem is the zero map for every field extension
$\Psi _{Y_L^\circ }$
in the above theorem is the zero map for every field extension
![]() $L/k$
. Applying this to the function field
$L/k$
. Applying this to the function field
![]() $L=k(Z)$
of Z and assuming that
$L=k(Z)$
of Z and assuming that
![]() $\bar X$
admits a decomposition of the diagonal with respect to
$\bar X$
admits a decomposition of the diagonal with respect to
![]() $W_{\bar X}$
, we get that the image of the diagonal point
$W_{\bar X}$
, we get that the image of the diagonal point
![]() $\delta _Z$
in
$\delta _Z$
in
![]() $\operatorname {CH}_0(Z^\circ \times k(Z))$
vanishes, and so, by the localization sequence, Z admits a decomposition with respect to
$\operatorname {CH}_0(Z^\circ \times k(Z))$
vanishes, and so, by the localization sequence, Z admits a decomposition with respect to
![]() $Z \cap W_Y$
. In other words,
$Z \cap W_Y$
. In other words,
![]() $\bar X$
admits no decomposition of the diagonal with respect to
$\bar X$
admits no decomposition of the diagonal with respect to
![]() $W_{\bar X}$
as long as Z admits no decomposition with respect to
$W_{\bar X}$
as long as Z admits no decomposition with respect to
![]() $Z \cap W_Y$
. Examples of this strategy are illustrated in Examples 4.5 and 4.6 below.
$Z \cap W_Y$
. Examples of this strategy are illustrated in Examples 4.5 and 4.6 below.
Since
![]() $\dim Z=\dim X-1$
, the above reasoning sets the stage for an inductive argument where one increases the dimension by one in each step. What makes this work is the observation that the examples of Fano hypersurfaces without a decomposition of the diagonal in [Reference Schreieder44, Reference Schreieder45] can in fact be shown to have no decomposition of the diagonal with respect to a large class of divisors, see Theorem 6.1 below. This will serve as the start of our induction. For the induction step we degenerate a given hypersurface of degree d to a union of two rational varieties which meet along the lower-dimensional hypersurface of degree d that we have produced in the previous step of the induction, see Section 5 below for the precise degeneration we pick. This step is inspired by [Reference Moe33]. The total space of our degeneration as well as the fibres and their components will be (very) singular. The singularities are not toric and so even in characteristic zero, the method in [Reference Kontsevich and Tschinkel29, Reference Nicaise and Shinder35, Reference Nicaise and Ottem34] does not seem to apply to our degeneration.
$\dim Z=\dim X-1$
, the above reasoning sets the stage for an inductive argument where one increases the dimension by one in each step. What makes this work is the observation that the examples of Fano hypersurfaces without a decomposition of the diagonal in [Reference Schreieder44, Reference Schreieder45] can in fact be shown to have no decomposition of the diagonal with respect to a large class of divisors, see Theorem 6.1 below. This will serve as the start of our induction. For the induction step we degenerate a given hypersurface of degree d to a union of two rational varieties which meet along the lower-dimensional hypersurface of degree d that we have produced in the previous step of the induction, see Section 5 below for the precise degeneration we pick. This step is inspired by [Reference Moe33]. The total space of our degeneration as well as the fibres and their components will be (very) singular. The singularities are not toric and so even in characteristic zero, the method in [Reference Kontsevich and Tschinkel29, Reference Nicaise and Shinder35, Reference Nicaise and Ottem34] does not seem to apply to our degeneration.
Remark 1.5. After completion of this paper, James Hotchkiss and David Stapleton informed us that they have independently obtained a different argument which shows that, over fields of characteristic zero, the hypersurfaces in Theorem 1.1 are not
![]() $\mathbb A^1$
-connected and hence not retract rational, see [Reference Hotchkiss and Stapleton21]. Their approach relies on a homotopy-theoretical lift of the obstruction from [Reference Nicaise and Shinder35, Reference Kontsevich and Tschinkel29]. As in [Reference Nicaise and Shinder35, Reference Kontsevich and Tschinkel29, Reference Nicaise and Ottem34, Reference Moe33], the assumption on the characteristic is needed to be able to apply weak factorization.
$\mathbb A^1$
-connected and hence not retract rational, see [Reference Hotchkiss and Stapleton21]. Their approach relies on a homotopy-theoretical lift of the obstruction from [Reference Nicaise and Shinder35, Reference Kontsevich and Tschinkel29]. As in [Reference Nicaise and Shinder35, Reference Kontsevich and Tschinkel29, Reference Nicaise and Ottem34, Reference Moe33], the assumption on the characteristic is needed to be able to apply weak factorization.
2 Preliminaries
2.1 Conventions
Rings are understood to be commutative with 1. The characteristic of a ring
![]() $\Lambda $
is the smallest positive integer
$\Lambda $
is the smallest positive integer
![]() $c\in {\mathbb {Z}}_{\geq 1} $
such that any element in
$c\in {\mathbb {Z}}_{\geq 1} $
such that any element in
![]() $\Lambda $
is c-torsion; it is zero if no such integer exists. The exponential characteristic of a field k is
$\Lambda $
is c-torsion; it is zero if no such integer exists. The exponential characteristic of a field k is
![]() $1$
if k has characteristic zero and it is equal to the characteristic of k otherwise.
$1$
if k has characteristic zero and it is equal to the characteristic of k otherwise.
An algebraic scheme is a separated scheme of finite type over a field. A variety is an integral algebraic scheme. Let Y be an algebraic scheme, then we denote by
![]() $\operatorname {CH}_i(Y)$
the Chow groups of dimension i cycles. For a ring
$\operatorname {CH}_i(Y)$
the Chow groups of dimension i cycles. For a ring
![]() $\Lambda $
, we let
$\Lambda $
, we let ![]() .
.
Let R be a ring. By an R-scheme we always mean a separated R-scheme of finite type, unless stated otherwise. For an R-scheme X and an R-algebra A, we denote the fibre product by ![]() or simply by
or simply by
![]() $X_A$
. We sometimes omit the ring R, if it is clear from context.
$X_A$
. We sometimes omit the ring R, if it is clear from context.
2.2 Strictly semi-stable degenerations
Definition 2.1. Let k be a field. An snc scheme of dimension n over k is a geometrically reduced algebraic scheme Y over k with irreducible components
![]() $Y_i$
,
$Y_i$
,
![]() $i\in I$
, such that for any subset
$i\in I$
, such that for any subset
![]() $J\subset I$
, the (scheme-theoretic) intersection
$J\subset I$
, the (scheme-theoretic) intersection ![]() is smooth over k and, if nonempty, equidimensional of dimension
is smooth over k and, if nonempty, equidimensional of dimension
![]() $n+1-|J|$
.
$n+1-|J|$
.
We recall the definition of strictly semi-stable schemes over a discrete valuation ring, see, for example, [Reference Hartl19, Definition 1.1].
Definition 2.2. Let R be a discrete valuation ring with fraction field K and residue field k. A strictly semi-stable R-scheme
![]() $\mathcal X\to \operatorname {Spec} R$
is an irreducible, reduced, separated scheme which is flat and of finite type over R with the following properties:
$\mathcal X\to \operatorname {Spec} R$
is an irreducible, reduced, separated scheme which is flat and of finite type over R with the following properties:
-
• the generic fibre
 $X=\mathcal X\times _R K$
is smooth over K;
$X=\mathcal X\times _R K$
is smooth over K; -
• the special fibre
 $Y=\mathcal X\times _R k$
is an snc scheme over k;
$Y=\mathcal X\times _R k$
is an snc scheme over k; -
• each component of the special fibre Y is a Cartier divisor on
 $\mathcal X$
.
$\mathcal X$
.
2.3 Fulton’s specialization map
Let R be a discrete valuation ring with fraction field K and residue field k. Let
![]() $\mathcal X\to \operatorname {Spec} R$
be a flat R-scheme of finite type with generic fibre
$\mathcal X\to \operatorname {Spec} R$
be a flat R-scheme of finite type with generic fibre
![]() $X=\mathcal X\times _RK$
and special fibre
$X=\mathcal X\times _RK$
and special fibre
![]() $Y=\mathcal X\times _Rk$
. Then, for any ring
$Y=\mathcal X\times _Rk$
. Then, for any ring
![]() $\Lambda $
, there is a specialization map on Chow groups
$\Lambda $
, there is a specialization map on Chow groups
defined as follows. If
![]() $\Lambda ={\mathbb {Z}}$
and
$\Lambda ={\mathbb {Z}}$
and
![]() $z=[Z]\in Z_i(X)$
is represented by an i-dimensional subvariety
$z=[Z]\in Z_i(X)$
is represented by an i-dimensional subvariety
![]() $Z\subset X$
, then
$Z\subset X$
, then
![]() $\operatorname {sp}(z)$
is represented by the restriction of the closure of Z in
$\operatorname {sp}(z)$
is represented by the restriction of the closure of Z in
![]() $\mathcal X$
to Y. (This restriction could be empty, in which case
$\mathcal X$
to Y. (This restriction could be empty, in which case
![]() $\operatorname {sp}(z)=[\emptyset ]=0$
.) This extends
$\operatorname {sp}(z)=[\emptyset ]=0$
.) This extends
![]() ${\mathbb {Z}}$
-linearly to a well-defined map by an argument of Fulton (see [Reference Fulton16, §4.4], [Reference Fulton17, §20.3], or [Reference Schreieder and Farkas46, proof of Theorem 8.2]). The case of arbitrary coefficients follows from this by functoriality of the tensor product. If k is algebraically closed, then the above map induces a well-defined map
${\mathbb {Z}}$
-linearly to a well-defined map by an argument of Fulton (see [Reference Fulton16, §4.4], [Reference Fulton17, §20.3], or [Reference Schreieder and Farkas46, proof of Theorem 8.2]). The case of arbitrary coefficients follows from this by functoriality of the tensor product. If k is algebraically closed, then the above map induces a well-defined map
where
![]() $\bar X=X\times _K\bar K$
denotes the base change to an algebraic closure. (In [Reference Fulton16, §4.4] and [Reference Fulton17, §20.3], this is shown for the completion
$\bar X=X\times _K\bar K$
denotes the base change to an algebraic closure. (In [Reference Fulton16, §4.4] and [Reference Fulton17, §20.3], this is shown for the completion
![]() $\hat R$
of R; the above case then follows via precomposing with the natural map
$\hat R$
of R; the above case then follows via precomposing with the natural map
![]() $\operatorname {CH}_i(\bar X)\to \operatorname {CH}_i(X\times _K \overline {\operatorname {Frac}(\hat R)})$
.)
$\operatorname {CH}_i(\bar X)\to \operatorname {CH}_i(X\times _K \overline {\operatorname {Frac}(\hat R)})$
.)
We will need the following specific result on Fulton’s specialization map.
Lemma 2.3. Let
![]() $\Lambda $
be a ring and let R be a discrete valuation ring with fraction field K and residue field k. Let
$\Lambda $
be a ring and let R be a discrete valuation ring with fraction field K and residue field k. Let
![]() $p:\mathcal X\to \operatorname {Spec} R$
and
$p:\mathcal X\to \operatorname {Spec} R$
and
![]() $q:\mathcal Y\to \operatorname {Spec} R$
be flat R-schemes of finite type. Denote by
$q:\mathcal Y\to \operatorname {Spec} R$
be flat R-schemes of finite type. Denote by
![]() $X_\eta ,Y_\eta $
and
$X_\eta ,Y_\eta $
and
![]() $X_0,Y_0$
the generic and special fibres of p, q, respectively. Assume that
$X_0,Y_0$
the generic and special fibres of p, q, respectively. Assume that
![]() $Y_\eta $
is geometrically integral and that there is a geometrically integral component
$Y_\eta $
is geometrically integral and that there is a geometrically integral component
![]() $Y_0'\subset Y_0$
, such that
$Y_0'\subset Y_0$
, such that
![]() $A=\mathcal O_{\mathcal Y,Y^{\prime }_0}$
is a discrete valuation ring and consider the flat A-scheme
$A=\mathcal O_{\mathcal Y,Y^{\prime }_0}$
is a discrete valuation ring and consider the flat A-scheme
![]() $\mathcal X_A\to \operatorname {Spec} A$
, given by base change of p. Then Fulton’s specialization map induces a specialization map
$\mathcal X_A\to \operatorname {Spec} A$
, given by base change of p. Then Fulton’s specialization map induces a specialization map
where
![]() $\bar K$
and
$\bar K$
and
![]() $\bar k$
denote algebraic closures of K and k, respectively, such that the following holds:
$\bar k$
denote algebraic closures of K and k, respectively, such that the following holds:
-
(1)
 $\operatorname {sp}$
commutes with pushforwards along proper maps and pullbacks along regular embeddings;
$\operatorname {sp}$
commutes with pushforwards along proper maps and pullbacks along regular embeddings; -
(2) If
 $\mathcal X=\mathcal Y$
and
$\mathcal X=\mathcal Y$
and
 $X_0$
is integral, then
$X_0$
is integral, then
 $\operatorname {sp}(\delta _{X_\eta })=\delta _{X_0}$
, where
$\operatorname {sp}(\delta _{X_\eta })=\delta _{X_0}$
, where
 $\delta _{X_\eta }\in \operatorname {CH}_0( X_\eta \times _{K} \bar {K}(X_\eta ),\Lambda )$
and
$\delta _{X_\eta }\in \operatorname {CH}_0( X_\eta \times _{K} \bar {K}(X_\eta ),\Lambda )$
and
 $\delta _{X_0}\in \operatorname {CH}_0( X_0 \times _{k} \bar {k}(X_0),\Lambda )$
denote the diagonal points.
$\delta _{X_0}\in \operatorname {CH}_0( X_0 \times _{k} \bar {k}(X_0),\Lambda )$
denote the diagonal points.
Proof. By functoriality of the tensor product, it suffices to prove the lemma in the case where
![]() $\Lambda ={\mathbb {Z}}$
. The lemma is then stated under the assumption that p and q are proper with connected fibres in [Reference Pavic and Schreieder36, Lemma 5.8], but the proof does not need those assumptions.
$\Lambda ={\mathbb {Z}}$
. The lemma is then stated under the assumption that p and q are proper with connected fibres in [Reference Pavic and Schreieder36, Lemma 5.8], but the proof does not need those assumptions.
2.4 Very general hypersurfaces and their degenerations
Definition 2.4. A hypersurface
![]() $X\subset {\mathbb {P}}^{N+1}_k$
over a field k is called very general, if the coefficients of a defining equation are algebraically independent over the prime field of k.
$X\subset {\mathbb {P}}^{N+1}_k$
over a field k is called very general, if the coefficients of a defining equation are algebraically independent over the prime field of k.
We say that a variety X over a field L degenerates to a variety Y over an algebraically closed field k if there is a discrete valuation ring R with residue field k and fraction field K with
![]() $K\subset L$
and a flat R-scheme
$K\subset L$
and a flat R-scheme
![]() $\mathcal X\to \operatorname {Spec} R$
of finite type whose special fibre is Y and such that
$\mathcal X\to \operatorname {Spec} R$
of finite type whose special fibre is Y and such that
![]() $\mathcal X\times _R L\cong X$
.
$\mathcal X\times _R L\cong X$
.
Lemma 2.5. Let ![]() be the universal family of degree d hypersurfaces of dimension N over a field k. Then the following hold:
be the universal family of degree d hypersurfaces of dimension N over a field k. Then the following hold:
-
(1) The locus of very general hypersurfaces
 $B_{vg}\subset B$
(as a set of schematic points) is the complement of a countable union of closed subsets; it is nonempty if the transcendence degree of k over the prime field is
$B_{vg}\subset B$
(as a set of schematic points) is the complement of a countable union of closed subsets; it is nonempty if the transcendence degree of k over the prime field is
 $\geq \dim B$
.
$\geq \dim B$
. -
(2) Let X be a very general hypersurface, namely,
 $X = X_b$
, where
$X = X_b$
, where
 $b \in B_{vg}$
. There are (algebraically closed) field extensions
$b \in B_{vg}$
. There are (algebraically closed) field extensions
 $L/k(B)$
and
$L/k(B)$
and
 $K/k$
together with an isomorphism of fields
$K/k$
together with an isomorphism of fields
 $\varphi :K\to L$
, such that
$\varphi :K\to L$
, such that
 $\varphi $
induces an isomorphism of schemes In particular, up to a base change, X degenerates to any other hypersurface
$\varphi $
induces an isomorphism of schemes In particular, up to a base change, X degenerates to any other hypersurface $$ \begin{align*}X\times_kK\stackrel{\sim}\longrightarrow \mathcal X\times_{k(B)}L. \end{align*} $$
$$ \begin{align*}X\times_kK\stackrel{\sim}\longrightarrow \mathcal X\times_{k(B)}L. \end{align*} $$
 $Y\subset {\mathbb {P}}_k^{N+1}$
of degree d in the above sense.
$Y\subset {\mathbb {P}}_k^{N+1}$
of degree d in the above sense.
Proof. We have
![]() $B={\mathbb {P}}^{N'}$
for some integer
$B={\mathbb {P}}^{N'}$
for some integer
![]() $N'$
. By definition, the complement of
$N'$
. By definition, the complement of
![]() $B_{vg}\subset B$
is given by the union of all hypersurfaces in
$B_{vg}\subset B$
is given by the union of all hypersurfaces in
![]() $B={\mathbb {P}}^{N'}$
that are defined over the prime field
$B={\mathbb {P}}^{N'}$
that are defined over the prime field
![]() $k_0$
of k. This is a countable union and the complement contains a point as soon as
$k_0$
of k. This is a countable union and the complement contains a point as soon as
![]() $\operatorname {trdeg}_{k_0} k\geq \dim B$
. This proves the first assertion.
$\operatorname {trdeg}_{k_0} k\geq \dim B$
. This proves the first assertion.
Consider the universal family
![]() $\mathcal X_0\to B_0={\mathbb {P}} ( H^0({\mathbb {P}}^{N+1}_{k_0},\mathcal O(d)))$
of degree d hypersurfaces of dimension N over the prime field
$\mathcal X_0\to B_0={\mathbb {P}} ( H^0({\mathbb {P}}^{N+1}_{k_0},\mathcal O(d)))$
of degree d hypersurfaces of dimension N over the prime field
![]() $k_0$
of k. The second item follows from the observation that any hypersurface of dimension N and degree d over a field extension of
$k_0$
of k. The second item follows from the observation that any hypersurface of dimension N and degree d over a field extension of
![]() $k_0$
, such that the coefficients of a defining equation are algebraically independent over
$k_0$
, such that the coefficients of a defining equation are algebraically independent over
![]() $k_0$
, is as an abstract scheme (i.e., without any structure morphism) a base change of the generic fibre of
$k_0$
, is as an abstract scheme (i.e., without any structure morphism) a base change of the generic fibre of
![]() $\mathcal X_0\to B_0$
. This concludes the proof of the lemma.
$\mathcal X_0\to B_0$
. This concludes the proof of the lemma.
3 Torsion orders and decompositions of the diagonal relative to a closed subset
Let X be a variety over a field k. We say that e times the diagonal of X decomposes if there is a zero-cycle
![]() $z\in \operatorname {CH}_0(X)$
such that
$z\in \operatorname {CH}_0(X)$
such that
for some cycle Z whose support does not dominate the second factor of
![]() $X\times _k X$
, see [Reference Bloch and Srinivas8]. The torsion order of X, denoted by
$X\times _k X$
, see [Reference Bloch and Srinivas8]. The torsion order of X, denoted by
![]() $\operatorname {Tor}(X)$
, is the smallest positive integer e such that a decomposition as above exists; it is
$\operatorname {Tor}(X)$
, is the smallest positive integer e such that a decomposition as above exists; it is
![]() $\infty $
if no such integer exists, see, for example, [Reference Chatzistamatiou and Levine10, Reference Kahn24, Reference Schreieder45]. We say that X admits a decomposition of the diagonal if
$\infty $
if no such integer exists, see, for example, [Reference Chatzistamatiou and Levine10, Reference Kahn24, Reference Schreieder45]. We say that X admits a decomposition of the diagonal if
![]() $\operatorname {Tor}(X)=1$
. By the localization exact sequence [Reference Fulton17, §1.8], this is equivalent to saying that
$\operatorname {Tor}(X)=1$
. By the localization exact sequence [Reference Fulton17, §1.8], this is equivalent to saying that
![]() $ \delta _X\in \operatorname {im}(\operatorname {CH}_0(W_{k(X)})\to \operatorname {CH}_0(X_{k(X)})) $
for a zero-dimensional closed subset
$ \delta _X\in \operatorname {im}(\operatorname {CH}_0(W_{k(X)})\to \operatorname {CH}_0(X_{k(X)})) $
for a zero-dimensional closed subset
![]() $W\subset X$
, where
$W\subset X$
, where
![]() $\delta _X\in X_{k(X)}$
denotes the point induced by the diagonal
$\delta _X\in X_{k(X)}$
denotes the point induced by the diagonal
![]() $\Delta _X\subset X\times _k X$
. This leads to the following simple but useful variant.
$\Delta _X\subset X\times _k X$
. This leads to the following simple but useful variant.
Definition 3.1. Let X be a variety over a field k and let
![]() $\Lambda $
be a ring. We say that X admits a
$\Lambda $
be a ring. We say that X admits a
![]() $\Lambda $
-decomposition of the diagonal relative to a closed subset
$\Lambda $
-decomposition of the diagonal relative to a closed subset
![]() $W\subset X$
if
$W\subset X$
if
where
![]() $\delta _X$
denotes the diagonal point induced by the diagonal
$\delta _X$
denotes the diagonal point induced by the diagonal
![]() $\Delta _X \subset X \times _k X$
. If
$\Delta _X \subset X \times _k X$
. If
![]() $\Lambda = {\mathbb {Z}}$
, we also say that X admits a decomposition (or integral decomposition) of the diagonal relative to W.
$\Lambda = {\mathbb {Z}}$
, we also say that X admits a decomposition (or integral decomposition) of the diagonal relative to W.
Variants of the notion of a decomposition of diagonal relative to a closed subscheme appear, for example, in [Reference Bloch and Srinivas8], [Reference Voisin50, Definition 1.2], and [Reference Chatzistamatiou and Levine10, Definition 1.1].
Remark 3.2. By the above discussion, X admits a decomposition of the diagonal if and only if it admits a decomposition relative to a closed subset of dimension zero.
By the localization sequence, the condition on
![]() $\delta _X$
in Definition 3.1 is equivalent to
$\delta _X$
in Definition 3.1 is equivalent to
where
![]() $U=X\setminus W$
. It follows that a
$U=X\setminus W$
. It follows that a
![]() $\Lambda $
-decomposition of the diagonal relative to
$\Lambda $
-decomposition of the diagonal relative to
![]() $W\subset X$
is the same thing as a
$W\subset X$
is the same thing as a
![]() $\Lambda $
-decomposition of the diagonal of U, relative to the empty set. These observations lead us to the following relative version of the aforementioned torsion order studied, for instance, in [Reference Chatzistamatiou and Levine10, Reference Kahn24, Reference Schreieder45].
$\Lambda $
-decomposition of the diagonal of U, relative to the empty set. These observations lead us to the following relative version of the aforementioned torsion order studied, for instance, in [Reference Chatzistamatiou and Levine10, Reference Kahn24, Reference Schreieder45].
Definition 3.3. Let X be a variety over a field k and let
![]() $\Lambda $
be a ring. The
$\Lambda $
be a ring. The
![]() $\Lambda $
-torsion order of X relative to a closed subset
$\Lambda $
-torsion order of X relative to a closed subset
![]() $W\subset X$
, denoted by
$W\subset X$
, denoted by
![]() $\operatorname {Tor}^\Lambda (X,W)$
, is the order of the element
$\operatorname {Tor}^\Lambda (X,W)$
, is the order of the element
where
![]() $U=X\setminus W$
.
$U=X\setminus W$
.
By definition,
![]() $\operatorname {Tor}^\Lambda (X,W)\in \mathbb N\cup \{\infty \}$
. If
$\operatorname {Tor}^\Lambda (X,W)\in \mathbb N\cup \{\infty \}$
. If
![]() $\Lambda $
has characteristic
$\Lambda $
has characteristic
![]() $c\neq 0$
, then
$c\neq 0$
, then
![]() $\operatorname {Tor}^\Lambda (X,W)$
divides c and hence is finite.
$\operatorname {Tor}^\Lambda (X,W)$
divides c and hence is finite.
We remark that the torsion order of proper varieties relative to the empty set has somewhat pathological behaviour. For instance, the
![]() ${\mathbb {Z}}$
-torsion order of a proper variety with respect to the empty set is always
${\mathbb {Z}}$
-torsion order of a proper variety with respect to the empty set is always
![]() $\infty $
, but it may or may not be finite relative to a nonempty closed subset
$\infty $
, but it may or may not be finite relative to a nonempty closed subset
![]() $W\subset X$
.
$W\subset X$
.
Remark 3.4. The
![]() $\Lambda $
-torsion order of X relative to W is
$\Lambda $
-torsion order of X relative to W is
![]() $1$
if and only if X admits a
$1$
if and only if X admits a
![]() $\Lambda $
-decomposition of the diagonal relative to W. Moreover, the
$\Lambda $
-decomposition of the diagonal relative to W. Moreover, the
![]() $\Lambda $
-torsion order of X relative to W is nothing but the
$\Lambda $
-torsion order of X relative to W is nothing but the
![]() $\Lambda $
-torsion order of
$\Lambda $
-torsion order of
![]() $X\setminus W$
, relative to the empty set.
$X\setminus W$
, relative to the empty set.
Remark 3.5. If X is an algebraic scheme over k (not necessarily irreducible) and
![]() $W\subset X$
is a closed subset such that
$W\subset X$
is a closed subset such that
![]() $U=X\setminus W$
is integral, then we can, in view of Remark 3.4, still define
$U=X\setminus W$
is integral, then we can, in view of Remark 3.4, still define
![]() $\operatorname {Tor}^\Lambda (X,W)$
via the order of the element
$\operatorname {Tor}^\Lambda (X,W)$
via the order of the element
Lemma 3.6. Let X be a variety over a field k and let
![]() $W\subset X$
be closed. Then the following hold:
$W\subset X$
be closed. Then the following hold:
-
(a) For all
 $m \in {\mathbb {Z}}$
,
$m \in {\mathbb {Z}}$
,
 $\operatorname {Tor}^{{\mathbb {Z}}/m}(X,W) \mid \operatorname {Tor}^{{\mathbb {Z}}}(X,W)$
.
$\operatorname {Tor}^{{\mathbb {Z}}/m}(X,W) \mid \operatorname {Tor}^{{\mathbb {Z}}}(X,W)$
. -
(b) Let
 $W' \subset W \subset X$
be a closed subset, then
$W' \subset W \subset X$
be a closed subset, then
 $\operatorname {Tor}^\Lambda (X,W) \mid \operatorname {Tor}^\Lambda (X,W')$
.
$\operatorname {Tor}^\Lambda (X,W) \mid \operatorname {Tor}^\Lambda (X,W')$
. -
(c)
 $\operatorname {Tor}(X)$
is the minimum of the relative torsion orders
$\operatorname {Tor}(X)$
is the minimum of the relative torsion orders
 $\operatorname {Tor}^{{\mathbb {Z}}}(X,W)$
where
$\operatorname {Tor}^{{\mathbb {Z}}}(X,W)$
where
 $W\subset X$
runs through all closed subsets of dimension zero.
$W\subset X$
runs through all closed subsets of dimension zero. -
(d) If X is proper and
 $\deg \colon \operatorname {CH}_0(X) \to {\mathbb {Z}}$
is an isomorphism, then
$\deg \colon \operatorname {CH}_0(X) \to {\mathbb {Z}}$
is an isomorphism, then
 $\operatorname {Tor}(X)=\operatorname {Tor}^{{\mathbb {Z}}}(X,W)$
for any closed subset
$\operatorname {Tor}(X)=\operatorname {Tor}^{{\mathbb {Z}}}(X,W)$
for any closed subset
 $W\subset X$
of dimension zero, which contains a zero-cycle of degree 1.
$W\subset X$
of dimension zero, which contains a zero-cycle of degree 1. -
(e) If
 $k=\bar k$
is algebraically closed, then
$k=\bar k$
is algebraically closed, then
 $\operatorname {Tor}^\Lambda (X,W)=\operatorname {Tor}^\Lambda (X_L,W_L)$
for any ring
$\operatorname {Tor}^\Lambda (X,W)=\operatorname {Tor}^\Lambda (X_L,W_L)$
for any ring
 $\Lambda $
and any field extension
$\Lambda $
and any field extension
 $L/k$
.
$L/k$
.
Proof. Items (a)–(d) follow easily from the definitions and the above discussions. To prove item (e), note that
![]() $\operatorname {Tor}^\Lambda (X_L,W_L)\mid \operatorname {Tor}^\Lambda (X,W)$
(even without asking that k is algebraically closed). The converse divisibility statement follows via a straightforward ‘spreading out and specialization at a k-point’ argument. This concludes the proof of the lemma.
$\operatorname {Tor}^\Lambda (X_L,W_L)\mid \operatorname {Tor}^\Lambda (X,W)$
(even without asking that k is algebraically closed). The converse divisibility statement follows via a straightforward ‘spreading out and specialization at a k-point’ argument. This concludes the proof of the lemma.
The next lemma explains the geometric meaning of
![]() $\Lambda $
-torsion orders.
$\Lambda $
-torsion orders.
Lemma 3.7. Let X be a proper variety over a field k and let
![]() $\Lambda $
be a ring. Assume that X admits a resolution of singularities or that the exponential characteristic of k is invertible in
$\Lambda $
be a ring. Assume that X admits a resolution of singularities or that the exponential characteristic of k is invertible in
![]() $\Lambda $
. If for some closed subset
$\Lambda $
. If for some closed subset
![]() $W\subset X$
the complement
$W\subset X$
the complement ![]() is smooth, then
is smooth, then
![]() $\operatorname {CH}_0(U_L,\Lambda )$
is
$\operatorname {CH}_0(U_L,\Lambda )$
is
![]() $\operatorname {Tor}^\Lambda (X,W)$
-torsion for all field extensions
$\operatorname {Tor}^\Lambda (X,W)$
-torsion for all field extensions
![]() $L/k$
.
$L/k$
.
Proof. Since
![]() $\operatorname {Tor}^\Lambda (X_L,W_L)$
divides
$\operatorname {Tor}^\Lambda (X_L,W_L)$
divides
![]() $\operatorname {Tor}^\Lambda (X,W)$
, we can assume without loss of generality that
$\operatorname {Tor}^\Lambda (X,W)$
, we can assume without loss of generality that
![]() $L=k$
. By work of Temkin [Reference Temkin47], we can pick an alteration
$L=k$
. By work of Temkin [Reference Temkin47], we can pick an alteration
![]() $\tau :X'\to X$
whose degree is a power of the exponential characteristic. Moreover, we can choose
$\tau :X'\to X$
whose degree is a power of the exponential characteristic. Moreover, we can choose
![]() $\tau $
to be of degree
$\tau $
to be of degree
![]() $1$
if X admits a resolution of singularities. We then let
$1$
if X admits a resolution of singularities. We then let ![]() and
and
![]() $U'=X'\setminus W'$
. We further let
$U'=X'\setminus W'$
. We further let
![]() $V\subset U$
be the locus over which
$V\subset U$
be the locus over which
![]() $\tau $
is étale and define
$\tau $
is étale and define ![]() .
.
Let ![]() . By assumption,
. By assumption,
![]() $m\cdot \delta _X\in \operatorname {CH}_0(X_{k(X)},\Lambda )$
vanishes when restricted to U. Hence,
$m\cdot \delta _X\in \operatorname {CH}_0(X_{k(X)},\Lambda )$
vanishes when restricted to U. Hence,
The base change of this class to the field extension
![]() $k(U')$
of
$k(U')$
of
![]() $k(U)$
still vanishes. If we spread this out and use the localization sequence, we find that
$k(U)$
still vanishes. If we spread this out and use the localization sequence, we find that
where
![]() $\Gamma \subset X'\times X'$
denotes the closure of the locus
$\Gamma \subset X'\times X'$
denotes the closure of the locus
and
![]() $Z_1$
,
$Z_1$
,
![]() $Z_2$
denote some cycles with
$Z_2$
denote some cycles with
for some nowhere dense closed subset
![]() $D\subsetneq X'$
.
$D\subsetneq X'$
.
Let now
![]() $z\in \operatorname {CH}_0(U,\Lambda )$
. By Chow’s moving lemma, we can assume that
$z\in \operatorname {CH}_0(U,\Lambda )$
. By Chow’s moving lemma, we can assume that
![]() $\operatorname {supp} z\subset V$
and
$\operatorname {supp} z\subset V$
and
![]() $\operatorname {supp} z\cap \tau (D)=\emptyset $
. We aim to show
$\operatorname {supp} z\cap \tau (D)=\emptyset $
. We aim to show
![]() $m\cdot z=0\in \operatorname {CH}_0(U,\Lambda )$
. To this end, let
$m\cdot z=0\in \operatorname {CH}_0(U,\Lambda )$
. To this end, let
![]() $p:X'\times X'\to X'$
and
$p:X'\times X'\to X'$
and
![]() $q:X'\times X'\to X'$
denote the projections to the first and second factors, respectively. Since
$q:X'\times X'\to X'$
denote the projections to the first and second factors, respectively. Since
![]() $X'$
is smooth and proper over k, we can define pullbacks along correspondences in
$X'$
is smooth and proper over k, we can define pullbacks along correspondences in
![]() $\operatorname {CH}^{\dim X}(X'\times X',\Lambda )$
.
$\operatorname {CH}^{\dim X}(X'\times X',\Lambda )$
.
By assumption, the support of z lies in the locus over which
![]() $\tau $
is étale:
$\tau $
is étale:
![]() $\operatorname {supp} z\subset V$
. We can thus define the zero-cycle
$\operatorname {supp} z\subset V$
. We can thus define the zero-cycle
![]() $\tau ^\ast z$
on
$\tau ^\ast z$
on
![]() $X'$
on the level of cycles via the preimages of the points in the support of z. We then apply the correspondence
$X'$
on the level of cycles via the preimages of the points in the support of z. We then apply the correspondence
![]() $\Gamma $
and get
$\Gamma $
and get
Since the support of z is contained in the locus V over which
![]() $\tau $
is étale, a direct computation shows that the above zero-cycle has the property that
$\tau $
is étale, a direct computation shows that the above zero-cycle has the property that
Conversely, by (3.1), we know that this cycle is rationally equivalent to
Since
![]() $ \operatorname {supp} Z_2\subset X'\times D$
and
$ \operatorname {supp} Z_2\subset X'\times D$
and
![]() $\operatorname {supp} z\cap \tau (D)=\emptyset $
, we have
$\operatorname {supp} z\cap \tau (D)=\emptyset $
, we have
![]() $[Z_2]^\ast (\tau ^\ast z)=0$
and so
$[Z_2]^\ast (\tau ^\ast z)=0$
and so
Since
![]() $\operatorname {supp} Z_1\subset W'\times X'$
, the above class lies in the image of
$\operatorname {supp} Z_1\subset W'\times X'$
, the above class lies in the image of
![]() $\operatorname {CH}_0(W',\Lambda )\to \operatorname {CH}_0(X',\Lambda )$
. Hence,
$\operatorname {CH}_0(W',\Lambda )\to \operatorname {CH}_0(X',\Lambda )$
. Hence,
By (3.2), it follows that
By the localization sequence, this implies
Since
![]() $\deg (\tau )^2$
is either one or a power of the exponential characteristic of k, it is invertible in
$\deg (\tau )^2$
is either one or a power of the exponential characteristic of k, it is invertible in
![]() $\Lambda $
by assumption. We deduce, as we want, that
$\Lambda $
by assumption. We deduce, as we want, that
![]() $z \in \operatorname {CH}_0(U,\Lambda )$
is m-torsion. This concludes the proof of the lemma.
$z \in \operatorname {CH}_0(U,\Lambda )$
is m-torsion. This concludes the proof of the lemma.
We will use that
![]() $\Lambda $
-torsion orders relative to closed subsets are well-behaved under specialization, as shown by the following lemma.
$\Lambda $
-torsion orders relative to closed subsets are well-behaved under specialization, as shown by the following lemma.
Lemma 3.8. Let R be a discrete valuation ring with fraction field K and residue field k. Let
![]() $\mathcal X\to \operatorname {Spec} R$
be a separated flat R-scheme of finite type with generic fibre
$\mathcal X\to \operatorname {Spec} R$
be a separated flat R-scheme of finite type with generic fibre
![]() $X=\mathcal X\times K$
and special fibre
$X=\mathcal X\times K$
and special fibre
![]() $Y=\mathcal X\times k$
. Let
$Y=\mathcal X\times k$
. Let
![]() $\bar X=X\times \bar K$
and
$\bar X=X\times \bar K$
and
![]() $\bar Y=Y\times \bar k$
be the base changes to algebraic closures of K and k, respectively. Let
$\bar Y=Y\times \bar k$
be the base changes to algebraic closures of K and k, respectively. Let
![]() $W_{\mathcal X}\subset \mathcal X$
be a closed subset with
$W_{\mathcal X}\subset \mathcal X$
be a closed subset with ![]() and
and ![]() . Assume that the fibres of
. Assume that the fibres of
![]() $U=\mathcal X\setminus W_{\mathcal X}$
over R are nonempty and geometrically integral.
$U=\mathcal X\setminus W_{\mathcal X}$
over R are nonempty and geometrically integral.
Then we have
Proof. By inflation of local rings [Reference Bourbaki7, Chapter IX, Appendice §2, Corollaire du Théorème 1 and Exercice 4], there is an unramified extension of discrete valuation rings
![]() $R'/R$
such that the residue field of
$R'/R$
such that the residue field of
![]() $R'$
is
$R'$
is
![]() $\bar k$
. Up to a base change along
$\bar k$
. Up to a base change along
![]() $R'/R$
we can thus assume that k is algebraically closed. (This uses item (e) in Lemma 3.6.)
$R'/R$
we can thus assume that k is algebraically closed. (This uses item (e) in Lemma 3.6.)
Let ![]() . Then there is a finite extension
. Then there is a finite extension
![]() $K'/K$
such that the
$K'/K$
such that the
![]() $\Lambda $
-torsion order of
$\Lambda $
-torsion order of
![]() $X\times K'$
relative to
$X\times K'$
relative to
![]() $W_{X}\times K'$
is m. Let
$W_{X}\times K'$
is m. Let
![]() $R_{K'}\subset K'$
be the integral closure of R in
$R_{K'}\subset K'$
be the integral closure of R in
![]() $K'$
and let
$K'$
and let
![]() $R'\subset K'$
be the localization of
$R'\subset K'$
be the localization of
![]() $R_{K'}$
at a maximal ideal lying over the maximal ideal of R. Then
$R_{K'}$
at a maximal ideal lying over the maximal ideal of R. Then
![]() $R'$
is a discrete valuation ring with
$R'$
is a discrete valuation ring with
![]() $\operatorname {Frac} R'=K'$
and
$\operatorname {Frac} R'=K'$
and
![]() $R\subset R'$
. Up to a base change along
$R\subset R'$
. Up to a base change along
![]() $\operatorname {Spec} R'\to \operatorname {Spec} R$
, we can then assume that
$\operatorname {Spec} R'\to \operatorname {Spec} R$
, we can then assume that
![]() $K=K'$
. Hence,
$K=K'$
. Hence,
![]() $m=\operatorname {Tor}^\Lambda ( X,W_{X})$
and it remains to show that
$m=\operatorname {Tor}^\Lambda ( X,W_{X})$
and it remains to show that
Let
![]() $U=\mathcal X\setminus W_{\mathcal X}$
with generic fibre
$U=\mathcal X\setminus W_{\mathcal X}$
with generic fibre ![]() and special fibre
and special fibre ![]() . By assumptions,
. By assumptions,
![]() $U\to \operatorname {Spec} R$
is flat with nonempty geometrically integral fibres. Let A be the local ring of U at the generic point of the special fibre
$U\to \operatorname {Spec} R$
is flat with nonempty geometrically integral fibres. Let A be the local ring of U at the generic point of the special fibre
![]() $U_0$
. Since
$U_0$
. Since
![]() $U_0$
is integral, A is a discrete valuation ring with residue field
$U_0$
is integral, A is a discrete valuation ring with residue field
![]() $k(U_0)$
and fraction field
$k(U_0)$
and fraction field
![]() $K(U_\eta )$
. We then apply Fulton’s specialization map on Chow groups to the base change
$K(U_\eta )$
. We then apply Fulton’s specialization map on Chow groups to the base change ![]() and obtain a group homomorphism
and obtain a group homomorphism
with
![]() $\operatorname {sp}(\delta _{U_\eta })=\delta _{U_0}$
, see Lemma 2.3. This implies (3.3), because
$\operatorname {sp}(\delta _{U_\eta })=\delta _{U_0}$
, see Lemma 2.3. This implies (3.3), because
![]() $m=\operatorname {Tor}^\Lambda ( X,W_{X})$
is the order of
$m=\operatorname {Tor}^\Lambda ( X,W_{X})$
is the order of
![]() $\delta _{U_\eta }$
, while
$\delta _{U_\eta }$
, while
![]() $\operatorname {Tor}^\Lambda ( Y,W_{Y})$
is the order of
$\operatorname {Tor}^\Lambda ( Y,W_{Y})$
is the order of
![]() $\delta _{U_0}$
.
$\delta _{U_0}$
.
4 Obstruction map
Let
![]() $Y = \bigcup _{i \in I} Y_i$
be an snc scheme over k (see Definition 2.1). We say that Y has no triple intersections if
$Y = \bigcup _{i \in I} Y_i$
be an snc scheme over k (see Definition 2.1). We say that Y has no triple intersections if
![]() $Y_i \cap Y_j \cap Y_l = \emptyset $
for all pairwise different
$Y_i \cap Y_j \cap Y_l = \emptyset $
for all pairwise different
![]() $i,j,l \in I$
.
$i,j,l \in I$
.
The following map is the key player in Theorem 1.4, stated in the introduction.
Definition 4.1. Let
![]() $Y = \bigcup _{i \in I} Y_i$
be an snc scheme over k which has no triple intersections. We fix a total order ‘
$Y = \bigcup _{i \in I} Y_i$
be an snc scheme over k which has no triple intersections. We fix a total order ‘
![]() $<$
’ on I. Let
$<$
’ on I. Let
![]() $\Lambda $
be a ring. Then we define the obstruction map
$\Lambda $
be a ring. Then we define the obstruction map
 $$ \begin{align} \Psi_Y^\Lambda \colon \bigoplus\limits_{l \in I} \operatorname{CH}_1(Y_l,\Lambda) \longrightarrow \bigoplus\limits_{\substack{i,j \in I \\ i < j}} \operatorname{CH}_0(Y_{ij},\Lambda), \quad (\gamma_l)_l \mapsto \left(\gamma_{i}|_{Y_{ij}} - \gamma_{j}|_{Y_{ij}} \right)_{i,j}, \end{align} $$
$$ \begin{align} \Psi_Y^\Lambda \colon \bigoplus\limits_{l \in I} \operatorname{CH}_1(Y_l,\Lambda) \longrightarrow \bigoplus\limits_{\substack{i,j \in I \\ i < j}} \operatorname{CH}_0(Y_{ij},\Lambda), \quad (\gamma_l)_l \mapsto \left(\gamma_{i}|_{Y_{ij}} - \gamma_{j}|_{Y_{ij}} \right)_{i,j}, \end{align} $$
where
![]() $Y_{ij} = Y_i \cap Y_j$
for
$Y_{ij} = Y_i \cap Y_j$
for
![]() $i,j \in I$
.
$i,j \in I$
.
In the above definition,
![]() $\gamma _i|_{Y_{ij}}$
is the intersection with the divisor
$\gamma _i|_{Y_{ij}}$
is the intersection with the divisor
![]() $Y_{ij} \subset Y_i$
; see [Reference Fulton17, §2.3]. In particular,
$Y_{ij} \subset Y_i$
; see [Reference Fulton17, §2.3]. In particular,
![]() $\gamma _{i}|_{Y_{ij}}$
is represented by a
$\gamma _{i}|_{Y_{ij}}$
is represented by a
![]() $0$
-cycle supported on the set-theoretic intersection
$0$
-cycle supported on the set-theoretic intersection
![]() $|\gamma _j|\cap Y_{ij}$
and hence can be viewed as a class in
$|\gamma _j|\cap Y_{ij}$
and hence can be viewed as a class in
![]() $\operatorname {CH}_0(Y_{ij},\Lambda )$
, see also [Reference Fulton17, Convention 1.4]. We further note that we have
$\operatorname {CH}_0(Y_{ij},\Lambda )$
, see also [Reference Fulton17, Convention 1.4]. We further note that we have
![]() $\operatorname {CH}_0(Y_{ij},\Lambda ) = 0$
if
$\operatorname {CH}_0(Y_{ij},\Lambda ) = 0$
if
![]() $Y_{ij} = \emptyset $
and we set
$Y_{ij} = \emptyset $
and we set
![]() $\gamma _{i}|_{Y_{ij}}=0$
in this case.
$\gamma _{i}|_{Y_{ij}}=0$
in this case.
Theorem 4.2. Let R be a discrete valuation ring with algebraically closed residue field k and fraction field K. Let
![]() $\Lambda $
be a ring of positive characteristic
$\Lambda $
be a ring of positive characteristic
![]() $c \in {\mathbb {Z}}_{\geq 1}$
such that the exponential characteristic of k is invertible in
$c \in {\mathbb {Z}}_{\geq 1}$
such that the exponential characteristic of k is invertible in
![]() $\Lambda $
. Let
$\Lambda $
. Let
![]() $\mathcal {X} \to \operatorname {Spec} R$
be a strictly semi-stable R-scheme (see Definition 2.1) with geometrically integral generic fibre
$\mathcal {X} \to \operatorname {Spec} R$
be a strictly semi-stable R-scheme (see Definition 2.1) with geometrically integral generic fibre
![]() $X = \mathcal {X} \times _R K$
and special fibre
$X = \mathcal {X} \times _R K$
and special fibre
![]() $Y = \mathcal {X} \times _R k$
. Assume that
$Y = \mathcal {X} \times _R k$
. Assume that
![]() $Y = \bigcup _{i \in I} Y_i$
has no triple intersections and fix a total order ‘
$Y = \bigcup _{i \in I} Y_i$
has no triple intersections and fix a total order ‘
![]() $<$
’ on I. Then the cokernel of the map
$<$
’ on I. Then the cokernel of the map
 $$ \begin{align*}\Psi^\Lambda_{Y_L} \colon \bigoplus\limits_{l \in I} \operatorname{CH}_1(Y_l \times_k L,\Lambda) \longrightarrow \bigoplus\limits_{\substack{i,j \in I \\ i < j}} \operatorname{CH}_0(Y _{ij} \times_k L,\Lambda) \end{align*} $$
$$ \begin{align*}\Psi^\Lambda_{Y_L} \colon \bigoplus\limits_{l \in I} \operatorname{CH}_1(Y_l \times_k L,\Lambda) \longrightarrow \bigoplus\limits_{\substack{i,j \in I \\ i < j}} \operatorname{CH}_0(Y _{ij} \times_k L,\Lambda) \end{align*} $$
from (4.1) is
![]() $\operatorname {Tor}^\Lambda (\bar {X},\emptyset )$
-torsion for every field extension
$\operatorname {Tor}^\Lambda (\bar {X},\emptyset )$
-torsion for every field extension
![]() $L/k$
.
$L/k$
.
Note that the family
![]() $\mathcal {X} \to \operatorname {Spec} R$
in the above theorem is not assumed to be proper. We can always choose a relative Nagata compactification of this morphism, see [1, Tag 0F41]. Replacing
$\mathcal {X} \to \operatorname {Spec} R$
in the above theorem is not assumed to be proper. We can always choose a relative Nagata compactification of this morphism, see [1, Tag 0F41]. Replacing
![]() $\operatorname {Tor}^\Lambda (\bar {X},\emptyset )$
by the relative torsion order of the compactification (cf. Definition 3.3 and Remark 3.4), we can then rephrase the above theorem as follows.
$\operatorname {Tor}^\Lambda (\bar {X},\emptyset )$
by the relative torsion order of the compactification (cf. Definition 3.3 and Remark 3.4), we can then rephrase the above theorem as follows.
Theorem 4.3. Let R be a discrete valuation ring with algebraically closed residue field k and fraction field K. Let
![]() $\Lambda $
be a ring of positive characteristic
$\Lambda $
be a ring of positive characteristic
![]() $c \in {\mathbb {Z}}_{\geq 1}$
such that the exponential characteristic of k is invertible in
$c \in {\mathbb {Z}}_{\geq 1}$
such that the exponential characteristic of k is invertible in
![]() $\Lambda $
. Let
$\Lambda $
. Let
![]() $\mathcal {X} \to \operatorname {Spec} R$
be a proper flat R-scheme with geometrically integral generic fibre
$\mathcal {X} \to \operatorname {Spec} R$
be a proper flat R-scheme with geometrically integral generic fibre
![]() $X=\mathcal X\times _RK$
and special fibre
$X=\mathcal X\times _RK$
and special fibre
![]() $Y=\mathcal X\times _Rk$
. Let
$Y=\mathcal X\times _Rk$
. Let
![]() $W_{\mathcal {X}} \subset \mathcal {X}$
be a closed subscheme and let
$W_{\mathcal {X}} \subset \mathcal {X}$
be a closed subscheme and let ![]() and
and ![]() be the respective intersections (i.e., fibre products). Assume that the following conditions are satisfied:
be the respective intersections (i.e., fibre products). Assume that the following conditions are satisfied:
-
(1)
 is a strictly semi-stable R-scheme (see Definition 2.2);
is a strictly semi-stable R-scheme (see Definition 2.2); -
(2)
 has no triple intersections.
has no triple intersections.
Given a total order ‘
![]() $<$
’ on I, the cokernel of the map
$<$
’ on I, the cokernel of the map
 $$ \begin{align*}\Psi^\Lambda_{Y_L^\circ} \colon \bigoplus\limits_{l \in I} \operatorname{CH}_1(Y_l^\circ \times_k L,\Lambda) \longrightarrow \bigoplus\limits_{\substack{i,j \in I \\ i < j}} \operatorname{CH}_0(Y_{ij}^\circ \times_k L,\Lambda) \end{align*} $$
$$ \begin{align*}\Psi^\Lambda_{Y_L^\circ} \colon \bigoplus\limits_{l \in I} \operatorname{CH}_1(Y_l^\circ \times_k L,\Lambda) \longrightarrow \bigoplus\limits_{\substack{i,j \in I \\ i < j}} \operatorname{CH}_0(Y_{ij}^\circ \times_k L,\Lambda) \end{align*} $$
from (4.1) is
![]() $\operatorname {Tor}^\Lambda (\bar {X},W_{\bar X})$
-torsion for every field extension
$\operatorname {Tor}^\Lambda (\bar {X},W_{\bar X})$
-torsion for every field extension
![]() $L/k$
, where
$L/k$
, where ![]() .
.
Corollary 4.4. Let the assumptions be as in Theorem 4.3. If
![]() $\bar {X}$
admits a
$\bar {X}$
admits a
![]() $\Lambda $
-decomposition of the diagonal relative to
$\Lambda $
-decomposition of the diagonal relative to
![]() $W_{\bar {X}}$
, then the map
$W_{\bar {X}}$
, then the map
 $$ \begin{align*}\Psi^\Lambda_{Y_L^\circ} \colon \bigoplus\limits_{l \in I} \operatorname{CH}_1(Y_l^\circ \times_k L,\Lambda) \longrightarrow \bigoplus\limits_{\substack{i,j \in I \\ i < j}} \operatorname{CH}_0(Y_{ij}^\circ \times_k L,\Lambda) \end{align*} $$
$$ \begin{align*}\Psi^\Lambda_{Y_L^\circ} \colon \bigoplus\limits_{l \in I} \operatorname{CH}_1(Y_l^\circ \times_k L,\Lambda) \longrightarrow \bigoplus\limits_{\substack{i,j \in I \\ i < j}} \operatorname{CH}_0(Y_{ij}^\circ \times_k L,\Lambda) \end{align*} $$
is surjective for every field extension
![]() $L/k$
.
$L/k$
.
We illustrate the mechanism of the above corollary in the following example, where we show formally that the fact that elliptic curves admit no decomposition of the diagonal with respect to a finite set of points implies that the same holds for certain quartic surfaces. The result itself is of course a well-known consequence of [Reference Bloch and Srinivas8] and the emphasis lies in the mechanism of the argument.
Example 4.5. Let
![]() $\Lambda $
be a ring of characteristic
$\Lambda $
be a ring of characteristic
![]() $c\geq 2$
. Let k be an algebraically closed field such that the exponential characteristic of k is invertible in
$c\geq 2$
. Let k be an algebraically closed field such that the exponential characteristic of k is invertible in
![]() $\Lambda $
and let
$\Lambda $
and let
![]() $f,g_0,g_1\in k[x_0,x_1,x_2,x_3]$
be general homogeneous polynomials of degrees
$f,g_0,g_1\in k[x_0,x_1,x_2,x_3]$
be general homogeneous polynomials of degrees
![]() $\deg f=4$
and
$\deg f=4$
and
![]() $\deg g_i=2$
. Consider the degeneration
$\deg g_i=2$
. Consider the degeneration
![]() ${\mathcal X=\{t\cdot f+ g_0g_1=0\}}$
over
${\mathcal X=\{t\cdot f+ g_0g_1=0\}}$
over
![]() $R=k[[t]]$
of a smooth quartic surface into the union
$R=k[[t]]$
of a smooth quartic surface into the union
![]() $Y_0\cup Y_1$
of two smooth quadric surfaces
$Y_0\cup Y_1$
of two smooth quadric surfaces
![]() $Y_i=\{g_i=0\}$
which meet along a smooth elliptic curve
$Y_i=\{g_i=0\}$
which meet along a smooth elliptic curve ![]() . Let
. Let
![]() $S \subset \mathcal X$
be a closed reduced subscheme which is finite and surjective over
$S \subset \mathcal X$
be a closed reduced subscheme which is finite and surjective over
![]() $\operatorname {Spec} R$
. We further let
$\operatorname {Spec} R$
. We further let
![]() $T_i\subset Y_i$
be the union of two lines contained in the two different rulings of the quadric surface
$T_i\subset Y_i$
be the union of two lines contained in the two different rulings of the quadric surface
![]() $Y_i$
and set
$Y_i$
and set
where we note that the singular locus
![]() $\mathcal X^{\operatorname {sing}}=\{f=g_0=g_1=t=0\}$
is a finite number of points on Z. In the above notation,
$\mathcal X^{\operatorname {sing}}=\{f=g_0=g_1=t=0\}$
is a finite number of points on Z. In the above notation,
![]() $Y_i^\circ =Y_i\setminus W_{\mathcal X}$
is an open subset of
$Y_i^\circ =Y_i\setminus W_{\mathcal X}$
is an open subset of
![]() $Y_i\setminus T_i\cong \mathbb A^2$
, hence
$Y_i\setminus T_i\cong \mathbb A^2$
, hence
![]() $\operatorname {CH}_1(Y_i^\circ \times _k L,\Lambda ) = 0$
for
$\operatorname {CH}_1(Y_i^\circ \times _k L,\Lambda ) = 0$
for
![]() $i=0,1$
and any field extension
$i=0,1$
and any field extension
![]() $L/k$
. By construction,
$L/k$
. By construction,
![]() $W_{\mathcal X}$
meets Z in finitely many points. Since the elliptic curve Z does not admit a
$W_{\mathcal X}$
meets Z in finitely many points. Since the elliptic curve Z does not admit a
![]() $\Lambda $
-decomposition of the diagonal with respect to a finite collection of points, the group
$\Lambda $
-decomposition of the diagonal with respect to a finite collection of points, the group
![]() $\operatorname {CH}_0(Z^\circ \times _kL,\Lambda )$
is nontrivial for
$\operatorname {CH}_0(Z^\circ \times _kL,\Lambda )$
is nontrivial for
![]() $L=k(Z)$
, where
$L=k(Z)$
, where
![]() $Z^\circ =Z\setminus W_{\mathcal X}$
. It follows that
$Z^\circ =Z\setminus W_{\mathcal X}$
. It follows that
![]() $\Psi ^\Lambda _{Y^\circ _L}$
is not surjective and so Corollary 4.4 implies that the geometric generic fibre
$\Psi ^\Lambda _{Y^\circ _L}$
is not surjective and so Corollary 4.4 implies that the geometric generic fibre
![]() $\bar X$
of our family does not admit a
$\bar X$
of our family does not admit a
![]() $\Lambda $
-decomposition of the diagonal with respect to the finite set of points
$\Lambda $
-decomposition of the diagonal with respect to the finite set of points
![]() $S\times _R \bar K$
.
$S\times _R \bar K$
.
The following example extends the argument in the previous example to the nontrivial case of quartic fivefolds, which was the main result in [Reference Pavic and Schreieder36]. We leave some details to the reader; similar constructions and arguments will be given with full details in the proof of Theorem 1.1 below.
Example 4.6. Let k be an algebraically closed field of characteristic different from
![]() $2$
and let
$2$
and let
![]() $\Lambda ={\mathbb {Z}}/2$
. Consider the homogeneous polynomial
$\Lambda ={\mathbb {Z}}/2$
. Consider the homogeneous polynomial
where ![]() . We consider the degeneration
. We consider the degeneration
over
![]() $R = k[[t]]$
of a singular
$R = k[[t]]$
of a singular
![]() $(2,4)$
-complete intersection X in
$(2,4)$
-complete intersection X in
![]() ${\mathbb {P}}^7_{k((t))}$
into a union
${\mathbb {P}}^7_{k((t))}$
into a union
![]() $Y = Y_0 \cup Y_1$
of two singular quartic fivefolds intersecting in the singular integral quartic fourfold
$Y = Y_0 \cup Y_1$
of two singular quartic fivefolds intersecting in the singular integral quartic fourfold
which is birational to the quadric surface bundle example in [Reference Hassett, Pirutka and Tschinkel20, Example 8]. Let
![]() $S\subset \mathcal X$
be the closure of a finite set of points in X and let
$S\subset \mathcal X$
be the closure of a finite set of points in X and let
One can check that ![]() is strictly semi-stable. The singular quartic fivefold
is strictly semi-stable. The singular quartic fivefold
![]() $Y_i$
(
$Y_i$
(
![]() $i=0,1$
) is birational to
$i=0,1$
) is birational to
![]() ${\mathbb {P}}^5$
via the projection from the singular point of multiplicity
${\mathbb {P}}^5$
via the projection from the singular point of multiplicity
![]() $3$
given by
$3$
given by
![]() $x_i=0$
and
$x_i=0$
and
![]() $y_j = 0$
for all
$y_j = 0$
for all
![]() $i,j$
and
$i,j$
and
![]() $z=1$
(resp.
$z=1$
(resp.
![]() $w=1$
). The restriction of this projection to the open subset
$w=1$
). The restriction of this projection to the open subset
![]() $Y_i^\circ = Y_i \setminus W_{\mathcal {X}}$
gives an isomorphism with an open subset of
$Y_i^\circ = Y_i \setminus W_{\mathcal {X}}$
gives an isomorphism with an open subset of
![]() $\mathbb {A}^5 = {\mathbb {P}}^5 \setminus \{x_0 = 0\}$
. Hence,
$\mathbb {A}^5 = {\mathbb {P}}^5 \setminus \{x_0 = 0\}$
. Hence,
![]() $\operatorname {CH}_1(Y_i^\circ \times _k L) = 0$
for every field extension
$\operatorname {CH}_1(Y_i^\circ \times _k L) = 0$
for every field extension
![]() $L/k$
. Recall the unramified class
$L/k$
. Recall the unramified class
![]() $\alpha =(x_1/x_0,x_2/x_0)\in H^2_{nr}(k(Z),{\mathbb {Z}}/2)$
from [Reference Hassett, Pirutka and Tschinkel20, Proposition 11]. A direct computation (using, e.g., [Reference Schreieder44, Theorem 2.3]) shows that this class vanishes on the generic points of the divisors
$\alpha =(x_1/x_0,x_2/x_0)\in H^2_{nr}(k(Z),{\mathbb {Z}}/2)$
from [Reference Hassett, Pirutka and Tschinkel20, Proposition 11]. A direct computation (using, e.g., [Reference Schreieder44, Theorem 2.3]) shows that this class vanishes on the generic points of the divisors
![]() $\{x_0 x_1x_2=0\}$
and
$\{x_0 x_1x_2=0\}$
and
![]() $\{y_1=0\}$
(the latter uses that
$\{y_1=0\}$
(the latter uses that
![]() $\langle \frac {g}{x_0^2} \rangle $
is a subform of the quadratic form
$\langle \frac {g}{x_0^2} \rangle $
is a subform of the quadratic form
![]() $\langle 1, \frac {x_1}{x_0} \rangle $
over
$\langle 1, \frac {x_1}{x_0} \rangle $
over
![]() $k({\mathbb {P}}^2)$
). We then pass to a resolution or alteration of Z and apply the vanishing result in [Reference Schreieder44, Proposition 5.1] to the unramified class from [Reference Hassett, Pirutka and Tschinkel20, Proposition 11], to conclude via an ‘action of correspondences’ argument that Z does not admit a
$k({\mathbb {P}}^2)$
). We then pass to a resolution or alteration of Z and apply the vanishing result in [Reference Schreieder44, Proposition 5.1] to the unramified class from [Reference Hassett, Pirutka and Tschinkel20, Proposition 11], to conclude via an ‘action of correspondences’ argument that Z does not admit a
![]() $\Lambda $
-decomposition of the diagonal relative to
$\Lambda $
-decomposition of the diagonal relative to
![]() $W_Z = W_{\mathcal {X}} \cap Z = (S \cap Z) \cup \{x_0 x_1 x_2 y_1 = 0\} \cup \operatorname {Sing} Z \subset Z$
; see Theorem 6.1 below for more details on this type of argument. Thus,
$W_Z = W_{\mathcal {X}} \cap Z = (S \cap Z) \cup \{x_0 x_1 x_2 y_1 = 0\} \cup \operatorname {Sing} Z \subset Z$
; see Theorem 6.1 below for more details on this type of argument. Thus,
![]() $\operatorname {CH}_0(Z^\circ \times k(Z),\Lambda )$
is nontrivial, where
$\operatorname {CH}_0(Z^\circ \times k(Z),\Lambda )$
is nontrivial, where
![]() $Z^\circ =Z\setminus W_Z$
. It follows that the map
$Z^\circ =Z\setminus W_Z$
. It follows that the map
![]() $\Psi ^\Lambda _{Y^\circ _{k(Z)}}$
in Corollary 4.4 is not surjective. Consequently,
$\Psi ^\Lambda _{Y^\circ _{k(Z)}}$
in Corollary 4.4 is not surjective. Consequently,
![]() $\bar {X}$
does not admit a
$\bar {X}$
does not admit a
![]() $\Lambda $
-decomposition of the diagonal relative to
$\Lambda $
-decomposition of the diagonal relative to
![]() $W_{\bar X} = (W_{\mathcal {X}} \cap X)_{\bar K}$
. The substitution
$W_{\bar X} = (W_{\mathcal {X}} \cap X)_{\bar K}$
. The substitution
![]() $y_1=zy_1/x_0$
and
$y_1=zy_1/x_0$
and
![]() $w=-tx_0^2/z $
shows that the
$w=-tx_0^2/z $
shows that the
![]() $(2,4)$
complete intersection X is birational to the singular quartic hypersurface
$(2,4)$
complete intersection X is birational to the singular quartic hypersurface
One checks that the restriction of the induced birational map
![]() $X \dashrightarrow X'$
to
$X \dashrightarrow X'$
to
![]() $X \setminus W_{\mathcal {X}}$
yields an isomorphism onto its image. It follows that, even after base change to an algebraic closure of
$X \setminus W_{\mathcal {X}}$
yields an isomorphism onto its image. It follows that, even after base change to an algebraic closure of
![]() $k((t))$
,
$k((t))$
,
![]() $X'$
does not admit a decomposition of the diagonal relative to the union of
$X'$
does not admit a decomposition of the diagonal relative to the union of
![]() $\{x_0x_1x_2 y_1 z = 0\} \subset X'$
with a finite set of points. This produces a singular quartic fivefold that does not admit a
$\{x_0x_1x_2 y_1 z = 0\} \subset X'$
with a finite set of points. This produces a singular quartic fivefold that does not admit a
![]() $\Lambda $
-decomposition of the diagonal relative to a finite set of points (union its singular locus). We can then apply Lemma 3.8 to conclude that any smooth quartic fivefold that degenerates to
$\Lambda $
-decomposition of the diagonal relative to a finite set of points (union its singular locus). We can then apply Lemma 3.8 to conclude that any smooth quartic fivefold that degenerates to
![]() $X'$
does not admit a decomposition of the diagonal relative to a finite set of points. Altogether, this yields a simplified argument for the main result in [Reference Pavic and Schreieder36].
$X'$
does not admit a decomposition of the diagonal relative to a finite set of points. Altogether, this yields a simplified argument for the main result in [Reference Pavic and Schreieder36].
Remark 4.7. In order to prove Theorem 1.1, we would like to replace in the above argument the example [Reference Hassett, Pirutka and Tschinkel20, Example 8] with the higher dimensional examples in [Reference Schreieder44, Section 4 and 7]. This does not work directly as the unramified class
![]() $\alpha $
from [Reference Schreieder44, Proposition 5.1] does not vanish along the divisor
$\alpha $
from [Reference Schreieder44, Proposition 5.1] does not vanish along the divisor
![]() $\{y_1 = 0\}$
. We circumvent this problem by introducing an additional parameter
$\{y_1 = 0\}$
. We circumvent this problem by introducing an additional parameter
![]() $\lambda $
in the family, see Section 5. Further technical difficulties appear because we aim to apply the above argument inductively, where we degenerate to
$\lambda $
in the family, see Section 5. Further technical difficulties appear because we aim to apply the above argument inductively, where we degenerate to
![]() $Y_0\cup Y_1$
such that
$Y_0\cup Y_1$
such that
![]() $Y_0\cap Y_1$
is birational to the example of lower dimension we had treated before.
$Y_0\cap Y_1$
is birational to the example of lower dimension we had treated before.
4.1 Comparison to the map in [Reference Pavic and Schreieder36]
We recall the obstruction map from [Reference Pavic and Schreieder36] in the generality needed in this paper. Let
![]() $\Lambda $
be a ring and let
$\Lambda $
be a ring and let
![]() $Y = \bigcup \limits _{i \in I} Y_i$
be an snc scheme over a field k. Then we consider for
$Y = \bigcup \limits _{i \in I} Y_i$
be an snc scheme over a field k. Then we consider for
![]() $i,j \in I$
the homomorphism
$i,j \in I$
the homomorphism
 $$ \begin{align} \Phi^\Lambda_{Y_i,Y_j} \colon \operatorname{CH}_1(Y_i,\Lambda) \longrightarrow \operatorname{CH}_0(Y_j,\Lambda), \quad \gamma_i \mapsto \begin{cases} \iota_{ij,j\, \ast} (\gamma_i|_{Y_{ij}}) & \text{if } i \neq j, \\ - \sum\limits_{l \neq i} \iota_{il,i\, \ast} (\gamma_i|_{Y_{il}}) & \text{if } i = j, \end{cases} \end{align} $$
$$ \begin{align} \Phi^\Lambda_{Y_i,Y_j} \colon \operatorname{CH}_1(Y_i,\Lambda) \longrightarrow \operatorname{CH}_0(Y_j,\Lambda), \quad \gamma_i \mapsto \begin{cases} \iota_{ij,j\, \ast} (\gamma_i|_{Y_{ij}}) & \text{if } i \neq j, \\ - \sum\limits_{l \neq i} \iota_{il,i\, \ast} (\gamma_i|_{Y_{il}}) & \text{if } i = j, \end{cases} \end{align} $$
where ![]() is the natural inclusion and
is the natural inclusion and ![]() is the pullback along the regular embedding
is the pullback along the regular embedding
![]() $\iota _{ij,i}$
of the Cartier divisor
$\iota _{ij,i}$
of the Cartier divisor
![]() $Y_{ij}$
in
$Y_{ij}$
in
![]() $Y_i$
, see [Reference Pavic and Schreieder36, Definition 3.1 and Lemma 3.2]. We additionally set
$Y_i$
, see [Reference Pavic and Schreieder36, Definition 3.1 and Lemma 3.2]. We additionally set
for
![]() $j \in I$
and
$j \in I$
and

Lemma 4.8. Let R be a discrete valuation ring with residue field k and let
![]() $\mathcal {X} \to \operatorname {Spec} R$
be a strictly semi-stable R-scheme with special fibre
$\mathcal {X} \to \operatorname {Spec} R$
be a strictly semi-stable R-scheme with special fibre ![]() . Then for
. Then for
![]() $i,j \in I$
and
$i,j \in I$
and
![]() $\gamma _i \in \operatorname {CH}_1(Y_i,\Lambda )$
, we have
$\gamma _i \in \operatorname {CH}_1(Y_i,\Lambda )$
, we have
where
![]() $\iota _i \colon Y_i \to \mathcal {X}$
is the natural inclusion.
$\iota _i \colon Y_i \to \mathcal {X}$
is the natural inclusion.
Proof. This follows from [Reference Fulton17, Theorem 6.2], see also [Reference Pavic and Schreieder36, Lemma 3.2].
The effect of base changes for
![]() $\Phi $
has previously been studied in [Reference Pavic and Schreieder36, Section 4] and [Reference Lange30, Theorem 1.1]; some version of
$\Phi $
has previously been studied in [Reference Pavic and Schreieder36, Section 4] and [Reference Lange30, Theorem 1.1]; some version of
![]() $\Psi $
appeared implicitly in the proof of [Reference Pavic and Schreieder36, Proposition 4.4].
$\Psi $
appeared implicitly in the proof of [Reference Pavic and Schreieder36, Proposition 4.4].
Proposition 4.11 below compares
![]() $\Phi $
and
$\Phi $
and
![]() $\Psi $
and shows that the morphism
$\Psi $
and shows that the morphism
![]() $\Psi $
introduced in (4.1) has excellent properties under base changes. This will play an important role in the proof of Theorem 4.2 below.
$\Psi $
introduced in (4.1) has excellent properties under base changes. This will play an important role in the proof of Theorem 4.2 below.
Recall that the dual graph
![]() $G = (V,E)$
of an snc scheme Y without triple intersections is the graph whose vertices V correspond to the irreducible components of Y and whose edges E encode the codimension
$G = (V,E)$
of an snc scheme Y without triple intersections is the graph whose vertices V correspond to the irreducible components of Y and whose edges E encode the codimension
![]() $1$
subvarieties of Y. Moreover, we explicitly fix a total order ‘
$1$
subvarieties of Y. Moreover, we explicitly fix a total order ‘
![]() $<$
’ on the set of vertices V. We denote for a vertex
$<$
’ on the set of vertices V. We denote for a vertex
![]() $v \in V$
and an edge
$v \in V$
and an edge
![]() $e \in E$
the corresponding irreducible subvariety by
$e \in E$
the corresponding irreducible subvariety by
![]() $Y_v$
and
$Y_v$
and
![]() $Y_e$
, respectively. For an edge
$Y_e$
, respectively. For an edge
![]() $e \in E$
, we denote its end points by
$e \in E$
, we denote its end points by
![]() $v(e),w(e) \in V$
and assume that
$v(e),w(e) \in V$
and assume that
![]() $v(e) < w(e)$
. (Note that every edge in G has two distinct vertices.)
$v(e) < w(e)$
. (Note that every edge in G has two distinct vertices.)
Lemma 4.9. Let
![]() $\Lambda $
be a ring of finite characteristic
$\Lambda $
be a ring of finite characteristic
![]() $c \in {\mathbb {Z}}_{\geq 1}$
. Let R be a discrete valuation ring with fraction field K and algebraically closed residue field k. Let
$c \in {\mathbb {Z}}_{\geq 1}$
. Let R be a discrete valuation ring with fraction field K and algebraically closed residue field k. Let
![]() $\mathcal {X} \to \operatorname {Spec} R$
be a strictly semi-stable R-scheme whose special fibre
$\mathcal {X} \to \operatorname {Spec} R$
be a strictly semi-stable R-scheme whose special fibre ![]() has no triple intersections with dual graph
has no triple intersections with dual graph
![]() $G = (V,E)$
. Let
$G = (V,E)$
. Let
![]() $R'/R$
be a finite ramified extension of discrete valuation rings such that the ramification index r is divisible by c. Let
$R'/R$
be a finite ramified extension of discrete valuation rings such that the ramification index r is divisible by c. Let
![]() $\mathcal {X}' \to \mathcal {X} \times _R R'$
be a resolution given by repeatedly blowing up the non-Cartier components of the special fibre as in [Reference Hartl19]. Then the following holds:
$\mathcal {X}' \to \mathcal {X} \times _R R'$
be a resolution given by repeatedly blowing up the non-Cartier components of the special fibre as in [Reference Hartl19]. Then the following holds:
-
(1)
 $\mathcal {X}'$
is strictly semi-stable and its special fibre
$\mathcal {X}'$
is strictly semi-stable and its special fibre
 $Y'$
has no triple intersections. The dual graph
$Y'$
has no triple intersections. The dual graph
 $G' = (V',E')$
of
$G' = (V',E')$
of
 $Y'$
consists of the vertices
$Y'$
consists of the vertices
 $V' = V \cup (E \times \{1,\dots ,r-1\})$
and edges
$V' = V \cup (E \times \{1,\dots ,r-1\})$
and edges
 $(v',w') \in V' \times V'$
of the form
$(v',w') \in V' \times V'$
of the form  $$ \begin{align*}\begin{aligned} v' &= (e,n), &&w'= (e,n+1) &&\text{for } e \in E,\ n \in \{1,\dots,r-2\}, \\ v' &= v(e), &&w'= (e,1) &&\text{for } e \in E, \text{ or} \\ v' &= (e,r-1), &&w'= w(e) &&\text{for } e \in E. \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} v' &= (e,n), &&w'= (e,n+1) &&\text{for } e \in E,\ n \in \{1,\dots,r-2\}, \\ v' &= v(e), &&w'= (e,1) &&\text{for } e \in E, \text{ or} \\ v' &= (e,r-1), &&w'= w(e) &&\text{for } e \in E. \end{aligned} \end{align*} $$
-
(2) The components
 $Y^{\prime }_v$
for
$Y^{\prime }_v$
for
 $v \in V$
are isomorphic to
$v \in V$
are isomorphic to
 $Y_v$
and the components
$Y_v$
and the components
 $Y^{\prime }_{(e,n)}$
for
$Y^{\prime }_{(e,n)}$
for
 $e \in E$
and
$e \in E$
and
 $1 \leq n < r$
are
$1 \leq n < r$
are
 ${\mathbb {P}}^1$
-bundles over
${\mathbb {P}}^1$
-bundles over
 $Y_{e}$
with two disjoint sections given by the natural inclusion, where we set
$Y_{e}$
with two disjoint sections given by the natural inclusion, where we set $$ \begin{align*} &s_{(e,n)} \colon Y^{\prime}_{(e,n)} \cap Y^{\prime}_{(e,n+1)} \longrightarrow Y^{\prime}_{(e,n)}, \\ &s^{\prime}_{(e,n)} \colon Y^{\prime}_{(e,n-1)} \cap Y^{\prime}_{(e,n)} \longrightarrow Y^{\prime}_{(e,n)}, \end{align*} $$
$$ \begin{align*} &s_{(e,n)} \colon Y^{\prime}_{(e,n)} \cap Y^{\prime}_{(e,n+1)} \longrightarrow Y^{\prime}_{(e,n)}, \\ &s^{\prime}_{(e,n)} \colon Y^{\prime}_{(e,n-1)} \cap Y^{\prime}_{(e,n)} \longrightarrow Y^{\prime}_{(e,n)}, \end{align*} $$
 $Y^{\prime }_{(e,0)} = Y^{\prime }_{v(e)}$
and
$Y^{\prime }_{(e,0)} = Y^{\prime }_{v(e)}$
and
 $Y^{\prime }_{(e,r)} = Y^{\prime }_{w(e)}$
.
$Y^{\prime }_{(e,r)} = Y^{\prime }_{w(e)}$
.
Proof. The geometry of the resolution after finite base-change is explained, for example, in [Reference Pavic and Schreieder36, Section 4.2] for chains. The same arguments work for any special fibre that has no triple intersections, see also [Reference Lange30, Proposition 4.11].
Remark 4.10. The graph
![]() $(V',E')$
is obtained by subdividing each edge of
$(V',E')$
is obtained by subdividing each edge of
![]() $(V,E)$
into r pieces, see, for example, [Reference Lange30, Example A.1].
$(V,E)$
into r pieces, see, for example, [Reference Lange30, Example A.1].
Proposition 4.11. In the notation of Lemma 4.9, let
![]() $L/k$
be a field extension. If the cokernel of
$L/k$
be a field extension. If the cokernel of
is m-torsion for some integer m, then the cokernel of the map
 $$ \begin{align*}\Psi^\Lambda_{Y_L} \colon \bigoplus\limits_{l \in V} \operatorname{CH}_1(Y_l \times_k L,\Lambda) \longrightarrow \bigoplus\limits_{\substack{i,j \in V \\ i < j}} \operatorname{CH}_0(Y_{ij} \times_k L,\Lambda) \end{align*} $$
$$ \begin{align*}\Psi^\Lambda_{Y_L} \colon \bigoplus\limits_{l \in V} \operatorname{CH}_1(Y_l \times_k L,\Lambda) \longrightarrow \bigoplus\limits_{\substack{i,j \in V \\ i < j}} \operatorname{CH}_0(Y_{ij} \times_k L,\Lambda) \end{align*} $$
from (4.1) is m-torsion.
Proof. For ease of notation, we will deal with the case
![]() $L=k$
in what follows; the general case follows verbatim via the same argument.
$L=k$
in what follows; the general case follows verbatim via the same argument.
Recall that
![]() $q_{(e,n)}:Y^{\prime }_{(e,n)} \to Y_{e}$
is a
$q_{(e,n)}:Y^{\prime }_{(e,n)} \to Y_{e}$
is a
![]() ${\mathbb {P}}^1$
-bundle for
${\mathbb {P}}^1$
-bundle for
![]() $1 \leq n < r$
by item (2) in Lemma 4.9. Thus there exist isomorphisms
$1 \leq n < r$
by item (2) in Lemma 4.9. Thus there exist isomorphisms
see [Reference Fulton17, Theorem 3.3 (b)]. Note that the subspace
![]() $q_{(e,n)}^\ast \operatorname {CH}_0(Y_e,\Lambda )$
is canonical, while the subspace
$q_{(e,n)}^\ast \operatorname {CH}_0(Y_e,\Lambda )$
is canonical, while the subspace
![]() $\operatorname {CH}_1(Y_{e},\Lambda )\subset \operatorname {CH}_1(Y^{\prime }_{(e,n)},\Lambda )$
depends on the choice of a section of
$\operatorname {CH}_1(Y_{e},\Lambda )\subset \operatorname {CH}_1(Y^{\prime }_{(e,n)},\Lambda )$
depends on the choice of a section of
![]() $q_{(e,n)}:Y^{\prime }_{(e,n)} \to Y_{e}$
.
$q_{(e,n)}:Y^{\prime }_{(e,n)} \to Y_{e}$
.
Step 1. We will show that for every
![]() $\gamma ' \in \bigoplus _{v' \in V'} \operatorname {CH}_1(Y^{\prime }_{v'},\Lambda )$
, there exists another class
$\gamma ' \in \bigoplus _{v' \in V'} \operatorname {CH}_1(Y^{\prime }_{v'},\Lambda )$
, there exists another class
![]() $\gamma \in \bigoplus _{v' \in V'} \operatorname {CH}_1(Y^{\prime }_{v'},\Lambda )$
with the same image
$\gamma \in \bigoplus _{v' \in V'} \operatorname {CH}_1(Y^{\prime }_{v'},\Lambda )$
with the same image
![]() $\Phi ^\Lambda _{Y'}(\gamma ) = \Phi ^\Lambda _{Y'}(\gamma ')$
, such that the component
$\Phi ^\Lambda _{Y'}(\gamma ) = \Phi ^\Lambda _{Y'}(\gamma ')$
, such that the component
![]() $\gamma _{(e,n)}\in \operatorname {CH}_1(Y^{\prime }_{(e,n)},\Lambda )$
of
$\gamma _{(e,n)}\in \operatorname {CH}_1(Y^{\prime }_{(e,n)},\Lambda )$
of
![]() $\gamma $
satisfies
$\gamma $
satisfies
for each
![]() $(e,n) \in E \times \{1,\dots ,r-1\}$
.
$(e,n) \in E \times \{1,\dots ,r-1\}$
.
This follows from the argument in [Reference Pavic and Schreieder36, Lemma 4.3], which we explain for the convenience of the reader. Let
![]() $\gamma ' =(\gamma ^{\prime }_{v'})_{v'} \in \bigoplus _{v' \in V'} \operatorname {CH}_1(Y^{\prime }_{v'},\Lambda )$
be a collection of one-cycles and let
$\gamma ' =(\gamma ^{\prime }_{v'})_{v'} \in \bigoplus _{v' \in V'} \operatorname {CH}_1(Y^{\prime }_{v'},\Lambda )$
be a collection of one-cycles and let
![]() $(e,n) \in E \times \{1,\dots ,r-1\}$
. Using (4.3), we can write
$(e,n) \in E \times \{1,\dots ,r-1\}$
. Using (4.3), we can write
![]() $\gamma ^{\prime }_{(e,n)}$
as
$\gamma ^{\prime }_{(e,n)}$
as
for some
![]() $\alpha _{(e,n)} \in \operatorname {CH}_0(Y_e,\Lambda )$
and some
$\alpha _{(e,n)} \in \operatorname {CH}_0(Y_e,\Lambda )$
and some
![]() $\zeta _{(e,n)} \in \operatorname {CH}_1(Y_e,\Lambda )$
, where
$\zeta _{(e,n)} \in \operatorname {CH}_1(Y_e,\Lambda )$
, where
![]() $s_{(e,n)}$
is the section given in item (2) of Lemma 4.9. Lemma 4.8 implies that
$s_{(e,n)}$
is the section given in item (2) of Lemma 4.9. Lemma 4.8 implies that
where
![]() $s^{\prime }_{(e,n+1)} \colon Y^{\prime }_{(e,n)} \cap Y^{\prime }_{(e,n+1)} \to Y^{\prime }_{(e,n+1)}$
is the natural inclusion. Thus
$s^{\prime }_{(e,n+1)} \colon Y^{\prime }_{(e,n)} \cap Y^{\prime }_{(e,n+1)} \to Y^{\prime }_{(e,n+1)}$
is the natural inclusion. Thus
where
![]() $\gamma " = (\gamma ^{\prime \prime }_{v'})_{v'} \in \bigoplus _{v' \in V'} \operatorname {CH}_1(Y^{\prime }_{v'},\Lambda )$
is given by
$\gamma " = (\gamma ^{\prime \prime }_{v'})_{v'} \in \bigoplus _{v' \in V'} \operatorname {CH}_1(Y^{\prime }_{v'},\Lambda )$
is given by
 $$ \begin{align*}\gamma^{\prime\prime}_{v'} = \begin{cases} q_{(e,n)}^\ast \alpha_{(e,n)} & \text{if } v' = (e,n), \\ \gamma^{\prime}_{(e,n+1)} + s^{\prime}_{(e,n+1) \, \ast} \zeta_{(e,n)} & \text{if } v' = (e,n+1), \\ \gamma^{\prime}_v & \text{otherwise,} \end{cases} \end{align*} $$
$$ \begin{align*}\gamma^{\prime\prime}_{v'} = \begin{cases} q_{(e,n)}^\ast \alpha_{(e,n)} & \text{if } v' = (e,n), \\ \gamma^{\prime}_{(e,n+1)} + s^{\prime}_{(e,n+1) \, \ast} \zeta_{(e,n)} & \text{if } v' = (e,n+1), \\ \gamma^{\prime}_v & \text{otherwise,} \end{cases} \end{align*} $$
where we set
![]() $\gamma ^{\prime }_{(e,r)} = \gamma ^{\prime }_{w(e)} \in \operatorname {CH}_1(Y^{\prime }_{w(e)},\Lambda )$
. Applying this argument to every edge
$\gamma ^{\prime }_{(e,r)} = \gamma ^{\prime }_{w(e)} \in \operatorname {CH}_1(Y^{\prime }_{w(e)},\Lambda )$
. Applying this argument to every edge
![]() $e \in E$
and
$e \in E$
and
![]() $1 \leq n \leq r-1$
(in increasing order) finishes Step 1.
$1 \leq n \leq r-1$
(in increasing order) finishes Step 1.
Since Y is an snc scheme without triple intersections, we have
![]() $Y_e \cap Y_{e'} = \emptyset $
for all different
$Y_e \cap Y_{e'} = \emptyset $
for all different
![]() $e,e' \in E$
. In particular,
$e,e' \in E$
. In particular,
 $$ \begin{align*} \bigoplus\limits_{\substack{i,j \in V \\ \substack i < j}} \operatorname{CH}_0(Y_{ij},\Lambda) = \bigoplus\limits_{e \in E} \operatorname{CH}_0(Y_e,\Lambda). \end{align*} $$
$$ \begin{align*} \bigoplus\limits_{\substack{i,j \in V \\ \substack i < j}} \operatorname{CH}_0(Y_{ij},\Lambda) = \bigoplus\limits_{e \in E} \operatorname{CH}_0(Y_e,\Lambda). \end{align*} $$
Using this identification, there is a natural projection homomorphism
 $$ \begin{align*}\operatorname{pr}_e \colon \bigoplus\limits_{\substack{i,j \in V \\ \substack i < j}} \operatorname{CH}_0(Y_{ij},\Lambda) \longrightarrow \operatorname{CH}_0(Y_e,\Lambda) \end{align*} $$
$$ \begin{align*}\operatorname{pr}_e \colon \bigoplus\limits_{\substack{i,j \in V \\ \substack i < j}} \operatorname{CH}_0(Y_{ij},\Lambda) \longrightarrow \operatorname{CH}_0(Y_e,\Lambda) \end{align*} $$
for every
![]() $e \in E$
. We denote the composition
$e \in E$
. We denote the composition
![]() $\operatorname {pr}_e \circ \Psi _Y^\Lambda $
by
$\operatorname {pr}_e \circ \Psi _Y^\Lambda $
by
![]() $\Psi ^\Lambda _{Y,Y_e}$
.
$\Psi ^\Lambda _{Y,Y_e}$
.
Step 2. Let
![]() $\gamma = (\gamma _{v'})_{v'} \in \bigoplus _{v' \in V'} \operatorname {CH}_1(Y^{\prime }_{v'},\Lambda )$
be a one-cycle satisfying (4.5) and let
$\gamma = (\gamma _{v'})_{v'} \in \bigoplus _{v' \in V'} \operatorname {CH}_1(Y^{\prime }_{v'},\Lambda )$
be a one-cycle satisfying (4.5) and let
![]() $q \colon Y' \to Y$
be the natural morphism. We will show that for every
$q \colon Y' \to Y$
be the natural morphism. We will show that for every
![]() $e \in E$
$e \in E$
 $$ \begin{align} \sum\limits_{n = 1}^{r-1} n \cdot \Phi^{\Lambda}_{Y',Y^{\prime}_{(e,n)}}(\gamma) = \Psi^\Lambda_{Y,Y_e}(q_\ast \gamma) \in \operatorname{CH}_0(Y_e,\Lambda), \end{align} $$
$$ \begin{align} \sum\limits_{n = 1}^{r-1} n \cdot \Phi^{\Lambda}_{Y',Y^{\prime}_{(e,n)}}(\gamma) = \Psi^\Lambda_{Y,Y_e}(q_\ast \gamma) \in \operatorname{CH}_0(Y_e,\Lambda), \end{align} $$
where we view the zero-cycles on the left hand side as zero-cycles on
![]() $Y_e$
using (4.4).
$Y_e$
using (4.4).
To prove the above claim, first note that by assumption there exists
![]() $\alpha _{(e,n)} \in \operatorname {CH}_0(Y_{e},\Lambda )$
for every
$\alpha _{(e,n)} \in \operatorname {CH}_0(Y_{e},\Lambda )$
for every
![]() $(e,n) \in E \times \{1,\dots ,r-1\}$
such that
$(e,n) \in E \times \{1,\dots ,r-1\}$
such that
To simplify the formulas below, we set additionally

where
![]() $\gamma _{v(e)}|_{Y_{e}}$
is the pullback of
$\gamma _{v(e)}|_{Y_{e}}$
is the pullback of
![]() $\gamma _{v(e)}$
along the regular embedding
$\gamma _{v(e)}$
along the regular embedding
![]() $Y_e \hookrightarrow Y_{v(e)}$
of the Cartier divisor
$Y_e \hookrightarrow Y_{v(e)}$
of the Cartier divisor
![]() $Y_e \subset Y_{v(e)}$
. Note that we used here the isomorphisms
$Y_e \subset Y_{v(e)}$
. Note that we used here the isomorphisms
![]() $Y^{\prime }_{v(e)} \cong Y_{v(e)}$
. By (4.2), we see that for such a collection of one-cycles
$Y^{\prime }_{v(e)} \cong Y_{v(e)}$
. By (4.2), we see that for such a collection of one-cycles
![]() $\gamma =(\gamma _{v'})_{v'}$
, for
$\gamma =(\gamma _{v'})_{v'}$
, for
![]() $e \in E$
and
$e \in E$
and
![]() $1 \leq n < r$
,
$1 \leq n < r$
,
The following computation then shows the claim in Step 2:
 $$ \begin{align*}\begin{aligned} \sum\limits_{n = 1}^{r-1} n \cdot \Phi^{\Lambda}_{Y',Y^{\prime}_{(e,n)}}(\gamma) &= \sum\limits_{n = 1}^{r-1} n \left(- 2\alpha_{(e,n)} + \alpha_{(e,n-1)} + \alpha_{(e,n+1)}\right) \\ &= \alpha_{(e,0)} - r \alpha_{(e,r-1)} + (r-1) \alpha_{(e,r)} + \sum\limits_{n=1}^{r-2} (-2n + n+1 + n -1) \alpha_{(e,n)} \\ &= \alpha_{(e,0)} - \alpha_{(e,r)} \\ &= \gamma_{v(e)}|_{Y_{e}} - \gamma_{w(e)}|_{Y_{e}} \\ &= \Psi^\Lambda_{Y,Y_e}(q_\ast \gamma), \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} \sum\limits_{n = 1}^{r-1} n \cdot \Phi^{\Lambda}_{Y',Y^{\prime}_{(e,n)}}(\gamma) &= \sum\limits_{n = 1}^{r-1} n \left(- 2\alpha_{(e,n)} + \alpha_{(e,n-1)} + \alpha_{(e,n+1)}\right) \\ &= \alpha_{(e,0)} - r \alpha_{(e,r-1)} + (r-1) \alpha_{(e,r)} + \sum\limits_{n=1}^{r-2} (-2n + n+1 + n -1) \alpha_{(e,n)} \\ &= \alpha_{(e,0)} - \alpha_{(e,r)} \\ &= \gamma_{v(e)}|_{Y_{e}} - \gamma_{w(e)}|_{Y_{e}} \\ &= \Psi^\Lambda_{Y,Y_e}(q_\ast \gamma), \end{aligned} \end{align*} $$
where we used in the third equality that r is divisible by the characteristic c of
![]() $\Lambda $
.
$\Lambda $
.
We finish the proof of the proposition. To this end, let
be a collection of zero-cycles. By assumption, there exists a one-cycle
![]() $\gamma \in \bigoplus _{v' \in V'} \operatorname {CH}_1(Y^{\prime }_{v'},\Lambda )$
such that
$\gamma \in \bigoplus _{v' \in V'} \operatorname {CH}_1(Y^{\prime }_{v'},\Lambda )$
such that
![]() $\Phi ^\Lambda _{Y'}(\gamma ) = \beta $
, where
$\Phi ^\Lambda _{Y'}(\gamma ) = \beta $
, where
![]() $\beta $
is the collection of zero-cycles
$\beta $
is the collection of zero-cycles
![]() $(\beta _{v'})_{v'}$
in
$(\beta _{v'})_{v'}$
in
![]() $\bigoplus _{v' \in V'} \operatorname {CH}_0(Y^{\prime }_{v'},\Lambda )$
with
$\bigoplus _{v' \in V'} \operatorname {CH}_0(Y^{\prime }_{v'},\Lambda )$
with
 $$ \begin{align*}\beta_{v'} = \begin{cases} m \cdot z_{e} & \text{for } v' = (e,1), \\ 0 & \text{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*}\beta_{v'} = \begin{cases} m \cdot z_{e} & \text{for } v' = (e,1), \\ 0 & \text{otherwise.} \end{cases} \end{align*} $$
By Step 1, we can assume that
![]() $\gamma $
satisfies the condition (4.5). Then Step 2 shows that
$\gamma $
satisfies the condition (4.5). Then Step 2 shows that
![]() $m \cdot z = \Psi ^\Lambda _Y(q_\ast \gamma )$
is contained in the image of
$m \cdot z = \Psi ^\Lambda _Y(q_\ast \gamma )$
is contained in the image of
![]() $\Psi ^\Lambda _{Y}$
, as we want.
$\Psi ^\Lambda _{Y}$
, as we want.
Remark 4.12. The key point in the above proof is (4.6). In the chain of equalities showing (4.6), we used that
![]() $\Lambda $
has positive characteristic c and r is divisible by c. We do not know how to perform this step integrally, despite the fact that the (more general) analysis of
$\Lambda $
has positive characteristic c and r is divisible by c. We do not know how to perform this step integrally, despite the fact that the (more general) analysis of
![]() $\Phi $
under base changes carried out in [Reference Lange30] does in fact work integrally.
$\Phi $
under base changes carried out in [Reference Lange30] does in fact work integrally.
Remark 4.13. In [Reference Pavic and Schreieder36], the obstruction morphism
![]() $\Phi ^{\mathbb {Z}}_{Y}$
is studied for strictly semi-stable degenerations
$\Phi ^{\mathbb {Z}}_{Y}$
is studied for strictly semi-stable degenerations
![]() $\mathcal X\to \operatorname {Spec} R$
that are proper. Under this assumption, the image of
$\mathcal X\to \operatorname {Spec} R$
that are proper. Under this assumption, the image of
![]() $\Phi _Y^{\mathbb {Z}}$
is contained in the kernel of the degree map. The obstruction to the existence of a decomposition of the diagonal used in [Reference Pavic and Schreieder36] is the cokernel of
$\Phi _Y^{\mathbb {Z}}$
is contained in the kernel of the degree map. The obstruction to the existence of a decomposition of the diagonal used in [Reference Pavic and Schreieder36] is the cokernel of
![]() $\Phi _Y^{\mathbb {Z}}$
, viewed as a map to the subspace of degree-zero classes. In the above discussion, properness is dropped and so we cannot talk about the degree anymore. This is the reason why we work directly with the cokernel of
$\Phi _Y^{\mathbb {Z}}$
, viewed as a map to the subspace of degree-zero classes. In the above discussion, properness is dropped and so we cannot talk about the degree anymore. This is the reason why we work directly with the cokernel of
![]() $\Phi $
and
$\Phi $
and
![]() $\Psi $
, respectively. An important difference between
$\Psi $
, respectively. An important difference between
![]() $\Phi $
and
$\Phi $
and
![]() $\Psi $
is the fact that
$\Psi $
is the fact that
![]() $\Phi $
maps to the Chow groups of zero-cycles of the components, while
$\Phi $
maps to the Chow groups of zero-cycles of the components, while
![]() $\Psi $
maps to
$\Psi $
maps to
![]() $\operatorname {CH}_0$
of the intersections
$\operatorname {CH}_0$
of the intersections
![]() $Y_{ij}$
of two irreducible components of Y.
$Y_{ij}$
of two irreducible components of Y.
4.2 Proof of Theorem 4.2
Proof of Theorem 4.2
Let ![]() . Then there exists a finite field extension
. Then there exists a finite field extension
![]() $F/K$
such that
$F/K$
such that
![]() $\operatorname {Tor}^\Lambda (X_F,\emptyset ) = m$
.
$\operatorname {Tor}^\Lambda (X_F,\emptyset ) = m$
.
A suitable localization
![]() $R'$
of the integral closure of R in F is also a discrete valuation ring with fraction field F and residue field k. (Note that k is algebraically closed.) Up to replacing
$R'$
of the integral closure of R in F is also a discrete valuation ring with fraction field F and residue field k. (Note that k is algebraically closed.) Up to replacing
![]() $R'$
by a ramified extension, we can assume that the ramification index r of
$R'$
by a ramified extension, we can assume that the ramification index r of
![]() $R'/R$
is divisible by the characteristic c of
$R'/R$
is divisible by the characteristic c of
![]() $\Lambda $
.
$\Lambda $
.
Recall that the special fibre of
![]() $\mathcal {X} \to \operatorname {Spec} R$
is an snc scheme Y which has no triple intersections by assumption and we denote its dual graph by
$\mathcal {X} \to \operatorname {Spec} R$
is an snc scheme Y which has no triple intersections by assumption and we denote its dual graph by
![]() $(V,E)$
. By Lemma 4.9, there exists a resolution
$(V,E)$
. By Lemma 4.9, there exists a resolution
![]() $\tilde {\mathcal {X}} \to \mathcal {X} \times _R R'$
by repeatedly blowing-up the non-Cartier components of the special fibre. The generic fibre of
$\tilde {\mathcal {X}} \to \mathcal {X} \times _R R'$
by repeatedly blowing-up the non-Cartier components of the special fibre. The generic fibre of
![]() $\tilde {\mathcal {X}} \to \operatorname {Spec} R'$
is isomorphic to
$\tilde {\mathcal {X}} \to \operatorname {Spec} R'$
is isomorphic to
![]() $X_F$
and the special fibre
$X_F$
and the special fibre
![]() $Y'$
has no triple intersections and its dual graph
$Y'$
has no triple intersections and its dual graph
![]() $(V',E')$
is as in Lemma 4.9 (1). It then suffices by Proposition 4.11 to show that
$(V',E')$
is as in Lemma 4.9 (1). It then suffices by Proposition 4.11 to show that
![]() $\operatorname {coker} \Phi ^\Lambda _{Y^{\prime }_L}$
is m-torsion for all field extensions
$\operatorname {coker} \Phi ^\Lambda _{Y^{\prime }_L}$
is m-torsion for all field extensions
![]() $L/k$
.
$L/k$
.
Let
![]() $L/k$
be a field extension. By inflation of local rings (see, e.g., [Reference Bourbaki7, Chapter IX, Appendice §2, Corollaire du Théorème 1 and Exercice 4]), there exists an unramified extension of discrete valuation rings
$L/k$
be a field extension. By inflation of local rings (see, e.g., [Reference Bourbaki7, Chapter IX, Appendice §2, Corollaire du Théorème 1 and Exercice 4]), there exists an unramified extension of discrete valuation rings
![]() $A/R'$
such that the induced extension of residue fields is
$A/R'$
such that the induced extension of residue fields is
![]() $L/k$
. Passing to the completion, we may in addition assume that A is complete. We consider the base-change
$L/k$
. Passing to the completion, we may in addition assume that A is complete. We consider the base-change
which is a strictly semi-stable A-scheme, see, for example, [Reference Hartl19, Proposition 1.3]. We aim to show that the cokernel of the map
defined in (4.2) is m-torsion, where ![]() . Let
. Let
be a collection of zero-cycles. (By a moving lemma, we can assume that no
![]() $z_{w'}$
lies in the intersection of
$z_{w'}$
lies in the intersection of
![]() $Y^{\prime }_{w'}$
with another component
$Y^{\prime }_{w'}$
with another component
![]() $Y^{\prime }_{v'}$
.) By Hensel’s lemma, see [Reference Grothendieck14, Théorème 18.5.17], there exists a horizontal one-cycle
$Y^{\prime }_{v'}$
.) By Hensel’s lemma, see [Reference Grothendieck14, Théorème 18.5.17], there exists a horizontal one-cycle
![]() $h \in Z_1(\tilde {\mathcal {X}}_A,\Lambda )$
such that
$h \in Z_1(\tilde {\mathcal {X}}_A,\Lambda )$
such that
holds for all
![]() $w'$
already on the level of cycles (without rational equivalence). Recall that m is the
$w'$
already on the level of cycles (without rational equivalence). Recall that m is the
![]() $\Lambda $
-torsion order of
$\Lambda $
-torsion order of
![]() $X_F$
with respect to the empty set. Lemma 3.7 together with Nagata’s compactification theorem thus imply that
$X_F$
with respect to the empty set. Lemma 3.7 together with Nagata’s compactification theorem thus imply that
![]() $\operatorname {CH}_0(X_F \times _F F',\Lambda )$
is m-torsion for all field extensions
$\operatorname {CH}_0(X_F \times _F F',\Lambda )$
is m-torsion for all field extensions
![]() $F'/F$
. It follows that the restriction of
$F'/F$
. It follows that the restriction of
![]() $m \cdot h$
to the generic fibre
$m \cdot h$
to the generic fibre
![]() $\tilde {\mathcal {X}}_A \times _A F' = X_F \times _F F'$
vanishes, where
$\tilde {\mathcal {X}}_A \times _A F' = X_F \times _F F'$
vanishes, where
![]() $F'$
is the fraction field of A. Thus the horizontal one-cycle
$F'$
is the fraction field of A. Thus the horizontal one-cycle
![]() $m \cdot h$
is rationally equivalent to a cycle
$m \cdot h$
is rationally equivalent to a cycle
![]() $\gamma $
supported on the special fibre
$\gamma $
supported on the special fibre
![]() $Y^{\prime }_L$
by the localization exact sequence, see [Reference Fulton17, §1.8]. Hence, we see from (4.7) and Lemma 4.8 that
$Y^{\prime }_L$
by the localization exact sequence, see [Reference Fulton17, §1.8]. Hence, we see from (4.7) and Lemma 4.8 that
![]() $m \cdot z = \Phi ^\Lambda _{Y^{\prime }_L}(\gamma )$
is contained in the image of
$m \cdot z = \Phi ^\Lambda _{Y^{\prime }_L}(\gamma )$
is contained in the image of
![]() $\Phi ^\Lambda _{Y^{\prime }_L}$
. This shows that the cokernel of the map
$\Phi ^\Lambda _{Y^{\prime }_L}$
. This shows that the cokernel of the map
![]() $\Phi ^\Lambda _{Y^{\prime }_L}$
is m-torsion, which finishes the proof of the theorem.
$\Phi ^\Lambda _{Y^{\prime }_L}$
is m-torsion, which finishes the proof of the theorem.
Remark 4.14. The assumption that the special fibre has no triple intersections in Theorem 4.2 appears to be crucial. In particular, there seems to be no useful generalization of
![]() $\Psi $
to snc schemes with deeper strata, despite the fact that the definition of
$\Psi $
to snc schemes with deeper strata, despite the fact that the definition of
![]() $\Phi $
in (4.2) makes sense in more generality, see [Reference Pavic and Schreieder36, Section 3]. Indeed, if
$\Phi $
in (4.2) makes sense in more generality, see [Reference Pavic and Schreieder36, Section 3]. Indeed, if
![]() $Z=Y_{i_1}\cap \dots \cap Y_{i_n}$
is a stratum of the special fibre Y, then we can always perform an
$Z=Y_{i_1}\cap \dots \cap Y_{i_n}$
is a stratum of the special fibre Y, then we can always perform an
![]() $n:1$
base change followed by a resolution as in [Reference Hartl19] to arrive at a special fibre
$n:1$
base change followed by a resolution as in [Reference Hartl19] to arrive at a special fibre
![]() $\tilde Y$
that contains a component
$\tilde Y$
that contains a component
![]() $P_Z$
that is birational to a projective bundle over Z. However, for
$P_Z$
that is birational to a projective bundle over Z. However, for
![]() $n\geq 3$
, one can show via similar arguments as in [Reference Lange30] that the diagonal point of
$n\geq 3$
, one can show via similar arguments as in [Reference Lange30] that the diagonal point of
![]() $P_Z$
will automatically be in the image of
$P_Z$
will automatically be in the image of
![]() $\Phi _{\tilde Y_{k(P_Z)}}$
. (The key difference to
$\Phi _{\tilde Y_{k(P_Z)}}$
. (The key difference to
![]() $n\leq 2$
is that the blow-up of a component
$n\leq 2$
is that the blow-up of a component
![]() $Y_{i_j}$
along Z contains a positive dimensional projective bundle over Z if
$Y_{i_j}$
along Z contains a positive dimensional projective bundle over Z if
![]() $n\geq 3$
.) Hence, the strategy for disproving (retract) rationality in [Reference Pavic and Schreieder36, Reference Lange30] cannot be applied to strata given by the intersection of more than 2 components.
$n\geq 3$
.) Hence, the strategy for disproving (retract) rationality in [Reference Pavic and Schreieder36, Reference Lange30] cannot be applied to strata given by the intersection of more than 2 components.
5 Double cone construction
In this section we consider an explicit degeneration of a variety birational to a degree d hypersurface
![]() $X'$
into a union of two rational varieties whose intersection Z is a degree d hypersurface of lower dimension. We aim to apply Theorem 4.3 to this particular family and show that the
$X'$
into a union of two rational varieties whose intersection Z is a degree d hypersurface of lower dimension. We aim to apply Theorem 4.3 to this particular family and show that the
![]() $\Lambda $
-torsion order of Z divides the
$\Lambda $
-torsion order of Z divides the
![]() $\Lambda $
-torsion order of
$\Lambda $
-torsion order of
![]() $X'$
. In particular, we can inductively increase the dimension of retract irrational hypersurfaces.
$X'$
. In particular, we can inductively increase the dimension of retract irrational hypersurfaces.
Let
![]() $k = \overline {k_0(\lambda )}$
be an algebraic closure of the purely transcendental field extension
$k = \overline {k_0(\lambda )}$
be an algebraic closure of the purely transcendental field extension
![]() $k_0(\lambda )$
of an algebraically closed field
$k_0(\lambda )$
of an algebraically closed field
![]() $k_0$
. Write
$k_0$
. Write
![]() $N = n + r+ s$
for some integers
$N = n + r+ s$
for some integers
![]() $n,r,s \in {\mathbb {Z}}_{\geq 0}$
and consider integers
$n,r,s \in {\mathbb {Z}}_{\geq 0}$
and consider integers
![]() $d \geq 4$
and
$d \geq 4$
and
![]() $l \geq 1$
such that
$l \geq 1$
such that
![]() $2l \leq d$
. We denote the homogeneous coordinates of
$2l \leq d$
. We denote the homogeneous coordinates of
![]() ${\mathbb {P}}_k^{N+3}$
by
${\mathbb {P}}_k^{N+3}$
by
![]() $x_0,\dots ,x_n,y_1,\dots ,y_{r+1},z_1,\dots ,z_s,z,w$
. Let
$x_0,\dots ,x_n,y_1,\dots ,y_{r+1},z_1,\dots ,z_s,z,w$
. Let
be homogeneous polynomials of degree
![]() $\deg f = d$
and
$\deg f = d$
and
![]() $\deg a_i = d-2i$
which do not contain the variable
$\deg a_i = d-2i$
which do not contain the variable
![]() $y_j$
for some
$y_j$
for some
![]() $1 \leq j \leq r+1$
. Assume that
$1 \leq j \leq r+1$
. Assume that
Let ![]() be the local ring of
be the local ring of
![]() $\mathbb A^1$
at the origin and consider the complete intersection R-scheme
$\mathbb A^1$
at the origin and consider the complete intersection R-scheme

Lemma 5.1. The singular locus of
![]() $\mathcal X$
in (5.3) is contained in
$\mathcal X$
in (5.3) is contained in
![]() $\{x_0 = 0\} \subset \mathcal X$
.
$\{x_0 = 0\} \subset \mathcal X$
.
Proof. Consider the part of the Jacobian given by the derivatives
![]() $\partial _t$
and
$\partial _t$
and
![]() $\partial _z$
$\partial _z$
 $$ \begin{align*}\begin{pmatrix} 0 & x_0^{d-1} \\ x_0^2 & w \end{pmatrix}. \end{align*} $$
$$ \begin{align*}\begin{pmatrix} 0 & x_0^{d-1} \\ x_0^2 & w \end{pmatrix}. \end{align*} $$
As the singular locus is given by the vanishing of all
![]() $2 \times 2$
minors of the Jacobian, we see that it is contained in
$2 \times 2$
minors of the Jacobian, we see that it is contained in
![]() $\{x_0 = 0\}$
as claimed.
$\{x_0 = 0\}$
as claimed.
The generic fibre of the family
![]() $\mathcal X \to \operatorname {Spec} R$
in (5.3) is birational to a degree d hypersurface. For the inductive argument to work, it will be important to understand the corresponding birational map, which is the content of the following lemma, where we denote by
$\mathcal X \to \operatorname {Spec} R$
in (5.3) is birational to a degree d hypersurface. For the inductive argument to work, it will be important to understand the corresponding birational map, which is the content of the following lemma, where we denote by ![]() the fraction field of
the fraction field of
![]() $R=k[t]_{(t)}$
.
$R=k[t]_{(t)}$
.
Lemma 5.2. The generic fibre
![]() $X = \mathcal X \times _R K$
of the family (5.3) is birational to a geometrically integral degree d hypersurface
$X = \mathcal X \times _R K$
of the family (5.3) is birational to a geometrically integral degree d hypersurface
![]() $X'$
of the form
$X'$
of the form
 $$ \begin{align} X' = \left\{f + \sum\limits_{i=0}^l a_i' y_j^i = 0\right\} \subset {\mathbb{P}}^{N+2}_K, \end{align} $$
$$ \begin{align} X' = \left\{f + \sum\limits_{i=0}^l a_i' y_j^i = 0\right\} \subset {\mathbb{P}}^{N+2}_K, \end{align} $$
where f is as in (5.1) and
![]() $a^{\prime }_0,\dots ,a^{\prime }_l \in K[x_0,\dots ,x_n,y_1,\dots ,\hat {y_j},\dots ,y_{r+1},z_1,\dots ,z_{s+1}]$
are homogeneous polynomials of degree
$a^{\prime }_0,\dots ,a^{\prime }_l \in K[x_0,\dots ,x_n,y_1,\dots ,\hat {y_j},\dots ,y_{r+1},z_1,\dots ,z_{s+1}]$
are homogeneous polynomials of degree
![]() $\deg a^{\prime }_i = d - i$
. (An explicit formula for them is given in (5.6) below.) Moreover, they satisfy the following properties:
$\deg a^{\prime }_i = d - i$
. (An explicit formula for them is given in (5.6) below.) Moreover, they satisfy the following properties:
-
(1) The birational map induces an isomorphism between the open subsets
 $\{x_0 \neq 0\} \subset X$
and
$\{x_0 \neq 0\} \subset X$
and
 $\{x_0z_{s+1} \neq 0\} \subset X'$
;
$\{x_0z_{s+1} \neq 0\} \subset X'$
; -
(2) If there exists
 $e \in \mathbb N$
such that
$e \in \mathbb N$
such that
 $x_0^{ie} \mid a_i$
for all
$x_0^{ie} \mid a_i$
for all
 $i = 0,\dots ,l$
, then
$i = 0,\dots ,l$
, then
 $x_0^{ie} \mid a^{\prime }_i$
for all
$x_0^{ie} \mid a^{\prime }_i$
for all
 $i = 0,\dots ,l$
;
$i = 0,\dots ,l$
; -
(3) If all
 $a_0,\dots ,a_l$
do not contain one of the coordinates
$a_0,\dots ,a_l$
do not contain one of the coordinates
 $x_1,\dots ,x_n$
,
$x_1,\dots ,x_n$
,
 $y_1,\dots ,y_{r+1},$
or
$y_1,\dots ,y_{r+1},$
or
 $z_1,\dots ,z_{s}$
, then so do all
$z_1,\dots ,z_{s}$
, then so do all
 $a^{\prime }_0,\dots ,a^{\prime }_l$
;
$a^{\prime }_0,\dots ,a^{\prime }_l$
; -
(4) The polynomial
 $f + a_0'$
is irreducible over
$f + a_0'$
is irreducible over
 $\bar {K}$
.
$\bar {K}$
.
Proof. The parameter t is nonzero on the generic fibre X of (5.3). We then work on the open subset
![]() $\{x_0z\neq 0\}$
and perform the substitution
$\{x_0z\neq 0\}$
and perform the substitution
![]() $w=-tx_0^2z^{-1}$
to obtain the equation
$w=-tx_0^2z^{-1}$
to obtain the equation
 $$ \begin{align} f + \sum\limits_{i=0}^l a_i x_0^i y_j^i + x_0^{d-1}z - x_0^{d-2}(\lambda y_j + x_0)tx_0^2 z^{-1} = 0. \end{align} $$
$$ \begin{align} f + \sum\limits_{i=0}^l a_i x_0^i y_j^i + x_0^{d-1}z - x_0^{d-2}(\lambda y_j + x_0)tx_0^2 z^{-1} = 0. \end{align} $$
After the change of coordinates
![]() $y_j \mapsto y_jz / x_0 - \lambda ^{-1} x_0$
we arrive at the degree d hypersurface given by the vanishing of the polynomial
$y_j \mapsto y_jz / x_0 - \lambda ^{-1} x_0$
we arrive at the degree d hypersurface given by the vanishing of the polynomial
 $$ \begin{align*}f + \sum\limits_{i = 0}^l a_i (y_j z - \lambda^{-1}x_0^2)^i + x_0^{d-1}z - t\lambda x_0^{d-1}y_j = 0. \end{align*} $$
$$ \begin{align*}f + \sum\limits_{i = 0}^l a_i (y_j z - \lambda^{-1}x_0^2)^i + x_0^{d-1}z - t\lambda x_0^{d-1}y_j = 0. \end{align*} $$
Reordering the terms and renaming the coordinate z to
![]() $z_{s+1}$
, yields the claim that X is birational to a degree d hypersurface
$z_{s+1}$
, yields the claim that X is birational to a degree d hypersurface
![]() $X'$
of the form (5.4), where
$X'$
of the form (5.4), where
 $$ \begin{align} a^{\prime}_i = z_{s+1}^i \left(\sum\limits_{m = i}^l \binom{m}{i} (-\lambda^{-1})^{m-i} x_0^{2 m - 2 i} a_{m}\right) - \delta_{i,1} t \lambda x_0^{d-1} + \delta_{i,0} x_0^{d-1}z_{s+1}. \end{align} $$
$$ \begin{align} a^{\prime}_i = z_{s+1}^i \left(\sum\limits_{m = i}^l \binom{m}{i} (-\lambda^{-1})^{m-i} x_0^{2 m - 2 i} a_{m}\right) - \delta_{i,1} t \lambda x_0^{d-1} + \delta_{i,0} x_0^{d-1}z_{s+1}. \end{align} $$
This shows (2) and (3). Item (1) follows immediately from the above construction. Indeed, the coordinate transformation
![]() $y_j \mapsto y_jz/x_0 - \lambda ^{-1}x_0$
is invertible on the set
$y_j \mapsto y_jz/x_0 - \lambda ^{-1}x_0$
is invertible on the set
![]() $\{x_0z \neq 0\}$
with inverse given by
$\{x_0z \neq 0\}$
with inverse given by
![]() ${y_j \mapsto x_0(y_j + \lambda ^{-1}x_0)/z}$
. Thus the birational map induces an isomorphism between the open subsets
${y_j \mapsto x_0(y_j + \lambda ^{-1}x_0)/z}$
. Thus the birational map induces an isomorphism between the open subsets
![]() $\{x_0 \neq 0\} = \{x_0z \neq 0\} \subset X$
and
$\{x_0 \neq 0\} = \{x_0z \neq 0\} \subset X$
and
![]() $\{x_0 z_{s+1} \neq 0\} \subset X'$
. (Note that we renamed the z-coordinate to
$\{x_0 z_{s+1} \neq 0\} \subset X'$
. (Note that we renamed the z-coordinate to
![]() $z_{s+1}$
.) Next we prove (4). Since
$z_{s+1}$
.) Next we prove (4). Since
![]() $a_0'$
contains the variable
$a_0'$
contains the variable
![]() $z_{s+1}$
linearly by (5.6) and f does not contain
$z_{s+1}$
linearly by (5.6) and f does not contain
![]() $z_{s+1}$
, the condition (5.2) implies that
$z_{s+1}$
, the condition (5.2) implies that
![]() $f + a_0'$
is irreducible, as claimed. The hypersurface
$f + a_0'$
is irreducible, as claimed. The hypersurface
![]() $X'$
is geometrically integral by (4).
$X'$
is geometrically integral by (4).
Remark 5.3. The name ‘double cone construction’ is taken from [Reference Moe33]; it is reflected by the fact that the generic fibre of our degeneration can birationally be described by the equation (5.5) above, which contains the variable z and its inverse linearly and so its Newton polytope is a double cone. We note, however, that the degenerations that we use in this paper in general do not have toric singularities (e.g., because the singular hypersurfaces in [Reference Schreieder44] do not have toric singularities) and hence are different from the degenerations suitable for the method of [Reference Nicaise and Ottem34, Reference Moe33].
Corollary 5.4. The generic fibre X of (5.3) is geometrically integral.
Proof. Since X is a complete intersection in
![]() ${\mathbb {P}}^{N+3}_K$
, it is equidimensional and Cohen-Macaulay. As X is Cohen-Macaulay, X has no embedded components. By Lemma 5.2, we know that the open subset
${\mathbb {P}}^{N+3}_K$
, it is equidimensional and Cohen-Macaulay. As X is Cohen-Macaulay, X has no embedded components. By Lemma 5.2, we know that the open subset
![]() $\{x_0 \neq 0\} \subset X$
is isomorphic to an open subset of the geometrically integral hypersurface
$\{x_0 \neq 0\} \subset X$
is isomorphic to an open subset of the geometrically integral hypersurface
![]() $X' \subset {\mathbb {P}}^{N+2}_K$
in (5.4). Hence it suffices to show that the subset
$X' \subset {\mathbb {P}}^{N+2}_K$
in (5.4). Hence it suffices to show that the subset
![]() $\{x_0 = 0\} \subset X$
is not an irreducible component of X, which is clear because
$\{x_0 = 0\} \subset X$
is not an irreducible component of X, which is clear because
![]() $f + a_0$
is an irreducible polynomial by (5.2).
$f + a_0$
is an irreducible polynomial by (5.2).
We turn to the special fibre of the family (5.3). The special fibre
![]() $Y = \mathcal X \times _R k$
of the family (5.3) has two components, namely
$Y = \mathcal X \times _R k$
of the family (5.3) has two components, namely


The intersection ![]() is the degree d hypersurface
is the degree d hypersurface

The assumption (see (5.2)) that
![]() $f + a_0$
is irreducible implies that Z is integral.
$f + a_0$
is irreducible implies that Z is integral.
Lemma 5.5. The singular locus of
![]() $Y_0$
is contained in
$Y_0$
is contained in
![]() $\{x_0 = 0\}$
and the singular locus of
$\{x_0 = 0\}$
and the singular locus of
![]() $Y_1$
is contained in the closed subset
$Y_1$
is contained in the closed subset
![]() $\{x_0(\lambda y_j + x_0) = 0\}$
. Moreover,
$\{x_0(\lambda y_j + x_0) = 0\}$
. Moreover,
Proof. The derivative of the defining equation of
![]() $Y_0$
with respect to z is given by
$Y_0$
with respect to z is given by
 $$ \begin{align*}\partial_z \left(f + \sum\limits_{i = 0}^l a_ix_0^iy_j^i + x_0^{d-1}z\right) = x_0^{d-1}. \end{align*} $$
$$ \begin{align*}\partial_z \left(f + \sum\limits_{i = 0}^l a_ix_0^iy_j^i + x_0^{d-1}z\right) = x_0^{d-1}. \end{align*} $$
Hence, the singular locus of
![]() $Y_0$
is contained in
$Y_0$
is contained in
![]() $\{x_0 = 0\}$
.
$\{x_0 = 0\}$
.
The derivative of the defining equation of
![]() $Y_1$
with respect to w is given by
$Y_1$
with respect to w is given by
 $$ \begin{align*}\partial_w \left(f + \sum\limits_{i = 0}^l a_ix_0^iy_j^i + x_0^{d-2}(\lambda y_j + x_0)w\right) = x_0^{d-2} (\lambda y_j + x_0). \end{align*} $$
$$ \begin{align*}\partial_w \left(f + \sum\limits_{i = 0}^l a_ix_0^iy_j^i + x_0^{d-2}(\lambda y_j + x_0)w\right) = x_0^{d-2} (\lambda y_j + x_0). \end{align*} $$
Hence, the singular locus of
![]() $Y_1$
is contained in
$Y_1$
is contained in
![]() $\{x_0(\lambda y_j + x_0)=0\}$
as claimed. Finally, the last claim in the lemma is clear, as
$\{x_0(\lambda y_j + x_0)=0\}$
as claimed. Finally, the last claim in the lemma is clear, as
![]() $Z \subset Y_1$
is a Cartier divisor in
$Z \subset Y_1$
is a Cartier divisor in
![]() $Y_1$
(given by
$Y_1$
(given by
![]() $\{w = 0\} \subset Y_1$
).
$\{w = 0\} \subset Y_1$
).
In order to understand the obstruction map (4.1) for the family (5.3), we need to control the Chow group of the two components
![]() $Y_0$
and
$Y_0$
and
![]() $Y_1$
.
$Y_1$
.
Lemma 5.6. Let
![]() $Y_0$
and
$Y_0$
and
![]() $Y_1$
be as in (5.7) and (5.8), that is, the irreducible components of the special fibre of the family (5.3). Consider the divisors
$Y_1$
be as in (5.7) and (5.8), that is, the irreducible components of the special fibre of the family (5.3). Consider the divisors ![]() and
and ![]() . Then the natural push-forward maps
. Then the natural push-forward maps
are surjective for every field extension
![]() $L/k$
.
$L/k$
.
Proof. Let
![]() $L/k$
be a field extension. Recall that
$L/k$
be a field extension. Recall that
 $$ \begin{align*} Y_0 \times_k L &= \left\{f + \sum\limits_{i=0}^l a_i x_0^i y_j^i + x_0^{d-1}z = 0\right\} \subset {\mathbb{P}}_L^{N+2}, \\ Y_1 \times_k L &= \left\{f + \sum\limits_{i=0}^l a_i x_0^i y_j^i + x_0^{d-2}(\lambda y_j + x_0)w = 0\right\} \subset {\mathbb{P}}_L^{N+2}. \end{align*} $$
$$ \begin{align*} Y_0 \times_k L &= \left\{f + \sum\limits_{i=0}^l a_i x_0^i y_j^i + x_0^{d-1}z = 0\right\} \subset {\mathbb{P}}_L^{N+2}, \\ Y_1 \times_k L &= \left\{f + \sum\limits_{i=0}^l a_i x_0^i y_j^i + x_0^{d-2}(\lambda y_j + x_0)w = 0\right\} \subset {\mathbb{P}}_L^{N+2}. \end{align*} $$
We consider
![]() $Y_1 \times _k L$
. The projection away from
$Y_1 \times _k L$
. The projection away from
![]() $P = [0:\dots :0:1] \in {\mathbb {P}}_L^{N+2}$
induces a rational map
$P = [0:\dots :0:1] \in {\mathbb {P}}_L^{N+2}$
induces a rational map
Since w appears only linearly in the defining equation of
![]() $Y_1 \times _k L$
, the restriction of
$Y_1 \times _k L$
, the restriction of
![]() $\varphi $
to
$\varphi $
to
![]() $Y_1 \times _k L$
yields a birational map
$Y_1 \times _k L$
yields a birational map
which induces an isomorphism between the complements of the closed subschemes
![]() $D_1 \times _k L \subset Y_1 \times _k L$
and
$D_1 \times _k L \subset Y_1 \times _k L$
and ![]() , respectively. Since
, respectively. Since
![]() $H_1$
is a union of two hyperplanes in
$H_1$
is a union of two hyperplanes in
![]() ${\mathbb {P}}_L^{N+1}$
, the pushforward along the natural inclusion
${\mathbb {P}}_L^{N+1}$
, the pushforward along the natural inclusion
is surjective. Thus, by the localization exact sequence (see [Reference Fulton17, Proposition 1.8]), we find that
is surjective, as
![]() $\operatorname {CH}_1(Y_1 \times _k L \setminus D_1 \times _k L) \cong \operatorname {CH}_1({\mathbb {P}}^{N+1}_L \setminus H_1) = 0$
by the above discussion. A similar argument shows that
$\operatorname {CH}_1(Y_1 \times _k L \setminus D_1 \times _k L) \cong \operatorname {CH}_1({\mathbb {P}}^{N+1}_L \setminus H_1) = 0$
by the above discussion. A similar argument shows that
is surjective. This finishes the proof of the lemma.
The following proposition is the main result of this section; it will be used for the induction step in our inductive argument.
Proposition 5.7. Let
![]() $\Lambda $
be a ring of positive characteristic such that the exponential characteristic of
$\Lambda $
be a ring of positive characteristic such that the exponential characteristic of
![]() $k_0$
is invertible in
$k_0$
is invertible in
![]() $\Lambda $
. Let
$\Lambda $
. Let
![]() $\mathcal X \to \operatorname {Spec} R$
be the projective family from (5.3) with generic fibre X for some
$\mathcal X \to \operatorname {Spec} R$
be the projective family from (5.3) with generic fibre X for some
![]() $l \geq 2$
. Let
$l \geq 2$
. Let
![]() $Y_0$
and
$Y_0$
and
![]() $Y_1$
be the irreducible components of the special fibre as in (5.7) and (5.8) and denote their scheme-theoretic intersection by
$Y_1$
be the irreducible components of the special fibre as in (5.7) and (5.8) and denote their scheme-theoretic intersection by ![]() . Let
. Let
be any homogeneous polynomial such that its reduction
![]() $h_0$
modulo the maximal ideal in R has coefficients in
$h_0$
modulo the maximal ideal in R has coefficients in
![]() $k_0$
, that is,
$k_0$
, that is,
![]() $h_0 \in k_0[x_0,\dots ,x_n,y_1,\dots ,y_{r+1},z_1,\dots ,z_s]$
and such that X is smooth over
$h_0 \in k_0[x_0,\dots ,x_n,y_1,\dots ,y_{r+1},z_1,\dots ,z_s]$
and such that X is smooth over
![]() $K=k(t)$
away from
$K=k(t)$
away from ![]() . Then
. Then
where ![]() and
and ![]() . In particular,
. In particular,
where
![]() $X'$
is as in Lemma 5.2,
$X'$
is as in Lemma 5.2, ![]() , and
, and ![]() .
.
Remark 5.8. As a consequence of Lemma 5.1, the smoothness of
![]() $X \setminus W_X$
is automatically satisfied in characteristic
$X \setminus W_X$
is automatically satisfied in characteristic
![]() $0$
. This is not true in general, but we will choose in our applications
$0$
. This is not true in general, but we will choose in our applications
![]() $W_X$
carefully so that the condition holds (over any field).
$W_X$
carefully so that the condition holds (over any field).
Proof. Since
![]() $\Lambda $
is a ring of positive characteristic,
$\Lambda $
is a ring of positive characteristic,
is a positive integer
![]() $m \in {\mathbb {Z}}_{\geq 1}$
.
$m \in {\mathbb {Z}}_{\geq 1}$
.
Step 1. We will check that the assumptions in Theorem 4.3 are satisfied for the projective family
![]() $\mathcal {X} \to \operatorname {Spec} R$
from (5.3) with the closed subset
$\mathcal {X} \to \operatorname {Spec} R$
from (5.3) with the closed subset
As in Theorem 4.3, let ![]() . We note that
. We note that
![]() $W_X$
agrees with
$W_X$
agrees with
![]() $W_{\mathcal {X}} \cap X$
. The generic fibre X of
$W_{\mathcal {X}} \cap X$
. The generic fibre X of
![]() $\mathcal X \to \operatorname {Spec} R$
is geometrically integral by Corollary 5.4. The special fibre
$\mathcal X \to \operatorname {Spec} R$
is geometrically integral by Corollary 5.4. The special fibre ![]() consists of two components
consists of two components
![]() $Y^\circ = Y_0^\circ \cup Y_1^\circ $
such that
$Y^\circ = Y_0^\circ \cup Y_1^\circ $
such that
![]() $Y_0^\circ $
,
$Y_0^\circ $
,
![]() $Y_1^\circ $
, and their intersection
$Y_1^\circ $
, and their intersection ![]() are smooth and integral, see also Lemma 5.5. In particular,
are smooth and integral, see also Lemma 5.5. In particular,
![]() $Y^\circ $
is an snc scheme, see Definition 2.1. The singular locus of
$Y^\circ $
is an snc scheme, see Definition 2.1. The singular locus of
![]() $\mathcal X$
is contained in
$\mathcal X$
is contained in
![]() $\{x_0 = 0\}$
by Lemma 5.1. It follows from this that
$\{x_0 = 0\}$
by Lemma 5.1. It follows from this that
![]() $Y^\circ _i$
is a Cartier divisor on
$Y^\circ _i$
is a Cartier divisor on
![]() $\mathcal X^\circ $
for
$\mathcal X^\circ $
for
![]() $i=0,1$
. The generic fibre of the R-scheme
$i=0,1$
. The generic fibre of the R-scheme ![]() is equal to
is equal to
![]() $X \setminus W_X$
and thus smooth by assumption. In particular,
$X \setminus W_X$
and thus smooth by assumption. In particular,
![]() $\mathcal {X}^\circ \to \operatorname {Spec} R$
is strictly semi-stable, see Definition 2.2. It follows that the assumptions (1) and (2) in Theorem 4.3 are satisfied for
$\mathcal {X}^\circ \to \operatorname {Spec} R$
is strictly semi-stable, see Definition 2.2. It follows that the assumptions (1) and (2) in Theorem 4.3 are satisfied for
![]() $\mathcal X \to \operatorname {Spec} R$
and the closed subset
$\mathcal X \to \operatorname {Spec} R$
and the closed subset
![]() $W_{\mathcal {X}} \subset \mathcal X$
. This concludes Step 1.
$W_{\mathcal {X}} \subset \mathcal X$
. This concludes Step 1.
Recall that Z is integral and let
![]() $\delta _{Z^\circ }\in Z^\circ _{k(Z)}$
denote the diagonal point of
$\delta _{Z^\circ }\in Z^\circ _{k(Z)}$
denote the diagonal point of
![]() $Z^\circ $
, which is dense open in Z.
$Z^\circ $
, which is dense open in Z.
Step 2. We will show that there is a one-cycle
![]() $\gamma \in \operatorname {CH}_1(Y_{1} \times _k k(Z),\Lambda )$
, supported on
$\gamma \in \operatorname {CH}_1(Y_{1} \times _k k(Z),\Lambda )$
, supported on
![]() $\{x_0(\lambda y_j + x_0) =0 \} \subset Y_1\times _k k(Z)$
, such that
$\{x_0(\lambda y_j + x_0) =0 \} \subset Y_1\times _k k(Z)$
, such that
where
![]() $ \iota \colon Y_1^\circ \times _k k(Z) \hookrightarrow Y_1 \times _k k(Z)$
denotes the natural open embedding and
$ \iota \colon Y_1^\circ \times _k k(Z) \hookrightarrow Y_1 \times _k k(Z)$
denotes the natural open embedding and
![]() $(\iota ^\ast \gamma )|_{Z^\circ _{k(Z)}}$
the pullback of the one-cycle to the Cartier divisor
$(\iota ^\ast \gamma )|_{Z^\circ _{k(Z)}}$
the pullback of the one-cycle to the Cartier divisor
![]() $Z^\circ _{k(Z)} \subset Y_1^\circ \times _k k(Z)$
along the natural regular embedding.
$Z^\circ _{k(Z)} \subset Y_1^\circ \times _k k(Z)$
along the natural regular embedding.
By Step 1, Theorem 4.3 implies that the cokernel of the map
from (4.1) (with
![]() $0 < 1$
) is m-torsion for every field extension
$0 < 1$
) is m-torsion for every field extension
![]() $L/k$
. In particular,
$L/k$
. In particular,
Note that
![]() $\operatorname {CH}_1(Y_0^\circ \times _k k(Z),\Lambda ) = 0$
by Lemma 5.6 and that the pull-back
$\operatorname {CH}_1(Y_0^\circ \times _k k(Z),\Lambda ) = 0$
by Lemma 5.6 and that the pull-back
is surjective by [Reference Fulton17, Proposition 1.8]. Hence there exists a one-cycle
![]() $\gamma \in \operatorname {CH}_1(Y_{1} \times _k k(Z),\Lambda )$
such that
$\gamma \in \operatorname {CH}_1(Y_{1} \times _k k(Z),\Lambda )$
such that
![]() $ m \cdot \delta _{Z^\circ } = (\iota ^\ast \gamma )|_{Z^\circ _{k(Z)}}$
. By Lemma 5.6 we can further assume that
$ m \cdot \delta _{Z^\circ } = (\iota ^\ast \gamma )|_{Z^\circ _{k(Z)}}$
. By Lemma 5.6 we can further assume that
![]() $\gamma $
is supported on
$\gamma $
is supported on
![]() $\{x_0(\lambda y_j + x_0) =0 \} \subset Y_1\times _k k(Z)$
. This concludes Step 2.
$\{x_0(\lambda y_j + x_0) =0 \} \subset Y_1\times _k k(Z)$
. This concludes Step 2.
Step 3. We now specialize
![]() $\lambda \to 0$
and aim to compute the image of (5.10) under the corresponding specialization map on Chow groups (see Lemma 2.3); we will show that the specialization of the one-cycle
$\lambda \to 0$
and aim to compute the image of (5.10) under the corresponding specialization map on Chow groups (see Lemma 2.3); we will show that the specialization of the one-cycle
![]() $\gamma $
vanishes and so does the specialization of
$\gamma $
vanishes and so does the specialization of
![]() $m\cdot \delta _{Z^\circ }$
.
$m\cdot \delta _{Z^\circ }$
.
Consider the discrete valuation ring
![]() $B = k_0[\lambda ]_{(\lambda )}$
with residue field
$B = k_0[\lambda ]_{(\lambda )}$
with residue field
![]() $k_0$
and fraction field
$k_0$
and fraction field
![]() $k_0(\lambda )$
. Recall that k is an algebraic closure of
$k_0(\lambda )$
. Recall that k is an algebraic closure of
![]() $k_0(\lambda )$
. Then consider the flat projective B-schemes
$k_0(\lambda )$
. Then consider the flat projective B-schemes

where f and
![]() $a_i$
are as in (5.1). Note that Z and
$a_i$
are as in (5.1). Note that Z and
![]() $Y_1$
are the geometric generic fibres of
$Y_1$
are the geometric generic fibres of
![]() $\mathcal {Z}$
and
$\mathcal {Z}$
and
![]() $\mathcal {Y}_1$
, respectively. Let
$\mathcal {Y}_1$
, respectively. Let
![]() $\mathcal {Z}^\circ \subset \mathcal {Z}$
and
$\mathcal {Z}^\circ \subset \mathcal {Z}$
and
![]() $\mathcal {Y}_{1}^\circ \subset \mathcal {Y}_1$
be the complement of the closure of
$\mathcal {Y}_{1}^\circ \subset \mathcal {Y}_1$
be the complement of the closure of
![]() $W_Z$
in
$W_Z$
in
![]() $\mathcal {Z}$
and of
$\mathcal {Z}$
and of
![]() $W_{Y_1}$
in
$W_{Y_1}$
in
![]() $\mathcal {Y}_1$
, respectively. Note that
$\mathcal {Y}_1$
, respectively. Note that
![]() $Z^\circ = Z \setminus W_Z$
and
$Z^\circ = Z \setminus W_Z$
and
![]() $Y_1^\circ = Y_1 \setminus W_{Y_1}$
are the geometric generic fibres of
$Y_1^\circ = Y_1 \setminus W_{Y_1}$
are the geometric generic fibres of
![]() $\mathcal {Z}^\circ $
and
$\mathcal {Z}^\circ $
and
![]() $\mathcal {Y}_1^\circ $
, respectively. We denote the special fibres by
$\mathcal {Y}_1^\circ $
, respectively. We denote the special fibres by
![]() $Z_0^\circ $
and
$Z_0^\circ $
and
![]() $Y_{1,0}^\circ $
, respectively. By Lemma 2.3, there exist specialization maps induced by Fulton’s specialization map for the flat
$Y_{1,0}^\circ $
, respectively. By Lemma 2.3, there exist specialization maps induced by Fulton’s specialization map for the flat
![]() $\mathcal {O}_{\mathcal {Z},Z_0}$
-schemes
$\mathcal {O}_{\mathcal {Z},Z_0}$
-schemes
![]() $\mathcal {Z}^\circ \times _B \mathcal {O}_{\mathcal {Z},Z_0}$
,
$\mathcal {Z}^\circ \times _B \mathcal {O}_{\mathcal {Z},Z_0}$
,
![]() $\mathcal {Y}_1^\circ \times _B \mathcal {O}_{\mathcal {Z},Z_0}$
, and
$\mathcal {Y}_1^\circ \times _B \mathcal {O}_{\mathcal {Z},Z_0}$
, and
![]() $\mathcal {Y}_1 \times _B \mathcal {O}_{\mathcal {Z},Z_0}$
$\mathcal {Y}_1 \times _B \mathcal {O}_{\mathcal {Z},Z_0}$
 $$ \begin{align*}\begin{aligned} \operatorname{sp}_{Z^\circ} &\colon \operatorname{CH}_0(Z^\circ \times_k k(Z),\Lambda) \longrightarrow \operatorname{CH}_0(Z_0^\circ \times_{k_0} k_0(Z_0),\Lambda), \\ \operatorname{sp}_{Y_1^\circ} &\colon \operatorname{CH}_1(Y_1^\circ \times_k k(Z),\Lambda) \longrightarrow \operatorname{CH}_1(Y_{1,0}^\circ \times_{k_0} k_0(Z_0),\Lambda), \\ \operatorname{sp}_{Y_1} &\colon \operatorname{CH}_1(Y_1 \times_k k(Z),\Lambda) \longrightarrow \operatorname{CH}_1(Y_{1,0} \times_{k_0} k_0(Z_0),\Lambda), \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} \operatorname{sp}_{Z^\circ} &\colon \operatorname{CH}_0(Z^\circ \times_k k(Z),\Lambda) \longrightarrow \operatorname{CH}_0(Z_0^\circ \times_{k_0} k_0(Z_0),\Lambda), \\ \operatorname{sp}_{Y_1^\circ} &\colon \operatorname{CH}_1(Y_1^\circ \times_k k(Z),\Lambda) \longrightarrow \operatorname{CH}_1(Y_{1,0}^\circ \times_{k_0} k_0(Z_0),\Lambda), \\ \operatorname{sp}_{Y_1} &\colon \operatorname{CH}_1(Y_1 \times_k k(Z),\Lambda) \longrightarrow \operatorname{CH}_1(Y_{1,0} \times_{k_0} k_0(Z_0),\Lambda), \end{aligned} \end{align*} $$
where
![]() $Y_{1,0}$
denotes the special fibre of the B-scheme
$Y_{1,0}$
denotes the special fibre of the B-scheme
![]() $\mathcal {Y}_1$
.
$\mathcal {Y}_1$
.
We now apply the specialization
![]() $\operatorname {sp}_{Z^\circ }$
to the zero-cycle (5.10). By Lemma 2.3, we get
$\operatorname {sp}_{Z^\circ }$
to the zero-cycle (5.10). By Lemma 2.3, we get
where
![]() $|_{Z^\circ _{k(Z)}}$
and
$|_{Z^\circ _{k(Z)}}$
and
![]() $|_{Z^\circ _{0,k_0(Z_0)}}$
denote the pullback along the regular embedding of the Cartier divisor
$|_{Z^\circ _{0,k_0(Z_0)}}$
denote the pullback along the regular embedding of the Cartier divisor
![]() $Z^\circ _{k(Z)}$
and
$Z^\circ _{k(Z)}$
and
![]() $Z^\circ _{0,k_0(Z_0)}$
in
$Z^\circ _{0,k_0(Z_0)}$
in
![]() $Y_1^\circ \times _k k(Z)$
and
$Y_1^\circ \times _k k(Z)$
and
![]() $Y_{1,0}^\circ \times _{k_0} k_0(Z_0)$
, respectively. Recall that the one-cycle
$Y_{1,0}^\circ \times _{k_0} k_0(Z_0)$
, respectively. Recall that the one-cycle
![]() $\gamma $
is supported on
$\gamma $
is supported on
![]() $\{x_0(\lambda y_j + x_0) =0 \} \subset Y_1\times _k k(Z)$
. Thus the specialization
$\{x_0(\lambda y_j + x_0) =0 \} \subset Y_1\times _k k(Z)$
. Thus the specialization
![]() $\operatorname {sp}_{Y_1}(\gamma ) \in \operatorname {CH}_1(Y_{1,0},\Lambda )$
is supported on
$\operatorname {sp}_{Y_1}(\gamma ) \in \operatorname {CH}_1(Y_{1,0},\Lambda )$
is supported on
![]() $\{x_0^2 =0\} \subset Y_{1,0}$
. In particular
$\{x_0^2 =0\} \subset Y_{1,0}$
. In particular
as the subset
![]() $\{x_0 = 0\} \subset Y_{1,0}$
is contained in the specialization of
$\{x_0 = 0\} \subset Y_{1,0}$
is contained in the specialization of
![]() $W_{Y_1}$
and
$W_{Y_1}$
and
![]() $\operatorname {sp}$
commutes with pullbacks along open immersions. Hence, the right hand side of (5.11) vanishes, which concludes Step 3.
$\operatorname {sp}$
commutes with pullbacks along open immersions. Hence, the right hand side of (5.11) vanishes, which concludes Step 3.
By Step 3,
where
![]() $W_{Z_0} \subset Z_0$
is the specialization of
$W_{Z_0} \subset Z_0$
is the specialization of
![]() $W_Z \subset Z$
. We note that
$W_Z \subset Z$
. We note that
![]() $Z = Z_0 \times _{k_0} k$
and
$Z = Z_0 \times _{k_0} k$
and
![]() $W_Z = W_{Z_0} \times _{k_0} k$
, because the defining equations of Z and
$W_Z = W_{Z_0} \times _{k_0} k$
, because the defining equations of Z and
![]() $W_Z$
are defined over
$W_Z$
are defined over
![]() $k_0$
. Hence, the proposition follows from Lemma 3.6 (e), as
$k_0$
. Hence, the proposition follows from Lemma 3.6 (e), as
![]() $m = \operatorname {Tor}^\Lambda (\bar {X},W_{\bar {X}})$
.
$m = \operatorname {Tor}^\Lambda (\bar {X},W_{\bar {X}})$
.
6 Base case
Our argument will rely on an inductive application of a degeneration as in Section 5. For the start of the induction we will use the explicit example of a singular hypersurface with nontrivial unramified cohomology from the proof of [Reference Schreieder45, Theorem 7.1]. We recall the example in what follows.
Let k be an algebraically closed field and let
![]() $m \geq 2$
be an integer coprime to the exponential characteristic of k. Let
$m \geq 2$
be an integer coprime to the exponential characteristic of k. Let
![]() $n \geq 2$
and
$n \geq 2$
and
![]() $r \leq 2^n-2$
be positive integers. Let
$r \leq 2^n-2$
be positive integers. Let
![]() $x_0,\dots ,x_n,y_1,\dots ,y_{r+1}$
be the coordinates of
$x_0,\dots ,x_n,y_1,\dots ,y_{r+1}$
be the coordinates of
![]() ${\mathbb {P}}^{n+r+1}$
and let
${\mathbb {P}}^{n+r+1}$
and let
![]() $\pi \in k$
be an element that is transcendental over the prime field of k. Consider the homogeneous polynomial from [Reference Schreieder45, Equation (21)]
$\pi \in k$
be an element that is transcendental over the prime field of k. Consider the homogeneous polynomial from [Reference Schreieder45, Equation (21)]

in
![]() $k[x_0,\dots ,x_n]$
of degree
$k[x_0,\dots ,x_n]$
of degree
![]() $\deg g = m \left \lceil \frac {n+1}{m}\right \rceil \leq n+m$
. Using this we define the homogeneous polynomial
$\deg g = m \left \lceil \frac {n+1}{m}\right \rceil \leq n+m$
. Using this we define the homogeneous polynomial

in
![]() $k[x_0,\dots ,x_n,y_1,\dots ,y_{r+1}]$
of degree
$k[x_0,\dots ,x_n,y_1,\dots ,y_{r+1}]$
of degree
![]() $m+n$
, where
$m+n$
, where
with
![]() $\varepsilon _i$
the
$\varepsilon _i$
the
![]() $(i-1)$
-th digit in the
$(i-1)$
-th digit in the
![]() $2$
-adic representation of j, that is,
$2$
-adic representation of j, that is,
![]() $j = \sum _{i} \varepsilon _i 2^{i-1}$
with
$j = \sum _{i} \varepsilon _i 2^{i-1}$
with
![]() $\varepsilon _i \in \{0,1\}$
. Consider the associated hypersurface
$\varepsilon _i \in \{0,1\}$
. Consider the associated hypersurface
of degree
![]() $m+n$
.
$m+n$
.
Theorem 6.1. Let
![]() $l\in k[x_0,\dots ,x_n]$
be any nontrivial homogeneous polynomial and consider
$l\in k[x_0,\dots ,x_n]$
be any nontrivial homogeneous polynomial and consider
where Z is as in (6.3). Then
![]() $\operatorname {Tor}^{{\mathbb {Z}}/m}(Z,W_Z)=m$
.
$\operatorname {Tor}^{{\mathbb {Z}}/m}(Z,W_Z)=m$
.
We have the following immediate corollary.
Corollary 6.2. Let
![]() $h,l',l" \in k[x_0,\dots ,x_n]$
be nontrivial homogeneous polynomials such that h is irreducible of degree
$h,l',l" \in k[x_0,\dots ,x_n]$
be nontrivial homogeneous polynomials such that h is irreducible of degree
![]() $m + n + \deg l'$
. Let
$m + n + \deg l'$
. Let
![]() $k' = k(\rho )$
be a purely transcendental field extension of k. Consider the hypersurface
$k' = k(\rho )$
be a purely transcendental field extension of k. Consider the hypersurface
of degree
![]() $m + n + \deg l'$
. Then
$m + n + \deg l'$
. Then
![]() $\operatorname {Tor}^{{\mathbb {Z}}/m}(\bar {Z}_\rho ,W_{\bar {Z}_\rho }) = m$
, where
$\operatorname {Tor}^{{\mathbb {Z}}/m}(\bar {Z}_\rho ,W_{\bar {Z}_\rho }) = m$
, where
![]() $\bar {Z}_\rho = Z_\rho \times _{k'} \bar {k'}$
and
$\bar {Z}_\rho = Z_\rho \times _{k'} \bar {k'}$
and
Proof. Consider the pair
![]() $(Z_\rho ,W_{Z_\rho })$
and let
$(Z_\rho ,W_{Z_\rho })$
and let
![]() $(Z_0,W_{Z_0})$
be the pair obtained by specializing
$(Z_0,W_{Z_0})$
be the pair obtained by specializing
![]() $\rho \to 0$
, that is,
$\rho \to 0$
, that is,
 $$ \begin{align*}\begin{aligned} Z_0 &= \{l' \cdot F = 0\} \subset {\mathbb{P}}^{n+r+1}_k, \\ W_{Z_0} &= \{y_{r+1}l'l" =0 \} \cup Z_{0}^{\operatorname{sing}} \subset Z_0. \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} Z_0 &= \{l' \cdot F = 0\} \subset {\mathbb{P}}^{n+r+1}_k, \\ W_{Z_0} &= \{y_{r+1}l'l" =0 \} \cup Z_{0}^{\operatorname{sing}} \subset Z_0. \end{aligned} \end{align*} $$
Note that the scheme
![]() $Z_0$
is reducible, but the open subscheme
$Z_0$
is reducible, but the open subscheme ![]() is integral as the polynomial F is irreducible. Hence, the torsion order
is integral as the polynomial F is irreducible. Hence, the torsion order
![]() $\operatorname {Tor}^{{\mathbb {Z}}/m}(Z_0,W_{Z_0})$
is defined, see Remark 3.5. We observe that
$\operatorname {Tor}^{{\mathbb {Z}}/m}(Z_0,W_{Z_0})$
is defined, see Remark 3.5. We observe that
![]() $U_0 = Z \setminus W_Z$
, where the pair
$U_0 = Z \setminus W_Z$
, where the pair
![]() $(Z,W_Z)$
is as in Theorem 6.1 with
$(Z,W_Z)$
is as in Theorem 6.1 with
![]() $l = l' \cdot l" \in k[x_0,\dots ,x_n]$
. Thus, we get
$l = l' \cdot l" \in k[x_0,\dots ,x_n]$
. Thus, we get
![]() $\operatorname {Tor}^{{\mathbb {Z}}/m}(Z_0,W_{Z_0}) = m$
by Theorem 6.1. Hence, m divides
$\operatorname {Tor}^{{\mathbb {Z}}/m}(Z_0,W_{Z_0}) = m$
by Theorem 6.1. Hence, m divides
![]() $\operatorname {Tor}^{{\mathbb {Z}}/m}(\bar {Z}_\rho ,W_{\bar {Z}_\rho })$
by Lemma 3.8. Conversely, any
$\operatorname {Tor}^{{\mathbb {Z}}/m}(\bar {Z}_\rho ,W_{\bar {Z}_\rho })$
by Lemma 3.8. Conversely, any
![]() ${\mathbb {Z}}/m$
-torsion order can be at most m. Hence,
${\mathbb {Z}}/m$
-torsion order can be at most m. Hence,
![]() $\operatorname {Tor}^{{\mathbb {Z}}/m}(\bar {Z}_\rho ,W_{\bar {Z_{\rho }}}) =m$
, as claimed.
$\operatorname {Tor}^{{\mathbb {Z}}/m}(\bar {Z}_\rho ,W_{\bar {Z_{\rho }}}) =m$
, as claimed.
Proof of Theorem 6.1
This follows from arguments similar to those in the proof of [Reference Schreieder45, Theorem 6.1 and 7.1]; we give some details for the reader’s convenience. Let
![]() $P=\{x_0=\dots =x_n=0 \}\subset {\mathbb {P}}^{n+r+1}_k$
and consider the blow-up
$P=\{x_0=\dots =x_n=0 \}\subset {\mathbb {P}}^{n+r+1}_k$
and consider the blow-up ![]() , which can be described via the vanishing locus of
, which can be described via the vanishing locus of
 $$ \begin{align} g(x_0,\dots,x_n) x_0^{m+n-\deg(g)} y_0^m + \sum\limits_{j = 1}^{r} x_0^{n-\deg c_j} c_j(x_1,\dots,x_n) y_j^m + (-1)^n x_1 x_2\dots x_n y_{r+1}^m, \end{align} $$
$$ \begin{align} g(x_0,\dots,x_n) x_0^{m+n-\deg(g)} y_0^m + \sum\limits_{j = 1}^{r} x_0^{n-\deg c_j} c_j(x_1,\dots,x_n) y_j^m + (-1)^n x_1 x_2\dots x_n y_{r+1}^m, \end{align} $$
inside the projective bundle
![]() $ {\mathbb {P}}_{{\mathbb {P}}^n}(\mathcal O(-1)\oplus \mathcal O^{\oplus (r+1)})$
over
$ {\mathbb {P}}_{{\mathbb {P}}^n}(\mathcal O(-1)\oplus \mathcal O^{\oplus (r+1)})$
over
![]() ${\mathbb {P}}^n$
, where
${\mathbb {P}}^n$
, where
![]() $y_0$
denotes a local coordinate that trivializes
$y_0$
denotes a local coordinate that trivializes
![]() $\mathcal O(-1)$
and
$\mathcal O(-1)$
and
![]() $y_1,\dots ,y_{r+1}$
trivialize
$y_1,\dots ,y_{r+1}$
trivialize
![]() $\mathcal O^{\oplus (r+1)}$
. The projection to the x-coordinates induces a morphism
$\mathcal O^{\oplus (r+1)}$
. The projection to the x-coordinates induces a morphism
![]() $f:Y\to {\mathbb {P}}^n_k$
. We furthermore pick an alteration
$f:Y\to {\mathbb {P}}^n_k$
. We furthermore pick an alteration
![]() $\tau ':Y'\to Y$
of order coprime to m, which can be done by [Reference Temkin47], see also [Reference Illusie and Temkin22]. The corresponding alteration of Z is denoted by
$\tau ':Y'\to Y$
of order coprime to m, which can be done by [Reference Temkin47], see also [Reference Illusie and Temkin22]. The corresponding alteration of Z is denoted by
![]() $\tau :Y'\to Z$
.
$\tau :Y'\to Z$
.
As detailed in [Reference Schreieder45, §7], an application of [Reference Schreieder45, Theorem 5.3] shows that the pullback of the class
![]() $\alpha =(x_1/x_0,\dots ,x_n/x_0)\in H^n(k({\mathbb {P}}^n),\mu _m^{\otimes n})$
yields an unramified class
$\alpha =(x_1/x_0,\dots ,x_n/x_0)\in H^n(k({\mathbb {P}}^n),\mu _m^{\otimes n})$
yields an unramified class
of order m such that for any subvariety
![]() $E\subset Y'$
which does not dominate
$E\subset Y'$
which does not dominate
![]() ${\mathbb {P}}^n$
via
${\mathbb {P}}^n$
via
![]() $ f\circ \tau '$
, the class
$ f\circ \tau '$
, the class
![]() $(\tau ')^\ast \gamma $
vanishes in
$(\tau ')^\ast \gamma $
vanishes in
![]() $H^n(k(E),\mu _m^{\otimes n})$
. Moreover, the class
$H^n(k(E),\mu _m^{\otimes n})$
. Moreover, the class
![]() $f^\ast \alpha $
vanishes at the generic point of the exceptional divisor
$f^\ast \alpha $
vanishes at the generic point of the exceptional divisor
![]() $D_0$
of
$D_0$
of
![]() $Y\to Z$
, which is cut out by
$Y\to Z$
, which is cut out by
![]() $y_0=0$
, and at the generic point of the strict transform
$y_0=0$
, and at the generic point of the strict transform
![]() $D_{r+1}$
of the divisor
$D_{r+1}$
of the divisor
![]() $\{y_{r+1} = 0\} \subset Z$
under the blow-up morphism
$\{y_{r+1} = 0\} \subset Z$
under the blow-up morphism
![]() $Y \to Z$
. Indeed, the divisors
$Y \to Z$
. Indeed, the divisors
![]() $D_0$
and
$D_0$
and
![]() $D_{r+1}$
in Y map via f onto
$D_{r+1}$
in Y map via f onto
![]() ${\mathbb {P}}^n$
and the generic fibres
${\mathbb {P}}^n$
and the generic fibres
![]() $D_{0,\eta }$
and
$D_{0,\eta }$
and
![]() $D_{r+1,\eta }$
of
$D_{r+1,\eta }$
of
![]() $\left .f\right |{}_{D_i}$
are the hypersurfaces in (different)
$\left .f\right |{}_{D_i}$
are the hypersurfaces in (different)
![]() ${\mathbb {P}}^r_{k({\mathbb {P}}^n)}$
given by
${\mathbb {P}}^r_{k({\mathbb {P}}^n)}$
given by
 $$ \begin{align*}\begin{aligned} &\sum\limits_{j = 1}^{r} c_j(x_1,\dots,x_n) y_j^m + (-1)^n x_1 x_2 \dots x_n y_{r+1}^m =0 \quad \text{and} \\ &\pi \cdot \left(1+\sum\limits_{i=1}^n x_i^{\left\lceil \frac{n+1}{m}\right\rceil}\right)^m y_0^m - (-1)^n x_1 x_2 \cdots x_n y_0^m + \sum\limits_{j = 1}^{r} c_j(x_1,\dots,x_n) y_j^m =0, \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} &\sum\limits_{j = 1}^{r} c_j(x_1,\dots,x_n) y_j^m + (-1)^n x_1 x_2 \dots x_n y_{r+1}^m =0 \quad \text{and} \\ &\pi \cdot \left(1+\sum\limits_{i=1}^n x_i^{\left\lceil \frac{n+1}{m}\right\rceil}\right)^m y_0^m - (-1)^n x_1 x_2 \cdots x_n y_0^m + \sum\limits_{j = 1}^{r} c_j(x_1,\dots,x_n) y_j^m =0, \end{aligned} \end{align*} $$
respectively, see (6.4) and (6.1). Thus
![]() $D_{0,\eta }$
and
$D_{0,\eta }$
and
![]() $D_{r+1,\eta }$
are each isomorphic as
$D_{r+1,\eta }$
are each isomorphic as
![]() $k({\mathbb {P}}^n)$
-varieties to a subvariety of the hypersurface given by the vanishing of the n-th Fermat-Pfister form of degree m
$k({\mathbb {P}}^n)$
-varieties to a subvariety of the hypersurface given by the vanishing of the n-th Fermat-Pfister form of degree m
with
![]() $j(\varepsilon ) = \sum \limits _{i=0}^n \varepsilon _i 2^{i-1}$
as defined in [Reference Schreieder45, Equation (7)]. The vanishing of
$j(\varepsilon ) = \sum \limits _{i=0}^n \varepsilon _i 2^{i-1}$
as defined in [Reference Schreieder45, Equation (7)]. The vanishing of
![]() $f^\ast \alpha $
along the generic points of
$f^\ast \alpha $
along the generic points of
![]() $D_0$
and
$D_0$
and
![]() $D_{r+1}$
follows from [Reference Schreieder45, Corollary 4.3]. Since the generic fibre of f is smooth (m is invertible in k), we conclude via [Reference Bloch and Ogus6] that
$D_{r+1}$
follows from [Reference Schreieder45, Corollary 4.3]. Since the generic fibre of f is smooth (m is invertible in k), we conclude via [Reference Bloch and Ogus6] that
for any subvariety
![]() $E\subset Y'$
with
$E\subset Y'$
with
![]() $\tau (E)\subset W_Z = Z^{\operatorname {sing}}\cup \{ y_{r+1} l=0\}$
, where
$\tau (E)\subset W_Z = Z^{\operatorname {sing}}\cup \{ y_{r+1} l=0\}$
, where
![]() $l\in k[x_0,\dots ,x_n]$
is any nontrivial homogeneous polynomial in
$l\in k[x_0,\dots ,x_n]$
is any nontrivial homogeneous polynomial in
![]() $x_0,\dots ,x_n$
as in the statement of the theorem.
$x_0,\dots ,x_n$
as in the statement of the theorem.
A computation with the Merkurjev pairing similar to [Reference Schreieder44, §3] or [Reference Schreieder and Farkas46, Theorem 8.6] then shows
![]() $\operatorname {Tor}^{{\mathbb {Z}}/m}(Z,W_Z)=m$
; we sketch the argument for convenience. For a contradiction assume that there is a positive integer
$\operatorname {Tor}^{{\mathbb {Z}}/m}(Z,W_Z)=m$
; we sketch the argument for convenience. For a contradiction assume that there is a positive integer
![]() $m'< m$
with
$m'< m$
with
for some zero-cycle z whose support
![]() $\operatorname {supp} z$
lies in
$\operatorname {supp} z$
lies in
![]() $(W_Z)_{k(Z)}$
and some zero-cycle
$(W_Z)_{k(Z)}$
and some zero-cycle
![]() $\zeta \in \operatorname {CH}_0(Z_{k(Z)})$
that reflects the fact that we work with
$\zeta \in \operatorname {CH}_0(Z_{k(Z)})$
that reflects the fact that we work with
![]() ${\mathbb {Z}}/m$
-torsion orders. We restrict the above identity to the regular locus of
${\mathbb {Z}}/m$
-torsion orders. We restrict the above identity to the regular locus of
![]() $Z_{k(Z)}$
and pull this back to
$Z_{k(Z)}$
and pull this back to
![]() $\tau ^{-1}(Z^{\operatorname {sm}}_{k(Z)})$
. The localization sequence then yields
$\tau ^{-1}(Z^{\operatorname {sm}}_{k(Z)})$
. The localization sequence then yields
where
![]() $\delta _\tau =\tau ^\ast \delta _Z$
is the point induced by the graph of
$\delta _\tau =\tau ^\ast \delta _Z$
is the point induced by the graph of
![]() $\tau :Y'\to Z$
,
$\tau :Y'\to Z$
,
![]() $z'$
is a zero-cycle with
$z'$
is a zero-cycle with
![]() $\operatorname {supp} z'\subset \tau ^{-1}(W_Z)_{k(Z)}$
and
$\operatorname {supp} z'\subset \tau ^{-1}(W_Z)_{k(Z)}$
and
![]() $\zeta '\in \operatorname {CH}_0(Y^{\prime }_{k(Z)}) $
. Note that this used
$\zeta '\in \operatorname {CH}_0(Y^{\prime }_{k(Z)}) $
. Note that this used
![]() $Z^{\operatorname {sing}}\subset W_Z$
. We pair the above zero-cycle via the Merkurjev pairing (see [Reference Merkurjev32, §2.4] or [Reference Schreieder and Farkas46, §5]) with the unramified class
$Z^{\operatorname {sing}}\subset W_Z$
. We pair the above zero-cycle via the Merkurjev pairing (see [Reference Merkurjev32, §2.4] or [Reference Schreieder and Farkas46, §5]) with the unramified class
![]() $\gamma $
from above. This yields
$\gamma $
from above. This yields
because
![]() $\gamma $
is m-torsion, hence pairs to zero with
$\gamma $
is m-torsion, hence pairs to zero with
![]() $m\cdot \zeta '$
, and it restricts to zero on generic points of subvarieties of
$m\cdot \zeta '$
, and it restricts to zero on generic points of subvarieties of
![]() $\tau ^{-1}(W_Z )$
by (6.5), hence pairs to zero with
$\tau ^{-1}(W_Z )$
by (6.5), hence pairs to zero with
![]() $z'$
. Conversely, the definition of the Merkurjev pairing directly implies that
$z'$
. Conversely, the definition of the Merkurjev pairing directly implies that
as
![]() $\delta _\tau \in Y^{\prime }_{k(Z)}$
is the point associated to the graph
$\delta _\tau \in Y^{\prime }_{k(Z)}$
is the point associated to the graph
![]() $\Gamma _\tau \subset Y'\times Z$
of
$\Gamma _\tau \subset Y'\times Z$
of
![]() $\tau $
. This contradicts the fact that
$\tau $
. This contradicts the fact that
![]() $ \deg (\tau )$
is coprime to m, that
$ \deg (\tau )$
is coprime to m, that
![]() $1\leq m'<m$
, and that
$1\leq m'<m$
, and that
![]() $\gamma $
has order m. This concludes the proof of the theorem.
$\gamma $
has order m. This concludes the proof of the theorem.
7 Proof of the main results
Let k be an algebraically closed field and let
![]() $X\subset {\mathbb {P}}^{N+1}_k$
be a smooth Fano hypersurface, that is, a smooth hypersurface of degree
$X\subset {\mathbb {P}}^{N+1}_k$
be a smooth Fano hypersurface, that is, a smooth hypersurface of degree
![]() $d\leq N+1$
. Then
$d\leq N+1$
. Then
![]() $\deg \colon \operatorname {CH}_0(X)\to {\mathbb {Z}}$
is an isomorphism and so the torsion order
$\deg \colon \operatorname {CH}_0(X)\to {\mathbb {Z}}$
is an isomorphism and so the torsion order
![]() $\operatorname {Tor}(X)$
of X is the torsion order
$\operatorname {Tor}(X)$
of X is the torsion order
![]() $\operatorname {Tor}^{\mathbb {Z}}(X,W)$
of X relative to any closed zero-dimensional subset
$\operatorname {Tor}^{\mathbb {Z}}(X,W)$
of X relative to any closed zero-dimensional subset
![]() $W \subset X$
, see Lemma 3.6 (d). The main results of this paper, stated in the introduction, will follow from the following result.
$W \subset X$
, see Lemma 3.6 (d). The main results of this paper, stated in the introduction, will follow from the following result.
Theorem 7.1. Let k be a field and let
![]() $m \geq 2$
be an integer invertible in k. Let
$m \geq 2$
be an integer invertible in k. Let
![]() $n \geq 2$
,
$n \geq 2$
,
![]() $r \leq 2^n-2$
, and let
$r \leq 2^n-2$
, and let
 $$ \begin{align*}s \leq \sum\limits_{l = 1}^n \binom{n}{l} \left\lfloor \frac{n-l}{m} \right\rfloor \end{align*} $$
$$ \begin{align*}s \leq \sum\limits_{l = 1}^n \binom{n}{l} \left\lfloor \frac{n-l}{m} \right\rfloor \end{align*} $$
be non-negative integers. Write ![]() . Then the torsion order
. Then the torsion order
![]() $\operatorname {Tor}(X_d)$
of a very general Fano hypersurface
$\operatorname {Tor}(X_d)$
of a very general Fano hypersurface
![]() $X_d \subset {\mathbb {P}}^{N+1}_k$
of degree
$X_d \subset {\mathbb {P}}^{N+1}_k$
of degree
![]() $d \geq m + n$
is divisible by m.
$d \geq m + n$
is divisible by m.
Remark 7.2. For
![]() $s=0$
, the result is proven in [Reference Schreieder45, Theorem 7.1].
$s=0$
, the result is proven in [Reference Schreieder45, Theorem 7.1].
Proof of Theorem 7.1
Note that the torsion order of any variety is divisible by the torsion order of the base-change to any field extension. Moreover, the definition of very general (see Definition 2.4) is stable under extension of the base field. Up to replacing k by a field extension, we can therefore assume that k is algebraically closed and uncountable.
We fix positive integers
![]() $n \geq 2$
and
$n \geq 2$
and
![]() $r \leq 2^{n} -2$
. For a non-negative integer s as in the theorem, we define inductively an integral degree d-hypersurface
$r \leq 2^{n} -2$
. For a non-negative integer s as in the theorem, we define inductively an integral degree d-hypersurface
![]() $Z = Z_s$
of dimension
$Z = Z_s$
of dimension
![]() $N = n + r + s$
.
$N = n + r + s$
.
Step 1. Suppose there exists an integral degree d-hypersurface
![]() $Z_s \subset {\mathbb {P}}_k^{n+r+s+1}$
given by the vanishing of a homogeneous polynomial of the form
$Z_s \subset {\mathbb {P}}_k^{n+r+s+1}$
given by the vanishing of a homogeneous polynomial of the form
 $$ \begin{align} f_0^{(s)} + a_0^{(s)} + a_{r+1}^{(s)} y_{r+1}^m + \sum\limits_{j=1}^{r} \sum\limits_{i=1}^m a_{i,j}^{(s)} \cdot y_j^i \in k[x_0,\dots,x_n,y_1,\dots,y_{r+1},z_1,\dots,z_s] \end{align} $$
$$ \begin{align} f_0^{(s)} + a_0^{(s)} + a_{r+1}^{(s)} y_{r+1}^m + \sum\limits_{j=1}^{r} \sum\limits_{i=1}^m a_{i,j}^{(s)} \cdot y_j^i \in k[x_0,\dots,x_n,y_1,\dots,y_{r+1},z_1,\dots,z_s] \end{align} $$
for some homogeneous polynomials
such that
-
(1)
 $f_0^{(s)} + a_0^{(s)} \in k[x_0,\dots ,x_n,z_1,\dots ,z_s]$
is an irreducible polynomial of degree d;
$f_0^{(s)} + a_0^{(s)} \in k[x_0,\dots ,x_n,z_1,\dots ,z_s]$
is an irreducible polynomial of degree d; -
(2) for each j, if
 $x_0^{e m} \mid a_{m,j}^{(s)}$
for a non-negative integer e, then
$x_0^{e m} \mid a_{m,j}^{(s)}$
for a non-negative integer e, then
 $x_0^{e i} \mid a_{i,j}^{(s)}$
for all
$x_0^{e i} \mid a_{i,j}^{(s)}$
for all
 $1 \leq i \leq m$
. We denote the maximal such e by
$1 \leq i \leq m$
. We denote the maximal such e by
 $e_j^{(s)}$
;
$e_j^{(s)}$
; -
(3)
 $\operatorname {Tor}^{{\mathbb {Z}}/m}(Z_s,W_{s}) = m$
, where
$\operatorname {Tor}^{{\mathbb {Z}}/m}(Z_s,W_{s}) = m$
, where  for some homogeneous polynomial
for some homogeneous polynomial
 $h^{(s)} \in k[x_0,\dots ,x_n,z_1,\dots ,z_s]$
.
$h^{(s)} \in k[x_0,\dots ,x_n,z_1,\dots ,z_s]$
.
Assume that there exists some
![]() $1 \leq j_0 \leq r$
such that
$1 \leq j_0 \leq r$
such that
![]() $e_{j_0}^{(s)} \geq 1$
. Then we construct an integral degree d-hypersurface
$e_{j_0}^{(s)} \geq 1$
. Then we construct an integral degree d-hypersurface
![]() $Z_{s+1}$
of the same form (7.1) satisfying conditions (1), (2), and (3) as follows.
$Z_{s+1}$
of the same form (7.1) satisfying conditions (1), (2), and (3) as follows.
Consider
![]() $k' = \overline {k(\lambda )}$
an algebraic closure of the purely transcendental field extension
$k' = \overline {k(\lambda )}$
an algebraic closure of the purely transcendental field extension
![]() $k(\lambda )$
of k. Rewrite the equation (7.1) as
$k(\lambda )$
of k. Rewrite the equation (7.1) as
 $$ \begin{align*}\left(f_0^{(s)} + a_{r+1}^{(s)} y_{r+1}^m + \sum\limits_{j\neq j_0} \sum\limits_{i=1}^m a_{i,j}^{(s)} \cdot y_j^i\right) + a_0^{(s)} + \sum\limits_{i=1}^m a_{i,j_0}^{(s)} y_{j_0}^i. \end{align*} $$
$$ \begin{align*}\left(f_0^{(s)} + a_{r+1}^{(s)} y_{r+1}^m + \sum\limits_{j\neq j_0} \sum\limits_{i=1}^m a_{i,j}^{(s)} \cdot y_j^i\right) + a_0^{(s)} + \sum\limits_{i=1}^m a_{i,j_0}^{(s)} y_{j_0}^i. \end{align*} $$
We are now in the situation of Section 5. Note that condition (1) implies the assumption (5.2). Let
![]() $Z_{s+1}$
be the integral degree d-hypersurface
$Z_{s+1}$
be the integral degree d-hypersurface
![]() $X' \times _{K} \bar {K} \subset {\mathbb {P}}^{n+r+s+2}_{\bar {K}}$
, where
$X' \times _{K} \bar {K} \subset {\mathbb {P}}^{n+r+s+2}_{\bar {K}}$
, where
![]() $X'$
is as in Lemma 5.2 and
$X'$
is as in Lemma 5.2 and
![]() $K = k'(t)$
. We choose an isomorphism
$K = k'(t)$
. We choose an isomorphism
![]() $k \cong \bar {K}$
, which exists because both fields are algebraically closed, have the same characteristic, and have the same uncountable transcendence degree over their prime fields. Thus we can view
$k \cong \bar {K}$
, which exists because both fields are algebraically closed, have the same characteristic, and have the same uncountable transcendence degree over their prime fields. Thus we can view
![]() $Z_{s+1}$
as a variety over k. We aim to check that
$Z_{s+1}$
as a variety over k. We aim to check that
![]() $Z_{s+1}$
satisfies the assumptions above. Recall from Lemma 5.2 that
$Z_{s+1}$
satisfies the assumptions above. Recall from Lemma 5.2 that
![]() $Z_{s+1}\subset {\mathbb {P}}^{n+r+s+2}_k$
is cut out by the homogeneous polynomial
$Z_{s+1}\subset {\mathbb {P}}^{n+r+s+2}_k$
is cut out by the homogeneous polynomial
 $$ \begin{align} \left(f_0^{(s)} + a_{r+1}^{(s)} y_{r+1}^m + \sum\limits_{j\neq j_0} \sum\limits_{i=1}^m a^{(s)}_{i,j} \cdot y_j^i\right) + a^{(s+1)}_0 + \sum\limits_{i=1}^m a^{(s+1)}_{i,j_0} y_{j_0}^i, \end{align} $$
$$ \begin{align} \left(f_0^{(s)} + a_{r+1}^{(s)} y_{r+1}^m + \sum\limits_{j\neq j_0} \sum\limits_{i=1}^m a^{(s)}_{i,j} \cdot y_j^i\right) + a^{(s+1)}_0 + \sum\limits_{i=1}^m a^{(s+1)}_{i,j_0} y_{j_0}^i, \end{align} $$
where
![]() $a^{(s+1)}_0,a^{(s+1)}_{i,j_0}\in k[x_0,\dots ,x_n,z_1,\dots ,z_{s+1}]$
are defined as in (5.6). Note that this uses also Lemma 5.2 (3). Hence, the defining equation of
$a^{(s+1)}_0,a^{(s+1)}_{i,j_0}\in k[x_0,\dots ,x_n,z_1,\dots ,z_{s+1}]$
are defined as in (5.6). Note that this uses also Lemma 5.2 (3). Hence, the defining equation of
![]() $Z_{s+1}$
has the form (7.1) with
$Z_{s+1}$
has the form (7.1) with
Since
![]() $f_{0}^{(s+1)}$
and
$f_{0}^{(s+1)}$
and
![]() $a_0^{(s+1)}$
do not contain any
$a_0^{(s+1)}$
do not contain any
![]() $y_i$
, condition (1) follows from Lemma 5.2 (4). As
$y_i$
, condition (1) follows from Lemma 5.2 (4). As
![]() $a_{i,j}^{(s+1)} = a_{i,j}^{(s)}$
for
$a_{i,j}^{(s+1)} = a_{i,j}^{(s)}$
for
![]() $j \neq j_0$
, condition (2) is clearly satisfied for
$j \neq j_0$
, condition (2) is clearly satisfied for
![]() $j \neq j_0$
and we note that
$j \neq j_0$
and we note that
![]() $e_j^{(s+1)} = e_j^{(s)}$
for
$e_j^{(s+1)} = e_j^{(s)}$
for
![]() $j \neq j_0$
. For
$j \neq j_0$
. For
![]() $j = j_0$
, condition (2) follows from Lemma 5.2 (2). Proposition 5.7 shows that
$j = j_0$
, condition (2) follows from Lemma 5.2 (2). Proposition 5.7 shows that
![]() $\operatorname {Tor}^{{\mathbb {Z}}/m}(Z_{s+1},W_{s+1}) = m$
, where
$\operatorname {Tor}^{{\mathbb {Z}}/m}(Z_{s+1},W_{s+1}) = m$
, where
![]() $W_{s+1} = \{x_0 a_{r+1}^{(s)} y_{r+1} h^{(s)} z_{s+1} = 0\} \subset Z_{s+1}$
. Note that the derivative of (7.2) with respect to
$W_{s+1} = \{x_0 a_{r+1}^{(s)} y_{r+1} h^{(s)} z_{s+1} = 0\} \subset Z_{s+1}$
. Note that the derivative of (7.2) with respect to
![]() $y_{r+1}$
is equal to
$y_{r+1}$
is equal to
![]() $m a_{r+1}^{(s)} y_{r+1}^{m-1}$
; thus the singular locus of
$m a_{r+1}^{(s)} y_{r+1}^{m-1}$
; thus the singular locus of
![]() $Z_{s+1}$
is contained in
$Z_{s+1}$
is contained in
![]() $\{a_{r+1}^{(s)} y_{r+1}=0\} \subset Z_{s+1}$
. By definition,
$\{a_{r+1}^{(s)} y_{r+1}=0\} \subset Z_{s+1}$
. By definition,
![]() $a_{r+1}^{(s+1)} = a_{r+1}^{(s)}$
and so condition (3) is satisfied for
$a_{r+1}^{(s+1)} = a_{r+1}^{(s)}$
and so condition (3) is satisfied for
![]() $h^{(s+1)} = h^{(s)} z_{s+1}$
.
$h^{(s+1)} = h^{(s)} z_{s+1}$
.
Step 2. Consider the hypersurface ![]() with defining equation
with defining equation
![]() $\rho h + x_0^{d-m-n} F$
as in Corollary 6.2, where
$\rho h + x_0^{d-m-n} F$
as in Corollary 6.2, where
![]() $h \in k[x_0,\dots ,x_n]$
is an irreducible polynomial of degree d, for example,
$h \in k[x_0,\dots ,x_n]$
is an irreducible polynomial of degree d, for example,
 $$ \begin{align*}h = \begin{cases} x_0^d + \sum\limits_{i = 1}^n x_{i-1} x_i^{d-1} & \text{if } p> 0 \text{ and } p \mid d, \\ \sum\limits_{i = 0}^n x_i^d & \text{otherwise,} \end{cases} \end{align*} $$
$$ \begin{align*}h = \begin{cases} x_0^d + \sum\limits_{i = 1}^n x_{i-1} x_i^{d-1} & \text{if } p> 0 \text{ and } p \mid d, \\ \sum\limits_{i = 0}^n x_i^d & \text{otherwise,} \end{cases} \end{align*} $$
where p is the characteristic of k. We will prove that
![]() $Z_0$
satisfies the condition (1), (2), and (3) above.
$Z_0$
satisfies the condition (1), (2), and (3) above.
Consider the following polynomials in
![]() $k[x_0,\dots ,x_n]$
$k[x_0,\dots ,x_n]$

where g is defined in (6.1) and the
![]() $c_j$
’s are defined in (6.2). Then, by construction,
$c_j$
’s are defined in (6.2). Then, by construction,
 $$ \begin{align*}\rho h + x_0^{d-m-n} F = f_0^{(0)} + a_0^{(0)} + a_{r+1}^{(s)} y_{r+1}^m + \sum\limits_{j=1}^r \sum\limits_{i=1}^m a_{i,j}^{(0)} \cdot y_j^i \in k[x_0,\dots,x_n,y_1,\dots,y_{r+1}] \end{align*} $$
$$ \begin{align*}\rho h + x_0^{d-m-n} F = f_0^{(0)} + a_0^{(0)} + a_{r+1}^{(s)} y_{r+1}^m + \sum\limits_{j=1}^r \sum\limits_{i=1}^m a_{i,j}^{(0)} \cdot y_j^i \in k[x_0,\dots,x_n,y_1,\dots,y_{r+1}] \end{align*} $$
is of the form (7.1). The polynomial
![]() $f_0^{(0)}$
is irreducible because the polynomial h is irreducible and
$f_0^{(0)}$
is irreducible because the polynomial h is irreducible and
![]() $\rho $
is a transcendental parameter over the prime field of k, which is algebraically independent from
$\rho $
is a transcendental parameter over the prime field of k, which is algebraically independent from
![]() $\pi $
. Hence condition (1) holds. Condition (2) is clearly satisfied as
$\pi $
. Hence condition (1) holds. Condition (2) is clearly satisfied as
![]() $a_{i,j}^{(0)} = 0$
for
$a_{i,j}^{(0)} = 0$
for
![]() $1 \leq i \leq m-1$
. In particular, we see from the definition of
$1 \leq i \leq m-1$
. In particular, we see from the definition of
![]() $a_{m,j}^{(0)}$
above that
$a_{m,j}^{(0)}$
above that
 $$ \begin{align} e_j^{(0)} = \left\lfloor \frac{d-m-\deg(c_j)}{m} \right\rfloor. \end{align} $$
$$ \begin{align} e_j^{(0)} = \left\lfloor \frac{d-m-\deg(c_j)}{m} \right\rfloor. \end{align} $$
Corollary 6.2 shows that condition (3) holds as well, where we note that we can choose
![]() $h^{(0)} = 1$
. This concludes Step 2.
$h^{(0)} = 1$
. This concludes Step 2.
By Steps 1 and 2 above, we can apply the double cone construction (see Section 5) as long as at least one of the
![]() $e_j$
’s defined in (2) is positive. In each step, we reduce one of them by
$e_j$
’s defined in (2) is positive. In each step, we reduce one of them by
![]() $1$
. Hence, the number of steps is equal to the sum
$1$
. Hence, the number of steps is equal to the sum
 $$ \begin{align*}\sum\limits_{j=1}^{r} e_j^{(0)} = \sum\limits_{j=1}^{r} \left\lfloor \frac{d-m-\deg(c_j)}{m} \right\rfloor. \end{align*} $$
$$ \begin{align*}\sum\limits_{j=1}^{r} e_j^{(0)} = \sum\limits_{j=1}^{r} \left\lfloor \frac{d-m-\deg(c_j)}{m} \right\rfloor. \end{align*} $$
This sum becomes maximal when r is maximal, that is,
![]() $r = 2^n -2$
. Then the sum reads
$r = 2^n -2$
. Then the sum reads
 $$ \begin{align*} \sum\limits_{j=1}^{2^n-2} e_j^{(0)} = \sum\limits_{l=1}^{n-1} \binom{n}{l} \left\lfloor \frac{d-m-l}{m} \right\rfloor. \end{align*} $$
$$ \begin{align*} \sum\limits_{j=1}^{2^n-2} e_j^{(0)} = \sum\limits_{l=1}^{n-1} \binom{n}{l} \left\lfloor \frac{d-m-l}{m} \right\rfloor. \end{align*} $$
Let now
![]() $X_d$
be a very general hypersurface of degree d and dimension N over k. Up to replacing k by a larger algebraically closed field (which does not affect the torsion order by Lemma 3.6), we can by Lemma 2.5 assume that
$X_d$
be a very general hypersurface of degree d and dimension N over k. Up to replacing k by a larger algebraically closed field (which does not affect the torsion order by Lemma 3.6), we can by Lemma 2.5 assume that
![]() $X_d$
degenerates to
$X_d$
degenerates to
![]() $Z_s$
. By choosing N general hyperplane sections through a closed point of
$Z_s$
. By choosing N general hyperplane sections through a closed point of
![]() $W_s$
, we can assume that there exists a closed subset W in the total space of the degeneration which has relative dimension
$W_s$
, we can assume that there exists a closed subset W in the total space of the degeneration which has relative dimension
![]() $0$
and whose restriction to the special fibre
$0$
and whose restriction to the special fibre
![]() $Z_s$
is contained in
$Z_s$
is contained in
![]() $W_s$
. Applying Lemma 3.8 to the degeneration with W as closed subset yields that
$W_s$
. Applying Lemma 3.8 to the degeneration with W as closed subset yields that
where ![]() is a closed nonempty zero-dimensional subset of
is a closed nonempty zero-dimensional subset of
![]() $X_d$
. Thus, Lemma 3.6 implies that m divides
$X_d$
. Thus, Lemma 3.6 implies that m divides
![]() $\operatorname {Tor}(X_d)$
, which finishes the proof of the theorem.
$\operatorname {Tor}(X_d)$
, which finishes the proof of the theorem.
The following lemmas yield explicit estimates for the bound given in Theorem 7.1.
Lemma 7.3. Let
![]() $n,m \geq 2$
be positive integers. Then
$n,m \geq 2$
be positive integers. Then
 $$ \begin{align} \left(\left\lfloor\frac{n}{m}\right\rfloor - 1 \right) (2^{n-1}-1) \leq \sum\limits_{l=1}^n \binom{n}{l} \left\lfloor \frac{n-l}{m} \right\rfloor \leq \left\lfloor\frac{n}{m}\right\rfloor (2^{n-1}-1). \end{align} $$
$$ \begin{align} \left(\left\lfloor\frac{n}{m}\right\rfloor - 1 \right) (2^{n-1}-1) \leq \sum\limits_{l=1}^n \binom{n}{l} \left\lfloor \frac{n-l}{m} \right\rfloor \leq \left\lfloor\frac{n}{m}\right\rfloor (2^{n-1}-1). \end{align} $$
Proof. The sum in question can be rewritten as follows
 $$ \begin{align*} \sum\limits_{l=1}^n \binom{n}{l} \left\lfloor \frac{n-l}{m} \right\rfloor &= \frac{1}{2} \sum\limits_{l=1}^{n-1} \binom{n}{l} \left\lfloor \frac{n-l}{m} \right\rfloor + \frac{1}{2} \sum\limits_{l=1}^{n-1} \binom{n}{n-l} \left\lfloor \frac{n-l}{m} \right\rfloor \\ &= \frac{1}{2} \sum\limits_{l=1}^{n-1} \binom{n}{l} \left\lfloor \frac{n-l}{m} \right\rfloor + \frac{1}{2} \sum\limits_{l=1}^{n-1} \binom{n}{l} \left\lfloor \frac{l}{m} \right\rfloor \\ &= \frac{1}{2} \sum\limits_{l=1}^{n-1} \binom{n}{l} \left(\left\lfloor \frac{n-l}{m} \right\rfloor + \left\lfloor \frac{l}{m} \right\rfloor\right). \end{align*} $$
$$ \begin{align*} \sum\limits_{l=1}^n \binom{n}{l} \left\lfloor \frac{n-l}{m} \right\rfloor &= \frac{1}{2} \sum\limits_{l=1}^{n-1} \binom{n}{l} \left\lfloor \frac{n-l}{m} \right\rfloor + \frac{1}{2} \sum\limits_{l=1}^{n-1} \binom{n}{n-l} \left\lfloor \frac{n-l}{m} \right\rfloor \\ &= \frac{1}{2} \sum\limits_{l=1}^{n-1} \binom{n}{l} \left\lfloor \frac{n-l}{m} \right\rfloor + \frac{1}{2} \sum\limits_{l=1}^{n-1} \binom{n}{l} \left\lfloor \frac{l}{m} \right\rfloor \\ &= \frac{1}{2} \sum\limits_{l=1}^{n-1} \binom{n}{l} \left(\left\lfloor \frac{n-l}{m} \right\rfloor + \left\lfloor \frac{l}{m} \right\rfloor\right). \end{align*} $$
The estimates in (7.4) follow now from the observation
 $$ \begin{align*}\left(\left\lfloor\frac{n}{m}\right\rfloor - 1 \right) \leq \left(\left\lfloor \frac{n-l}{m} \right\rfloor + \left\lfloor \frac{l}{m} \right\rfloor\right) \leq \left\lfloor \frac{n}{m} \right\rfloor \end{align*} $$
$$ \begin{align*}\left(\left\lfloor\frac{n}{m}\right\rfloor - 1 \right) \leq \left(\left\lfloor \frac{n-l}{m} \right\rfloor + \left\lfloor \frac{l}{m} \right\rfloor\right) \leq \left\lfloor \frac{n}{m} \right\rfloor \end{align*} $$
for all
![]() $0 \leq l \leq n$
together with the summation formula for binomial coefficients.
$0 \leq l \leq n$
together with the summation formula for binomial coefficients.
We provide more explicit formulas for
![]() $m = 2$
and
$m = 2$
and
![]() $m = 3$
. These bounds are used in Theorem 1.1 and Theorem 1.2.
$m = 3$
. These bounds are used in Theorem 1.1 and Theorem 1.2.
Lemma 7.4. Let n be a positive integer. Then the following formulas hold
 $$ \begin{align} \sum\limits_{l=1}^n \binom{n}{l} \left\lfloor \frac{n-l}{2} \right\rfloor &= (n-1) 2^{n-2} - \left\lfloor \frac{n}{2} \right\rfloor, \end{align} $$
$$ \begin{align} \sum\limits_{l=1}^n \binom{n}{l} \left\lfloor \frac{n-l}{2} \right\rfloor &= (n-1) 2^{n-2} - \left\lfloor \frac{n}{2} \right\rfloor, \end{align} $$
 $$ \begin{align} \sum\limits_{l=1}^n \binom{n}{l} \left\lfloor \frac{n-l}{3} \right\rfloor &= \frac{n-2}{3} 2^{n-1} - \frac{n}{3} + \delta, \end{align} $$
$$ \begin{align} \sum\limits_{l=1}^n \binom{n}{l} \left\lfloor \frac{n-l}{3} \right\rfloor &= \frac{n-2}{3} 2^{n-1} - \frac{n}{3} + \delta, \end{align} $$
where
![]() $\delta $
depends on the remainder of n modulo
$\delta $
depends on the remainder of n modulo
![]() $6$
and is given by the following table.
$6$
and is given by the following table.
 $$ \begin{align*}\begin{array}{l|c|c|c|c|c|c} n\quad \pmod 6& 0 & 1 & 2 & 3 & 4 & 5 \\ \hline \delta & \frac{1}{3} & \frac{2}{3} & \frac{2}{3} & -\frac{1}{3} & 0 & \frac{2}{3}. \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{l|c|c|c|c|c|c} n\quad \pmod 6& 0 & 1 & 2 & 3 & 4 & 5 \\ \hline \delta & \frac{1}{3} & \frac{2}{3} & \frac{2}{3} & -\frac{1}{3} & 0 & \frac{2}{3}. \end{array} \end{align*} $$
Proof. We check (7.5) by the following computation:
 $$ \begin{align*} \sum\limits_{l=1}^n \binom{n}{l} \left\lfloor \frac{n-l}{2} \right\rfloor &= \sum\limits_{l=1}^n \frac{n-l}{2} \binom{n}{l} - \frac{1}{2}\sum\limits_{\substack{l=1 \\ n -l \text{ odd}}}^n \binom{n}{l} \\ &= \frac{n}{2} (2^{n} - 1) - \frac{1}{2}\sum\limits_{l=1}^n l \binom{n}{l} - \frac{1}{2} \sum\limits_{\substack{l=1 \\ n-l \text{ odd}}}^n \left[\binom{n-1}{l-1} + \binom{n-1}{l}\right] \\ &= \frac{n}{2} (2^{n} - 1) - n 2^{n-2} - 2^{n-2} + \left(\frac{1}{4} - (-1)^n \frac{1}{4}\right) \\ &= (n-1)2^{n-2} - \left\lfloor \frac{n}{2} \right\rfloor. \end{align*} $$
$$ \begin{align*} \sum\limits_{l=1}^n \binom{n}{l} \left\lfloor \frac{n-l}{2} \right\rfloor &= \sum\limits_{l=1}^n \frac{n-l}{2} \binom{n}{l} - \frac{1}{2}\sum\limits_{\substack{l=1 \\ n -l \text{ odd}}}^n \binom{n}{l} \\ &= \frac{n}{2} (2^{n} - 1) - \frac{1}{2}\sum\limits_{l=1}^n l \binom{n}{l} - \frac{1}{2} \sum\limits_{\substack{l=1 \\ n-l \text{ odd}}}^n \left[\binom{n-1}{l-1} + \binom{n-1}{l}\right] \\ &= \frac{n}{2} (2^{n} - 1) - n 2^{n-2} - 2^{n-2} + \left(\frac{1}{4} - (-1)^n \frac{1}{4}\right) \\ &= (n-1)2^{n-2} - \left\lfloor \frac{n}{2} \right\rfloor. \end{align*} $$
We turn to (7.6) and prove first a combinatorial formula for a lacunary sum of binomial coefficients, see, for example, [Reference Riordan39, Section 4, Problem 8, p.161]. Let
![]() $\xi $
be a primitive third root of unity in
$\xi $
be a primitive third root of unity in
![]() ${\mathbb {C}}$
, then the following holds
${\mathbb {C}}$
, then the following holds
 $$ \begin{align*}\begin{aligned} 3 \sum\limits_{l \equiv r \ (3)} \binom{n}{l} &= \sum\limits_{l = 0}^n \binom{n}{l} (1 + \xi^{l-r} + \xi^{{2l-2r}}) \\ &= 2^n + \xi^{-r}(1+\xi)^{n} + \xi^{-2r} (1+\xi^2)^n \\ &= 2^n + (-1)^n (\xi^{n+r})^2 + (-1)^n\xi^{n+r}. \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} 3 \sum\limits_{l \equiv r \ (3)} \binom{n}{l} &= \sum\limits_{l = 0}^n \binom{n}{l} (1 + \xi^{l-r} + \xi^{{2l-2r}}) \\ &= 2^n + \xi^{-r}(1+\xi)^{n} + \xi^{-2r} (1+\xi^2)^n \\ &= 2^n + (-1)^n (\xi^{n+r})^2 + (-1)^n\xi^{n+r}. \end{aligned} \end{align*} $$
Write
![]() $n = 3a + b$
for integers
$n = 3a + b$
for integers
![]() $a \in {\mathbb {Z}}_{\geq 0}$
and
$a \in {\mathbb {Z}}_{\geq 0}$
and
![]() $b \in \{0,1,2\}$
. Then we get
$b \in \{0,1,2\}$
. Then we get
 $$ \begin{align*}\begin{aligned} \sum\limits_{l=1}^n \binom{n}{l} \left\lfloor \frac{n-l}{3} \right\rfloor &= \sum\limits_{l=1}^n \frac{n-l}{3} \binom{n}{l} - \frac{1}{3}\sum\limits_{\substack{n-l \equiv 1 \ (3) \\ l \neq 0}} \binom{n}{l} - \frac{2}{3}\sum\limits_{\substack{n-l \equiv 2 \ (3) \\ l \neq 0}} \binom{n}{l} \\ &= \frac{n}{3} (2^{n-1}-1) - \frac{1}{3}\sum\limits_{l \equiv 1 \ (3)} \binom{n}{l} - \frac{2}{3}\sum\limits_{l \equiv 2 \ (3)} \binom{n}{l} + \frac{b}{3}\\ &= \frac{n-2}{3} 2^{n-1} - \frac{n}{3} + \frac{b}{3} - \frac{(-1)^n}{9} \left(\xi^{2b+2} + \xi^{b+1} + 2 \xi^{2b+1} + 2 \xi^{b+2}\right). \\ \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} \sum\limits_{l=1}^n \binom{n}{l} \left\lfloor \frac{n-l}{3} \right\rfloor &= \sum\limits_{l=1}^n \frac{n-l}{3} \binom{n}{l} - \frac{1}{3}\sum\limits_{\substack{n-l \equiv 1 \ (3) \\ l \neq 0}} \binom{n}{l} - \frac{2}{3}\sum\limits_{\substack{n-l \equiv 2 \ (3) \\ l \neq 0}} \binom{n}{l} \\ &= \frac{n}{3} (2^{n-1}-1) - \frac{1}{3}\sum\limits_{l \equiv 1 \ (3)} \binom{n}{l} - \frac{2}{3}\sum\limits_{l \equiv 2 \ (3)} \binom{n}{l} + \frac{b}{3}\\ &= \frac{n-2}{3} 2^{n-1} - \frac{n}{3} + \frac{b}{3} - \frac{(-1)^n}{9} \left(\xi^{2b+2} + \xi^{b+1} + 2 \xi^{2b+1} + 2 \xi^{b+2}\right). \\ \end{aligned} \end{align*} $$
A simple computation shows that
which proves (7.6) and thus the lemma.
Proof of Theorem 1.1
If
![]() $d = 4$
, then the statement follows from [Reference Totaro48] for
$d = 4$
, then the statement follows from [Reference Totaro48] for
![]() $N \leq 4$
(see also [Reference Schreieder44, Theorem 1.1]) and [Reference Pavic and Schreieder36, Theorem 1.1] for
$N \leq 4$
(see also [Reference Schreieder44, Theorem 1.1]) and [Reference Pavic and Schreieder36, Theorem 1.1] for
![]() $N = 5$
, see also Example 4.6. Let now
$N = 5$
, see also Example 4.6. Let now
![]() $d \geq 5$
and
$d \geq 5$
and
![]() $N \leq \frac {d+1}{16} 2^d$
be positive integers. If
$N \leq \frac {d+1}{16} 2^d$
be positive integers. If
![]() $3 \leq N \leq (d-2) + 2^{d-2}-2$
, then the theorem follows from [Reference Schreieder44, Theorem 1.1], because we can then write N uniquely as
$3 \leq N \leq (d-2) + 2^{d-2}-2$
, then the theorem follows from [Reference Schreieder44, Theorem 1.1], because we can then write N uniquely as
![]() $N = n + r$
for integers
$N = n + r$
for integers
![]() $n,r \geq 1$
satisfying
$n,r \geq 1$
satisfying
![]() $2 \leq n \leq d-2$
and
$2 \leq n \leq d-2$
and
![]() $2^{n-1}-2 \leq r \leq 2^n - 2$
. Hence we can assume that
$2^{n-1}-2 \leq r \leq 2^n - 2$
. Hence we can assume that
![]() $N \geq d-4+2^{d-2}$
. Let
$N \geq d-4+2^{d-2}$
. Let
![]() $n = d-2$
,
$n = d-2$
,
![]() $r = 2^{d-2} - 2$
and
$r = 2^{d-2} - 2$
and
![]() $s = N - n - r$
be non-negative integers. We claim that
$s = N - n - r$
be non-negative integers. We claim that
 $$ \begin{align*}s \leq (d-3) 2^{d-4} - \left\lfloor \frac{d-2}{2} \right\rfloor. \end{align*} $$
$$ \begin{align*}s \leq (d-3) 2^{d-4} - \left\lfloor \frac{d-2}{2} \right\rfloor. \end{align*} $$
Indeed, otherwise we get
 $$ \begin{align*}N = n+r+s> d-4 + 2^{d-2} + (d-3) 2^{d-4} - \left\lfloor \frac{d-2}{2} \right\rfloor \geq \frac{d+1}{16}2^d, \end{align*} $$
$$ \begin{align*}N = n+r+s> d-4 + 2^{d-2} + (d-3) 2^{d-4} - \left\lfloor \frac{d-2}{2} \right\rfloor \geq \frac{d+1}{16}2^d, \end{align*} $$
which yields a contradiction to the assumption
![]() $N \leq \frac {d+1}{16} 2^d$
. Thus, Theorem 7.1 implies by Lemma 7.4 that
$N \leq \frac {d+1}{16} 2^d$
. Thus, Theorem 7.1 implies by Lemma 7.4 that
![]() $\operatorname {Tor}(X_d)$
is divisible by
$\operatorname {Tor}(X_d)$
is divisible by
![]() $2$
for a very general degree d hypersurface
$2$
for a very general degree d hypersurface
![]() $X_d \subset {\mathbb {P}}^{N+1}$
. In particular,
$X_d \subset {\mathbb {P}}^{N+1}$
. In particular,
![]() $X_d$
does not admit an integral decomposition of the diagonal.
$X_d$
does not admit an integral decomposition of the diagonal.
Proof of Theorem 1.2
Let
![]() $d \geq 5$
and
$d \geq 5$
and
![]() $3 \leq N \leq \frac {d+1}{48} 2^d$
be integers. If
$3 \leq N \leq \frac {d+1}{48} 2^d$
be integers. If
![]() $3 \leq N \leq (d-3) + 2^{d-3} - 2$
, then the theorem follows from [Reference Schreieder45, Theorem 7.1], because we can write
$3 \leq N \leq (d-3) + 2^{d-3} - 2$
, then the theorem follows from [Reference Schreieder45, Theorem 7.1], because we can write
![]() $N = n+r$
for unique positive integers
$N = n+r$
for unique positive integers
![]() $n,r$
satisfying
$n,r$
satisfying
![]() $2 \leq n \leq d-3$
and
$2 \leq n \leq d-3$
and
![]() $2^{n-1}-2 \leq r \leq 2^n -2$
. Hence we can assume that
$2^{n-1}-2 \leq r \leq 2^n -2$
. Hence we can assume that
![]() $N \geq d-5 + 2^{d-3}$
. Let
$N \geq d-5 + 2^{d-3}$
. Let
![]() $n = d-3$
,
$n = d-3$
,
![]() $r = 2^{d-3}-2$
and
$r = 2^{d-3}-2$
and
![]() $s = N -n-r$
be non-negative integers. We claim that
$s = N -n-r$
be non-negative integers. We claim that
where
![]() $\delta $
is defined as in Lemma 7.4. (Note that
$\delta $
is defined as in Lemma 7.4. (Note that
![]() $n = d-3$
.) Indeed, otherwise we get
$n = d-3$
.) Indeed, otherwise we get
 $$ \begin{align*}N = n + r + s> d-3 + 2^{d-3}-2 + \frac{d-5}{3} 2^{d-4} - \frac{d-3}{3} + \delta = \frac{d+1}{48} 2^d + \frac{2d}{3} + \delta - 4 \geq \left\lfloor\frac{d+1}{48} 2^d\right\rfloor, \end{align*} $$
$$ \begin{align*}N = n + r + s> d-3 + 2^{d-3}-2 + \frac{d-5}{3} 2^{d-4} - \frac{d-3}{3} + \delta = \frac{d+1}{48} 2^d + \frac{2d}{3} + \delta - 4 \geq \left\lfloor\frac{d+1}{48} 2^d\right\rfloor, \end{align*} $$
which yields a contradiction to the assumption that N is an integer satisfying
![]() $N \leq \frac {d+1}{48}2^d$
. Thus, Theorem 7.1 implies by Lemma 7.4 that
$N \leq \frac {d+1}{48}2^d$
. Thus, Theorem 7.1 implies by Lemma 7.4 that
![]() $3 \mid \operatorname {Tor}(X_d)$
for a very general degree d hypersurface
$3 \mid \operatorname {Tor}(X_d)$
for a very general degree d hypersurface
![]() $X_d \subset {\mathbb {P}}^{N+1}$
. In particular,
$X_d \subset {\mathbb {P}}^{N+1}$
. In particular,
![]() $X_d$
does not admit an integral decomposition of the diagonal.
$X_d$
does not admit an integral decomposition of the diagonal.
Acknowledgements
We are grateful to Simen Moe for discussions and to Jean-Louis Colliot-Thélène and the anonymous referee for comments that improved the exposition.
Competing interest
The authors have no competing interest to declare.
Funding statement
The first named author is supported by the Studienstiftung des deutschen Volkes. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme under grant agreement No 948066 (ERC-StG RationAlgic).