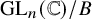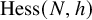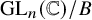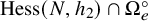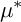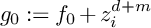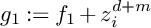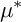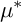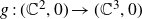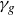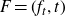Refine search
Actions for selected content:
106 results
Combinatorial cusp count and clover invariants
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 03 October 2025, pp. 1-9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stable degeneration of families of klt singularities with constant local volume
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 29 September 2025, e158
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EFFECTIVE BOUND FOR SINGULARITIES ON TORIC FIBRATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 260 / December 2025
- Published online by Cambridge University Press:
- 17 September 2025, pp. 779-795
- Print publication:
- December 2025
-
- Article
-
- You have access
- HTML
- Export citation
ON THE SINGULARITIES OF QUOTIENTS BY 1-FOLIATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 261 / 2026
- Published online by Cambridge University Press:
- 30 June 2025, e6
- Print publication:
- 2026
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Inversion of Adjunction for the minimal exponent
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 22 May 2025, e92
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Motivic Vitushkin invariants
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 20 August 2025, pp. 959-992
- Print publication:
- May 2025
-
- Article
- Export citation
GENERAL HYPERPLANE SECTIONS OF LOG CANONICAL THREEFOLDS IN POSITIVE CHARACTERISTIC
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 14 April 2025, pp. 1867-1894
- Print publication:
- September 2025
-
- Article
- Export citation
TRIANGULATED CHARACTERIZATIONS OF SINGULARITIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 261 / 2026
- Published online by Cambridge University Press:
- 24 February 2025, e3
- Print publication:
- 2026
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Local Normal Forms of Noncommutative Functions
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 18 February 2025, e8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Coordinate rings of regular nilpotent Hessenberg varieties in the open opposite schubert cell
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 17 February 2025, e44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Complements and coregularity of Fano varieties
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 07 February 2025, e39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the embedded Nash problem
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 16 October 2024, e15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equisingularity in pencils of curves on germs of reduced complex surfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 04 June 2024, pp. 990-1012
-
- Article
- Export citation
Strict positivity of Kähler–Einstein currents
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 27 May 2024, e68
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONSTANCY OF THE HILBERT–SAMUEL FUNCTION
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 256 / December 2024
- Published online by Cambridge University Press:
- 24 May 2024, pp. 938-952
- Print publication:
- December 2024
-
- Article
- Export citation
Convexity of multiplicities of filtrations on local rings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 13 March 2024, pp. 878-914
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A bound of the number of weighted blow-ups to compute the minimal log discrepancy for smooth 3-folds
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 08 March 2024, pp. 495-515
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
How to determine a curve singularity
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 09 January 2024, pp. 633-647
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
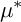 $\mu ^*$-ZARISKI PAIRS OF SURFACE SINGULARITIES
$\mu ^*$-ZARISKI PAIRS OF SURFACE SINGULARITIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 254 / June 2024
- Published online by Cambridge University Press:
- 05 December 2023, pp. 488-497
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
On the topology of the transversal slice of a quasi-homogeneous map germ
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 06 October 2023, pp. 339-359
- Print publication:
- March 2024
-
- Article
- Export citation