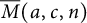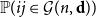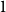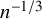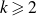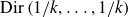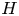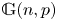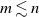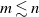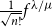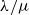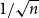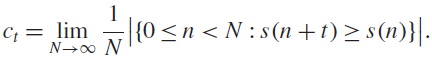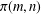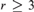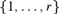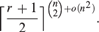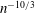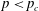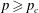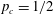Refine search
Actions for selected content:
41 results
Asymptotics for crank of overpartitions
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-34
-
- Article
- Export citation
Smooth permutations and polynomials revisited
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 3 / November 2024
- Published online by Cambridge University Press:
- 11 December 2024, pp. 455-480
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Embedding theorems for random graphs with specified degrees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 16 October 2024, pp. 115-130
-
- Article
- Export citation
INEQUALITIES AND UNIFORM ASYMPTOTIC FORMULAE FOR SPT-CRANK OF PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 13 September 2024, pp. 56-67
- Print publication:
- February 2025
-
- Article
- Export citation
The distribution of the maximum protection number in simply generated trees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 12 April 2024, pp. 518-553
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotic expansions relating to the distribution of the length of longest increasing subsequences
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 15 March 2024, e36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotics for symmetrized positive moments of odd ranks
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 09 October 2023, pp. 1731-1752
- Print publication:
- October 2024
-
- Article
- Export citation
Dirichlet law for factorisation of integers, polynomials and permutations
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 3 / November 2023
- Published online by Cambridge University Press:
- 06 September 2023, pp. 649-676
- Print publication:
- November 2023
-
- Article
- Export citation
Subgraph distributions in dense random regular graphs
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 25 August 2023, pp. 2125-2148
- Print publication:
- October 2023
-
- Article
- Export citation
Parking functions: interdisciplinary connections
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 17 January 2023, pp. 768-792
- Print publication:
- September 2023
-
- Article
- Export citation
Percolation probability and critical exponents for site percolation on the UIPT
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 20 October 2022, pp. 1869-1903
- Print publication:
- December 2023
-
- Article
- Export citation
Degree sequences of sufficiently dense random uniform hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 15 August 2022, pp. 183-224
-
- Article
- Export citation
Asymptotics for the number of standard tableaux of skew shape and for weighted lozenge tilings
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 18 October 2021, pp. 550-573
-
- Article
- Export citation
A lower bound for Cusick’s conjecture on the digits of n + t
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 24 February 2021, pp. 139-161
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- Export citation
Subgraph counts for dense random graphs with specified degrees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 05 November 2020, pp. 460-497
-
- Article
- Export citation
Graph limits of random unlabelled k-trees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 5 / September 2020
- Published online by Cambridge University Press:
- 18 May 2020, pp. 722-746
-
- Article
-
- You have access
- Open access
- Export citation
UNIFORM ASYMPTOTIC FORMULAS FOR RESTRICTED BIPARTITE PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 05 February 2020, pp. 217-225
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
DISCRETE METRIC SPACES: STRUCTURE, ENUMERATION, AND 0-1 LAWS
-
- Journal:
- The Journal of Symbolic Logic / Volume 84 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 19 August 2019, pp. 1293-1325
- Print publication:
- December 2019
-
- Article
- Export citation
A Boltzmann Approach to Percolation on Random Triangulations
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 1-43
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
Combinatorial Analysis of Growth Models for Series-Parallel Networks
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 4 / July 2019
- Published online by Cambridge University Press:
- 14 August 2018, pp. 574-599
-
- Article
- Export citation