Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-01-10T22:16:16.774Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotics for crank of overpartitions

Part of: Combinatorics Additive number theory; partitions

Published online by Cambridge University Press:  09 January 2025

Edward Y.S. Liu Open the ORCID record for Edward Y.S. Liu [Opens in a new window] ,
Helen W.J. Zhang  and
Ying Zhong
Edward Y.S. Liu
Affiliation:
School of Science, Chongqing University of Posts and Telecommunications, Chongqing 400065, P.R. China e-mail: liuyongshan@cqupt.edu.cn
Helen W.J. Zhang*
Affiliation:
School of Mathematics, Hunan University, Changsha 410082, P.R. China and Research Institute of Hunan University in Chongqing, Chongqing 401120, P.R. China
Ying Zhong
Affiliation:
School of Mathematics, Hunan University, Changsha 410082, P.R. China e-mail: YingZhong@hnu.edu.cn
*
e-mail: helenzhang@hnu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 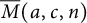$\overline {M}(a,c,n)$ denote the number of overpartitions of n with first residual crank congruent to a modulo c with $c\geq 3$ being odd and $0\leq a<c$. The central objective of this paper is twofold: firstly, to establish an asymptotic formula for the crank of overpartitions; and secondly, to establish several inequalities concerning $\overline {M}(a,c,n)$ that encompasses crank differences, positivity, and strict log-subadditivity.

Keywords

OverpartitionHardy–Ramanujan circle methodasymptoticscrank differences

MSC classification

Primary: 05A16: Asymptotic enumeration 05A17: Partitions of integers 05A20: Combinatorial inequalities 11P82: Analytic theory of partitions
Type
Article
Information
Canadian Journal of Mathematics , First View , pp. 1 - 34
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author is supported by the National Natural Science Foundation of China (Grant No. 12401432) and the Science and Technology Research Program of Chongqing Municipal Education Commission (Grant No. KJQN202200614). The second author is supported by the National Natural Science Foundation of China (Grant No. 12371327) and the Natural Science Foundation of Chongqing (Grant No. cstc2021jcyj-msxmX0107).

References

Andrews, G., On the theorems of Watson and Dragonette for Ramanujan’s mock theta functions . Amer. J. Math. 88(1966), no. 2, 454–490.CrossRefGoogle Scholar
Andrews, G. E. and Garvan, F., Dysonł crank of a partition . Bull. Amer. Math. Soc. 18(1988), no. 2, 167–171.CrossRefGoogle Scholar
Atkin, A. O. L. and Swinnerton-Der, H. P. F., Some properties of partitions . Proc. Lond. Math. Soc. (3) 4(1954), 84–106.CrossRefGoogle Scholar
Bessenrodt, C. and Ono, K., Maximal multiplicative properties of partitions . Ann. Comb. 20(2016), no. 1, 59–64.CrossRefGoogle Scholar
Bringmann, K., Asymptotics for rank partition functions . Trans. Amer. Math. Soc. 361 (2009) 3483–3500.CrossRefGoogle Scholar
Bringmann, K. and Lovejoy, J., Dyson’s rank, overpartitions, and weak Maass forms . Int. Math. Res. Not. IMRN (19) 2007(2007), rnm063, 34 pp.Google Scholar
Bringmann, K., Lovejoy, J., and Osburn, R., Rank and crank moments for overpartitions . J. Number Theory 129(2009), no. 7, 1758–1772.CrossRefGoogle Scholar
Bringmann, K. and Kane, B., Inequalities for differences of Dyson’s rank for all odd moduli . Math. Res. Lett. 17(2010), no. 5, 927–942.CrossRefGoogle Scholar
Ciolan, A., Ranks of overpartitions: asymptotics and inequalities . J. Math. Anal. Appl. 480(2019), (2), 123444, 28 pp.CrossRefGoogle Scholar
Ciolan, A., Inequalities between overpartition ranks for all moduli . Ramanujan J. 58(2022), no. 2, 463–489.CrossRefGoogle Scholar
Corteel, S. and Lovejoy, J., Overpartitions . Trans. Amer. Math. Soc. 356(2004), 1623–1635.CrossRefGoogle Scholar
Cui, S.-P., Gu, N. S. S., and Su, C.-Y., Ranks of overpartitions modulo 4 and 8 . Int. J. Number Theory 16(2020), no. 10, 2293–2310.CrossRefGoogle Scholar
Dyson, F. J., Some guesses in the theory of partitions, vol. 8. Eureka, Cambridge, 1944, pp. 10–15.Google Scholar
Garvan, F. G., New combinatorial interpretations of Ramanujanł partition congruences mod 5, 7 and 11 . Trans. Am. Math. Soc. 305(1988), no. 1, 47–77.Google Scholar
Jennings-Shaffer, C., Overpartition rank differences modulo 7 by Maass forms . J. Number Theory 163(2016), 331–358.CrossRefGoogle Scholar
Ji, K. Q., Zhang, H. W. J., and Zhao, A. X. H., Ranks of overpartitions modulo 6 and 10 . J. Number Theory 184(2018), 235–269.CrossRefGoogle Scholar
Lovejoy, J., Rank and conjugation for the Frobenius representation of an overpartition . Ann. Comb. 9(2005), 321–334.CrossRefGoogle Scholar
Zapata Rolon, J. M., Asymptotics of crank generating functions and Ramanujan congruences . Ramanujan J. 38(2015), no. 1, 147–178.CrossRefGoogle Scholar
Watson, G. N., A Treatise on the Theory of Bessel Functions, second edition, Cambridge University Press, Cambridge, 1944.Google Scholar
Zhang, H. W. J. and Zhong, Y., Strict log-subadditivity for overpartition rank . Ann. Comb. 27(2023), 799–817.CrossRefGoogle Scholar
Zuckerman, H. S., On the coefficients of certain modular forms belonging to subgroups of the modular group . Trans. Amer. Math. Soc. 45(1939), no. 2, 298–321.CrossRefGoogle Scholar