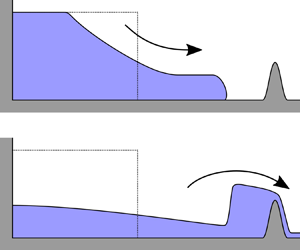
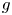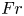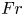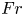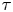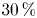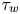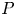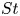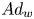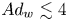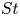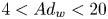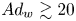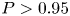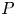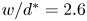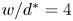doi:10.1017/jfm.2023.185 Gidreta et al. Effects of physical property changes of expelled respiratory liquid on atomization morphology
Contents
JFM Papers
Similarity for dissipation-scaled wall turbulence
-
- Published online by Cambridge University Press:
- 31 March 2023, A18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Polymer and surfactant flows through a periodically constricted tube
-
- Published online by Cambridge University Press:
- 31 March 2023, A19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Water wave propagation through arrays of closely spaced surface-piercing vertical barriers
-
- Published online by Cambridge University Press:
- 31 March 2023, A20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Shocked confined-granular flow over obstacles
-
- Published online by Cambridge University Press:
- 31 March 2023, A21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Effects of surface tension reduction on wind-wave growth and air–water scalar transfer
-
- Published online by Cambridge University Press:
- 03 April 2023, A22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Translational momentum of deformable submarine landslides off a slope
-
- Published online by Cambridge University Press:
- 03 April 2023, A23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the role of the laminar/turbulent interface in energy transfer between scales in bypass transition
-
- Published online by Cambridge University Press:
- 03 April 2023, A24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Three-dimensional sedimentation patterns of two interacting disks in a viscous fluid
-
- Published online by Cambridge University Press:
- 05 April 2023, A25
-
- Article
- Export citation
Penetrative convection: heat transport with marginal stability assumption
-
- Published online by Cambridge University Press:
- 05 April 2023, A26
-
- Article
- Export citation
The unsteady overtopping of barriers by gravity currents and dam-break flows
-
- Published online by Cambridge University Press:
- 05 April 2023, A27
-
- Article
- Export citation
Wall-pressure fluctuations in an axisymmetric boundary layer under strong adverse pressure gradient
-
- Published online by Cambridge University Press:
- 05 April 2023, A28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Wall-modelled large-eddy simulation of three-dimensional turbulent boundary layer in a bent square duct
-
- Published online by Cambridge University Press:
- 11 April 2023, A29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Reinforcement learning of control strategies for reducing skin friction drag in a fully developed turbulent channel flow
-
- Published online by Cambridge University Press:
- 11 April 2023, A30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Two-dimensional study on the motion and interactions of squirmers under gravity in a vertical channel
-
- Published online by Cambridge University Press:
- 11 April 2023, A31
-
- Article
- Export citation
Sessile drop evaporation in a gap – crossover between diffusion-limited and phase transition-limited regime
-
- Published online by Cambridge University Press:
- 11 April 2023, A32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On coupled envelope evolution equations in the Hamiltonian theory of nonlinear surface gravity waves
-
- Published online by Cambridge University Press:
- 13 April 2023, A33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hydrodynamic clogging of micro-particles in planar channels under electrostatic forces
-
- Published online by Cambridge University Press:
- 11 April 2023, A34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
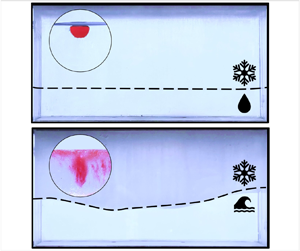
Sea water freezing modes in a natural convection system
-
- Published online by Cambridge University Press:
- 11 April 2023, A35
-
- Article
- Export citation
Computing Lagrangian means
-
- Published online by Cambridge University Press:
- 11 April 2023, A36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A linear-elastic-nonlinear-swelling theory for hydrogels. Part 1. Modelling of super-absorbent gels
-
- Published online by Cambridge University Press:
- 11 April 2023, A37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation