Article contents
The unsteady overtopping of barriers by gravity currents and dam-break flows
Published online by Cambridge University Press: 05 April 2023
Abstract
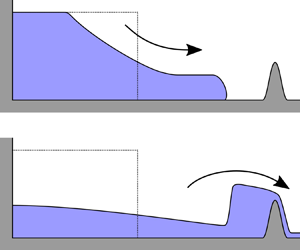
The collision of a gravitationally driven horizontal current with a barrier following release from a confining lock is investigated using a shallow water model of the motion, together with a sophisticated boundary condition capturing the local interaction. The boundary condition permits several overtopping modes: supercritical, subcritical and blocked flow. The model is analysed both mathematically and numerically to reveal aspects of the unsteady motion and to compute the proportion of the fluid trapped upstream of the barrier. Several problems are treated. Firstly, the idealised problem of a uniform incident current is analysed to classify the unsteady dynamical regimes. Then, the extreme regimes of a very close or distant barrier are tackled, showing the progression of the interaction through the overtopping modes. Next, the trapped volume of fluid at late times is investigated numerically, demonstrating regimes in which the volume is determined purely by volumetric considerations, and others where transient inertial effects are significant. For a Boussinesq gravity current, even when the volume of the confined region behind the barrier is equal to the fluid volume,  $30\,\%$ of the fluid escapes the domain, and a confined volume three times larger is required for the overtopped volume to be negligible. For a subaerial dam-break flow, the proportion that escapes is in excess of
$30\,\%$ of the fluid escapes the domain, and a confined volume three times larger is required for the overtopped volume to be negligible. For a subaerial dam-break flow, the proportion that escapes is in excess of  $60\,\%$ when the confined volume equals the fluid volume, and a barrier as tall as the initial release is required for negligible overtopping. Finally, we compare our predictions with experiments, showing a good agreement across a range of parameters.
$60\,\%$ when the confined volume equals the fluid volume, and a barrier as tall as the initial release is required for negligible overtopping. Finally, we compare our predictions with experiments, showing a good agreement across a range of parameters.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 6
- Cited by


