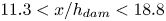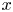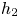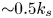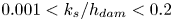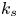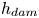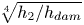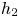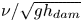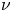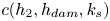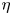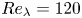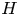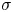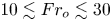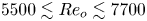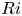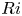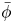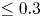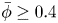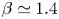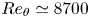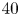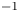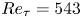Graphical abstract from Di Vaira, N., Łaniewski-Wołłk, Ł., Johnson, R., Aminossadati, S. & Leonardi, C. 2022 Influence of particle polydispersity on bulk migration and size segregation in channel flows. J. Fluid Mech. 939, A30. doi:10.1017/jfm.2022.166.
Contents
JFM Papers
Unsteady interaction of crossflow instability with a forward-facing step
-
- Published online by Cambridge University Press:
- 30 March 2022, A19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the role of heat source location and multiplicity in topographically controlled Marangoni–Rayleigh–Bénard convection
-
- Published online by Cambridge University Press:
- 30 March 2022, A20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Friction effects on quasi-steady dam-break wave propagation on horizontal beds
-
- Published online by Cambridge University Press:
- 30 March 2022, A21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamics of finite-size spheroids in turbulent flow: the roles of flow structures and particle boundary layers
-
- Published online by Cambridge University Press:
- 30 March 2022, A22
-
- Article
- Export citation
Motion of asymmetric bodies in two-dimensional shear flow
-
- Published online by Cambridge University Press:
- 30 March 2022, A23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the shear-driven surfactant layer instability
-
- Published online by Cambridge University Press:
- 30 March 2022, A24
-
- Article
- Export citation
Non-homogeneous analysis of rogue wave probability evolution over a shoal
-
- Published online by Cambridge University Press:
- 30 March 2022, A25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A one-dimensional model for the pulsating flow of cerebrospinal fluid in the spinal canal
-
- Published online by Cambridge University Press:
- 30 March 2022, A26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Brachistochronous motion of a flat plate parallel to its surface immersed in a fluid
-
- Published online by Cambridge University Press:
- 30 March 2022, A27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A theoretical model for the growth of spherical bubbles by rectified diffusion
-
- Published online by Cambridge University Press:
- 30 March 2022, A28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Characterising entrainment in fountains and negatively buoyant jets
-
- Published online by Cambridge University Press:
- 31 March 2022, A29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Influence of particle polydispersity on bulk migration and size segregation in channel flows
-
- Published online by Cambridge University Press:
- 31 March 2022, A30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Violent droplet impacts with non-flat surfaces
-
- Published online by Cambridge University Press:
- 31 March 2022, A31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hydrodynamics of an inertial squirmer and squirmer dumbbell in a tube
-
- Published online by Cambridge University Press:
- 31 March 2022, A32
-
- Article
- Export citation
Receptivity of crossflow instability to discrete roughness amplitude and location
-
- Published online by Cambridge University Press:
- 31 March 2022, A33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An adverse-pressure-gradient turbulent boundary layer with nearly constant
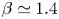 $\beta \simeq 1.4$ up to
$\beta \simeq 1.4$ up to 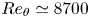 $Re_{\theta } \simeq 8700$
$Re_{\theta } \simeq 8700$
-
- Published online by Cambridge University Press:
- 01 April 2022, A34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamics of pulsed laser-induced cavities on a liquid–gas interface: from a conical splash to a ‘bullet’ jet
-
- Published online by Cambridge University Press:
- 31 March 2022, A35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Self-similar mechanisms in wall turbulence studied using resolvent analysis
-
- Published online by Cambridge University Press:
- 01 April 2022, A36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Gyrotactic trapping of micro-swimmers in simple shear flows: a study directly from the fundamental Smoluchowski equation
-
- Published online by Cambridge University Press:
- 31 March 2022, A37
-
- Article
- Export citation
Compressible high-pressure lubrication flows in thrust bearings
-
- Published online by Cambridge University Press:
- 31 March 2022, A38
-
- Article
- Export citation