Article contents
On the shear-driven surfactant layer instability
Published online by Cambridge University Press: 30 March 2022
Abstract
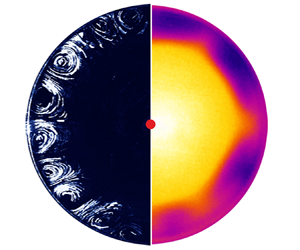
The convective flow generated by a source located at a water surface containing an insoluble surfactant has been investigated experimentally. The application of various sources, which differ in the way in which they drive the interface into motion, and two surfactants with different rheological properties made it possible to generalize the results and to develop a unified approach to describing the problem. We show that the threshold occurrence of a two-zone flow structure with an axisymmetric flow nearby the source and stagnant zone at the periphery results from the competition between two counter-directed shear stresses caused by surfactant concentration inhomogeneity and source influence. We demonstrate that, regardless of the source type, the ratio of these stresses, known as the elasticity number, can be used to predict the formation of a two-zone flow and to define the position of the boundary between the zones. We examined in detail the conditions for formation of the multi-vortex flow within the stagnant zone. Although this phenomenon has been observed by many researchers, it has not yet met a consistent physical explanation. We hypothesized that the formation of vortices can be considered as the instability of the mechanical equilibrium of the surfactant layer caused by the shear on the side of the underlying bulk flow. Based on the mechanism suggested, we introduced a non-dimensional parameter, called the surface Rayleigh number, and estimated its critical value. Finally we analysed the conditions for the occurrence of this instability, called the shear-driven surfactant layer instability in some famous problems of interfacial hydrodynamics.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
REFERENCES
- 8
- Cited by


