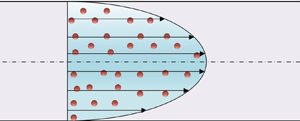
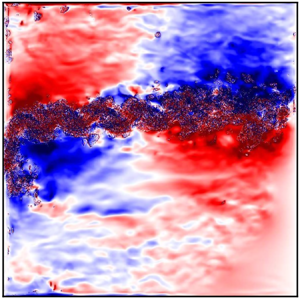
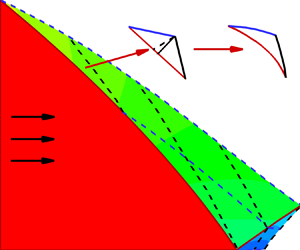
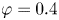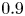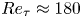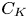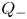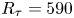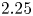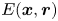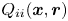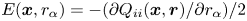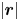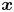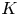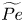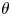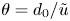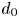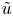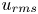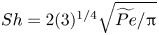Graphical abstract from Boujo, E. 2021 Second-order adjoint-based sensitivity for hydrodynamic stability and control. J. Fluid Mech. 920, A12. doi:10.1017/jfm.2021.425.
Contents
JFM Papers
Decomposition of available potential energy for networks of connected volumes
-
- Published online by Cambridge University Press:
- 09 June 2021, A17
-
- Article
- Export citation
Interactions of internal tides with a heterogeneous and rotational ocean
-
- Published online by Cambridge University Press:
- 10 June 2021, A18
-
- Article
- Export citation
Instability of the tip vortices shed by an axial-flow turbine in uniform flow
-
- Published online by Cambridge University Press:
- 11 June 2021, A19
-
- Article
- Export citation
Does dissipative anomaly hold for compressible turbulence?
-
- Published online by Cambridge University Press:
- 10 June 2021, A20
-
- Article
- Export citation
Information transfer between turbulent boundary layers and porous media
-
- Published online by Cambridge University Press:
- 10 June 2021, A21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Time domain modelling of a Helmholtz resonator analogue for water waves
-
- Published online by Cambridge University Press:
- 10 June 2021, A22
-
- Article
- Export citation
Effect of surfactant on the linear stability of a shear-imposed fluid flowing down a compliant substrate
-
- Published online by Cambridge University Press:
- 10 June 2021, A23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Trapped waves in supersonic and hypersonic turbulent channel flow over porous walls
-
- Published online by Cambridge University Press:
- 11 June 2021, A24
-
- Article
- Export citation
Effect of micromagnetorotation on magnetohydrodynamic Poiseuille micropolar flow: analytical solutions and stability analysis
-
- Published online by Cambridge University Press:
- 11 June 2021, A25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Linear stability analysis of two fluid columns of different densities and viscosities in a gravity field
-
- Published online by Cambridge University Press:
- 11 June 2021, A26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Coherent structure identification in turbulent channel flow using latent Dirichlet allocation
-
- Published online by Cambridge University Press:
- 11 June 2021, A27
-
- Article
- Export citation
Direct numerical simulation of roughness-induced transition controlled by two-dimensional wall blowing
-
- Published online by Cambridge University Press:
- 11 June 2021, A28
-
- Article
- Export citation
Aerofoil wake-induced transition characteristics on a flat-plate boundary layer
-
- Published online by Cambridge University Press:
- 11 June 2021, A29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Helicity dynamics in reconnection events of topologically complex vortex flows
-
- Published online by Cambridge University Press:
- 11 June 2021, A30
-
- Article
- Export citation
Scale-space energy density function transport equation for compressible inhomogeneous turbulent flows
-
- Published online by Cambridge University Press:
- 11 June 2021, A31
-
- Article
- Export citation
On non-uniqueness of the mesoscale eddy diffusivity
-
- Published online by Cambridge University Press:
- 11 June 2021, A32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Turbulent and wave kinetic energy budgets in the airflow over wind-generated surface waves
-
- Published online by Cambridge University Press:
- 14 June 2021, A33
-
- Article
- Export citation
Bubble-mediated transfer of dilute gas in turbulence
-
- Published online by Cambridge University Press:
- 14 June 2021, A34
-
- Article
- Export citation
High-Rayleigh-number convection in porous–fluid layers
-
- Published online by Cambridge University Press:
- 14 June 2021, A35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Method of curved-shock characteristics with application to inverse design of supersonic flowfields
-
- Published online by Cambridge University Press:
- 14 June 2021, A36
-
- Article
- Export citation