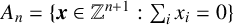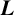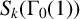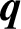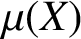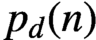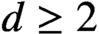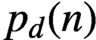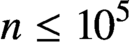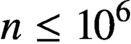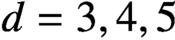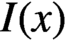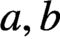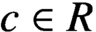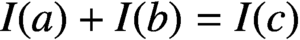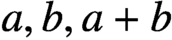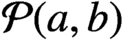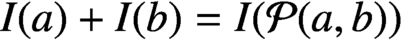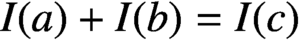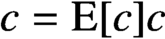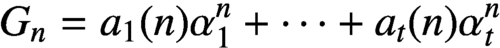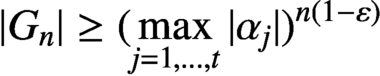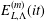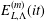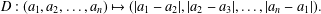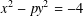Open access
Contents
Research Article
ABELIAN DIFFERENCE SETS AS LATTICE COVERINGS AND LATTICE TILINGS
- Part of:
-
- Published online by Cambridge University Press:
- 24 January 2022, pp. 177-184
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COUNTING HECKE EIGENFORMS WITH NONVANISHING
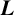 $\boldsymbol {L}$-VALUE
$\boldsymbol {L}$-VALUE
- Part of:
-
- Published online by Cambridge University Press:
- 24 January 2022, pp. 28-47
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
APÉRY LIMITS FOR ELLIPTIC
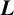 $\boldsymbol {L}$-VALUES
$\boldsymbol {L}$-VALUES
- Part of:
-
- Published online by Cambridge University Press:
- 19 January 2022, pp. 273-279
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
HEDGEHOGS IN LEHMER’S PROBLEM
- Part of:
-
- Published online by Cambridge University Press:
- 07 September 2021, pp. 236-242
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A FAMILY OF
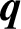 $\boldsymbol {q}$-SUPERCONGRUENCES MODULO THE CUBE OF A CYCLOTOMIC POLYNOMIAL
$\boldsymbol {q}$-SUPERCONGRUENCES MODULO THE CUBE OF A CYCLOTOMIC POLYNOMIAL
- Part of:
-
- Published online by Cambridge University Press:
- 03 September 2021, pp. 296-302
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON CERTAIN PRODUCTS OF PERMUTABLE SUBGROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 16 August 2021, pp. 278-285
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A UNIQUE PERFECT POWER DECAGONAL NUMBER
- Part of:
-
- Published online by Cambridge University Press:
- 06 August 2021, pp. 212-216
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GROUPS WITH MANY PRONORMAL SUBGROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 11 May 2021, pp. 75-86
-
- Article
-
- You have access
- Open access
- Export citation
REVISITING THE RECTANGULAR CONSTANT IN BANACH SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 26 April 2021, pp. 124-133
-
- Article
-
- You have access
- Open access
- Export citation
AN UNBOUNDED OPERATOR WITH SPECTRUM IN A STRIP AND MATRIX DIFFERENTIAL OPERATORS
- Part of:
-
- Published online by Cambridge University Press:
- 16 April 2021, pp. 146-153
-
- Article
-
- You have access
- Open access
- Export citation
CONNECTED COMPONENTS IN THE INVARIABLY GENERATING GRAPH OF A FINITE GROUP
- Part of:
-
- Published online by Cambridge University Press:
- 25 March 2021, pp. 453-463
-
- Article
-
- You have access
- Open access
- Export citation
SOME OBSERVATIONS AND SPECULATIONS ON PARTITIONS INTO d-TH POWERS
- Part of:
-
- Published online by Cambridge University Press:
- 28 January 2021, pp. 406-414
-
- Article
-
- You have access
- Open access
- Export citation
TRIPLET INVARIANCE AND PARALLEL SUMS
- Part of:
-
- Published online by Cambridge University Press:
- 25 January 2021, pp. 118-126
-
- Article
-
- You have access
- Open access
- Export citation
STRICTLY REAL FUNDAMENTAL THEOREM OF ALGEBRA USING POLYNOMIAL INTERLACING
- Part of:
-
- Published online by Cambridge University Press:
- 18 January 2021, pp. 249-255
-
- Article
-
- You have access
- Open access
- Export citation
ON THE GROWTH OF LINEAR RECURRENCES IN FUNCTION FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 09 November 2020, pp. 11-20
-
- Article
-
- You have access
- Open access
- Export citation
BLOCKS WITH SMALL-DIMENSIONAL BASIC ALGEBRA
- Part of:
-
- Published online by Cambridge University Press:
- 21 September 2020, pp. 461-474
-
- Article
-
- You have access
- Open access
- Export citation
ON A LATTICE GENERALISATION OF THE LOGARITHM AND A DEFORMATION OF THE DEDEKIND ETA FUNCTION
- Part of:
-
- Published online by Cambridge University Press:
- 20 February 2020, pp. 118-125
-
- Article
-
- You have access
- Open access
- Export citation
PERIODS OF DUCCI SEQUENCES AND ODD SOLUTIONS TO A PELLIAN EQUATION
- Part of:
-
- Published online by Cambridge University Press:
- 03 July 2019, pp. 201-205
-
- Article
-
- You have access
- Open access
- Export citation
A COMPACT QUALITATIVE UNCERTAINTY PRINCIPLE FOR SOME NONUNIMODULAR GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 28 November 2018, pp. 114-120
-
- Article
-
- You have access
- Open access
- Export citation
SOME HYPERGEOMETRIC INTEGRALS FOR LINEAR FORMS IN ZETA VALUES
- Part of:
-
- Published online by Cambridge University Press:
- 19 July 2018, pp. 372-375
-
- Article
-
- You have access
- Open access
- Export citation