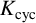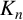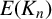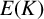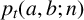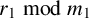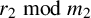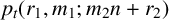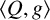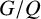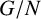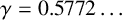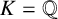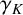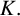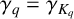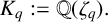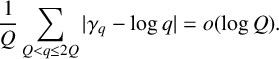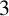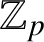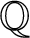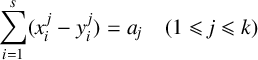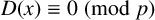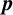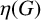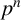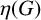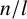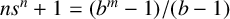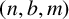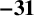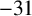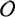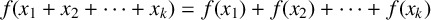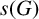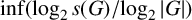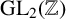Open access
Contents
Research Article
SPACINGS BETWEEN SELECTED PRIME DIVISORS OF AN INTEGER
- Part of:
-
- Published online by Cambridge University Press:
- 15 September 2022, pp. 403-415
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
REMARKS ON HILBERT’S TENTH PROBLEM AND THE IWASAWA THEORY OF ELLIPTIC CURVES
- Part of:
-
- Published online by Cambridge University Press:
- 30 August 2022, pp. 440-450
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE NUMBER OF 2-HOOKS AND 3-HOOKS OF INTEGER PARTITIONS
- Part of:
-
- Published online by Cambridge University Press:
- 18 August 2022, pp. 432-439
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GROUPS WITH A LARGE PERMUTABLY EMBEDDED SUBGROUP
- Part of:
-
- Published online by Cambridge University Press:
- 13 July 2022, pp. 276-283
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EULER–KRONECKER CONSTANTS FOR CYCLOTOMIC FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 30 May 2022, pp. 79-84
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE CAYLEYNESS OF PRAEGER–XU GRAPHS
- Part of:
-
- Published online by Cambridge University Press:
- 11 May 2022, pp. 353-356
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NEW NONLOCAL NONLINEAR DIFFUSION EQUATION: THE ONE-DIMENSIONAL CASE
- Part of:
-
- Published online by Cambridge University Press:
- 05 May 2022, pp. 333-339
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONTACT SURGERY GRAPHS
- Part of:
-
- Published online by Cambridge University Press:
- 25 April 2022, pp. 146-157
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON FINE SELMER GROUPS AND SIGNED SELMER GROUPS OF ELLIPTIC MODULAR FORMS
- Part of:
-
- Published online by Cambridge University Press:
- 19 April 2022, pp. 419-430
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE INHOMOGENEOUS VINOGRADOV SYSTEM
- Part of:
-
- Published online by Cambridge University Press:
- 19 April 2022, pp. 396-403
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON A QUESTION OF MORETÓ
- Part of:
-
- Published online by Cambridge University Press:
- 13 April 2022, pp. 306-309
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A CONTINUOUS HOMOMORPHISM OF A THIN SET ONTO A FAT SET
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2022, pp. 500-503
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SOLVABILITY OF A SYSTEM OF POLYNOMIAL EQUATIONS MODULO PRIMES
- Part of:
-
- Published online by Cambridge University Press:
- 23 March 2022, pp. 404-407
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONJUGACY CLASSES OF MAXIMAL CYCLIC SUBGROUPS AND NILPOTENCE CLASS OF
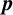 $\boldsymbol {p}$-GROUPS
$\boldsymbol {p}$-GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 21 March 2022, pp. 463-469
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON REPUNIT CULLEN NUMBERS
- Part of:
-
- Published online by Cambridge University Press:
- 08 February 2022, pp. 264-268
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN APPLICATION OF BINARY QUADRATIC FORMS OF DISCRIMINANT
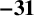 $\boldsymbol {-31}$ TO MODULAR FORMS
$\boldsymbol {-31}$ TO MODULAR FORMS
- Part of:
-
- Published online by Cambridge University Press:
- 08 February 2022, pp. 269-272
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON A
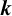 $\boldsymbol {k}$-ADDITIVE UNIQUENESS SET FOR MULTIPLICATIVE FUNCTIONS
$\boldsymbol {k}$-ADDITIVE UNIQUENESS SET FOR MULTIPLICATIVE FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 08 February 2022, pp. 209-214
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE NUMBER OF SET ORBITS OF PERMUTATION GROUPS AND THE GROUP ORDER
- Part of:
-
- Published online by Cambridge University Press:
- 27 January 2022, pp. 89-101
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON ÉTALE REPRESENTATIONS FROM NILPOTENT ORBITS
- Part of:
-
- Published online by Cambridge University Press:
- 25 January 2022, pp. 113-125
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AUTOMORPHISM AND OUTER AUTOMORPHISM GROUPS OF RIGHT-ANGLED ARTIN GROUPS ARE NOT RELATIVELY HYPERBOLIC
- Part of:
-
- Published online by Cambridge University Press:
- 24 January 2022, pp. 102-112
-
- Article
-
- You have access
- Open access
- HTML
- Export citation